Abstract
In this short review we tried to give an outline of investigations of charged pion condensation (PC) in dense baryonic (quark) matter in the framework of effective Nambu–Jona-Lasinio (NJL)-type models. The possibility of charged PC phase in dense quark matter with isospin asymmetry is investigated. First, it is demonstrated that this phase can be realized in the framework of massless NJL model. However, the existence of this phase is enormously fragile to the values of current quark mass and we show that charged PC phase is forbidden in electrically neutral dense quark matter with -equilibrium when current quark masses are close to their physical value of 5.5 MeV. Nevertheless, then it is shown that in real physical systems there could be conditions promoting the appearance of charged PC phenomenon in dense quark matter; specifically, it was shown that if one takes into consideration the fact that system can have finite size, then a dense charged PC phase can be realized there. It was also demonstrated that the possibility of inhomogeneous pion condensate might allow this phase to appear. In addition, more recently it was revealed that there is another interesting factor that can induce a charged PC phase in dense quark matter even without isospin imbalance. It is a chiral imbalance of the system (non-zero difference between densities of left- and right-handed quarks). These results can be interesting in heavy ion collision experiments, where it is expected to get high baryon densities. It is of interest also in the context of neutron stars, where quark matter might be realized in the core and very high baryon and isospin densities are attained.
1. Introduction
Recently, great efforts have been made in trying to understand the properties and the phase diagram of strongly interacting (quark) matter under high temperatures and/or baryon densities (or high values of the baryon chemical potential ). It is believed that quark matter under such extreme conditions can exist in cores of neutron stars, where baryon density is much higher than the density of ordinary nuclear matter, where is 0.15 baryon per fm, or can be formed as a result of a collision of heavy ions [1,2,3,4,5]. (In this case, there are no reasons to speak of protons and neutrons as particles that make up baryonic matter, and it would be more correct to say that we are dealing with dense quark matter.) However, in reality, within the framework of quantum chromodynamics (QCD), the fundamental theory designed to describe strongly interacting systems, it is rather problematic to get at least some information about the phase structure of dense quark matter. The fact is that despite asymptotic freedom and feasibility of perturbative calculations at extremely high temperature and the baryon density in real physical conditions (in compact stars or heavy ion collision experiments) the temperature and the baryon density of quark matter are usually not that great, which leads to the fact that the effective interaction constant of the particles is quite large. Therefore, one of the main research methods in the framework of QCD, perturbative analysis over a small coupling constant, is not applicable. Another well-known first-principle calculation approach to QCD is the method of lattice QCD simulations. However, unfortunately, due to the sign problem (complex fermion determinant) it encounters insurmountable difficulties at .
Due to these reasons, to study the QCD phase diagram at non-zero baryon density, effective field theories are employed and the most frequently used one is the Nambu–Jona-Lasinio (NJL) model [6] (for a review one can see Refs. [7,8,9]). This model uses quarks as the degrees of freedom instead of hadrons, and it can be used as an effective field theory for QCD in the low-energy regime to describe dense quark matter. The most appealing feature of NJL model is the description of the phenomenon of the dynamical chiral symmetry breaking when quarks get a rather large mass compared to the value of the current quark mass. The NJL model can be used to get insights not only in meson physics [10], but also in color superconductivity phenomenon [11,12], etc.
As mentioned above, dense quark matter can be formed inside neutron stars, i.e., it consists of different numbers of u and d quarks (it is the so-called isotopic asymmetry of quark matter). Hence, the ground state of such matter is characterized by baryon and isotopic (or isospin) densities and can be investigated in the framework of QCD or other alternative effective approaches using quark degrees of freedom and extended by baryon and isotopic (or isospin) chemical potentials. Then, as shown in Refs. [13,14,15,16,17,18,19,20,21,22,23,24], in the corresponding systems there might appear a Bose–Einstein condensate (even at ) of quark-antiquark pairs of the form , which has quantum numbers of charged pions. In this case, the charged pion condensation (PC) phase is realized in matter. However, the presence of this phase of dense quark matter is not a well-established fact. Indeed, it was shown in Refs. [13,14] that charged PC phase with non-zero quark density occupies a very narrow part of the phase diagram of the massless NJL model when and . However, this phase is extremely fragile to the effect of explicit chiral symmetry breaking via a non-zero current quark mass, and is ruled out from the phase diagram of electrically neutral dense quark matter with -equilibrium, when quark masses are larger than or of the order of 10 keV (see, e.g., in Refs. [22,25,26,27,28]). The same results were found in the framework of the Polyakov NJL model [27], where it was shown that the value of isospin chemical potential turns out to be not large enough for charged PC phase to take place in electrically neutral dense quark matter. A similar qualitative picture of the charged PC has been also found in an analysis in the framework of the toy (1+1)-dimensional massive Gross–Neveu model with isospin and baryon chemical potentials [29]. In particular, for example, it was found that baryon density is equal to zero in the charged PC phase of this model, i.e., this model does not predict dense quark matter with charged PC phenomenon.
Before continuing our discussion on the fate of the charged PC phase in dense quark matter, let us say a few words about the PC phenomenon in dense nuclear matter. It is clear that in this case the baryon density is around or greater than the normal baryon density , i.e., much less than in dense quark matter. It is clear that the main elementary objects forming nuclear matter are nucleons and pions. Therefore, a long time ago, in the early 1970s, it was understood that pions and pion condensates can play a significant role in the physical processes of dense nuclear matter [30,31] (see also, for example, the reviews [32,33]). As for physics of neutron stars, where in nuclear matter there is a large isotopic asymmetry (the predominance of neutrons over protons), here, of course, processes with the formation of charged pion condensate can play a prominent role. Indeed, in a series of papers [34,35,36,37,38,39,40] it was shown that charged PC phase has a significant effect on the cooling scenario of a neutron star, on its equation of state, on the phenomenon of superfluidity of nucleons in neutron stars, etc. The main thing for us is that different effective approaches (such as the -model, etc.) used in these studies to describe neutron matter, in principle, do not reject the possibility of the existence of a phase with charged PC. (Though let us note that the s-wave charged PC is considered highly unlikely to be realized in dense matter [41] but it was argued that p-wave charged PC is possible [42,43,44].) In contrast, as it follows from the above discussion, the possibility of the charged PC phenomenon in dense quark matter, in which baryon density is much higher than , described in the framework of the effective NJL model remains in question.
In this mini-review we discuss the present status of the charged PC phase in dense quark matter and, especially, pay attention to the factors promoting the emergence of charged PC phenomenon in dense quark matter. Specifically, in the paper [45] it was found that this phase might be realized in dense baryonic system that has finite size. It was also demonstrated in [46] that in dense baryonic matter spatially inhomogeneous charged PC might appear, and more recently it was found in [47,48,49,50,51,52,53,54] that chiral imbalance is another interesting factor that can induce a charged PC phase. Let us recall that chiral imbalance is a non-zero difference between densities of left-handed and right-handed fermions and it may appear in the fireball after heavy ion collisions and possibly lead to the so-called chiral magnetic effect [55,56]. It is a remarkable phenomenon that stems from highly nontrivial interplay of chiral symmetry, chiral (axial) anomaly of QCD and the topological structure of gluon configurations. It might be also realized in compact stars [54] or even in condensed matter systems [57,58,59].
The promotion of the charged PC phase in dense quark matter by finite size and spatial inhomogeneity of the charged pion condensate was demonstrated using a (1+1)-dimensional toy model with four-quark interactions, whereas the generation of the charged PC phase by chiral imbalance was shown as in (1+1)-dimensional toy model [47,48,49,50] as well as in more realistic effective QCD motivated NJL model [51,52,53].
The paper is organized as follows. In Section 2 NJL model with two quark flavors (u and d quarks) and with two kinds of chemical potentials, and , is presented and the charged PC phenomenon in dense isospin asymmetric quark matter is discussed. Here we show that it is unlikely to appear in the simplest case. Then in Section 3 it is revealed that there exist the conditions and factors promoting the appearance of charged PC in dense quark matter and different possibilities are discussed. In Section 3.2 the influence of finite size effect and nontrivial space topology is considered, then in Section 3.3 the possibility of inhomogeneous charged PC is discussed, finally in Section 3.4 it is shown that charged PC can appear in dense chiral imbalanced quark matter. Section 4 contains the summary and conclusions. Throughout the paper, for simplicity, all the considerations are made in the case of zero temperature .
2. Charged Pion Condensation in the Framework of NJL Model
2.1. The Model and Its Thermodynamic Potential
Since the considered studies are mostly performed in the framework of the (3+1)-dimensional NJL model, let us recall the two-flavored NJL model Lagrangian (there are no gluons and it is symmetric under global color group). It has the following form
where is a flavor doublet and and (u and d quarks) are four-component Dirac spinors as well as color -plets. The summation over flavor, color, and spinor indices is implied; () are Pauli matrices. In addition, m is current quark mass.
Moreover, since in (3+1)-space-time dimensions the four-fermion interaction operator has a mass dimension 6, the NJL model is not renormalizable and may be considered only as an effective QCD-like model. Hence, some regularization is needed to avoid usual ultraviolet divergences and throughout the paper we will use the simplest momentum cutoff regularization, i.e., the integration region in all momentum integrals is restricted by a cutoff , . In addition, the model parameters are fixed as follows: GeV, GeV.
Since our paper is devoted to the dense baryonic (quark) matter at various conditions, now, as a starting point, let us first consider the dense quark matter with isospin asymmetry. The Lagrangian of two-flavored NJL model with baryon and isopin chemical potentials has the following form
Since the Lagrangian (2) contains baryon and isospin chemical potentials, it can describe quark matter with non-zero baryon and isospin densities. Baryon and isospin densities are the quantities, thermodynamically conjugated to chemical potentials and , respectively, and can be obtained if one takes a derivative of the thermodynamic potential (TDP) of the system (2) with respect to and chemical potentials.
The quantities and are densities of conserved charges corresponding to the invariance of Lagrangian (2) with respect to the abelian groups , , where (recall that the following relations hold .)
So, one can show that and . One can also see that in addition to (3), Lagrangian (2) is invariant under the transformation of the electromagnetic group,
where .
To find the TDP of the system it is convenient to use a semibosonized version of the Lagrangian (2), with auxiliary composite bosonic fields and ,
Here the summation over repeated indices is implied. Hereafter, we will use the notations for quark chemical potential and . One can get the equations of motion for the bosonic fields from the auxiliary Lagrangian (5),
Using Equation (6), it is possible to show that the semibosonized Lagrangian (5) is equivalent to the initial Lagrangian (2). Please note that the auxiliary composite bosonic field can be identified with the physical -meson field, whereas the physical -meson fields are the following combinations of the composite bosonic fields, . In addition, let us note that the composite bosonic fields (6) are transformed under the isospin group in the following manner (it can be shown from (6)):
From the auxiliary Lagrangian (5), it is possible to obtain in the leading order of the large- expansion (i.e., in the one loop approximation) the effective action of the model. This quantity is a functional of the auxiliary bosonic and fields and has the following form:
It is easy to obtain for the following expression
in which the last term (i.e., the term in (8)) is a quark contribution to the effective action,
where is a normalization constant and is the Dirac operator acting in the flavor, spinor, and coordinate spaces. Now let us use the general formula and obtain the following expression for the effective action (8)
where the Tr operation is performed in spinor (s), flavor (f) and four-dimensional space-time coordinate (x) spaces, respectively.
Now the ground state expectation values and of composite bosonic fields can be found from the saddle point equations,
where . The knowledge of values and , namely their behavior with respect to chemical potentials, provides us with phase structure of the model.
It is clear that if there is a non-zero ground state expectation values of composite bosonic and/or fields, i.e., and/or , then in the chiral limit we have a spontaneous breaking of the axial isospin symmetry in the model (if we consider the chiral limit , when the Lagrangian (2) is symmetric in addition with respect to group, which is defined as ), whereas if another component of pion field acquires non-zero ground state expectation value, i.e., and/or , then, as it is obvious from (7), the isospin symmetry ( group) is spontaneously broken down. Since in this latter case the condensates, or the ground state expectation values, of the charged pion fields and are non-zero, this phase is usually called the charged PC phase. Furthermore, one can see from (6) that the non-zero condensates (or ) are not invariant with respect to the transformations of the electromagnetic group (4) and this leads to spontaneous breaking of electromagnetic symmetry. Hence one can say that the electromagnetic invariance in the charged PC phase is broken down and superconductivity is an unavoidable property of the charged PC phase.
As a rule, one supposes that in the ground state of the system expectation values and do not depend on space-time coordinates x,
where M and () are already constant quantities and they can be found as coordinates of the global minimum point of the TDP .
The TDP is defined by the following expression in the leading order of the large- expansion:
To find the phase portrait of the model one needs to investigate the dependence on of the global minimum point (GMP) of the TDP vs . To this end let us simplify the task and note that due to a invariance of the model, the TDP (13) depends really only on the three combinations of bosonic fields, , and (this can be seen from (7)). So, without loss of generality, it can be assumed that . Moreover, it is also possible to prove that at (see, e.g., in [60]). Hence, one can study the TDP as a function of only two variables, and . It means that we use the following ansatz
The expression for the TDP (13) of the dense (baryon density) and isospin asymmetric quark matter can be easily obtained in the mean field approximation and it has the form
where there have been introduced the following notations , and , . Let us recall also that the integration in the momentum space is restricted by a cutoff . From (15) it is possible to obtain the gap equations
Please note that the quark gap M is just the dynamical quark mass.
2.2. Phase Diagram at and in the Chiral Limit
First, let us discuss the phase diagram and the charged PC in dense quark matter with isospin asymmetry in the chiral limit. This case has been considered and the phase portrait of the model at both and has been obtained in [13,51]. Since, in general, it is a rather hard task to consider the phase diagram at the physical point, in these papers, for simplicity, the current quark mass m was assumed to be zero, i.e., the chiral limit was used. The corresponding -phase portrait is depicted in Figure 1. Let us discuss its content. One can see there is a huge region of PC phase at this phase diagram. Please note that it has been shown already in [15,16,17,61] that at the charged PC phase appears at . However, in the chiral limit (see in Figure 1) the same relation is also valid since in this case.
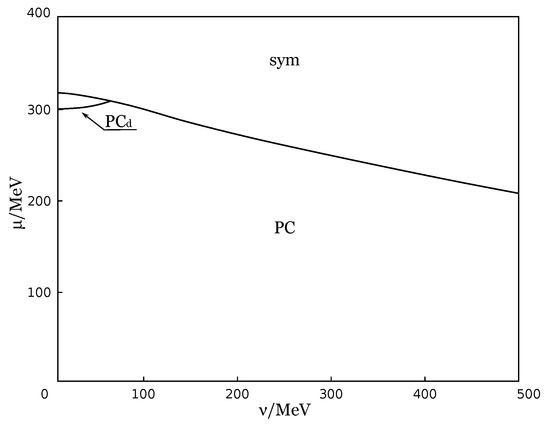
Figure 1.
The (, ) phase portrait in the chiral limit in the framework of NJL model. PC phase is charged pion condensation phase. Subscript d means that in this phase baryon density is non-zero. The sym denotes the symmetric phase.
Now let us discuss all possible phases in this case. The system of the gap equations (16) at has three different types of solutions: (i) , ; (ii) , ; (iii) , . The (i) solution corresponds to the symmetric phase, where all condensates are zero. If the GMP of the TDP is located at the point of the form (ii), then the charged pion condensate is equal to zero in the ground state and the quark condensate is non-zero. This phase is called a chiral symmetry breaking (CSB) phase. Finally, the (iii) solution corresponds to charged PC phase, where the quark condensate is equal to zero, but the charged pion one has a non-zero value.
If the GMP of the TDP is achieved on the solution of type (i), then one can see that the ground state of the system is invariant with respect to the initial symmetry group of the model, which at (in the chiral limit) and is . The (ii)-type solution (CSB phase) corresponds to the phase symmetric with respect to group. In the charged PC phase, the ground state is invariant under transformations from group. Moreover, it is clear that in the ground state of quark matter with non-zero charged pion condensate parity is also broken down.
Let us return to the discussion of the (, )-phase portrait of the model (see in Figure 1). One can see that apart from the PC phase there is a region of the PC phase at the phase diagram of Figure 1. This phase denotes the ground state of quark matter, in which besides non-zero charged pion condensate the baryon density is also non-zero. This consideration in terms of NJL model shows that the charged PC can be realized in dense quark matter with isospin asymmetry. However, let us recall once again that considerations have been performed in the chiral limit when pions are genuine Goldstone bosons and have zero masses.
2.3. Account of Electric Neutrality and -Equilibrium Conditions in the Chiral Limit
After the prediction of the charged PC phenomenon in the dense and isospin asymmetric quark matter (that can be realized, for example, in relativistic heavy ion collisions or inside the cores of the compact stars) it was interesting to take into account the charge neutrality and -equilibrium constraints that are important inside compact stars. The possibility of the charged PC phenomenon in cold and electrically neutral dense baryonic matter was investigated in -equilibrium in [14], where the consideration was also performed in the chiral limit.
Let us first elaborate on how to implement all these constraints. As it has been said above, the electric charge is conserved in the model and it can be written as , where is the generator of the third isospin component in the flavor space and is the baryon charge generator. Due to the -equilibrium requirement, one should incorporate electrons in our consideration. They are necessary to neutralize the electric charge of quarks. Moreover, -equilibrium of quark matter means that all -processes that include quarks and leptons should go in both directions with equal rates. As argued above, full Lagrangian of the system should include the electron field and electron chemical potential, but since our system is in -equilibrium, one can show that the electron chemical potential should be equal to charge chemical potential of quarks with opposite sign.
It was also supposed that one can neglect the mass of the electron and put it to zero for simplicity for their mass is quite small in the considered scale.
Since in the system composed of quarks and electrons both baryon charge and electric charge are conserved quantities, its properties in equilibrium are described by the following Lagrangian
where is the Lagrangian of NJL model (1), e is the electron spinor field; and are baryon and electric charge density operators, respectively, and , are corresponding chemical potentials. It is clear that
Hence the Lagrangian (17) can be presented in the form
In particular, it is clear from this relation that is just the isospin chemical potential .
The TDP in this case was obtained in [14] in the mean field approximation. In contrast to the previous sections where the large approximation was used, here (since in neutral quark matter the electrons are taken into account and the count of color degrees of freedom matters) it is important that there are three colors of quarks () and one should work in the mean field approximation. One should be careful as in this paper slightly different definitions are used compared to [14]. In the chiral limit the TDP has the following form (the definition of the TDP is the same as in (13))
where the first term in the right-hand side of (20) is the TDP of free massless electrons. The summation in the third term of (20) runs over all quasiparticles (), where
and , , , . As always, to avoid usual ultraviolet divergences, the integration region in (20) is restricted by a cutoff , i.e., . The gap equations that can be obtained from (20) look like
To impose the neutrality constraint locally, we should look for the ground state of the system with the electric charge density equals identically to zero. One can rephrase it in other words as the study of the GMP of the TDP under the constraint that has the following form
Then, it was shown in [14] by numerical investigations of the gap and neutrality Equations (22) and (23) that at sufficiently small quark chemical potential, namely at 301 MeV, the ground state of the system corresponds to CSB phase. As it has been discussed above, in this case the GMP has the form (ii) and the dynamical quark mass 301 MeV. There is no need to neutralize the quark electric charge because in this phase both the baryon and the isospin densities are zero. It means that in this phase.
At 323.5 MeV the GMP has already the form (iii), meaning that in this case the charged PC phase is realized. In this phase the baryon density is non-zero, so it is PC phase. At Figure 2 the pion condensate is depicted as a function of . Then, at larger values of the chemical potential (i.e., at at Figure 2) symmetric phase is realized, where both condensates are zero. So, one can see that in electrically neutral dense baryonic matter in -equilibrium there might appear charged PC phenomenon. Let us stress once more that in [14] this result was obtained in the chiral limit.
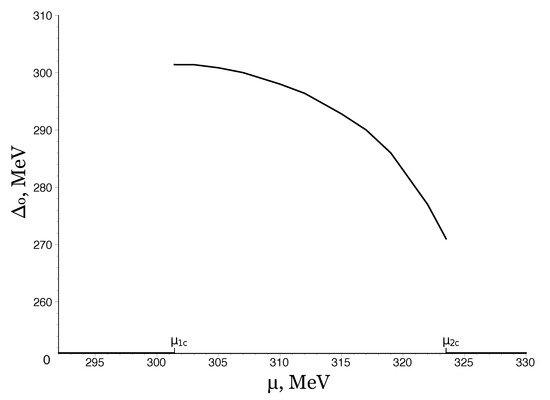
Figure 2.
The value of charged pion condensate as a function of quark number chemical potential in electric charge neutral quark matter.
2.4. Phase Diagram at and at the Physical Point ()
Though current quark mass is small compared to the scales studied in the paper, it was shown in [15,16,17] that charged PC phenomenon at not so large values of isospin imbalance is strongly influenced by current quark mass values. As we have already said above, charged PC phenomenon takes place only at values of . In addition, at physical point () it happens only at values of isospin chemical potential larger than approximately 139 MeV. So non-zero current quark mass can be of importance for the investigations of the phase structure.
After the prediction of the charged PC phase of dense matter, it was necessary to consider this phenomenon at the physical point. It means that one needs to use the Lagrangian (1) and (2) with non-zero physical value of current (bare) quark mass MeV. The consideration at the physical point but without electric neutrality condition showed that there remains marginal region of PC phase at the phase portrait. The corresponding () phase diagram is shown at Figure 3 and one can see that in this case the region of PC phase is much smaller than at Figure 1 corresponding to the chiral limit. However, charged PC phenomenon can still take place in this case, even at the physical point (even though one should bear in mind that the very small size of this phase and the fact that it is obtained in the framework of the effective model makes it not a very robust prediction).
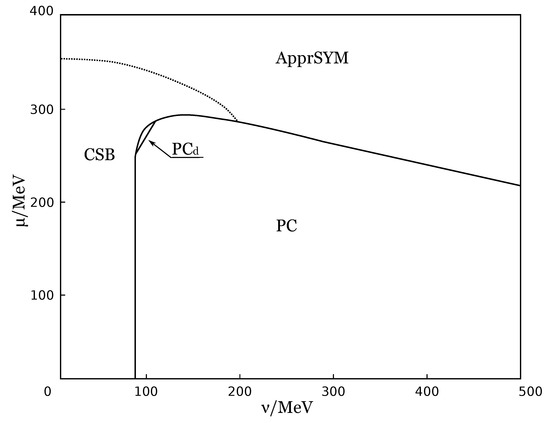
Figure 3.
The (, ) phase portrait of the model at the physical point (). CSB phase denotes chiral symmetry breaking phase and the notation ApprSYM means the phase where dynamical quark mass is close to the current quark mass value , i.e., the chiral symmetry is approximately restored in this phase. There is no a real phase transition between CSB and ApprSYM phases but a continuous crossover. Other notations are the same as in Figure 1.
Now let us turn to the discussion on what happens if one takes into play the electric neutrality and beta-equilibrium conditions at the physical point. In [22,25,26] the consideration of the electrically neutral dense baryonic matter in -equilibrium has been performed in the framework of NJL model at the physical point.
In this case the expression for the TDP (20) should be slightly changed, specifically the non-zero current quark mass should be added, and one obtains
Numerical studies of this case have been performed in [22,25,26] and the phase structure has been obtained. In these studies, the current quark mass m has been treated as a free parameter, therefore, the corresponding pion mass at was a free parameter as well.
Let us say a couple of words on the results obtained. At Figure 4 the phase diagram is presented. The solid line denotes the border between the two phases, CSB phase (which is arranged at rather small values of ) and ApprSYM one (this phase lies in the region of large ). ApprSYM means an approximate symmetrical phase and corresponds to a GMP of the TDP with and , but in contrast to the CSB phase, dynamical quark mass M in ApprSYM drops rapidly and incessantly to the current quark mass value m at increasing temperature or baryon chemical potential. The bold dot at the end of the line is the critical endpoint of the first order phase transition. The shaded region denotes the charged PC phase. Now if we go to the chiral limit (the line at ) these results are in good agreement with the ones discussed above. There are two critical values of the chemical potential, and that corresponding to the onset and disappearance of charged PC, respectively. However, increasing the value of the current quark mass the shaded region shrinks until these two points meet, . They meet at the value of pion mass that corresponds to a current quark mass of , much less than the physical values, . The (,) phase portrait at the physical point is depicted at Figure 5 [25], where one can also see that the electric neutrality line does not cross the PC phase. Hence, one can infer that charged PC is an extremely fragile phenomenon with respect to the explicit CSB effect (non-zero current quark mass).
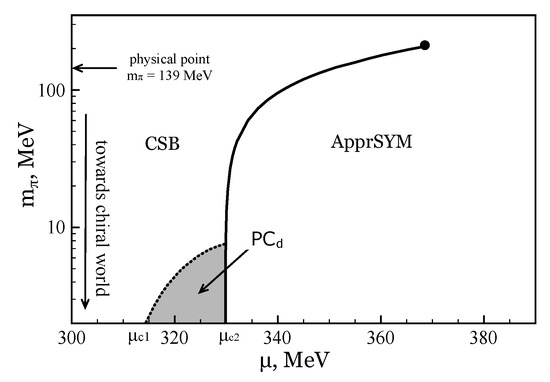
Figure 4.
The (,) phase diagram of neutral quark matter. The figure is taken from [25].
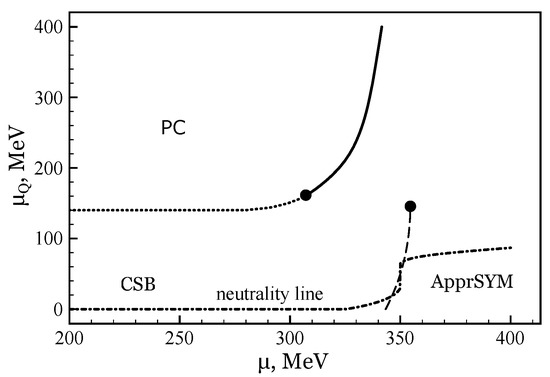
Figure 5.
The (,) phase diagram at the physical point, MeV. The figure is taken from [25].
In the papers [25,26] it was also shown that the equality between the electric chemical potential (in essence the isospin one) and the pion mass in medium, , is a threshold to the charged PC phase provided the transition to the charged PC phase is of second order. And the absence of the charged PC can be understood in the following way. Please note that increase of current quark mass leads to a drastic amplification of the vacuum pion mass because at small masses m pion mass depends on quark mass as , whereas the change in the value of the quark mass in keV scale brings about no considerable modification to the value of electric chemical potential .
So, let us note that not only PC phase is absent at the charge neutrality line, but there is no PC at all and electrically neutral quark matter never meets the regions occupied by the charged PC phase. Thus, one can summarize that at the physical quark mass the NJL model consideration of neutral quark matter forbids the charged PC to take place in the ground state.
3. Conditions Promoting the Appearance of Charged Pion Condensation in Dense Quark Matter
In the previous Section 2 (see Section 2.4) it was shown that charged PC does not take place in neutral quark matter with isospin asymmetry. However, recently there have been found conditions that can be realized in real physical situations and can lead to the appearance of charged PC in dense quark matter [45,46,47,50,51,53]. Some of these conditions are elaborated in the framework of the (3+1)-dimensional NJL model discussed in the previous section [51,53]. Other physical constraints that may lead to a generation of the charged PC phase of dense quark matter are investigated, for simplicity, within the framework of a toy (1+1)-dimensional NJL model (NJL) [45,46,47,50]. So first, let us remind the basic properties of the NJL model in the presence of baryon and isospin chemical potentials (see, e.g., in Ref. [29]).
3.1. The NJL2 Model and Its Phase Structure
As noted above, the NJL model can be used to get quite common qualitative information about the properties of real dense quark matter with isospin asymmetry. Formally, its Lagrangian has the same form as the Lagrangian (1) and (2) of the NJL model in (3+1)-dimensional space-time. However, u and d quark fields are now (in two dimensions) the two-component Dirac spinors and, moreover, the () and matrices are the 2 × 2 matrices in the two-dimensional spinor space,
It is clear that the NJL model is a direct generalization of the (1+1)-dimensional Gross–Neveu model [62] with a single flavor (i.e., single massless color -plet) to the case of two flavors of massive quarks.
To find the TDP of the NJL model in the leading order of the large- expansion, one can use the technique of the previous section, where we have obtained the corresponding TDP of the (3+1)-dimensional NJL model. Specifically, it is possible to introduce the auxiliary composite bosonic fields and as well as their ground state expectation values and , respectively (see in Equations (6) and (12), for more details). Moreover, without loss of generality, it can be assumed that and . Then the expression for the unrenormalized TDP of the NJL model can be easily shown to have the following form
where , , and . It is possible to perform in Equation (26) the integration with respect to , as in the (3+1)-dimensional case. Then, one can see that the TDP (26) is ultraviolet divergent, hence to get any physical information, one should first renormalize it (in contrast to the (3+1)-dimensional NJL model, the NJL model is renormalizable). For this purpose, one can use a special assumption that the bare coupling constant G depends on the cutoff parameter (where restricts the region of integration in the divergent integral of (26), ). At zero bare quark mass, , the renormalization procedure was discussed in the literature, see, e.g., in Refs. [45,47,63]. In short, it is evident in this case that cutting off the divergent integral in (26) and then using the following dependence of the bare coupling constant on the cutoff parameter, ,
one has a new free finite renormalization group invariant (does not depend on the cutoff ) massive parameter (and it can be shown that it is just a dynamically generated quark mass in vacuum, i.e., at and ). Then in the limit one can obtain a finite renormalization group invariant expression for the TDP. In particular, in vacuum, where we denote the TDP as , it looks like
It can be shown that the global minimum of the TDP (28) is reached at and , and chiral symmetry of the model is broken down. In the chiral limit () the phase structure of NJL model was studied in detail in Refs. [45,63], and it follows from these considerations that at arbitrary values of and the phase portrait of the NJL model does not contain the charged PC phase with non-zero density of baryons. The same property is valid for the phase structure of the massive NJL model, which does not predict the charged PC phenomenon in dense quark matter (see, e.g., in Refs. [29,46]).
Let us note that (1+1)-dimensional NJL model has the same chiral structure as the corresponding (3+1)-dimensional NJL model and it possesses a lot of common properties and features with real QCD. For example, QCD and NJL models are both renormalizable, both have asymptotic freedom, dimensional transmutation and the spontaneous CSB (in vacuum) [61,64,65,66,67,68,69]. Moreover, they have similar phase diagrams. Hence, NJL model can be used as a laboratory for the qualitative simulation of specific features of QCD and, since it is renormalizable, it can be done at arbitrary energies in contrast to effective (3+1)-dimensional NJL model.
Let us now discuss the breaking of continuous symmetry and the famous no-go theorem [70,71] that in general, forbids in two-dimensional space-time the spontaneous breaking of any continuous symmetry. Currently it is well understood (see, e.g., the discussion in [61,68,69,72,73]) that in the limit ( is the number of quark colors) the usual no-go theorem [70,71] does not work. This fact follows directly from the observation that the quantum fluctuations, which at finite usually washes away a long range order corresponding to a spontaneous breakdown of symmetry, are suppressed by the powers of factor in the large- limit. Thus, it is possible to simulate the phenomena taking place in real hadronic (quark) matter, such as spontaneous breaking of continuous chiral symmetry or charged PC (spontaneous breaking of the continuous isospin symmetry), in the framework of a comparatively simple (1+1)-dimensional NJL-type models, although only in the limit of the large .
3.2. Finite Size Effect and Nontrivial Topology
Now let us return to the factors that can generate the appearance of charged PC in dense quark matter. Physical phenomena, in general, usually occur in a restricted space. For instance, the quark gluon matter droplets produced in heavy ion collisions (for example, at RHIC) always has a finite size. A volume of the droplets can range and can be as large as of order of several dozens or even hundreds of fm, while size of the smallest system produced is estimated to be as low as 2 fm [74,75,76]. So, it is interesting to account for the influence of the finite size effects on (,) phase diagram and in particular on charged PC and it has been done in [45]. The analysis has been performed in the framework of NJL model. To study the influence of finite size effects on the phase structure of quark matter, one needs to assume from the beginning some boundary conditions. In finite temperature field theory one can introduce temperature by replacing integral over the temporal direction to a summation of the Matsubara frequencies with the requirement that fermion field satisfies the antiperiodic boundary conditions. However, in contrast to the temporal direction (thermal case), where boundary conditions are fixed just by the statistics, there is no such restriction in the case of spatial directions. So, for the system with the finite size there is always important issue concerning the choice of the boundary conditions for the fermion fields.
In the papers on this subject, both antiperiodic and periodic boundary conditions have been used and neither of them has been decisively excluded. Let us emphasize what the most substantial difference between these two boundary conditions is. It is actually whether one includes zero-momentum mode contribution or not. The zero-mode contribution is taken into account in the periodic boundary condition, whereas it is excluded in the case of antiperiodic one. For bosons, the most natural choice of boundary condition is periodic. However, it has been always not clear what boundary conditions one should use for fermions, for example, quarks.
In some cases, the antiperiodic spatial boundary condition is used to keep symmetry between the time and space directions or to get a consistent picture with the dependence of pion mass on the finite size obtained from chiral perturbation theory (ChPT).
Various boundary conditions induce opposite results on vacuum properties of QCD: the antiperiodic spatial boundary condition for quarks induces the chiral symmetry restoration in the small system (analogously to the thermal effects), while the periodic boundary condition enhances the CSB in vacuum (similar to the catalysis of CSB under the influence of magnetic field) [77,78,79,80].
There are many discussions of the finite size effects [77,78,79,81,82,83,84,85,86,87,88,89], and to incorporate it different strategies are employed, for example, replacing momentum integrals by the summations over discrete momentum [77,78,81,82,83,84,85], introducing a lower momentum cutoff in integrals [89] or one can use the multiple reflection expansion [86,87].
The above discussion was devoted to the quark models such as NJL model, but finite size effects have been also studied in the framework of different hadronic models such as ChPT, Walecka model, hadron resonance gas model etc. Let us elaborate on that a little bit. To get the extrapolation to infinite volume limit for lattice QCD finite size effects have been investigated in the framework of ChPT ([90] and references therein), where the periodic boundary conditions were imposed. Meanwhile, twisted boundary conditions (similar to the general case of the (29)) have been used in ChPT in [91,92]. In terms of hadron resonance gas model, the finite size effects were investigated in [93] employing a lower momentum cutoff, and the multiple reflection expansion formalism has been used to study influence of finite size on the chemical freeze-out [94]. Walecka model in a finite volume with antiperiodic spatial boundary conditions have been considered in [95] and both types of boundary conditions (periodic and antiperiodic) have been investigated in the framework of parity-doublet and Walecka model in [96]. Other methods not directly involving boundary conditions were used in studies of finite size matter in nuclei [97,98].
To simulate the influence of finite size effect, in Ref. [45] the (1+1)-dimensional system with Lagrangian of the form (1) and (2) was placed into a confined space region of the form (where x is the space coordinate). It is well-known that such a constraint is tantamount to the investigation in a space-time with nontrivial topology, for example in our case, one of the space coordinates are compactified. It means that one can consider the model in space-time with topology and quark quantum fields should satisfy the boundary conditions of the following form
where is the parameter fixing the boundary conditions, for example, corresponds to periodic boundary condition and to the antiperiodic one, the parameter L is the length of the circumference .
As a result, to obtain the TDP of the NJL system with Lagrangian (1) and (2) in the confined domain, one should make a standard replacement of the integration over momentum in the expression (26) to the summation according to the rule:
Let us briefly discuss the analogy of parameter with imaginary baryon chemical potential. For temporal dimension, the Matsubara frequencies are . Here the antiperiodic boundary conditions have been used. One can note that in the case of imaginary chemical potential the Matsubara frequencies are and the temporal boundary condition can be transformed into the imaginary chemical potential divided by temperature . In recent years, a great effort has been made in studying the phase diagram at imaginary chemical potential as in lattice QCD [99] as well as in effective models including NJL model ([100] and references therein).
Now let us introduce the notations used in [45]. Instead of dimensionful quantities such as M, , , (see Section 3.1) and L it is convenient to use the dimensionless quantities:
So is just the inverse length of the circumference and shows how large the volume of space, in which our system is confined, is. The case corresponds to the topology (infinite space) and the case corresponds to , where the length of compactified dimension is . One can think in the following way: the larger corresponds to smaller volume and stronger finite size effects.
The influence of nontrivial topology on the phase structure of NJL model has been studied in [45], where both periodic and antiperiodic boundary conditions have been studied. Let us present a couple of phase portraits. For example, in Figure 6 and Figure 7 the (,) phase diagrams are presented for various values of in the case of periodic boundary conditions. In addition, one can see that there is a region of the PC phase at both plots, it spans around the small values of isospin chemical potential. One can also notice that PC phase is presented in a wide interval of and it is enlarged if the system becomes smaller. In the case of antiperiodic boundary conditions this phase has not been found and it is probably natural, as in this case the finite size effect is similar to the effect of the finite temperature on the system (it usually restores all the symmetries and leads to the vanishing condensates). However, PC phase has been found in quark matter system of a finite size at least for periodic boundary conditions, so probably one can conclude that finite size and nontrivial topology effects might lead to the appearance of the charged PC phase with non-zero baryon density at least in the framework of the NJL model. It would be interesting to consider this situation in the framework of more realistic (3+1)-dimensional model approach, but unfortunately, to the best of our knowledge, this consideration has not been performed.
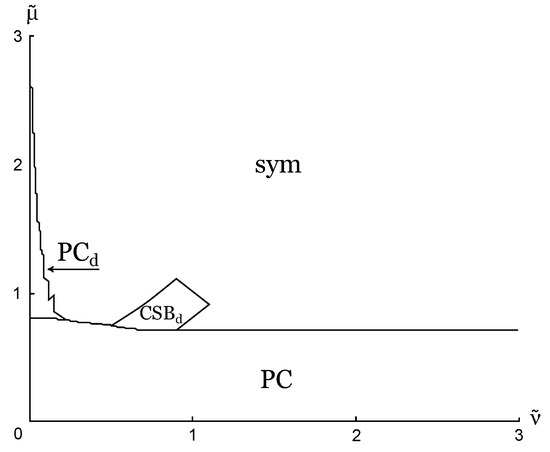
Figure 6.
The phase portrait at (where , and , see the text). The case of periodic boundary conditions.
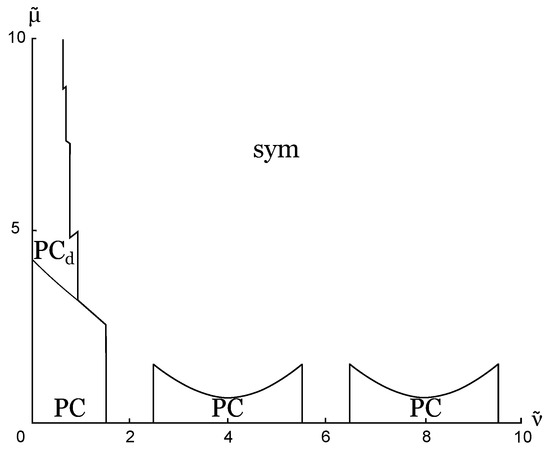
Figure 7.
The phase portrait at . The case of periodic boundary conditions.
Now let us mention another interesting feature of the phase structure characteristic to the finite size systems at zero temperature. One can see at Figure 6 and Figure 7 that there are small spikes at the border line between PC and symmetrical phases. At the first glance one can think that they are numerical calculations artifacts. However, they are actually physical and comes from the fact that in the finite systems the momentum spectrum became discrete and when one changes external parameters new momentum eigenvalues go into play and this can lead to the non-analyticity of critical lines, condensates, and some thermodynamic quantities. Similar oscillations were observed in [101].
3.3. Inhomogeneous Pion Condensation in Dense Baryonic Matter
Now let us turn our attention and discuss another factor that can lead to the generation of charged PC in dense quark matter, namely the possibility of inhomogeneity of condensates i.e., dependence of condensates on the spatial space-time dimensions. The phase structure of dense quark matter with isospin asymmetry has been studied in the framework of NJL model with possibility of inhomogeneous charged pion condensate [46]. The consideration was performed at the physical point, i.e., for physical values of current quark mass.
Let us say a couple of words about why one should consider inhomogeneous condensates. In vacuum, i.e., in empty space without particle density and, equivalently, at zero values of the chemical potentials and , the vacuum expectation values and do not depend on space-time coordinates. Although in dense quark medium or, in other words, at non-zero values of the chemical potentials , , the ground state expectation values of bosonic fields might assume a nontrivial dependence on spatial coordinate x. For example, in the considerations of Ref. [46] there has been used the following ansatz
where , and are quantities that do not depend on space-time coordinates.
In [46] the phase structure in this approach was explored and it was found that in the inhomogeneous case there is charged PC phase with non-zero baryon density at the phase portrait and it is quite extensive. At Figure 8 the phase portrait of the model NJL model is shown. There the phase IPC are inhomogeneous phases with charged PC and with non-zero baryon density, and one can see that it occupies the large part of the phase diagram.
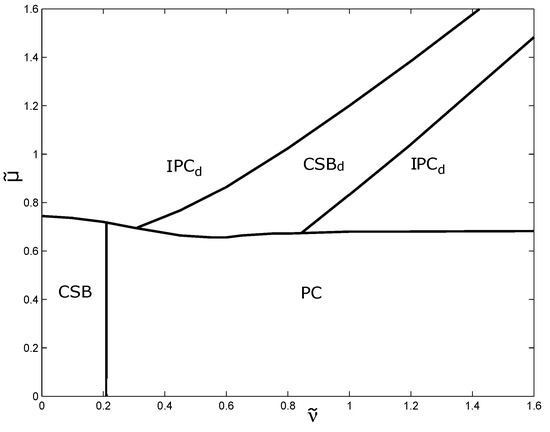
Figure 8.
The phase portrait of the model with the possibility of inhomogeneous pion condensation. IPC stand for inhomogeneous charged PC phases. All other notations are the same.
So, one can conclude that spatial inhomogeneity of charged pion condensate is also a factor promoting the appearance of PC phases at the phase diagram of dense quark matter.
3.4. Chiral Imbalanced Dense Quark Matter
Now let us return to the (3+1)-dimensional NJL (1) model and talk about another factor that can generate charged pion condensation in dense quark matter. Besides non-zero temperature and baryon density (non-zero baryon chemical potential), there exist additional parameters that may be relevant to the properties of the QCD phase diagram. We have already talked about isotopic chemical potential. There is another captivating phenomenon that fell into spotlight quite recently, it is the chiral imbalance (different average densities of right- () and left-handed () quarks). This phenomenon is a remarkable effect originating from highly nontrivial interplay of different features of QCD such as chiral symmetry, chiral (axial) anomaly, and possible gluon configuration topology. It is expected to appear in the processes in heavy ion collisions violating P and CP on the event-by-event basis [56] and possibly may lead to interesting phenomena such as chiral magnetic effect [55]. Chiral imbalance might be also realized in interiors of compact stars [54]. In addition, chiral media, i.e., media with non-zero chiral imbalance, can be attained in condensed matter systems such as Dirac and Weyl semimetals [57,58]. Also, note that phenomena regarding a chiral imbalance in the context of QCD are usually studied in the framework of NJL models with a chiral chemical potential [102,103,104,105,106,107,108,109,110].
The chiral imbalance of the system is described by the chiral charge density but instead of it one can use the corresponding chiral chemical potential in the grand canonical ensemble approach. In general, the chiral charge is a more relevant quantity, but due to technical reasons when studying the phase diagram, it is easier to work with chemical potential , and we will follow this way in this paper. Let us also note that the chiral charge is not a strictly conserved quantity, because of non-zero quark condensate as well as quantum chiral anomaly. Therefore, chemical potential is not a quantity conjugated to a strictly conserved charge. However, it is possible to treat as the chemical potential describing a system in thermodynamic equilibrium in the state with non-zero value of , although, on a larger time scale than the one needed for chirality changing processes to occur. Moreover, let us talk about other possibility and note that can be introduced for individual quark flavor, and , and it is evident that . Then it is possible to consider chiral isospin charge as well as the corresponding chiral isospin chemical potential . Unlike the chiral charge , the chiral isospin charge turns out to be a conserved quantity at least in the massless NJL model. Since gluons interact with different quark flavors in exactly the same way, it is usually assumed that in QCD matter the chiral charges and are equal and therefore and . However, the chiral isospin chemical potential can be generated due to chiral separation effect in dense quark matter.
In [51,53,54] the phase diagram of dense quark matter both with chiral and isospin imbalances has been considered and the influence of chiral and chiral isospin chemical potentials on the phase structure and charged PC, in particular, has been studied. The investigations have been performed in the framework of two-flavored (3+1)-dimensional massless NJL model with baryon , isospin , chiral and chiral isospin chemical potentials. Its Lagrangian has the form
where and other notations are presented in Equation (1). In the following we use the notations , and .
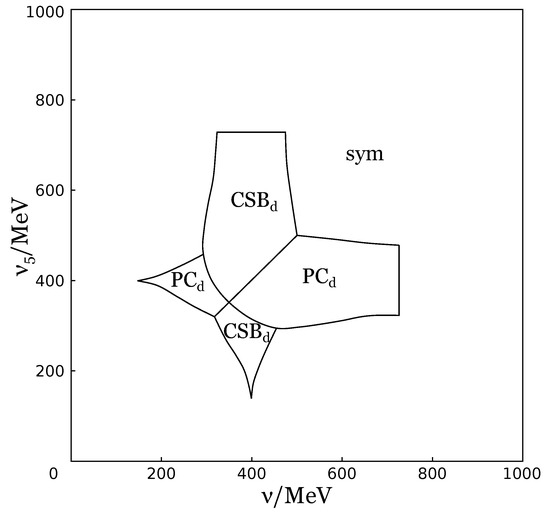
The phase diagram of NJL model with baryon , isospin , and chiral isospin chemical potentials (at ) has been considered in [51] and the phase portrait of the model is shown at Figure 9. It is clear from this figure that chiral imbalance (chiral isospin chemical potential ) leads to the generation of charged PC in dense quark matter with isotopic asymmetry. However, let us note that for the PC phase to be generated the matter should have non-zero isospin imbalance (isospin chemical potential ). One can also observe that in contrast to the first prediction of PC phase in dense quark matter with isotopic asymmetry (see Section 2.2, Section 2.4 and Figure 1 and Figure 3), the generation is quite extensive and the region of PC phase is quite large (not marginal in any way).
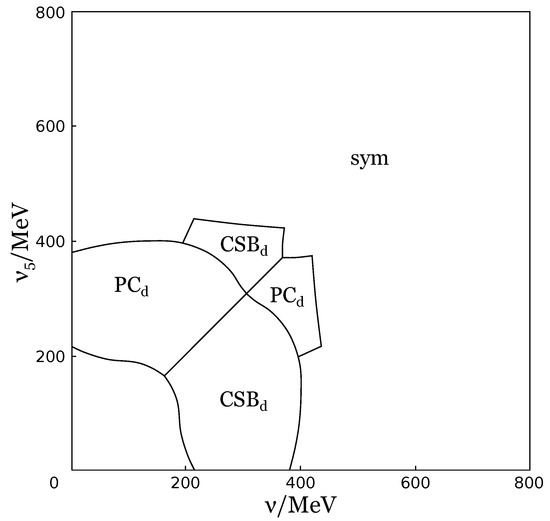
Then in [53] the influence of chiral chemical potential was studied in addition, and it was shown that chiral chemical potential generates charged PC phase in dense baryonic (quark) matter as well. It is easily seen from Figure 10, where the phase portrait of the NJL model is presented at . However, this generation is not that vast and occurs at not so large baryon densities. The case of the joint effect of two chiral chemical potentials, and , on the phase structure of the NJL model was also considered in this work. The -phase diagram (at ) is depicted at Figure 11 and one can see that at non-zero values of there is a large patch of PC phase. Moreover, this phase can be generated even at zero values of isospin chemical potential . The fact that there is no need for isospin imbalance to generate the PC phase is clearly presented at Figure 12, where the -phase diagram is depicted at zero value of isospin chemical potential, , and it exhibits a large region containing PC phase. So, one can conclude that chiral and chiral isospin chemical potentials together generate PC phase very efficiently. Summarizing, one can say that chiral imbalance is a factor that leads to the generation of charged PC in dense quark matter.
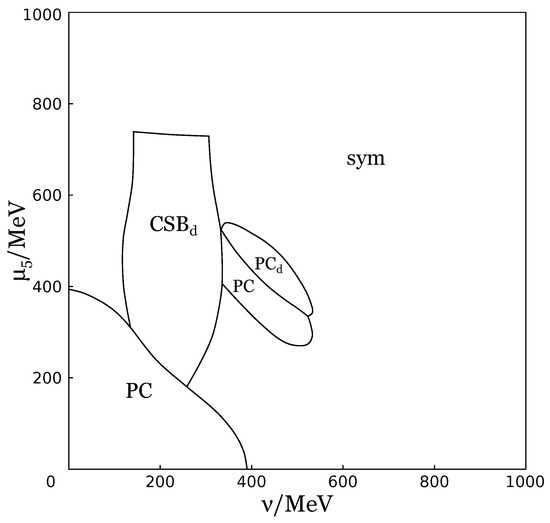
Figure 10.
The -phase diagram at and GeV.
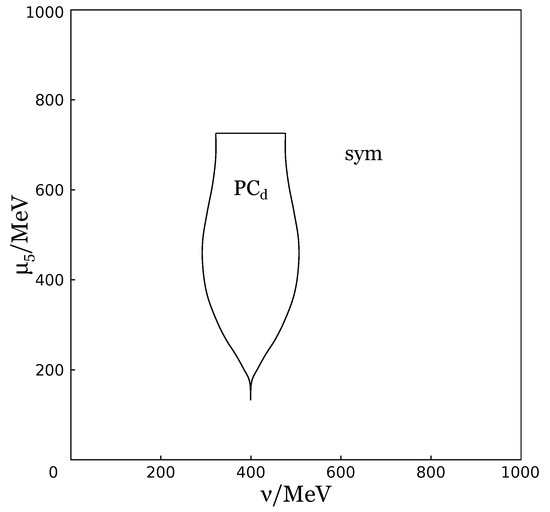
Figure 12.
The -phase diagram at and GeV.
4. Summary and Conclusions
In this short review we tried to give an outline of investigations of charged PC in dense baryonic (quark) matter in the framework of effective (3+1)-dimensional NJL model and toy QCD motivated (1+1)-dimensional NJL model (NJL model).
The possibility of charged PC phase with non-zero baryon density was shown for the first time in the framework of the massless NJL model in Ref. [13] and then in Ref. [14] it was found that this phase persists even in electrically neutral dense baryonic (quark) matter. However, later it was shown in Refs. [22,25,26,27,28] that charged PC condensation in neutral dense quark matter is enormously frail with respect to explicit CSB effect (non-zero current quark mass), and it was shown, in particular that it is forbidden for the physical values of current quark masses.
Nevertheless, recently there have been found factors and conditions that can be realized in real physical systems and can promote the appearance of charged PC phenomenon in dense baryonic (quark) matter. Specifically, in the paper [45] it was shown that if one takes into consideration the fact that system can have finite size, then charged PC phase with non-zero baryon density can be realized in the system. It was also revealed in [46] that the possibility of spatially inhomogeneous charged PC condensate allows this phase to appear as well. In addition, more recently [47,50,51,53] it was found that there is another interesting factor that can induce a charged PC phase in dense baryonic matter, it is a chiral imbalance of the system (non-zero difference between densities of left-handed and right-handed quarks).
The finite size effect and spatially inhomogeneous charged PC have been considered in Refs. [45,46] in the framework of a toy QCD motivated NJL model, and the influence of chiral imbalance has been investigated both in the framework of NJL model [47,50] and in more realistic (3+1)-dimensional NJL model [51,53]. These models allow one to consider the region of non-zero baryon densities of QCD phase diagram, which cannot be studied in lattice QCD (simulations are almost impossible due to the infamous sign problem). For simplicity, the whole review is devoted to the consideration of the case of zero temperature only. However, our recent investigation [54], made in the framework of the NJL model with non-zero bare quark masses, shows that in chirally asymmetric dense quark matter charged PC phenomenon can be realized even at sufficiently high temperatures.
Let us once more recapitulate the conditions that can lead to the generation of charged PC phenomenon in dense baryonic matter:
- (1)
- finite size effects and nontrivial topology,
- (2)
- possibility of inhomogeneous charged pion condensates,
- (3)
- chiral imbalance.
These results can be interesting in the context of heavy ion collision experiments such as NICA and FAIR, where it is expected to get high baryon densities. It is of interest also in neutron star physics, since quark matter might be produced in their cores, where very high baryon and isospin densities are attained.
Author Contributions
All authors contribute equally to this article.
Funding
This research received no external funding
Acknowledgments
We would like to thank Sergei D. Odintsov and Tomohiro Inagaki for information about this special issue and the opportunity to contribute.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shuryak, E.V. Quantum Chromodynamics and the Theory of Superdense Matter. Phys. Rept. 1980, 61, 71–158. [Google Scholar] [CrossRef]
- Schäfer, T. Quark matter. arXiv 2003, arXiv:hep-ph/0304281. [Google Scholar]
- Stone, J.R. High Density Matter. EPJ Web Conf. 2013, 63, 03009. [Google Scholar] [CrossRef]
- Fukushima, K.; Sasaki, C. The phase diagram of nuclear and quark matter at high baryon density. Prog. Part. Nucl. Phys. 2013, 72, 99–154. [Google Scholar] [CrossRef]
- Shuryak, E.V. The QCD vacuum, hadrons and the superdense matter. World Sci. Lect. Notes Phys. 2004, 71, 1–618. [Google Scholar]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 112, 345. [Google Scholar] [CrossRef]
- Hatsuda, T.; Kunihiro, T. QCD phenomenology based on a chiral effective Lagrangian. Phys. Rept. 1994, 247, 221–367. [Google Scholar] [CrossRef]
- Klevansky, S.P. The Nambu-Jona-Lasinio model of quantum chromodynamics. Rev. Mod. Phys. 1992, 64, 649. [Google Scholar] [CrossRef]
- Buballa, M. NJL model analysis of quark matter at large density. Phys. Rept. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Ebert, D.; Kalinovsky, Y.L.; Münchow, L.; Volkov, M.K. Mesons and diquarks in a NJL model at finite temperature and chemical potential. Int. J. Mod. Phys. 1993, A8, 1295. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455. [Google Scholar] [CrossRef]
- Shovkovy, I.A. Two lectures on color superconductivity. Found. Phys. 2005, 35, 1309–1358. [Google Scholar] [CrossRef]
- Ebert, D.; Klimenko, K.G. Gapless pion condensation in quark matter with finite baryon density. J. Phys. G 2006, 32, 599. [Google Scholar] [CrossRef]
- Ebert, D.; Klimenko, K.G. Pion condensation in electrically neutral cold matter with finite baryon density. Eur. Phys. J. C 2006, 46, 771–776. [Google Scholar] [CrossRef]
- He, L.; Jin, M.; Zhuang, P. Effect of U(A)(1) breaking on chiral phase structure and pion superfluidity at finite isospin chemical potential. Mod. Phys. Lett. A 2007, 22, 637–643. [Google Scholar] [CrossRef]
- He, L.; Jin, M.; Zhuang, P. Pion superfluidity and meson properties at finite isospin density. Phys. Rev. D 2005, 71, 116001. [Google Scholar] [CrossRef]
- He, L.; Zhuang, P. Phase structure of Nambu-Jona-Lasinio model at finite isospin density. Phys. Lett. B 2005, 615, 93–101. [Google Scholar] [CrossRef]
- Barducci, A.; Casalbuoni, R.; Pettini, G.; Ravagli, L. A Calculation of the QCD phase diagram at finite temperature, and baryon and isospin chemical potentials. Phys. Rev. D 2004, 69, 096004. [Google Scholar] [CrossRef]
- Loewe, M.; Villavicencio, C. Two-flavor condensates in chiral dynamics: Temperature and isospin density effects. Phys. Rev. D 2005, 71, 094001. [Google Scholar] [CrossRef]
- Splittorff, K.; Son, D.T.; Stephanov, M.A. QCD—Like theories at finite baryon and isospin density. Phys. Rev. D 2001, 64, 016003. [Google Scholar] [CrossRef]
- Son, D.T.; Stephanov, M.A. QCD at finite isospin density. Phys. Rev. Lett. 2001, 86, 592. [Google Scholar] [CrossRef] [PubMed]
- Andersen, J.O.; Kyllingstad, L.T. Pion Condensation in a two-flavor NJL model: The role of charge neutrality. J. Phys. G 2009, 37, 015003. [Google Scholar] [CrossRef]
- Kogut, J.B.; Sinclair, D.K. Quenched lattice QCD at finite isospin density and related theories. Phys. Rev. D 2002, 66, 014508. [Google Scholar] [CrossRef]
- Gupta, S. Critical behavior in QCD at finite isovector chemical potential. arXiv 2002, arXiv:hep-lat/0202005. [Google Scholar]
- Abuki, H.; Anglani, R.; Gatto, R.; Pellicoro, M.; Ruggieri, M. The Fate of pion condensation in quark matter: From the chiral to the real world. Phys. Rev. D 2009, 79, 034032. [Google Scholar] [CrossRef]
- Anglani, R. A Microscopic study of pion condensation within Nambu-Jona-Lasinio model. Acta Phys. Pol. Suppl. 2010, 3, 735. [Google Scholar]
- Abuki, H.; Ciminale, M.; Gatto, R.; Ippolito, N.D.; Nardulli, G.; Ruggieri, M. Electrical neutrality and pion modes in the two flavor PNJL model. Phys. Rev. D 2008, 78, 014002. [Google Scholar] [CrossRef]
- Abuki, H.; Anglani, R.; Gatto, R.; Nardulli, G.; Ruggieri, M. Chiral crossover, deconfinement and quarkyonic matter within a Nambu-Jona Lasinio model with the Polyakov loop. Phys. Rev. D 2008, 78, 034034. [Google Scholar] [CrossRef]
- Ebert, D.; Klimenko, K.G. Properties of the massive Gross-Neveu model with nonzero baryon and isospin chemical potentials. Phys. Rev. D 2009, 80, 125013. [Google Scholar] [CrossRef]
- Migdal, A.B. Stability of Vacuum and Limiting Fields. Zh. Eksp. Teor. Fiz. 1971, 61, 2210. [Google Scholar] [CrossRef]
- Migdal, A.B. Phase Transition in Nuclear Matter and Non-pair Nuclear Forces. Sov. Phys. JETP 1973, 36, 1052. [Google Scholar]
- Migdal, A.B.; Saperstein, E.E.; Troitsky, M.A.; Voskresensky, D.N. Pion degrees of freedom in nuclear matter. Phys. Rept. 1990, 192, 179. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Levenfish, K.P.; Shibanov, Y.A. Cooling neutron stars and superfluidity in their interiors. Phys. Usp. 1999, 42, 737. [Google Scholar] [CrossRef]
- Tatsumi, T. Alternating Layer Spin Structure Realized In The Sigma Model. Prog. Theor. Phys. 1980, 63, 1252–1267. [Google Scholar] [CrossRef]
- Tatsumi, T. A Realistic Approach To Charged Pion Condensation In Neutron Matter. Prog. Theor. Phys. 1982, 68, 1231–1247. [Google Scholar] [CrossRef]
- Tatsumi, T. A Realistic Calculation of the Cooling Rate of Neutron Stars with the Charged Pion Condensate. Prog. Theor. Phys. 1983, 69, 1137–1145. [Google Scholar] [CrossRef][Green Version]
- Takatsuka, T.; Tamagaki, R. Nucleon superfluidity under pion condensation in neutron star matter. Prog. Theor. Phys. Suppl. 1993, 112, 107–122. [Google Scholar] [CrossRef]
- Takatsuka, T.; Tamagaki, R. Effects of charged-pion condensation on neutron 3P2 superfluidity. Prog. Theor. Phys. 1997, 97, 263–281. [Google Scholar] [CrossRef]
- Takatsuka, T.; Tamagaki, R.; Tatsumi, T. Characteristic aspects of pion condensed phases. Prog. Theor. Phys. Suppl. 1993, 112, 67–106. [Google Scholar] [CrossRef]
- Suzuki, T.; Tatsumi, T.; Sakai, H. The Landau-Migdal Parameters, G-prime(N N) and G-prime(N Delta) and Pion Condensations. arXiv 1999, arXiv:nucl-Th/9901097. [Google Scholar]
- Ohnishi, A.; Jido, D.; Sekihara, T.; Tsubakihara, K. Possibility of s-wave pion condensates in neutron stars revisited. Phys. Rev. C 2009, 80, 038202. [Google Scholar] [CrossRef]
- Ericson, T.E.O.; Weise, W. Pions and Nuclei; Oxford University Press: Oxford, UK, 1988. [Google Scholar]
- Wakasa, T.; Sakai, H.; Okamura, H.; Otsu, H.; Fujita, S.; Ishida, S.; Sakamoto, N.; Uesaka, S.; Satou, N.; Greenfield, M.B.; et al. Gamow-Teller strength of Nb-90 in the continuum studied via multipole decomposition analysis of the Zr-90 (p, n) reaction at 295 MeV. Phys. Rev. C 1997, 55, 2909. [Google Scholar] [CrossRef]
- Suzuki, T.; Sakai, H. The Landau-Migdal parameters, g’(NN) and g’(N Delta). Phys. Lett. B 1999, 455, 25. [Google Scholar] [CrossRef]
- Ebert, D.; Khunjua, T.G.; Klimenko, K.G.; Zhukovsky, V.C. Charged pion condensation phenomenon of dense baryonic matter induced by finite volume: The NJL(2) model consideration. Int. J. Mod. Phys. A 2012, 27, 1250162. [Google Scholar] [CrossRef]
- Gubina, N.V.; Klimenko, K.G.; Kurbanov, S.G.; Zhukovsky, V.C. Inhomogeneous charged pion condensation phenomenon in the NJL2 model with quark number and isospin chemical potentials. Phys. Rev. D 2012, 86, 085011. [Google Scholar] [CrossRef]
- Khunjua, T.G.; Klimenko, K.G.; Zhokhov, R.N.; Zhukovsky, V.C. Inhomogeneous charged pion condensation in chiral asymmetric dense quark matter in the framework of NJL2 model. Phys. Rev. D 2017, 95, 105010. [Google Scholar] [CrossRef]
- Khunjua, T.G.; Klimenko, K.G.; Zhokhov-Larionov, R.N. Affinity of NJL2 and NJL4 model results on duality and pion condensation in chiral asymmetric dense quark matter. EPJ Web Conf. 2018, 191, 05016. [Google Scholar] [CrossRef]
- Khunjua, T.G.; Zhukovsky, V.C.; Klimenko, K.G.; Zhokhov, R.N. Duality and Charged Pion Condensation in Chirally Asymmetric Dense Quark Matter in the Framework of an NJL2 Model. Int. J. Mod. Phys. Conf. Ser. 2018, 47, 1860093. [Google Scholar] [CrossRef]
- Ebert, D.; Khunjua, T.G.; Klimenko, K.G. Duality between chiral symmetry breaking and charged pion condensation at large Nc: Consideration of an NJL2 model with baryon, isospin, and chiral isospin chemical potentials. Phys. Rev. D 2016, 94, 116016. [Google Scholar] [CrossRef]
- Khunjua, T.G.; Klimenko, K.G.; Zhokhov, R.N. Dense baryon matter with isospin and chiral imbalance in the framework of NJL4 model at large Nc: Duality between chiral symmetry breaking and charged pion condensation. Phys. Rev. D 2018, 97, 054036. [Google Scholar] [CrossRef]
- Khunjua, T.; Klimenko, K.; Zhokhov, R. Dense quark matter with chiral and isospin imbalance: NJL-model consideration. EPJ Web Conf. 2018, 191, 05015. [Google Scholar] [CrossRef]
- Khunjua, T.G.; Klimenko, K.G.; Zhokhov, R.N. Dualities in dense quark matter with isospin, chiral, and chiral isospin imbalance in the framework of the large-Nc limit of the NJL4 model. Phys. Rev. D 2018, 98, 054030. [Google Scholar] [CrossRef]
- Khunjua, T.G.; Klimenko, K.G.; Zhokhov, R.N. Chiral imbalanced hot and dense quark matter: NJL analysis at the physical point and comparison with lattice QCD. Eur. Phys. J. C 2019, 79, 151. [Google Scholar] [CrossRef]
- Fukushima, K.; Kharzeev, D.E.; Warringa, H.J. The Chiral Magnetic Effect. Phys. Rev. D 2008, 78, 074033. [Google Scholar] [CrossRef]
- Kharzeev, D.E.; McLerran, L.D.; Warringa, H.J. The Effects of topological charge change in heavy ion collisions: ‘Event by event P and CP violation’. Nucl. Phys. A 2008, 803, 227. [Google Scholar] [CrossRef]
- Li, Q.; Kharzeev, D.E.; Zhang, C.; Huang, Y.; Pletikosic, I.; Fedorov, A.V.; Zhong, R.D.; Schneeloch, J.A.; Gu, G.D.; Valla, T. Observation of the chiral magnetic effect in ZrTe5. Nat. Phys. 2016, 12, 550–554. [Google Scholar] [CrossRef]
- Braguta, V.V.; Katsnelson, M.I.; Kotov, A.Y.; Trunin, A.M. Catalysis of Dynamical Chiral Symmetry Breaking by Chiral Chemical Potential in Dirac semimetals. arXiv 2019, arXiv:1904.07003. [Google Scholar]
- Boyda, D.L.; Braguta, V.V.; Katsnelson, M.I.; Kotov, A.Y. Lattice Quantum Monte Carlo Study of Chiral Magnetic Effect in Dirac Semimetals. Ann. Phys. 2018, 396, 78–86. [Google Scholar] [CrossRef]
- Ebert, D.; Klimenko, K.G.; Zhukovsky, V.C.; Fedotov, A.M. Quark and pion condensation in a chromomagnetic background field. Eur. Phys. J. C 2007, 49, 709–719. [Google Scholar] [CrossRef]
- Barducci, A.; Casalbuoni, R.; Gatto, R.; Modugno, M.; Pettini, G. Thermodynamics of the massive Gross-Neveu model. Phys. Rev. D 1995, 51, 3042. [Google Scholar] [CrossRef]
- Gross, D.J.; Neveu, A. Dynamical symmetry breaking in asymptotically free field theories. Phys. Rev. D 1974, 10, 3235. [Google Scholar] [CrossRef]
- Ebert, D.; Klimenko, K.G. Pion condensation in the Gross-Neveu model with nonzero baryon and isospin chemical potentials. arXiv 2009, arXiv:0902.1861. [Google Scholar]
- Wolff, U. The phase diagram of the infinite-N Gross-Neveu model at finite temperature and chemical potential. Phys. Lett. B 1985, 157, 303. [Google Scholar] [CrossRef]
- Inagaki, T.; Kouno, T.; Muta, T. Phase Structure of Four-Fermion Theories at Finite Temperature and Chemical Potential in Arbitrary Dimensions. Int. J. Mod. Phys. A 1995, 10, 2241–2268. [Google Scholar] [CrossRef]
- Kanemura, S.; Sato, H.-T. Phase Diagram of Gross-Neveu Model at Finite Temperature, Density and Constant Curvature. Mod. Phys. Lett. A 1995, 10, 1777–1786. [Google Scholar] [CrossRef]
- Klimenko, K.G. Massive Gross-Neveu model in the leading order of the 1/N expansion. Allowance for the temperature and the chemical potential. Theor. Math. Phys. 1988, 75, 487–493. [Google Scholar] [CrossRef]
- Chodos, A.; Minakata, H.; Cooper, F.; Singh, A.; Mao, W. Two-dimensional model with chiral condensates and Cooper pairs having a QCD-like phase structure. Phys. Rev. D 2000, 61, 045011. [Google Scholar] [CrossRef]
- Ohwa, K. Crystalline ground state in chiral Gross-Neveu and Cooper pair models at finite densities. Phys. Rev. D 2002, 65, 085040. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 1966, 17, 1133. [Google Scholar] [CrossRef]
- Coleman, S. There are no Goldstone bosons in two dimensions. Commun. Math. Phys. 1973, 31, 259. [Google Scholar] [CrossRef]
- Schon, V.; Thies, M. 2d Model Field Theories at Finite Temperature and Density. Phys. Rev. D 2000, 62, 096002. [Google Scholar]
- Brzoska, A.; Thies, M. No first-order phase transition in the Gross-Neveu model? Phys. Rev. D 2002, 65, 125001. [Google Scholar] [CrossRef]
- Wang, Q.W.; Xia, Y.; Zong, H.S. Finite volume effects with stationary wave solution from Nambu–Jona-Lasinio model. arXiv 2018, arXiv:1802.00258. [Google Scholar]
- Wang, Q.W.; Xia, Y.; Zong, H.S. Nambu-Jona-Lasinio model with proper time regularization in a finite volume. Mod. Phys. Lett. A 2018, 33, 1850232. [Google Scholar] [CrossRef]
- Palhares, L.F.; Fraga, E.S.; Kodama, T. Chiral transition in a finite system and possible use of finite size scaling in relativistic heavy ion collisions. J. Phys. G 2011, 38, 085101. [Google Scholar] [CrossRef]
- Xu, K.; Huang, M. Quantized first-order phase transition and two sets of critical end point in droplet quark matter. arXiv 2019, arXiv:1904.01154. [Google Scholar]
- Xu, K.; Huang, M. Zero-mode contribution and quantized first order phase transition in a droplet quark matter. arXiv 2019, arXiv:1903.08416. [Google Scholar]
- Inagaki, T.; Matsuo, Y.; Shimoji, H. Four-Fermion Interaction Model on MD−1⊗S1. Symmetry 2019, 11, 451. [Google Scholar] [CrossRef]
- Inagaki, T.; Muta, T.; Odintsov, S.D. Dynamical symmetry breaking in curved space-time: Four fermion interactions. Prog. Theor. Phys. Suppl. 1997, 127, 93–193. [Google Scholar] [CrossRef]
- Malbouisson, A.P.C.; Malbouisson, J.M.C.; Pereira, R.C. Boundary effects on the mass and coupling constant in the compactified Ginzburg–Landau model: The boundary dependent critical temperature. J. Math. Phys. 2009, 50, 083304. [Google Scholar] [CrossRef]
- Abreu, L.M.; Khanna, F.C.; Malbouisson, A.P.; Malbouisson, J.M.; Santana, A.E. Finite-size effects on the phase transition in a four- and six-fermion interaction model. Phys. Lett. A 2014, 378, 2597–2602. [Google Scholar] [CrossRef]
- Corrêa, E.B.; Linhares, C.A.; Malbouisson, A.P.; Malbouisson, J.M.; Santana, A.E. Finite-size, chemical-potential and magnetic effects on the phase transition in a four-fermion interacting model. Eur. Phys. J. C 2017, 77, 261. [Google Scholar] [CrossRef]
- Khanna, F.C. Thermal Quantum Field Theory—Algebraic Aspects and Applications; World Scientific: Hackensack, NJ, USA, 2009. [Google Scholar]
- Khanna, F.C.; Malbouisson, A.P.; Malbouisson, J.M.; Santana, A.E. Quantum field theory on toroidal topology: Algebraic structure and applications. Phys. Rept. 2014, 539, 135–224. [Google Scholar] [CrossRef]
- Kiriyama, O. Colour-superconducting strangelets in the Nambu-Jona-Lasinio model. Phys. Rev. D 2005, 72, 054009. [Google Scholar] [CrossRef]
- Kiriyama, O.; Hosaka, A. Chiral phase properties of finite size quark droplets in the Nambu-Jona-Lasinio model. Phys. Rev. D 2003, 67, 085010. [Google Scholar] [CrossRef]
- Grunfeld, A.G.; Lugones, G. Finite size effects in strongly interacting matter at zero chemical potential from Polyakov loop Nambu-Jona-Lasinio model in the light of lattice data. Eur. Phys. J. C 2018, 78, 640. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Ray, R.; Sur, S. Fluctuation of strongly interacting matter in the Polyakov–Nambu–Jona-Lasinio model in a finite volume. Phys. Rev. D 2015, 91, 051501. [Google Scholar] [CrossRef]
- Colangelo, G. Finite volume effects in chiral perturbation theory. Nucl. Phys. Proc. Suppl. 2005, 140, 120–126. [Google Scholar] [CrossRef]
- Sachrajda, C.T.; Villadoro, G. Twisted boundary conditions in lattice simulations. Phys. Lett. B 2005, 609, 73–85. [Google Scholar] [CrossRef]
- Bijnens, J.; Relefors, J. Chiral Perturbation Theory at Finite Volume and/or with Twisted Boundary Conditions. arXiv 2016, arXiv:1611.06068. [Google Scholar] [CrossRef]
- Samanta, S.; Ghosh, S.; Mohanty, B. Finite size effect of hadronic matter on its transport coefficients. J. Phys. G 2018, 45, 075101. [Google Scholar] [CrossRef]
- Sarkar, N.; Deb, P.; Ghosh, P. Incomplete equilibration in high-multiplicity pp and pPb events at LHC. arXiv 2019, arXiv:1905.06532. [Google Scholar]
- Abreu, L.M.; Nery, E.S. Finite-size effects on the phase structure of the Walecka model. Phys. Rev. C 2017, 96, 055204. [Google Scholar] [CrossRef]
- Ishikawa, T.; Nakayama, K.; Suzuki, K. Casimir effect for nucleon parity doublets. Phys. Rev. D 2019, 99, 054010. [Google Scholar] [CrossRef]
- De, J.N.; Agrawal, B.K.; Samaddar, S.K. Equation of state of finite nuclei and liquid gas phase transition. Phys. Rev. C 1999, 59, 1. [Google Scholar] [CrossRef]
- Moretto, L.G.; Bugaev, K.A.; Elliott, J.B.; Ghetti, R.; Helgesson, J.; Phair, L. The Complement: A Solution to liquid drop finite size effects in phase transitions. Phys. Rev. Lett. 2005, 94, 202701. [Google Scholar] [CrossRef] [PubMed]
- Lombardo, M.P. Lattice QCD at finite density: Imaginary chemical potential. PoS CPOD 2006, 2006, 003. [Google Scholar] [CrossRef]
- Kashiwa, K. Imaginary Chemical Potential, NJL-Type Model and Confinement–Deconfinement Transition. Symmetry 2019, 11, 562. [Google Scholar] [CrossRef]
- Ebert, D.; Klimenko, K.G. Cooper pairing and finite-size effects in a NJL-type four-fermion model. Phys. Rev. D 2010, 82, 025018. [Google Scholar] [CrossRef]
- Andrianov, A.A.; Espriu, D.; Planells, X. An effective QCD Lagrangian in the presence of an axial chemical potential. Eur. Phys. J. C 2013, 73, 2294. [Google Scholar] [CrossRef]
- Andrianov, A.A.; Espriu, D.; Planells, X. Chemical potentials and parity breaking: the Nambu–Jona-Lasinio model. Eur. Phys. J. C 2014, 74, 2776. [Google Scholar] [CrossRef]
- Gatto, R.; Ruggieri, M. Hot Quark Matter with an Axial Chemical Potential. Phys. Rev. D 2012, 85, 054013. [Google Scholar] [CrossRef]
- Yu, L.; Liu, H.; Huang, M. Spontaneous generation of local CP violation and inverse magnetic catalysis. Phys. Rev. D 2014, 90, 074009. [Google Scholar] [CrossRef]
- Yu, L.; Liu, H.; Huang, M. Effect of the chiral chemical potential on the chiral phase transition in the NJL model with different regularization schemes. Phys. Rev. D 2016, 94, 014026. [Google Scholar] [CrossRef]
- Braguta, V.V.; Kotov, A.Y. Catalysis of Dynamical Chiral Symmetry Breaking by Chiral Chemical Potential. Phys. Rev. D 2016, 93, 105025. [Google Scholar] [CrossRef]
- Cao, G.; Zhuang, P. Effects of chiral imbalance and magnetic field on pion superfluidity and color superconductivity. Phys. Rev. D 2015, 92, 105030. [Google Scholar] [CrossRef]
- Khunjua, T.G.; Klimenko, K.G.; Zhokhov, R.N. Dualities and inhomogeneous phases in dense quark matter with chiral and isospin imbalances in framework of effective model. arXiv 2019, arXiv:1901.02855 [hep-ph]. JHEP 06 (2019) 006. [Google Scholar]
- Ruggieri, M.; Peng, G.X. Critical Temperature of Chiral Symmetry Restoration for Quark Matter with a Chiral Chemical Potential. J. Phys. G 2016, 43, 125101. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).