Generalized Scheme Based on Octagon-Shaped Shell for Data Hiding in Steganographic Applications

Abstract

The exploiting modification direction scheme is a well-known data hiding method because of its high payload and low distortion. Its most criticized drawback is that the secret data must be converted to a non-binary numeral system before the embedding procedure. To overcome this drawback, one study proposed a turtle shell-based scheme for data hiding, in which a reference matrix was constructed based on a hexagon-shaped shell to embed three secret bits into each pixel group of a pair of pixels of the cover image. In a subsequent work, the embedding capacity was increased by using an octagon-shaped shell instead of a hexagon-shaped shell in the reference matrix. The above scheme was extended by utilizing a regular octagon-shaped shell in the reference matrix to reduce the distortion of the worst case. In another approach, the payload of the octagon-shaped-shell-based data hiding scheme was maximized by searching for the appropriate width and height of the octagon. In this study, we generalize the data hiding scheme based on an octagon-shaped shell so that the above-mentioned four schemes can be regarded as specific cases of the proposed method.

1. Introduction

The popularity of computers and rapid growth of the internet makes digital data widely used all over the world. It is very convenient to easily share enormous multimedia data through ubiquitous channels. However, it also raises concerns regarding threats to consumers’ personal privacy. Traditionally, Cryptology has been used as a reliable and safe method of transmission. However, the encrypted data may evoke suspicion from eavesdroppers. Data hiding techniques were invented to overcome this drawback by imperceptibly embedding secret data into a cover media (text, image, audio, or video) and satisfies the imperceptibility requirement. Once a cover media embeds the secret data, it becomes a stego-media. In this study, we use a grayscale image as the cover media. Data hiding can be broadly classified into two categories: reversible and irreversible. In some applications, such as military, medical, and astronomical imagery, besides the requirement of a high embedding capacity and visual quality of the stego-image, recovering a cover image without any distortion is also necessary. Reversible data hiding can restore the cover image after extracting the secret data from the stego-image, whereas irreversible data hiding cannot. However, irreversible data hiding is well-known because of its high payload and easy implementation.

The least significant bit (LSB) substitution scheme is a prominent irreversible data hiding scheme; it directly substitutes n secret bits into n LSBs of each pixel of the cover image. It achieves a high payload and a stego-image of good visual quality [1]. Two important strategies are applied to the LSB scheme for improving the visual quality of the stego-image: the optimal pixel adjustment process (OPAP) proposed by Chan and Cheng [2] and the modulus function proposed by Thien and Lin [3]. To overcome the asymmetry of an LSB, Li et al. proposed the LSB matching scheme (LSBM) [4]. Mielikainen proposed the LSB matching revisited scheme, in which one is added or subtracted from a pixel pair of two consecutive secret bits [5]. However, the embedded secret data by the LSB scheme can be detected by RS-steganalysis [6].

To increase the resistance to steganalysis, Zhang and Wang proposed the exploiting modification direction (EMD) scheme [7]. The EMD scheme uses n pixels as a group to embed one secret digit in a (2n + 1)-ary numeral system, and it defines an extraction function to construct a hypercube as a reference to modify the cover pixels. In the EMD scheme, a maximum of one pixel in the group is increased or decreased by 1; therefore, it has a low distortion.

For example, when n = 2 and the extraction function is defined as f(x₁,x₂) = (1 × x₁ + 2 × x₂) mod 5, we can construct a hypercube as shown in Figure 1. Suppose (x₁,x₂) = (3,2) is a pixel pair of the cover image. If the to-be-embedded 5-ary secret digit is 0, 1, 2, 3, or 4, then we choose stego-pixels (3,1), (2,2), (3,2), (4,2), or (3,3), respectively.

There are two weaknesses to the EMD scheme. One is the limitation of the payload. To increase the payload, many researchers use two pixels as a group and define different extraction functions for the embedding and extraction procedures [8,9,10,11,12,13]. Chao et al. employed a diamond-shaped shell to embed a (2k² + 2k + 1)-ary numeral system secret digit and increased the payload up to 2.68 bpp (k = 4) [8]. Kim et al. proposed the 2-EMD and EMD-2 schemes based on a log₂ (2 (5n − 7) + 1)-ary numeral system secret digit and achieved a maximum payload of log₂ (10) bpp (about 3.22 bpp) [9]. Kieu and Chang improved the EMD scheme by using eight modification directions on a square-shaped shell of size s × s and attained a maximum payload of up to 4.5 bpp (s = 23) [10]. Kim used a codebook to embed a (2^n+x − 1)-ary numeral system secret digit and achieved a maximum payload of up to 2.48 bpp [11]. Liu et al. extended the EMD scheme to realize a payload of 2.5 bpp [12]. Leng and Tseng extended the EMD scheme on a three-dimensional (3D)-hypercube sized w × w × w and generalized the EMD scheme on an n-dimensional hypercube with a maximum payload of up to 4.75 bpp (w = 27) [13].

Another shortcoming of the EMD scheme is that the secret data must be converted to a non-binary numeral system. To overcome this issue, Chang et al. proposed a novel turtle-based data hiding scheme. In this, a reference matrix is constructed based on a hexagon-shaped shell to embed three secret bits in each pixel pair of the cover image [14]. It achieved a payload of 1.5 bpp with a high visual quality of the stego-image (about 49.42 dB). Kurup et al. proposed a data hiding scheme based on an octagon-shaped shell to embed four secret bits in the cover pixel pairs and achieved a payload of 2 bpp [15]. Subsequently, Leng improved the scheme of Kurup et al. by using a regular octagon-shaped shell to embed five secret bits in the cover pixel pairs and realized a payload of 2.5 bpp [16]. In addition, this scheme has the best combination of a high payload and low distortion. Leng and Tseng extended the scheme of Leng to maximize the payload of the octagon-shaped-shell-based data hiding scheme and achieved a payload of 3.5 bpp with a stego-image of a good visual quality (about 30.61 dB) [17].

In this study, we consider the size of an octagon-shaped shell. The proposed method generalizes the data hiding scheme based on an octagon-shaped shell in the reference matrix. Therefore, the schemes of Kurup, Leng, and Leng and Tseng can be regarded as specific cases of the proposed method.

The remainder of this paper is organized as follows. Section 2 reviews the schemes of Chang et al., Kurup et al., and Leng. Section 3 describes the proposed method. The experimental results are given in Section 4. Finally, Section 5 draws the conclusions.

2. Related Works

In this section, the schemes of Chang et al., Kurup et al., and Leng are introduced briefly. According to the scheme of Chang et al., a reference-matrix-based data hiding scheme is used in the embedding and extraction procedure. First, a reference matrix with a size of 256 × 256 is constructed for the grayscale cover image in the embedding and extraction procedure. Then, the cover image is divided into pixel pairs of two neighbor pixels. For each pixel pair (x₁,x₂), the location of M (x₁,x₂) determines the to-be-embedded secret digits. To embed the secret digit, s, into the pixel pair, (x₁,x₂), the pixel pair is first located in the reference matrix, M, as M (x₁,x₂), and the element, M (x₁′,x₂′), which has the shortest distance with M (x₁,x₂) and M (x₁′,x₂′) = s, is searched. Subsequently, the original pixel pair, (x₁,x₂), is modified to (x₁′,x₂′). In the extraction procedure, the secret digit is extracted correctly from the stego pixel pair that is mapped to the element, M(x₁′,x₂′), in the reference matrix, M.

2.1. Scheme of Chang et al.

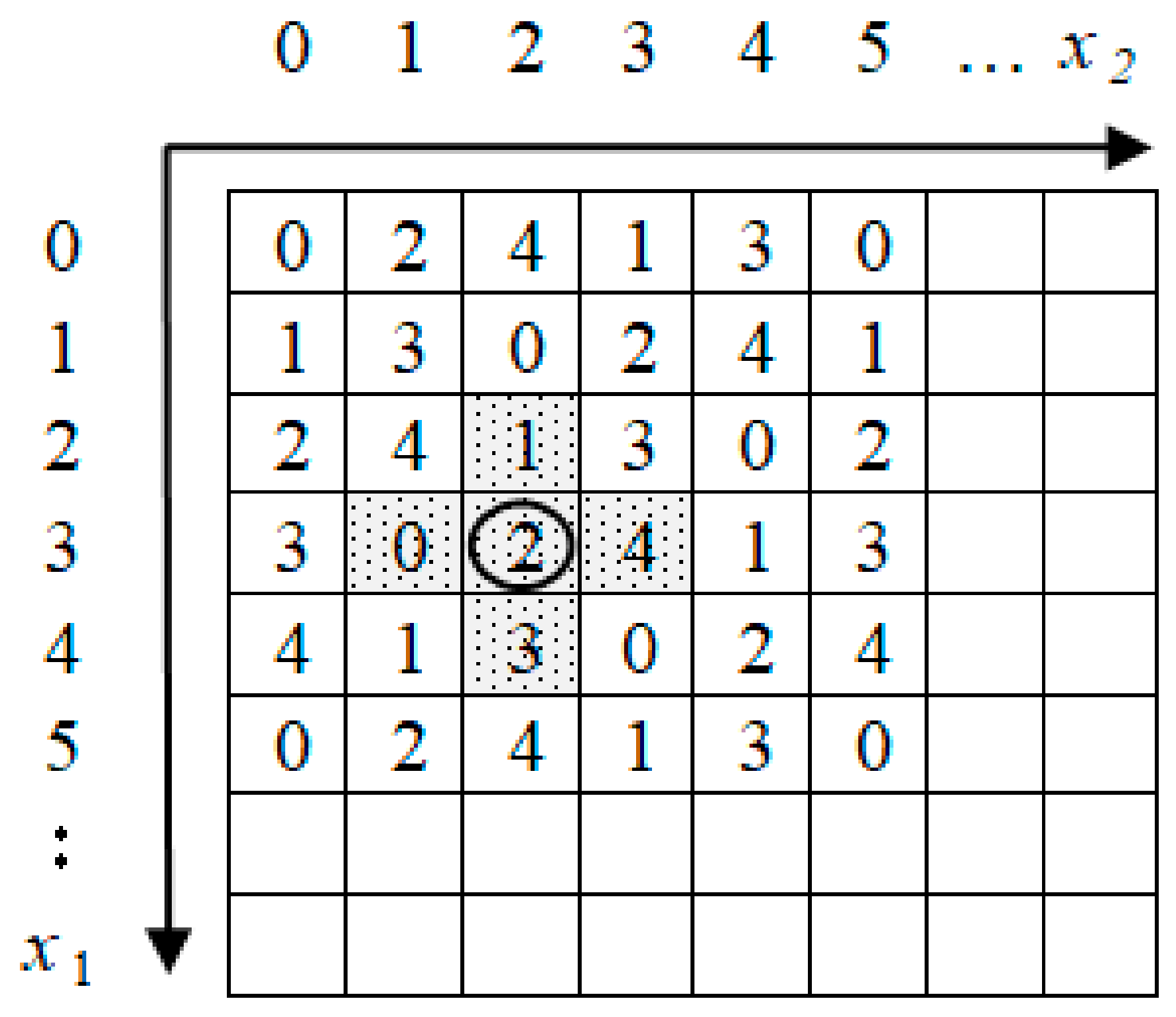
In the scheme of Chang et al., the reference matrix is composed of numerous contiguous hexagons called turtle shells, where each hexagon contains eight different digits ranging from 0 to 7, which include two back digits and six edge digits. For each pixel pair, the scheme of Chang et al. embeds three secret bits. The construction of the reference matrix is based on two rules. The value difference between two adjacent columns in the same row is set as 1, and the value between two adjacent rows in the same column is set alternately as +2 and +3. Figure 2 illustrates an example of a reference matrix, M, based on hexagon-shaped shells.

For example, a cover pixel pair, (3,4), and the to-be-embedded secret bits are (111)₂ = 7. The cover pixel pair, (3,4), is mapped to M (3,4) = 3 in the reference matrix, M. Then, the candidate stego pixel pairs, M (1,5) = 7, M (2,2) = 7, M (4,5) = 7, and M (5,3) = 7, choose (4,5) as the stego pixel pair to ensure the lowest distortion. In the extraction procedure, if M (4,5) = 7 = (111)₂; then, the secret digits are extracted correctly.

The scheme of Chang et al. makes an important contribution in that it overcomes the drawback of the tradition EMD scheme of converting the secret data into a non-binary numeral system before the embedding and extraction. The construction of the reference matrix has become a new topic in data hiding.

2.2. Scheme of Kurup et al.

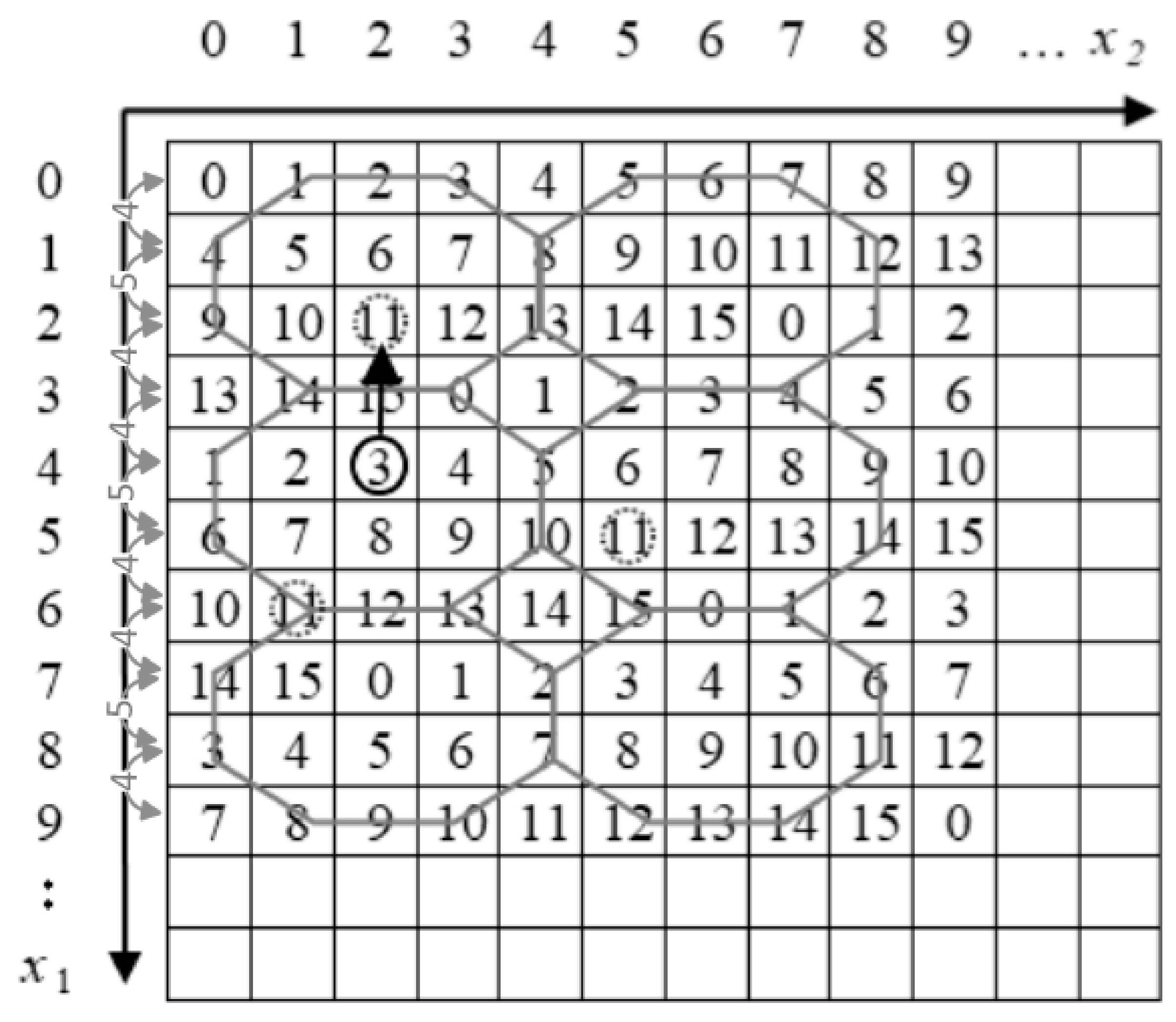
In the scheme of Kurup et al., the reference matrix is constructed based on the concept of octagon shells. The octagon-shaped shells contain 16 different digits ranging from 0 to 15, including six back digits and ten edge digits. For each pixel pair, the scheme of Kurup et al. embeds four secret bits. The construction of the reference matrix is based on two rules. The value difference between two adjacent columns in the same row is set as 1, and the value between two adjacent rows in the same column is set alternately as +4, +5, and +4. Figure 3 illustrates an example of a reference matrix, M, based on octagon-shaped shells.

For example, a cover pixel pair (4,2) and the to-be-embedded secret bits are (1011)₂ = 11. The cover pixel pair, (4,2), is mapped to M (4,2) = 3 in the reference matrix, M. Then, the candidate stego pixel pairs are M (2,2) = 11, M (5,5) = 11, and M (6,1) = 11, and (2,2) is selected as the stego pixel pair to ensure the lowest distortion. In the extraction procedure, if M (2,2) = 11 = (1011)₂, then the secret digit can be extracted correctly.

It is trivial that based on the reference matrix, the schemes of Chang et al. and Kurup et al. have the same embedding and extraction procedure; the only difference is in the method to construct the reference matrix for the trade-off between the payload and visual quality of the stego-image.

2.3. Scheme of Leng

In the scheme of Kurup et al., if the octagon-shaped shell is not regular, then the worst case will decrease the distortion. The scheme of Leng summarizes this problem as Equation (1),

n² − 4 = 2^k

(1)

where n is the octagon size, k is a positive integer, and $1\le k\le 8$.

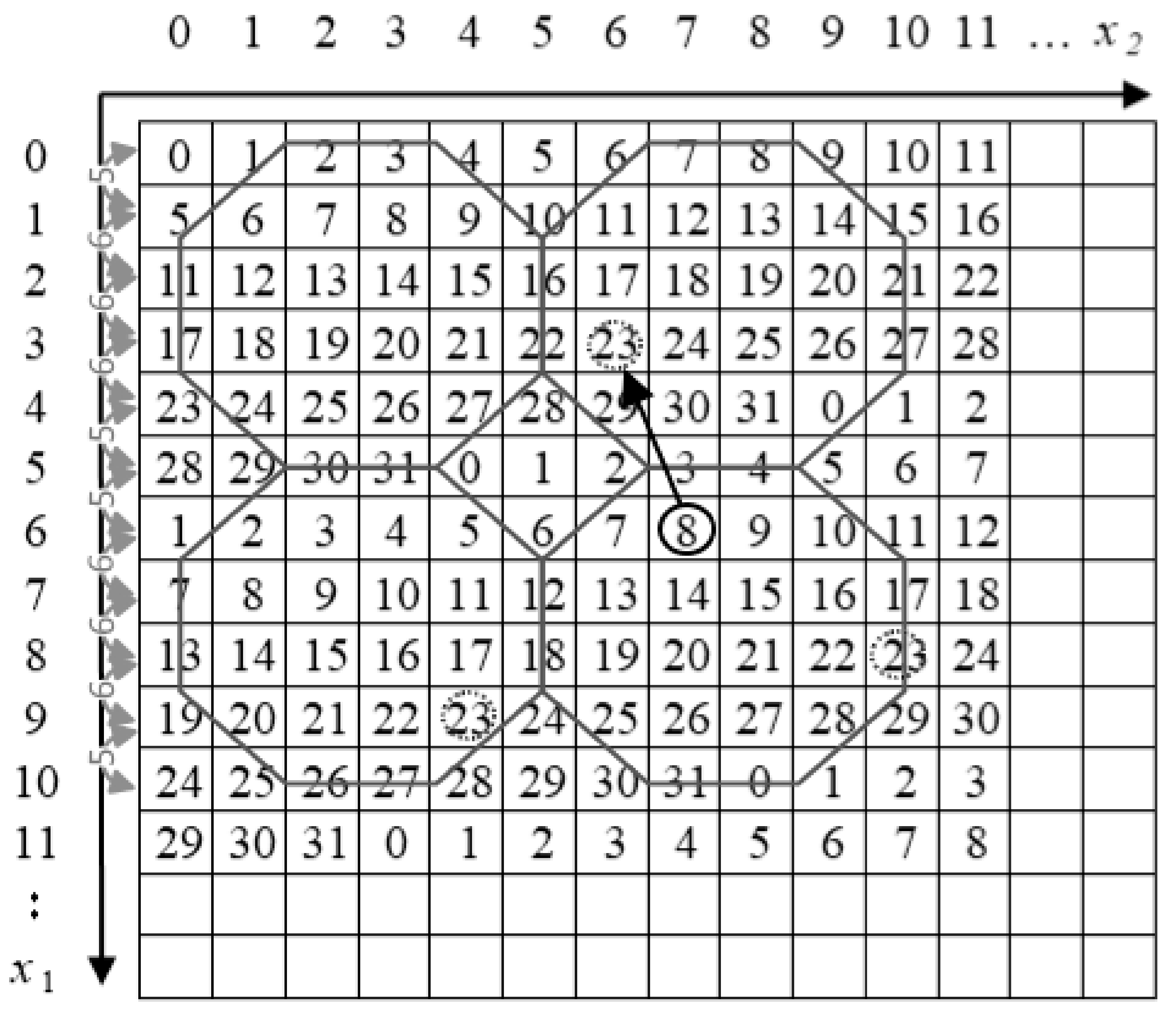
In the scheme of Leng, the reference matrix is constructed based on the concept of regular octagon shells. It denotes n = 6 and k = 5 and then constructs a regular octagon-shaped shell reference matrix. For each pixel pair, the scheme of Leng embeds five secret bits. The construction of the reference matrix is based on two rules. The value difference between two adjacent columns in the same row is set as 1, and the value between two adjacent rows in the same column is set alternately as +5, +6, +6, +6, and +5. Figure 4 illustrates an example of reference matrix M, based on regular octagon-shaped shells.

For example, a cover pixel pair is (6,7) and the to-be-embedded secret bits are (10111)₂ = 23. The cover pixel pair, (6,7), is mapped to M (6,7) = 8 in the reference matrix, M. Then, the candidate stego pixel pairs are M (3,6) = 23, M(6,10) = 23, and M (9,4) = 23, and (3,6) is selected as the stego pixel pair to ensure the lowest distortion. In the extraction procedure, if M (3,6) = 23 = (10111)₂, then the secret digits can be extracted correctly.

The scheme of Leng constructs reference-matrix-based data hiding with the best balance between the payload and visual quality of the stego-image.

3. The Proposed Method

In the section, we generalize the data hiding scheme based on octagon-shaped shells. We improve Equation (1) as Equation (2),

$$m·n-4·\frac{k\left(k+1\right)}{2}=2^w$$

(2)

where m and n are the width and height of an octagon ($\mathrm{m}\le \mathrm{n}$), respectively, k is the width and height of the corner of the octagon ($k\le \lfloor \raisebox{1ex}{$m$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\rfloor$), respectively, and w is a positive integer ($1\le w\le 8$).

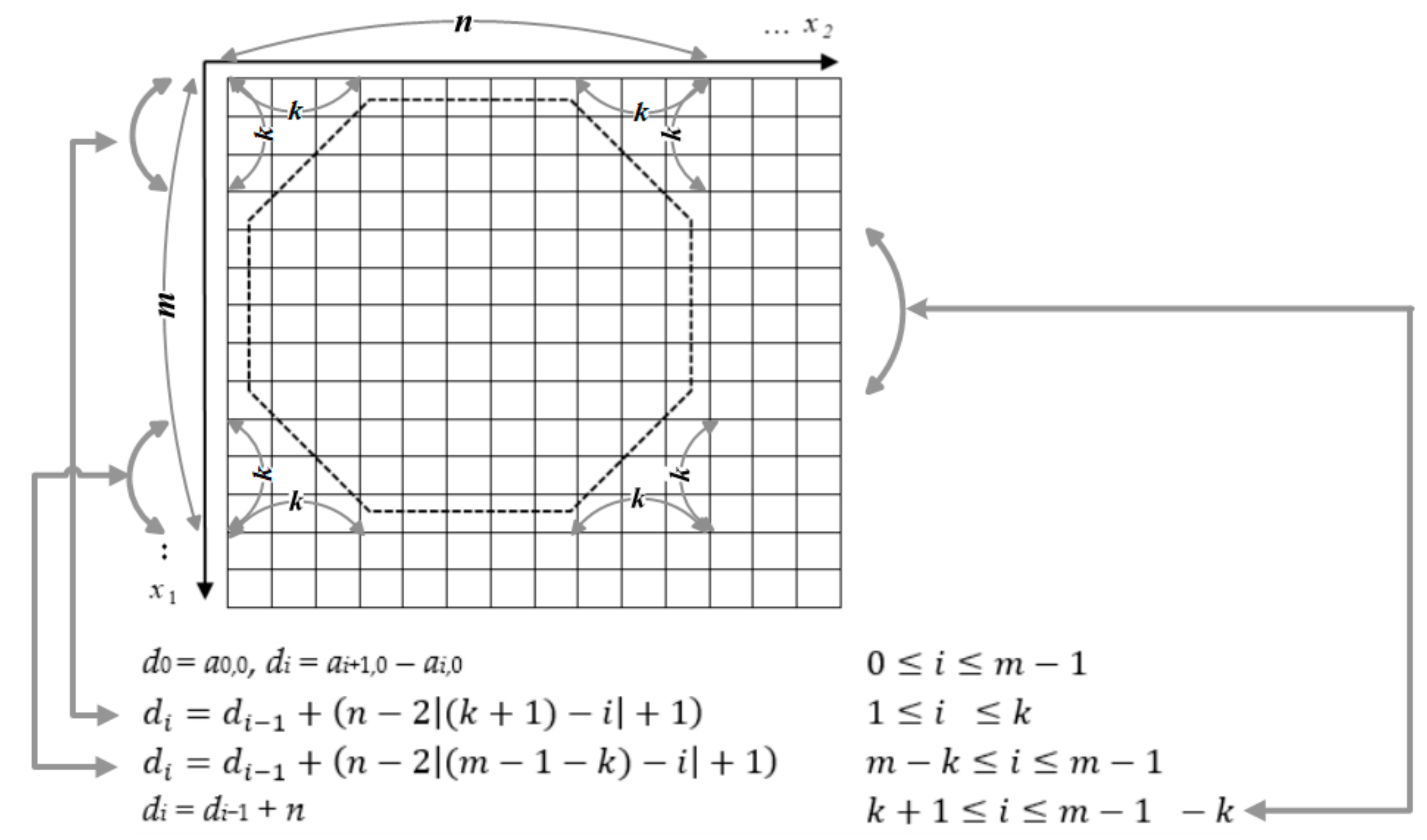
In addition, we demand that this octagon-shaped shell contains 2^w different digits ranging from 0 to 2^w − 1 digits. Then, for each pixel pair, the proposed method embeds w secret bits. The construction of reference matrix M, sized 256 × 256, is based on the following three rules. Let M = (a_i,j)_256×256; then, element a_0,0 can choose any number from the range [0,2^w−1] and serve as a key. The value difference between two adjacent columns in the same row is set as 1, and the value between the two adjacent rows is set alternately as d₀, d₁, d₂, …, d_m−1, where d_i is defined as follows:

d0 = a0,0, di = ai+1,0 − ai,0	$0\le i\le m-1$
$d_i=d_{i-1}+\left(n-2\left|\left(k+1\right)-i\right|+1\right)$	$1\le i\le k$
$d_i=d_{i-1}+\left(n-2\left|\left(m-1-k\right)-i\right|+1\right)$	$m-k\le i\le m-1$
di = di−1 + n	$k+1\le i\le m-1-k$

Figure 5 illustrates an example of the reference matrix, M, of the proposed method.

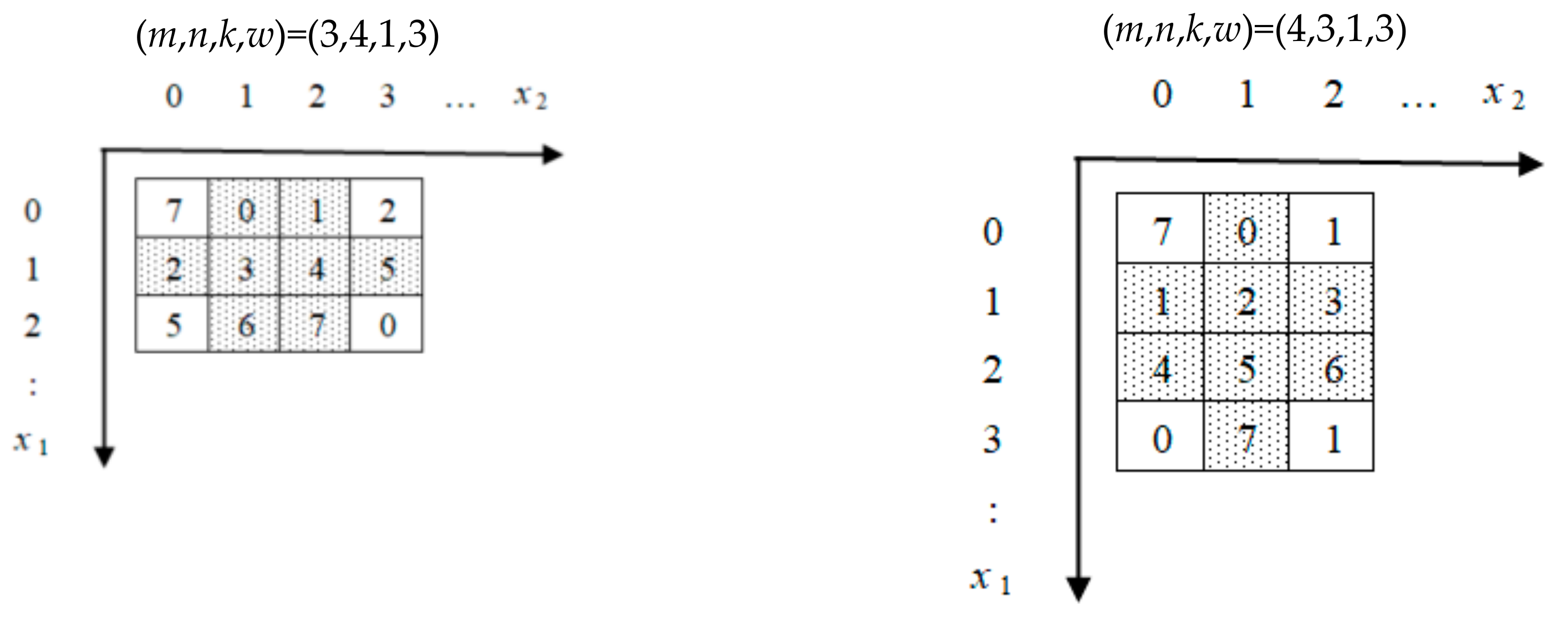
Notice that we suppose $m\le n$; if m > n, then the reference matrix is different but the payload and quality of the stego-image are the same. For example, (m,n,k,w) = (3,4,1,3) and (m,n,k,w) = (4,3,1,3) are illustrated in Figure 6.

Based on Figure 5, we obtain all the solutions of Equation (2). There are 29 solutions: 14 solutions for k = 1, three solutions for k = 2, seven solutions for k = 3, one solution for k = 4, one solution for k = 6, two solutions for k = 7, and one solution for k = 8.

The distortion of a stego-image is determined by the longest distance of the reference matrix. In the embedding procedure, for each cover pixel pair (x₁,x₂), if the to-be-embedded secret digits are s, then the element M (x₁′,x₂′), which has the shortest distance with M (x₁,x₂) and M (x₁′,x₂′) = s, is searched. In the extraction procedure, the secret digit is extracted correctly from the stego pixel pair, which is mapped to the element, M (x₁′,x₂′), in the reference matrix, M.

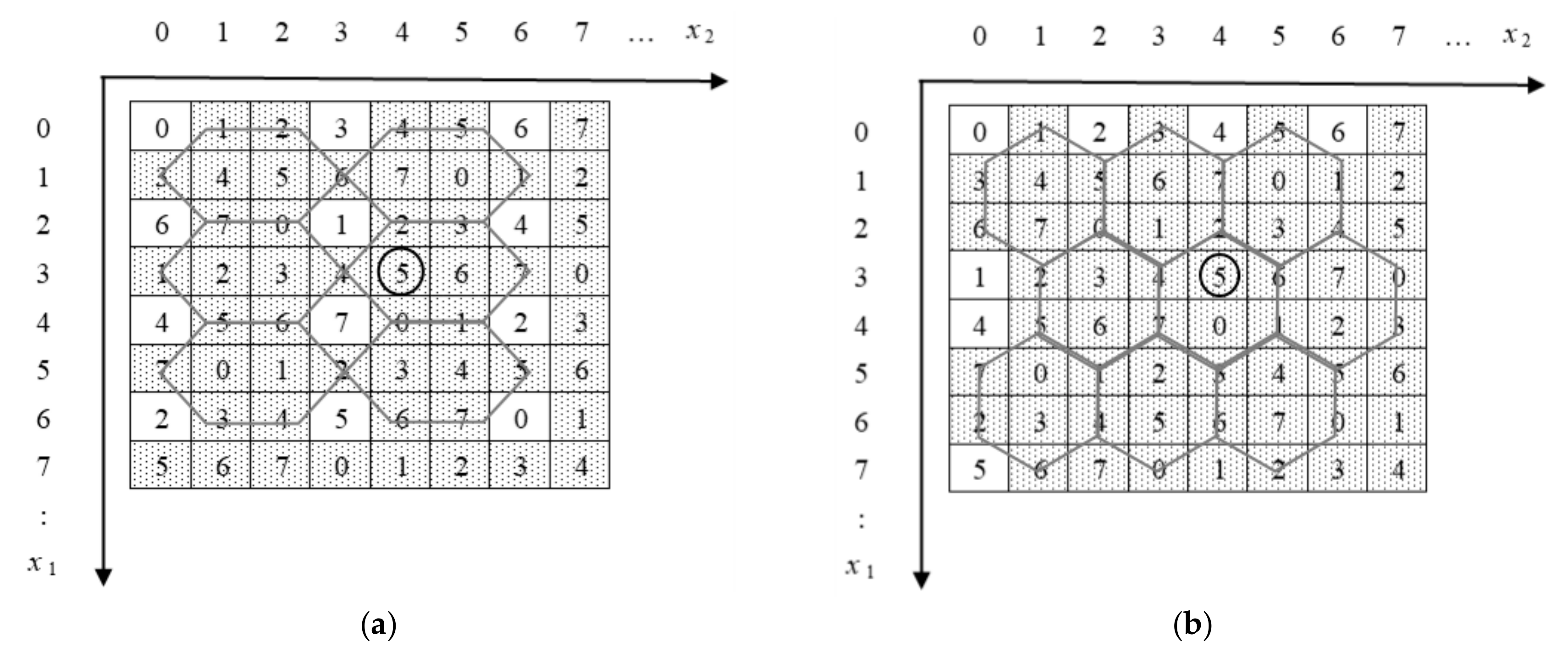
From

Table 1. All the solutions of the proposed method.

	k = 1	k = 2	k = 3	k = 4	k = 6	k = 7	k = 8
(m,n,w)	(3,4,3)1, (3,12,5), (3,44,7), (4,5,4)2, (4,9,5), (4,17,6), (4,33,7), (4,65,8), (5,52,8), (6,6,5)3, (6,22,7), (10,26,8), (11,12,7)4, (13,20,8)	(5,28,7), (7,20,7), (10,14,7)	(7,8,5), (7,40,8), (8,11,6), (8,19,7), (8,35,8), (10,28,8), (14,20,8)	(12,14,7)	(17,20,8)	(15,16,7), (16,23,8)	(20,20,8)
solutions	14	3	7	1	1	2	1

¹ Scheme of Chang et al. is the case of (m,n,k,w) = (3,4,1,3). ² Scheme of Kurup et al. is the case of (m,n,k,w) = (4,5,1,4). ³ Scheme of Leng is the case of (m,n,k,w) = (6,6,1,5). ⁴ Scheme of Leng and Tseng is the case of (m,n,k,w) = (11,12,1,7).

, we denote (m,n,k,w) = (3,4,1,3), and in Figure 7b, we reconstruct the reference matrix by hexagon-shaped shells to compare with the scheme of Chang et al. (Figure 2). This achieves the same payload and visual quality of the stego-image of the scheme of Chang et al. In addition, the scheme of Kurup et al. is the case of (m,n,k,w) = (6,6,1,5), the scheme of Leng scheme is the case of (m,n,k,w) = (6,6,1,5), and that of Leng and Tseng is the case of (m,n,k,w) = (11,12,1,7).

4. Results and Discussion

In the experiment, six 512 × 512 grayscale images: Tiffany, Baboon, Lena, Jet, Scene, and Peppers, were chosen from the SIPI image database; they are adopted as the cover image and illustrated in Figure 8. Random secret bits are used in the following experiments.

The performance of the stego-image is measured by the peak signal to noise ratio (PSNR). The PSNR and mean square error (MSE) are defined as follows:

$$PSNR=10\times lo{g}_{10}\frac{{255}^2}{MSE}$$

(3)

$$MSE=\frac{1}{M\times N}{\displaystyle \sum _{i=1}^M\sum _{j=1}^N}{\left(x_{i,j}-{x_{i,j}}^{\prime }\right)}^2$$

(4)

where M and N are the length and width of the cover image, respectively, x_i,j and x_i,j′ are the pixel values of the cover image and stego-image, respectively.

Table 2. Performance of the proposed method.

(m,n,k)	w = 3	(m,n,k)	w = 4	(m,n,k)	w = 5	(m,n,k)	w = 6	(m,n,k)	w = 7	(m,n,k)	w = 8
(3,4,1)	49.74	(4,5,4)	46.82	(3,12,1)	41.34	(4,17,1)	37.95	(3,44,1)	$\underset{=}{29.05}$	(4,65,1)	$\underset{=}{25.05}$
				(4,9,1)	43.14	(8,11,3)	40.71	(4,33,1)	31.83	(5,52,1)	$\underset{=}{27.28}$
				(6,6,1)	43.94			(6,22,1)	35.17	(10,26,1)	33.05
				(7,8,3)	43.31			(11,12,1)	37.83	(13,20,1)	34.40
								(5,28,2)	34.02	(7,40,3)	30.79
								(7,20,2)	36.49	(8,35,3)	31.96
								(10,14,2)	37.77	(10,28,3)	33.45
								(8,19,3)	37.23	(14,20,3)	34.70
								(12,14,4)	37.61	(17,20,6)	34.51
								(15,16,7)	36.49	(16,23,7)	34.53
										(20,20,8)	33.79

present the PSNR values of the proposed method as a function of the payloads (w = 3, 4, 5, 6, 7, and 8).

When w = 3, the payload is 1.5 bpp, and there is only one case. Compared to the scheme of Chang et al. (49.42 dB), the proposed method provides a better image quality (49.74 dB) with the same payload (1.5 bpp), because the octagon-shaped shells can better complete coverage the reference matrix. When w = 4, the payload is 2 bpp, and there is only one case. The case (m,n,k) = (4,5,4) is the same as the scheme of Kurup et al. When w = 5, the payload is 2.5 bpp and there are four cases. The case (m,n,k) = (6,6,1) is the same as that of the scheme of Leng. It has the highest image quality because its m value is closer to the n value, i.e., the octagon-shaped shell is closer to the circle shape so that it causes less distortion. When w = 6, the payload is 3 bpp, and there are two cases. For the same reason as described above, the case (m,n,k) = (8,11,3) has a better image quality than the case (m,n,k) = (4,17,1). When w = 7, the payload is 3.5 bpp, and there are ten cases. The case (m,n,k) = (11,12,1) is the same as that of the scheme of Leng and Tseng. In the case (m,n,k) = (3,44,1), the m value is extremely far from the n value, such that it causes a large distortion. In addition, if the pixel pair M (x₁,x₂) is located in the border area of the reference matrix, it causes a large distortion when it searches the element, M (x₁′,x₂′) = s. When w = 8, the payload is 4 bpp and there are eleven cases. Similarly, the cases (m,n,k) = (4,65,1) and (m,n,k) = (5,52,1) are two poor cases. However, the case (m,n,k) = (14,20,3) achieves a high payload (4 bpp) with a good visual stego-image quality (34.70 dB).

The proposed method improves Equation (1) as Equation (2) and generalizes the data hiding scheme based on an octagon-shaped shells. The reason why the proposed method achieves better performance is because the octagon-shaped shells can better complete coverage of the reference matrix. Table 2 shows that the proposed method can provide various hiding capacities (i.e., parameter (m,n,k)) with good and acceptable visual qualities to satisfy different requirements of users.

5. Conclusions

In this study, the proposed method is based on the concept of using a reference matrix. The proposed method also improves the scheme of Leng to generalize the data hiding scheme based on octagon-shaped shells. Therefore, the schemes of Chang et al., Kurup et al., Leng, and Leng and Tseng can be regarded as specific cases of the proposed method. The payload and image quality depend on the width and height of both the octagon and the corner of the octagon. If the value m is close to the value n then the octagon-shaped shell is close to a circle shape and will cause less distortion. Contrastingly, if the pixel pair M(x₁,x₂) is located in the border area of the reference matrix, it causes a large distortion when it searches the element M(x₁′,x₂′) = s. In the future, we plan to improve Equation (2) so that the number of digits contains in an octagon-shape shells is m × n instead of 2^w.