Discrete Orthogonality of Bivariate Polynomials of A2, C2 and G2
Abstract
1. Introduction
2. Weyl Groups and Corresponding Domains
2.1. Roots, Coroots, Weights, Coweights
- the basis of simple roots , ,
- the basis of coroots , ,
- the basis of the fundamental weights , ,
- the basis of coweights , .
2.2. Weyl Group and Affine Weyl Group
2.3. Dual Affine Weyl Group
3. Orbit Functions and Corresponding Characters
3.1. Orbit Functions and Characters of Two Variables
3.2. Orbit Functions of
3.3. Orbit Functions of
3.4. Orbit Functions of
3.5. Discrete Orthogonality of Orbit Functions
4. Orthogonal Polynomials
4.1. Four Types of Orthogonal Polynomials of Two Variables
4.2. Orthogonal Polynomials of
4.2.1. Recurrence Relations for polynomials of .
4.2.2. Recurrence Relations for polynomials of .
4.3. Orthogonal Polynomials of
4.3.1. Recurrence Relations for polynomials of .
4.3.2. Recurrence Relations for polynomials of .
4.3.3. Recurrence Relations for polynomials of .
4.3.4. Recurrence Relations for polynomials of .
4.4. Orthogonal Polynomials of
4.4.1. Recurrence Relations for polynomials of .
4.4.2. Recurrence Relations for polynomials of .
4.4.3. Recurrence Relations for polynomials of .
4.4.4. Recurrence Relations for polynomials of .
5. Discrete Orthogonality
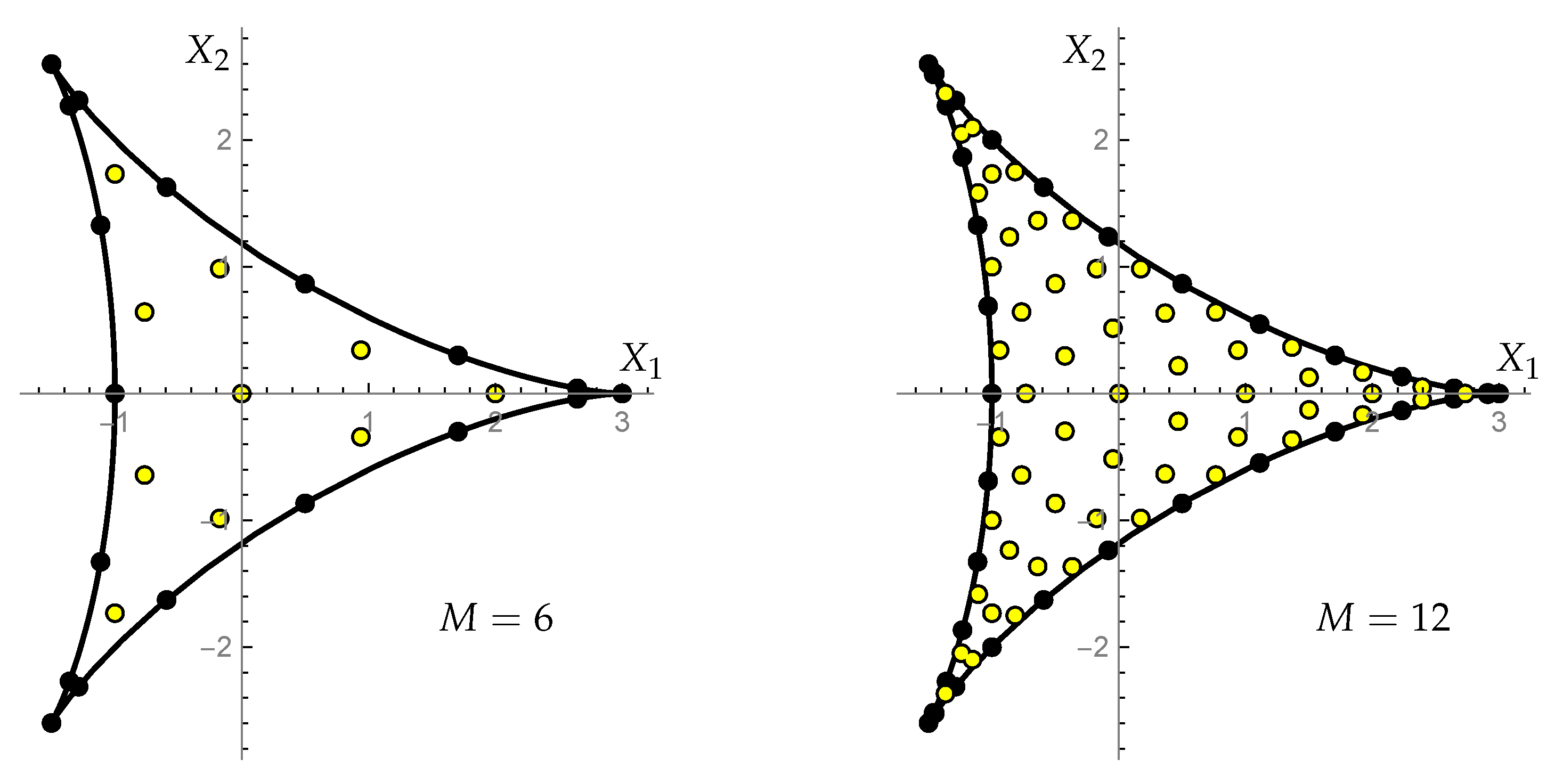
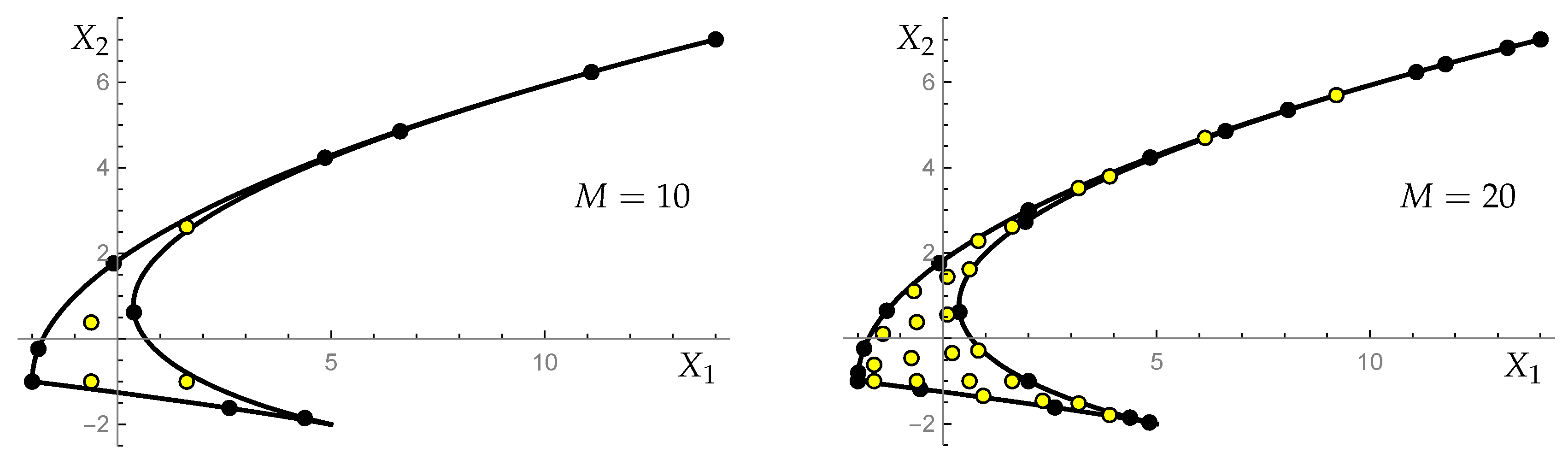
5.1. Sets of Points
5.2. General Orthogonality Relations
5.3. Sets of Weights
5.4. Discrete Orthogonality of Polynomials
5.5. Discrete Orthogonality of Polynomials
5.6. Discrete Orthogonality of Polynomials
5.7. Polynomial Interpolation
6. Concluding Remarks
- The orthogonality of our polynomials is expressed as the sum of values of the polynomials over the points of the domain. Crucial for the orthogonality are the weight functions that are determined here. The weight functions are different for polynomials of each type and for each of the three groups , , . Let us emphasize that the set of points in the domain for any value of is not a fragment of a lattice. It would be interesting to characterize such sets of isolated points without reference to the orthogonality of orbit functions on lattices.
- Our approach begins with the sums of exponential functions (‘orbit functions’) determined by the orbits of the Weyl groups of , , on the corresponding weight lattice and their refinements. Discrete orthogonality of orbit functions [19,21] on finite fragments of 2D lattices of any density is the input that makes our work possible. Such functions serve us as a departure point for a description of the polynomials of two discrete variables that are orthogonal on a set of isolated points inside of a finite domain of a complex space. Moreover, their orthogonality is maintained when the finite domain is populated by ever increasing set of points. The density is determined by our choice of any positive integer M. The greater M, the greater number of points is in the domain.
- The classical product-to-sum formula for the Chebyshev polynomials [7] of the first kind , which is for of the form has a straightforward generalization to the polynomials. This 2D product-to-sum formula is readily derived from the product-to-sum formulas of orbit functions, see e.g. [25], and has the following formwhere denotes the unique point of orbit which lies in . Even though the existence of more complicated formulas, which would generalize product-to-sum formulas for the Chebyshev polynomials of the second kind to 2D relations for , and polynomials, may be expected, their explicit form deserves further study.
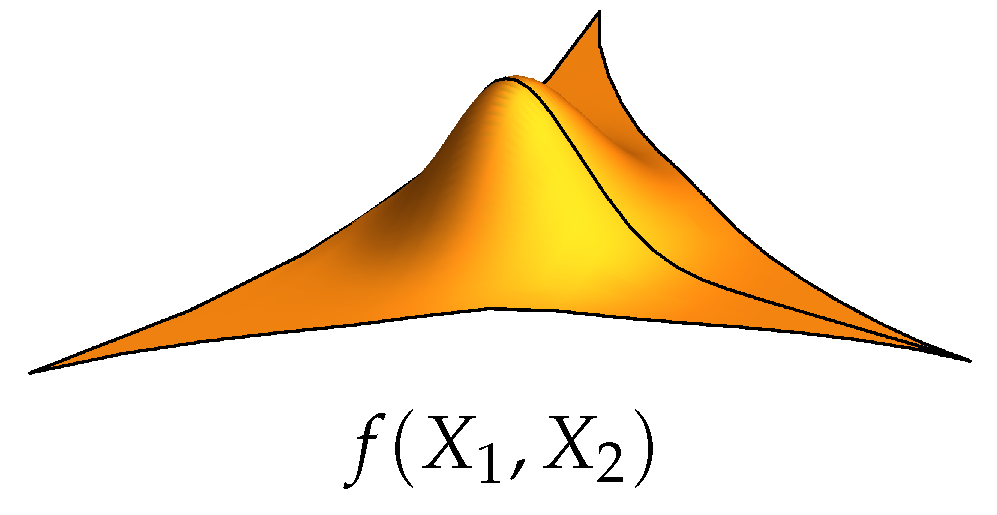
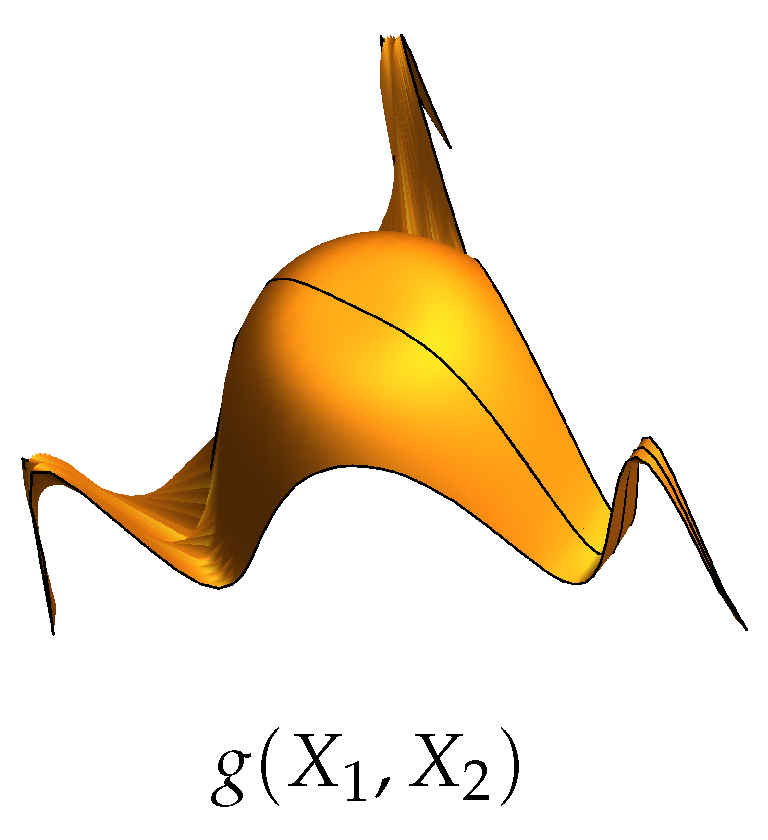
- The example of interpolation demonstrates promising behavior of the polynomial interpolation . Visual inspection and the integral error estimates of the interpolations of the model function f lead to the conclusion that the interpolation error is small once the minimal distances of the points become smaller than the variance of the model function. The existence of general conditions for the convergence of the functional series of polynomials poses an open problem. The aliasing problem of the classical Chebyshev polynomials is generalized via the action of the magnified dual affine Weyl group . Two polynomials and are identical on the nodes if there exists an element of the magnified dual affine Weyl group such that . Possible generalization of the current Weyl group multivariate approach to wavelet analysis [30,31,32] poses open problem.
- Another practical aspect of the discrete orthogonality relations is the possibility of deriving inherent cubature formulas [2,33]. For successful computer implementation of these numerical integration formulas the data contained in the presented discrete orthogonality relations, it is necessary to include the weight functions. The data specifying the groups , , are different. However, our approach is uniform to the extent that it can be directly applied to study the polynomials of higher rank groups, their discrete orthogonality, polynomial interpolation properties, cubature formulas and other practical aspects.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bourbaki, N. Groupes et Algèbres de Lie, Chapters IV, V, VI; Hermann: Paris, France, 1968. [Google Scholar]
- Moody, R.V.; Motlochová, L.; Patera, J. Gaussian cubature arising from hybrid characters of simple Lie groups. J. Fourier Anal. Appl. 2014, 20, 1257–1290. [Google Scholar] [CrossRef]
- Dunn, K.B.; Lidl, R. Multi-dimensional generalizations of the Chebyshev polynomials, I. Proc. Jpn. Acad. Ser. A Math. Sci. 1980, 156, 154–159. [Google Scholar] [CrossRef]
- Heckman, G.J.; Opdam, E.M. Root systems and hypergeometric functions. I, II. Compos. Math. 1987, 64, 329–373. [Google Scholar]
- Koornwinder, T.H. Orthogonal polynomials in two variables which are eigenfunctions of two algebraically independent partial differential operators. III, IV. Indag. Math. 1974, 77, 357–381. [Google Scholar] [CrossRef]
- Macdonald, I.G. Orthogonal polynomials associated with root systems. In Orthogonal Polynomials; Springer: Dordrecht, The Netherlands, 1990; pp. 311–318. [Google Scholar]
- Rivlin, T.J. Chebyshev Polynomials: From Approximation Theory to Algebra and Number Theory; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Van Diejen, J.F. Finite-Dimensional Orthogonality Structures for Hall-Littlewood Polynomials. Acta Appl. Math. 2007, 99, 301–308. [Google Scholar] [CrossRef]
- Van Diejen, J.F.; Emsiz, E. Orthogonality of Macdonald polynomials with unitary parameters. Math. Z. 2014, 276, 517–542. [Google Scholar] [CrossRef]
- Dunkl, C.F. Orthogonal Polynomials in Two Variables of q-Hahn and q-Jacobi Type. SIAM J. Algebr. Discret. Methods 1980, 1, 137–151. [Google Scholar] [CrossRef]
- Van Diejen, J.F.; Vinet, L. The quantum dynamics of the compactified trigonometric Ruijsenaars-Schneider model. Commun. Math. Phys. 1998, 197, 33–74. [Google Scholar] [CrossRef][Green Version]
- Scarabotti, F. The tree method for multidimensional q-Hahn and q-Racah polynomials. Ramanujan J. 2011, 25, 57–91. [Google Scholar] [CrossRef]
- Li, H.; Sun, J.; Xu, Y. Discrete Fourier analysis and Chebyshev polynomials with G2 group. SIGMA 2012, 8, 067. [Google Scholar]
- Li, H.; Xu, Y. Discrete Fourier analysis on fundamental domain of Ad lattice and on simplex in d-variables. J. Fourier Anal. Appl. 2010, 16, 383–433. [Google Scholar] [CrossRef]
- Li, H.; Sun, J.; Xu, Y. Discrete Fourier analysis, cubature, and interpolation on a hexagon and a triangle. SIAM J. Numer. Anal. 2008, 46, 1653–1681. [Google Scholar] [CrossRef]
- Czyżycki, T.; Hrivnák, J.; Patera, J. Generating functions for orthogonal polynomials of A2, C2 and G2. Symmetry 2018, 10, 354. [Google Scholar] [CrossRef]
- Damaskinsky, E.V.; Sokolov, M.A. The generating function of bivariate Chebyshev polynomials associated with the Lie algebra G2. Theor. Math. Phys. 2017, 192, 1115–1128. [Google Scholar] [CrossRef]
- Hrivnák, J. Discretization of four types of Weyl group orbit functions. J. Phys. Conf. Ser. 2013, 474, 012021. [Google Scholar] [CrossRef]
- Hrivnák, J.; Patera, J. On discretization of tori of compact simple Lie groups. J. Phys. A Math. Theor. 2009, 42, 385208. [Google Scholar] [CrossRef]
- Hrivnák, J.; Motlochová, L. Dual-Root Lattice Discretization of Weyl Orbit Functions. J. Fourier Anal. Appl. 2017, 1–49. [Google Scholar] [CrossRef]
- Hrivnák, J.; Motlochová, L.; Patera, J. On discretization of tori of compact simple Lie groups II. J. Phys. A Math. Theor. 2012, 45, 255201. [Google Scholar] [CrossRef]
- Hrivnák, J.; Walton, M.A. Weight-lattice discretization of Weyl-orbit functions. J. Math. Phys. 2016, 57, 083512. [Google Scholar] [CrossRef]
- Humphreys, J.E. Introduction to Lie Algebras and Representation Theory; Springer: New York, NY, USA, 1972. [Google Scholar]
- Kane, R. Reflection Groups and Invariant Theory; Springer: New York, NY, USA, 2001. [Google Scholar]
- Klimyk, A.; Patera, J. Orbit functions. Symmetry Integr. Geom. Methods Appl. 2006, 2, 006. [Google Scholar] [CrossRef]
- Klimyk, A.; Patera, J. Antisymmetric functions. SIGMA 2007, 3, 23. [Google Scholar]
- Patera, J.; Zaratsyan, A. Discrete and continuous cosine transform generalized to Lie groups SU(3) and G(2). J. Math. Phys. 2005, 46, 113506. [Google Scholar] [CrossRef]
- Szajewska, M. Four types of special functions of G2 and their discretization. Integr. Trans. Spec. Funct. 2012, 23, 455–472. [Google Scholar] [CrossRef]
- Mason, J.C.; Handscomb, D.C. Chebyshev Polynomials; Chapman & Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Guariglia, E. Primality, Fractality, and Image Analysis. Entropy 2019, 21, 304. [Google Scholar] [CrossRef]
- Pilipović, S.; Rakić, D.; Vindas, J. New Classes of Weighted Hölder-Zygmund Spaces and the Wavelet Transform. J. Funct. Spaces Appl. 2012, 2012, 815475. [Google Scholar] [CrossRef]
- Saneva, K.; Vindas, J. Wavelet expansions and asymptotic behavior of distributions. J. Math. Anal. Appl. 2010, 370, 543–554. [Google Scholar] [CrossRef][Green Version]
- Hrivnák, J.; Motlochová, L.; Patera, J. Cubature formulas of multivariate polynomials arising from symmetric orbit functions. Symmetry 2016, 8, 63. [Google Scholar] [CrossRef]
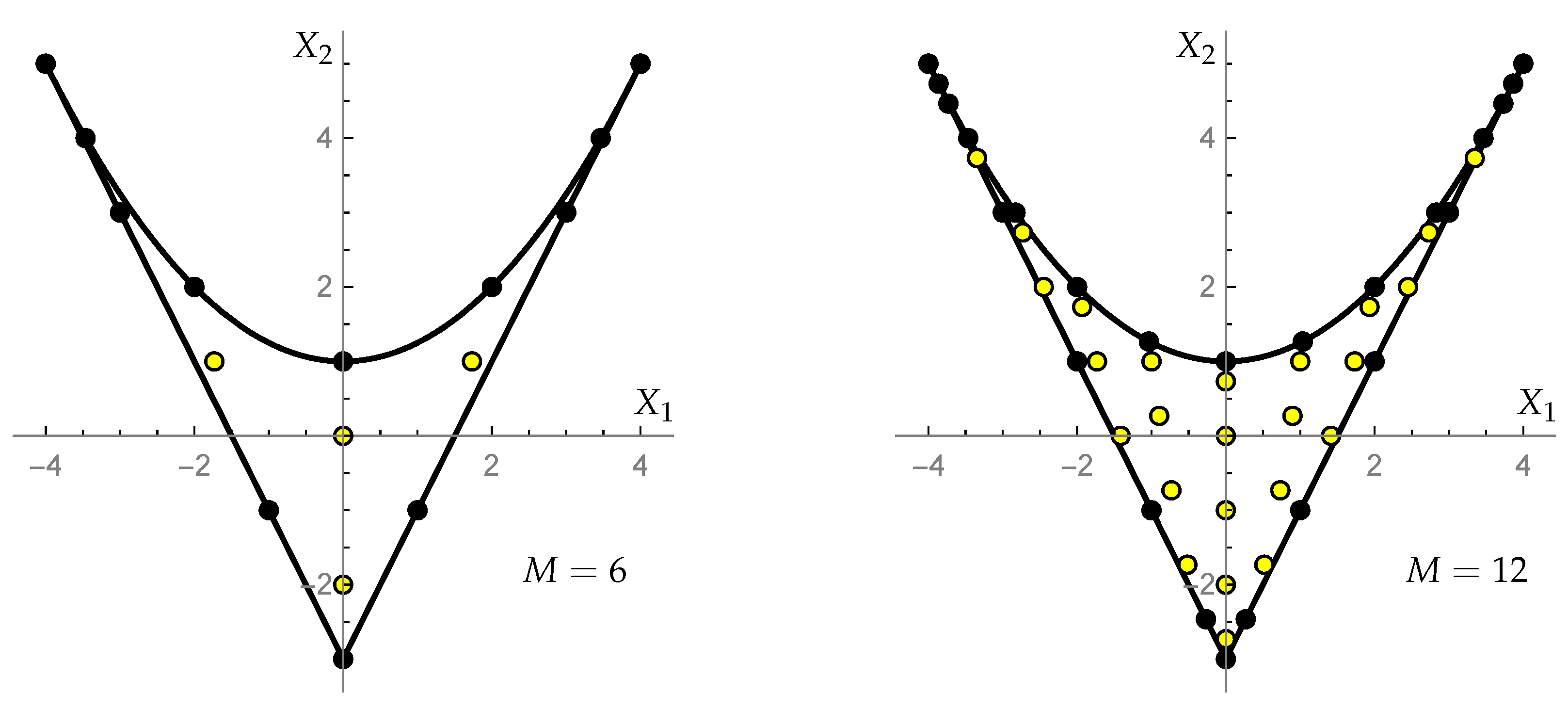
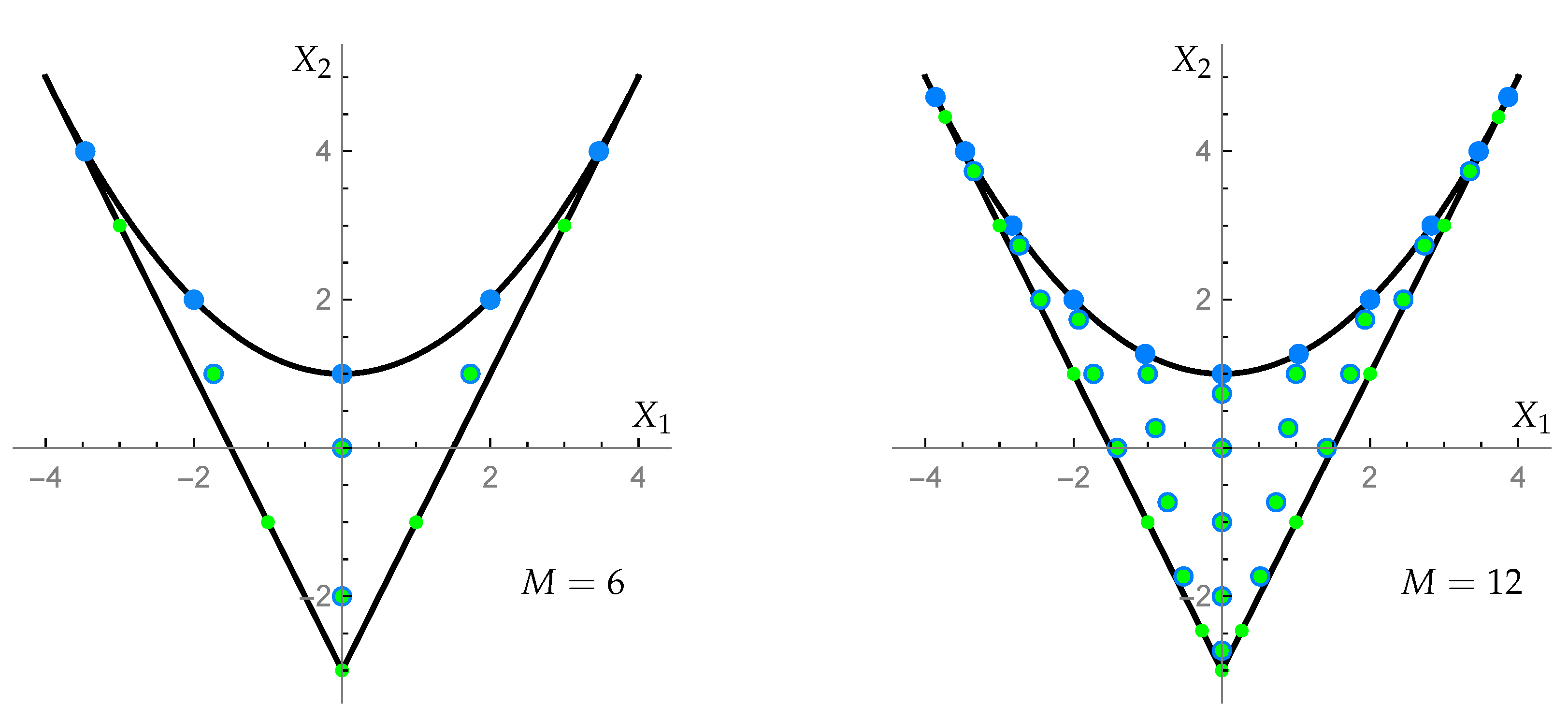
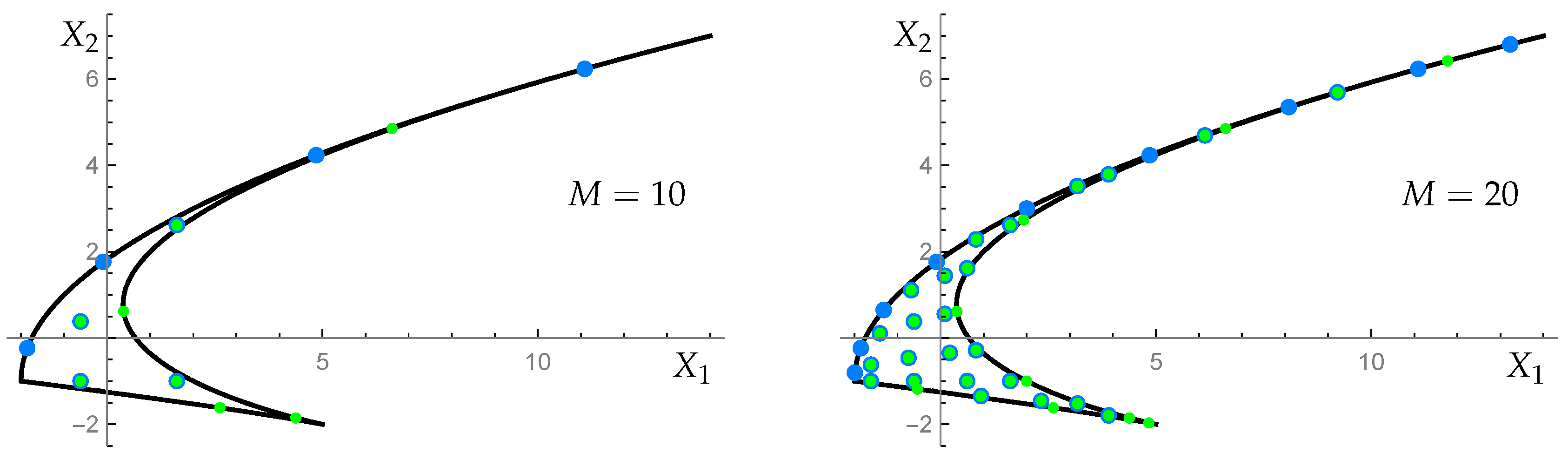
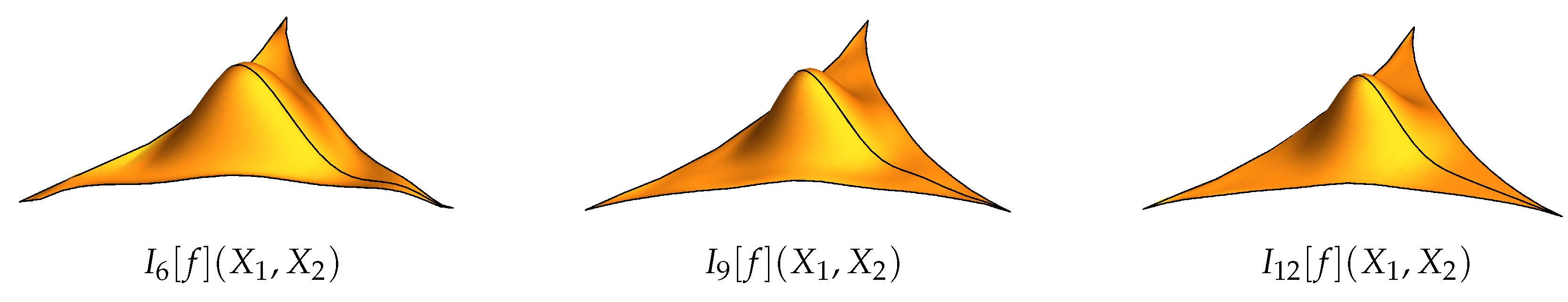
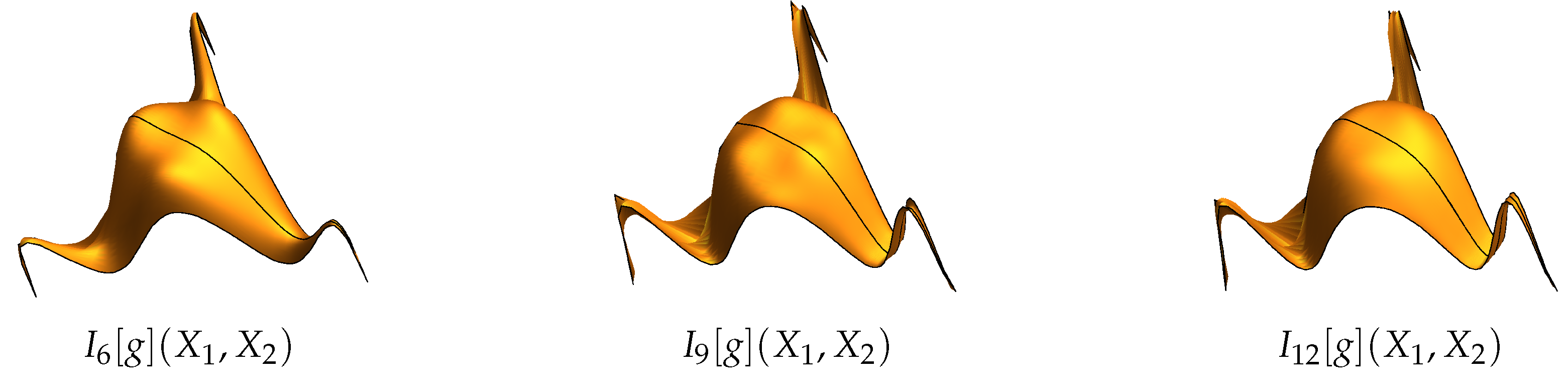
| 6 | |
| 1 | |
| 8 | |
| 1 | |
| 1 | |
| 1 | |
| 12 | |
| 1 | |
| 1 | |
| 1 | |
| 6 | 8 | 12 | |
| 3 | 4 | 6 | |
| 3 | 4 | 6 | |
| 3 | 4 | 6 | |
| 1 | 1 | 2 | |
| 1 | 2 | 3 | |
| 1 | 1 | 1 |
| 1 | 1 | 1 | |
| 2 | 2 | 2 | |
| 2 | 2 | 2 | |
| 2 | 2 | 2 | |
| 6 | 4 | 4 | |
| 6 | 8 | 6 | |
| 6 | 8 | 12 |
| M | Number of Points | ||
|---|---|---|---|
| 3 | 10 | ||
| 6 | 28 | ||
| 9 | 55 | ||
| 12 | 91 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hrivnák, J.; Patera, J.; Szajewska, M. Discrete Orthogonality of Bivariate Polynomials of A2, C2 and G2. Symmetry 2019, 11, 751. https://doi.org/10.3390/sym11060751
Hrivnák J, Patera J, Szajewska M. Discrete Orthogonality of Bivariate Polynomials of A2, C2 and G2. Symmetry. 2019; 11(6):751. https://doi.org/10.3390/sym11060751
Chicago/Turabian StyleHrivnák, Jiří, Jiří Patera, and Marzena Szajewska. 2019. "Discrete Orthogonality of Bivariate Polynomials of A2, C2 and G2" Symmetry 11, no. 6: 751. https://doi.org/10.3390/sym11060751
APA StyleHrivnák, J., Patera, J., & Szajewska, M. (2019). Discrete Orthogonality of Bivariate Polynomials of A2, C2 and G2. Symmetry, 11(6), 751. https://doi.org/10.3390/sym11060751





