Hybrid Particle Swarm Algorithm for Products’ Scheduling Problem in Cellular Manufacturing System
Abstract
1. Introduction
2. Literature Review
3. Performance Analysis
- No pre-emption is allowed and setup times are sequence independent.
- Breakdown and re-work is neglected and all parts are available.
- Buffer size is not considered.
4. Methodology
4.1. Mathematical Modeling
- = Arrival time of part “i” on machine “j”
- = Process time of part “i” on machine “j”
- = Setup time of part “i” on machine “j”
- = Start time of part “i” on machine “j”
- = Completion time of part “i” on machine “j”
- = Waiting time in queue of part “i” on machine “j”
4.2. Genetic Algorithm
- Evaluation: Determine the aptitude of each individual according to certain criteria or measure, that is, which individuals are the most apt to survive.
- Selection: Select the strongest individuals of a generation that must pass to the next generation or must reproduce. In our case, roulette wheel selection scheme [38] was applied.
- Crossing: Take two individuals to reproduce and cross their genetic information to generate new individuals that will form a new population. Several crossover operators have been proposed for the permutation encoded chromosomes. In the current study, the Similar Block 2—Point Order Crossover (SB2OX) was applied as according to results of [39], it is an efficient technique for a permutation solution space. The crossover probability considered was for two levels (0.2 and 0.3)
- Mutation: Randomly alters the genes of an individual because of errors in the reproduction or deformation of genes. In other words, genetic variability is introduced into the population for diversity enhancement of a population. In addition, early convergence is also avoided to any local optimum. In this study, swap technique was used with two level probabilities, 0.01 and 0.02.
- Replacement: Procedure to create a new generation of individuals.
4.3. NEPSO in Scheduling
4.3.1. PSO Terms to clear:
- Particle: At iteration k, ith particle in swarm is denoted by and is represented by number of dimensions as = ; refers to position value of ith particle w.r.t to dimension j (j = 1,..., n).
- Population: The group of m particles in swarm at iteration k, i.e. = .
- Sequence: is a sequence of jobs inferred by the particle . = ; is the arrangement of job j in domain of the particle i at iteration k w.r.t. jth dimension.
- Particle velocity: is the velocity of ith particle at kth iteration; = .
- Inertia weight: Parameter used for controlling impact of the previous velocity on the current velocity and denoted by wk.
- Personal best: Position values determining best fitness values for ith particle so far until iteration k is known as personal best denoted by . Updated for every particle in swarm, such as when fitness () < fitness (), personal best is updated else it stays the same.
- Global best: Among all particles in the swarm at iteration k, position values with a sequence giving overall best fitness represents global best particle.
4.3.2. Initial Seed Solution
- For each job i, find the total processing time Ti with help of (14).
- Sort the n jobs in descending order of their total processing times.
- Take the first four jobs from the sorted list and form 4! = 24 partial sequences. The best k out of these 24 partial sequences is selected for further processing. The relative positions of jobs in any partial sequence are not altered in any later (larger) sequence.
- Let x be the position numbers. Set x = 5, because we are already filled with 4 positions, that is, jobs.
- The next job on the sorted list is inserted at each of the x positions in each of the k (x−1)-job partial sequences, resulting in x × k x-job partial sequences.
- The best k out of the x × k sequences is selected for further processing. Here we distinguish and find out two sequences, that is, kth sequence with minimum total flow time and kth sequence with minimum makespan.
- Increment x by 1.
- If x > n, accept the best of the k n-job sequences as the final solution and stop.
- Otherwise go to step 7.
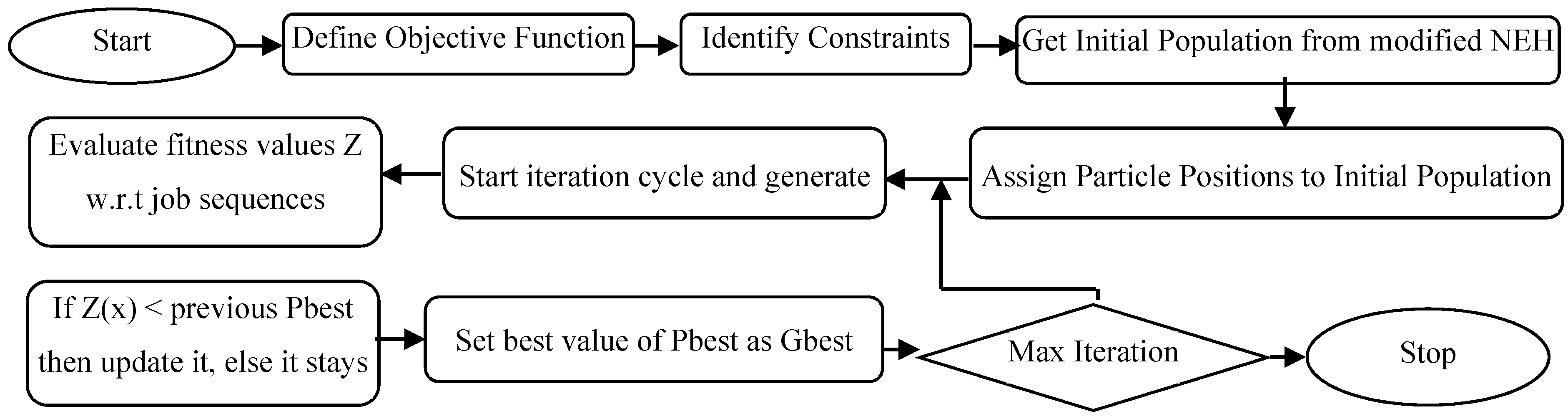
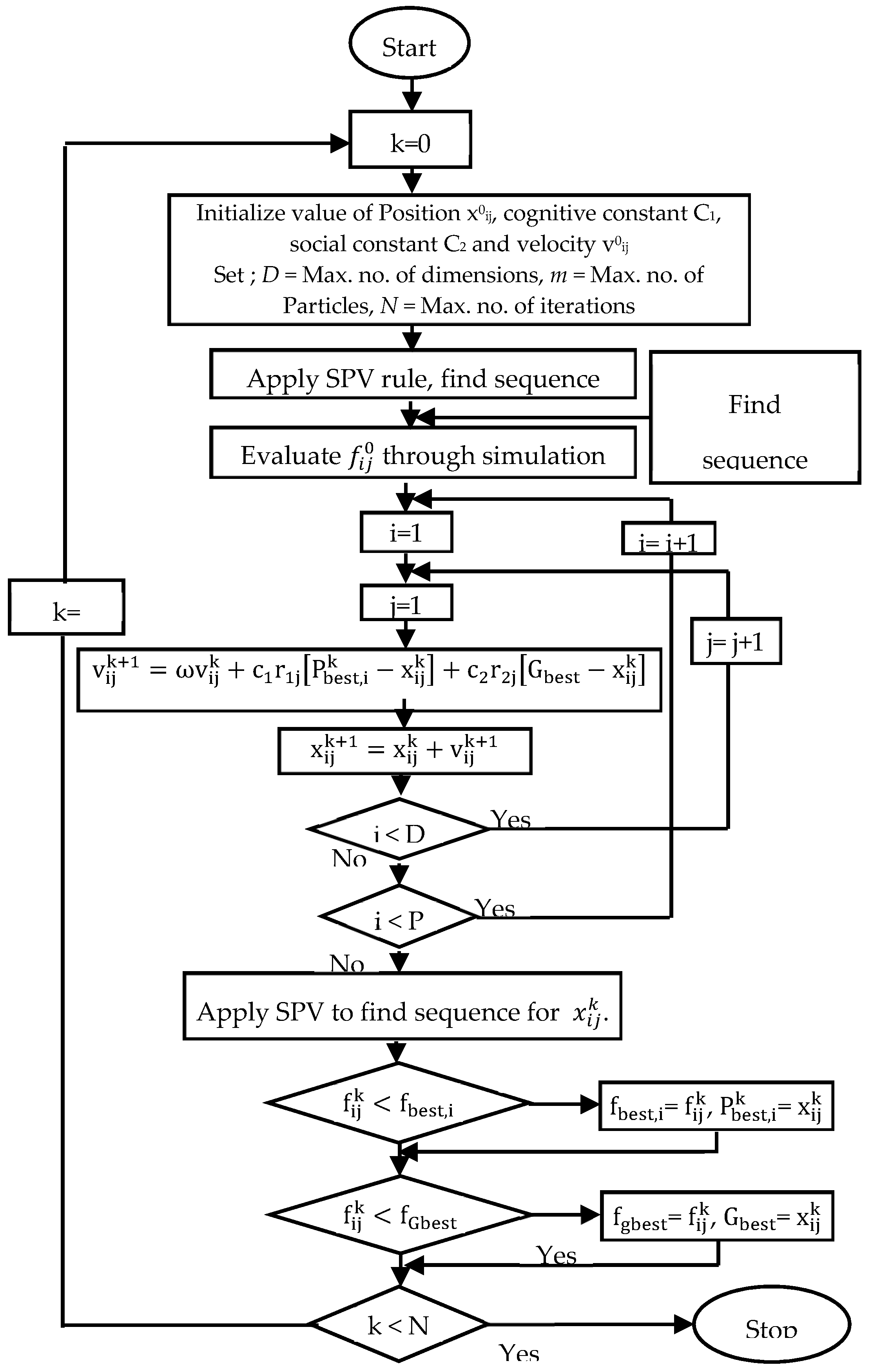
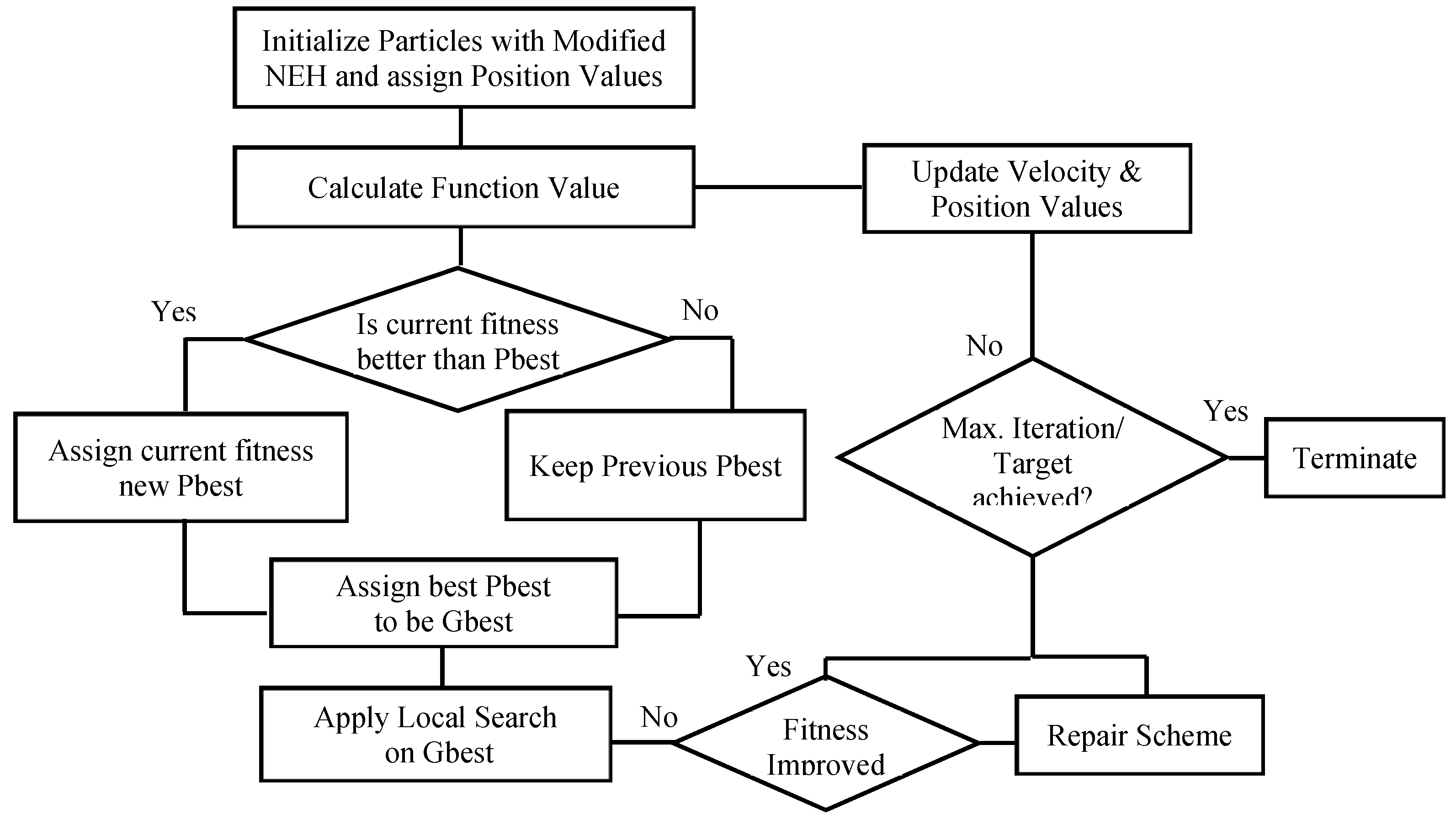
- Determine the initial solution with the aid of proposed heuristic.
- Set iteration k=0 and number of particles—each job represent a dimension. Set values of cognitive and social co-efficient C1, C2 [18].
- Linking to the initial solution, generate position values according to SPV rule for m particles in search space, i.e.{} where and n is last job’s dimension.
- Generate initial velocities for the particles in random manner with help of Equation (15), where Rn(0,1) is random number in between 0 and 1, where we have
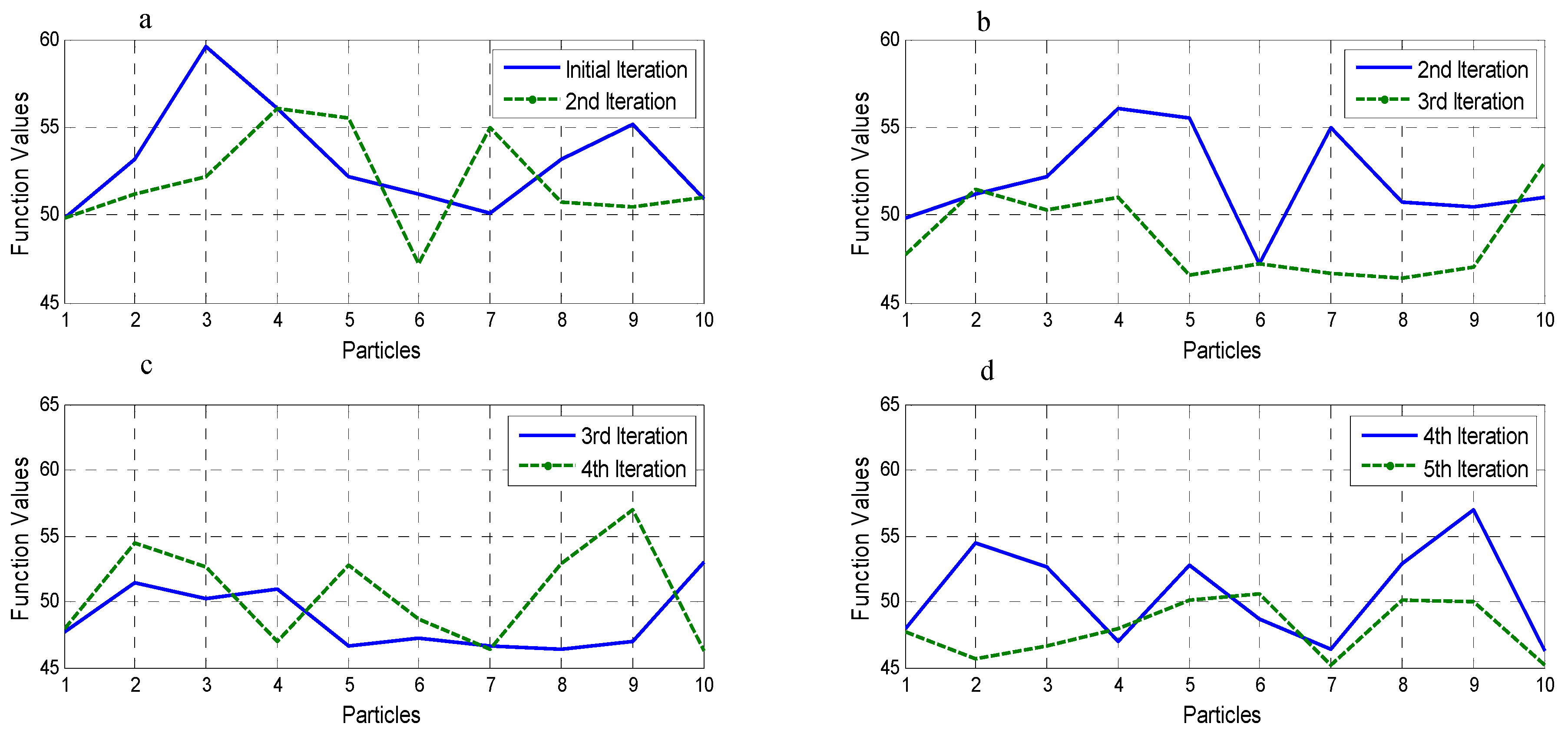
- Evaluate the sequences by finding out the function values with help of simulation.
- Simulation model assists in finding throughput time for machines on basis of which WIP is calculated.
- Model also determines if component of time machine is idle, calculating average utilization of the machines.
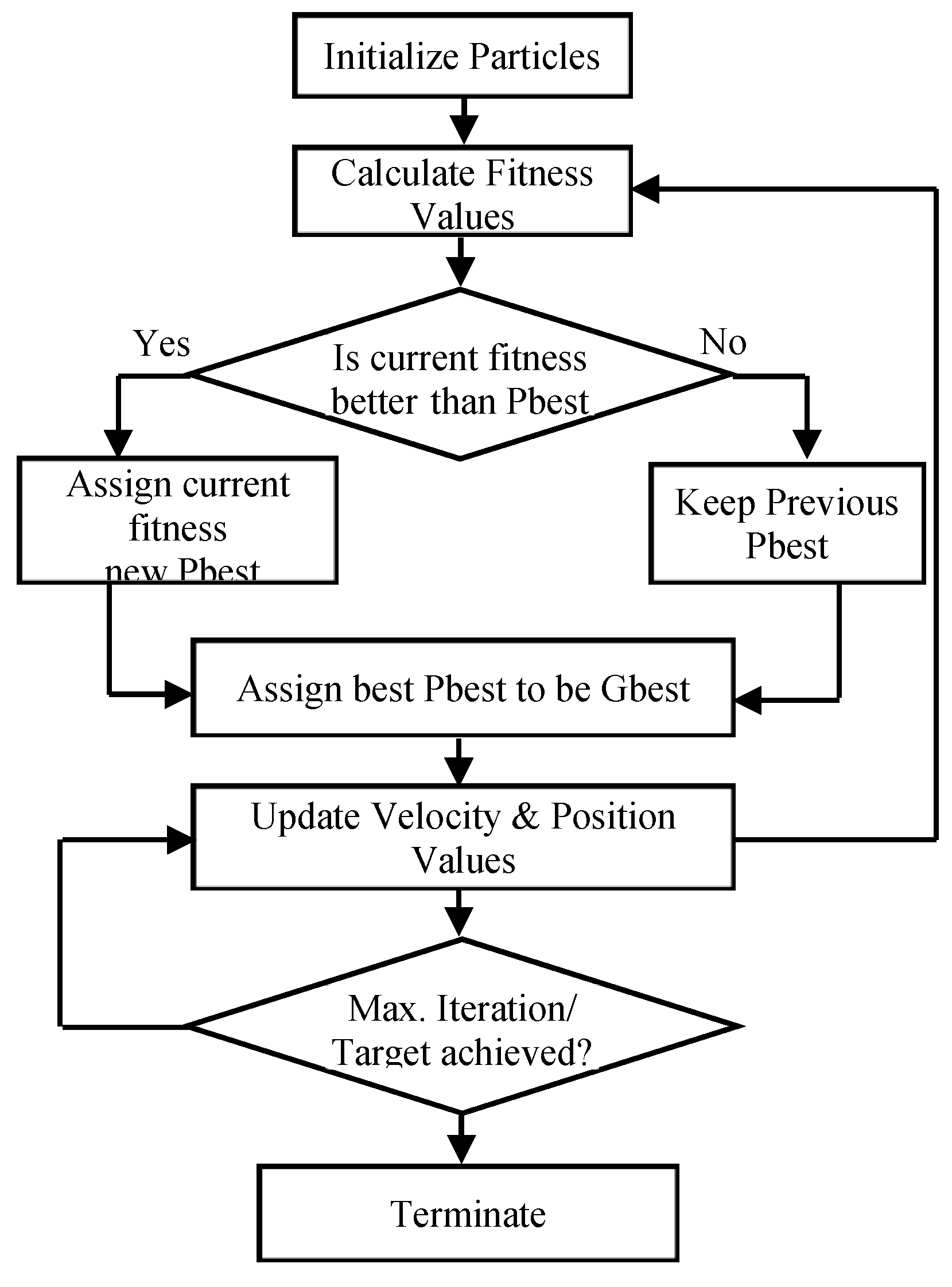
- Set these function values to be personal best for each particle in the swarm at first iteration.
- Select minimum of the personal best values and set it as global best.
- In next step, update velocity for the particles, keeping track of previous personal best value of the particle and global best of the swarm; this helps in convergence to achieve good fitness values.
- Updated velocities change the particles position and new sequence is developed and evaluated.
- Apply smallest position value (SPV) rule on the positions of generated particles, thus, determining its sequence. SPV rule gives the job its sequential number according to its dimensions adjusted by arranging particle position values in ascending order. = , where is the assignment of job j of the particle i in the processing order at iteration k with respect to the jth dimension.
- Evaluate function values; if the achieved are minimum than previous, their particle positions are updated in library of personal and global best positions.
- If stopping criteria is met, stop the iteration.
- Interchange the two jobs between yth and zth dimension, y ≠ z (interchange).
- Remove the job at the yth dimension and then insert in zth dimension, y ≠ z (insert).
5. Case Problems
5.1. Application of NEPSO on Case Study
5.2. Comparison and Model Analysis
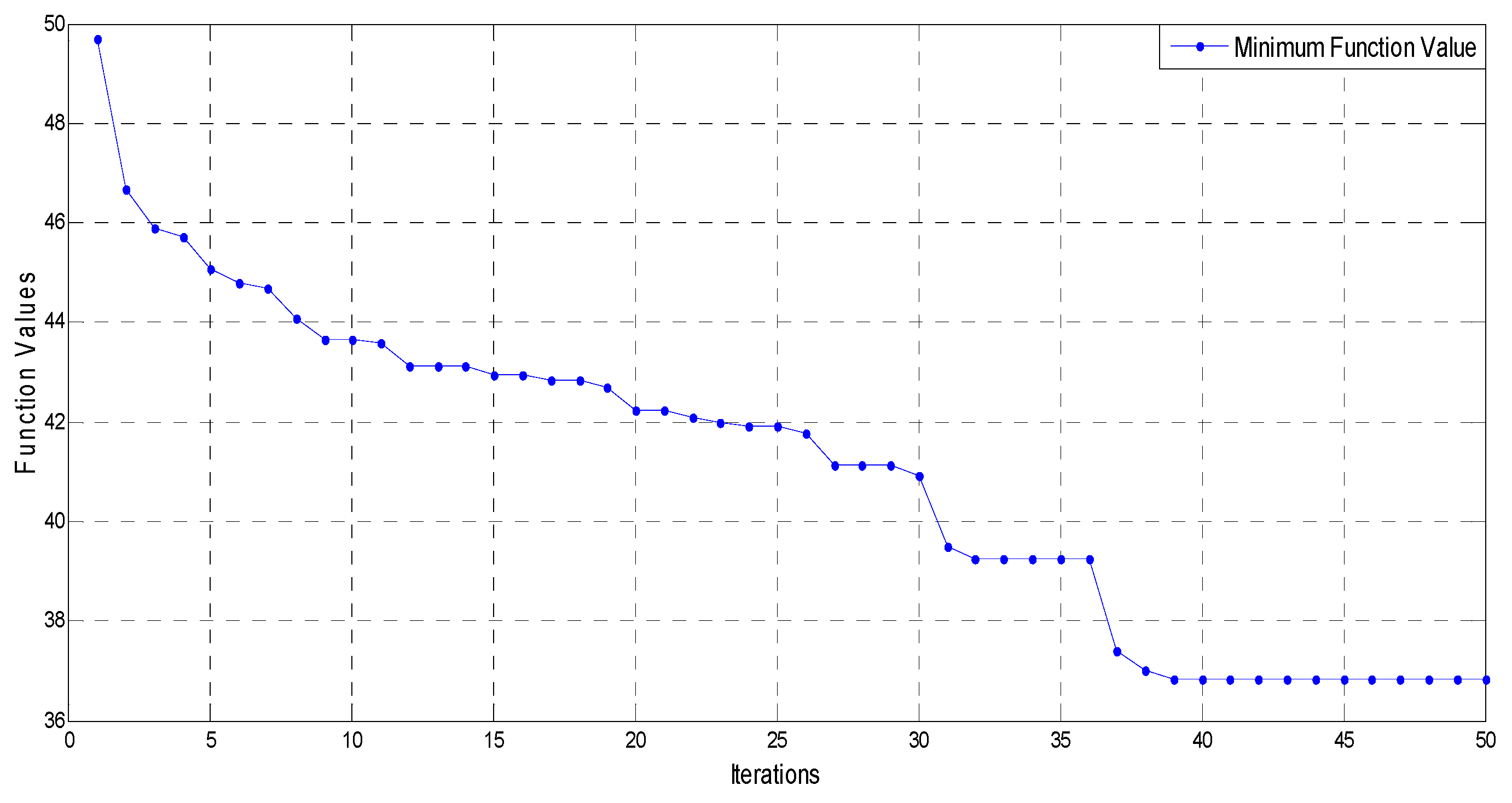
6. Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Baker, K.R. Scheduling a Full-Time Workforce to Meet Cyclic Staffing Requirements. Manag. Sci. 1974, 20, 1561–1568. [Google Scholar] [CrossRef]
- Baker, K.R. Introduction to Sequencing and Scheduling; John Wiley & Sons: Hoboken, NJ, USA, 1974. [Google Scholar]
- Conway, R.W.; Maxwell, W.L.; Miller, L.W. Theory of Scheduling; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Swamidass, P.M. Encyclopedia of Production and Manufacturing Management; Springer Science & Business Media: Berlin, Germany, 2000. [Google Scholar]
- Ham, I.; Hitomi, K.; Yoshida, T. Production scheduling for group technology. In Group Technology; Springer: Berlin, Germany, 1985; pp. 93–107. [Google Scholar]
- Sridhar, J.; Rajendran, C. Scheduling in flowshop and cellular manufacturing systems with multiple objectives—A genetic algorithmic approach. Prod. Plan. Control 1996, 7, 374–382. [Google Scholar] [CrossRef]
- Wemmerlov, U.; Johnson, D.J. Cellular manufacturing at 46 user plants: implementation experiences and performance improvements. Int. J. Prod. Res. 1997, 35, 29–49. [Google Scholar] [CrossRef]
- Shafer, S.; Charnes, J. A simulation analyses of factors influencing loading practices in cellular manufacturing. Int. J. Prod. Res. 1995, 33, 279–290. [Google Scholar] [CrossRef]
- Suer, G.A.; Saiz, M.; Gonzalez, W. Evaluation of manufacturing cell loading rules for independent cells. Int. J. Prod. Res. 1999, 37, 3445–3468. [Google Scholar] [CrossRef]
- Logendran, R.; Nudtasomboon, N. Minimizing the makespan of a group scheduling problem: a new heuristic. Int. J. Prod. Econ. 1991, 22, 217–230. [Google Scholar] [CrossRef]
- Akturk, M.S.; Wilson, G.R. A hierarchical model for the cell loading problem of cellular manufacturing systems. Int. J. Prod. Res. 1998, 36, 2005–2023. [Google Scholar] [CrossRef]
- Schaller, J. A comparison of heuristics for family and job scheduling in a flow-line manufacturing cell. Int. J. Prod. Res. 2000, 38, 287–308. [Google Scholar] [CrossRef]
- Flynn, B. The effects of setup time on output capacity in cellular manufacturing. Int. J. Prod. Res. 1987, 25, 1761–1772. [Google Scholar]
- Eberhart, R.C.; Shi, Y. Guest Editorial Special Issue on Particle Swarm Optimization. IEEE Trans. Evolut. Comput. 2004, 8, 201–203. [Google Scholar] [CrossRef]
- Hassan, R.; Cohanim, B.; De Weck, O.; Venter, G. A Comparison of Particle Swarm Optimization and the Genetic Algorithm. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 21 April 2005. [Google Scholar]
- Das, S.; Abraham, A.; Konar, A. Particle Swarm Optimization and Differential Evolution Algorithms: Technical Analysis, Applications and Hybridization Perspectives. In Advances of Computational Intelligence in Industrial Systems; Liu, Y., Sun, A., Loh, H.T., Lu, W.F., Lim, E.-P., Eds.; Springer: Berlin, Germany, 2008; pp. 1–38. [Google Scholar]
- Reyes-Sierra, M.; Coello, C.C. Multi-objective particle swarm optimizers: A survey of the state-of-the-art. Int. J. Comput. Intell. Res. 2006, 2, 287–308. [Google Scholar]
- Tasgetiren, M.F.; Liang, Y.C.; Sevkli, M.; Gencyilmaz, G. A particle swarm optimization algorithm for makespan and total flowtime minimization in the permutation flowshop sequencing problem. Eur. J. Oper. Res. 2007, 177, 1930–1947. [Google Scholar] [CrossRef]
- Tasgetiren, M.F.; Sevkli, M.; Liang, Y.C.; Yenisey, M.M. A particle swarm optimization and differential evolution algorithms for job shop scheduling problem. J. Oper. Res. 2006, 3, 120–135. [Google Scholar]
- Xia, W.; Wu, Z. An effective hybrid optimization approach for multi-objective flexible job-shop scheduling problems. Comput. Ind. Eng. 2005, 48, 409–425. [Google Scholar] [CrossRef]
- Xia, W.J.; Wu, Z.M. A hybrid particle swarm optimization approach for the job-shop scheduling problem. Int. J. Adv. Manuf. Technol. 2006, 29, 360–366. [Google Scholar] [CrossRef]
- Liu, H.; Abraham, A.; Choi, O.; Moon, S.H. Variable Neighborhood Particle Swarm Optimization for Multi-objective Flexible Job-Shop Scheduling Problems. In Simulated Evolution and Learning; Wang, T.D., Li, X., Chen, S.H., Wang, X., Abbass, H., Iba, H., Chen, G., Yao, X., Eds.; Springer: Berlin, Germany, 2006; pp. 197–204. [Google Scholar]
- Jia, Z.; Chen, H.; Sun, Y. Hybrid particle swarm optimization for flexible job-shop scheduling. J. Syst. Simul. 2007, 19, 4743–4747. [Google Scholar]
- Jerald, J.; Asokan, P.; Prabaharan, G.; Saravanan, R. Scheduling optimisation of flexible manufacturing systems using particle swarm optimisation algorithm. Int. J. Adv. Manuf. Technol. 2005, 25, 964–971. [Google Scholar] [CrossRef]
- Tavakkoli-Moghaddam, R.; Jafari-Zarandini, Y.; Gholipour-Kanani, Y. Multi-objective Particle Swarm Optimization for Sequencing and Scheduling a Cellular Manufacturing System. In Advanced Intelligent Computing Theories and Applications; Huang, D.-S., McGinnity, M., Heutte, L., Zhang, X.-P., Eds.; Springer: Berlin, Germany, 2010; pp. 69–75. [Google Scholar]
- Yang, J.; Posner, M.E. Flow shops with WIP and value added costs. J. Schedul. 2010, 13, 3–16. [Google Scholar] [CrossRef]
- Massim, Y.; Yalaoui, F.; Amodeo, L.; Châtelet, É.; Zeblah, A. Efficient combined immune-decomposition algorithm for optimal buffer allocation in production lines for throughput and profit maximization. Comput. Oper. Res. 2010, 37, 611–620. [Google Scholar] [CrossRef]
- Conway, R.; Maxwell, W.; McClain, J.O.; Thomas, L.J. The Role of Work-in-Process Inventory in Serial Production Lines. Oper. Res. 1988, 36, 229–241. [Google Scholar] [CrossRef]
- Yang, J. 7. Flow-shop Scheduling Problem with Weighted Work-In-Process. Available online: http://www.dbpia.co.kr/journal/articleDetail?nodeId=NODE00596702&language=ko_KR (accessed on 19 April 2019).
- Zhang, Q.; Manier, H.; Manier, M.-A. A modified shifting bottleneck heuristic and disjunctive graph for job shop scheduling problems with transportation constraints. Int. J. Prod. Res. 2014, 52, 985–1002. [Google Scholar] [CrossRef]
- Tavakkoli-Moghaddam, R.; Ranjbar-Bourani, M.; Amin, G.R.; Siadat, A. A cell formation problem considering machine utilization and alternative process routes by scatter search. J. Intell. Manuf. 2012, 23, 1127–1139. [Google Scholar] [CrossRef]
- Mahdavi, I.; Javadi, B.; Fallah-Alipour, K.; Slomp, J. Designing a new mathematical model for cellular manufacturing system based on cell utilization. Appl. Math. Comput. 2007, 190, 662–670. [Google Scholar] [CrossRef]
- Li, W.D.; McMahon, C.A. A simulated annealing-based optimization approach for integrated process planning and scheduling. Int. J. Comput. Integrated Manuf. 2007, 20, 80–95. [Google Scholar] [CrossRef]
- Campos, J.; Silva, M. Structural techniques and performance bounds of stochastic Petri net models. In Advances in Petri Nets; Springer: Berlin, HDB, Germany, 1992; pp. 352–391. [Google Scholar]
- Alanazi, H.O.; Abdullah, A.H.; Larbani, M. Dynamic weighted sum multi-criteria decision making: Mathematical Model. Int. J. Math. Statistics Invent. 2013, 1, 16–18. [Google Scholar]
- Chen, C.H.; Liu, T.K.; Chou, J.H. A novel crowding genetic algorithm and its applications to manufacturing robots. IEEE Trans. Ind. Inf. 2014, 10, 1705–1716. [Google Scholar] [CrossRef]
- Gong, X.; Plets, D.; Tanghe, E.; De Pessemier, T.; Martens, L.; Joseph, W. An efficient genetic algorithm for large-scale planning of dense and robust industrial wireless networks. Expert Syst. Appl. 2018, 96, 311–329. [Google Scholar] [CrossRef]
- Oĝuz, C.; Ercan, M.F. A genetic algorithm for hybrid flow-shop scheduling with multiprocessor tasks. J. Sched. 2005, 8, 323–351. [Google Scholar] [CrossRef]
- Ruiz, R.; Maroto, C. A genetic algorithm for hybrid flowshops with sequence dependent setup times and machine eligibility. Eur. J. Oper. Res. 2006, 169, 781–800. [Google Scholar] [CrossRef]
- Man, K.F.; Tang, K.S.; Kwong, S.; Ip, W.H. Genetic algorithm to production planning and scheduling problems for manufacturing systems. Prod. Plan. Control 2000, 11, 443–458. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A comprehensive survey on particle swarm optimization algorithm and its applications. Math. Probl. Eng. 2015, 15, 1–38. [Google Scholar] [CrossRef]
- Tasgetiren, M.F.; Sevkli, M.; Liang, Y.C.; Gencyilmaz, G. Particle swarm optimization algorithm for single machine total weighted tardiness problem. In Proceedings of the 2004 Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004. [Google Scholar]
- Anghinolfi, D.; Paolucci, M. A new discrete particle swarm optimization approach for the single-machine total weighted tardiness scheduling problem with sequence-dependent setup times. Eur. J. Oper. Res. 2009, 193, 73–85. [Google Scholar] [CrossRef]
- Chen, W.N.; Zhang, J.; Chung, H.S.; Zhong, W.L.; Wu, W.G.; Shi, Y.H. A novel set-based particle swarm optimization method for discrete optimization problems. IEEE Trans. Evolut. Comput. 2010, 14, 278–300. [Google Scholar] [CrossRef]
- Cui, W.W.; Lu, Z.; Zhou, B.; Li, C.; Han, X. A hybrid genetic algorithm for non-permutation flow shop scheduling problems with unavailability constraints. Int. J. Comput. Integrated Manuf. 2016, 29, 944–961. [Google Scholar] [CrossRef]

| Dimension J | PV | Velocity | Ascending Order of PV | Sequence |
|---|---|---|---|---|
| 1 | 5.160 | 1.073 | 1.476 | 6 |
| 2 | 9.000 | −0.288 | 2.810 | 5 |
| 3 | 5.449 | −0.348 | 5.160 | 1 |
| 4 | 8.916 | 3.184 | 5.449 | 3 |
| 5 | 2.810 | −3.214 | 8.916 | 4 |
| 6 | 1.476 | 3.918 | 9.000 | 2 |
| 7 | 11.844 | 0.371 | 9.156 | 8 |
| 8 | 9.156 | 2.016 | 11.844 | 7 |
| Dimension J | PV | Sequence | ||
|---|---|---|---|---|
| 1 | 5.16 | 6 | 5.16 | 6 |
| 2 | 9 | 5 | 9 | 5 |
| 3 | 5.44 | 1 | 5.44 | 3 |
| 4 | 8.91 | 3 | 8.91 | 1 |
| 5 | 2.81 | 4 | 2.81 | 4 |
| 6 | 1.47 | 2 | 1.47 | 2 |
| 7 | 11.84 | 8 | 11.84 | 8 |
| 8 | 9.15 | 7 | 9.15 | 7 |
| Dimension J | PV | Sequence | ||
|---|---|---|---|---|
| 1 | 5.16 | 6 | 5.44 | 6 |
| 2 | 9 | 5 | 9 | 5 |
| 3 | 5.44 | 1 | 5.16 | 3 |
| 4 | 8.91 | 3 | 8.91 | 1 |
| 5 | 2.81 | 4 | 2.81 | 4 |
| 6 | 1.47 | 2 | 1.47 | 2 |
| 7 | 11.84 | 8 | 11.84 | 8 |
| 8 | 9.15 | 7 | 9.15 | 7 |
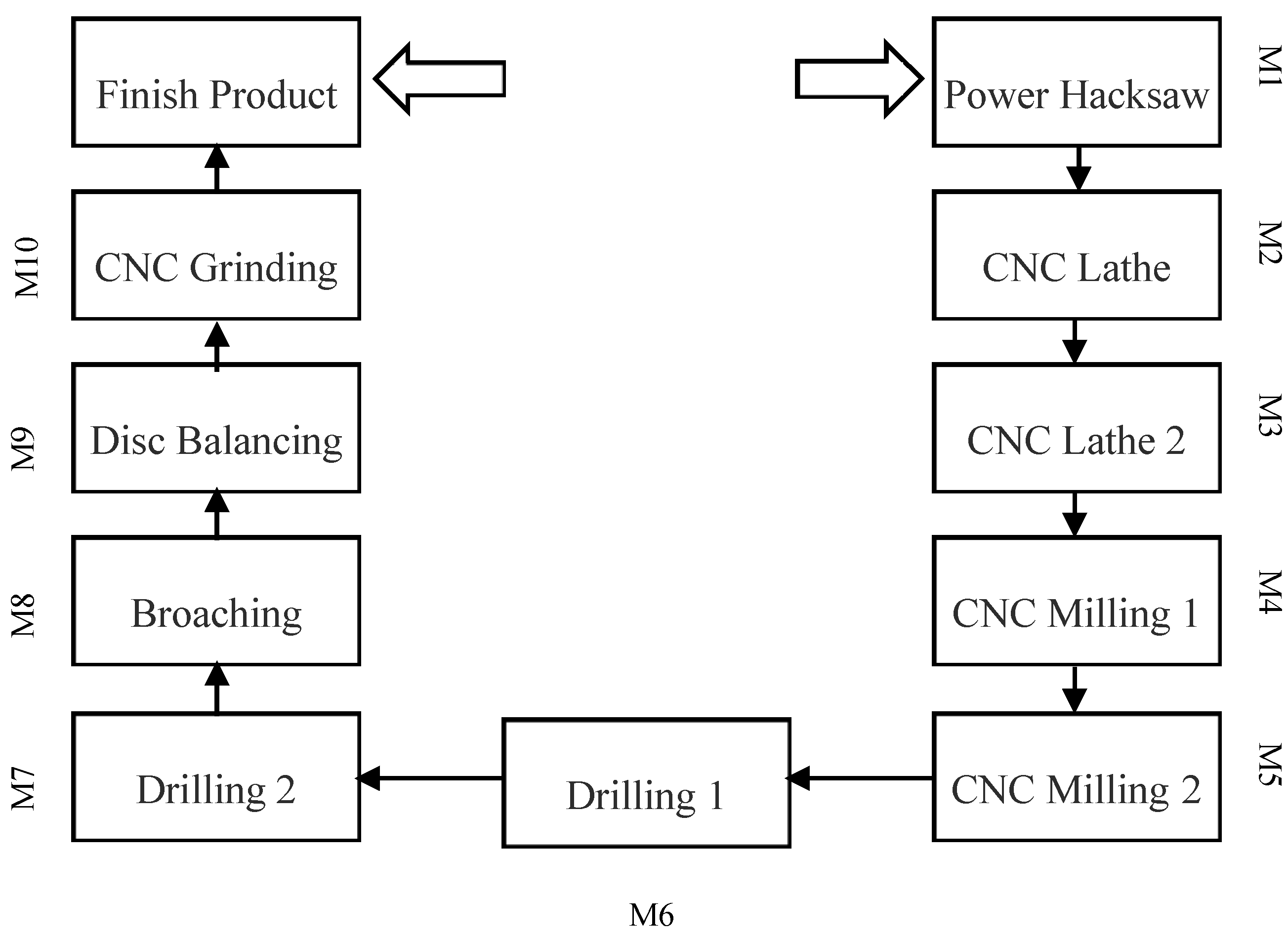
| Machines. Parts | M1 | M2 | M3 | M4 | M5 | M6 | M7 | M8 | M9 | M10 |
|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 2.3/1/0 | 2.5/0.15/0.15 | 0/0/0.25 | 2/0.65/0.15 | 0/0/0.15 | 0/0/0.2 | 2.8/0.25/0.25 | 1.75/0.5/0.15 | 0/0/0.2 | 0/0/0.25 |
| P2 | 2.5/0.25/0 | 1.6/0.3/0.15 | 0/0/0.2 | 3.3/0.25/0.25 | 1.25/0.75/0.15 | 0/0/0.25 | 0/0/0.2 | 0/0/0.15 | 3.25/0.33/0.3 | 0/0/0.2 |
| P3 | 0/0/0 | 2.31/0.25/0.2 | 2.4/0.2/0.2 | 1.5/0.5/0.25 | 1.55/0.25/0.2 | 3.1/0.45/0.3 | 0/0/0.25 | 1.5/1/0.2 | 0/0/0.15 | 2.35/0.15/0.25 |
| P4 | 3.2/1.25/0 | 0/0/0.2 | 2.3/0.26/0.25 | 0/0/0.15 | 4/0.55/0.15 | 0/0/0.2 | 2.25/0.35/0.25 | 2.75/0.85/0.15 | 1.6/1.11/0.2 | 1.85/0.45/0.3 |
| P5 | 1.2/0.35/0 | 2.25/0.35/0.2 | 2.5/0.15/0.15 | 2/0.75/0.25 | 0/0/0.2 | 3.25/0.75/0.25 | 1.75/0.75/0.3 | 0/0/0.2 | 0/0/0.2 | 3.33/0.75/0.3 |
| P6 | 2.25/0.45/0 | 1.51/0.5/0.15 | 1.6/1/0.2 | 2.75/0.35/0.15 | 2.85/0.35/0.35 | 0/0/0.15 | 1.25/0.56/0.2 | 3.5/1/0.3 | 2/1.52/0.15 | 0/0/0.15 |
| P7 | 1.35/1.5/0 | 0/0/0.2 | 2.33/0.55/0.15 | 0/0/0.2 | 0/0/0.2 | 2.45/0.35/0.15 | 1.85/0.85/0.2 | 1.75/0.65/0.3 | 0/0/0.2 | 2/1.5/0.15 |
| P8 | 1.9/0.5/0 | 1.35/0.52/0.15 | 0/0/0.2 | 2.6/0.25/0.25 | 1.85/0.26/0.15 | 0/0/0.15 | 1.45/0.15/0.25 | 0/0/0.15 | 2.33/0.45/0.2 | 0/0/0.2 |
| P9 | 1.75/0.4/0 | 0/0/0.2 | 1.3/0.75/0.25 | 1.85/0.46/0.15 | 0/0/0.2 | 1.75/0.5/0.3 | 3.5/0.45/0.2 | 1.5/0.75/0.25 | 2.25/0.5/0.35 | 0/0/0.2 |
| P10 | 1.5/0.75/0 | 0/0/0.15 | 2/1.5/0.3 | 0/0/0.25 | 2/1.1/0.15 | 2.25/0.75/0.15 | 0/0/0.2 | 2.45/0.35/0.35 | 3.5/1.75/0.3 | 3.5/0.25 |
| Particles | Iteration | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 7 | 9 | 2 | 5 | 1 | 3 | 10 | 4 | 6 |
| 2 | 8 | 7 | 6 | 2 | 5 | 1 | 3 | 10 | 4 | 9 |
| 3 | 8 | 7 | 9 | 2 | 5 | 1 | 3 | 10 | 6 | 4 |
| 4 | 2 | 5 | 1 | 8 | 7 | 9 | 3 | 10 | 4 | 6 |
| 5 | 10 | 4 | 6 | 2 | 5 | 1 | 3 | 8 | 7 | 9 |
| 6 | 2 | 10 | 7 | 8 | 4 | 9 | 6 | 5 | 3 | 1 |
| 7 | 2 | 1 | 7 | 8 | 4 | 9 | 6 | 5 | 3 | 10 |
| 8 | 2 | 7 | 10 | 8 | 4 | 9 | 6 | 5 | 3 | 1 |
| 9 | 8 | 4 | 9 | 2 | 10 | 7 | 6 | 5 | 3 | 1 |
| 10 | 5 | 3 | 1 | 8 | 4 | 9 | 6 | 2 | 10 | 7 |
| Criteria | Value |
|---|---|
| Swarm/Population Size | 10 |
| Inertia Weight | 1.2 |
| Constriction Factor | 0.97 |
| Total Number of Generations | 50 × 3 |
| Problem Set | Iterations | ILOG IB CPLEX | Time (sec) | Proposed NEPSO | Time (sec) |
|---|---|---|---|---|---|
| 5 × 10 | 20 | 40.9 | 31.232 | 37.2 | 12.133 |
| 7 × 7 | 20 | 48.8 | 29.220 | 44.6 | 11.544 |
| 8 × 10 | 20 | 52.3 | 52.644 | 45.1 | 15.330 |
| 12 × 5 | 20 | 46.7 | 48.321 | 39.5 | 14.221 |
| Problem Set | Iterations | % Gap | |||
|---|---|---|---|---|---|
| ILOG IB CPLEX | Time (sec) | Proposed MPSO | Time (sec) | ||
| 5 × 10 | 20 | 0.091 | 0.612 | 0.00 | 0.00 |
| 7 × 7 | 20 | 0.86 | 0.605 | 0.00 | 0.00 |
| 8 × 10 | 20 | 0.16 | 0.709 | 0.00 | 0.00 |
| 12 × 5 | 20 | 0.154 | 0.706 | 0.00 | 0.00 |
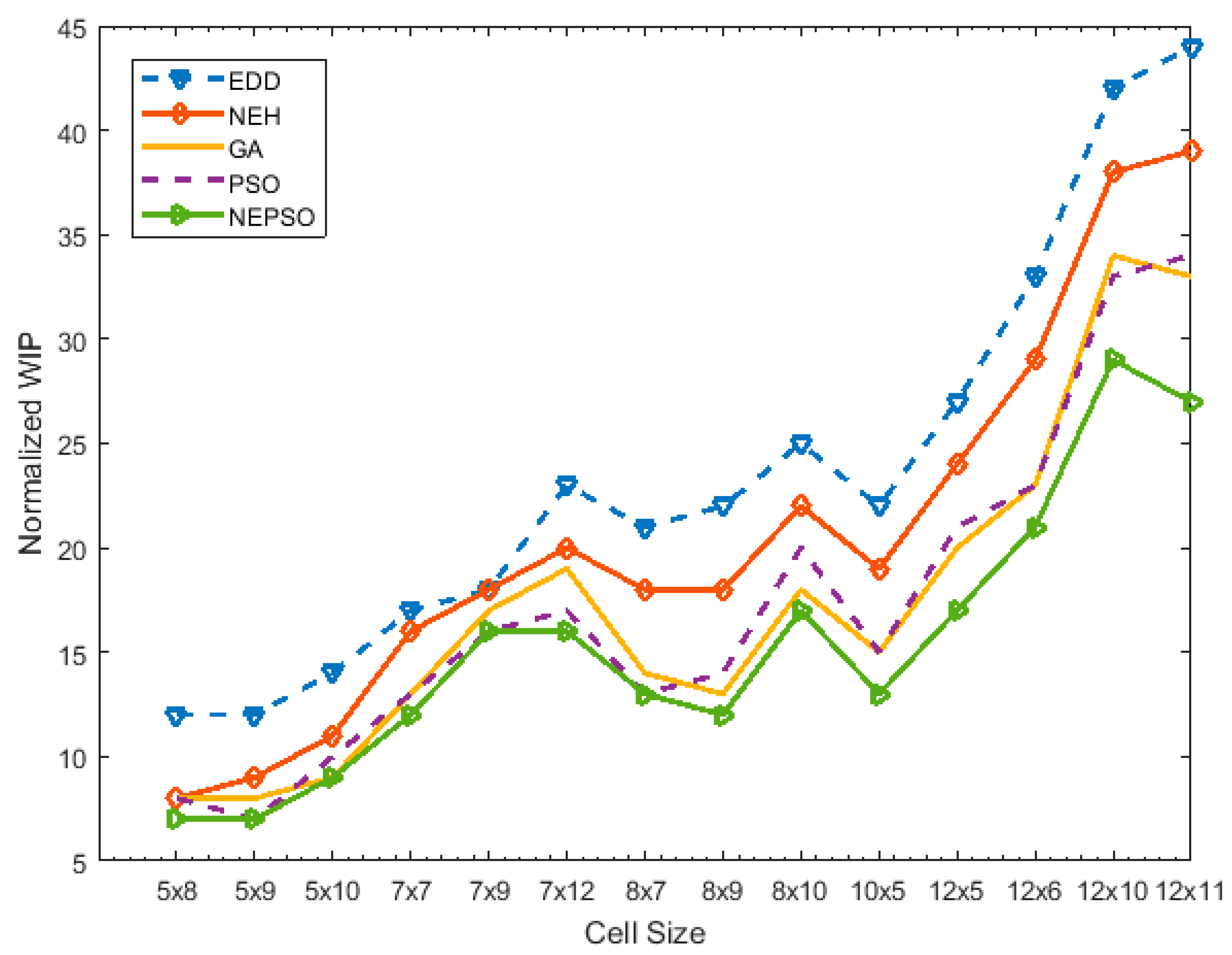
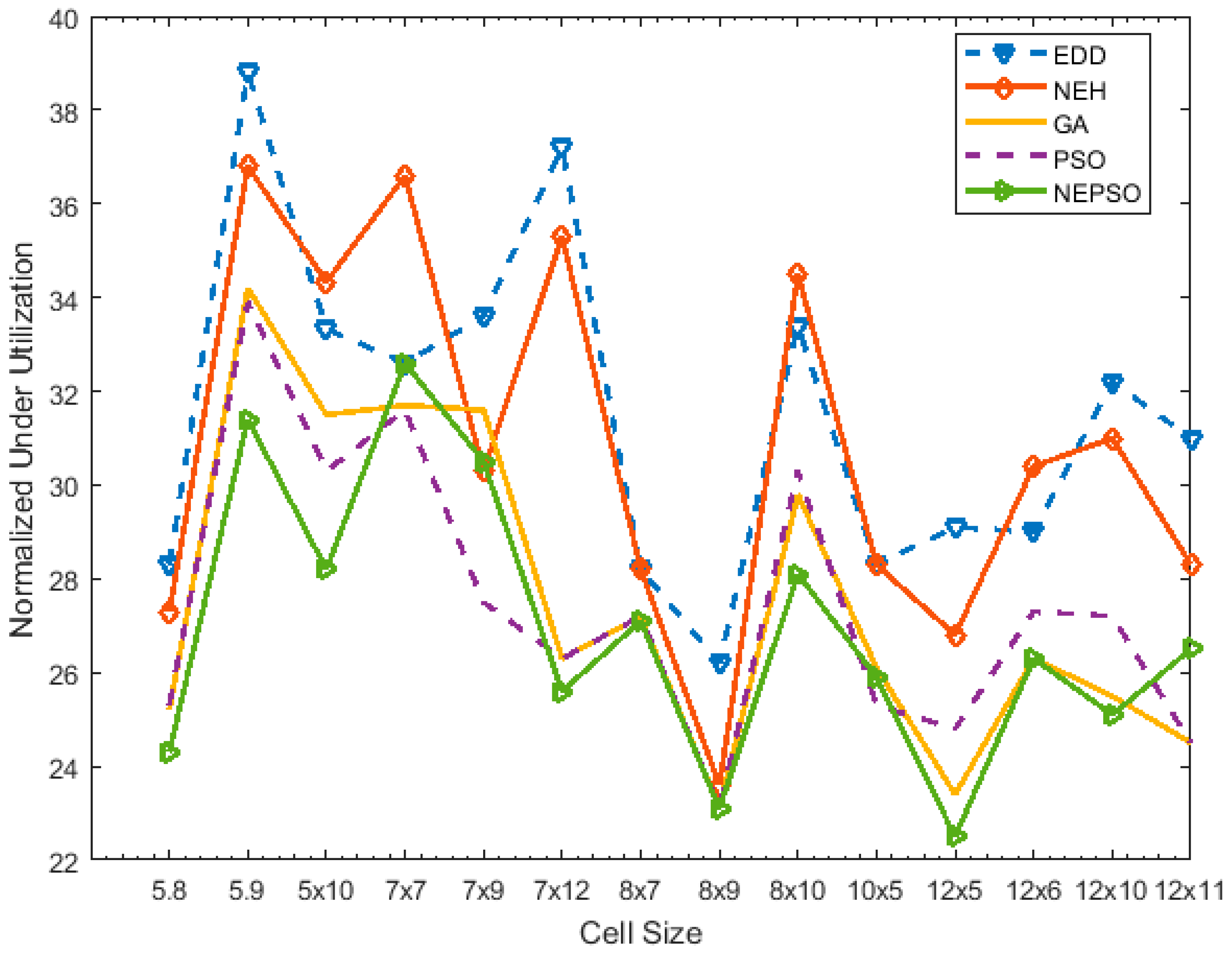
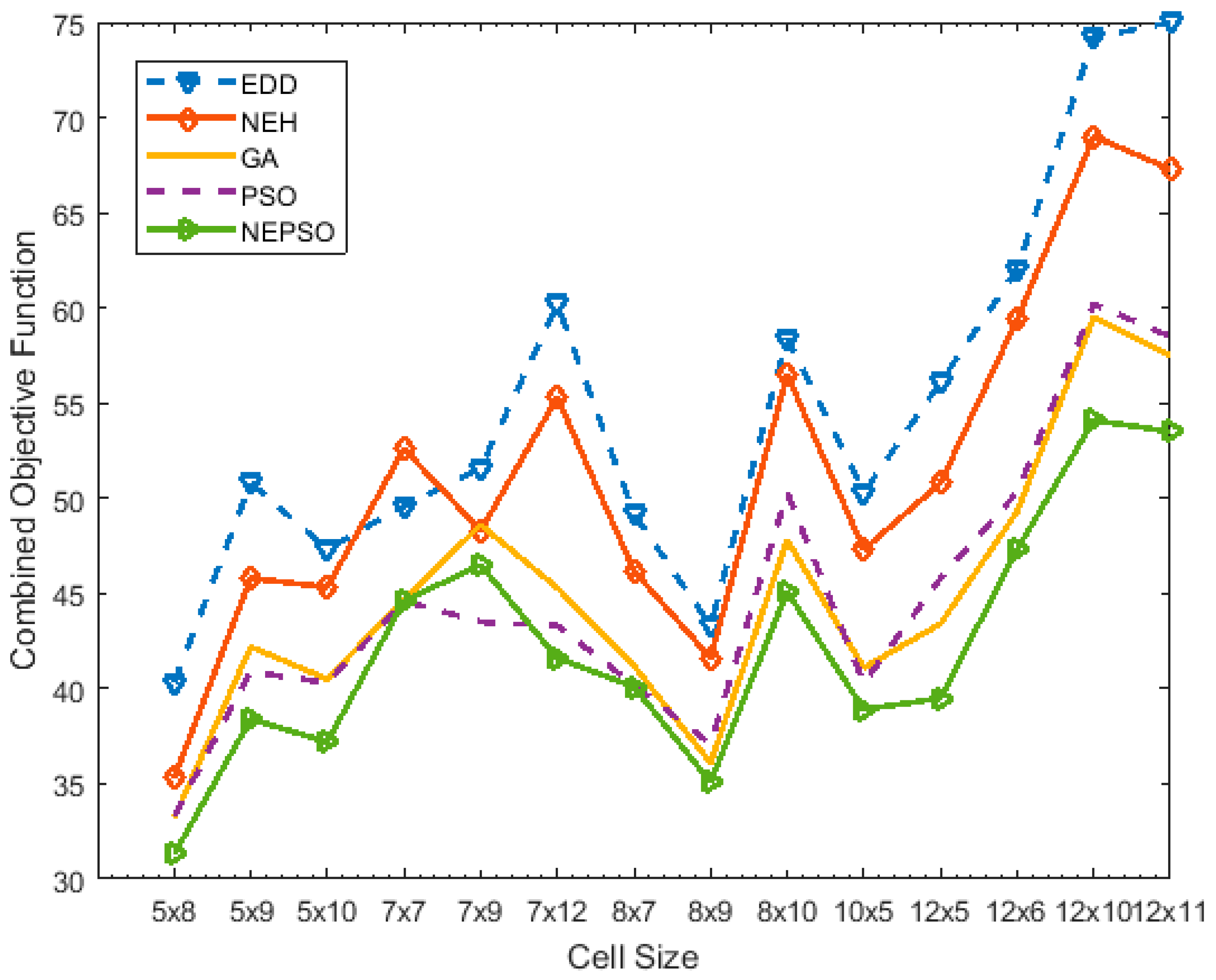
| S.No. | Cell Size | EDD | NEH | GA | PSO | NEPSO | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Normalized WIP | Normalized UU | C.O.F | Normalized WIP | Normalized UU | C.O.F | Normalized WIP | Normalized UU | C.O.F | Normalized WIP | Normalized UU | C.O.F | Normalized WIP | Normalized UU | C.O.F | % Improvement | ||
| 1 | 5 × 8 | 12 | 28.3 | 40.3 | 8 | 27.3 | 35.3 | 8 | 25.2 | 33.2 | 8 | 25.3 | 33.3 | 7 | 24.3 | 31.3 | 22.3 |
| 2 | 5 × 9 | 12 | 38.8 | 50.8 | 9 | 36.8 | 45.8 | 8 | 34.2 | 42.2 | 7 | 33.9 | 40.9 | 7 | 31.4 | 38.4 | 24.4 |
| 3 | 5 × 10 | 14 | 33.33 | 47.33 | 11 | 34.33 | 45.33 | 9 | 31.5 | 40.5 | 10 | 30.3 | 40.3 | 9 | 28.2 | 37.2 | 21.4 |
| 4 | 7 × 7 | 17 | 32.6 | 49.6 | 16 | 36.6 | 52.6 | 13 | 31.7 | 44.7 | 13 | 31.6 | 44.6 | 12 | 32.6 | 44.6 | 10.1 |
| 5 | 7 × 9 | 18 | 33.6 | 51.6 | 18 | 30.3 | 48.3 | 17 | 31.6 | 48.6 | 16 | 27.5 | 43.5 | 16 | 30.5 | 46.5 | 9.9 |
| 6 | 7 × 12 | 23 | 37.2 | 60.2 | 20 | 35.3 | 55.3 | 19 | 26.3 | 45.3 | 17 | 26.3 | 43.3 | 16 | 25.6 | 41.6 | 30.9 |
| 7 | 8 × 7 | 21 | 28.2 | 49.2 | 18 | 28.2 | 46.2 | 14 | 27.2 | 41.2 | 13 | 27.2 | 40.2 | 13 | 27.1 | 40.1 | 18.5 |
| 8 | 8 × 9 | 22 | 21.3 | 43.3 | 18 | 23.6 | 41.6 | 13 | 23.1 | 36.1 | 14 | 23.1 | 37.1 | 12 | 23.1 | 35.1 | 18.9 |
| 9 | 8 × 10 | 25 | 33.4 | 58.4 | 22 | 34.5 | 56.5 | 18 | 29.8 | 47.8 | 20 | 30.3 | 50.3 | 17 | 28.1 | 45.1 | 22.8 |
| 10 | 10 × 5 | 22 | 28.3 | 50.3 | 19 | 28.3 | 47.3 | 15 | 26.1 | 41.1 | 15 | 25.3 | 40.3 | 13 | 25.9 | 38.9 | 22.7 |
| 11 | 12 × 5 | 27 | 29.1 | 56.1 | 24 | 26.8 | 50.8 | 20 | 23.4 | 43.4 | 21 | 24.8 | 45.8 | 17 | 22.5 | 39.5 | 29.6 |
| 12 | 12 × 6 | 33 | 29 | 62 | 29 | 30.4 | 59.4 | 23 | 26.3 | 49.3 | 23 | 27.3 | 50.3 | 21 | 26.3 | 47.3 | 23.7 |
| 13 | 12 × 10 | 42 | 32.2 | 74.2 | 38 | 31 | 69 | 34 | 25.5 | 59.5 | 33 | 27.2 | 60.2 | 29 | 25.1 | 54.1 | 27.1 |
| 14 | 12 × 11 | 44 | 31 | 75 | 39 | 28.3 | 67.3 | 33 | 24.5 | 57.5 | 34 | 24.5 | 58.5 | 27 | 26.5 | 53.5 | 28.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalid, Q.S.; Arshad, M.; Maqsood, S.; Jahanzaib, M.; Babar, A.R.; Khan, I.; Mumtaz, J.; Kim, S. Hybrid Particle Swarm Algorithm for Products’ Scheduling Problem in Cellular Manufacturing System. Symmetry 2019, 11, 729. https://doi.org/10.3390/sym11060729
Khalid QS, Arshad M, Maqsood S, Jahanzaib M, Babar AR, Khan I, Mumtaz J, Kim S. Hybrid Particle Swarm Algorithm for Products’ Scheduling Problem in Cellular Manufacturing System. Symmetry. 2019; 11(6):729. https://doi.org/10.3390/sym11060729
Chicago/Turabian StyleKhalid, Qazi Salman, Muhammad Arshad, Shahid Maqsood, Mirza Jahanzaib, Abdur Rehman Babar, Imran Khan, Jabir Mumtaz, and Sunghwan Kim. 2019. "Hybrid Particle Swarm Algorithm for Products’ Scheduling Problem in Cellular Manufacturing System" Symmetry 11, no. 6: 729. https://doi.org/10.3390/sym11060729
APA StyleKhalid, Q. S., Arshad, M., Maqsood, S., Jahanzaib, M., Babar, A. R., Khan, I., Mumtaz, J., & Kim, S. (2019). Hybrid Particle Swarm Algorithm for Products’ Scheduling Problem in Cellular Manufacturing System. Symmetry, 11(6), 729. https://doi.org/10.3390/sym11060729





