Vibration Analysis of a Guitar considered as a Symmetrical Mechanical System

Abstract

This paper aimed to use the symmetry that exists to the body of a guitar to ease the analysis behavior to vibrations. Symmetries can produce interesting properties when studying the dynamic and steady-state response of such systems. These properties can, in some cases, considerably decrease the effort made for dynamic analysis at the design stage. For a real guitar, these properties are used to determine the eigenvalues and eigenvectors. Finite element method (FEM) is used for a numerical modeling and to prove the theoretically determined properties in this case. In this paper, different types of guitar plates related to symmetrical reinforcement patterns were studied in terms of modal analysis performed using finite element analysis (FEA). The dynamic response differs in terms of amplitude, eigenvalues, modal shapes in accordance with number and pattern of stiffening bars. In this study, the symmetrical and asymmetric modes of modal analysis were highlighted in the case of constructive symmetrical structures.

1. Introduction

The dynamical study of mechanical systems with elastic elements that present symmetries or have identical parts occurs in many engineering fields, especially in mechanical engineering and civil engineering, but also in the automotive industry and aerospace engineering. In all engineering fields, there are certain products or parts of products or components containing repetitive or identical elements where different types of symmetry can occur. The study of such systems was made by many researchers [1,2,3]. In civil engineering for example, most buildings, works of art or halls have, in their structure, identical parts and symmetries. This has happened since antiquity for different causes. First, as an easier, faster and a cheaper way to design, then for easy manufacturing and (less important for engineers but important to the beneficiaries) for aesthetic reasons. Systems consisting of two identical parts represent a particular case of these types of problems. Such systems exhibit interesting vibration properties which computation is presented in literature [4,5,6]. Depending on the types of structural elements (rod and shell), two methods were developed, namely asymptotic and variational, which are presented by Le [7] from a mathematical point of view, emphasizing the formulation of boundary-value problems. Zhou [8] presents an exact solution of free vibration of a thin rectangular plate attached with sprung masses based on differential equations.

For this type of problem, its eigenmodes can be classified in symmetrical modes and skew-symmetrical modes. The guitar is a vibrant mechanical system where we can easily identify a symmetry plan in terms of model geometry. For this reason, it can fit into the class of mechanical systems described above and the vibration study of it can be much simplified. In this paper, the symmetrical system of the guitar is analyzed and the vibration properties that are the result of considering this symmetry are revealed. An example for a real system is made in the second part of the paper. Derveaux et al. [9] developed a guitar model based on advanced numerical methods to simulate the three-dimensional sound-pressure field of a guitar in the time domain. Due to the complexity of the problem, the main parts of guitar (plates, body, strings, air from cavity, holes) that are implied in acoustic radiation and vibration were simplified in terms of mathematical models and interactions. Compare to [9], in this paper, the frequency spectrum and eigenmodes of different symmetric types of guitar plates were analyzed and in future works, the guitars bodies with different bars pattern will be numerical modeled. Elejabarrieta et al. [10] analyzed the influence of each component from acoustic box of guitar on the vibrational behavior using finite element method in a progressive manner of constructive system.

These types of problems occur frequently in practical applications; many mechanical systems exhibit different kinds of symmetry properties, resulting from a design process for constructive, simplistic, logistic or cost considerations. Knowing these properties allows to increase the precision of calculations in such issues. Properties determined by symmetries have been observed by researchers and are mainly used in the static analysis. They are presented in the classical courses of Strength of Material or Structural Analysis. From a historical point of view, the symmetries in mechanics have been studied by mathematicians [11,12]. Symmetry effects occur in the writing the motion equations, but the solutions can be symmetric and antisymmetric according to the assumed boundary conditions [7]. In accordance with [13], the methods of mechanics (Lagrangian and Hamiltonian) use symmetry to solve complex problems. Moreover, these methods and symmetry principles are based on the developments of string theory. In case of the sandwich plate, [13] present the solution of symmetric vibration and the effects of the elastic, geometric and inertia parameters on dynamic behavior of plate.

Unfortunately, there are fewer applications in practice. In January 2018, a special issue of the Symmetry magazine dedicated to applications in Structural Mechanics (Civil Engineering and Symmetry - 2018, A special issue of Symmetry -ISSN 2073-8994) was launched. A European project was also funded for the study of these types of problems (Mechanics and Symmetry in Europe: the FP5-Human Potential). The latter held courses at the Solid Mechanics Centre—International Center for Mechanical Sciences (CISM) at UDINE (similarly, the Symmetry and Group Theoretical Methods in Mechanics held lectures in the International Centre for Mechanical Sciences in September 7, 2015–September 11, 2015) [14,15,16,17,18,19]. In the vibration field, the effect of symmetries was less used, but there are papers that began to study this type of problem [20,21]. There are, however, many situations that can be studied and that is why paper aims to complete the studied case.

The aim of this study is to present the solutions of eigenvalues and eigenvectors based on symmetry principles in case of a symmetric structure as guitar plate. The effect of inertia parameters (fan struts and bars) with respect the symmetry provided in this paper can be used as benchmark for optimal soundboard strutting system of guitar during the manufacturing.

2. Guitar as a Mechanical System Subjected to Vibration

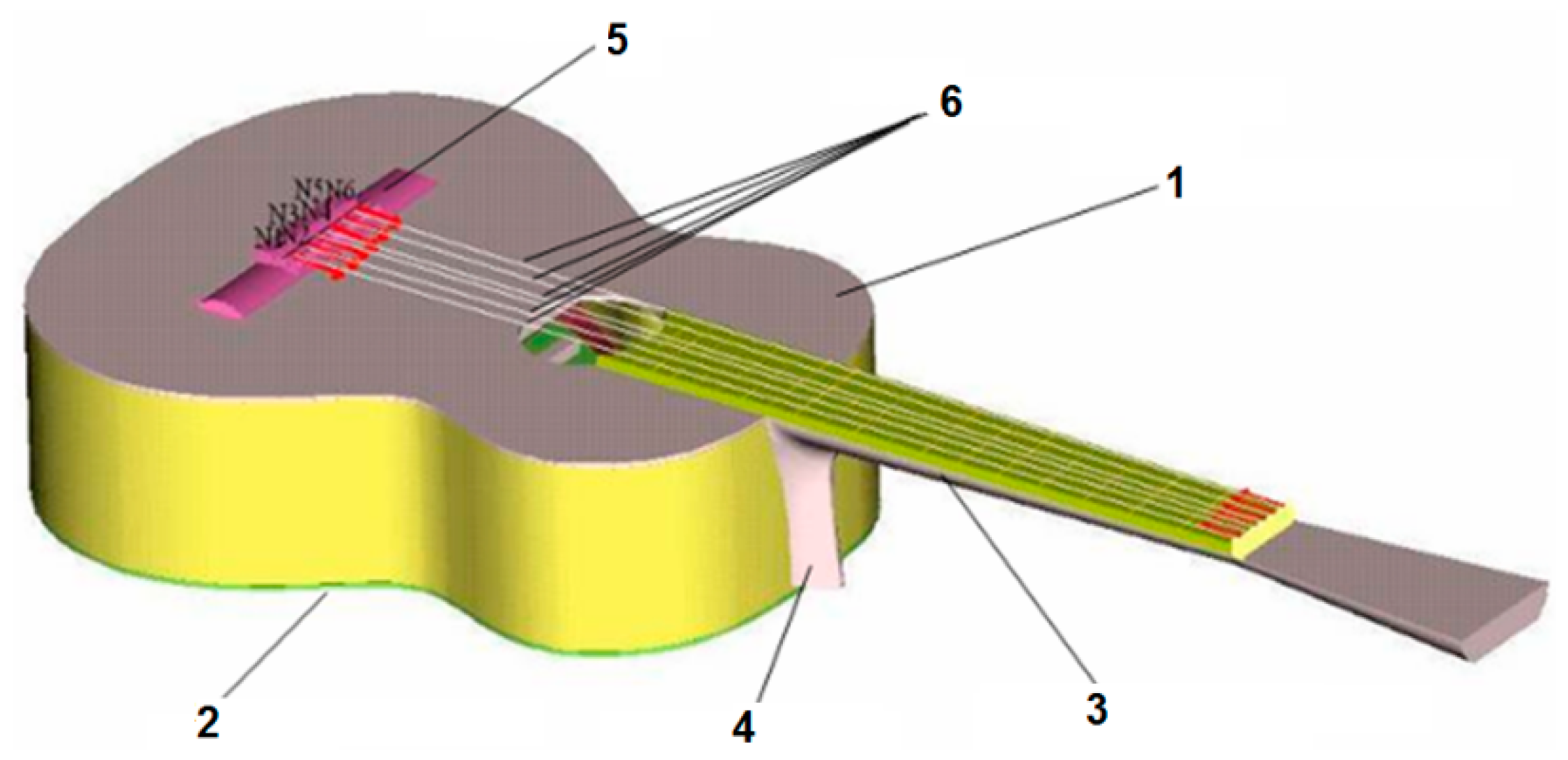
Being a complex structure, modeling of the guitar requires the identification of the component parts from the point of view of the geometric model represented by them, the system of loads acting on them, as well as the mechanical connections between the structures and the ground. Thus, in the structure of the guitar, nearly all types of geometric models can be identified by the strength of the materials, namely: wire, plates, trusses, massive blocks (Figure 1). In the paper the object of the main theoretical interest is the structure of plates with different degrees of complexity and with various stiffening systems [21,22,23].

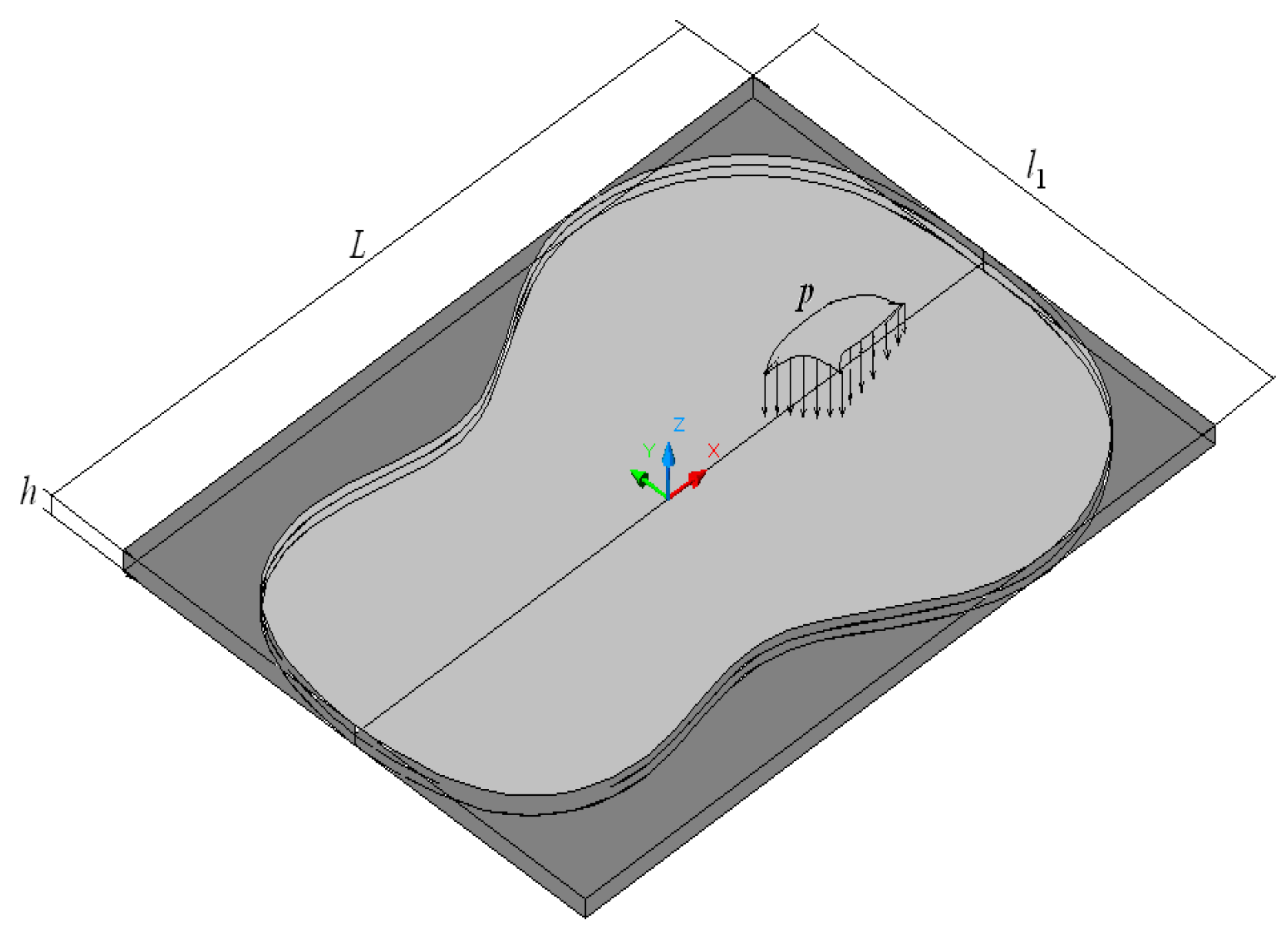
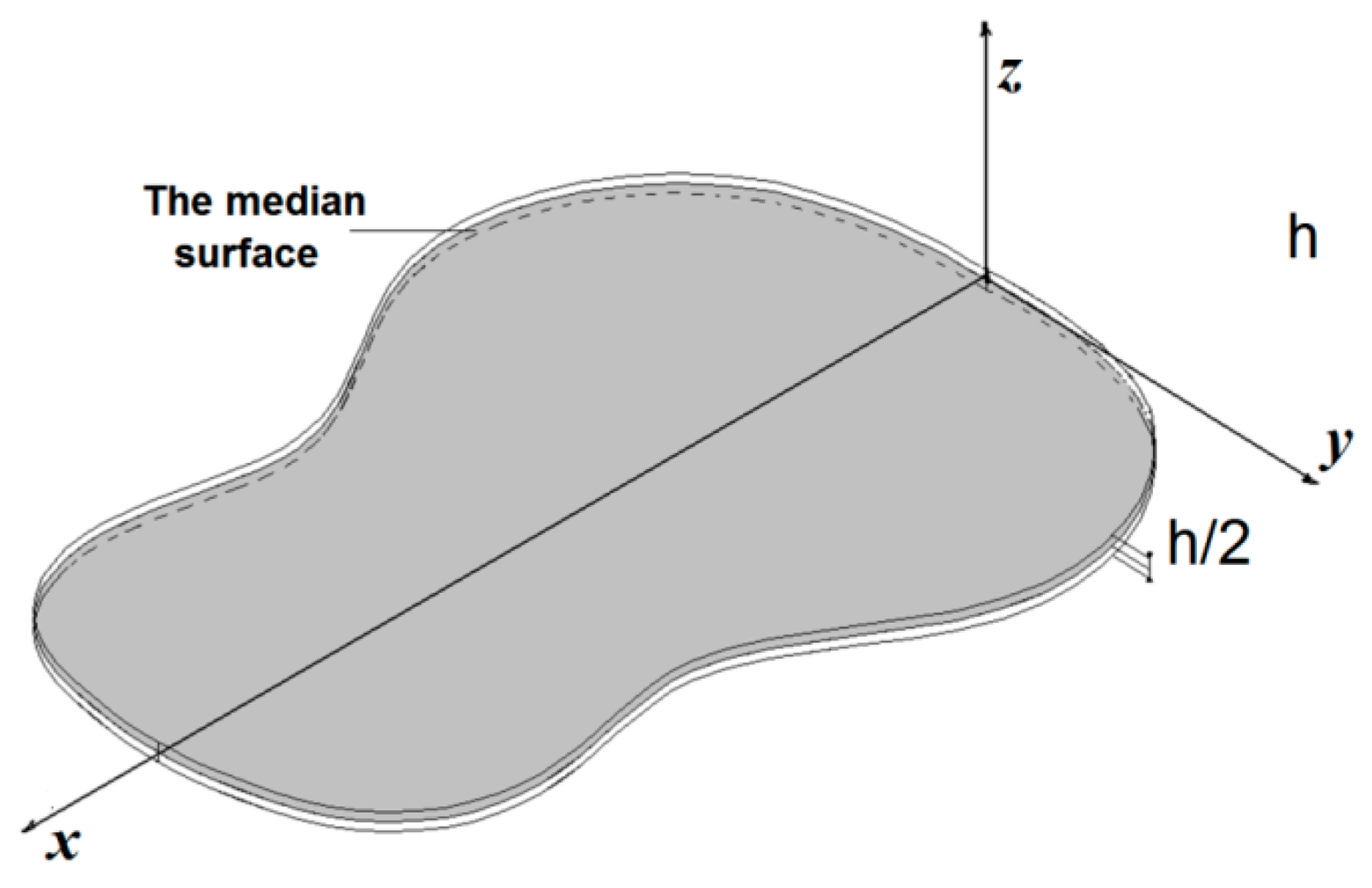
Consider the guitar plate, presented in Figure 2. The density of the material is $\rho$. This it is in transverse bending vibration.

Based on Kirchhoff’s hypotheses and applying the d’Alembert principle or another energy method, it is obtained the dynamic response of the plate [23,24]:

$$\Delta \Delta w\left(x,y,t\right)+\frac{\rho h}{D}\frac{{\partial }^{2}w\left(x,y,t\right)}{\partial t^2}=\frac{p\left(x,y,t\right)}{D},$$

(1)

where $w\left(x,y,t\right)$—the normal instantaneous displacement on the median surface of the plate; $D=\frac{E{h}^3}{12\left(1-{\nu }^2\right)}$—bending modulus of the plate, h—thickness of plate, E—the modulus of elasticity and ν—Poisson’s coefficient; $p\left(x,y,t\right)$—the distributed load acting perpendicular to the median surface of the plate; $\Delta =\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}$—Laplacian differential operator.

If $p\left(x,y,t\right)=0$, from (1) it results in the free transverse vibration Equations (2):

$$\frac{{\partial }^{4}w\left(x,y,t\right)}{\partial x^4}+2\frac{{\partial }^{4}w\left(x,y,t\right)}{\partial x^2\partial y^2}+\frac{{\partial }^{4}w\left(x,y,t\right)}{\partial y^4}=-\rho \frac{h}{D}\frac{{\partial }^{2}w\left(x,y,t\right)}{\partial t^2},$$

(2)

To solve (1), the Fourier-Bernoulli method is used, finding a solution under the form:

$$w\left(x,y,t\right)=w\left(x,y\right)\cdot w\left(t\right),$$

(3)

Using (3) in (2) results in:

$$\frac{D}{\rho h}\frac{1}{w\left(x,y\right)}\left[\frac{d^{4}w\left(x,y\right)}{d{x}^4}+2\frac{d^{4}w\left(x,y\right)}{d{x}^{2}d{y}^2}+\frac{d^{4}w\left(x,y\right)}{d{y}^4}\right]=-\frac{1}{w\left(t\right)}\frac{d^2{w}_t\left(t\right)}{d{t}^2}={\omega }_{}^2,$$

(4)

where $\omega$ is an arbitrary constant.

From (4), we have:

$$\{\begin{array}{c}\frac{d^2{w}_t\left(t\right)}{d{t}^2}+{\omega }_{}^2{w}_t\left(t\right)=0\\ \frac{d^{4}w\left(x,y\right)}{d{x}^4}+2\frac{d^{4}w\left(x,y\right)}{d{x}^{2}d{y}^2}+\frac{d^{4}w\left(x,y\right)}{d{y}^4}={\omega }_{}^2\frac{\rho h}{d}w\left(x,y\right)\end{array},$$

(5)

For Equation (5), the solution is [25,26,27]:

$$w_t\left(t\right)=A_{}^{\left(t\right)}\cos \left({\omega }_{}t-{\varphi }_{}\right),$$

(6)

$A_{}^{\left(t\right)}$ and $\varphi$ are integration constants depending on boundary conditions.

A good approximation for the guitar domain is a rectangular domain (Figure 2). In this case, the second Equation (5) should satisfy the boundary conditions. Some common boundary conditions are:

• In case of plate with one free edge (where $x=x_0$), we assume that the bending moment $M_y$ and shear force $T_{zx}$ are zero. Thus, the condition where the bending moment along the free edge is zero, is:

  $$\begin{array}{c}{\left(\frac{{\partial }^{2}w\left(x,y\right)}{\partial x^2}+\nu \frac{{\partial }^{2}w\left(x,y\right)}{\partial y^2}\right)|}_{x=x_0}=0,\\ {\left(\frac{{\partial }^{3}w\left(x,y\right)}{\partial x^3}+(2-\nu )\frac{{\partial }^{3}w\left(x,y\right)}{\partial x\partial y^2}\right)|}_{x=x_0}=0,\end{array}$$

  (7)
• In case of the plate being supported at all edges $\left(x=x_0\right)$, the displacement are null and along the all edges, the bending moment is zero, too. In Equation (8), the boundary conditions are readily seen to be satisfied exactly:

  $$\begin{array}{l}{w\left(x,y\right)|}_{x=x_0}=0\\ {\left(\frac{{\partial }^{2}w\left(x,y\right)}{\partial x^2}+\nu \frac{{\partial }^{2}w\left(x,y\right)}{\partial y^2}\right)|}_{x=x_0}=0\end{array}$$

  (8)
• For a plate with one clamped edge $\left(x=x_0\right)$, the displacement and rotation in a perpendicular plan to the side are null:

  $$\begin{array}{l}{w\left(x,y\right)|}_{x=x_0}=0\\ {\left(\frac{\partial w}{\partial x}\right)|}_{x=x_0}=0\end{array}$$

  (9)

In [7], Le makes the difference between the clamped edge and the fixed edge of a structure considering based on the variational principle.

When the contour is not rectangular or circular and when the support is continuous, as is the case with the guitar plates, the boundary conditions become more complicated. In the particular case of the guitar plate supported at all edges, the boundary conditions (8) result in:

$$\{\begin{array}{c}{w\left(x,y\right)|}_{\begin{array}{c}x=0\\ x=a\end{array}}=0,{\left(\frac{{\partial }^{2}w\left(x,y\right)}{\partial x^2}+\nu \frac{{\partial }^{2}w\left(x,y\right)}{\partial y^2}\right)|}_{\begin{array}{c}x=0\\ x=a\end{array}}=0\\ {w\left(x,y\right)|}_{\begin{array}{c}y=0\\ y=b\end{array}}=0,{\left(\frac{{\partial }^{2}w\left(x,y\right)}{\partial y^2}+\nu \frac{{\partial }^{2}w\left(x,y\right)}{\partial x^2}\right)|}_{\begin{array}{c}y=0\\ y=b\end{array}}=0\end{array},$$

(10)

It can be shown that the function $w\left(x,y\right)$ in the conditions (10) is expressed by (11):

$$w\left(x,y\right)=A_{}^{\left(x,y\right)}\sin \frac{\pi m}{L}x\sin \frac{\pi n}{l_1}y,\left(m,n=1,2,\dots \right),$$

(11)

where m and n are the numbers of vibration nodes.

The eigenvalues corresponding of the plate with the eigenmode “mn” are:

$${\omega }_{m,n}={\pi }^2\left(\frac{m^2}{L^2}+\frac{n^2}{l_1{}^2}\right)\sqrt{\frac{D}{\rho h}},\left(m,n=1,2,\dots \right),$$

(12)

According to Equation (12) the considered rectangular plate has duplicate eigenfrequencies due to an arbitrary linear combination of the two modes [28]. Thus, one of the two eigenfrequencies will hold the line, while the other varies with the parameters of the system [9].

3. Properties of a System Consisting of Two Identical Parts

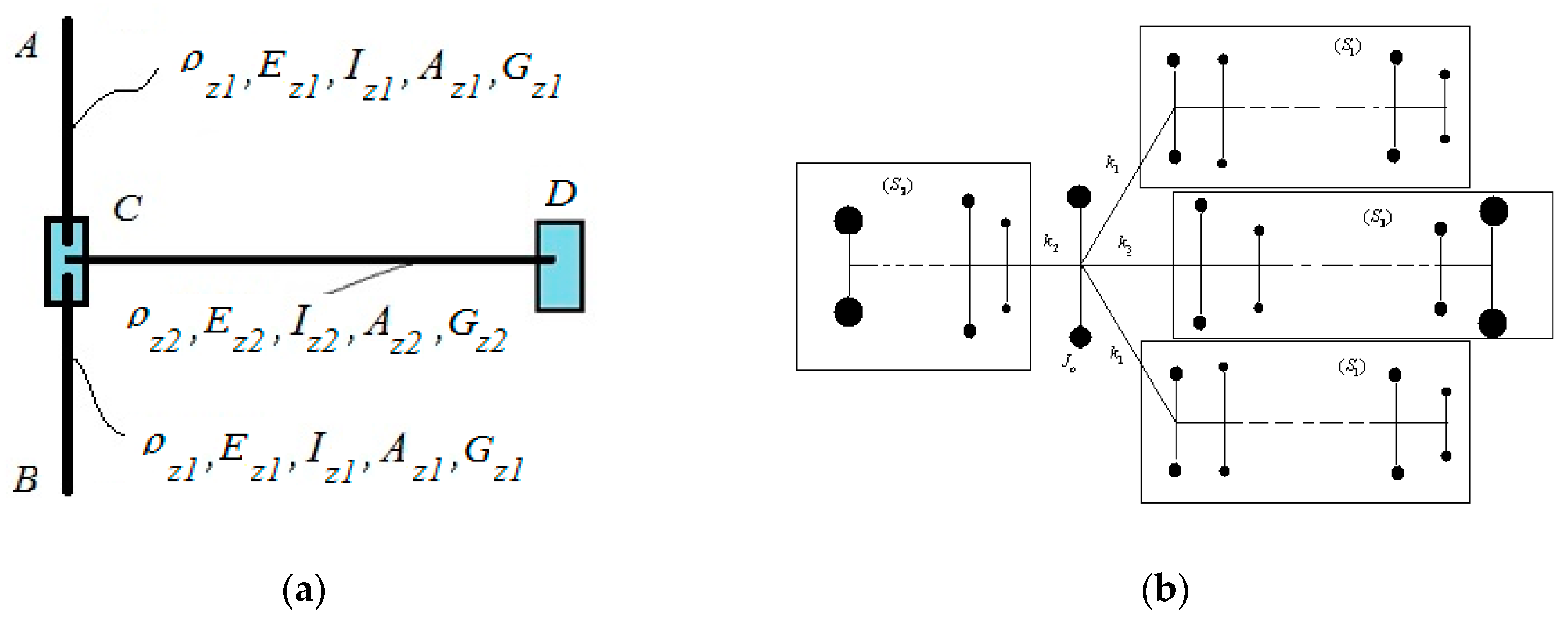
From the big class of systems that have different types of symmetry, we will study a particular one: a system made by two identical parts. Two example are presented in Figure 3a,b, [12,19].

From a mechanical point of view, the guitar can be reduced to a structure consisting of two parts: a bar represented by the neck of the guitar that is clamped on the body and the sound box (guitar body), which is made of coupled plates. The strings system that loads the two components is compounded by simple and complex wires which give an asymmetry of the entire acoustical structure.

If the strings are neglected, from the geometrical point of view, the guitar plate has a symmetry plan (xz) and can be considered as being composed of two identical parts connected to each other, as can be seen in Figure 4 [29]. This symmetry is also respected as material so that the wood used in the structure of the guitar plates has a symmetrical structure. In the following, we will highlight the vibration properties of such a system.

To determine the mechanical response of such type of structure we try to model the system. The whole structure (S) can be considered as being composed by two identical sub-structure, denoted with (S₁) and (S_r) (Figure 3 and Figure 4). We denote by Δ_a the common nodes of the two structures (S₁), with Δ_l the nodes of the left structure (S₁), different from Δ_a and with Δ_r the nodes of the right structure (S_r), different from Δ_a. The equations of the undamped free vibrations of the entire structure (S), the left substructure (S₁) (Equation (13)) and the right substructure (S_r) (Equation (14)) are, respectively [4,28,29,30]:

$$\left[\begin{array}{cc}{m}_a& m_{ab}\\ m_{ab}& m_b\end{array}\right]\left\{\begin{array}{c}{\ddot{\Delta }}_l\\ {\ddot{\Delta }}_a\end{array}\right\}+\left[\begin{array}{cc}{k}_a& k_{ab}^{}\\ k_{ab}^T& k_b\end{array}\right]\left\{\begin{array}{c}{\Delta }_l\\ {\Delta }_a\end{array}\right\}=0,$$

(13)

$$\left[\begin{array}{cc}{m}_a& m_{ab}\\ m_{ab}& m_b\end{array}\right]\left\{\begin{array}{c}{\ddot{\Delta }}_r\\ {\ddot{\Delta }}_a\end{array}\right\}+\left[\begin{array}{cc}{k}_a& k_{ab}^{}\\ k_{ab}^T& k_b\end{array}\right]\left\{\begin{array}{c}{\Delta }_r\\ {\Delta }_a\end{array}\right\}=0,$$

(14)

$$\left[\begin{array}{ccc}{m}_a& 0& m_{ab}\\ 0& m_a& m_{ab}\\ m_{ab}& m_{ab}& m_{bb}\end{array}\right]\left\{\begin{array}{c}{\ddot{\Delta }}_l\\ {\ddot{\Delta }}_r\\ {\ddot{\Delta }}_a\end{array}\right\}+\left[\begin{array}{ccc}{k}_a& 0& k_{ab}\\ 0& k_a& k_{ab}\\ k_{ab}^T& k_{ab}^T& k_{bb}\end{array}\right]\left\{\begin{array}{c}{\Delta }_l\\ {\Delta }_r\\ {\Delta }_a\end{array}\right\}=0,$$

(15)

It is obvious that the matrices involved in the Equations (13) and (14) are the same. This means that the problem of eigenvalues and eigenvectors offer the same solution in the both cases. For the full system (Equation (15)), we have the following property (proved for a more general context in [26]): P1—the eigenvalues for the subsystem (S_l) (for the differential, Equations (1) or (2)) are eigenvalues for the system (S)).

This property expresses the fact that the eigenvalues corresponding to the subsystem (S_l) verified the eigenvalues problem for the whole system (S). That means that the solutions of Equations (16) are also solutions of the algebraic Equation (17):

$$\left|\begin{array}{cc}{k}_a-{\omega }^2{m}_a& k_{ab}^T-{\omega }^2{m}_{ab}\\ k_{ab}^T-{\omega }^2{m}_{ab}& k_b-{\omega }^2{m}_b\end{array}\right|=0,$$

(16)

$$\left|\begin{array}{ccc}{k}_a-{\omega }^2{m}_a& 0& k_{ab}-{\omega }^2{m}_{ab}\\ 0& k_a-{\omega }^2{m}_a& k_{ab}-{\omega }^2{m}_{ab}\\ k_{ab}^T-{\omega }^2{m}_{ab}^T& k_{ab}^T-{\omega }^2{m}_{ab}^T& k_b-{\omega }^2{m}_b\end{array}\right|=0,$$

(17)

which implies that the polynomial in ${\omega }^2$ expressed by the Equation (17) is divided by the polynomial in ${\omega }^2$ expresses by the Equation (16).

If we denote:

$$A_{11}=\left[k_a-{\omega }^2{m}_a\right];A_{13}=A_{31}=\left[k_{ab}-{\omega }^2{m}_{ab}\right];A_{33}=\left[k_b-{\omega }^2{m}_b\right],$$

(18)

and:

$$S=\left[\begin{array}{ccc}{A}_{11}& 0& A_{13}\\ 0& A_{11}& A_{13}\\ A_{31}& A_{31}& A_{33}\end{array}\right],$$

(19)

the characteristic Equation of (17) can be written:

$$\det \left[\begin{array}{ccc}{A}_{11}& 0& A_{13}\\ 0& A_{11}& A_{13}\\ A_{31}& A_{31}& A_{33}\end{array}\right]=\det \left[S\right]=0$$

(20)

To determine the eigenvectors, once the eigenvalues are known, it must to solve the linear system [17,19,31]:

$$\left[S\right]\left\{\mathsf{\Phi }\right\}=0,$$

(21)

where we noted with $\left\{\mathsf{\Phi }\right\}$ as the eigenvectors. Any eigenvalue corresponds to an eigenvector. Concerning these, the following two properties are interesting for our research: P2—for the common eigenvalues of the system presented in Figure 3a and of the system presented in Figure 3b, the eigenvectors are of the form:

$$\mathsf{\Phi }=\left\{\begin{array}{c}{\mathsf{\Phi }}_1\\ -{\mathsf{\Phi }}_1\\ 0\end{array}\right\},$$

(22)

The components of the eigenmodes, corresponding to the two identical parts are skew symmetric, the other components are zero-we call these skewsymmetric eigenmodes.

Proof: 

the existence of common eigenvalues for the system presented in Figure 3a,b is proven by the previous presented theorem P1. With the eigenvalues obtained from (20), the linear homogeneous system offers the eigenvectors:

$$\left[\begin{array}{ccc}{A}_{11}& 0& A_{13}\\ 0& A_{11}& A_{13}\\ A_{31}& A_{31}& A_{33}\end{array}\right]\left\{\begin{array}{c}{\mathsf{\Phi }}_l\\ {\mathsf{\Phi }}_r\\ {\mathsf{\Phi }}_a\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\\ 0\end{array}\right\},$$

(23)

with:

$$\det A_{11}=0,$$

(24)

Equation (24) implies that we can find a vector $\mathsf{\Phi }{}_l$, so that:

$$A_{11}{\mathsf{\Phi }}_l=0,$$

(25)

and then (23) becomes:

$$A_{13}{\mathsf{\Phi }}_a=0,$$

(26)

$$A_{11}{\mathsf{\Phi }}_r+A_{13}{\mathsf{\Phi }}_a=0,$$

(27)

$$A_{31}\left({\mathsf{\Phi }}_l+{\mathsf{\Phi }}_r\right)+A_{33}{\mathsf{\Phi }}_a=0,$$

(28)

From (26), we immediately have:

$${\mathsf{\Phi }}_a=0,$$

(29)

and by replacing in (28), we obtain ${\mathsf{\Phi }}_l={\mathsf{\Phi }}_r$, which also verifies (27) if we consider (25). If we note: ${\mathsf{\Phi }}_l={\mathsf{\Phi }}_1$, we easily obtain (22).

P3—for the other eigenvalues, (not obtained from (S_l)), the eigenvectors are of the form (symmetric eigenmodes) [32,33]:

$$\mathsf{\Phi }=\left\{\begin{array}{c}{\mathsf{\Phi }}_1\\ {\mathsf{\Phi }}_1\\ {\mathsf{\Phi }}_3\end{array}\right\},$$

(30)

The components of the eigenmodes corresponding to the two identical beams are the same—we call this symmetric eigenmodes [34]. ☐

Proof: 

for these eigenvalues we have to solve the system (23), considering $\det A_{11}\ne 0$, or:

$$A_{11}{\mathsf{\Phi }}_l+A_{13}{\mathsf{\Phi }}_a=0,$$

(31)

$$A_{11}{\mathsf{\Phi }}_r+A_{13}{\mathsf{\Phi }}_a=0,$$

(32)

$$A_{31}\left({\mathsf{\Phi }}_l+{\mathsf{\Phi }}_r\right)+A_{33}{\mathsf{\Phi }}_a=0$$

(33)

By subtracting (31) from (32), the following can be obtained:

$$A_{11}\left({\mathsf{\Phi }}_l-{\mathsf{\Phi }}_r\right)=0$$

(34)

However, $\det A_{11}\ne 0$, then we have ${\mathsf{\Phi }}_l-{\mathsf{\Phi }}_r=0$ so ${\mathsf{\Phi }}_l={\mathsf{\Phi }}_r={\mathsf{\Phi }}_1$. ☐

4. Finite Element Analysis (FEA) of Guitar Plates

The behavior of wood (a commonly used material for the guitar plate) under the action of sound is influenced by the sound energy that comes into contact with the wood and, on the other hand, by the quality of the wood material. It is known that wood is an orthotropic material characterized by three planes of symmetry. The macro and microscopic structure of the wood: cell membrane construction, dimensions and cohesion fibers, chemicals structure, the humidity and temperature of the wood, the elastic properties and orientation of the structure with respect to the dynamic force influences the dynamic response of plates [35]. As a result of vibrations, the internal friction occurring in the wood transforms the original sound energy into a modified sound energy, obtaining a resonance phenomenon as well as a caloric energy due to intermolecular energy exchanges.

The most important acoustic property of wood is the ability to receive sounds with a frequency close to or identical to the frequency of its membranes. This produces the resonance phenomenon that leads to the amplification of sounds and their timber enriched with overtones due to its complex and anisotropic structure. Depending on the external excitation frequency period, the resonance occurs whenever the pulse of forced vibration passes in the vicinity of eigenfrequency of the wood [28,29]. The complex phenomena that develop during cyclical stresses are structural and acoustic in nature, interdependent with each other. From this point of view, the analytical theories underlying the dynamic guitars’ response mainly deal with one aspect, which is why a series of simplifying hypotheses are introduced. However, the calculations that use these theories are numerous and laborious. 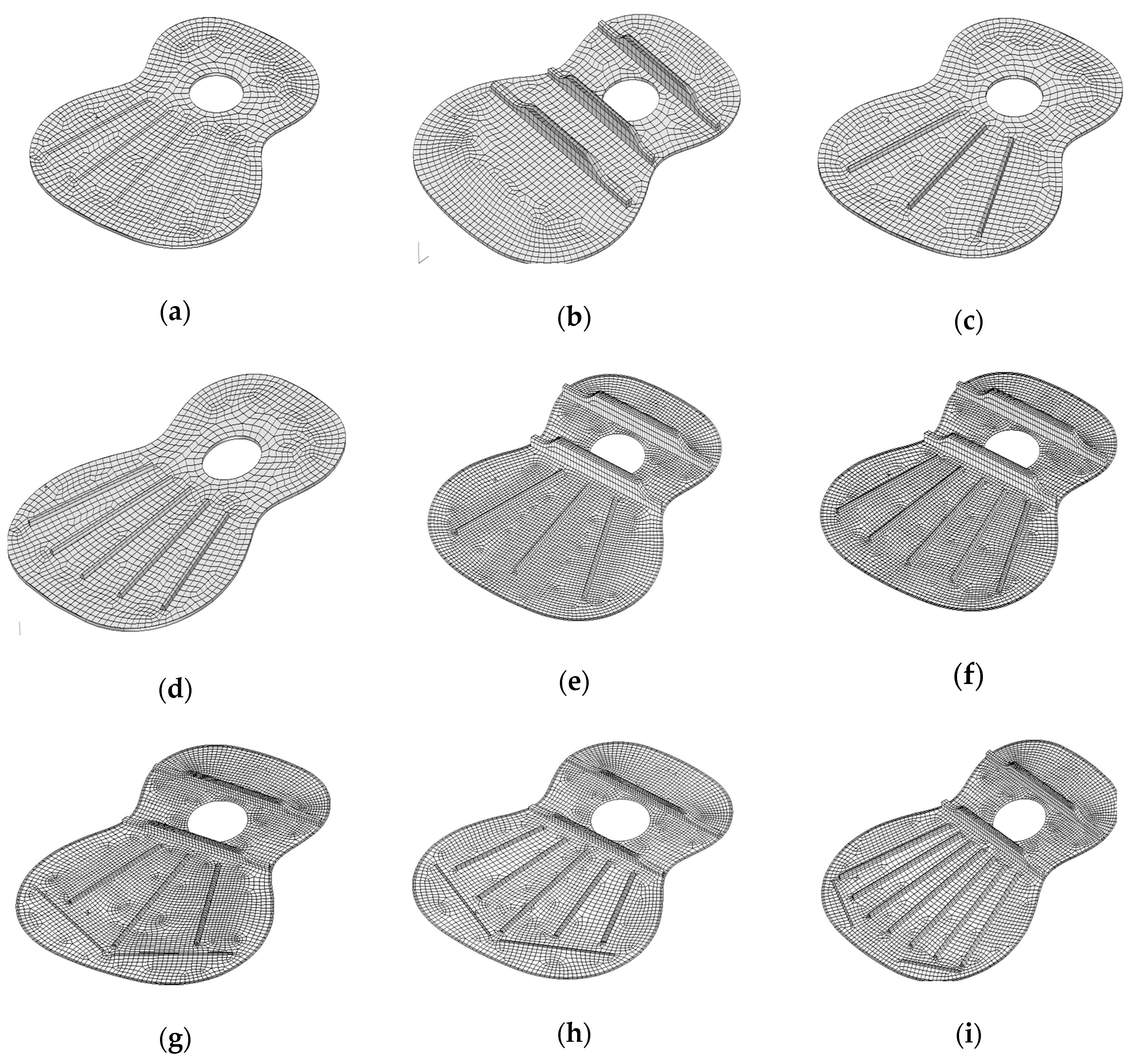At present, the mathematical and analytical modeling of the guitar is replaced by numerical methods: the finite element method (FEM) or finite difference method (DFM) underlying the numerical modeling software [30,31]. For the modal analysis of the guitar plates, nine symmetric variants of plates were geometrically shaped respecting the dimensions practiced for a real guitar: a simple plate with an acoustic hole (denoted PSah) without stiffening elements (Figure 5a); a plate with three transversal reinforcing bars (denoted P3BT) (Figure 5b); a plate with three radial resonance bars, symmetric disposed related to longitudinal axis of plate (denoted P3BR) (Figure 5c); a plate with five radial resonance bars, symmetric disposed related to longitudinal axis of plate radial (denoted P5BR) (Figure 5d); a plate with three radial and two transversal bars (denoted P3BR2T) (Figure 5e); a plate with five radial and two transverse bars (denoted P5BR2T) (Figure 6f); a plate with three radial bars, two transverse and two oblique (denoted P3BR2V) (Figure 5g); a plate with five radial bars, two transverse and two oblique bars (denoted P5BR2V) (Figure 5h); a plate with seven radial bars two transverse and two oblique bars (denoted P7BR2V) (Figure 5i) [35].

Modeling and simulation were done using the Patran Nastran 2004 package. For the meshing in finite elements, elements shell type (QUAD4) were used; the number of degrees of freedom on the element node being 6. For all the nodes on the contour, all the degrees of freedom were fixed. In the preprocessing stage, the following parameters specific to the material and the geometry of the plate were introduced: thickness (h = 1.5, 2, 2.5, 3, 3.5 mm), Young’s modulus (E = 10,000, 12,000, 14,000 MPa), density (ρ = 350, 400, 450, 500 kg/m³), system of beams; keeping Poisson’s coefficient constant (ν = 0.36) and shear’s modulus (G = 5000 MPa). The values of the Young’s modulus E and the density ρ were taken from the literature and based on the results of the analytical modeling [35,36,37].

5. Discussion: Use of the Symmetry in the Calculus of the Eigenvalues of the Guitar

In the following, we will present the procedure that facilitates the calculation, taking into account the mentioned symmetry properties the case of free vibrations of such a system. First of all, we will examine an example to see if these properties are met in the case of guitars. The calculation is done for the entire structure and then only for half of the structure, with a numerical example; for a guitar that is considered in two cases: once without the acoustic hole and the second time with the acoustic hole. The results are shown in

Table 1. Influence of the acoustic hole on the eigenvalues of the guitar plates for: E = 13,000 MPa, G = 2300 MPa, $\nu$ = 0.4, ρ = 500 kg/m³, h =2.5 mm.

All Eigen-Mode	Eigen Frequency of Plate without Acoustic Hole, (Hz)	Eigen Frequency of Plate with Acoustic Hole, (Hz)	Difference between the Two Cases (%)	Symmetrical/ Skew Symmetrical Modes	Eigen Frequency of Plate without Acoustic Hole, (Hz)	Eigen Frequency of Plate with Acoustic Hole, (Hz)
1	191.64	191.65	+0.00052	Symmetric
2	295.79	310.84	+4.5	Symmetric	296.21	310.23
3	405.56	404.99	−0.14	Skew (1)
4	437.14	428.00	−2.09	Symmetric
5	638.70	598.35	−6.8	Skew (2)	638.22	598.43
6	646.94	619.39	−4.258	Symmetric
7	702.26	695.79	−0.921	Symmetric
8	727.18	698.61	−3.92	Skew (3)	727.67	698.35
9	931.33	914.99	−1.754	Skew (4)	931.73	914.46
10	943.61	944.98	+0.145	Symmetric

. It is noted that the first four frequencies for the guitar half are the 2, 5, 8, 9 skew-symmetrical eigenmodes of the guitar taken in its entirety. It follows that the properties listed above are met by the guitar structure. This means that we can ease the calculation in this case using the following method: first, we calculate eigenvalues for a half guitar. Then, the polynomial characteristic equation for the entire structure is divided into the characteristic equation for half structure. The result obtained, which is a polynomial, provides the rest of the structure’s eigenvalues, which will define the symmetrical eigenmodes.

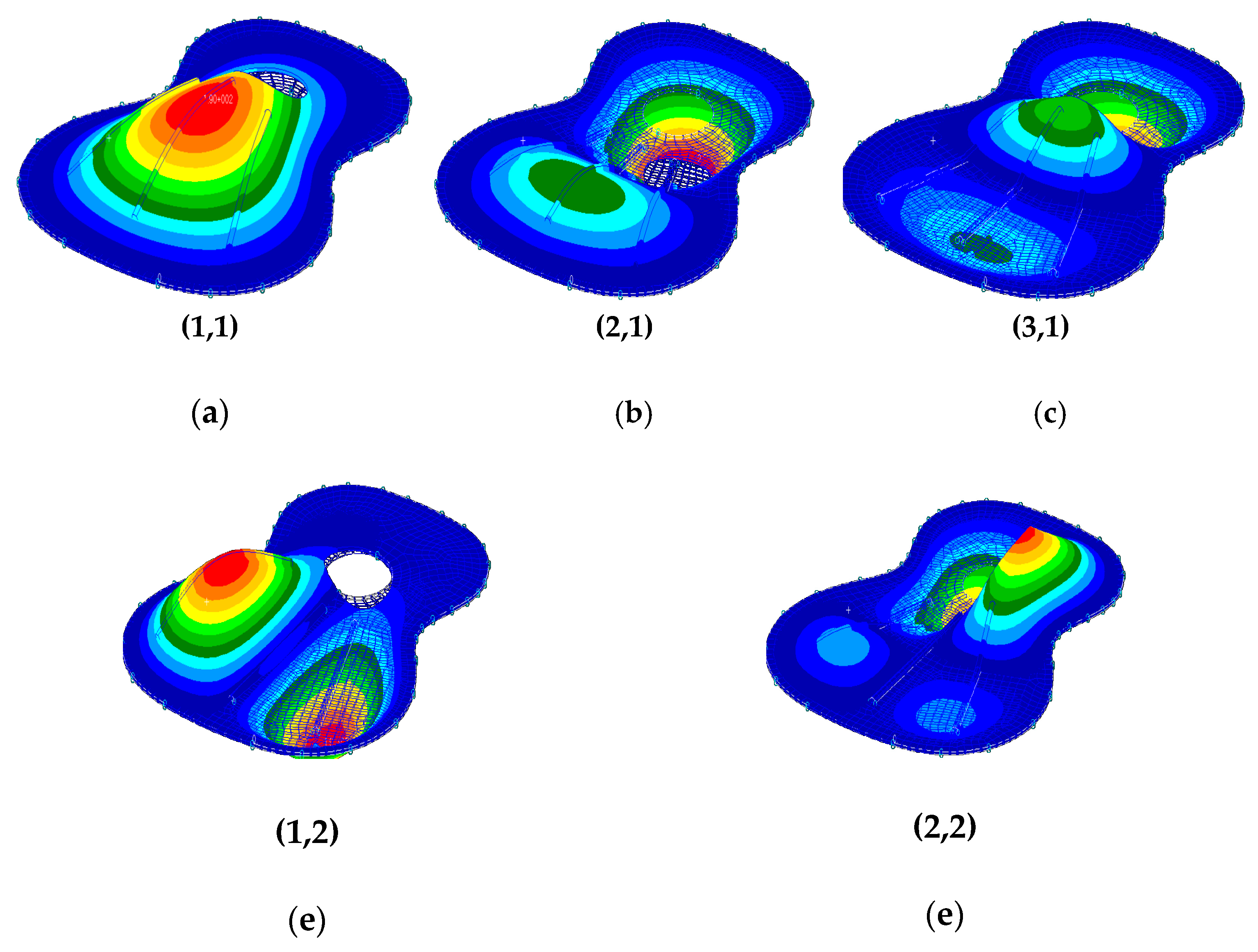
In the studied case, after the reduction of the dimension of the characteristic equation, the calculated values are obtained with a very good approximation. In the following study, this method is used to determine the eigenvalues, which reduces the time required to study. The properties P2 and P3 (from previous chapter) offer the eigenmodes of the structure. In order to determine how the existence of the acoustic hole influences the eigenmodes and the eigenfrequencies, the element of the guitar plate, without stiffening elements and without the acoustic hole was analyzed using FEA and the same plate provided with a rosette. In the preprocessing step, the same characteristics of the material were introduced, so as to obtain the eigenfrequencies determined by the change of the plate structure in the presence of the sound hole. In Figure 6 and Figure 7 are shown the eigenmodes, and in Table 1 the eigenfrequencies. This study was previously used to verify the properties presented in the Section 2 of this paper.

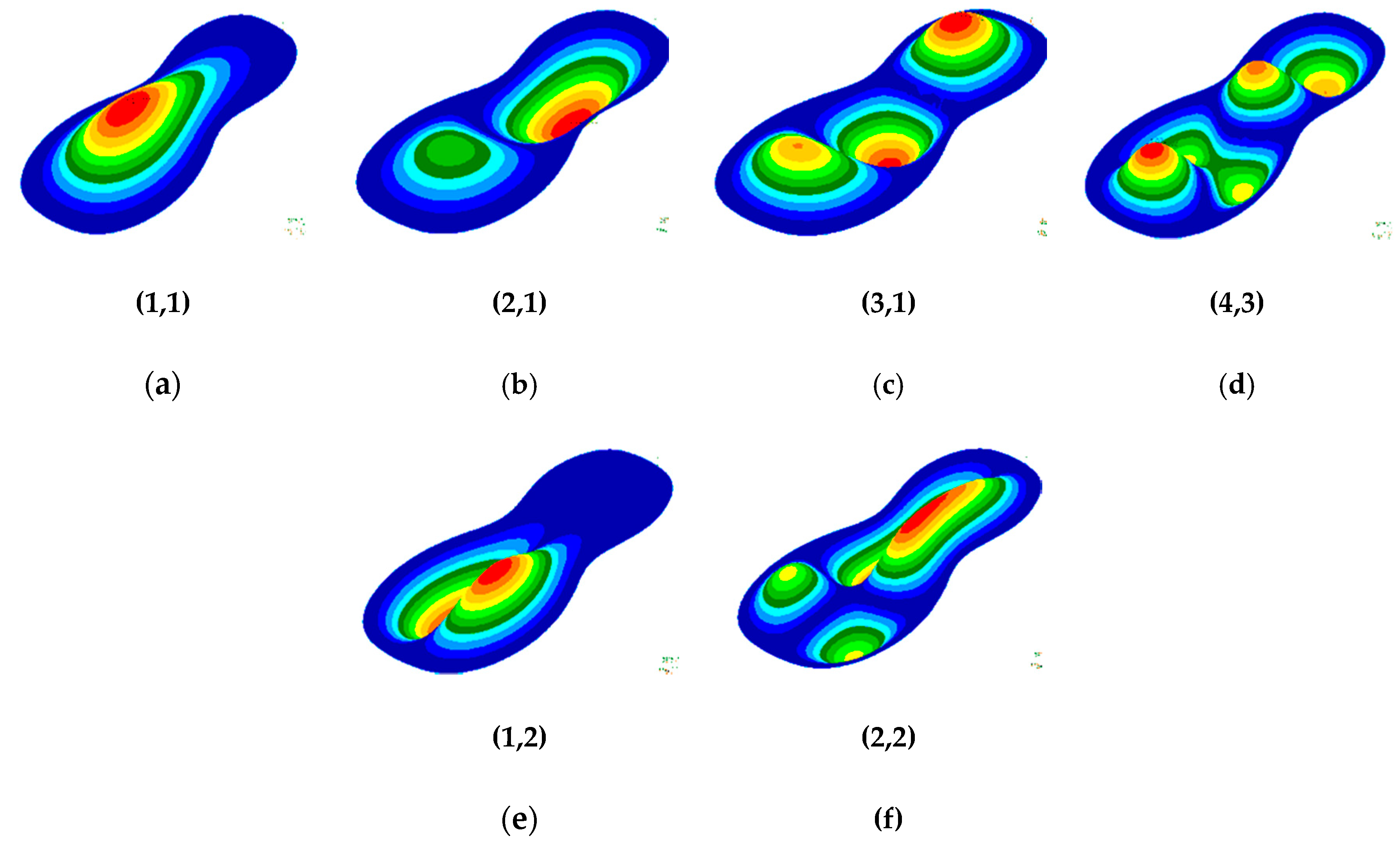
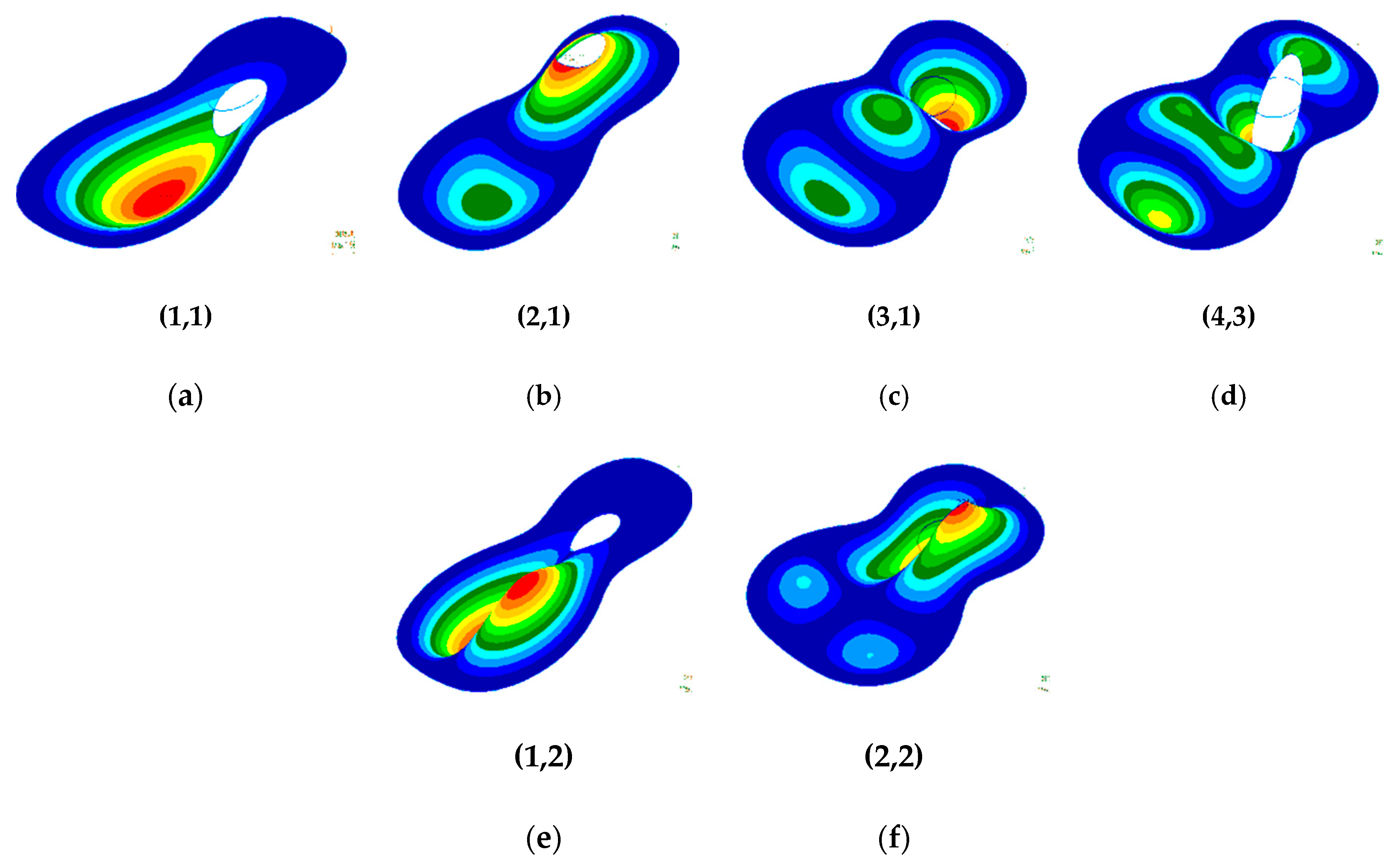
It has been found that the presence of the acoustic hole does not produce major differences in the eigenvalues of eigenmodes as can be seen in Figure 6 and Figure 7 and in Table 1. From the point of view of eigenmodes, there are no differences between the first six eigenmodes between the single bezel plate and the acoustic hole; starting with the seventh mode, there are differences in the distribution of nodal lines. We highlighted symmetrical and skewsymmetrical modes. Figure 8, Figure 9 and Figure 10 show eigenmodes of the plates with different stiffening systems. We have presented a selection from the multitude of the model studied. It has been observed that the eigenmodes are not influenced by the shape, size and order by the material parameters used in the preprocessing stage, namely: density, thickness, Young’s modulus, etc. [38]. However, the structure and stiffening elements of the plate has a significant influence on eigenmodes. 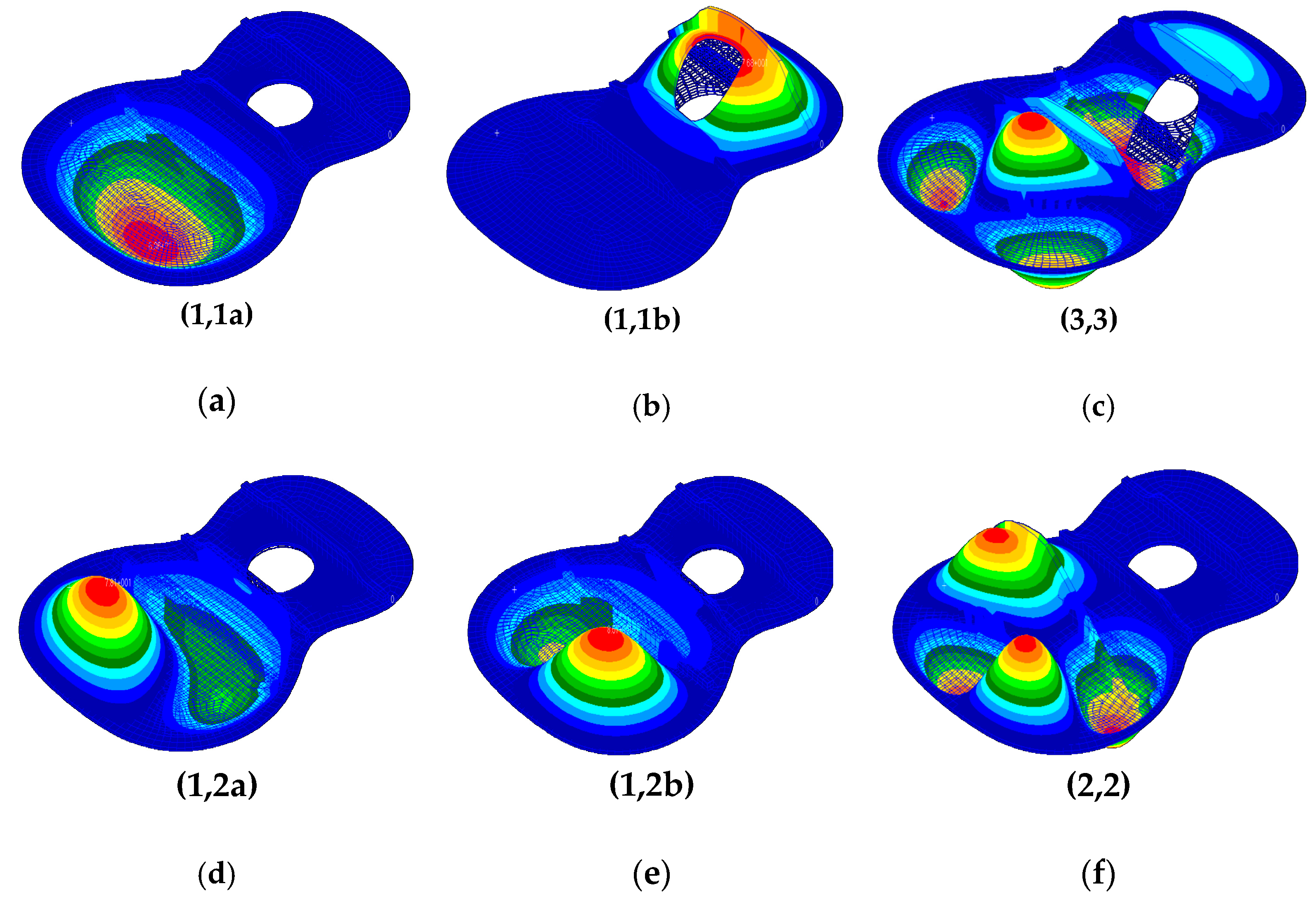In Figure 8, the modal shapes of plate with three symmetrical radial bars are presented. If the bars are setting perpendicular to the longitudinal axis, the skew eigenmodes change in shape and orientation as can be seen in Figure 9.

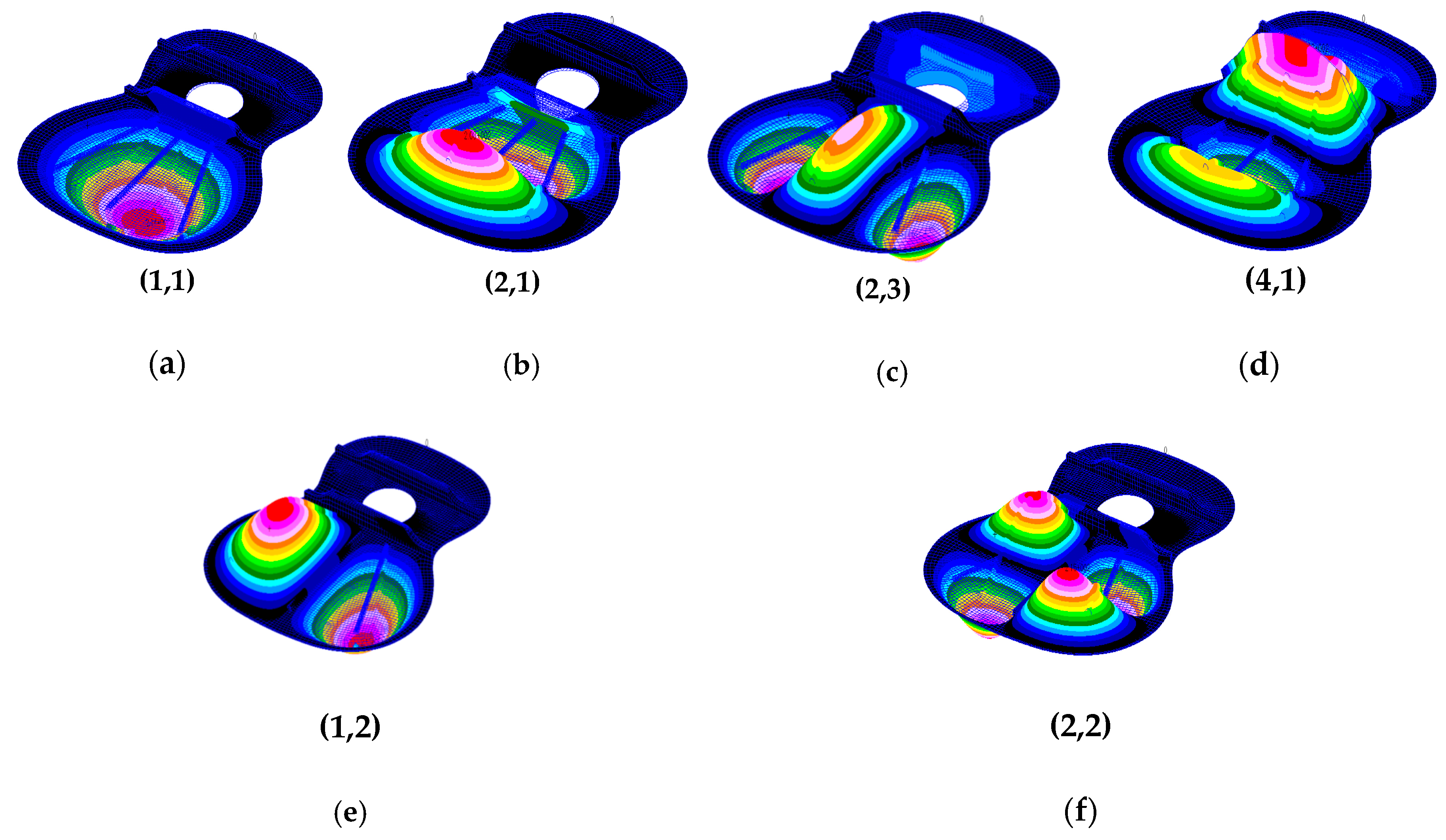
In Figure 10, the symmetrical eigenmodes correspond to breathing mode or synclastic (1,1), to anticlastic bending of first order (2,1) and second order (4,1). The skew symmetrical eigenmodes reported to plane of symmetry are the center bout rotation (1,2) and transverse dipole in plane (2,2).

Analyzing the eigenmodes obtained in the case of studied plates, it was observed that:

• The first eigenmode of vibration (1,1) presents the same shape, regardless the stiffening pattern. Compare to plates with transversal bars, the plates without them (Figure 6, Figure 7 and Figure 8) are characterized by a more extended shape along the longitudinal axis. Additionally, the plates without transverse stiffening elements have the second eigenmode of the type (1,2) compared to the other plates whose eigenmode is of the shape (2,1);
• The stiffening bars change the eigenmodes and the order on the plates. Additionally, the increases of number of bars leads to the natural frequency also increased (

  Table 2. The eigenvalues of the guitar plates with different stiffening pattern, for: G = 2300 MPa, $\nu$ = 3.6, ρ = 450 kg/m³, h = 2.5 mm (Legend: PS – simple plate without acoustic hole; PSah - simple plate with acoustic hole, without stiffening bars; P3BR – plate with three radial resonance bars, symmetric disposed related to longitudinal axis of plate; P5BR – plate with five radial resonance bars, symmetric disposed related to longitudinal axis of plate radial; P3BT – plate with three transversal reinforcing bars; P3BR2T – plate with three radial and two transversal bars; P5BR2T – plate with five radial and two transverse bars; P3BR2V – plate with three radial bars, two transverse and two oblique; P5BR2V – plate with five radial bars, two transverse and two oblique bars; P7BR2V - plate with seven radial bars two transverse and two oblique bars.

  	Frequency (Hz)
  Plates	14,000 MPa	12,000 MPa	10,000 MPa
  PS	101	92	87
  PSah	106	98	89
  P3BR	207	175	155
  P5BR	209	193	176
  P3BT	210	194	178
  P3BR2T	262	242	221
  P5BR2T	264	243	223
  P3BR2V	261	241	220
  P5BR2V	264	243	224
  P7BR2V	265	245.72	224.43

  );
• The eigenmodes for the plates with the complete stiffening bars: radial, oblique and transverse bars, regardless of their number, are similar;
• An interesting situation is recorded for plate with only three transversal bars (Figure 9), where the antisymmetric modes (1,2a) and (1,2b) are obtained related to a different plane from longitudinal symmetry plane, which is inclined to about 40-45 degrees (Figure 9d,e).

In Table 2, the values of the first natural frequency obtained by means FEA, for the different elasticity moduli are shown.

For plates without stiffening bars, the eigenmodes are formed over the entire surface of the plate; the plate’s eigenmodes are not significantly influenced by thickness and material (density, Young’s modulus, Poisson’s ratio).

6. Conclusions

For some practical reasons related to material costs, execution and design, identical parts in the engineering are commonly used. Using identical parts in a project a device or a machine can be designed and can be executed cheaper and faster. The paper made an analysis of such a structure to determine if these repetitive parts can induce characteristic properties and can bring some advantages in design and calculus. The paper studied a particular case of a structure made by two identical parts with application to real guitar plates. Although the modal analysis of the guitar plates does not provide a comprehensive eigenmodes map of the whole guitar, the natural modes of soundboards presented in this paper play an important role on the vibrational behavior of coupled plates on the entire guitar structure.

In this way, the computational time decreases significantly. The dimension of the system decrease and it’s easier to make a vibration analysis. The FEA allowed verification of the stated properties and was used for the numerical study of the problem.