LPI Radar Waveform Recognition Based on CNN and TPOT
Abstract
1. Introduction
2. CNN-TPOT Identification System Structure
3. Preprocessing
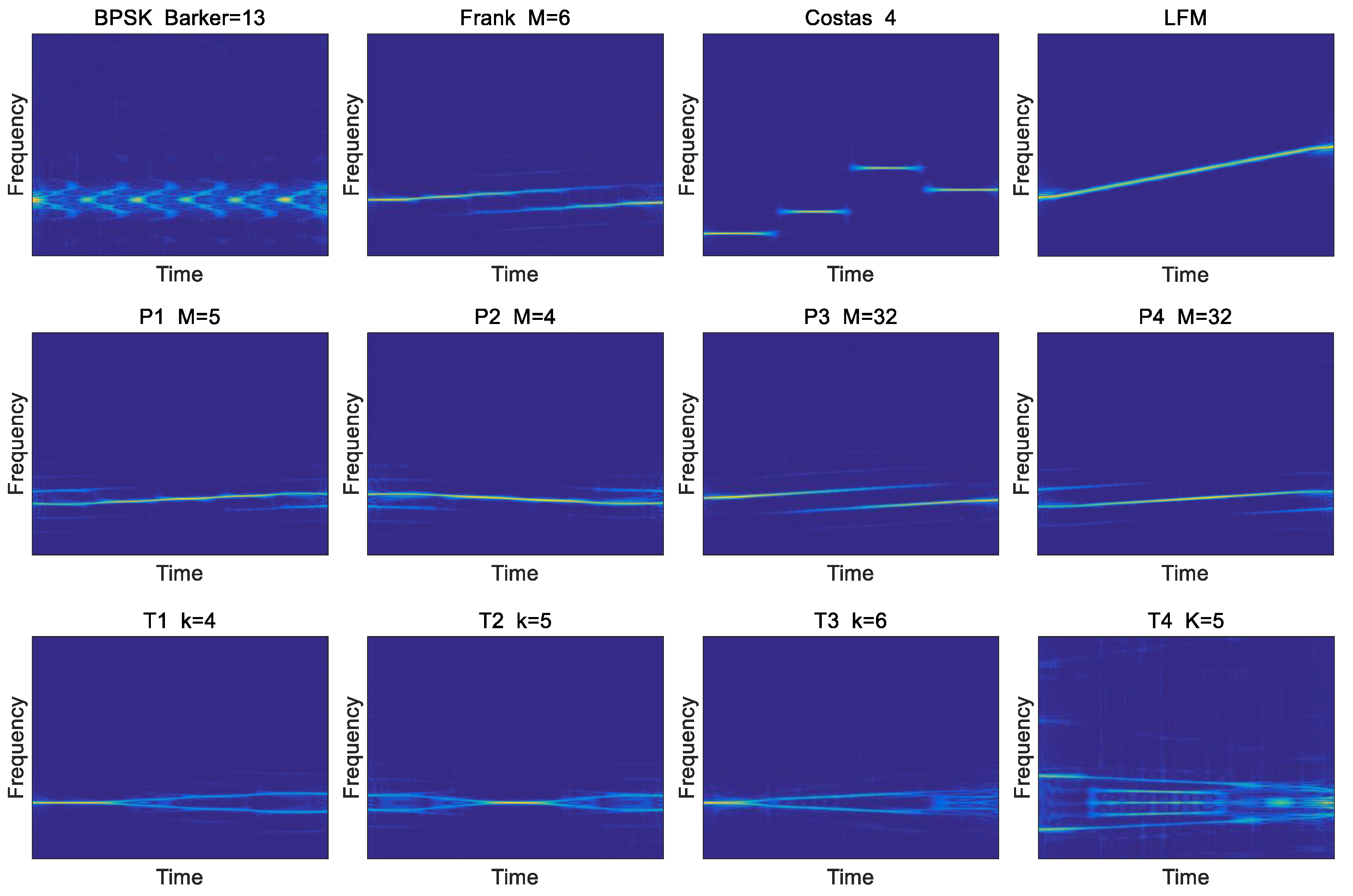
3.1. Signal Model
3.2. Choi–Williams Distribution
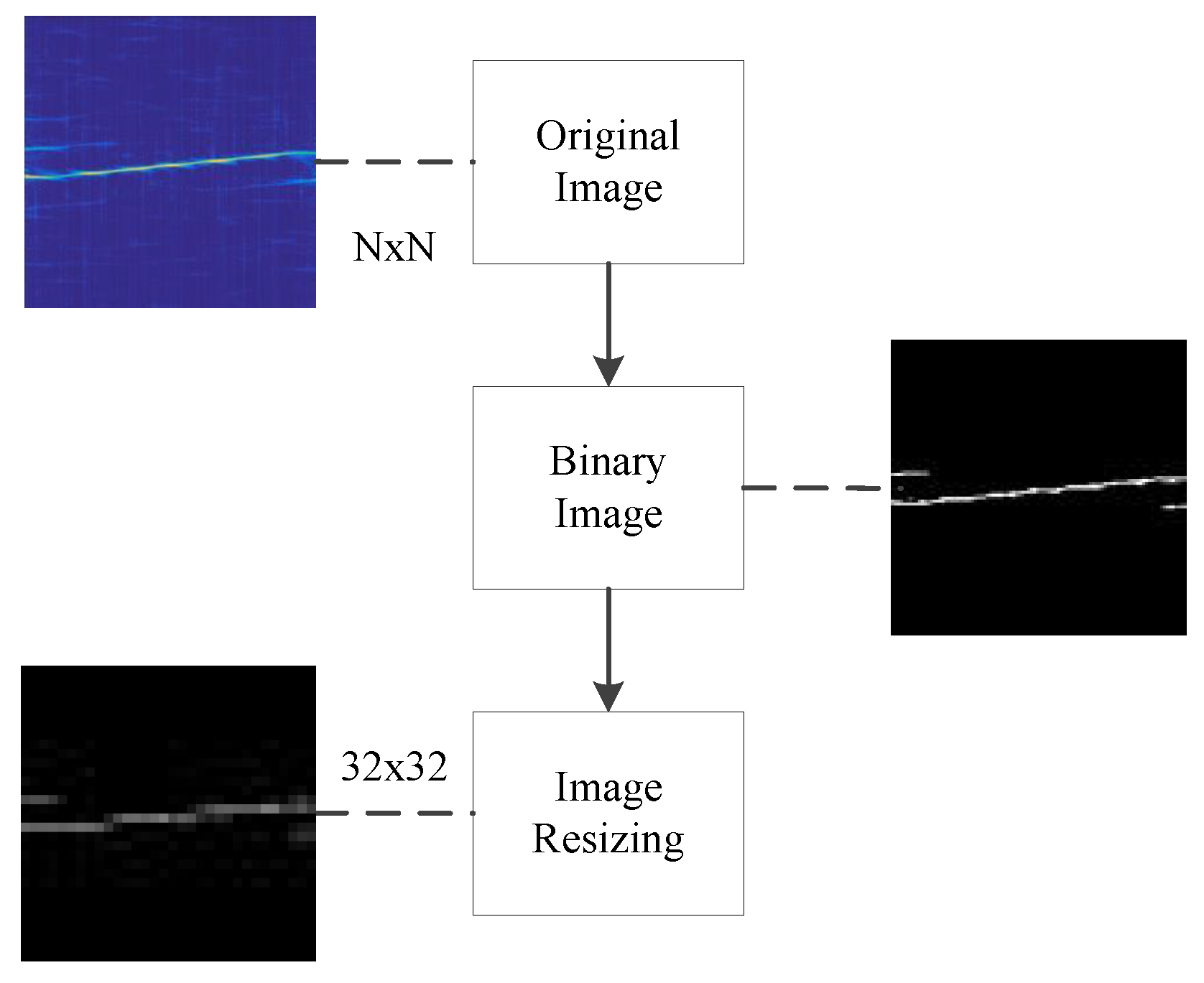
3.3. Binary Image
- Get the probability of occurrence of each gray value that appears in the picture. For example, stores the gray value of the ith pixel in the image, and stores the probability that the ith gray value appears.
- Calculate the discrete function distribution of the gray value.where i is the total number of types of gray values from zero to the image.
- Find the sum of the probabilities of the occurrence of the previous i kinds of gray values, .
- Obtain the gray average value AGray of the overall image, that is, sum the gray value of all the pixels in the image and then divide by the total number of pixels.
- Calculate the threshold weight at different gray values.
- Obtain the gray value corresponding to the i value of the maximum as a global binarization threshold.
4. CNN Feature Extractor Design
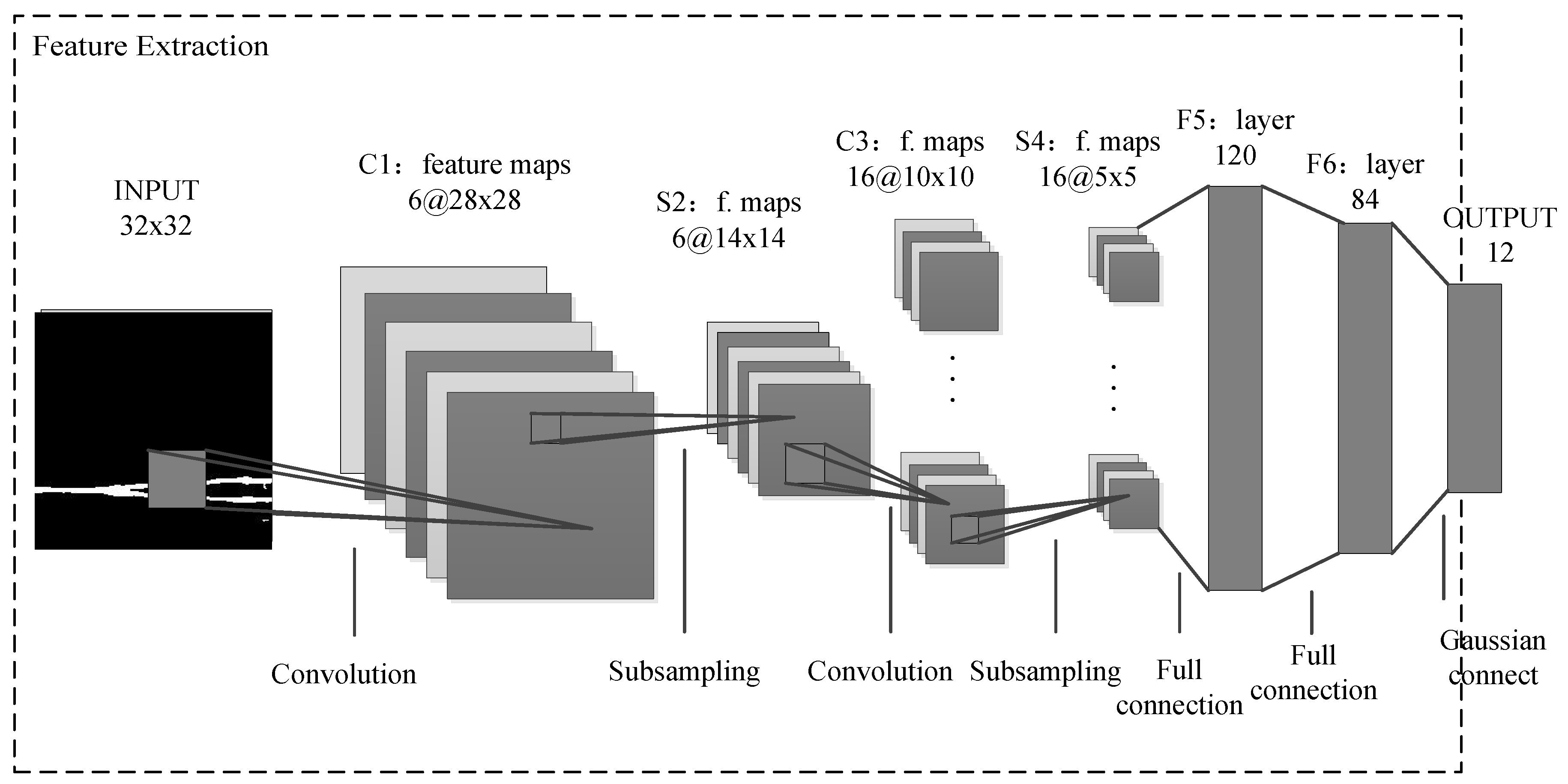
4.1. CNN Model
- The input image is a standardized CNN training data structure with a size of . The detected LPI radar waveform is subjected to CWD time–frequency transform and image binarization. However, since the image size is too large to train the CNN network, we use image size conversion to size.
- The C1 layer is a convolutional layer with six feature maps. The size of the convolution kernel is , thus each feature map has , i.e., Neurons. Each neuron is connected to a size region of the input layer.
- The S2 layer is a down sampling layer with six feature maps, and each neuron in each feature map is connected to a region in the feature map corresponding to the C1 layer.
- C3 is also a convolutional layer that uses a convolution kernel to process the S2 layer. The number of neurons that calculate the feature map of the C3 layer is , that is, . C3 has 16 feature maps, each of which is composed of different combinations between the individual feature maps of the previous layer, as shown in Table 1.
- The S4 layer is a down sampling layer composed of 16 size feature maps, each of which is connected to a size region of the corresponding feature map in C3.
- The C5 layer is another convolutional layer. The same is used for a size convolution kernel. Each feature map has , i.e., neurons. Each unit is fully connected to the area of all 16 feature maps of S4. The C5 layer has 120 feature maps.
- The F6 fully connected layer has 84 feature maps, and each feature map has only one neuron connected to the C5 layer.
- The output layer is also a fully connected layer with a total of 12 nodes representing the 12 different LPI radar waveforms, respectively.
4.2. Feature Extraction
5. TPOT Optimization Classifier
5.1. Genetic Programming
- Replace mutation: The operational nodes in the individual process structure are randomly selected and replaced with new randomly generated process sequences.
- Insert mutation: A new randomly generated sequence of processes is inserted into the random location of the inserted individual.
- Remove mutation: A random culling sequence is performed on the processes of the deleted individual.
5.2. Classifier Model Selection and Optimization
6. Simulation Experiment
6.1. Create Sample
6.2. CNN Feature Validity Experiment
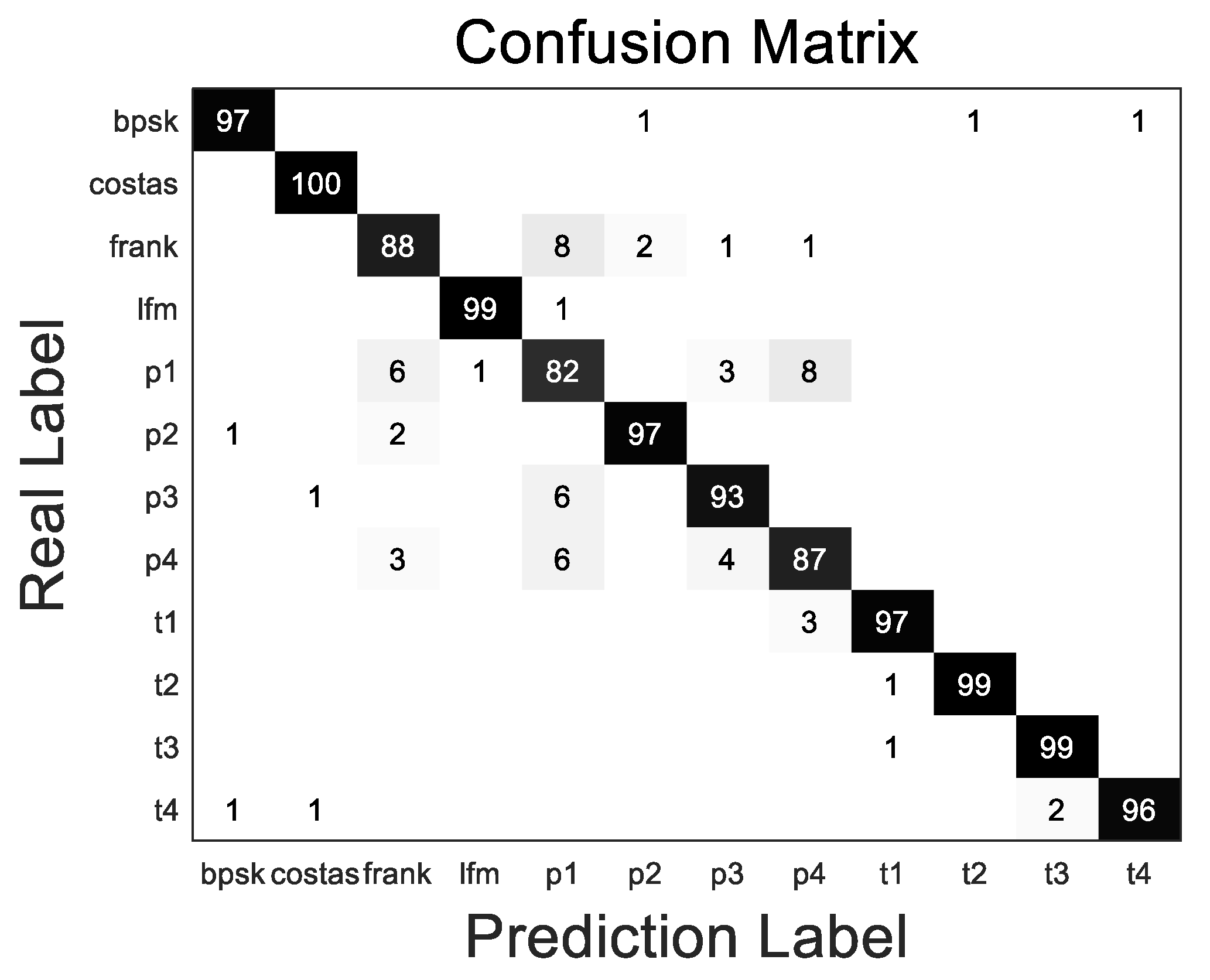
6.3. TPOT Optimized Classifier Performance Test
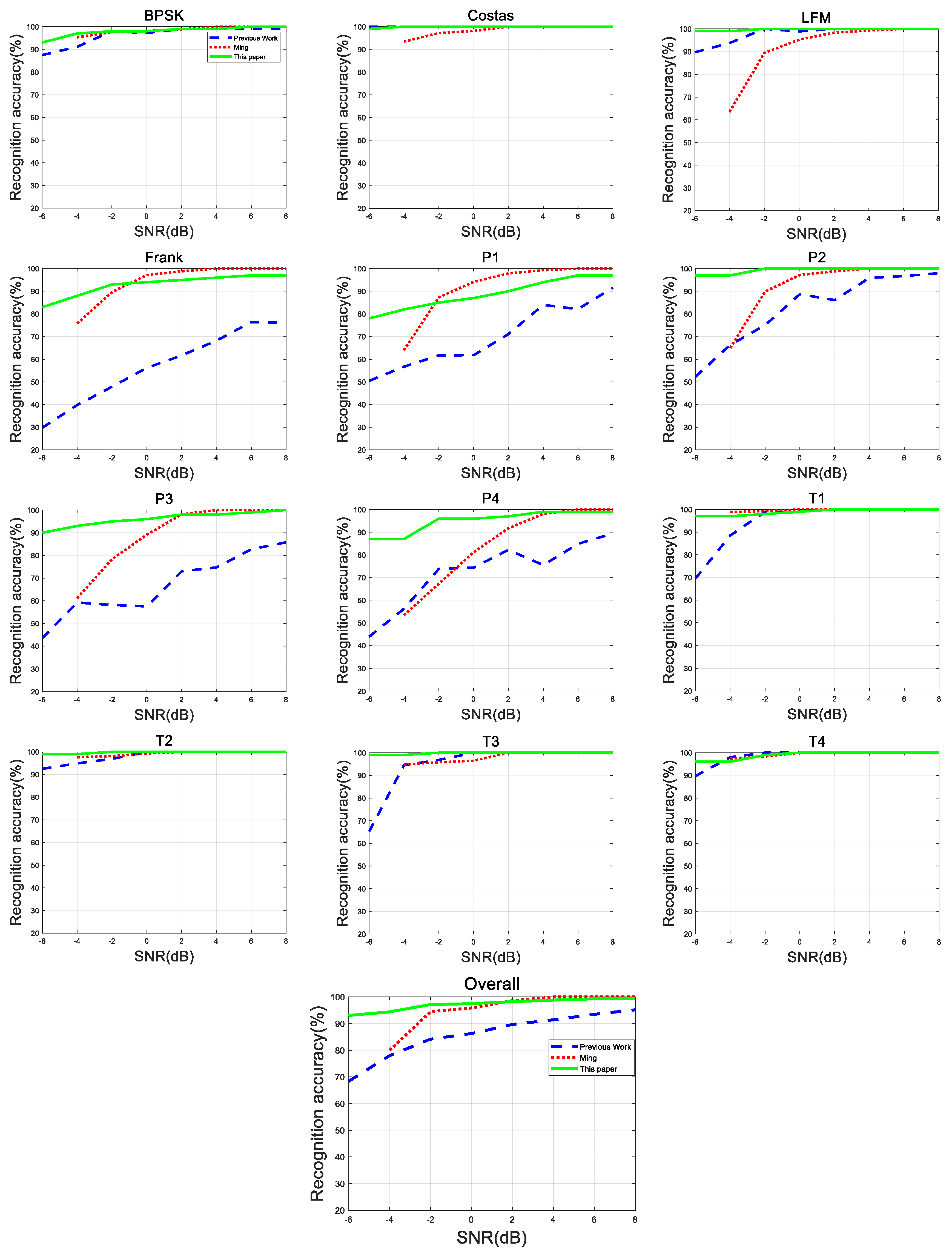
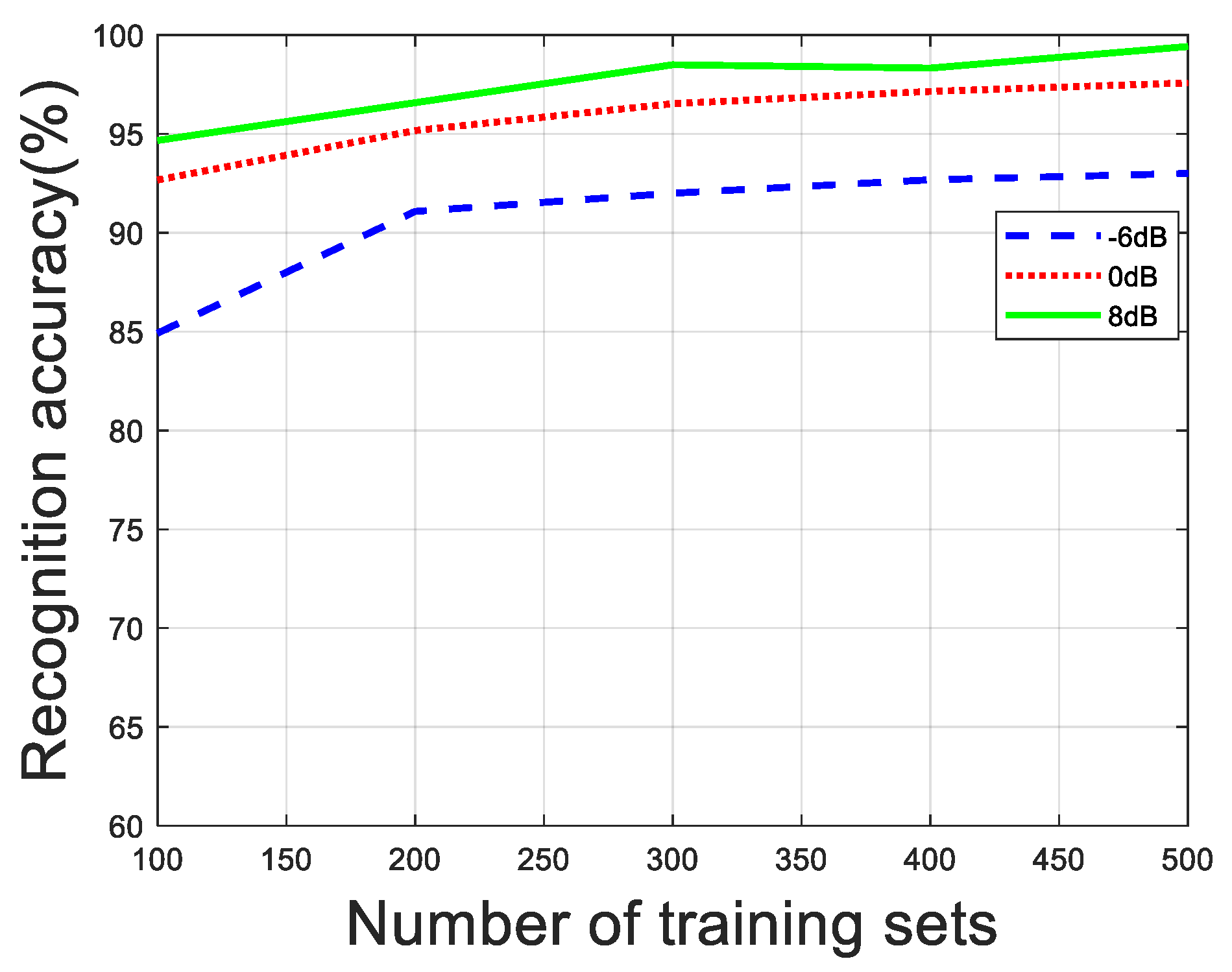
6.4. Experiment Results with SNR
6.5. Experiment with Robustness
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| LPI | low probability interception |
| LFM | linear frequency modulation |
| CNN | convolutional neural network |
| TPOT | tree structure-based machine learning process optimization |
| SNR | signal-to-noise ratio |
| CWD | Choi–Williams distribution |
| WVD | Wigner–Ville distribution |
| ENN | Herman neural network |
| PCA | principal components analysis |
| GP | genetic programming |
| SVM | support vector machine |
| KNN | K-nearest neighbor method |
References
- Chen, T.; Liu, L.; Huang, X. LPI Radar Waveform Recognition Based on Multi-Branch MWC Compressed Sampling Receiver. IEEE Access 2018, 6, 30342–30354. [Google Scholar] [CrossRef]
- Kishore, T.R.; Rao, K.D. Automatic intrapulse modulation classification of advanced LPI radar waveforms. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 901–914. [Google Scholar] [CrossRef]
- Dezfuli, A.A.; Shokouhm, A.; Oveis, A.H.; Norouzi, Y. Reduced complexity and near optimum detector for linear-frequency-modulated and phase-modulated LPI radar signals. IET Radar Sonar Navig. 2019, 13, 593–600. [Google Scholar] [CrossRef]
- Jenn, D.C.; Pace, P.E.; Romero, R.A. An Antenna for a Mast-Mounted Low Probability of Intercept Continuous Wave Radar. J. Abbr. 2019, 61, 63–70. [Google Scholar]
- Zilberman, E.R.; Pace, P.E. Autonomous time-frequency morphological feature extraction algorithm for LPI radar modulation classification. In Proceedings of the 2006 International Conference on Image Processing, Atlanta, GA, USA, 8–11 October 2006. [Google Scholar]
- Ma, J.; Huang, G.; Zuo, W.; Wu, X.; Gao, J. Robust radar waveform recognition algorithm based on random projections and sparse classification. IET Radar Sonar Navig. 2013, 8, 290–296. [Google Scholar] [CrossRef]
- Lunden, J.; Koivunen, V. Automatic radar waveform recognition. IEEE J. Sel. Top. Signal Process. 2007, 1, 124–136. [Google Scholar] [CrossRef]
- Zhang, M.; Diao, M.; Guo, L. Convolutional Neural Networks for Automatic Cognitive Radio Waveform Recognition. IEEE Access 2017, 5, 11074–11082. [Google Scholar] [CrossRef]
- Ming, Z.; Ming, D.; Lipeng, G.; Lutao, L. Neural Networks for Radar Waveform Recognition. Symmetry 2017, 9, 75. [Google Scholar] [CrossRef]
- Lutao, L.; Shuang, W.; Zhongkai, Z. Radar Waveform Recognition Based on Time-Frequency Analysis and Artificial Bee Colony-Support Vector Machine. Electronics 2018, 7, 59. [Google Scholar]
- Zhang, M.; Liu, L.; Diao, M. LPI Radar Waveform Recognition Based on Time-Frequency Distribution. Sensors 2017, 16, 1682. [Google Scholar] [CrossRef]
- Xu, B.; Sun, L.; Xu, L.; Xu, G. Improvement of the Hilbert method via ESPRIT for detecting rotor fault in induction motors at low slip. IEEE Trans. Energy Convers. 2013, 28, 225–233. [Google Scholar]
- Feng, Z.; Liang, M.; Chu, F. Recent advances in time Ű frequency analysis methods for machinery fault diagnosis: A review with application examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar]
- Hou, J.; Yan, X.P.; Li, P.; Hao, X.H. Adaptive time-frequency representation for weak chirp signals based on Duffing oscillator stopping oscillation system. Int. J. Adapt. Control Signal Process. 2018, 32, 777–791. [Google Scholar] [CrossRef]
- Qu, Z.Y.; Mao, X.J.; Deng, Z.A. Radar Signal Intra-Pulse Modulation Recognition Based on Convolutional Neural Network. IEEE Access 2018, 6, 43874–43884. [Google Scholar] [CrossRef]
- Ataie, R.; Zarandi, A.A.E.; Mehrabani, Y.S. An efficient inexact Full Adder cell design in CNFET technology with high-PSNR for image processing. Int. J. Electron. 2019, 106, 928–944. [Google Scholar] [CrossRef]
- Zhang, A.J.; Yang, X.Z.; Jia, L.; Ai, J.Q.; Xia, J.F. SRAD-CNN for adaptive synthetic aperture radar image classification. Int. J. Remote Sens. 2019, 40, 3461–3485. [Google Scholar]
- Li, Y.; Zeng, J.B.; Shan, S.G.; Chen, X.L. Occlusion Aware Facial Expression Recognition Using CNN With Attention Mechanism. IEEE Trans. Image Process. 2019, 28, 2439–2450. [Google Scholar] [CrossRef]
- Baloglu, U.B.; Talo, M.; Yildirim, O.; Tan, R.S.; Acharya, U.R. Classification of myocardial infarction with multi-lead ECG signals and deep CNN. Pattern Recognit. Lett. 2019, 122, 23–30. [Google Scholar] [CrossRef]
- Zeng, K.; Wang, Y.N.; Mao, J.X.; Liu, J.Y.; Peng, W.X.; Chen, N.K. A Local Metric for Defocus Blur Detection Based on CNN Feature Learning. IEEE Trans. Image Process. 2019, 28, 2107–2115. [Google Scholar] [CrossRef]
- Zhang, G.W.; Tang, B.P.; Chen, Z. Operational modal parameter identification based on PCA-CWT. Measurement 2019, 139, 334–345. [Google Scholar] [CrossRef]
- Yun, L.; Li, W.; Garg, A.; Maddila, S.; Gao, L.; Fan, Z.; Buragohain, P.; Wang, C.T. Maximization of extraction of Cadmium and Zinc during recycling of spent battery mix: An application of combined genetic programming and simulated annealing approach. J. Clean. Prod. 2019, 218, 130–140. [Google Scholar] [CrossRef]
- Wang, B.; Tian, R.F. Judgement of critical state of water film rupture on corrugated plate wall based on SIFT feature selection algorithm and SVM classification method. Nucl. Eng. Des. 2019, 347, 132–139. [Google Scholar] [CrossRef]




| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | X | X | X | X | X | X | X | X | X | X | ||||||
| 1 | X | X | X | X | X | X | X | X | X | X | X | |||||
| 2 | X | X | X | X | X | X | X | X | X | X | ||||||
| 3 | X | X | X | X | X | X | X | X | X | X | X | |||||
| 4 | X | X | X | X | X | X | X | X | X | X | ||||||
| 5 | X | X | X | X | X | X | X | X | X | X |
| GP Parameter | Content |
|---|---|
| Population size | 100 |
| Number of iterations | 10 |
| Individual mutation rate | 90% |
| Crossover rate | 5% |
| Method of choosing | 10% elite reserve, 3 choice 2 bidding selection method, according to complexity 2 choose 1 |
| Mutation | Replace, insert, delete, each type of mutation each accounted for 1/3 |
| Repeated operation | 5 |
| Item | Model/Version |
|---|---|
| CPU | i5-8300H(Intel) |
| GPU | NVIDIA GeForce GTX 1050 Ti |
| Memory | 16 GB(DDR4 @2667 MHZ) |
| MATLAB | R2018b |
| Spyder | Python 3.5 |
| Radar Waveform | Simulation Parameter | Ranges |
|---|---|---|
| Sampling frequency | 1( HZ) | |
| BPSK | Barker codes | {7,11,13} |
| Carrier frequency | U(1/8,1/4) | |
| Cycles per phase code cpp | [1, 5] | |
| Number of code periods np | [100, 300] | |
| LFM | Number of samples N | [500, 1024] |
| Bandwidth | U(1/16,1/8) | |
| Initial frequency | U(1/16,1/8) | |
| Costas | Fundamental frequency | U(1/24,1/20) |
| Number change | [3, 6] | |
| Number of samples N | [512, 1024] | |
| Frank&P1 | Carrier frequency | U(1/8,1/4) |
| Cycles per phase code cpp | [1, 5] | |
| Samples of frequency stem M | [4, 8] | |
| P2 | Carrier frequency | U(1/8,1/4) |
| Cycles per phase code cpp | [1, 5] | |
| Samples of frequency stem M | 2 × [2, 4] | |
| P3&P4 | Carrier frequency | U(1/8,1/4) |
| Cycles per phase code cpp | [1, 5] | |
| Samples of frequency stem M | 2 × [16, 35] | |
| T1–T4 | Number of segments k | [4, 6] |
| Overall code duration T | [0.07, 0.1] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, J.; Yu, X.; Guo, Q. LPI Radar Waveform Recognition Based on CNN and TPOT. Symmetry 2019, 11, 725. https://doi.org/10.3390/sym11050725
Wan J, Yu X, Guo Q. LPI Radar Waveform Recognition Based on CNN and TPOT. Symmetry. 2019; 11(5):725. https://doi.org/10.3390/sym11050725
Chicago/Turabian StyleWan, Jian, Xin Yu, and Qiang Guo. 2019. "LPI Radar Waveform Recognition Based on CNN and TPOT" Symmetry 11, no. 5: 725. https://doi.org/10.3390/sym11050725
APA StyleWan, J., Yu, X., & Guo, Q. (2019). LPI Radar Waveform Recognition Based on CNN and TPOT. Symmetry, 11(5), 725. https://doi.org/10.3390/sym11050725





