Improvement on Meshing Stiffness Algorithms of Gear with Peeling
Abstract
:1. Introduction
2. The Algorithm Model of Meshing Stiffness
2.1. Calculate Hertz Contact Stiffness and Wheel Stiffness
2.2. Calculate Bending Stiffness, Shear Stiffness, and Compression Stiffness
3. Improvement on Meshing Stiffness Algorithms of Gear with Peeling
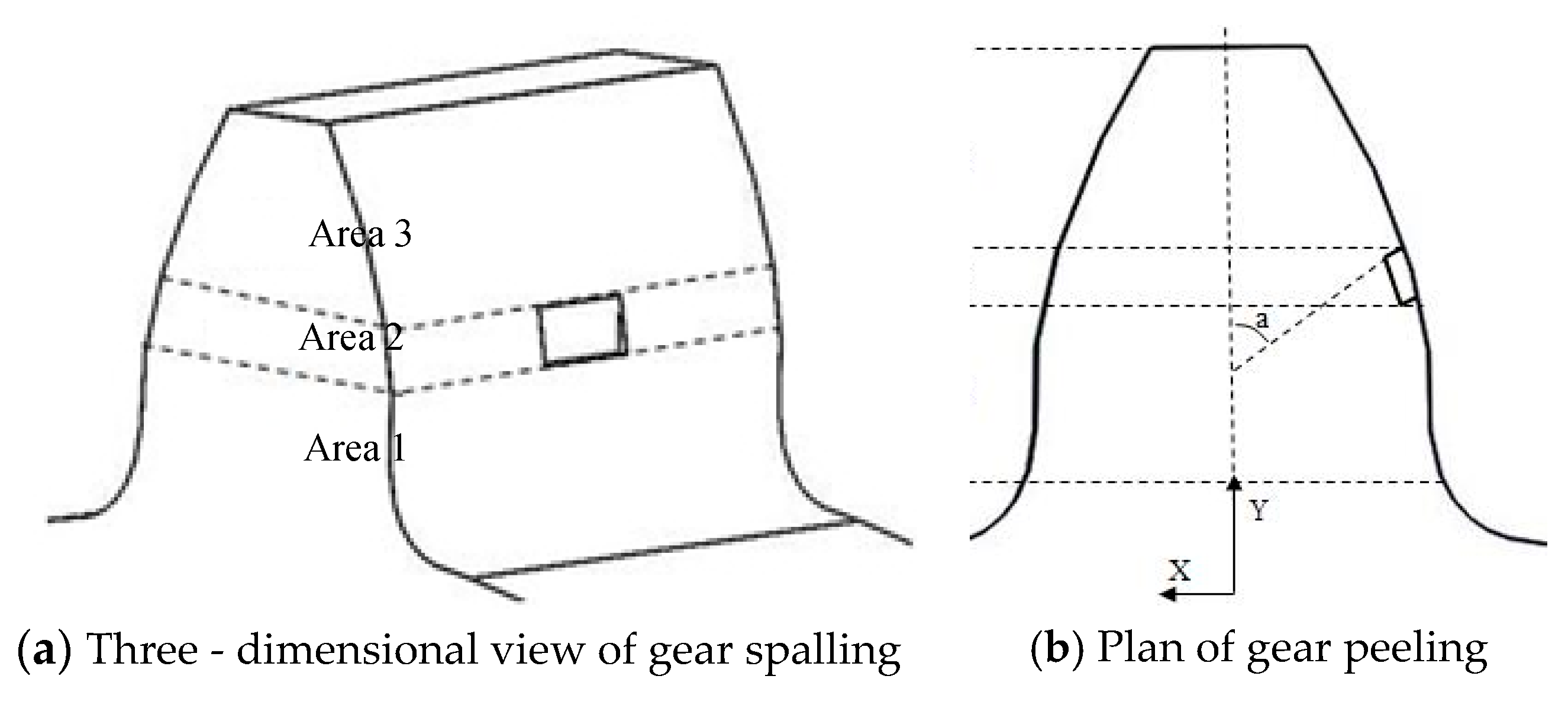
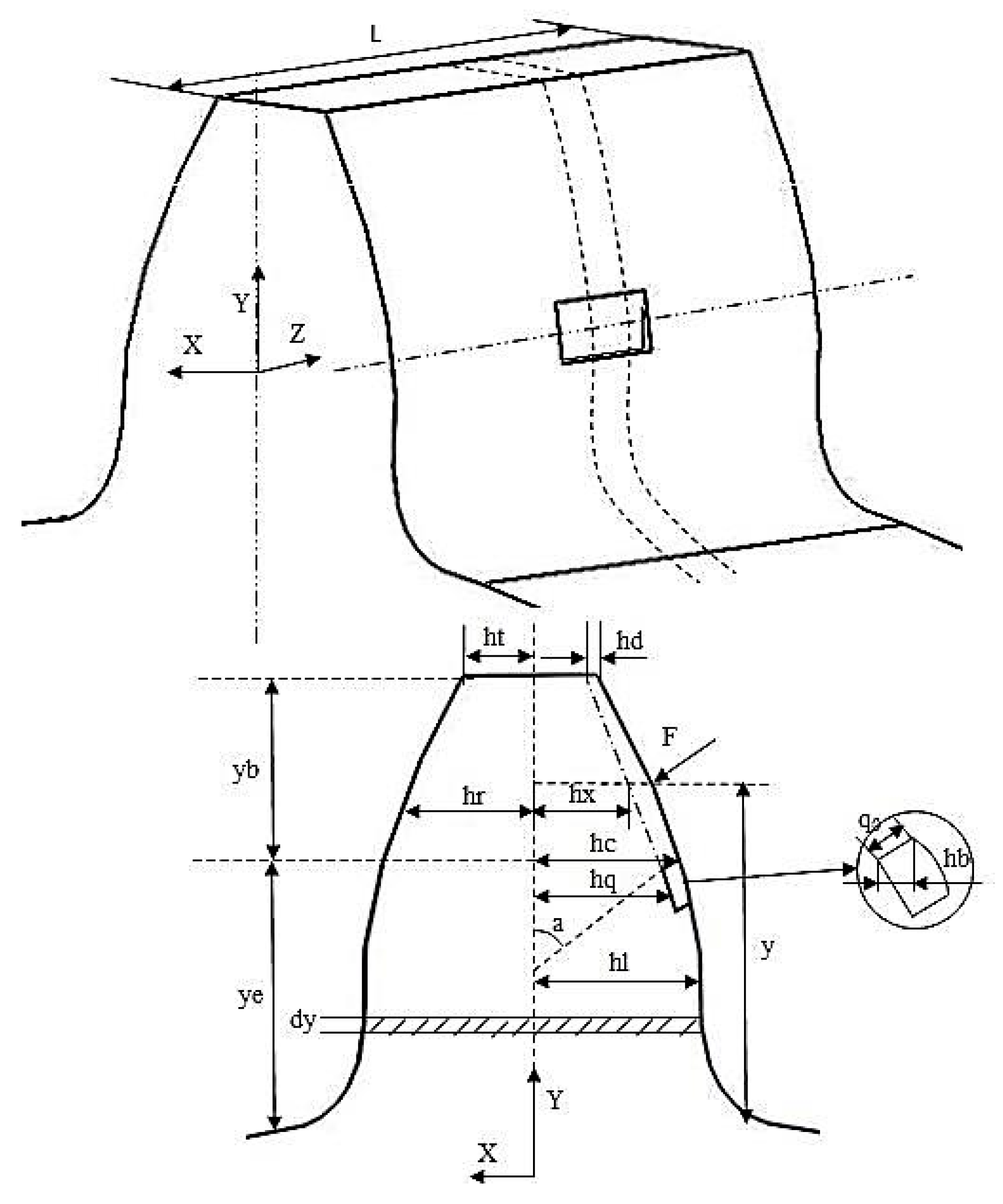
3.1. Establishing a Calculation Model of Peeling Failure Meshing Stiffness
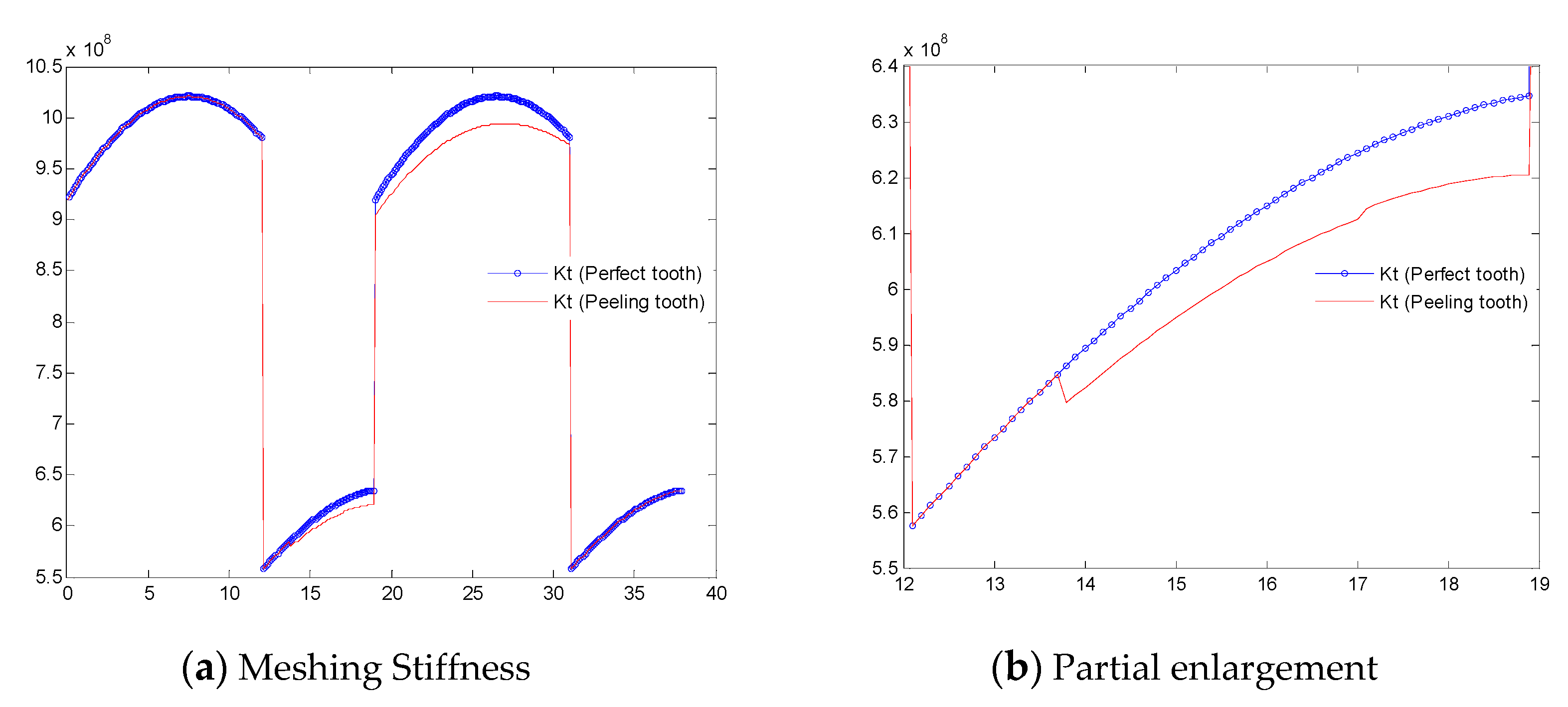
3.2. Solve Peeling Failure Meshing Stiffness
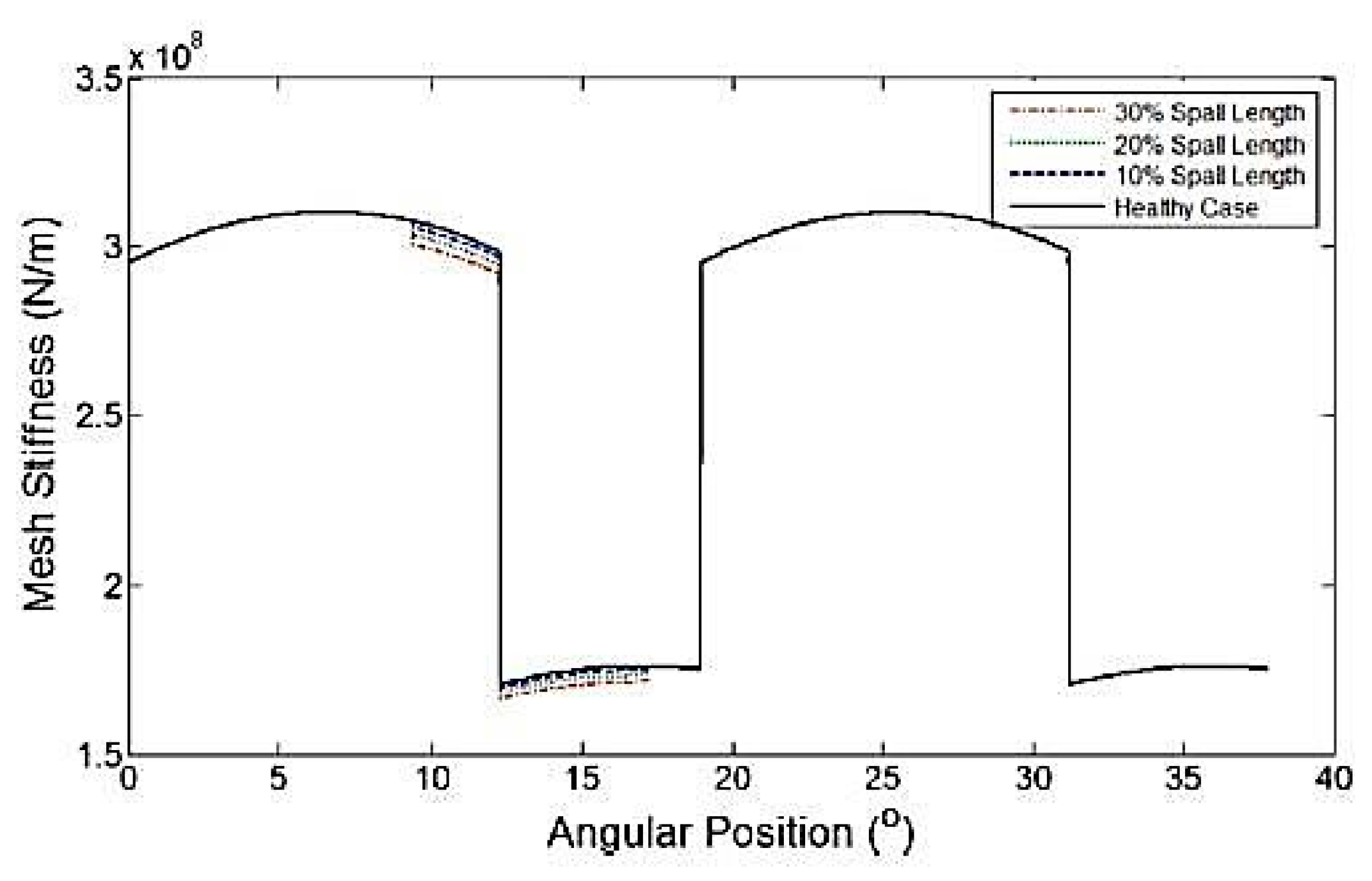
4. The Meshing Stiffness of Gear with Variable Peeling Parameter
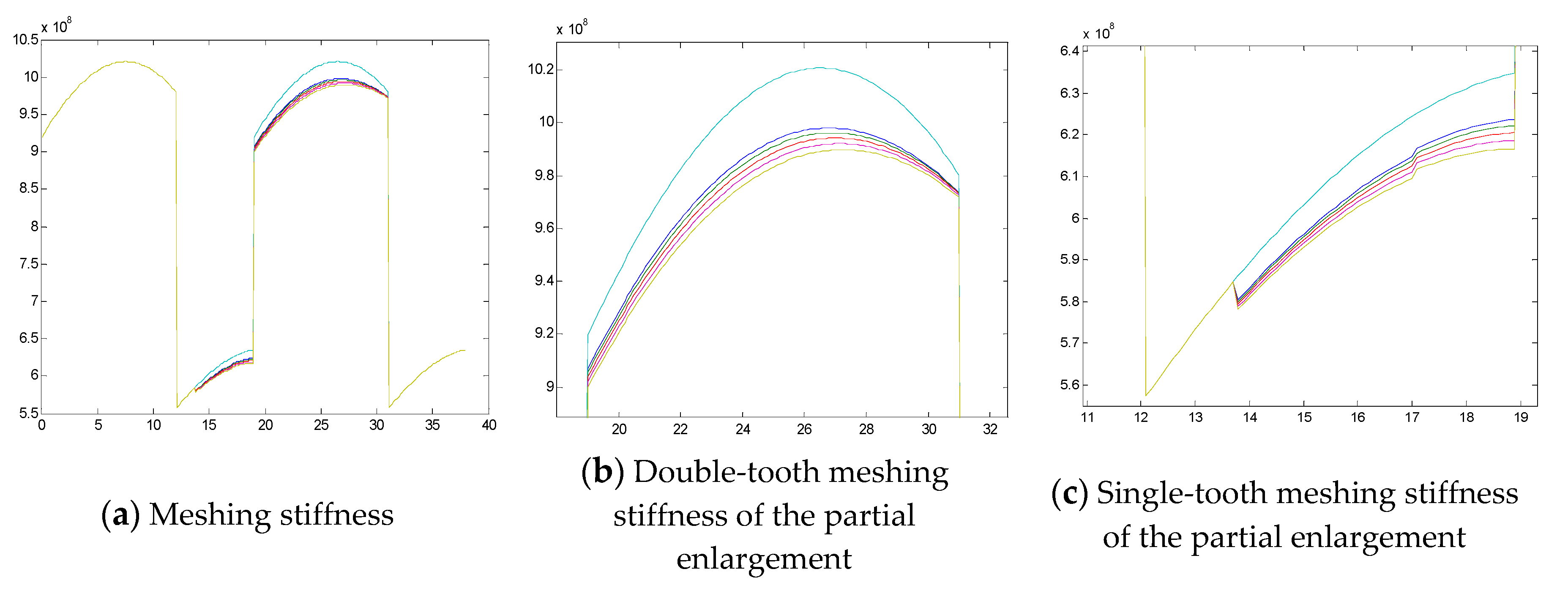
4.1. Variable Depth Variable Meshing Stiffness
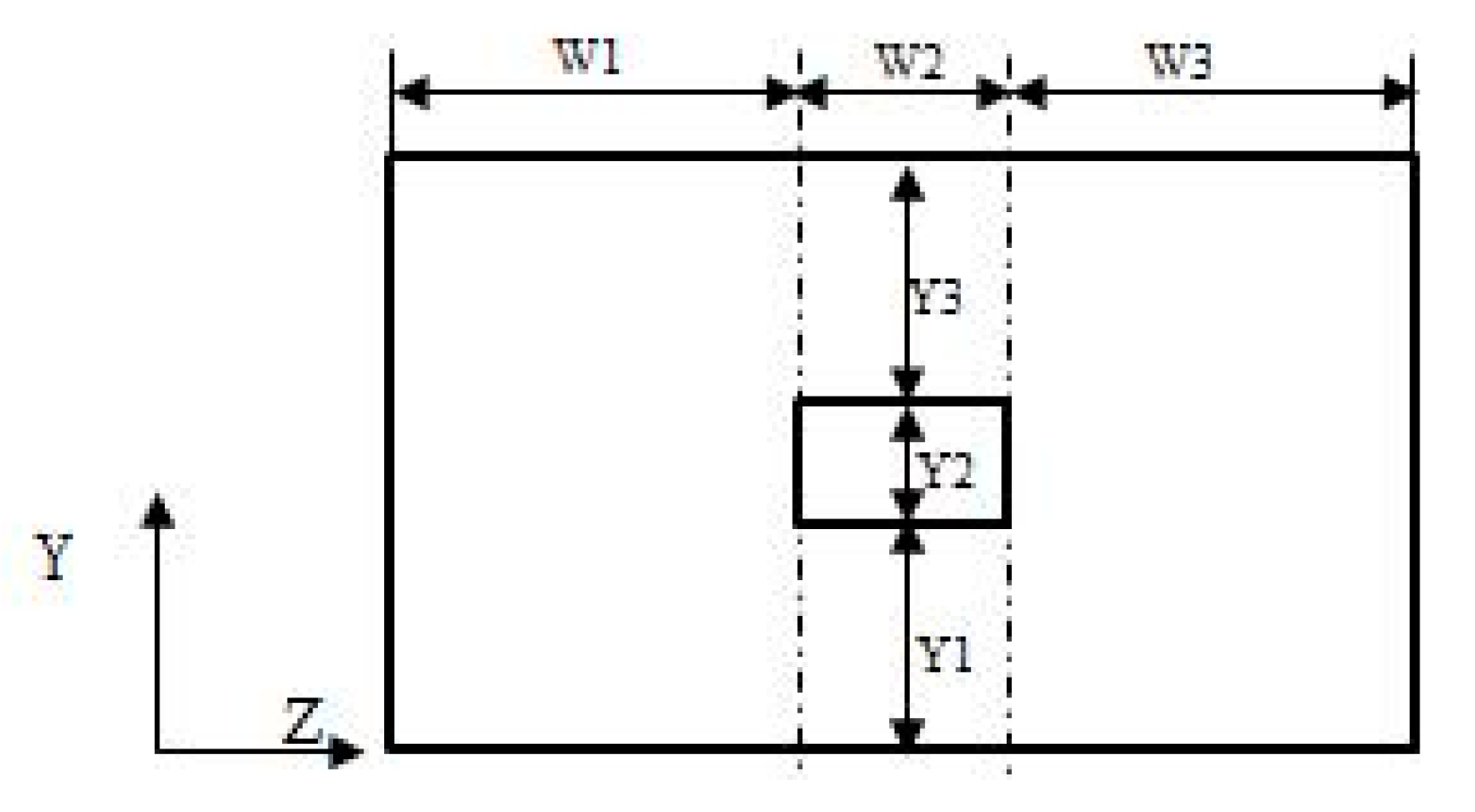
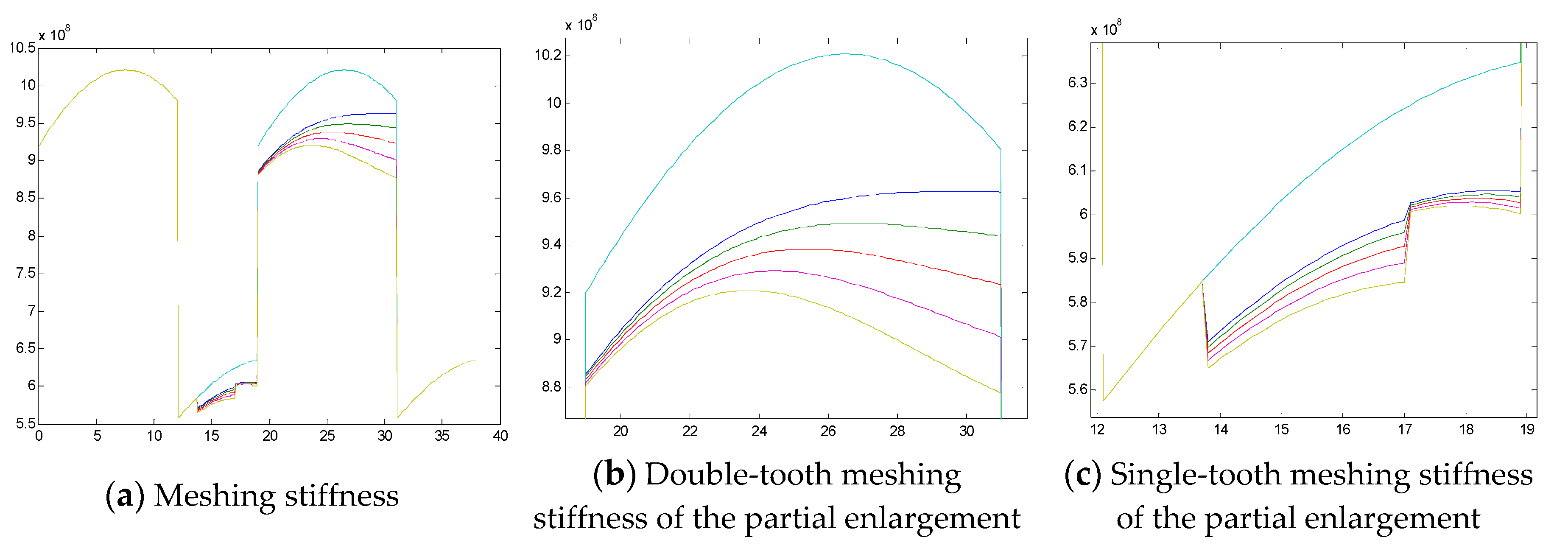
4.2. Variable Width Variable Meshing Stiffness
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cui, L.L.; Li, B.B.; Ma, J.F.; Jin, Z. Quantitative trend fault diagnosis of a rolling bearing based on Sparsogram and Lempel-Ziv. Measurement 2018, 128, 410–418. [Google Scholar] [CrossRef]
- Song, L.Y.; Wang, H.Q.; Chen, P. Vibration-Based Intelligent Fault Diagnosis for Roller Bearings in Low-Speed Rotating Machinery. IEEE Trans. Instrum. Meas. 2018, 67, 1887–1899. [Google Scholar] [CrossRef]
- Cui, L.L.; Wang, X.; Xu, Y.G.; Jiang, H.; Zhou, J.P. A novel Switching Unscented Kalman Filter method for remaining useful life prediction of rolling bearing. Measurement 2019, 135, 678–684. [Google Scholar] [CrossRef]
- Han, T.; Jiang, D.; Zhao, Q.; Wang, L.; Yin, K. Comparison of random forest, artificial neural networks and support vector machine for intelligent diagnosis of rotating machinery. Trans. Inst. Meas. Control 2018, 40, 2681–2693. [Google Scholar] [CrossRef]
- Cui, L.; Huang, J.; Zhang, F. Quantitative and localization diagnosis of a defective ball bearing based on vertical-horizontal synchronization signal analysis. IEEE Trans. Ind. Electron. 2017, 64, 8695–8705. [Google Scholar] [CrossRef]
- 6. Hao, Y.S.; Song, L.Y.; Wang, M.Y.; Cui, L.I.; Wang, H. Underdetermined Source Separation of Bearing Faults Based on Optimized Intrinsic Characteristic-Scale Decomposition and Local Non-Negative Matrix Factorization. IEEE Access 2019, 7, 11427–11435. [Google Scholar] [CrossRef]
- Cui, L.; Wang, J.; Lee, S. Matching Pursuit of an Adaptive Impulse Dictionary for Bearing Fault Diagnosis. J. Sound Vib. 2014, 333, 2840–2862. [Google Scholar] [CrossRef]
- Wang, H.; Li, S.; Song, L.Y. A novel convolutional neural network based fault recognition method via image fusion of multi-vibration-signals. Comput. Ind. 2019, 105, 182–190. [Google Scholar] [CrossRef]
- Cui, L.; Huang, J.F.; Zhang, F.B. HVSRMS localization formula and localization law: Localization diagnosis of a ball bearing outer ring fault. Mech. Syst. Signal Process. 2019, 120, 608–629. [Google Scholar] [CrossRef]
- Wang, H.Q.; Ren, B.Y.; Song, L.Y. A Novel Weighted Sparse Representation Classification Strategy based on Dictionary Learning for Rotating Machinery. IEEE Trans. Instrum. Meas. 2019. [Google Scholar] [CrossRef]
- Cui, L.L.; Yao, T.C.; Zhang, Y.; Gong, X.Y.; Kang, C.H. Application of pattern recognition in gear faults based on the matching pursuit of a characteristic waveform. Measurement 2017, 104, 212–222. [Google Scholar] [CrossRef]
- Hao, Y.; Song, L.; Cui, L.; Wang, H. A three-dimensional geometric features-based SCA algorithm for compound faults diagnosis. Measurement 2019, 134, 480–491. [Google Scholar] [CrossRef]
- Cui, L.; Jin, Z.; Huang, J.; Wang, H. Fault severity classification and size estimation for ball bearings based on vibration mechanism. IEEE Access 2019. [Google Scholar] [CrossRef]
- Wang, H.; Wang, P.; Song, L. A Novel Feature Enhancement Method based on Improved Constraint Model of Online Dictionary Learning. IEEE Access 2019, 7, 17599–17607. [Google Scholar] [CrossRef]
- Al-Meshari, A.; Al-Zahrani, E.; Diab, M. Failure analysis of cooling fan gearbox. Eng. Fail. Anal 2012, 20, 166–172. [Google Scholar] [CrossRef]
- Amarnath, M.; Chandramohan, S. Experimental investigations of surface wear assessment of spur gear teeth. J. Vib. Control 2012, 7, 1009–1024. [Google Scholar] [CrossRef]
- Subramanian, R.B.; Srinivasan, K. Vibration analysis of an influence of groove in the bottom land of a spur gear. J. Vib. Control 2014, 6, 847–858. [Google Scholar] [CrossRef]
- Cui, L.L.; Wang, X.; Wang, H.Q.; Wu, N. Improved Fault Size Estimation Method for Rolling Element Bearings Based on Concatenation Dictionary. IEEE Access 2019, 7, 22710–22718. [Google Scholar] [CrossRef]
- Song, L.Y.; Wang, H.Q.; Chen, P. Step-by-step Fuzzy Diagnosis Method for Equipment Based on Symptom Extraction and Trivalent Logic Fuzzy Diagnosis Theory. IEEE Trans. Fuzzy Syst. 2018, 26, 3467–3478. [Google Scholar] [CrossRef]
- Lin, J.; Robert, G.P. Mesh stiffness variation instabilities in two-stage gear systems. J. Vib. Acoust. 2002, 124, 68–76. [Google Scholar] [CrossRef]
- Li, R.Z. Ring-wheel strength design material. Japan Society of Mechanical Engineers. Mach. Tool Ind. Ed. 1984, 56–58. [Google Scholar]
- Weber, C. The deformation of loaded gears and the effect on their load-carrying capacity. In Scientific and Industrial Research in British; EReport No.3; Department of Scientific and Industrial Research: New Delhi, India, 1949. [Google Scholar]
- Yang, D.C.H.; Lin, J.Y. Hertzian damping, tooth friction and bending elasticity in gear impact dynamics. J. Mesh. Trans. Auto. Des. 1987, 109, 189–196. [Google Scholar] [CrossRef]
- Wang, Q.B.; Zhang, Y.M. A model for analyzing stiffness and stress in a helical gear pair with tooth profile errors. J. Vib. Control 2017, 23, 272–289. [Google Scholar] [CrossRef]
- Wang, X. Study on the Calculation of Gear Crack Dynamics and Gear Tooth Crack Stiffness. Master’s Thesis, Chongqing University, Chongqing, China, 2012. [Google Scholar]
- Mohammed, O.D.; Rantatalo, M.; AIDANPÄÄ, J.O. Improving mesh stiffness calculation of cracked gears for the purpose of vibration-based fault analysis. Eng. Fail. Anal. 2013, 34, 235–251. [Google Scholar] [CrossRef]
- Tian, X.H. Dynamic Simulation for System Response of Gearbox Including Localized Gear Faults. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2004. [Google Scholar]
- Zhao, S.B.; Hong, R.J. Function law calculation Calculation peeling breakdown time at the time of ringing. Mach. Des. Manuf. 2014, 10, 171–176. [Google Scholar]
- Del Rincon, A.F.; Viadero, F.; Iglesias, M.; De-Juan, A.; Garcia, P.; Sancibrian, R. Effect of cracks and pitting defects on gear meshing. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 2805–2815. [Google Scholar] [CrossRef]
- Shao, Y.M.; Wang, X.L. Contact surface time hardness surface surface peeling dynamics model robustness application. J. Vib. Shock 2014, 33, 8–14. [Google Scholar]
- Fernandez-del-Rincon, A.; Garcia, P.; Diez-Ibarbia, A.; de-Juan, A.; Iglesias, M.; Viadero, F. Enhanced model of gear transmission dynamics for condition monitoring applications: Effects of torque, friction and bearing clearance. Mech. Syst. Signal Process. 2017, 85, 445–467. [Google Scholar] [CrossRef]
- Del Rincon, A.F.; de-Juan, A.P.; Garcia, P.A.; Diez-Ibarbia, A.; Viadero, F. Planetary transmission load sharing: Manufacturing errors and system configuration study Iglesias. Mech. Mach. Theory 2017, 111, 21–38. [Google Scholar]
- Saxena, A.; Parey, A. Time varying mesh stiffness calculation of spur gear pair considering sliding friction and peeling defects. Eng. Fail. Anal. 2016, 70, 200–211. [Google Scholar] [CrossRef]
- Yang, D.C.H.; Sun, Z.S. A Rotary Model for Spur Gear Dynamics. J. Mech. Transm. Autom. Des. 1985, 107, 529–535. [Google Scholar] [CrossRef]
- Steward, J.H. Elastic analysis of load distribution in wide-faced spur gears. Master’s Thesis, University of Newcastle, Galan, Australian, 1989. [Google Scholar]
- Chen, Z.; Shao, Y. Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth. Eng. Fail. Anal 2011, 18, 2149–2164. [Google Scholar] [CrossRef]
- Mohammed, O.D.; Rantatalo, M.; Aidanpää, J.O. Vibration signal analysis for gear fault diagnosis with various crack progression scenarios. Mech. Syst. Signal Process. 2013, 41, 176–195. [Google Scholar] [CrossRef]



| Parameters | Drive Wheel | Driven Wheel |
|---|---|---|
| Modulus | 5 | 5 |
| Number of teeth | 19 | 48 |
| Pressure angle | 20° | 20° |
| Addendum coefficient | 1 | 1 |
| Tip clearance coefficient | 0.25 | 0.25 |
| Elastic Modulus | 2.06 × 1011 | 2.06 × 1011 |
| Poisson’s ratio | 0.3 | 0.3 |
| Tooth width | 20 | 20 |
| Ai | Bi | Ci | Di | Ei | Fi | |
|---|---|---|---|---|---|---|
| −5.574e−5 | −1.9986e−3 | −2.3015e−4 | 4.7702e−3 | 0.0271 | 6.8045 | |
| 60.111e−5 | 28.100e−3 | −83.431e−4 | −9.9256e−3 | 0.1624 | 0.9086 | |
| −50.952e−5 | 185.50e−3 | 0.0538e−4 | 53.300e−3 | 0.2895 | 0.9236 | |
| −6.2042e−5 | 9.0889e−3 | −4.0964e−4 | 7.8297e−3 | −0.1472 | 0.6904 |
| 7 mm | 2 mm | 7 mm | 2.5 mm | 1.0 mm | 4.33 mm | 45° |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, L.; Liu, T.; Huang, J.; Wang, H. Improvement on Meshing Stiffness Algorithms of Gear with Peeling. Symmetry 2019, 11, 609. https://doi.org/10.3390/sym11050609
Cui L, Liu T, Huang J, Wang H. Improvement on Meshing Stiffness Algorithms of Gear with Peeling. Symmetry. 2019; 11(5):609. https://doi.org/10.3390/sym11050609
Chicago/Turabian StyleCui, Lingli, Tongtong Liu, Jinfeng Huang, and Huaqing Wang. 2019. "Improvement on Meshing Stiffness Algorithms of Gear with Peeling" Symmetry 11, no. 5: 609. https://doi.org/10.3390/sym11050609
APA StyleCui, L., Liu, T., Huang, J., & Wang, H. (2019). Improvement on Meshing Stiffness Algorithms of Gear with Peeling. Symmetry, 11(5), 609. https://doi.org/10.3390/sym11050609





