The Bessel Expansion of Fourier Integral on Finite Interval
Abstract
1. Introduction
2. Some Basic Theoretical Results
3. The Bessel Expansion of Normal Fourier Integral
3.1. Hermite Series of Analytic Functions
3.2. The Bessel Expansion of Fourier Integral With Analytic Function
4. The Bessel Expansion of Fourier Integral With Symmetric Branch Points
4.1. Hermite Series with Symmetric Branch Points
4.2. The Bessel Expansion of Fourier Integral with Symmetric Branch Points
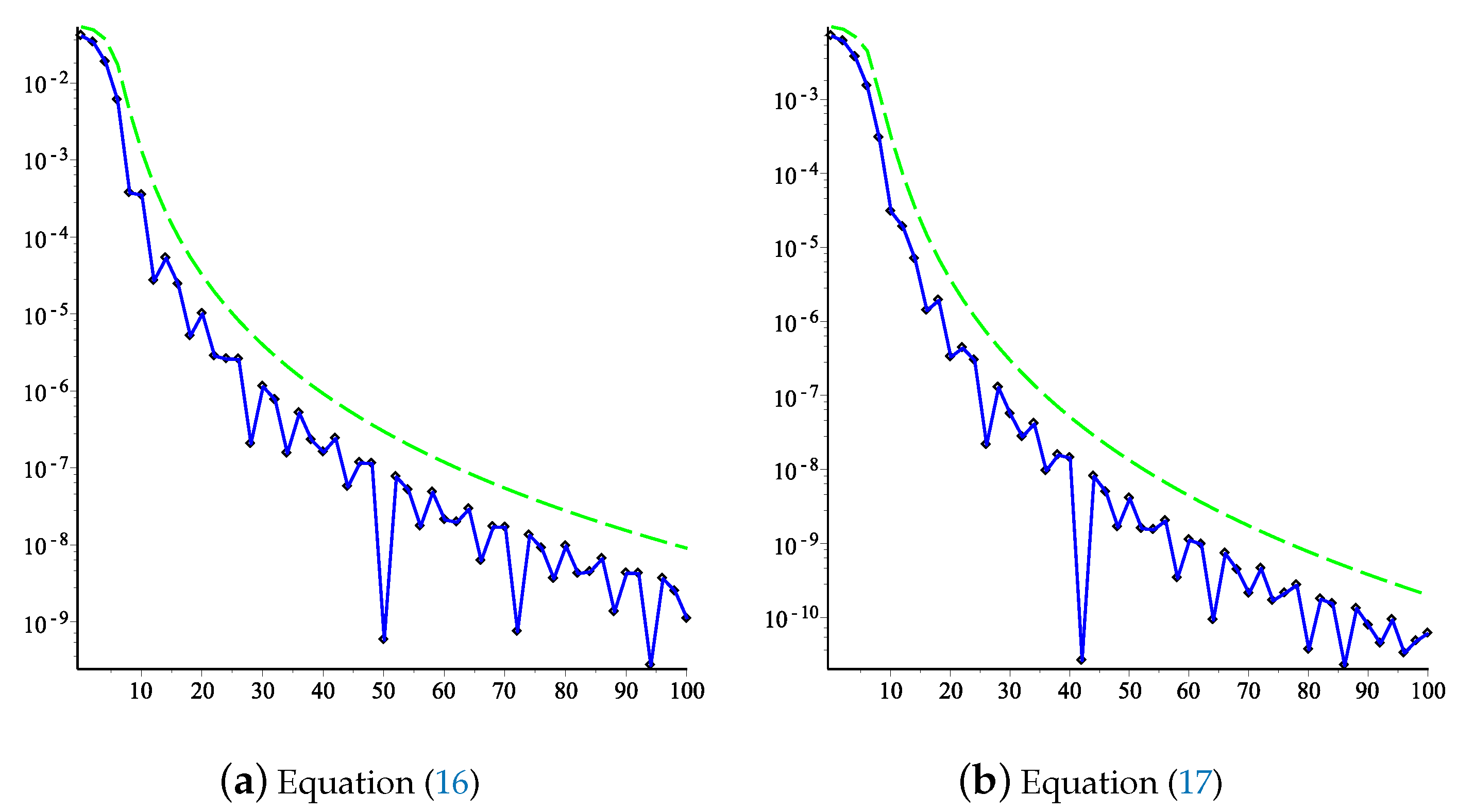
5. The Numerical Experiments
6. The Conclusions and Acknowledgement
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Watson, G.N. A Treatise on the Theory of Bessel Function; Cambridge University Press: Cambridge, UK, 1966. [Google Scholar]
- Deaño, A.; Huybrechs, D.; Iserles, A. Computing Highly Oscillatory Integrals; SIAM: Philadelphia, PA, USA, 2018. [Google Scholar]
- Huybrechs, D.; Iserles, A.; Nørsett, S.P. From high oscillation to rapid approximation V: The equilateral triangle. IMA J. Numer. Anal. 2010, 30, 755–785. [Google Scholar] [CrossRef][Green Version]
- Xiang, S.H. Efficient Filon-type methods for f(x)eiωg(x)dx. Numer. Math. 2007, 105, 633–658. [Google Scholar] [CrossRef]
- Xiang, S.H.; Brunner, H. Efficient methods for Volterra integral equations with highly oscillatory Bessel kernels. BIT Numer. Math. 2013, 53, 241–263. [Google Scholar] [CrossRef]
- Kang, H. Efficient calculation and asymptotic expansions of many different oscillatory infinite integrals. Appl. Math. Comput. 2019, 346, 305–318. [Google Scholar] [CrossRef]
- Filon, L.N.G. On a quadrature formula for trigonometric integrals. Proc. R. Soc. Edinb. 1928, 49, 38–47. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Elsevier/Academic Press: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Dover Publications Inc.: New York, NY, USA, 1965. [Google Scholar]
- Wang, Z.X.; Guo, D.R. Special Functions; World Scientific: Singapore, 1989. [Google Scholar]
- Ahlfors, L.V. Complex Analysis: An Introduction to the Theory of Analytic Functions of One Complex Variable; McGraw-Hill Book Company, Inc.: New York, NY, USA; Toronto, ON, Canada; London, UK, 1979. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Zhao, Z. The Bessel Expansion of Fourier Integral on Finite Interval. Symmetry 2019, 11, 607. https://doi.org/10.3390/sym11050607
Zhou Y, Zhao Z. The Bessel Expansion of Fourier Integral on Finite Interval. Symmetry. 2019; 11(5):607. https://doi.org/10.3390/sym11050607
Chicago/Turabian StyleZhou, Yongxiong, and Zhenyu Zhao. 2019. "The Bessel Expansion of Fourier Integral on Finite Interval" Symmetry 11, no. 5: 607. https://doi.org/10.3390/sym11050607
APA StyleZhou, Y., & Zhao, Z. (2019). The Bessel Expansion of Fourier Integral on Finite Interval. Symmetry, 11(5), 607. https://doi.org/10.3390/sym11050607