A Pairing-Based Three-Party Authenticated Encryption Scheme without Shared Secrets

Abstract

The Traditional Authenticated Encryption (AE) scheme is a single-user cryptographic mechanism which only enables one designated verifier to authenticate the ciphertext. Although several group-oriented AE variants have also been proposed to eliminate such a limitation, they require shared verification. This motivated us to think of a scenario of three-party communication environments where each party runs independent processes without cooperation. In this paper, we realize a novel three-party AE (abbreviated to TPAE) scheme in which two designated verifiers can solely decrypt the same ciphertext and then inspect the validity of embedded signature. Additionally, we also show that our TPAE construction is computationally secure using the well-defined IND-CCA2 and the EF-CMA adversary games in the proof model of random oracles. The comparison results will demonstrate the computational efficiency of our mechanism.

1. Introduction

In public key cryptosystems [1], digital signature schemes [2,3,4] are important mechanisms that serve the same function of handwritten signatures in the real world. A significant property of digital signatures is nonrepudiation [5], which guarantees that a signer cannot deny their generated signatures later.

To further provide the property of confidentiality [6,7] for some special signature applications such as online auction and electronic transactions, one can employ the so-called two-step measure which means an encryption process is performed after a signing operation. Nevertheless, this approach is inefficient.

In 1994, to provide a better solution, Horster et al. [8] introduced a hybrid method known as the authenticated encryption (AE) scheme that can fulfill the characteristic of confidentiality and authenticity [9]. In such an approach, a signer combines the intended recipient’s public key with the signing operation. In this way, the resulted authenticated ciphertext must be verified by the person holding the knowledge of correct private key. Thus, an AE scheme no longer exhibits the characteristic of public verification due to the confidentiality concern. However, this trait also leads to another problem of later dispute provided that a signer denies his/her behavior of making the signature. A designated verifier will have a difficulty in proving the signer’s dishonesty without revealing his private key information.

To handle the above issue, Araki et al. [10] addressed a signature mechanism of limited verifier and an optional arbitration procedure is supplied. Yet, the procedure requires the signer’s assistance to announce an extra parameter. Once the signer refuses cooperation, the arbitration mechanism is useless. Moreover, Zhang and Kim [11] showed that an adversary can choose an arbitrary message to launch universal forgery attacks against Araki et al.’s work successfully.

Later, Wu and Hsu [12] proposed a convertible AE protocol admitting a designated verifier to solely conduct the arbitration steps and then reveal a converted signature for public verification. A noticeable property of the Wu–Hsu scheme is that the signature conversion steps are computation-free, i.e., an originally signed signature would be acquired within the ciphertext decryption procedure. Next, Huang and Chang [13] also presented another enhanced scheme. However, Lv et al. [14] specified that the semantic security is not satisfied in both the Huang-Chang and the Wu–Hsu schemes. Concretely speaking, an adversary can easily distinguish a given authenticated ciphertext from only two candidate messages.

In 2005, Yang [15] proposed a secure scheme with provable security. In 2008, Chien [16] came up with a new AE variant permitting either an original signer or a determined recipient to run the conversion steps of signature. Constructed from famous ElGamal cryptosystems, in 2009, Lee et al. [17] introduced the ElGamal-based variant. In the same year, Wu and Lin [18] showed how to use RSA cryptosystems to build a concrete AE construction with convertibility. Aim at reducing the impact caused by key-compromise attacks, Hsu and Lin [19] presented a key-insulated AE scheme in which a helper is able to renew users’ short-term private keys periodically with the increment of time periods.

Consider group-oriented applications, in 2011, Hsu and Lin [20] presented a convertible variation of multi-AE (a.k.a. MAE) method. To provide more flexible signing policy, in 2014 Lin [21] further introduced a threshold-AE scheme. In 2017, a new AE scheme supporting multisigner and the functionality of proxy delegation was also introduced [22]. Up to present, lots of AE variants [23,24,25,26,27,28,29,30,31] have been proposed. However, all of existing mechanisms puts the emphasis on either the single-user setting or the group-oriented environments with cooperative groups. In this paper, we aim at proposing a better alternative for three-party communication environments where each entity usually runs independent processes without sharing their secrets with each other.

2. Preliminaries

Before presenting the proposed mechanism, we first revisit the operations of bilinear pairing together with some famous cryptographic assumptions, which will be utilized as the underlying building blocks of our work.

Concept of Bilinear Pairing

Let the symbols of G₁ and G₂ be an additive and a multiplicative group, respectively. Both groups have the same prime order q. A bilinear pairing e is expressed as e: G₁ × G₁ → G₂. Some properties of bilinear pairing e are described as follows:

(i)

Bilinearity:

e(Q₁ + Q₂, W) = e(Q₁, W)e(Q₂, W);

e(Q, W₁ + W₂) = e(Q, W₁)e(Q, W₂);

(ii)

Nondegeneracy:

We say that in the group G₂, the value e(Q, Q) is regarded as a generator provided that, in the group G₁, Q is also a generator.

(iii)

Computability:

There exists an efficient polynomial-time algorithm to compute e(P, Q) for any P, Q ∈ G₁.

Elliptic Curve Discrete Logarithm Problem and Assumption

An Elliptic Curve Discrete Logarithm Problem (ECDLP) is to find some x ∈ $Z_q^{*}$ satisfying the equality of X = xQ, where X and Q are two known points over an elliptic curve E. The ECDL assumption asserts that it is almost negligible advantage ε for any probabilistic algorithm $\mathcal{A}$ running in polynomial-time to solve ECDLPs. More precisely, the ECDL assumption is denoted by the following probability inequality:

$$\mathrm{Pr}\left[\mathcal{A}\right(Q,xQ)=x;x\leftarrow Z_q^{*},(Q,xQ)\leftarrow {{\mathit{G}}_1}^2]\le \epsilon .$$

Bilinear Diffie–Hellman Problem and Assumption

A Bilinear Diffie–Hellman Problem (BDHP) was used to calculate e(Q, Q)^xyz ∈ G₂ from four given values (Q, X, Y, and Z) of the group G₁. In particular, X = xQ, Y = yQ and Z = zQ for some x, y, z ∈ $Z_q^{*}$. The BDH assumption asserts that it is almost negligible advantage ε for any probabilistic algorithm $\mathcal{A}$ running in polynomial-time to solve BDHPs. Precisely speaking, the BDH assumption is denoted by the following probability inequality.

$$\mathrm{Pr}\left[\mathcal{A}\right(Q,xQ,yQ,zQ)=e(Q,Q{)}^{xyz};x,y,z\leftarrow Z_q^{*},Q,xQ,yQ,zQ\leftarrow {\mathit{G}}_1]\le \epsilon .$$

3. Proposed TPAE Construction

Using the operation and properties of bilinear pairing, this section is going to present the designed TPAE construction. At first, the roles of participated entities will be briefly described. Then we display the definition of constituted algorithms followed by a secure construction.

3.1. Participated Entity

A general TPAE construction has three participated entities, which cover an original signer and two designated receivers. The former will produce an authenticated ciphertext. Then, both specified receivers can independently decrypt the obtained ciphertext and inspect the validity of embedded signature. A TPAE scheme is said to be correct provided that a signer creates a valid authenticated ciphertext and merely the specified receivers have the privilege to decrypt it and check the validity of embedded signature. Each of the designated receivers could exhibit a transformed signature suitable for public proof when encountering a repudiation dispute, too.

3.2. Constituted Algorithms

The designed TPAE scheme can be divided into four algorithms. We describe the definition of each algorithm as follows.

Setup: This algorithm is used to initialize the constructed system by taking a security parameter k and then generates public parameters params.

Reg_U: The input of this algorithm is an index i while the corresponding output includes a private–public keypair (x_i, Y_i) together with a public key certificate Cert_i.

ESign: The input of this algorithm includes m, x_s, Y_a, and Y_b, which separately represents a message, a signing key, and two verification keys. It will finally generate a corresponding authenticated ciphertext δ.

EVerify: The input of this algorithm includes δ, x_a, ID_s, ID_a, and ID_b, which separately denote a ciphertext, a decryption key, and the identities of one signer and two recipients. The output could be either a transformed signature Ω with the original message m or an error symbol ⊥. The latter case occurs if the input contains a false ciphertext.

3.3. Substantial Construction

Setup: Let k be a security parameter of the input. The algorithm first selects two groups, i.e., G₁ and G₂, which have an identical order of prime q. There is a generator P in the group G₁ and a bilinear map e is defined as G₁ × G₁ → G₂. Assume that h₁: {0, 1}^k × G₁² → Z_q, h₂: G₁³ → {0, 1}^k and h₃: G₂ → G₁ are collision resistant hash functions. The algorithm outputs public params which are composed of G₁, G₂, q, P, and e along with three hash functions.

Reg_U: Given an index i, the algorithm randomly chooses an integer x_i ∈ Z_q as the corresponding private key and then calculates the value Y_i = x_iP to be its public key. Note that a public key certificate named Cert_i is also returned by employing the standard of X.509 [32].

ESign: To produce an authenticated ciphertext for a message m in relation to two verification keys (Y_a and Y_b) and a signing key x_s, the algorithm chooses w ∈ $Z_q^{*}$ to compute

W = wP,

(1)

T = h₃(e(wY_a, Y_b)),

(2)

σ = (x_s + h₁(m, W, T))⁻¹W,

(3)

c = m ⊕ h₂(W, σ, T),

(4)

and then outputs the authenticated ciphertext δ = (W, σ, c).

Note that in Equation (4), the ciphertext parameter c is computed by XOR-ing the message m and the hash result of h₂(W, σ, T). This implies that the original message has to be split into k-bit blocks for facilitating the XOR operation. Therefore, the ciphertext parameter c is constituted by concatenating all XORed blocks.

EVerify: Given an authenticated ciphertext δ = (W, σ, c), one private key x_i (for i ∈ {a, b}) of participated receivers and the signing key Y_s, this algorithm can easily derive

T = h₃(e(x_aW, Y_b)) = h₃(e(Y_a, x_bW)),

(5)

to decrypt the original message m as

m = c ⊕ h₂(W, σ, T)

(6)

and then inspects the embedded redundancy of m. The algorithm further checks its signature by testing whether

e(σ, Y_s + h₁(m, W, T)P) = e(W, P).

(7)

When the above equality is fulfilled, the algorithm returns the decrypted message m together with a transformed signature Ω = (W, σ, T). If not, an error symbol ⊥ is outputted to denote the false ciphertext.

The correctness of Equations (6) and (7) could be confirmed by the following derivations. In Equation (6), the right side can be written as

	c ⊕ h2(W, σ, T)
=	c ⊕ h2(W, σ, h3(e(xaW, Yb)))	(by Equation (5))
=	c ⊕ h2(W, σ, h3(e(xatP, Yb)))	(by Equation (1))
=	c ⊕ h2(W, σ, h3(e(wYa, Yb)))
=	c ⊕ h2(W, σ, T)	(by Equation (2))
=	m	(by Equation (4))

which is just the left side of Equation (6).

In Equation (7), the left side can be written as

	e(σ, Ys + h1(m, W, T)P)
=	e((xs + h1(m, W, T))−1W, Ys + h1(m, W, T)P)	(by Equation (3))
=	e((xs + h1(m, W, T))−1W, (xs + h1(m, W, T))P)
=	e(W, P)

which is the right side of Equation (7).

4. Security Model and Proof

To prove the security of our TPAE scheme, we first revisit the general security models of confidentiality and unforgeability below.

Definition 1

(Requirement of IND-CCA2). The proposed TPAE scheme satisfies the characteristic of indistinguishability for the confidentiality requirement provided that no probabilistic polynomial-time (PPT) adversary $\mathcal{A}$ plotting adaptive chosen ciphertext attacks has a non-negligible advantage to beat a player $\mathcal{B}$ acting as a challenger in the following game.

Setup (1^k): By initializing the Setup(1^k) algorithm, the challenger $\mathcal{B}$ first provides the adversary $\mathcal{A}$ with public params.

Phase 1: The querying capability of adversary $\mathcal{A}$ consists of the following oracles.

Reg_U query:$\mathcal{A}$ could choose an index i to request its Reg_U query. $\mathcal{B}$ would run the Reg_U algorithm and return the output of (Y_i, Cert_i).

ESign query:$\mathcal{A}$ could request an ESign query for his/her chosen m, Y_s, Y_a, and Y_b. $\mathcal{B}$ outputs a corresponding authenticated ciphertext δ to $\mathcal{A}$.

EVerify query:$\mathcal{A}$ could request an EVerify query for his/her chosen ciphertext δ. $\mathcal{B}$ would send either an error symbol ⊥ or a message m along with its transformed signature Ω to $\mathcal{A}$.

Challenge: After requesting several queries, the adversary $\mathcal{A}$ would create messages, say, m₀ and m₁, where | m₀ | = | m₁ |. Then $\mathcal{B}$ determines λ ← {0, 1} by flipping an internal coin. An authenticated ciphertext δ* on m_λ is also computed as a challenge designated for $\mathcal{A}$.

Phase 2: In this phase, the adversary $\mathcal{A}$ continues to request new queries, but does not include any EVerify query on the target challenge.

Guess: At last, we say that the adversary $\mathcal{A}$ is the winner of this game provided that his/her guessed bit λ′ = λ. The advantage of $\mathcal{A}$, denoted as Adv($\mathcal{A}$), could be written as | Pr[λ′ = λ] – 0.5 |.

Definition 2

(Requirement of EF-CMA). The proposed TPAE scheme satisfies the characteristic of existential unforgeability provided that no PPT adversary $\mathcal{A}$ plotting adaptive chosen-message attacks has a non-negligible advantage to beat a player $\mathcal{B}$ acting as a challenger in the following game:

Setup(1^k): By initializing the Setup(1^k) algorithm, the challenger $\mathcal{B}$ first provides the adversary $\mathcal{A}$ with public params.

Phase 1: The querying capability of adversary $\mathcal{A}$ consists of Reg_U and ESign oracles just like those described in Definition 1.

Forgery: At the end of this game, we say that the winner is $\mathcal{A}$ if he/she outputs a valid δ* on an arbitrarily chosen m*. It should be noted that δ* could not be obtained via an ESign oracle.

We then adopt the techniques of random oracle proof models to formally show that the proposed mechanism satisfies the security of Definitions 1 and 2.

Theorem 1

(Proof of IND-CCA2)1 It is said that the proposed TPAE scheme is (t, q_h1, q_h2, q_h3, q_{Reg_U}, q_ESign, q_EVerify, ε)-secure in the requirement of IND-CCA2 when no PPT adversary has the non-negligible advantage ε′ to solve the BDHP within the running time t′, where

$${\epsilon }^{\prime }\ge (\frac{1}{q_{h_3}})(2\epsilon -\frac{q_{EVerify}}{2^k}),$$

t’ ≈ t + t_λ(2q_EVerify).

Here, t_λrepresents the required computation time of a bilinear map.

Proof. 

We first assume that within the running time, t, there is a PPT adversary, $\mathcal{A}$, whose capability is sufficient to break the proposed TPAE construction by plotting adaptive chosen ciphertext attacks. The advantage of the adversary $\mathcal{A}$ is ε and the maximum query times of oracle i is denoted as q_i. By utilizing $\mathcal{A}$ as a subroutine, it enables us to create a new algorithm, say $\mathcal{B}$, to break the assumption of BDH within the expected time t′ and the success probability is ε′. Let P, xP, yP, and zP be the inputted BDHP instance for $\mathcal{B}$ and the desired output would be e(P, P)^xyz. In the following interactive processes, $\mathcal{B}$ acts as a challenger to answer queries submitted by $\mathcal{A}$. □

Setup: By performing the initial Setup(1^k) algorithm, the challenger $\mathcal{B}$ provides the adversary $\mathcal{A}$ with public params = {G₁, G₂, q, P, e}.

Phase 1: In the beginning, $\mathcal{A}$ designates (ID_s, ID_a, and ID_b) as the identities of the signer and two designated verifiers, and could adaptively request queries stated below.

h₁oracle:$\mathcal{A}$ could submit an h₁(m, W, T) oracle to get the value v₁ ∈ _R Z_q. A record of (m, W, T, v₁) would also be written into a maintained h₁-list by $\mathcal{B}$.

h₂oracle:$\mathcal{A}$ could submit an h₂(W, σ, T) oracle to get the value v₂ ∈ _R {0, 1}^k. A record of (W, σ, T, v₂) would also be written into a maintained h₂-list by $\mathcal{B}$.

h₃oracle:$\mathcal{A}$ could submit an h₃(E) oracle to get the value v₃ ∈ _RG₁. A record of (E, v₃) would also be written into a maintained h₃-list by $\mathcal{B}$.

Reg_U query:$\mathcal{A}$ could choose an index i to request its Reg_U query. If i = a, $\mathcal{B}$ sends (Y_a = xP, Cert_a) to $\mathcal{A}$. If i = b, $\mathcal{B}$ returs (Y_b = yP, Cert_b) to $\mathcal{A}$. When i = s, $\mathcal{B}$ calls the Reg_U algorithm to get (x_s, Y_s, Cert_s) and then returns (Y_s, Cert_s) to $\mathcal{A}$.

ESign query:$\mathcal{A}$ could request an ESign query on an arbitrarily chosen message m. $\mathcal{B}$ would run the ESign algorithm to return the corresponding result.

EVerify query:$\mathcal{A}$ could request an EVerify query on a ciphertext δ = (W, σ, c). $\mathcal{B}$ utilizes (W, σ) as keywords to search the h₂-list for all matched v_2′s. If one of matched v_2′s satisfies that e(σ, Y_s + h₁(c ⊕ v₂, W, T)P) = e(W, P), $\mathcal{B}$ returns (c ⊕ v₂, W, σ, T). If not, $\mathcal{A}$ will receive an error symbol.

Challenge: After requesting several queries, the adversary $\mathcal{A}$ would create messages, say m₀ and m₁, where | m₀ | = | m₁ |. Then $\mathcal{B}$ determines λ ← {0, 1} by flipping an internal coin and computes a ciphertext δ* for the selected m_λ with the following steps:

Step 1

Randomly choose v₁ ∈ Z_q along with v₂ ∈ {0, 1}^k;

Step 2

Let W* = zP;

Step 3

Compute σ* = (x_s + v₁)⁻¹W* and c* = m_λ ⊕ v₂;

Step 4

Add the record of (m_λ, W*, null, v₁) into h₁-list;

Step 5

Add the record of (W*, σ*, null, v₂) into h₂-list.

The ciphertext δ* = (W*, σ*, c*) is served as a target challenge for $\mathcal{A}$.

Phase 2: In this phase, the adversary $\mathcal{A}$ continues to request new queries, but does not include any EVerify queries on the target challenge δ*.

Analysis of the game: In this game interaction, it is possible for the adversary $\mathcal{A}$ to get an error symbol with respect to an EVerify query on some valid δ = (W, σ, c). Such an event will happen in the case that the corresponding h₂(W, σ, T) oracle had never been made before. We express this event as EVerify_Fat and Pr[EVerify_Fat] during the entire simulation game is not greater than $\frac{q_{EVerify}}{2^k}$, as $\mathcal{A}$ can issue at most q_EVerify EVerify queries. Besides, in the challenge phase, $\mathcal{B}$ sets W* = zP, which infers that the component Z* is formulated as h₃(e(x(zP), yP)) = h₃(e(P, P)^xyz). If the adversary $\mathcal{A}$ queries an h₃ oracle on the value e(P, P)^xyz during the second phase, the simulation game would accidentically terminate. We denote such an event as QH₃* and let PSG be the event of perfect simulation game. When the event PSG occurs, $\mathcal{A}$ has no better change to guess λ, i.e.,

Pr[λ′ = λ | PSG] = 0.5.

(8)

Modified from the probability event of Pr[λ′ = λ], it could be obtained that

Pr[λ′ = λ] = Pr[λ′ = λ | PSG] Pr[PSG] + Pr[λ′ = λ | ¬PSG] Pr[¬PSG]

≤ 0.5Pr[PSG] + Pr[¬PSG]

(by Equation (8))

= 0.5(1 − Pr[¬PSG]) + Pr[¬PSG]

= 0.5 + 0.5Pr[¬PSG].

(9)

Additionally, it could also be learned that

Pr[λ′ = λ] ≥ Pr[λ′ = λ | PSG] Pr[PSG]

= 0.5(1 − Pr[¬PSG])

= 0.5 − 0.5Pr[¬PSG].

(10)

Integrating inequalities (9) with (10), we have

| Pr[λ′ = λ] − 0.5 | ≤ 0.5Pr[¬PSG].

(11)

According to the proof assumption, the adversary $\mathcal{A}$ is sufficient to break our TPAE construction with a non-negligible chance ε, which indicates that

ε	= | Pr[λ′ = λ] − 0.5 |	(by Definition 1)
	≤ 0.5Pr[¬PSG]	(by Equation (11))
	= 0.5(Pr[QH3* ∨ EVerify_Fat])
	≤ 0.5(Pr[QH3*] + Pr[EVerify_Fat]).

Further rewrite this inequality and it will have that

Pr[QH₃*] ≥ 2ε − Pr[EVerify_Fat]

$$\ge 2\epsilon -\frac{q_{EVerify}}{2^k}.$$

When the event QH₃* happens, we claim that e(P, P)^xyz would be contained in a record of h₃-list. For that reason, we could mean that the advantage of the algorithm $\mathcal{B}$ for breaking the designated BDHP instance is ε′ ≥ $(\frac{1}{q_{h_3}})(2\epsilon -\frac{q_{EVerify}}{2^k})$. The expected running time of $\mathcal{B}$ is calculated as t′ ≈ t + t_λ(2q_EVerify).

Theorem 2.

(Proof of EF-CMA). It is said that the proposed TPAE scheme is (t, q_h1, q_h2, q_h3, q_{Reg_U}, q_ESign, ε)-secure in the requirement of EF-CMA when no PPT adversary having the non-negligible advantage ε′ solves the ECDLP within the running time t′, where

ε′ ≥ 10(q_ESign + 1)(q_ESign + q_h1)/2^k,

t′ ≤ 120686q_h1t/ε.

Proof. 

We first assume that within the running time t, there is a PPT adversary, $\mathcal{A}$, whose capability is sufficient to break the proposed TPAE construction by plotting adaptive chosen message attacks. The advantage of the adversary $\mathcal{A}$ is ε and the maximum query times of oracle i is denoted as q_i. By utilizing $\mathcal{A}$ as a subroutine, it enables us to create a new algorithm, say $\mathcal{B}$, to break the assumption of ECDL within the expected time t’ and the success probability is ε’. Let (P, zP) be the inputted ECDLP instance for $\mathcal{B}$ and the purpose is to obtain z. In this proof, we use the technique of Forking Lemma [33] and $\mathcal{B}$ acts as a challenger to answer queries submitted by $\mathcal{A}$. □

Setup: By performing the initial Setup(1^k) algorithm, the challenger $\mathcal{B}$ provides the adversary $\mathcal{A}$ with public params = {G₁, G₂, q, P, e} and a random tape which is constituted of a series of random bits. Given public params and an identical random tape, $\mathcal{B}$ would play two rounds of games with the adversary $\mathcal{A}$ below.

Phase 1: In the beginning, $\mathcal{A}$ designates (ID_s, ID_a, and ID_b) as the selected identities of the signer together with two intended verifiers, and then adaptively makes new queries as follows. For all h_i (i∈{1, 2, 3}) oracles, $\mathcal{B}$ returns as those defined in Theorem 1.

Reg_U query: When $\mathcal{A}$ requests an Reg_U query on the index i = s, $\mathcal{B}$ directly sends (Y_s = zP, Cert_s) to $\mathcal{A}$. Otherwise, $\mathcal{B}$ calls the Reg_U algorithm for getting (x_i, Y_i, and Cert_i) and then returns (Y_i, Cert_i) to $\mathcal{A}$.

ESign query: When $\mathcal{A}$ submits an ESign query on his/her chosen m, Y_s, Y_a, and Y_b, $\mathcal{B}$ performs the subsequent procedures:

Step 1

Randomly pick two integers d, v₁ ∈ $Z_q^{*}$;

Step 2

Run the Reg_U algorithm to get (x_a, Y_a, Cert_a) and (x_b, Y_b, Cert_b);

Step 3

Compute

• σ = dP,
• W = d(zP) + v₁dP,
• T = h₃(e(x_aW, Y_b)),
• c = m ⊕ h₂(W, σ, T);

Step 4

Add the entry (m, W, T, v₁) into h₁-list;

The ciphertext δ = (W, σ, c) is then returned to $\mathcal{A}$.

Analysis of the game: In the above simulation, it is obvious that the ESign query always returns a valid authenticated ciphertext, such that the adversary $\mathcal{A}$ is incapable of distinguishing it from the one outputted by the real scheme. When $\mathcal{A}$ successfully forges a fresh ciphertext δ = (W, σ, c) for the message m denoted by the event PF, we obtain Pr[PF] = ε as $\mathcal{A}$ owns a non-negligible chance ε of breaking our TPAE construction. Now we evaluate the probability that $\mathcal{A}$ does not query the corresponding h₁ oracle and we know that Pr[¬QH₁] ≤ 2^−k. Hence, it could be further expressed that the probability of $\mathcal{A}$ to generate a valid ciphertext δ = (W, σ, c) following making the corresponding h₁(m, W, T) oracle to be Pr[PF ∧ QH₁] ≥ (ε − 1/2^k). Afterwards, $\mathcal{B}$ plays the second round with $\mathcal{A}$ in the same environment. Because the inputted tape is formed by identical series of randomized bits, the challenger $\mathcal{B}$ is able to anticipate $\mathcal{A}$’s next query. According to the responses made in first run, $\mathcal{B}$ returns the same results until $\mathcal{A}$ queries the critical h₁(m, W, T) oracle. Instead of returning original v₁, $\mathcal{B}$ outputs a new value v₁*. By the Forking Lemma, if $\mathcal{A}$ finally forges a valid ciphertext δ* = (W, σ*, c*) with h₁(m, W, T) = v₁*, $\mathcal{B}$ can solve the ECDLP. Concretely speaking, when the adversary $\mathcal{A}$ finally outputs two valid ciphertext (δ, δ*) with h₁(m, W, T) ≠ h₁*(m, W, T), we can obtain two equations:

σ = (x_s + h₁(m, W, T))⁻¹W = (z + v₁)⁻¹W,

σ* = (x_s + h₁*(m, W, T))⁻¹W = (z + v₁*)⁻¹W.

Thus, the ECDLP instance can be solved by computing z = $\frac{{\sigma }^{*}{v_1}^{*}-\sigma v_1}{\sigma -{\sigma }^{*}}$. We could evaluate $\mathcal{B}$’s success probability after two simulation games as ε ≥ 10(q_ESign+ 1)(q_ESign+ q_h1)/2^k and the expected running time spent by $\mathcal{B}$ is t’ ≤ 120686q_h1t/ε.

Note that an adversary might try to derive a valid ciphertext if he/she has access to multiple ciphertexts. Yet, each valid ciphertext will also contain a valid signature which is randomly generated and protected by a secret value chosen by the signer. Consequently, it is computationally infeasible for any adversary to plot the forgery attacks from multiple known ciphertexts.

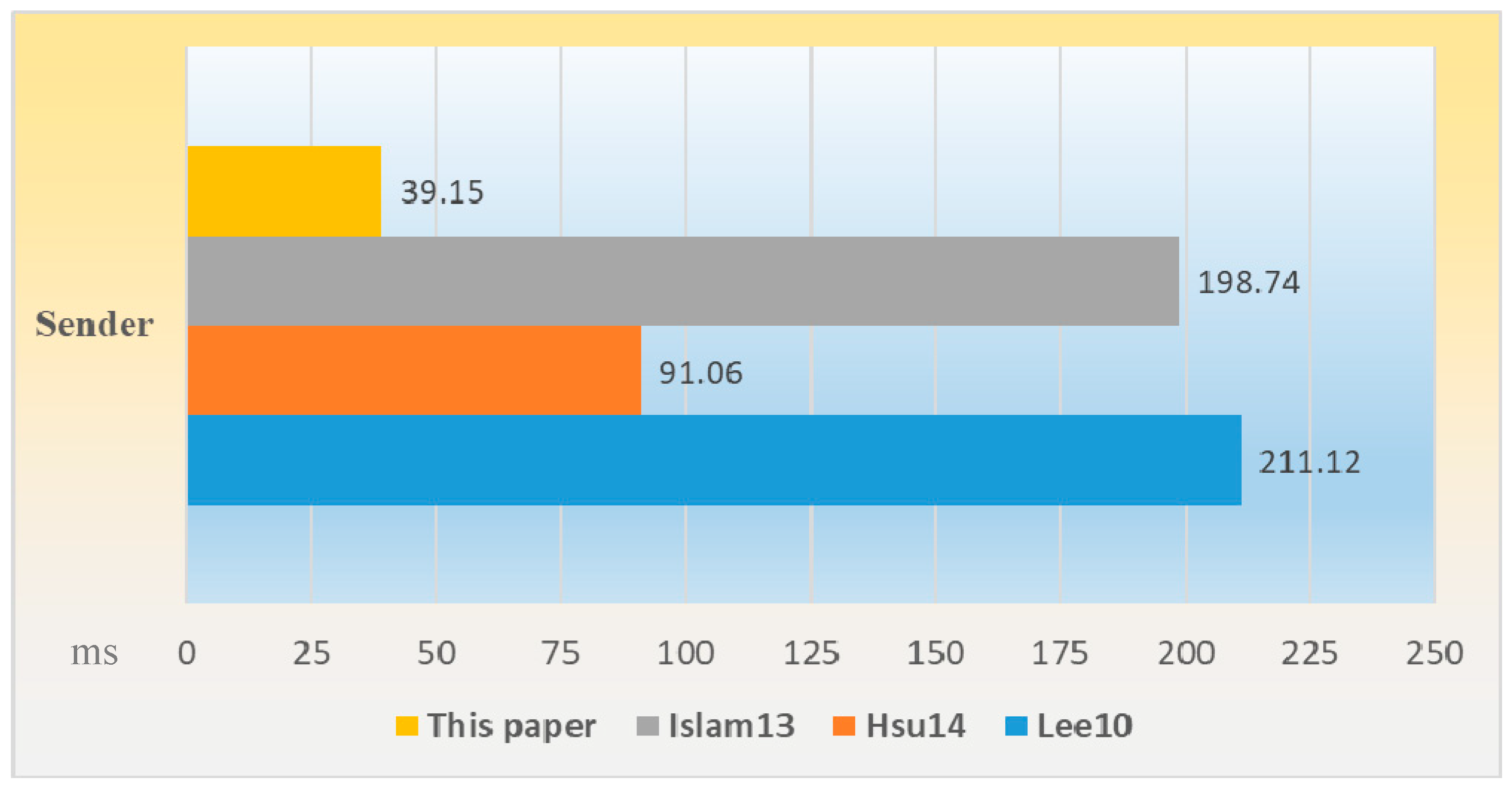
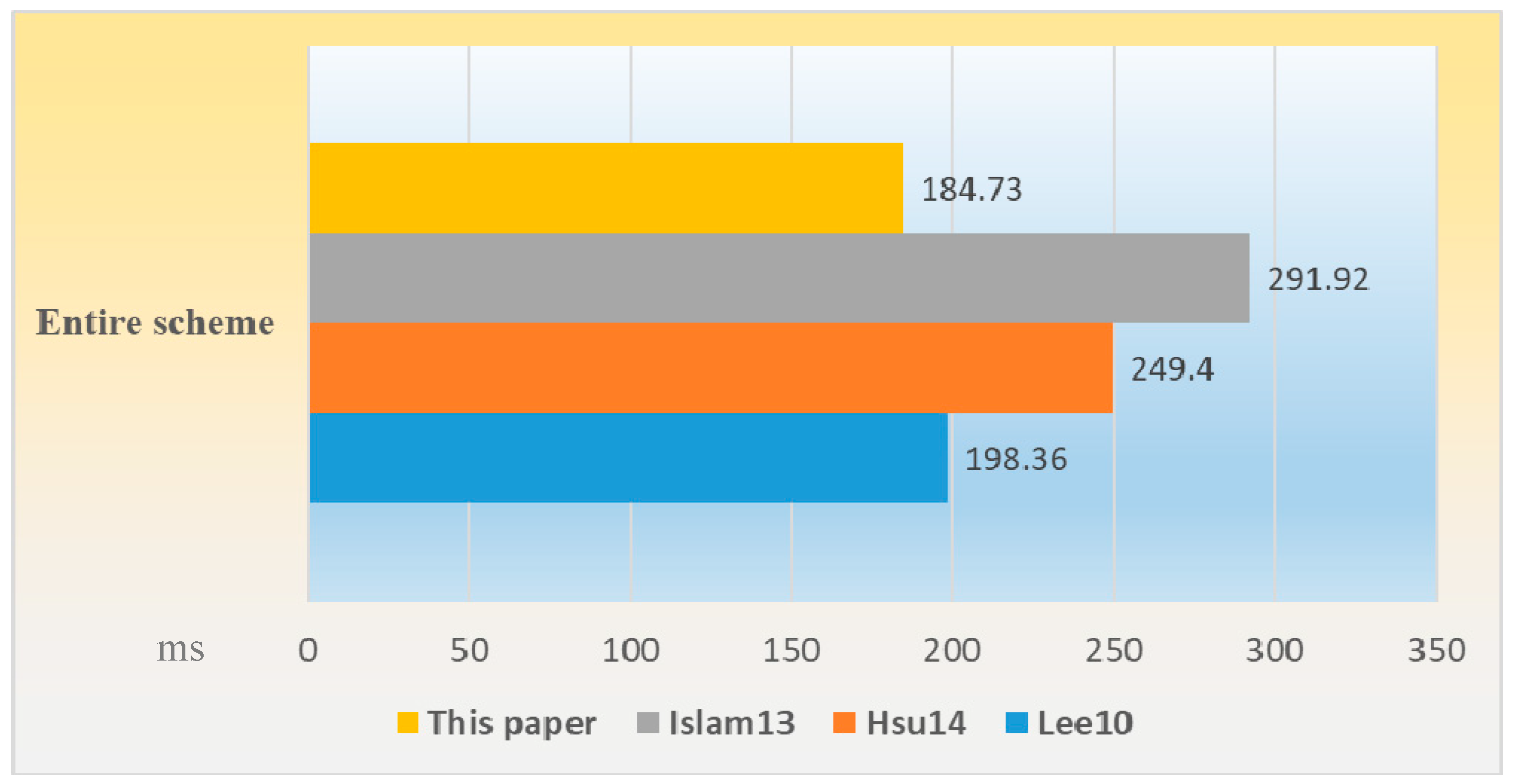
5. Performance Evaluation

In a three-party communication environment, a party usually has to transmit the same message to the other two parties. When the message is encrypted with traditional asymmetric approaches, the sender is required to run the encryption process twice for two recipients who do not want to share their private keys with each other. In such a way, a sender engaged in three-party communication environments often incurs higher computational costs. From the above computational perspective, we will show that the proposed scheme is better than previous single-user setting mechanisms.

As our protocol is implemented on pairing-based systems, we only consider some time-consuming operations such as bilinear map, exponentiation, and scalar multiplication. The operations of XOR, addition and one-way hash function are ignored. We present the used symbols as

Table 1. The used symbols.

Symbol	Description
C1	To execute a bilinear pairing computation
C2	To execute an exponentiation computation over G2
C3	To execute a scalar multiplication over G1

.

Table 2. Computational comparison in three-party communication environments.

	Sender	Each Recipient	Entire Scheme
Lee10	4C1 + 4C3	2C1 + C3	8C1 + 6C3
Hsu14	2C1 + 8C3	3C1 + 3C3	8C1 + 14C3
Islam13	6C1 + 6C3 + 2C2	C1 + C3 + C2	8C1 + 8C3 + 4C2
This paper	C1 + 3TM	3C1 + 2C3	7C1 + 7C3

is the summary of computational comparisons among our TPAE scheme and thee similar protocols involving Lee et al.’s (Lee10) [34], the Hsu–Lin (Hsu14) [24], and the Islam–Biswas (Islam13) [35]. In order to obtain more united comparison results, we adopt Cao et al.’s experimental figures [36] to transform the above computation into approximate running time as Figure 1, Figure 2 and Figure 3. Specifically, the computation of a bilinear pairing, exponentiation and scalar multiplication will take approximately 20.01 ms, 11.2 ms, and 6.38 ms, respectively.

In Figure 1, a sender of the proposed scheme has to spend about 39.15 ms for generating a ciphertext intended for two recipients. The required time is minimal among all compared mechanisms. Although in Figure 2, each recipient’s running time of both Lee et al.’s [34] and the Islam–Biswas [35] is better than that of ours and the proposed scheme still exhibits better performance as a whole in Figure 3. Accordingly, it is evident that our proposed scheme outperforms compared ones from either the sender side or the entire mechanism.

6. Conclusions

AE schemes with convertibility have found numerous applications in online transactions such as e-auction and confidential contract signing. In this paper, we focused on the applications of three-party communication environments and proposed a novel three-party AE (TPAE) scheme. Unlike most group-oriented AE mechanisms which require cooperative verification, our TPAE scheme allows two designated recipients to solely decrypt acquired ciphertext along with inspecting the recovered signature without utilizing shared secrets. Moreover, the signature conversion process also exhibits the property of computation-free and can be carried out by each designated recipient alone. To make certain the realistic feasibility, the requirement of IND-CCA2 and that of EF-CMA for our construction are both fulfilled in the formal proof model of random oracles. Compared to previous similar protocols in terms of computational efforts, the designed approach is particularly appealing to the three-party applications.