Weights-Based Image Demosaicking Using Posteriori Gradients and the Correlation of R–B Channels in High Frequency
Abstract
1. Introduction
2. Related Work
2.1. The Outline of G Interpolation in ACP
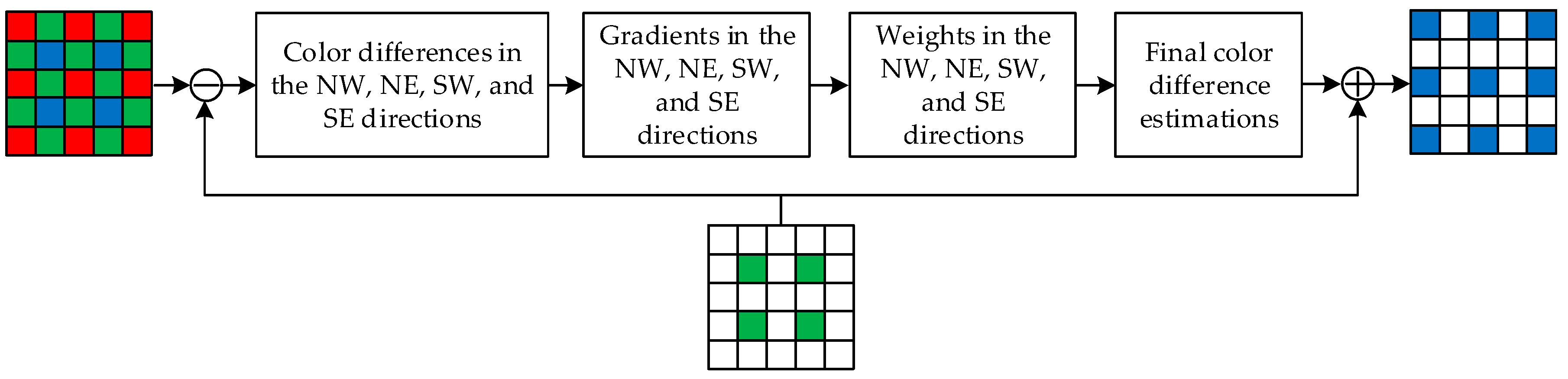
2.2. The Process of R/B Interpolation at B/R Positions in LDI-NAT
3. The Proposed Algorithm
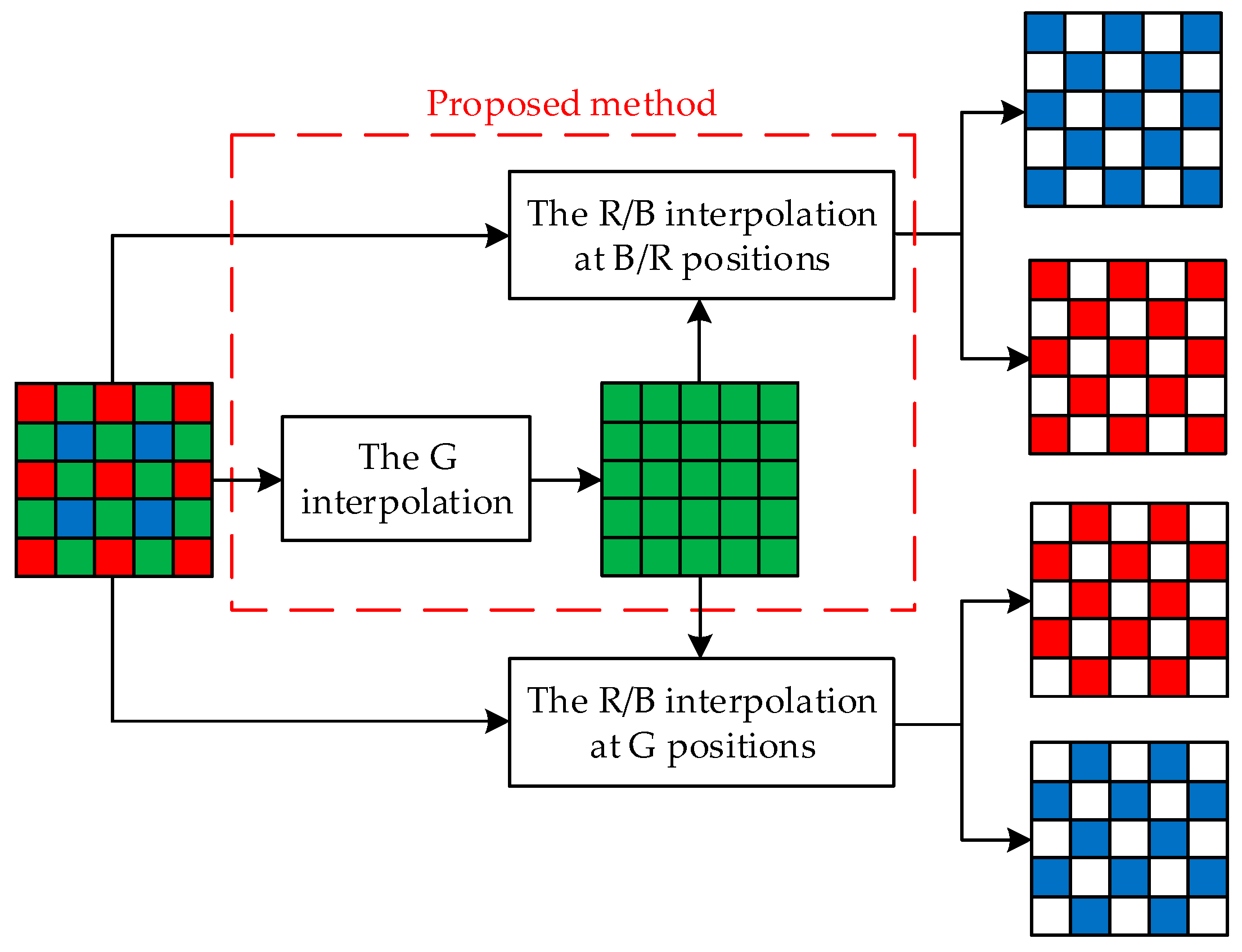
3.1. The Outline of the Proposed Algorithm
3.2. The G Interpolation at R/B Positions
3.3. The R/B Interpolation at G Positions
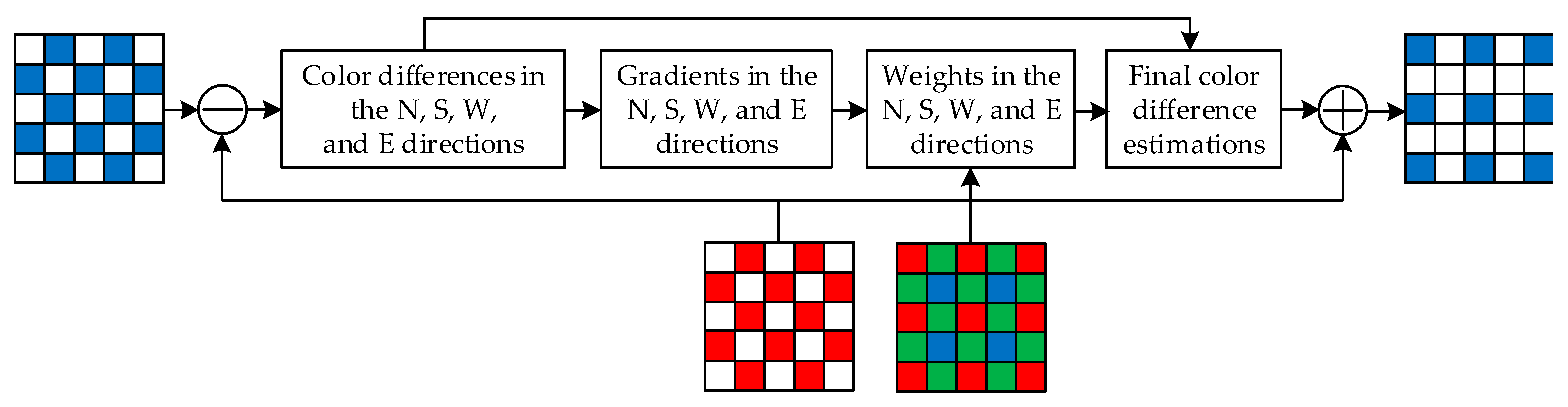
3.4. The R/B Interpolation at B/R Positions
4. Experimental Results and Performance Analyses
5. Conclusions and Remarks on Possible Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Menon, D.; Calvagno, G. Color image demosaicking: An overview. Signal Process. Image Commun. 2011, 26, 518–533. [Google Scholar] [CrossRef]
- Bayer, B.E. Color imaging array. U.S. Patent 3,971,065, 20 July 1976. [Google Scholar]
- Longere, P.; Zhang, X.M.; Delahunt, P.B.; Brainard, D.H. Perceptual assessment of demosaicing algorithm performance. Proc. IEEE 2002, 90, 123–132. [Google Scholar] [CrossRef]
- Malvar, H.S.; He, L.W.; Cutler, R. High-quality linear interpolation for demosaicing of Bayer-patterned color images. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004; pp. 485–488. [Google Scholar]
- Luo, X.; Sun, H.J.; Chen, Q.P.; Chen, J.; Wang, Y.J. Real-time demosaicing of Bayer pattern images. Chin. J. Opt. Appl. Opt. 2010, 3, 182–187. [Google Scholar]
- Wang, D.Y.; Yu, G.; Zhou, X.; Wang, C.Y. Image demosaicking for Bayer-patterned CFA images using improved linear interpolation. In Proceedings of the 7th International Conference on Information Science and Technology, Da Nang, Vietnam, 16–19 April 2017; pp. 464–469. [Google Scholar]
- Zhou, X.; Yu, G.; Yu, K.; Wang, C.Y. An effective image demosaicking algorithm with correlation among Red-Green-Blue channels. Int. J. Eng. Trans. B 2017, 30, 1190–1196. [Google Scholar]
- Adams, J.E.; Hamilton, J.F. Adaptive color plan interpolation in single sensor color electronic camera. U.S. Patent 5,629,734, 13 May 1997. [Google Scholar]
- Lee, J.; Jeong, T.; Lee, C. Improved edge-adaptive demosaicking method for artifact suppression around line edges. In Proceedings of the Digest of Technical Papers International Conference on Consumer Electronics, Las Vegas, NV, USA, 10–14 January 2007; pp. 1–2. [Google Scholar]
- Menon, D.; Andriani, S.; Calvagno, G. Demosaicing with directional filtering and a posteriori decision. IEEE Trans. Image Process. 2007, 16, 132–141. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.J.; Chang, P.Y. Effective demosaicking algorithm based on edge property for color filter arrays. Digit. Signal Process. 2012, 22, 163–169. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.L. Color demosaicking via directional linear minimum mean square-error estimation. IEEE Trans. Image Process. 2005, 14, 2167–2178. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Wang, C.Y.; Zhang, S.Y. Region-adaptive demosaicking with weighted values of multidirectional information. J. Commun. 2014, 9, 930–936. [Google Scholar] [CrossRef]
- Chung, K.H.; Chan, Y.H. Low-complexity color demosaicing algorithm based on integrated gradients. J. Electron. Imaging 2010, 19, 021104. [Google Scholar] [CrossRef]
- Pekkucuksen, I.; Altunbasak, Y. Gradient based threshold free color filter array interpolation. In Proceedings of the 17th IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 137–140. [Google Scholar]
- Zhang, L.; Wu, X.L.; Buades, A.; Li, X. Color demosaicking by local directional interpolation and nonlocal adaptive thresholding. J. Electron. Imaging 2011, 20, 023016. [Google Scholar]
- Chen, X.D.; Jeon, G.; Jeong, J. Voting-based directional interpolation method and its application to still color image demosaicking. IEEE Trans. Circuits Syst. Video Technol. 2014, 24, 255–262. [Google Scholar] [CrossRef]
- Wu, J.J.; Anisetti, M.; Wu, W.; Damiani, E.; Jeon, G. Bayer demosaicking with polynomial interpolation. IEEE Trans. Image Process. 2016, 25, 5369–5382. [Google Scholar] [CrossRef] [PubMed]
- Kiku, D.; Monno, Y.; Tanaka, M.; Okutomi, M. Residual interpolation for color image demosaicking. In Proceedings of the 20th IEEE International Conference on Image Processing, Melbourne, VIC, Australia, 15–18 September 2013; pp. 2304–2308. [Google Scholar]
- He, K.M.; Sun, J.; Tang, X.Q. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Kiku, D.; Monno, Y.; Tanaka, M.; Okutomi, M. Minimized-Laplacian residual interpolation for color image demosaicking. In Proceedings of the SPIE-IS and T Electronic Imaging - Digital Photography X, San Francisco, CA, USA, 3–5 February 2014; pp. 1–8. [Google Scholar]
- Yu, K.; Wang, C.Y.; Yang, S.; Lu, Z.W.; Zhao, D. An effective directional residual interpolation algorithm for color image demosaicking. Appl. Sci. 2018, 8, 680. [Google Scholar] [CrossRef]
- Wang, L.; Jeon, G. Bayer pattern CFA demosaicking based on multi-directional weighted interpolation and guided filter. IEEE Signal Process. Lett. 2015, 22, 2083–2087. [Google Scholar] [CrossRef]
- Monno, Y.; Kiku, D.; Tanaka, M.; Okutomi, M. Adaptive residual interpolation for color and multispectral image demosaicking. Sensors 2017, 17, 2787. [Google Scholar] [CrossRef] [PubMed]
- Thomas, J.B.; Farup, I. Demosaicing of periodic and random color filter arrays by linear anisotropic diffusion. J. Imaging Sci. Technol. 2018, 62, 050401. [Google Scholar] [CrossRef]
- Zhang, L.; Lukac, R.; Wu, X.L.; Zhang, D. PCA-based spatially adaptive denoising of CFA images for single-sensor digital cameras. IEEE Trans. Image Process. 2009, 18, 797–812. [Google Scholar] [CrossRef] [PubMed]
- Djeddi, M.; Ouahabi, A.; Batatia, H.; Basarab, A.; Kouamé, D. Discrete wavelet for multifractal texture classification: Application to medical ultrasound imaging. In Proceedings of the 17th IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 637–640. [Google Scholar]
- Ahmed, S.S.; Messali, Z.; Ouahabi, A.; Trepout, S.; Messaoudi, C.; Marco, S. Nonparametric denoising methods based on Contourlet transform with sharp frequency localization: Application to low exposure time electron microscopy images. Entropy 2015, 17, 3461–3478. [Google Scholar] [CrossRef]
- Eastman Kodak Company. Kodak lossless true color image suite—Photo CD PCD0992. Available online: http://r0k.us/graphics/kodak/index.html (accessed on 25 April 2019).
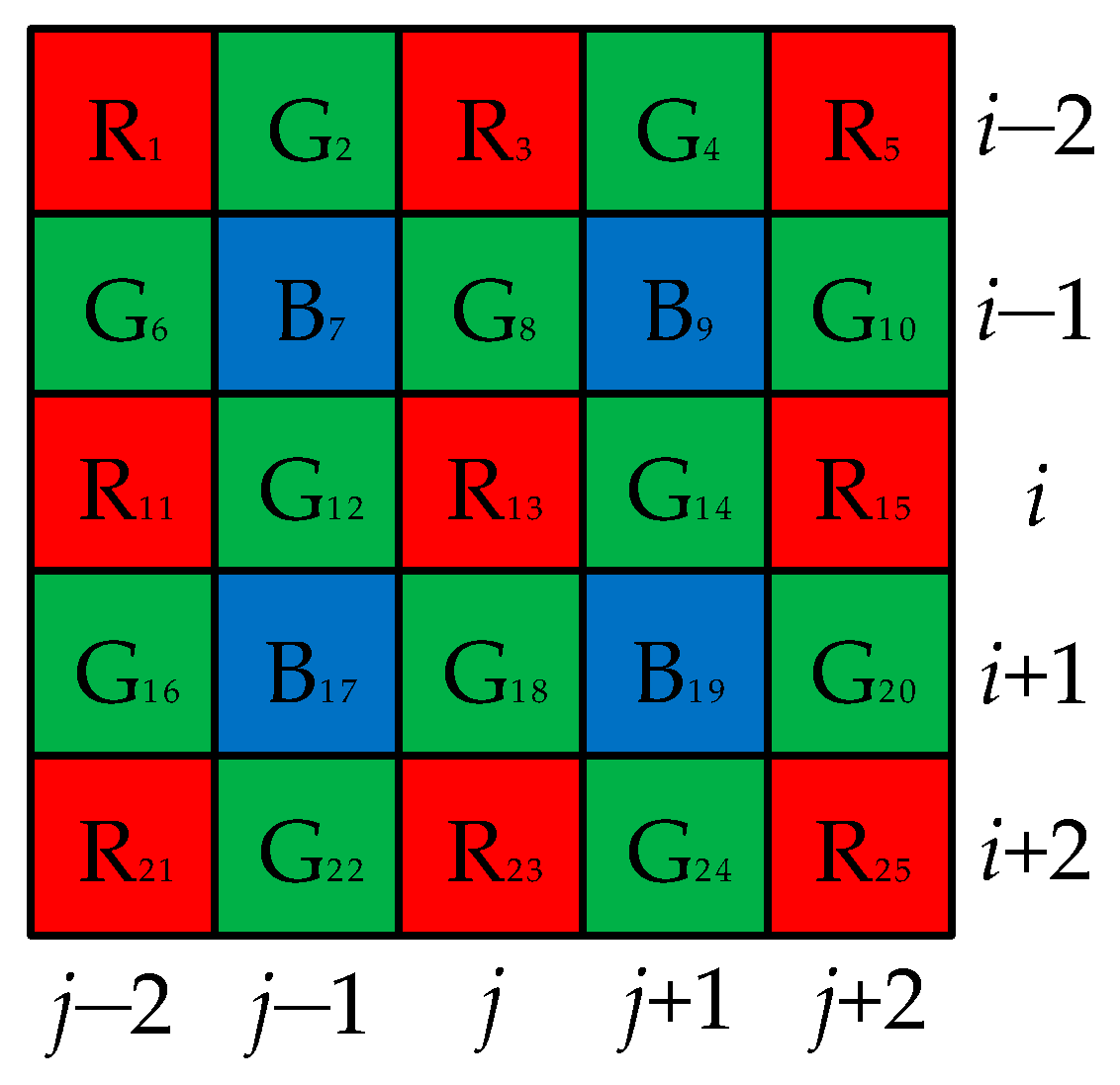






| Images | ACP [8] | DWDF [10] | DLMMSE [12] | RAD [13] | IG [14] | LDI-NAT [16] | OAO | IAO | OAI | Proposed |
|---|---|---|---|---|---|---|---|---|---|---|
| Figure 7a | 34.02 | 35.27 | 34.98 | 34.36 | 35.44 | 35.82 | 34.07 | 36.21 | 34.65 | 36.51 |
| Figure 7b | 38.93 | 40.22 | 38.57 | 38.83 | 37.21 | 40.19 | 38.94 | 40.38 | 39.78 | 41.24 |
| Figure 7c | 39.26 | 41.66 | 40.12 | 39.23 | 41.51 | 41.48 | 40.45 | 41.81 | 41.14 | 41.85 |
| Figure 7d | 38.76 | 39.87 | 37.90 | 38.29 | 38.90 | 40.17 | 39.04 | 40.44 | 39.66 | 40.83 |
| Figure 7e | 34.17 | 36.14 | 36.98 | 34.69 | 36.27 | 37.00 | 34.97 | 37.02 | 35.37 | 37.08 |
| Figure 7f | 33.86 | 37.56 | 36.15 | 33.99 | 37.14 | 36.27 | 35.20 | 37.39 | 35.98 | 37.63 |
| Figure 7g | 41.53 | 41.14 | 40.66 | 40.86 | 40.88 | 41.45 | 40.30 | 41.27 | 41.05 | 41.94 |
| Figure 7h | 32.10 | 33.81 | 33.29 | 31.78 | 33.85 | 33.82 | 32.41 | 33.54 | 33.00 | 33.69 |
| Figure 7i | 41.93 | 41.31 | 41.93 | 40.52 | 41.47 | 40.75 | 39.16 | 40.54 | 39.64 | 42.08 |
| Figure 7j | 41.19 | 41.06 | 40.86 | 40.87 | 41.38 | 41.16 | 39.45 | 41.44 | 40.23 | 41.95 |
| Figure 7k | 35.56 | 37.98 | 36.05 | 35.83 | 38.00 | 37.98 | 36.26 | 38.39 | 37.07 | 38.75 |
| Figure 7l | 40.55 | 42.22 | 39.98 | 38.99 | 41.57 | 41.08 | 40.36 | 42.11 | 41.42 | 42.55 |
| Figure 7m | 30.41 | 31.64 | 31.37 | 31.20 | 32.09 | 32.03 | 30.49 | 32.62 | 30.96 | 32.70 |
| Figure 7n | 35.62 | 36.34 | 37.10 | 35.56 | 36.75 | 37.14 | 35.84 | 36.98 | 36.13 | 37.00 |
| Figure 7o | 36.87 | 38.82 | 35.95 | 36.22 | 38.43 | 38.86 | 37.50 | 39.34 | 38.20 | 39.42 |
| Figure 7p | 39.21 | 41.48 | 40.89 | 38.64 | 40.79 | 39.24 | 38.50 | 41.02 | 39.31 | 41.04 |
| Figure 7q | 37.85 | 39.70 | 39.68 | 38.50 | 41.14 | 39.92 | 38.54 | 40.05 | 39.13 | 40.06 |
| Figure 7r | 34.47 | 34.71 | 34.20 | 35.14 | 35.55 | 35.29 | 33.86 | 35.78 | 34.22 | 35.81 |
| Figure 7s | 37.71 | 38.13 | 38.17 | 37.51 | 38.58 | 38.15 | 36.78 | 38.71 | 37.41 | 38.82 |
| Figure 7t | 37.12 | 37.95 | 37.81 | 37.10 | 38.99 | 39.28 | 37.86 | 39.27 | 38.43 | 39.66 |
| Figure 7u | 34.62 | 36.43 | 34.69 | 35.00 | 37.02 | 37.08 | 35.57 | 37.46 | 36.03 | 37.71 |
| Figure 7v | 35.71 | 36.65 | 36.12 | 36.04 | 37.89 | 37.54 | 36.27 | 37.67 | 36.79 | 38.08 |
| Figure 7w | 39.86 | 40.87 | 40.52 | 39.32 | 42.62 | 42.33 | 41.45 | 41.59 | 40.98 | 41.61 |
| Figure 7x | 31.54 | 30.06 | 32.39 | 32.52 | 34.21 | 33.16 | 31.98 | 33.75 | 32.58 | 33.81 |
| Average | 36.79 | 37.96 | 37.56 | 36.71 | 38.24 | 38.20 | 36.89 | 38.53 | 37.47 | 38.84 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, M.; Wang, C.; Ge, W. Weights-Based Image Demosaicking Using Posteriori Gradients and the Correlation of R–B Channels in High Frequency. Symmetry 2019, 11, 600. https://doi.org/10.3390/sym11050600
Xia M, Wang C, Ge W. Weights-Based Image Demosaicking Using Posteriori Gradients and the Correlation of R–B Channels in High Frequency. Symmetry. 2019; 11(5):600. https://doi.org/10.3390/sym11050600
Chicago/Turabian StyleXia, Meidong, Chengyou Wang, and Wenhan Ge. 2019. "Weights-Based Image Demosaicking Using Posteriori Gradients and the Correlation of R–B Channels in High Frequency" Symmetry 11, no. 5: 600. https://doi.org/10.3390/sym11050600
APA StyleXia, M., Wang, C., & Ge, W. (2019). Weights-Based Image Demosaicking Using Posteriori Gradients and the Correlation of R–B Channels in High Frequency. Symmetry, 11(5), 600. https://doi.org/10.3390/sym11050600







