Boosting Memory-Based Collaborative Filtering Using Content-Metadata

Abstract

Recommendation systems are widely used in conjunction with many popular personalized services, which enables people to find not only content items they are currently interested in, but also those in which they might become interested. Many recommendation systems employ the memory-based collaborative filtering (CF) method, which has been generally accepted as one of consensus approaches. Despite the usefulness of the CF method for successful recommendation, several limitations remain, such as sparsity and cold-start problems that degrade the performance of CF systems in practice. To overcome these limitations, we propose a content-metadata-based approach that uses content-metadata in an effective way. By complementarily combining content-metadata with conventional user-content ratings and trust network information, our proposed approach remarkably increases the amount of suggested content and accurately recommends a large number of additional content items. Experimental results show a significant enhancement of performance, especially under a sparse rating environment.

1. Introduction

As recommendation services are widely used on-line, many recommendation techniques have been developed. Memory-based collaborative filtering (CF) has been used most widely because it indirectly predicts the rating score of content for an active user (without any direct calculation of user-content similarity) based on a number of similar users (or similar content) [1,2]. Especially, with the popularity of personalized devices such as smartphones and smart TV, coverage of CF services has received more attention because many users desire not only content they are currently interested in, but also more diverse content in which they might become interested. However, conventional CF has often failed to reach its potential success level because it suffers from sparsity and cold-start problems [3,4,5,6]. For example, the Epinions dataset (http://www.epinions.com), which is a publicly available movie rating benchmark, has less than 2% user-movie pair ratings among all its rating pairs. This inadequacy, commonly referred to as the sparsity problem, often causes CF to recommend few content items to some users. Apart from the sparsity problem, the cold-start problem arises when a new user or content is introduced into the CF system. In this situation, CF cannot generate useful recommendation for the new user or content item due to the lack of their rating information.

Researchers have suggested many recommendation methods using the content-metadata [7,8,9,10,11] that are typically provided in the form of textual descriptions of content features. Such recommendation methods usually construct each user’s profile or predictor using metadata from all content the user rates and then estimate the rating score of content using the user’s profile or predictor. Those methods are often incorporated into CF by first filling in all possible parts of the user-content rating matrix with their estimates and then applying conventional CF using a less sparse matrix. However, these methods are not particularly effective in practice because it is hard to construct a useful profile or predictor for many users, especially when we consider the large number of users and the relatively small number of content items that each user rates.

In this paper, we suggest a novel method of applying content-metadata to well-known item-based CF methods, which effectively employs content-metadata for calculating inter-similarities among content items and building a content link network. Based on this method, we propose several content-metadata-based approaches for boosting conventional CF. Our approach significantly mitigates the inadequacy of commonly used CF methods and also provides effective recommendations in a large-scale and evolving environment where a large number of users and content items newly join and the user-content rating matrix gradually becomes less sparse. Particularly, our approach makes satisfactory recommendations even with a sparse user-content rating matrix because content-metadata is used to complement conventional CF methods by calculating content similarities using its metadata, even without user-content ratings. Furthermore, as user-content ratings are accumulated, our approach consistently shows much better performance (relative to other existing methods) regarding both coverage and precision.

This paper is organized as follows. The second section outlines related works and the background to our approach and the third section describes selected content-metadata-based boosting approaches for CF. The fourth section presents several experiments using a benchmark dataset in comparison with conventional methods. The fifth section provides discussions about our proposed approaches and the final section gives conclusions and guidance for our future work.

2. Background

2.1. Related Works

Typical CF methods predict rating scores of target contents for an active user based on preferences (generally expressed by rating scores) of similar users (or contents). User-based CF finds other users (neighbors) who have similar preferences to an active user and then predicts the active user’s preference based on his/her neighbors’ preferences [12,13]. Item-based CF identifies rated content similar to target content and predicts the rating score of the target content by using rating scores of similar content [13,14]. To identify the set of content items similar to the target content, item-based CF estimates inter-similarities among content items based on users’ ratings of each item.

The recommendation performance of traditional CF methods can be more enhanced by utilizing trust networks of diverse users. Trust-based recommendation systems such as MoleTrust [15] and TrustWalker [16] use trust network information to enhance the performance of traditional CF [17,18,19]. The idea of trust-based recommendation systems is not to search for similar users from a rating score matrix (as conventional user-based CF does), but to search for trustable users by exploiting trust propagation [20] over the trust network. The content appreciated by these trustable users is recommended to an active user. Implementation of trust-based recommendation systems has revealed that a well-constructed trust network that may be quite useful to improve precision can cause another problem; the precision decreases drastically if the distance of trust propagation is increased above a certain limit to enhance coverage.

Meanwhile, in order to more enhance recommendation performance of traditional CF methods, a number of methods exploiting content-metadata have been proposed. Content-boosted CF [21,22,23] suggests a framework for combining content-metadata and collaboration. Using content-metadata, this approach constructs a content-based naïve Bayesian predictor (CBNB) that boosts a sparse rating score matrix into a dense matrix. Such a content-based predictor helps overcome some drawbacks of traditional CF by constructing a machine learning model using content-metadata. However, there remain several problems that render this approach inadequate. First, it is challenging to learn effective content-based predictors for every active user; thus, this strategy may often be inapplicable in practice. Second, in a large-scale and evolving recommendation environment, the content-based predictor has to be relearned for each user and is then used frequently to reboost the rating score matrix, which may lead to severe inefficiencies due to heavy computational overhead.

Content-metadata can be utilized in various ways. For example, Seo et al. [10] used content-metadata to construct a k-partite graph on the basis of content-attributes such as content-actor, content-director, content-genres, and so on. This method performs random walk propagation on the k-partite graph for an active user and then discovers the hidden distribution of the user’s content preference. A large-scale recommendation environment often suffers from low performance because a limited number of content-attributes are used in nature and available in practice. Mittal et al. [11] employed historical ratings along with user metadata, such as age, gender, occupation, and ethnicity, to alleviate the cold-start problem. Different from conventional user-based CF, this approach redefines the neighborhood based on user metadata so that more robust recommendations can be obtained. However, the premise of this method is based on the existence of sufficient metadata for all users and is thus impractical in a real environment; consequently, performance improvement is imperceptible in many cases.

Finally, unlike traditional CF methods, model-based recommendation methods employed rating scores to build a model using machine learning or data mining techniques. The well-known matrix factorization techniques [24,25,26,27,28] are among the best model-based recommendation methods. They predict the unobserved rating scores by decomposing the user-content matrix into the product of two lower dimensionality rectangular matrices. To maximize the enhancement of performance, some of them use Collaborative Topic Model (CTM) [24], Probabilistic Matrix Factorization (PMF) [25], or Bayesian Probabilistic Matrix Factorization (BPMF) [26] models, and others use a novel BPMF model fused with trust network information (called social relations) and content-metadata (called item contents) (BPMFSRIC) [27]. The main drawback of those model-based recommendation methods is high computational overhead that makes it impractical to relearn the model frequently, although an incremental recommendation method is tried with implicit feedback for fast matrix factorization [29].

2.2. Using Content-Metadata for CF

Content-metadata, textual information that describes content features, has been used widely in many information retrieval and extraction applications [21,30,31,32]. In our work, our key intuition is that this content-metadata can be used effectively in a different way from existing methods to enhance performance. Because content-metadata involves general information and key features of content, it can be utilized to extract mutual relationships between the content. By applying the mutual relationships effectively into existing CF methods, significant performance improvement can be achieved, especially under a sparse rating environment.

In this subsection, we introduce two content representations constructed from content-metadata. They are utilized in our recommendation methods that will be given in the next section.

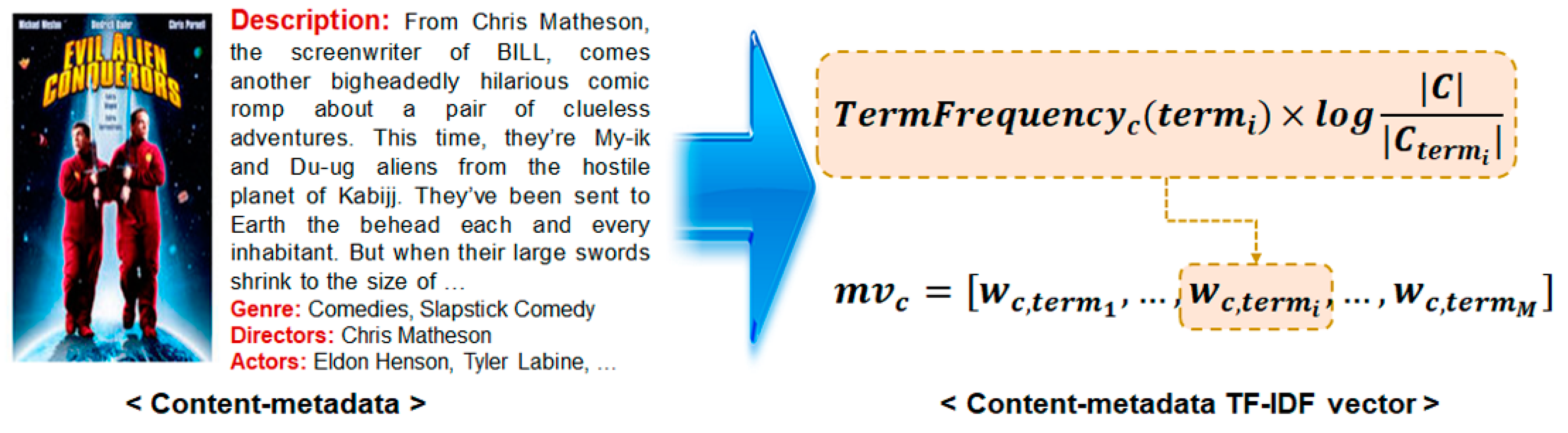
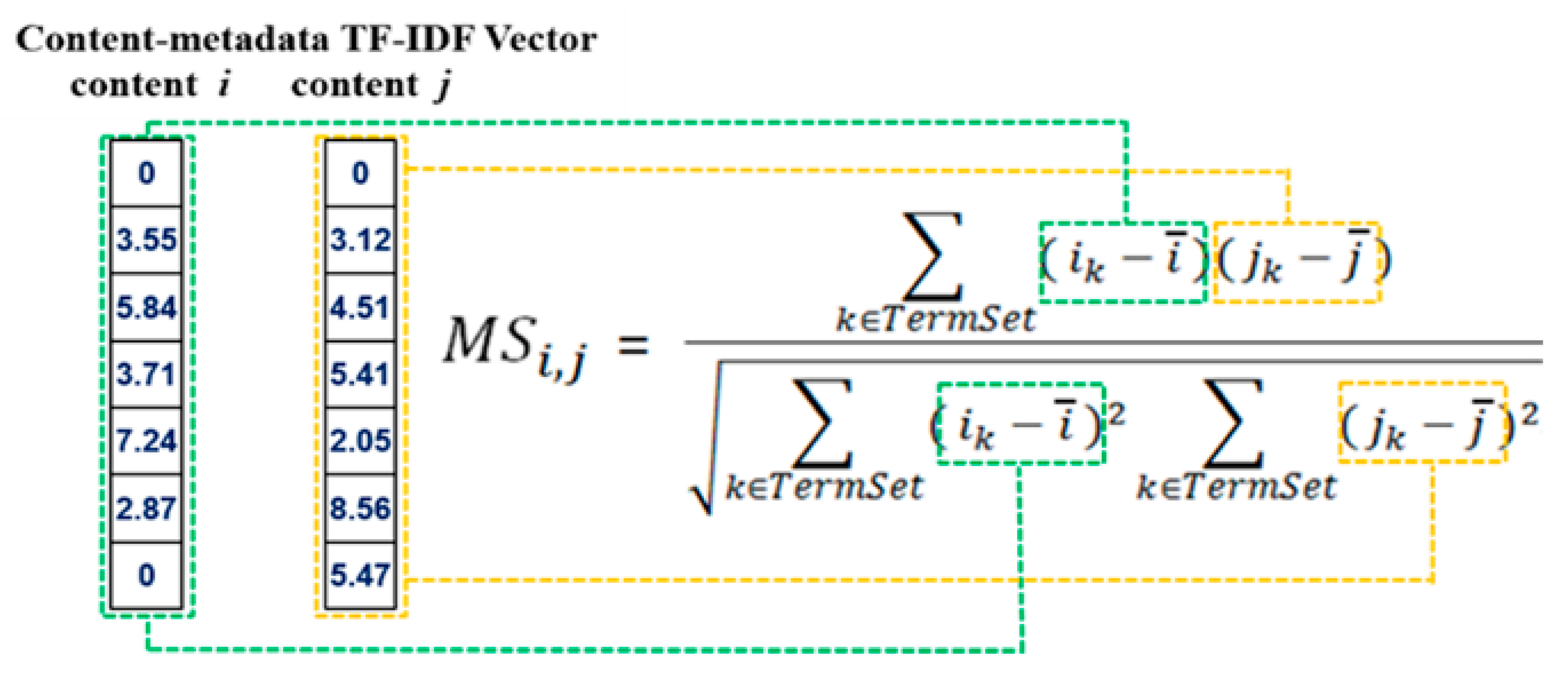
2.2.1. Content-Metadata TF-IDF Vector

Content-metadata is given as a set of sentences (term sequence) describing content features. After crawling content-metadata that is easily accessible on the web, we converted this content-metadata to a TF-IDF (term frequency-inverse document frequency) vector whose component represents a TF-IDF score for each term using general information retrieval techniques.

As shown in Figure 1, the content-metadata TF-IDF vector $m{v}_c$ of content item c corresponds to a sequence of the weight value (TF-IDF score) $W_{c, ter{m}_i}$ of term_i in content item c. $TermFrequenc{y}_c\left(ter{m}_i\right)$ refers to the appearance frequency of term i in content item c, |C| is the total number of content items, and |$C_{ter{m}_i}$| is the number of content items that contain term_i in a collection.

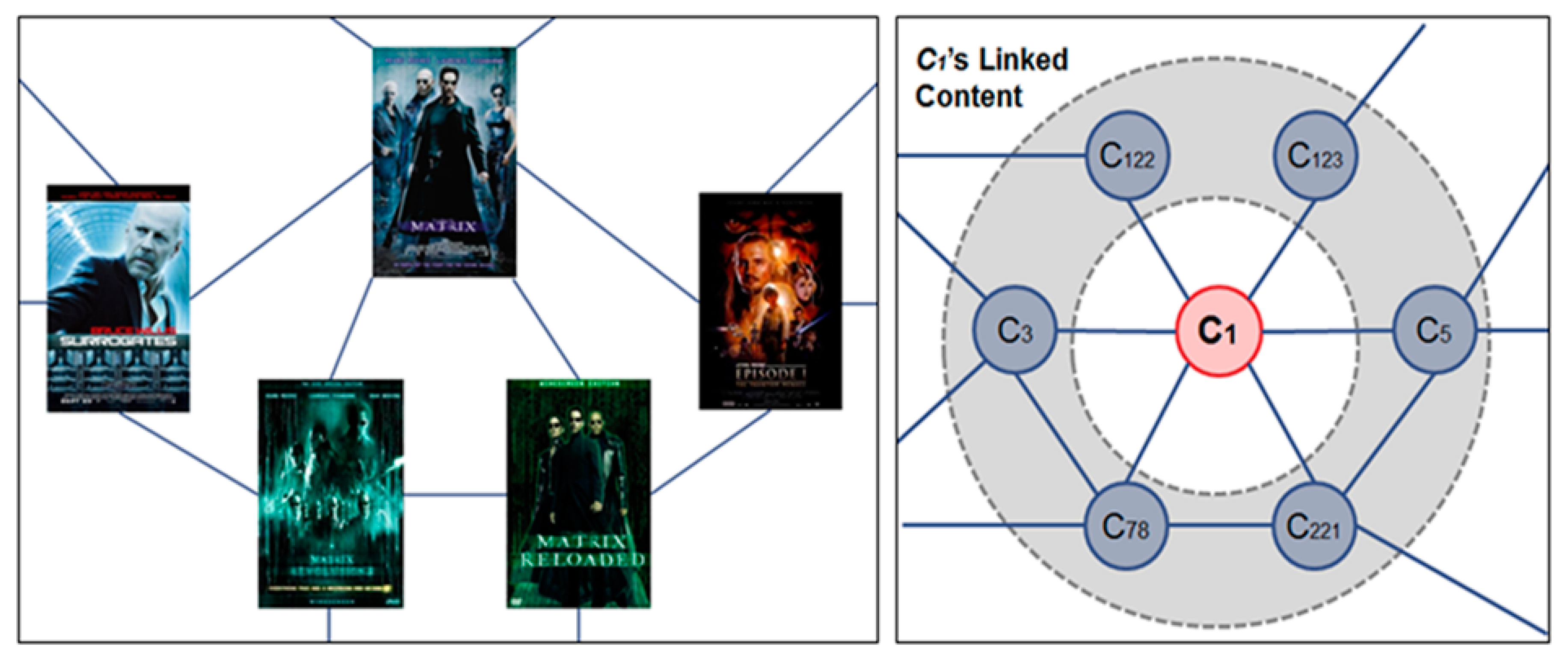
2.2.2. Content Link Network

We also built a content link network by extracting associative relationships between content items using tree pattern expression (TPE)-based text mining process [33,34,35]. In this process, the content link network was constructed by connecting content items whose metadata contains the same TPE semantic patterns and significant terms. For example, if two content items share similar metadata descriptions, containing many common terms and semantic structures, such as in “The Matrix” movie series, these content items would be connected with each other in TPE-based text mining process. Figure 2 describes a detailed pseudocode to construct the content link network using TPEMatcher [34], a TPE-based pattern matching and mining tool.

In Figure 2, in order to link the contents $C_i$ and $C_j$, two descriptions, $De{s}_i$ and $De{s}_j$, involved in the content-metadata of $C_i$ and $C_j$, respectively, are matched by TPEMatcher to identify semantic similarities between them. TPEMatcher first parses $De{s}_i$ and $De{s}_j$ using an NLP (natural language processing) full parser. Then, parse trees of $De{s}_i$ are matched to parse trees of $De{s}_j$ by a tree pattern matching algorithm [33,34]. If $De{s}_i$ and $De{s}_j$ are semantically similar, they may share similar grammatical patterns and terms, which are effectively extracted by matching the parse trees of $De{s}_i$ and $De{s}_j$ in TPEMatcher. Therefore, if $De{s}_i$ and $De{s}_j$ are matched by TPEMatcher, $C_i$ and $C_j$ are linked. Finally, by conducting the pattern matching for all content pairs, a content link network is constructed.

In the content link network, each content item is represented as a vertex and a connection between two associated content items is represented as an edge. For example, as shown in Figure 3, we can build a content link network and then find neighborhood content items (C3, C5, C78, C122, C123, C221) of a content item C1, which are used to predict the rating score of C1 in Section 3.4.

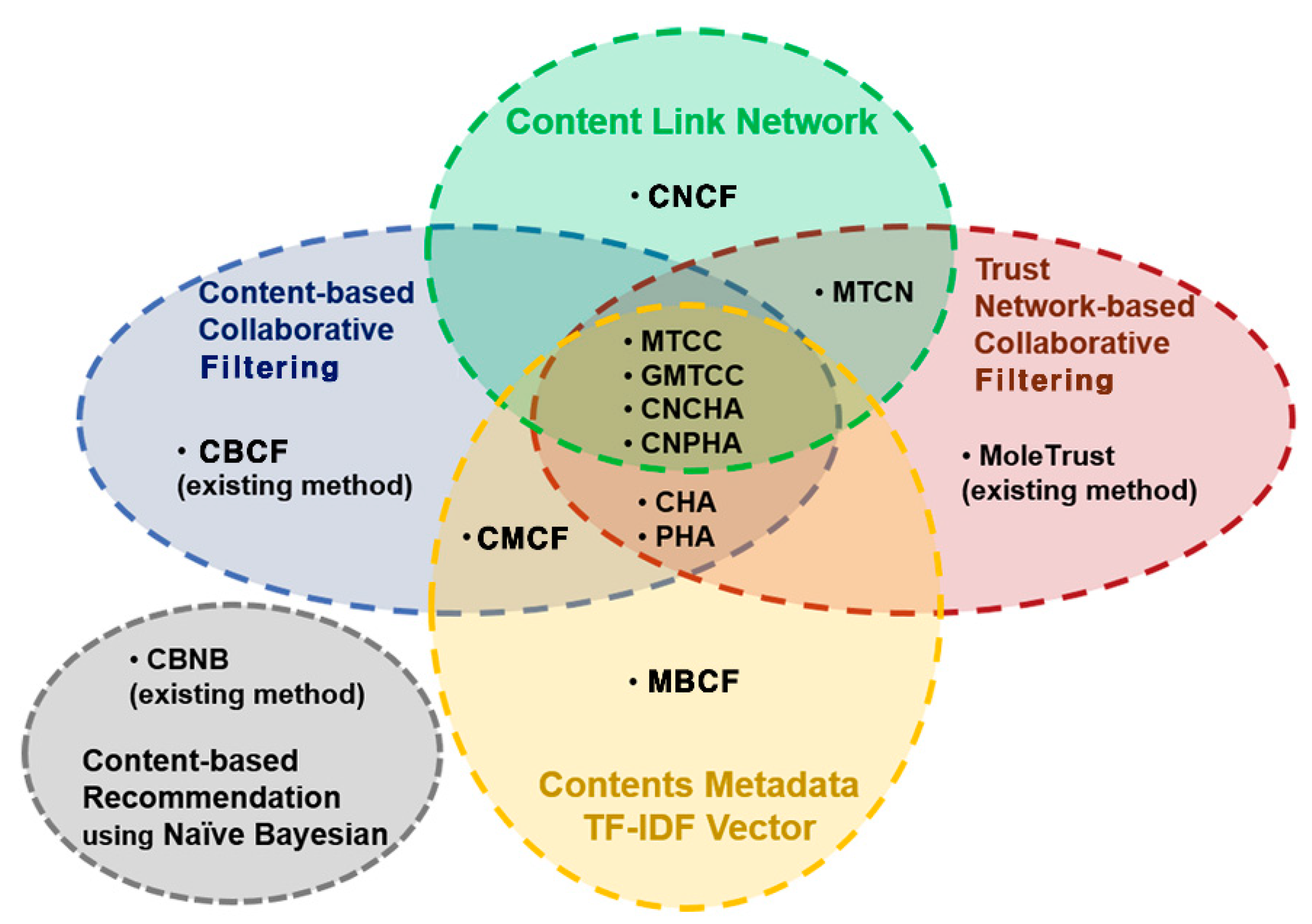
3. Metadata-Based Boosting Approaches

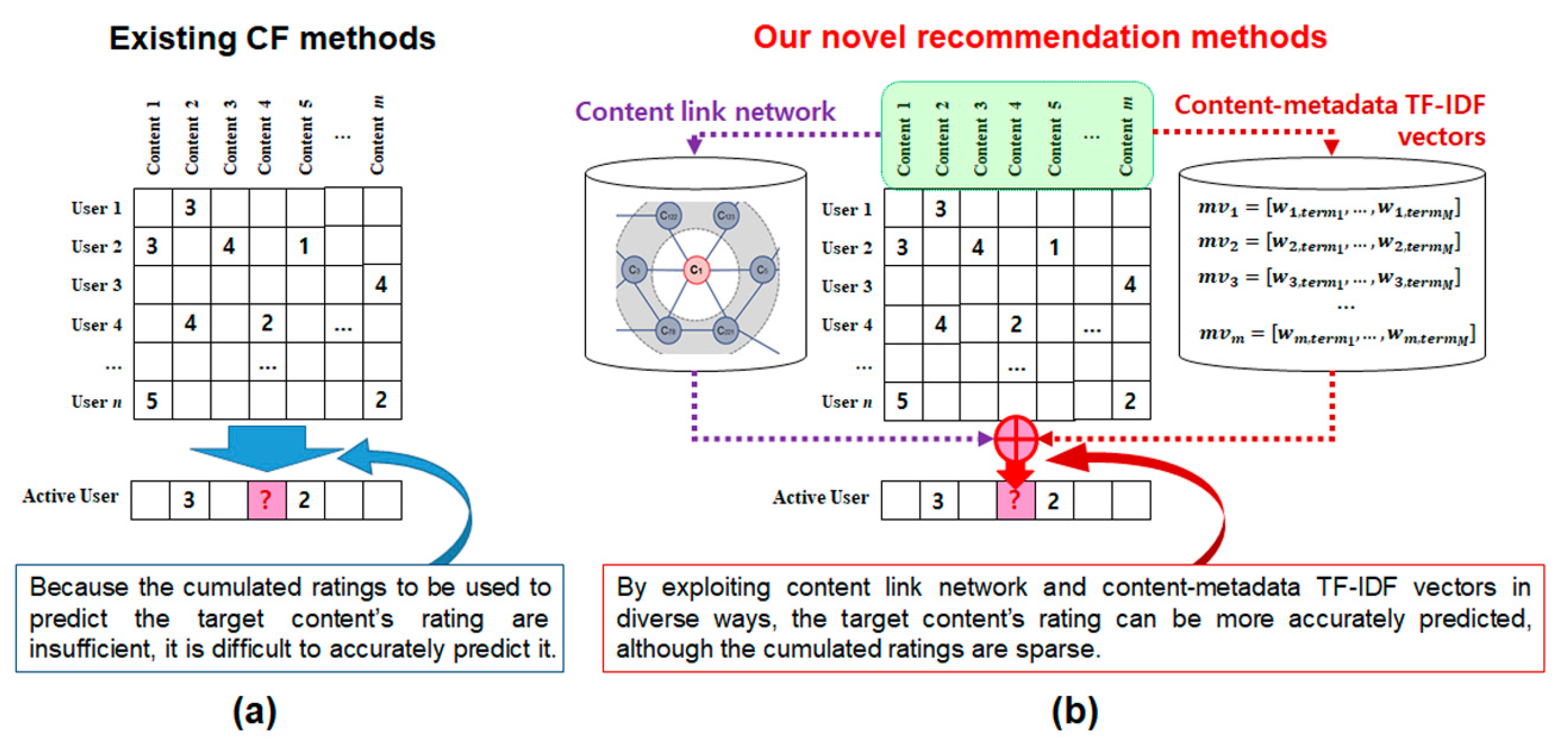
3.1. Motivation

While many well-known CF systems use a user-content rating matrix and/or trust network, our approach exploits content-metadata effectively to provide more robust recommendation services. Specifically, in our recommendation method, content-metadata was used to improve the process of finding neighborhood content for a target content item in the context of item-based CF. Figure 4a illustrates a typical problem that may occur in conventional CF methods; if sufficient rating scores in the recommendation system do not exist, it is difficult to predict accurate rating scores for some target contents. In order to overcome this problem, we exploited content-metadata with existing user-content rating scores and trust networks to more accurately predict rating scores of the target contents. Figure 4b describes our approach that boosts traditional CF methods effectively.

As shown in Figure 4b, after building up two forms of content representation (TF-IDF vector and content link network) as mentioned in Section 2.2, they are complementarily coupled with traditional CF methods (using the existing user-content rating scores and trust network) for maximizing recommendation performance. Thus, we can expect to mitigate main problems caused by a lack of the accumulated rating scores, such as an inaccurate prediction of rating scores and a decrease of the number of predictable rating scores.

In this section, we developed several boosting approaches by incorporating the two content-metadata-based representations into conventional CF methods in different ways as follows: (i) Content and metadata-based CF (CMCF); (ii) the combined harmonic approach (CHA); (iii) the priority-based harmonic approach (PHA); (iv) content link network-based CF (CNCF); (v) MoleTrust combined with CNCF (MTCN); (vi) MoleTrust combined with CNCF and CMCF (MTCC); (vii) generalized MTCC (GMTCC); (viii) CNCF combined with CHA (CNCHA); and (ix) CNCF combined with PHA (CNPHA). These approaches combine content-metadata with traditional item-based CF (termed content-based CF, CBCF) and/or a trust network-based CF (MoleTrust). Figure 5 depicts our approaches, other existing CF methods, and their intersecting relationships. The detailed methods of our boosting approaches are described in Section 3.2, Section 3.3, Section 3.4, Section 3.5, Section 3.6, Section 3.7, Section 3.8, Section 3.9 and Section 3.10.

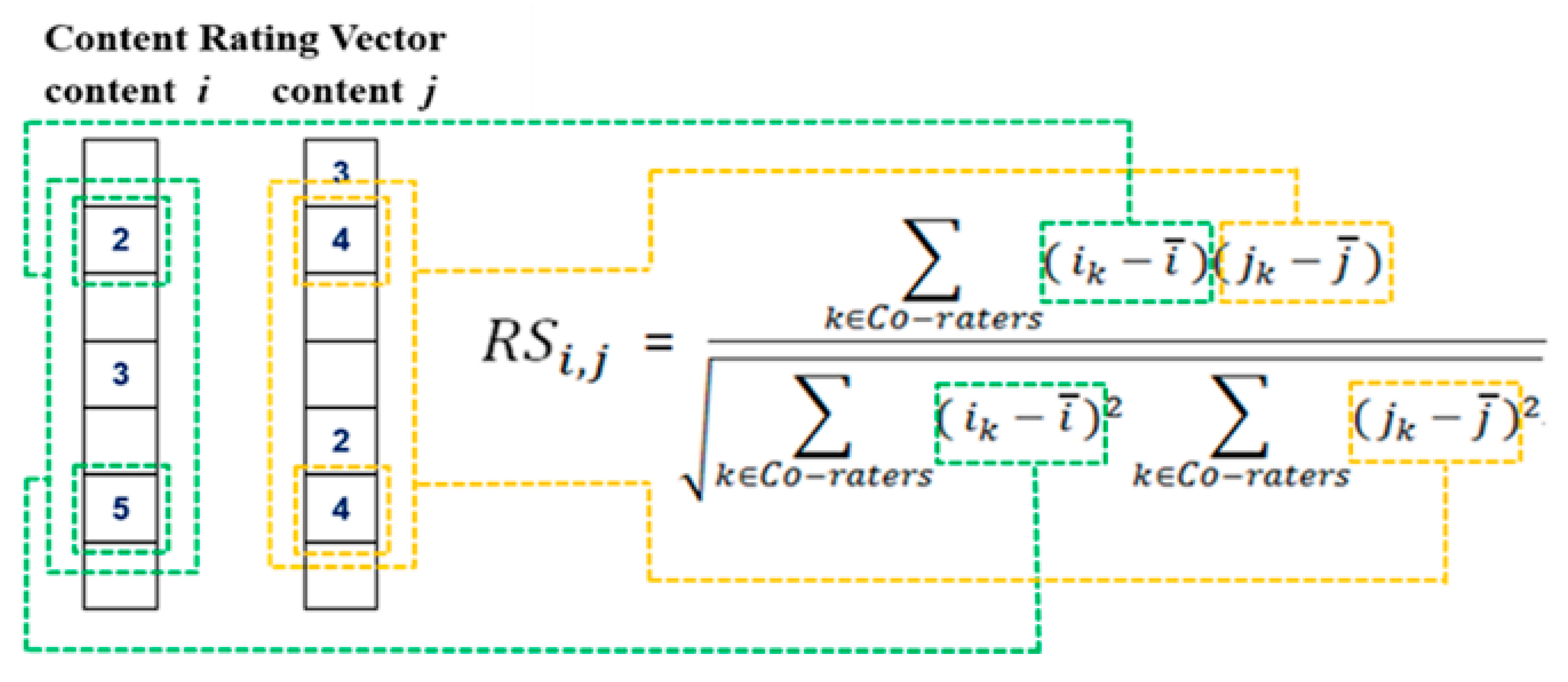
3.2. Content and Metadata-Based CF

CMCF uses content-metadata to complement the process of calculating inter-similarities between content items in traditional CBCF. More concretely, if the number of co-raters for two content items i and j is less than a threshold τ, then the content similarity ($R{S}_{i,j}$) (based on user-content ratings) is combined with the similarity ($M{S}_{i,j}$), based on content-metadata. $R{S}_{i,j}$ is represented by the correlation coefficient [36] between two co-rating scores of content items i and j, as shown in Figure 6, and $M{S}_{i,j}$ is represented in the same way as $R{S}_{i,j}$ except for using TF-IDF vectors of the two content items, as shown in Figure 7.

$M{S}_{i,j}$ and $R{S}_{i,j}$ are combined in Equation (1), where n is the number of co-raters for content items i and j and where τ is a threshold value that is the maximum number of co-raters that allows $R{S}_{i,j}$ to be combined with $M{S}_{i,j}$. From Equation (1), if n is lower than τ, then $R{S}_{i,j}$ is combined with $M{S}_{i,j}$ to a degree equal to the difference between threshold τ and n.

$$w_{i,j}^{*}=\{\begin{array}{l}\frac{n*R{S}_{i,j}+\left(\tau -n\right)*M{S}_{i,j}}{\tau },n<\tau ,\\ R{S}_{i,j},otherwise\end{array}$$

(1)

Based on the above similarity $w_{i,j}^{*}$ between content items i and j, the rating score $r_{a,i}{}^{\left(CMCF\right)}$ for active user a and content item i is predicted as in Equation (2), where N is a set of content items rated by active user a and where $r_{a,j}$ is the rating score of active user a for content item j.

$$r_{a,i}{}^{\left(CMCF\right)}=\frac{1}{{{\displaystyle \sum }}_{j\in N}{w}_{i,j}^{*}}{\displaystyle \sum }_{j\in N\mathrm{s}.\mathrm{t}.W_{i,j}^{*}>0}{w}_{i,j}^{*}{r}_{a,j}$$

(2)

From Equation (1) and Equation (2), if n is zero, then CMCF reduces to metadata-based CF (MBCF) and if n ≥ τ, then it reduces to CBCF.

3.3. Combined Harmonic Approach

CHA combines the well-known MoleTrust algorithm with our CMCF in a complementary fashion. The MoleTrust rating score $r_{a,i}{}^{\left(MT\right)}$ is given in Equation (3), where $U_i$ is a set of users who rated content item i and ${\mathrm{Linked}}_d\left(a,u\right)$ returns whether active user a and user u are linked to each other (True = 1 or False = 0) within the depth d in trust network.

$$r_{a,i}{}^{\left(MT\right)}=\overline{r_a}+\frac{{{\displaystyle \sum }}_{u\in U_i}{\mathrm{Linked}}_d\left(a,u\right)*\left(r_{u,i}-\overline{r_u}\right)}{{{\displaystyle \sum }}_{u\in U_i}{\mathrm{Linked}}_d\left(a,u\right)}$$

(3)

The CHA rating score $r_{a,i}{}^{\left(CHA\right)}$ is calculated as in Equation (4), where $n_1={\displaystyle \sum }_{u\in U_i}{\mathrm{Linked}}_d\left(a,u\right)$, $n_2$ is the number of content items used to calculate $r_{a,i}{}^{\left(CMCF\right)}$, and α is a correction factor that compensates for the scale difference between $n_1$ and $n_2$. In this way, CHA can apply the two rating scores of CMCF and MoleTrust more reliably.

$$r_{a,i}{}^{\left(CHA\right)}=\frac{\alpha ·n_1·r_{a,i}{}^{\left(MT\right)}+n_2·r_{a,i}{}^{\left(CMCF\right)}}{\alpha ·n_1+n_2}$$

(4)

3.4. Priority-Based Harmonic Approach

PHA combines three rating scores by giving priorities in the order of CBCF first, MoleTrust second, and MBCF last. Equation (5) describes how to combine three rating scores, where $r_{a,i}{}^{\left(CB\right)}$ is the rating score predicted by CBCF, $r_{a,i}{}^{\left(MT\right)}$ is the rating score by MoleTrust, $r_{a,i}{}^{\left(MB\right)}$ is the rating score by MBCF, $n_1$ is the number of content items used to calculate $r_{a,i}{}^{\left(CB\right)}$, and $n_2$ is the number (= $n_1$ in Equation (4)) of the active user’s friends used to calculate $r_{a,i}{}^{\left(MT\right)}$. The threshold value ${\tau }_1$ is the maximum value of $n_1$ that allows $r_{a,i}{}^{\left(CB\right)}$ to be combined with $r_{a,i}{}^{\left(MT\right)}$ and $r_{a,i}{}^{\left(MB\right)}$ and the threshold value ${\tau }_2$ is the maximum value of $n_2$ that allows $r_{a,i}{}^{\left(MT\right)}$ to be combined with $r_{a,i}{}^{\left(MB\right)}$.

$$r_{a,i}{}^{\left(PHA\right)}=\{\begin{array}{c}\frac{1}{{\tau }_1}(n_1{r}_{a,i}{}^{\left(CB\right)}+({\tau }_1-n_1)\frac{n_2{r}_{a,i}{}^{\left(MT\right)}+({\tau }_2-n_2)r_{a,i}{}^{\left(MB\right)}}{{\tau }_2}),n_1<{\tau }_{1}and{n}_2<{\tau }_2,\\ \frac{n_1{r}_{a,i}{}^{\left(CB\right)}+({\tau }_1-n_1)r_{a,i}{}^{\left(MT\right)}}{{\tau }_1},n_1<{\tau }_{1}and{n}_2\ge {\tau }_2,\\ r_{a,i}{}^{\left(CB\right)},otherwise\end{array}$$

(5)

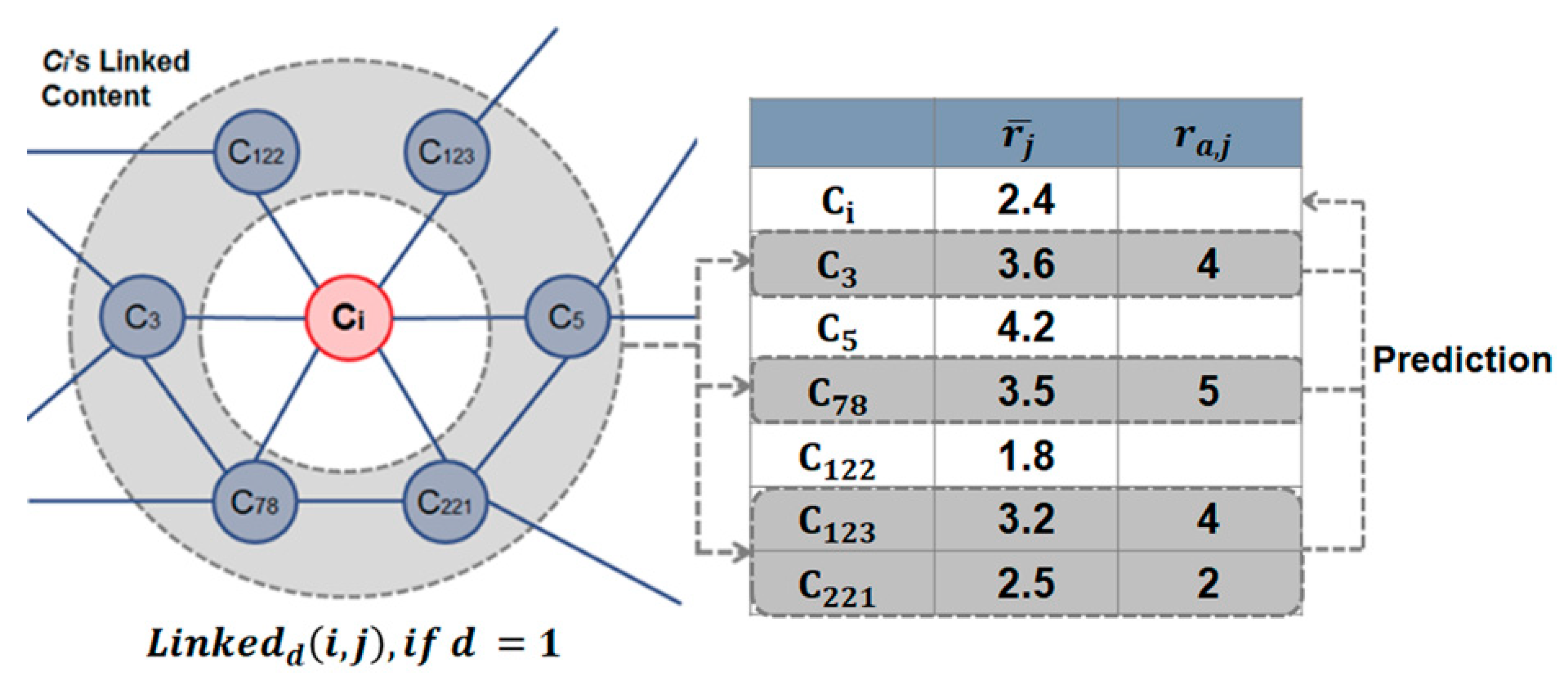
3.5. Content Link Network-Based CF

CNCF predicts the rating score using a number of content items linked to the target content by the breadth-first search of the content link network. As shown in Figure 8, if the searching depth is set to 1 in the content link network for a target content item i, then the linked content items (3, 78, 123, 221) are found from the list of content items rated by an active user. By increasing the searching depth, CNCF can recommend more target content items because it uses more (indirectly) linked content items, possibly at the expense of accuracy.

After finding the linked content items in the content link network, the CNCF rating score $r_{a,i}{}^{\left(CNCF\right)}$ is calculated as in Equation (6), where N is a set of content items rated by an active user a and ${\mathrm{Linked}}_d\left(i,j\right)$ returns whether content items i and j are linked to each other (True = 1 or False = 0) within depth d in the content link network.

$$r_{a,i}{}^{\left(CNCF\right)}=\frac{{{\displaystyle \sum }}_{j\in N}{\mathrm{Linked}}_d\left(i,j\right)*r_{a,j}}{{{\displaystyle \sum }}_{j\in N}{\mathrm{Linked}}_d\left(i,j\right)}$$

(6)

3.6. Combining MoleTrust with CNCF

MTCN combines the rating score of MoleTrust with CNCF. The MTCN rating score $r_{a,i}{}^{\left(MTCN\right)}$ is calculated as in Equation (7), where $r_{a,i}{}^{\left(MT\right)}$ is the rating score predicted by MoleTrust, $n_1$ is the number of the active user’s friends used to calculate $r_{a,i}{}^{\left(MT\right)}$, and $n_2$ (= the denominator ${\displaystyle \sum }_{j\in N}{\mathrm{Linked}}_d\left(i,j\right)$ of Equation (6)) is the number of content items (used to calculate $r_{a,i}{}^{\left(CNCF\right)}$) rated by an active user and linked to the target content in the content link network.

$$r_{a,i}{}^{\left(MTCN\right)}=\frac{n_1{r}_{a,i}{}^{\left(MT\right)}+n_2{r}_{a,i}{}^{\left(CNCF\right)}}{n_1+n_2}$$

(7)

3.7. Combining MoleTrust with CNCF and CMCF

MTCC combines the rating score of MoleTrust with CNCF or CMCF. Equation (8) describes how to combine the MoleTrust rating score $r_{a,i}{}^{\left(MT\right)}$ with the CNCF rating score $r_{a,i}{}^{\left(CNCF\right)}$ or the CMCF rating score $r_{a,i}{}^{\left(CMCF\right)}$. In Equation (8), $n_1$ is the number of the active user’s friends used to calculate $r_{a,i}{}^{\left(MT\right)}$ and $n_2$ is the number of content items that are used to calculate $r_{a,i}{}^{\left(CNCF\right)}$ or $r_{a,i}{}^{\left(CMCF\right)}$. More specifically, if there exists some (active user’s) rated content linked to the target content in the content link network of CNCF, $n_2$ is the total number of those content items and the binary value b is set to 1. Otherwise, $n_2$ is the number of content items used to calculate $r_{a,i}{}^{\left(CMCF\right)}$ and b is set to 0. Accordingly, MTCC tries to combine MoleTrust with CNCF first and if this process fails, MTCC combines MoleTrust with CMCF.

$$r_{a,i}{}^{\left(MTCC\right)}=\frac{n_1{r}_{a,i}{}^{\left(MT\right)}+n_2\left(b{r}_{a,i}{}^{\left(CNCF\right)}+\left(1-b\right)r_{a,i}{}^{\left(CMCF\right)}\right)}{n_1+n_2}$$

(8)

3.8. Generalized MTCC

GMTCC is a more generalized version of MTCC. Equation (9) describes an intermediate rating score $r_{a,i}{}^{\left(GCM\right)}$ by combining the CNCF rating score $r_{a,i}{}^{\left(CNCF\right)}$ and the CMCF rating score $r_{a,i}{}^{\left(CMCF\right)}$. In Equation (9), $n$ is the number (= $n_2$ in Equation (7)) of the (active user’s) rated content items linked to the target content in the content link network of CNCF and ${\tau }_0$ is a threshold value that is the maximum value of $n$ that allows $r_{a,i}{}^{\left(CNCF\right)}$ to be combined with $r_{a,i}{}^{\left(CMCF\right)}$.

$$r_{a,i}{}^{\left(GCM\right)}=\{\begin{array}{l}\frac{n{r}_{a,i}{}^{\left(CNCF\right)}+\left({\tau }_0-n\right)r_{a,i}{}^{\left(CMCF\right)}}{{\tau }_0}, n<{\tau }_0,\\ r_{a,i}{}^{\left(CNCF\right)},otherwise\end{array}$$

(9)

GMTCC combines the rating score of MoleTrust with the above $r_{a,i}{}^{\left(GCM\right)}$ and its rating score $r_{a,i}{}^{\left(GMTCC\right)}$ is calculated as in Equation (10), where $n_1$ is the number of the active user’s friends used to calculate $r_{a,i}{}^{\left(MT\right)}$ and $n_2$ is the number of content items used to calculate $r_{a,i}{}^{\left(GCM\right)}$.

$$r_{a,i}{}^{\left(GMTCC\right)}=\frac{n_1{r}_{a,i}{}^{\left(MT\right)}+n_2{r}_{a,i}{}^{\left(GCM\right)}}{n_1+n_2}$$

(10)

3.9. Combining CNCF with CHA

CNCHA combines the rating score of CNCF with CHA (in Section 3.3), and its rating score $r_{a,i}{}^{\left(CNCHA\right)}$ is calculated as in Equation (11), where $n$ is the number (= $n_2$ in Equation (7)) of content items used to calculate $r_{a,i}{}^{\left(CNCF\right)}$ and where ${\tau }_0$ is a threshold value that is the maximum value of $n$ that allows $r_{a,i}{}^{\left(CNCF\right)}$ to be combined with $r_{a,i}{}^{\left(CHA\right)}$.

$$r_{a,i}{}^{\left(CNCHA\right)}=\{\begin{array}{l}\frac{n{r}_{a,i}{}^{\left(CNCF\right)}+\left({\tau }_0-n\right)r_{a,i}{}^{\left(CHA\right)}}{{\tau }_0},n<{\tau }_0,\\ r_{a,i}{}^{\left(CNCF\right)},otherwise\end{array}$$

(11)

3.10. Combining CNCF with PHA

CNPHA combines the rating score of CNCF with PHA (in Section 3.4) and its rating score $r_{a,i}{}^{\left(CNPHA\right)}$ is calculated as in Equation (12), where $n$ is the number (= $n_2$ in Equation (7)) of content items used to calculate $r_{a,i}{}^{\left(CNCF\right)}$ and where ${\tau }_0$ is a threshold value that is the maximum value of $n$ that allows $r_{a,i}{}^{\left(CNCF\right)}$ to be combined with $r_{a,i}{}^{\left(PHA\right)}$.

$$r_{a,i}{}^{\left(CNPHA\right)}=\{\begin{array}{l}\frac{n{r}_{a,i}{}^{\left(CNCF\right)}+\left({\tau }_0-n\right)r_{a,i}{}^{\left(PHA\right)}}{{\tau }_0},n<{\tau }_0,\\ r_{a,i}{}^{\left(CNCF\right)},otherwise\end{array}$$

(12)

4. Experiment

4.1. Experimental Configuration

We collected a large amount of user-movie ratings (in the form of a Likert scale, 1–5) and users’ trust network information from Epinions.com and we additionally crawled movie metadata from the web. The collected dataset consisted of 91,735 users, 611,741 trust links between users, 26,527 movie content items along with their metadata, and 170,797 user-content ratings. We also assembled a content link network by extracting 39,959 content-to-content relationships by the text mining process described in Section 2.2.2. The user-content rating matrix was very sparse (the mean number of ratings for each content item was close to 5) and its total sparsity was approximately 99%.

In order to evaluate the performance of all the recommendation methods, our experiments were conducted by 5-fold cross validation. Specifically, we used 80% of all the user-content rating scores as a training dataset and the remaining 20% as a test dataset. For each of the real user-content rating scores in the test dataset, we predicted their rating scores by the recommendation methods. Finally, we measured the overall recommendation performance of each method from all the predicted rating scores and the real user-content rating scores. To provide performance measures in our experiment, we used the precision (in terms of the normalized inverse root mean squared error), the coverage (the ratio of predictable rating scores), and the F-measure (the harmonic mean of precision and coverage) [37] as detailed in Section 4.1.1–4.1.3. By implementing our proposed methods and also all the existing methods, we evaluated our content-metadata-based approaches in comparison with three existing CF methods (conventional content-based CF (CBCF), MoleTrust with depth 2, and content-boosted CF (CBNB)) and three model-based recommendation methods (PMF, BPMF, and BPMFSRIC).

Meanwhile, our experiments were designed in two ways. In the first method, we randomly selected 80% of all user-content ratings and used them to predict the remaining 20%. In the second method, we measured the performance by gradually increasing the portion size of user-content ratings from 20% to 80% to predict the remaining 20%. In our approaches, we set parameters as $\tau$ = 50, $\alpha$ = 20, d = 2, ${\tau }_0$ = 30, ${\tau }_1$ = 20, and ${\tau }_2$ = 50 by finding (sub)optimal values through local-searching of the space of those parameters with multiple random retrials.

4.1.1. Precision

Representing precision, the root mean squared error (RMSE) between the real rating score and the predicted score is defined in Equation (13), where $r_i$ is the predicted rating score, $r_i{}^{*}$ is the real rating score, and N is the total number of real rating scores that are predictable.

$$RMSE=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^N{\left(r_i-r_i{}^{*}\right)}^2}{N}}$$

(13)

After computing the RMSE, we converted the RMSE to precision by Equation (14), in which MaxError represents the maximum error range of the rating score (the Likert scale, 1–5, is used for the rating; thus, MaxError is 4).

$$Precision=1-\frac{RMSE}{MaxError}$$

(14)

4.1.2. Coverage

Generally, CF often fails to be successful because the coverage is substantially degraded by the sparsity of the rating score dataset. Therefore, it is necessary to measure the coverage of the CF method to characterize the practical usefulness of the recommendation service. Coverage means how much the portion of content items can be a target of recommendation on average. In Equation (15), coverage is obtained by dividing the number of predictable rating scores by the number of all possible rating scores (M is the number of all users).

$$Coverage=\frac{{{\displaystyle \sum }}_{a=1}^{\mathrm{M}}\mathrm{the}\mathrm{number}\mathrm{of}\mathrm{predictable}\mathrm{content}\mathrm{items}\mathrm{for}\mathrm{user}a}{\mathrm{M}\times \mathrm{the}\mathrm{number}\mathrm{of}\mathrm{content}\mathrm{items}}$$

(15)

4.1.3. F-Measure

To evaluate the overall performance of the CF methods, we used the F-measure, that is, the harmonic mean of precision and coverage as shown in Equation (16). This measure, which represents a single metric of the effectiveness of the CF method, is bound by 0 and 1.

$$F-Measure=\frac{2\times Precision\times Coverage}{Precision+Coverage}$$

(16)

4.2. Experimental Results

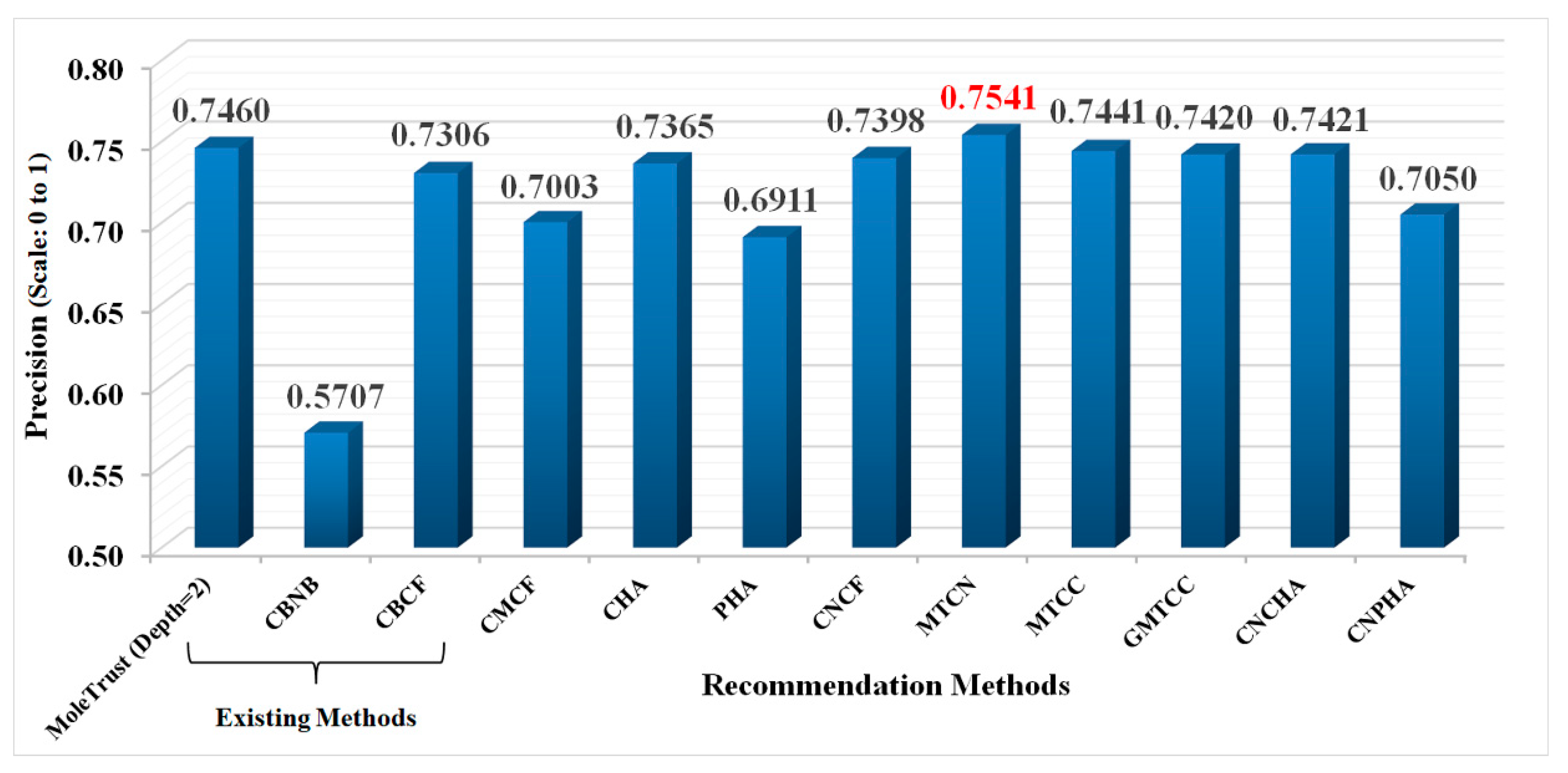
4.2.1. Overall Performance

Figure 9 shows the precision performances of our recommendation methods and the existing methods. In this figure, our methods show overall better precision than existing methods (particularly CBNB and CBCF). Specifically, MoleTrust shows the best precision, 0.7460 among the existing methods, but our method, MTCN, outperforms all the existing methods with the highest precision, 0.7541. Moreover, the experimental results indicate that exploiting neighbor users’ preference information (of trust network) along with user-content rating scores can improve the precision effectively. A more notable fact is that combining content-metadata with a trust network complementarily can contribute considerably to boosting the precision of recommendation.

The coverage performances of the recommendation methods are shown in Figure 10. Most of our methods show dramatically improved coverage performance when compared to the existing methods. Especially, CHA, MTCC, GMTCC, CNCHA, and CNPHA show excellent coverage performance over 0.8, which is a notable result when considering the coverage performance, about 0.7 of MoleTrust and CBNB. Specifically, MTCC and CNCHA show the best coverage performance, 0.8954. It indicates that our methods increased the number of predictable user-content ratings considerably by combining content-metadata and trust network. It is because content-metadata provides additional information effectively to compute the rating scores of target contents, regardless of the amount of accumulated user-content ratings in the recommendation system. On the other hand, CBCF and CNCF show the worst coverage performances (0.4568 and 0.3796, respectively), even though they use content-metadata. These results imply that using content-metadata complementarily along with other information such as a trust network can contribute significantly to predicting more user-content ratings than using content-metadata only.

Finally, F-measure performances are shown in Figure 11. Our methods significantly improve recommendation performance (except for CNCF) because their F-measure (and also coverage) is better than that of other existing methods without any prominent degradation of precision. When compared to MoleTrust, which has the best performance among the existing methods, our best methods, MTCC and CNCHA, improve recommendation performance by 17.17%. More specifically, MTCC, GMTCC, CNCHA, and CHA all show very good performance over 0.8, that is, over 43% higher than CBCF, and even CMCF shows much better performance than its most comparable method, CBNB, which also uses content-metadata without any trust network information. These results indicate that our methods can make effective use of content-metadata to improve the recommendation effectiveness by recommending much more useful content items that cannot be recommended by conventional methods.

From the detailed analysis of the experimental dataset, we explain these results as follows: (i) Conventional CBCF methods cannot effectively recommend many content items that have few ratings because such content items’ similarities may be insignificant and (ii) our approach can recommend such content items well by complementing the conventional CBCF method with content-metadata effectively, as explained in detail in Section 5.

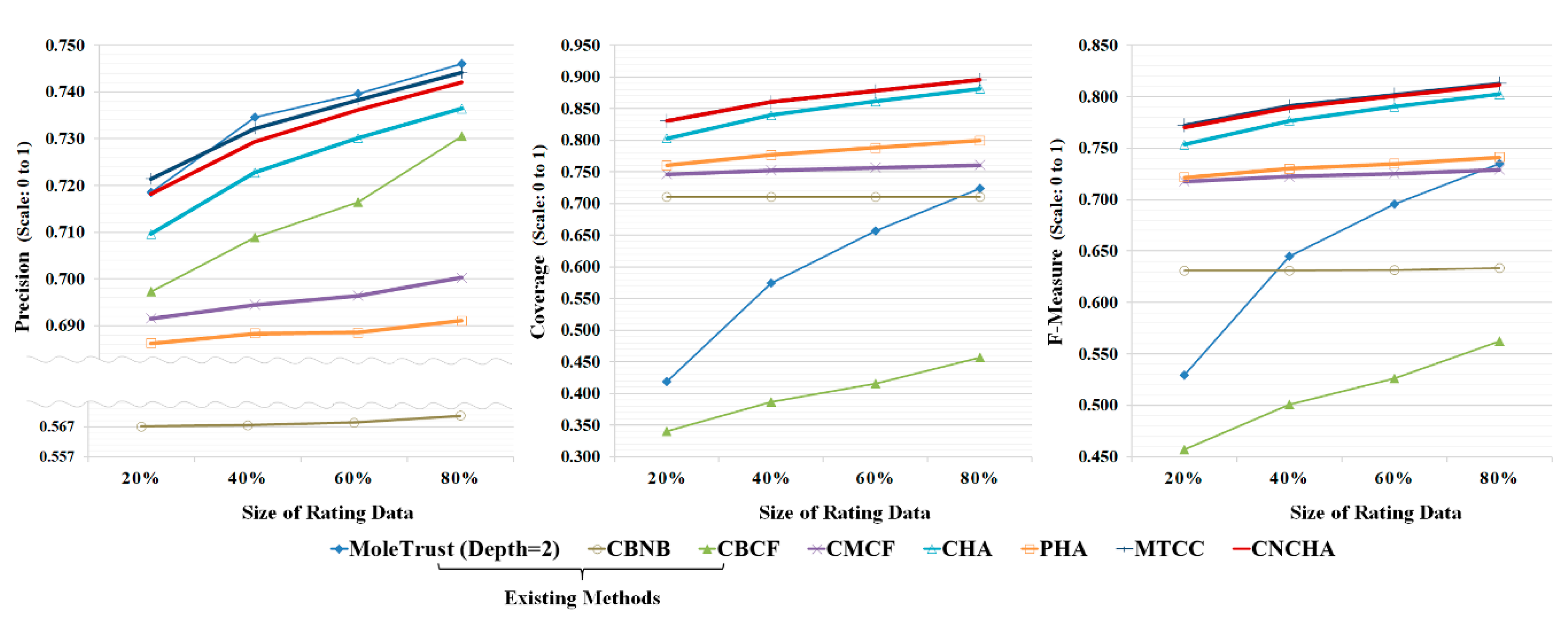
4.2.2. Performance over Size of Rating Data

In this experiment, we measure the performance incrementally by gradually increasing the (randomly selected) portion size of the complete set of user-content rating scores. We configured the experiment with accumulation ratios of user-content rating scores as 20%, 40%, 60%, and 80% (from high sparsity to relatively low sparsity).

As shown in Figure 12, all recommendation methods show a gradual increase in precision as the size of the user-content rating set increases. Relative to the existing methods, our content-metadata-based boosting approaches show almost the same or a slightly higher level of precision on average. In terms of coverage and F-measure, our methods all outperform the existing methods for all the sizes of user-content rating data. Specifically, MTCC and CNCHA show the highest performance and CHA also shows much higher performance than the existing methods for all the sizes of rating data. Particularly, the outperformance of our methods is more highlighted when the rating data is very sparse.

Therefore, it is easily confirmed that the performances of conventional methods are largely influenced by the amount of accumulated user-content rating scores, while our proposed approaches are much less vulnerable to the sparsity of user-content ratings. In other words, our content-metadata-based approaches can enable a recommendation system to predict rating scores for much more content items effectively under a sparse rating environment. The main reason for such results is that our approach makes efficient use of content-metadata available online to supplement sparse rating data. When considering challenges in the effective prediction of the rating score in the initial phase of recommendation service due to the lack of user-content ratings, these experimental results confirm the strong practical potential of our approach in many recommendation services.

4.2.3. Comparison with Model-Based Recommendation Methods

Finally, we compared our selected approaches with several model-based recommendation methods (PMF, BPMF, and BPMFSRIC) that are known to show the best precision in many recommendation tasks. Overall, as shown in

Table 1. Precision of our approach in comparison with model-based methods.

Methods	Size of Rating Data
	20%	40%	60%	80%
PMF	0.6756	0.6730	0.6766	0.6851
BPMF	0.6927	0.7103	0.7264	0.7355
BPMFSRIC	0.7149	0.7311	0.7381	0.7420
MTCC	0.7214	0.7322	0.7384	0.7441
GMTCC	0.7191	0.7318	0.7379	0.7420
CNCHA	0.7182	0.7294	0.7363	0.7421

, our approaches are not worse than those methods even when they all use both trust network information and content-metadata. Especially, MTCC shows the best precision for all the sizes of rating data. It shows a consistently better performance even when compared to BPMFSRIC, which boosts the performance of the Bayesian probabilistic matrix factorization method by combining trust network and content-metadata. Moreover, GMTCC and CNCHA also show comparable performance with the model-based methods. More specifically, GMTCC and CNCHA show 0.7327 and 0.7315 precisions, respectively, on average, which are all not worse than the average precisions of PMF, BPMFSR, and BPMFSRIC (0.6776, 0.7162, and 0.7315, respectively).

Those model-based methods use a pre-computed model to quickly recommend content items and thus the model is learnt usually in a batch and offline manner. They can predict all unobserved rating scores, which means their coverage rises up to 1.0 but the prediction of many unobserved ratings could be poor. In our experiment, all the predictions of unobserved ratings are excluded when calculating precision due to the lack of real rating scores. Importantly, their model-building process is computationally very expensive, with highly intensive memory usage, which can make real-time and online recommendation difficult in practice. From that perspective, it is meaningful that our memory-based approach is competitive with the ones of the best model-based recommendation methods.

5. Discussion

In the baseline CF CBCF, the content-to-content similarity is calculated based on users’ co-rating scores for two content items and thus is likely to be insignificant when the number of co-raters is small, which results in inaccurate prediction of rating scores. To increase significance, CMCF uses not only co-rating scores but also content-metadata whose similarity is weighted more highly as fewer co-raters exist (as in Equation (1)) when calculating the content-to-content similarity. Overall, CMCF shows satisfactory performance, similar to MoleTrust, and is apparently much less vulnerable to the sparsity of rating data than MoleTrust. On the other hand, CNCF uses a content link network that is constructed by connecting similar content items using text mining techniques for content-metadata and this framework shows satisfactory precision but not satisfactory coverage at all because content items are connected in a relatively limited way based on the semantic similarities of content.

To increase the strength and mitigate the limitations of each recommendation method, our successful combinations are based on two basic principles that (i) the more precise method (a method with higher precision in our experiment) is used in higher priority and/or (ii) the more reliable prediction is preferably applied to calculate target rating scores. We assume that the reliability of the prediction is proportional to the number of content rating scores referenced to calculate the rating score of target content because satisfactory statistical reliability requires a sufficient amount of data. As an example, the target rating scores of MTCN and GMTCC are reliability-weighted averages of MoleTrust and CNCF predictions and MoleTrust and GCM predictions, respectively, to support principle (ii). As another example, MTCC combines MoleTrust with the more precise CNCF method first and then (if this method fails) the less precise CMCF to support principle (i). Other examples, namely, CNCHA, CNPHA, and GCM (in Section 3.8) use a more precise method in terms of priority; only if the prediction is not reliable enough, weighted averaging is performed with the less precise prediction to support both principles (i) and (ii). As a special example that follows principle (ii) but not principle (i), PHA combines three basic methods in different priorities from their precision-based ones, and its performance enhancement is trivial. Similar to PHA and its variation CNPHA, other combinations (that do not follow the above principles) do not show as strong a performance as expected and thus are not presented in this paper.

To make traditional CF more successful, our approach uses content-metadata information for calculating content-to-content similarity or constructing content link network, while MoleTrust incorporates a user’s trust network information apart from user-content rating scores. By using two kinds of information in a suitable combination with rating scores, the performance can be improved considerably, which means that each piece of information can complement rating scores accurately; more importantly, two kinds of information can complement each other successfully in our approach.

Although our methods show high precision and coverage performances especially in a very sparse rating environment, they still cannot predict some user-content rating scores. It may be caused by a basic characteristic of memory-based recommendation methods, such as conventional CF methods whose predictions are based on the relationship information of users (or contents). This limitation will be further addressed and overcome in our future studies.

6. Conclusions

In this paper, we proposed a content-metadata-based approach for boosting CF which might suffer from deficiencies such as sparsity and cold-start problems in real recommendation systems. To mitigate such deficiencies, our proposed approach effectively uses content-metadata for complementing conventional CF methods and also combines content-metadata with trust network information. The experimental results indicate that our approach can provide a recommendation service with high-level performance even under the environment of sparse user-content ratings by using pre-crawled content-metadata in a supplementary way. More specifically, relative to existing methods, our approach recommends much more content by relaxing the insufficiency problem of the rating dataset, which considerably improves the recommendation performance, especially in terms of coverage. Furthermore, by effectively combining content-metadata with trust network information, a large amount of additional content can be recommended accurately; thus, our approach outperforms existing methods significantly and consistently irrespective of the size of the rating dataset in terms of the F-measure. These results are quite promising when considering that our approach showed significant improvement in comparison with one of the best conventional methods (MoleTrust, using a very large users’ trust network) and even CMCF performed at least as well as MoleTrust despite not using any trust network information. We expect that our metadata-based approach can be effectively applied for a variety of CF services with/without trust network to enhance the recommendation performance.

In the near future, we anticipate performing additional in-depth experiments by developing multiple different approaches (with more sophisticated parameter settings) using other existing CF methods, such as TrustWalker. Moreover, we will conduct comprehensive studies to further improve our recommendation methods using state-of-the-art machine-learning techniques including deep learning models.