Abstract
In the present paper, an analytical solution of rectified diffusion of processes of gas bubbles in molten metal is derived for the purpose of predicting the diffusion behaviors of gas bubbles during ultrasonic degassing. In the present model, a theoretical threshold (in terms of the amplitude of the applied ultrasonic field) is determined for the evaluation of the ultrasonic degassing effects. The diffusion of hydrogen bubbles in molten aluminum is predicted, so as to provide examples to illustrate the important findings of the present work.
1. Introduction
Ultrasonic degassing is an important topic for high-quality casting production [1,2,3,4,5]. For a comprehensive review of this technique, please see Eskin et al. [1]. During ultrasonic degassing, the existing bubbles could be forced to oscillate with significant amplitudes (termed as ‘acoustic cavitation’ [6,7,8]). During the oscillation process, gas shows prominent diffusion across the bubble interface with both the diffusion into and out of the bubble [9]. The overall diffusion direction is very important in regard to degassing efficiency. Based on our previous works on bubble dynamics in water [9], it has been proved that the amplitude of the ultrasonic field plays an important role on the determination of the diffusion direction. Hence, a rigorous theoretical determination of the phenomenon is necessary in order to promote further applications in the field.
First, the mechanisms of gas formations in the castings will be introduced. For this example, we will use aluminum alloys. At the aluminum melting interface with air, the existing moisture could react with the aluminum, forming atomic hydrogen and also molecular hydrogen. In conditions of oversaturation, hydrogen bubbles will be formed. During solidification, due to the prominent solubility of the hydrogen in the liquid aluminum, a great amount of porosity will be observed. As the porosity could significantly affect the performance of the alloys (e.g., yield strengths), some further treatments are essential to remove the pores.
When the ultrasonic fields are applied to the liquid aluminum, the existing bubbles will oscillate dramatically. During the oscillations, and in proper conditions, the dissolved hydrogen could be diffused into the bubble through the bubble–liquid interface [9]. With the growth of the bubble, the hydrogen in the liquid will be reduced, as the hydrogen will be inside the bubbles in increasing quantity. When the bubble is of a significant size, it will float to the liquid interface and then the hydrogen will be removed. During the whole process, there is no introduction of additives into the system. Hence, compared with other mechanical methods (e.g., stirring facilities), the ultrasonic treatment is a clean method. Furthermore, ultrasonic treatment does not need expensive instruments, making it both a cheap and convenient method. It is necessary to mention that, except for the aforementioned degassing effects, ultrasonic treatment could achieve other benefits e.g., micro-structure modification [10,11] and grain refinement [12,13]. The applicable melts of ultrasonic treatment include aluminum–magnesium alloys [14]. Unfortunately, the theoretical basis for ultrasonic degassing is still absent in the literature (e.g., in terms of the theoretical predictions of the suitable conditions for the process).
In the present paper, an analytical solution to the rectified diffusion of gas bubbles in molten metal is derived and discussed, with the aid of typical examples. Specifically, the coupled equations of diffusion and bubble motion are solved together, with the corresponding initial and boundary conditions. Compared with the previous work, Sievert’s law is employed for the closure of the model. For the demonstrating cases, the diffusion process of the hydrogen bubbles in the liquid aluminum is analyzed in detail to illustrate the importance of the present paper.
2. Theoretical Analysis
In this section, the formulas for rectified diffusion of gas bubbles in molten metal under acoustic fields are derived. The following assumptions are employed:
- The involved sizes of the bubble is far beyond the molecular level [15].
- The interactions between the bubble and the boundaries are ignored. Here, we only consider a bubble in an infinite liquid melt. In fact, near the boundaries (e.g., wall and particle), the cavitation phenomenon is very complex [16,17,18].
- The bubbles are assumed to be spherical. In fact, because of the high viscosity involved here, the bubble could be safely treated as spherical ones. For a more recent work on the bubble stability theory, readers could refer to Klapcsik and Hegedűs [19,20].
- The viscosity and the compressibility of molten metal are both considered.
- The relationship between the volume and the internal pressure of gas bubbles is described by the polytropic model [21].
- Thermal damping is currently ignored. As shown in our previous work [21], this damping mechanism often does not serve as a dominant one.
The equation of bubble motion is given as [9],
where
Here, R is the instantaneous radius of the gas bubble oscillating in the melting metals; overdot denotes the time derivative; ρl is the density of the molten metal; t is the time; cl is the sound speed propagating in the molten metal; Pg is the instantaneous pressure in the bubble; σ is the surface tension coefficient; μl is the viscosity of the molten metal; P∞ is the ambient pressure; R0 is the initial and equilibrium radius of the given bubble; η is the polytropic exponent; PA is the amplitude of the applied acoustic field; f is the frequency of the applied acoustic field.
The mass transfer equation is [22]
where c is the concentration of certain gas in the molten metal; u is the velocity of the molten metal surrounding the gas bubble; D is the diffusion constant. The initial and boundary conditions are [22]
Here, Ci is the initial concentration or the concentration at infinity; CS is the local gas concentration at the inner bubble wall. The solubility of gases in molten metal is controlled by Sievert’s law [23] as follows
Here, C0 is the saturation concentration of gas in the molten metal; kS is a constant. Equations (1) to (5) with initial and boundary conditions of Equations (6) to (8) can be solved following our previous framework [9]. Because the solubility of gas in the molten metal is controlled by the Sievert’s law rather than Henry’s law, some modifications on the previous works will be performed as follows. The time derivative of the gas amount change (n) inside the bubble is given by [22]
where
with
Here, Tb is the bubble oscillation period; < > denotes time averages of the given parameter. By using the Sievert’s law, F0 can be expressed as,
The required time averages in dn/dt can be determined based on the solution of Equations (1) to (4) using the perturbation method with direct series expansions. Only second-order terms are considered, and the harmonic term can be neglected ([22], p. 501). Following the framework of reference [9], the bubble growth rate in the given molten metal is as shown in [9]
with
Here, Rg is the universal constant; T is the temperature (unit: K). Compared with previous work (e.g., [9]) based on the Henry’s law, Equations (9), and (12) are different owing to the use of Sievert’s law (e.g., the terms with Pg in the Equations (9) and (12)). Based on Equations (9) to (15), one can find that the growth or dissolution rate of gas bubbles in molten metal under acoustic excitation is dependent on many parameters, e.g., acoustic pressure, amplitude, and frequency, saturation conditions, ambient pressure, temperature, bubble radius, and time. By integration of Equation (9), the quasi-equilibrium bubble radius could be obtained. If one set dR0/dt = 0 in Equation (9), the corresponding acoustic amplitude will be the threshold for the diffusion (PT) as follows
For a given bubble radius, the bubble will grow if PA > PT and dissolve if PA < PT.
3. Results and Discussions
In this section, the predictions of the rectified diffusion of gas bubbles in molten metal are demonstrated and discussed. Here, hydrogen bubbles in molten aluminum is considered as an example. For the physical properties of molten aluminum, the following constants are used [24]: melting point Tm = 933.4 K; σ = 868 − 0.152(T − Tm) dyn/m; ρl = 2375 kg/m3; cl = 6187 m/s; μl = 0.1492exp(1984.5/T) Pa·s.
The solubility of hydrogen in molten aluminum can be expressed as [25],
Here, S is the solubility of hydrogen in aluminum.
The diffusion coefficient of hydrogen in molten aluminum is [26]
Here, D is the diffusion coefficient (m2/s); D0 is the maximum diffusion coefficient at the infinite temperature (m2/s); Q is the activation energy for diffusion. Here, a group of values suggested by [26] are used: D0 = 3.8 × 10−6 m2/s; Q = 19320 J/mol. The constants are highlighted in Table 1 with the following acoustic parameters given: P∞ = 1.01 × 105 Pa; f = 18 kHz; PA = 1.1 × 105 Pa. For some cases, the polytropic exponent could not be regarded as a pure constant. Instead, it will depend on the external frequency and the bubble radius. For more details for the predictions of the polytropic exponent, readers could consider our previous model [21].

Table 1.
Detailed values of the employed parameters.
Figure 1 shows the predictions of the threshold of rectified diffusion (PT) based on Equation (16) for hydrogen bubbles in molten aluminum. The threshold is minimal near resonance and increases gradually for non-resonance conditions. For oversaturation conditions (e.g., Ci/C0 = 1.05), the threshold is lower while for subsaturation conditions (e.g., Ci/C0 = 0.95), the threshold is higher. In Figure 1, Eskin’s predictions [6] were not compared with ours because Eskin’s model cannot be used to predict the threshold phenomenon of the rectified diffusion owing to the assumption of gas always flowing into bubbles embedded in his model ([6], Equation (3)). It should be emphasized that for effective ultrasonic degassing, the amplitude of applied ultrasonic fields should be strong enough (i.e., above the threshold of rectified diffusion) to facilitate the growth of a gas bubble.
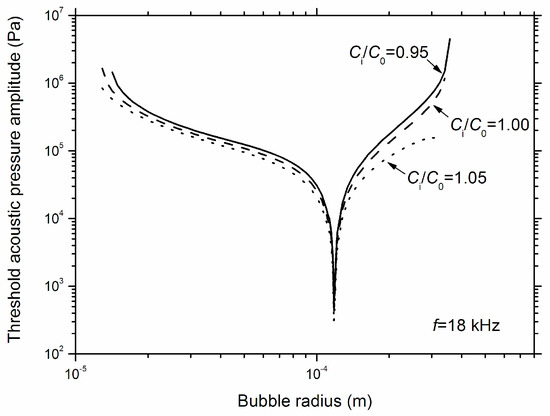
Figure 1.
Predicted threshold of acoustic pressure amplitude of rectified diffusion of hydrogen bubbles in molten aluminum. Ci/C0 = 0.95, 1.00 and 1.05. f = 18 kHz.
Figure 2 shows the dynamic change of the equilibrium bubble radius of hydrogen bubbles in molten aluminum. The bubble growth rate (the gradient of the curves shown in Figure 2) firstly increases to a maximum value near the bubble resonance regime and then decreases quickly. It should be noticed that the growth of hydrogen bubbles is rather rapid on average, i.e., about fifteen-fold of the initial bubble radius after 0.1s. When the bubble radius reaches a critical value (determined by the liquid densities), the dissolved hydrogen could be successfully removed through the bubble floatation. Figure 2 reflects the detailed process for hydrogen degasification in molten aluminum, which can be used for the further optimization of efficient ultrasonic degassing technique.
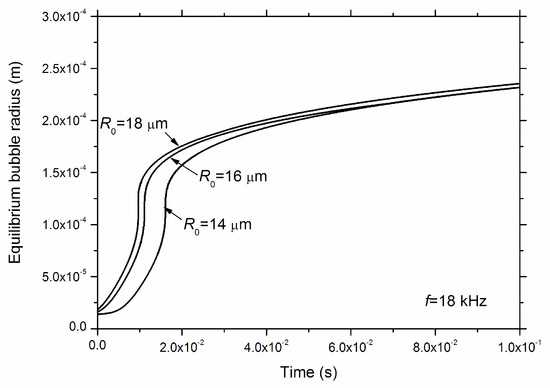
Figure 2.
Predicted dynamic change of equilibrium bubble radius against time during rectified diffusion processes of hydrogen bubbles in molten aluminum. Initial bubble radius (R0) employed for the predictions are 14, 16 and 18 μm respectively. Ci/C0 = 1. f = 18 kHz. PA = 1.1 × 106 Pa.
Finally, the validation of the present model will be briefly discussed. In our previous work, the present framework has been well proved by the experimental studies as shown in figure 8 of Zhang and Li [9]. As shown in the above figure, the agreement between the theoretical predictions and the experimental data is fairly good. As a future work, an experimental system based on the high speed photography [27] will be employed to further reveal the interesting bubble phenomenon (e.g., micro-jet formation) and the complex fluid flow (e.g., vortex [28,29,30]). For related reviews on the cavitation and bubble dynamics based on high-speed camera, Lauterborn and Kurz [31] and Wang et al. [32] are suggested.
The limitations of the present model will be also further briefly discussed. When the acoustic wave passing through the liquids containing bubbles, many complex phenomenon will be induced by the mutual interactions between the acoustic waves and the bubbles. For example, the wave will be greatly attenuated by the oscillating bubbles within a short distance [33,34,35], leading to the frequency locking of the wave [34]. On the contrary, the acoustic wave could also manipulate the distributions of the bubbles through inducing the Bjerknes forces between them [36,37,38,39], leading to the coalescence of the bubbles. In the present model, for the sake of the simplicity, those effects are not accounted with neglecting the strong interactions between the waves and bubbles.
4. Conclusions
Rectified diffusion process of gas bubbles in molten metal during ultrasonic degassing has been theoretically investigated based on analytical analysis. Theoretical expressions of the threshold and the bubble growth (or dissolution) rate have been derived and interpreted. The features of the diffusion phenomenon have been demonstrated through predictions of the behaviors of hydrogen bubbles in molten aluminum. In the present work, the nonlinearity of the bubble oscillator (e.g., sub-harmonics [40,41]) is not fully considered, and its effects on bubble dynamics will be further explored in future work.
Author Contributions
The authors contributed equally to the work reported.
Funding
This research was funded by the National Natural Science Foundation of China (Project Nos.: 51506051 and 51606221).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eskin, D.; Alba-Baena, N.; Pabel, T.; Silva, M. Ultrasonic degassing of aluminium alloys: basic studies and practical implementation. Mater. Sci. Technol. 2015, 31, 79–84. [Google Scholar] [CrossRef]
- Xu, H.; Han, Q.; Meek, T.T. Effects of ultrasonic vibration on degassing of aluminum alloys. Mater. Sci. Eng. A 2008, 473, 96–104. [Google Scholar] [CrossRef]
- Meidani, A.N.; Meidani, A.N.; Hasan, M. A study of hydrogen bubble growth during ultrasonic degassing of Al–Cu alloy melts. J. Mater. Process. Technol. 2004, 147, 311–320. [Google Scholar] [CrossRef]
- Meidani, A.N.; Hasan, M. Mathematical and physical modelling of bubble growth due to ultrasound. Appl. Math. Model. 2004, 28, 333–351. [Google Scholar] [CrossRef]
- Lebon, G.S.B.; Pericleous, K.; Tzanakis, I.; Eskin, D.G. Dynamics of two interacting hydrogen bubbles in liquid aluminum under the influence of a strong acoustic field. Phys. Rev. E 2015, 92, 043004. [Google Scholar] [CrossRef]
- Eskin, G. Cavitation mechanism of ultrasonic melt degassing. Ultrason. Sonochemistry 1995, 2, 137. [Google Scholar] [CrossRef]
- Xu, W.; Tzanakis, I.; Srirangam, P.; Mirihanage, W.; Eskin, D.; Bodey, A.; Lee, P.; Xu, W.; Mirihanage, W.; Lee, P. Synchrotron quantification of ultrasound cavitation and bubble dynamics in Al–10Cu melts. Ultrason. Sonochemistry 2016, 31, 355–361. [Google Scholar] [CrossRef] [PubMed]
- Eskin, G.I. Prospects of ultrasonic (cavitational) treatment of the melt in the manufacture of aluminum alloy products. Metallurgist 1998, 42, 284–291. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S. Mass transfer during radial oscillations of gas bubbles in viscoelastic mediums under acoustic excitation. Int. J. Heat Mass Transf. 2014, 69, 106–116. [Google Scholar] [CrossRef]
- Feng, X.; Zhao, F.; Jia, H.; Li, Y.; Yang, Y. Numerical simulation of non-dendritic structure formation in Mg-Al alloy solidified with ultrasonic field. Ultrason. Sonochemistry 2018, 40, 113–119. [Google Scholar] [CrossRef] [PubMed]
- Moussa, M.; Waly, M.; Amin, M. Effect of high intensity ultrasonic treatment on microstructural modification and hardness of a nickel-aluminum bronze alloy. J. Alloy. Compd. 2018, 741, 804–813. [Google Scholar] [CrossRef]
- Nagasivamuni, B.; Wang, G.; StJohn, D.H.; Dargusch, M.S. The effect of ultrasonic treatment on the mechanisms of grain formation in as-cast high purity zinc. J. Cryst. 2018, 495, 20–28. [Google Scholar] [CrossRef]
- Feng, X.; Zhao, F.; Jia, H.; Zhou, J.; Li, Y.; Li, W.; Yang, Y. Effect of temperature conditions on grain refinement of Mg–Al alloy under ultrasonic field. Int. J. Cast Met. Res. 2017, 30, 341–347. [Google Scholar] [CrossRef]
- Mills, K.; Wang, G.; StJohn, D.; Dargusch, M. Ultrasonic Processing of Aluminum–Magnesium Alloys. Materials 2018, 11, 1994. [Google Scholar] [CrossRef]
- Wang, H.-S.; Fu, G.-S.; Cheng, C.-Z.; Song, L.-L.; Wang, L.-D. Molecular mechanics and dynamics simulation of hydrogen diffusion in aluminum melt. China Foundry 2017, 14, 478–484. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, F.; Zhang, Y.; Zhang, Y.; Du, X. Experimental investigations of interactions between a laser-induced cavitation bubble and a spherical particle. Exp. Therm. Sci. 2018, 98, 645–661. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, X.; Zhang, Y.; Zhang, Y. High-speed experimental photography of collapsing cavitation bubble between a spherical particle and a rigid wall. J. Hydrodyn. 2018, 30, 1012–1021. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, X.; Zhang, Y.; Zhang, Y.; Du, X. Experimental study of influences of a particle on the collapsing dynamics of a laser-induced cavitation bubble near a solid wall. Exp. Therm. Sci. 2019. [Google Scholar] [CrossRef]
- Klapcsik, K.; Hegedűs, F. Study of non-spherical bubble oscillations under acoustic irradiation in viscous liquid. Ultrason. Sonochemistry 2019. [Google Scholar] [CrossRef]
- Klapcsik, K.; Hegedűs, F. The effect of high viscosity on the evolution of the bifurcation set of a periodically excited gas bubble. Chaos Solitons Fractals 2017, 104, 198–208. [Google Scholar] [CrossRef][Green Version]
- Zhang, Y.; Li, S.C. Notes on radial oscillations of gas bubbles in liquids: Thermal effects. J. Acoust. Soc. Am. 2010, 128, EL306–EL309. [Google Scholar] [CrossRef]
- Eller, A.I.; Flynn, H.G. Rectified diffusion during nonlinear pulsations of cavitation bubbles. J. Acoust. Soc. Am. 1965, 37, 493–503. [Google Scholar] [CrossRef]
- Gupta, C.K. Chemical Metallurgy: Priciples and Practice; Viley-VCH Verlag GmbH&Co. KGaA: Weinheim, Germany, 2003; p. 273. ISBN 3-527-30376-6. [Google Scholar]
- Hatch, J.E. Aluminum: properties and physical metallurgy. Am. Soc. Met. 1984, 1, 1–24. [Google Scholar]
- Opie, W.R.; Grant, N.J. Hydrogen solubility in aluminum and some aluminum alloys. JOM 1950, 2, 1237–1241. [Google Scholar] [CrossRef]
- Eichenauer, W.; Markopoulos, J. Measurement of the diffusion coefficients of hydrogen in liquid aluminum. WAA Trans. Z. Met. 1974, 65, 649–652. [Google Scholar]
- Lv, L.; Zhang, Y.; Zhang, Y.; Zhang, Y. Experimental investigations of the particle motions induced by a laser-generated cavitation bubble. Ultrason. Sonochemistry 2019. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiu, X.; Chen, F.; Liu, K.; Zhang, Y.; Liu, C. A selected review of vortex identification methods with applications. J. Hydrodyn. 2018, 30, 767–779. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Zhang, Y.; Liu, C. Comparisons of and analyses of vortex identification between omega method and Q criterion. J. Hydrodyn. 2019, 31, 224–230. [Google Scholar] [CrossRef]
- Dong, X.; Wang, Y.; Chen, X.; Dong, Y.; Zhang, Y.; Liu, C. Determination of epsilon for Omega vortex identification method. J. Hydrodyn. 2018, 30, 541–548. [Google Scholar] [CrossRef]
- Lauterborn, W.; Kurz, T. Physics of bubble oscillations. Rep. Prog. Phys. 2010, 73, 106501. [Google Scholar] [CrossRef]
- Wang, S.-P.; Zhang, A.-M.; Liu, Y.-L.; Zhang, S.; Cui, P. Bubble dynamics and its applications. J. Hydrodyn. 2018, 30, 975–991. [Google Scholar] [CrossRef]
- Ganesh, H.; Mäkiharju, S.A.; Ceccio, S.L. Bubbly shock propagation as a mechanism of shedding in separated cavitating flows. J. Hydrodyn. 2017, 29, 907–916. [Google Scholar] [CrossRef]
- Yuan, Y.; Miao, B.; An, Y. Cavitation clouds in gas-containing liquids block low-frequency components of ultrasonic waves. J. Appl. Phys. 2018, 124, 224902. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Z.; Yuan, J.; Chen, T.; Tang, N.; Du, X. Influences of bubble size distribution on propagation of acoustic waves in dilute polydisperse bubbly liquids. J. Hydrodyn. 2019, 31, 50–57. [Google Scholar] [CrossRef]
- Chen, H.; Lai, Z.; Chen, Z.; Li, Y. The secondary Bjerknes force between two oscillating bubbles in Kelvin-Voigt-type viscoelastic fluids driven by harmonic ultrasonic pressure. Ultrason. Sonochemistry 2018. [Google Scholar] [CrossRef]
- Baresch, D.; Garbin, V. Acoustic manipulation and actuation of bubbles in complex environments: Beyond the Bjerknes force. J. Acoust. Soc. Am. 2018, 144, 1933. [Google Scholar] [CrossRef]
- Xu, Z. Numerical simulation of the coalescence of two bubbles in an ultrasound field. Ultrason. Sonochemistry 2018, 49, 277–282. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Li, S. The secondary Bjerknes force between two gas bubbles under dual-frequency acoustic excitation. Ultrason. Sonochemistry 2016, 29, 129–145. [Google Scholar] [CrossRef]
- Klapcsik, K.; Varga, R.; Hegedűs, F. Bi-parametric topology of subharmonics of an asymmetric bubble oscillator at high dissipation rate. Nonlinear Dyn. 2018, 94, 2373–2389. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Li, S. Combination and simultaneous resonances of gas bubbles oscillating in liquids under dual-frequency acoustic excitation. Ultrason. Sonochemistry 2017, 35, 431–439. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).