Symmetrical Uncertainty-Based Feature Subset Generation and Ensemble Learning for Electricity Customer Classification

Abstract

The use of actual electricity consumption data provided the chance to detect the change of customer class types. This work could be done by using classification techniques. However, there are several challenges in computational techniques. The most important one is to efficiently handle a large number of dimensions to increase customer classification performance. In this paper, we proposed a symmetrical uncertainty based feature subset generation and ensemble learning method for the electricity customer classification. Redundant and significant feature sets are generated according to symmetrical uncertainty. After that, a classifier ensemble is built based on significant feature sets and the results are combined for the final decision. The results show that the proposed method can efficiently find useful feature subsets and improve classification performance.

1. Introduction

In the electricity market, the type of customer class is the predefined electricity usage contract. Therefore, The customer class is usually identified at the beginning of the contract and it is difficult to be updated once it has been determined. The load consumption pattern of a customer is represented with the customer class (contract type)-specific load profiles (e.g., hourly load profiles). Electricity consumers with the same customer class type show similar load consumption patterns. In reality, the type of customer class may change due to several reasons, for example, an addition of new devices, or the customers’ abnormal behavior that they do not correspond to the predefined customer class types. That means actual consumption patterns of a customer is changed. The automatic meter-reading (AMR) system is used to measure the customers’ electricity consumption in real time and there are several studies based on actual electricity consumption data [1,2,3]. If we have the information about the real consumption pattern of a customer, then we can judge if the customer class is changed or not according to the consumption behavior of customers. One of the effective approaches is to apply classification method on electricity consumption data.

1.1. Customer Classification

Normally, electricity consumption data are used in load profiling and customer classification. There are studies about data mining based customer classification [1,4,5,6,7,8,9,10,11,12,13]. We can see that the most often used approach is to directly apply the classification method on the raw electricity consumption data.

The actual electricity consumption of customers is measured per several minutes (e.g., 15 min) or hourly. If the data is the daily use of the customer and it is measured per 15 min, then the number of dimensions is 96. If the data is the weekly data, then there are 672 features (dimensions). In the view of data mining, handling such a large number of dimensions is time-consuming and has a big chance to decrease customer classification performance. Therefore, the dimensionality reduction method is necessary for saving the computational cost and guarantee for the performance.

For the purpose of dimensionality reduction, there are several solutions like field indices extraction [14,15,16,17,18,19,20], harmonic analysis (discrete Fourier transform) [21,22], and principal component analysis [23]. These solutions are often used on hourly consumption diagrams.

1.2. Field Indices Extraction

Feature extraction is a very useful approach to dimensionality reduction. Field indices extraction is the application of a feature extraction technique in electricity customer classification. There are two types of indices: priori indices and field indices. Priori indices are contractual information, for example, power usage type and economic activity type. Most of the time, priori indices are hard to use to represent the customer’s actual consumption behaviors.

Field indices are directly extracted from actual consumption patterns [14,15,16,17,18,19,20]. The field indices definition is based on the descriptive statistical analysis of the particular interval (section) in actual consumption patterns. For example, $P_{min}$ is the minimum power demand of the weekend; $P_{av}$ is the average power demand of the weekend. Then, we can get a field index $P_{min}$/$P_{av}$ according to $P_{min}$ and $P_{av}$ of weekend.

It has been proved that field indices have a positive effect on customer classification. However, the definition of the field indices is varying in different studies and countries. Most of them look like they are artificially defined. Piao et al. [20] have proposed a method to explain how to define the field indices according to given data. However, it still needs time to train the parameters to achieve an appropriate result.

1.3. Data Transformation

Data transformation is the application of a deterministic mathematical function to each point in a data set. Each data point p is replaced with the transformed value tp = f(p), where f is a function. Transforms are usually applied so that the data can be easier to visualize. Some studies have applied transformation functions to electricity consumption data like harmonic analysis (discrete Fourier transform) [21,22], principal component analysis [23].

Harmonic analysis extracts a series of indices from the frequency domain of the load profiles. The frequency domain of the electrical profile is computed by using the discrete Fourier transform (DFT). The DFT transforms a sequence of N complex numbers $\left\{x_n\right\}:=x_0,x_1,\dots ,x_{N-1}$ into another sequence of complex numbers, $\left\{X_k\right\}:=X_0,X_1,\dots ,X_{N-1}$, it is stated as:

$$X_k=\sum _{n=0}^{N-1}{x}_n·e^{-\frac{i2\pi }{N}}kn.$$

(1)

If applying the DFT on the electricity consumption data, the data will be transformed into the frequency based format.

The principal component analysis will map the original variables into a new space of uncorrelated variables, and not all new variables are kept. Consider a data matrix X with column-wise zero empirical means, the first weight vector $w_1$ can be calculated as:

$$w_1=argmax\left\{\sum _i^b{(X_i·w^T)}^2\right\},\Vert w\Vert =1.$$

(2)

The k-th component can be calculated by subtracting the first $k-1$ principal component from X:

$${\widehat{X}}_k=X-\sum _{s=1}^{k-1}X{w}_s{w}_s^T$$

(3)

The use of such transformation will cause the loss of the original information of the consumption patterns like the geometrical shape information of the consumption pattern.

In our study, we propose a symmetrical uncertainty based feature subset generation and ensemble learning method for the electricity customer classification. Remain paper is organized as follows: Section 2 describes the details of the proposed method; Section 3 shows the experimental results and the conclusion is given in Section 4.

2. Proposed Method

Dimensionality reduction techniques were used to reduce the number of features under consideration. In data mining, dimensionality reduction was done by using feature selection methods. The feature selection method was used to detect a subset of the features (also called variable, attributes or dimensions). There were three types: one is the filter type method, the feature selection is independent of the model. The selection was done by considering some measurements, for example, the correlation between the feature and the target class (e.g., information gain, gain ratio); and wrapper type methods, the subset selection took place based on the learning algorithm used to train the model, and embedded types tried to perform the feature selection as a part of the learning method. The learning method had its own built-in feature selection methods (e.g., decision tree).

2.1. Symmetrical Uncertainty

The most often used feature selection method was filter-based such as mutual information, Pearson correlation, chi-squared test, information gain, gain ratio and relief. Yu and Liu [24] proposed the fast correlation-based filter (FCBF) method to remove the irrelevant and redundant features. The measurement of symmetrical uncertainty (SU) was defined to measure the redundancy:

$$IG\left(X\right|Y)=E(X)-E(X\left|Y\right)$$

(4)

$$SU(X,Y)=2\times \frac{IG\left(X\right|Y)}{E\left(X\right)+E\left(Y\right)},$$

(5)

where E(X) and E(Y) are the entropy of features X and Y, and IG(X|Y) is the information gain of X after observing Y. C-correlation and F-correlation are defined based on SU to measure the correlation between features.

C-correlation: the SU between any feature $F_i$ and the class C, denoted by $S{U}_{i,c}$.

F-correlation: the SU between any pair of features $F_i$ and $F_j$ ($i\ne j$), denoted by $S{U}_{i,j}$.

The use of symmetrical uncertainty has been proved to be useful in dimensionality reduction in previous studies [24,25,26,27,28,29].

2.2. SUFSE

For easy use, we call the proposed algorithm the symmetrical uncertainty based-feature subset generation and ensemble learning (SUFSE). The main idea is to find a number of feature subsets to build a classifier ensemble to perform the classification work.

Significant feature and redundant feature: suppose there are two relevant features $F_i$ and $F_j$ ($i\ne j$), and given a SU threshold $\sigma$, if $S{U}_{i,c}\ge \sigma$, $S{U}_{j,c}\ge \sigma$ and $S{U}_{i,j}\ge min(S{U}_{i,c},S{U}_{j,c})$. Then, we call $F_i$ a significant feature, and $F_j$ is the redundant feature of $F_i$.

The proposed method consists of several steps:

• Suppose there are features $F_1,F_2,···,F_i$, and class C. At the beginning of the algorithm, all of the features $F_1,F_2,···,F_i$ are sorted in descending order according to the C-correlation $S{U}_{i,c}$. If the value of $S{U}_{i,c}$ is smaller than a given threshold $\sigma$, then the feature $F_i$ is removed. Otherwise, feature $F_i$ is inserted into a candidate list C-list.
• Redundancy analysis is performed for features in C-list, and features in the C-list are named as $C_i$. Starting from the first element $C_i$ of C-list, the F-correlation $S{U}_{i,j}$ ($i\ne j$) is calculated for $C_i$ and $C_j$. If $S{U}_{i,j}\ge min(S{U}_{i,c},S{U}_{j,c})$, then $C_j$ is removed to the non-candidate list (NC-list) and $C_i$ is inserted into significant feature list (SF-list). Repeat the steps for remaining elements in C-list.
• Check the first element of NC-list, and the element is named as $N{C}_1$. For the element $C_i$ of C-list, if the C-correlation of $C_i$ is greater than $N{C}_1$, then $C_i$ is removed from C-list because it is already inserted into the SF-list. Initialize the NC-list.
• Repeat steps 2 to 3 until there are no elements in C-list.

Figure 1 shows the example of the proposed method. Suppose there are features F1, F2, F3, F4, F5, F6 in the candidate feature list C-list which are in descending order according to C-correlation.

The first iteration starts from F1, the redundancy between the first element of the C-list F1 and other features are checked. F2 and F3 are removed to NC-list since they are redundant with F1. F6 is also removed since it is redundant with F5. F1, F4, F5 are inserted into the SF-list.

At the second iteration, F1 is removed from C-list since its $S{U}_{1,c}$ is greater than $S{U}_{2,c}$ where F2 is the first element of NC-list. The redundancy analysis is performed for F2, F3, F4, F5, F6. F4 is removed to NC-list since it is redundant with F2. F6 is also removed since it is redundant with F5. F2, F3, F5 are inserted into significant feature list SF-list.

At the third iteration, F2 and F3 are removed from the C-list since its $S{U}_{2,c}$ and $S{U}_{3,c}$ are greater than $S{U}_{4,c}$. Remain steps are the same as first and second iteration.

For defining significant and redundant features, the important thing is to decide the SU threshold $\sigma$ value. According to the definition of the significant and redundant feature, we can see that the use of a high SU threshold value will result in a small number of significant features.

2.3. Ensemble Learning-Based Evaluation

The decision tree was easy to use when compared to other classification methods. Furthermore, the result of the decision tree is simple and easy to understand without explanation. It reduces the ambiguity in decision-making. Therefore, the decision tree C4.5 [30] was used to evaluate the performance of the significant feature subsets. For the significant feature subsets selected at each iteration, C4.5 was applied to generate classifiers and the average of the posterior probability was used to combine the result of classifiers.

The posterior probability was used to evaluate the probability that a given object belongs to one of the classes. For a given instance, the sum of the probabilities from each base classifier was derived and then the average is obtained by dividing the sum by the number of base classifiers [25]. In other words, it sums up the discriminating power of generated feature subsets to evaluate them.

2.4. Final Significant Feature Set Generation

The proposed method SUFSE has two parameters: the threshold $\sigma$ for C-correlation $S{U}_{i,c}$; and the number of iterations. The parameter number of iterations was provided for users to decide the number of feature subsets according to the ensemble learning based evaluation.

If the performance of the ensemble learning satisfies the expectation, then significant feature subsets generated from each iteration were combined to generate the final significant feature set by removing the redundancy. For example, if there are two generated feature subsets a,b,c and b,c,d, we can get the final significant feature set a,b,c,d.

3. Experimental Results

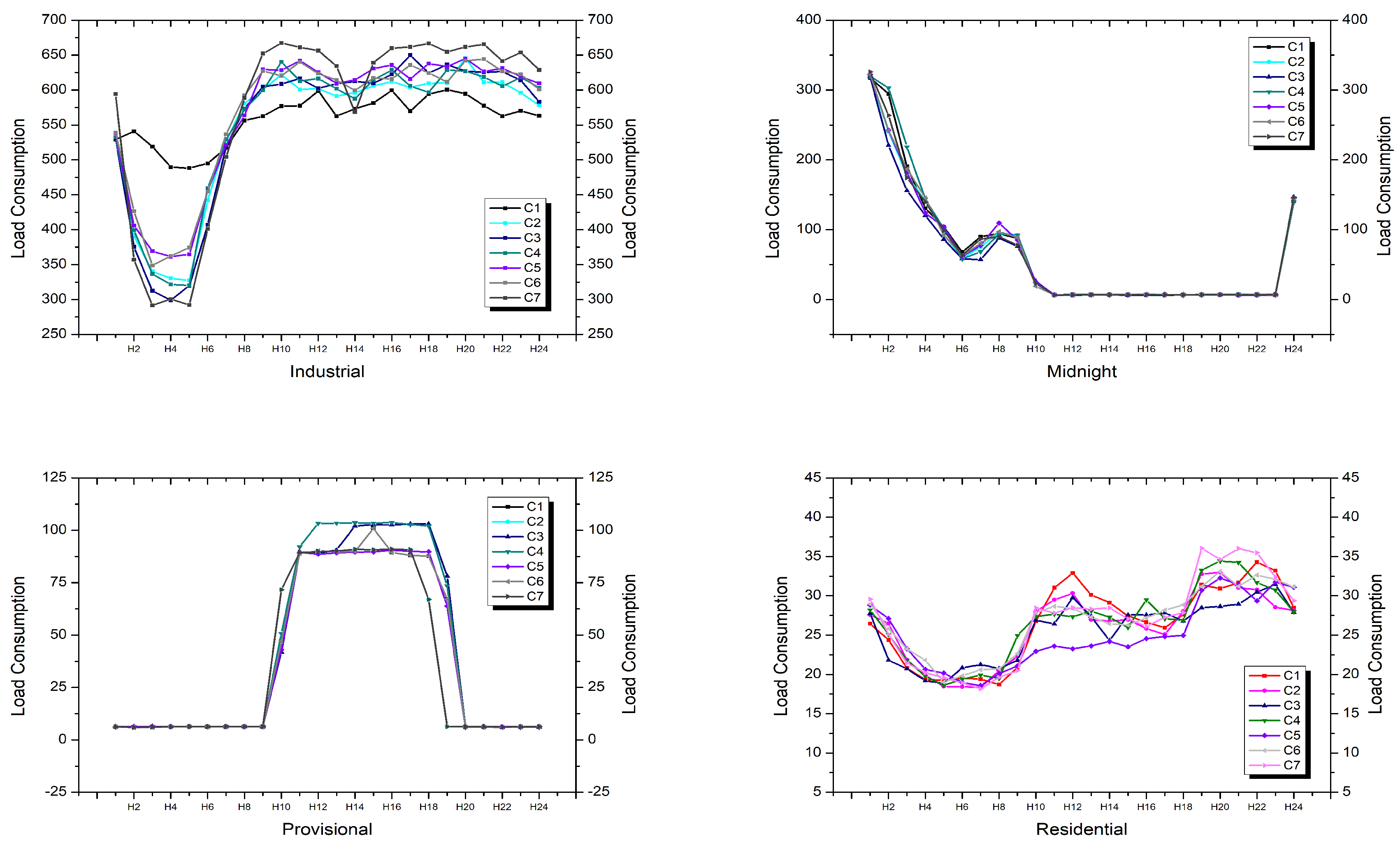
The given data set was the customers’ electricity consumption use of working days. Each customer’s data consisted of (1) one single load consumption diagram with 24 variables (i.e., 24 dimensions, denoted as H1, H2, ⋯, H23, H24) and (2) one class label which was the consumers contract type information (contract type: midnight, provisional, industrial, residential). There were 90 number of the midnight type, 63 number of the provisional type, 52 number of the industrial type, and 36 number of the residential type, i.e., a total 241 instances. Example instances are shown in

Table 1. Example instances of used electricity consumption data. H1 to H24 indicates the measuring time, i.e., H1 means 1:00 A.M., H2 means 2:00 A.M., and etc.

No.	H1	H2	H3	...	H22	H23	H24	Class
1	233.55	220.5	179.73	...	306.36	314.55	282.06	industrial
2	98.21	191.26	183.51	...	22.66	24.66	139.98	midnight
4	27.6	26.49	21.84	...	30.78	28.56	28.16	residential
5	16.94	17.07	16.77	...	15.5	15.36	15.55	provisional
.	.	.	.	...	.	.	.	.
.	.	.	.	...	.	.	.	.
.	.	.	.	...	.	.	.	.

.

The typical load profiles of these contract types are shown in Figure 2. From Figure 2, we can see that load profiles of different contract types had totally different geometrical shape information. The application of the feature selection method on load profiles was to find a smaller number of dimensions to represent the geometrical shape information of load profiles. For validation of the classification methods, 10 cross-validation was used to partition the data into training and validation data.

After a number of tests, the threshold $\sigma$ for C-correlation $S{U}_{i,c}$ was given as 0.4. Only one feature H1 was selected with low performance when the threshold $\sigma$ was given as 0.6. That means the threshold should be smaller than 0.6 because the high SU threshold value resulted in a small number of significant features. The performance was best when the threshold $\sigma$ was given as 0.4. The used measurements were accuracy, sensitivity, and specificity. They can be calculated according to the confusion matrix as shown in

Table 2. Confusion matrix.

		Predicted Class
		Positive	Negative
Actual Class	Positive	True Positive (TP)	False Negative (FN)
	Negative	False Positive (FP)	True Negative (TN)

. Table 2 shows the binary classification problem. If there were more than two classes, the class was estimated is considered as positive whereas others were considered as negative.

For easy understanding, we simply used a medical diagnosis example to describe the used measurements. Suppose that patients were positive for the disease and healthy were negative for the disease.

Accuracy: it is the ability to predict either patient and healthy cases correctly. We had to calculate the proportion of true positive and true negative in a population. It is stated as:

$$\mathbf{Accuracy}=\frac{TP+TN}{TP+TN+FP+FN}$$

(6)

Sensitivity (true positive rate): it is the ability to determine the patient cases correctly. We had to calculate the proportion of patient cases that are correctly identified. It is stated as:

$$\mathbf{Sensitivity}(\mathbf{TPR},\mathbf{Recall})=\frac{TP}{TP+FN}$$

(7)

Specificity (true negative rate): it is the ability to determine the healthy cases correctly. We should calculate the proportion of the healthy cases correctly identified. It is stated as:

$$\mathbf{Specificity}\left(\mathbf{TNR}\right)=\frac{TN}{TN+FP}$$

(8)

At first, the best result of SUFSE was derived.

Table 3. Selected significant features ($\sigma$ = 0.4).

Iteration	Selected Features	Iteration	Selected Features
1	1	9	5, 16
2	2, 22	10	15
3	13, 3, 24	11	19, 7
4	4, 24, 17	12	23
5	21, 6	13	20, 7
6	14, 6	14	11
7	18, 6	15	7
8	12, 6

shows the generated feature subsets. There were no feature subsets generated when the parameter number of iterations was bigger than 15.

Table 4. Performance evaluation ($\sigma$ = 0.4).

No. Classifiers	Accuracy (%)	Sensitivity (%)	Specificity (%)
1	86.3	86.3	95.8
2	88.8	88.8	96.7
3	89.6	89.6	97.0
4	87.6	87.6	96.5
5	89.6	89.6	97.0
6	90.5	90.5	97.2
7	92.1	92.1	97.6
8	91.7	91.7	97.3
9	91.7	91.7	97.3
10	91.7	91.7	97.3
11	92.1	92.1	97.4
12	92.1	92.1	97.4
13	92.1	92.1	97.4
14	92.1	92.1	97.4
15	91.7	91.7	97.2

shows the performance evaluation of the feature subsets during ensemble learning based evaluation. From the table, we can see that the performance was best when the number of classifiers was 7, 11, 12, 13, and 14. Here, the number of classifiers is the same as the number of iterations in Table 3. We can see that the minimum number of iterations with the highest performance is 7. Therefore, we generated a significant feature set from 1 to 7 iterations. It resulted in a minimum number of features with the highest accuracy. Generated final significant feature set is {1, 2, 3, 4, 6, 13, 14, 17, 18, 21, 22, 24}.

After the best ensemble was built, the performance was compared to other classification methods: Bayes Net [31], naive Bayes [32], logistic [33], SVM [34], and C4.5 [30]. From

Table 5. Comparison with other classifiers.

Classifiers	Accuracy (%)	Sensitivity (%)	Specificity (%)
Bayes Net	89.6	89.6	97.1
Naive Bayes	73.9	73.9	91.4
Logistic	84.6	84.6	95.2
SVM	67.6	67.6	88.3
C4.5	88.8	88.8	96.3
SUFSE	92.1	92.1	97.6

, we can see that SUFSE outperformed other classification methods. Also, the performance of the SUFSE was compared to other ensemble methods which were supported from WEKA. WEKA is an open data mining toolkit supported by the Machine Learning Group at the University of Waikato. It can be downloaded from http://www.cs.waikato.ac.nz/ml/weka/.

Table 6. Comparison with other ensemble methods. The base classifier is C4.5.

Ensemble Methods	Accuracy (%)	Sensitivity (%)	Specificity (%)
Grading	37.3	37.3	62.7
Dagging	79.7	79.7	93.6
MultiBoostAB	91.7	91.7	97.4
SUFSE	92.1	92.1	97.6
Decorate	92.1	92.1	97.7
Bagging	92.5	92.5	97.7
AdaBoostM1	92.5	92.5	97.9
RandomForest	95.9	95.9	98.7

shows the comparison results. The proposed method outperforms grading, dagging, and MultiBoostAB. It has achieved a similar result when compared to decorate. Bagging, AdaBoostM1, and random forest show a better result than SUFSE.

For evaluating the final significant feature set {1, 2, 3, 4, 6, 13, 14, 17, 18, 21, 22, 24}, the performance was compared to the entire set of features by using classification methods.

Table 7. Performance comparison of entire vs. significant feature set.

Classifiers	Used Features	Accuracy (%)	Sensitivity (%)	Specificity (%)
Bayes Net	Entire	89.6	89.6	97.1
	Significant	90.5	90.5	97.3
Naive Bayes	Entire	73.9	73.9	91.4
	Significant	75.5	75.5	92.0
Logistic	Entire	84.6	84.6	95.2
	Significant	82.6	82.6	95.2
SVM	Entire	67.6	67.6	88.3
	Significant	66.0	66.0	87.1
C4.5	Entire	88.8	88.8	96.3
	Significant	90.5	90.5	96.8

shows the comparison result by using Bayes net, naive Bayes, logistic, SVM, and C4.5. When comparing the performance on entire and significant features, we can see that the performance of Bayes net, naive Bayes, and C4.5 were improved whereas logistic and SVM are decreased when tested on significant features. That does not mean the significant features were meaningless. The purpose of using feature selection was to improve performance while saving the cost, but it was not absolute.

For proving the stability of the proposed method, we tested the method on several public datasets and compared to other methods. The used datasets are supported by the open data mining tool kit WEKA. The used datasets are Breast cancer, Credit-g, Diabetes, Ionosphere, Labor, Segment-challenge, Soybean, and Vote. These data sets consist of a number of input features and a target feature named class. Details of the used datasets are shown in

Table 8. Details of the used datasets.

Data	Number of Attributes	Attribute Type	Number of Instances
Breast-Cancer	10	Nominal	286
Credit-g	21	Nominal, Numeric	1000
Diabetes	9	Numeric	768
Ionosphere	35	Numeric	351
Labor	17	Nominal, Numeric	57
Segment-challenge	20	Numeric	1500
Soybean	36	Nominal	683
Vote	17	Nominal	435

.

Table 9. Verification on public datasets (accuracy (%)).

Data	SUFSE	Bayes Net	Naive Bayes	Logistic	SVM	C4.5
Breast-Cancer	75.9	72.0	71.7	68.9	69.6	75.5
Credit-g	74.8	75.5	75.4	75.2	75.1	70.5
Diabetes	74.7	74.3	76.3	77.2	77.3	73.8
Ionosphere	92.3	89.5	82.6	88.9	88.6	91.5
Labor	86.0	87.7	89.5	93.0	89.5	73.7
Segment-challenge	95.5	90.4	81.1	96.1	92.0	95.7
Soybean	90.6	93.3	93.0	93.9	93.9	91.5
Vote	96.3	90.1	90.1	96.1	96.1	96.3
Average	85.8	84.1	82.5	86.3	85.3	83.6
Standard Deviation	8.7	8.1	7.3	9.9	9.2	10.4

shows the verification of the SUFSE on public datasets by comparing with various algorithms. We can see that the performance of the SUFSE was similar or better than other used algorithms. The average performance was also top-ranked which means that SUFSE has acceptable stability. When comparing the proposed method and the logistic which shows the best average performance, we can see that the proposed method showed a smaller deviation. It indicates that the proposed method was more stable than the logistic method.

4. Conclusions

In our study, we have proposed a symmetrical uncertainty based feature subset generation and ensemble learning method for electricity customer classification. Significant feature sets are generated after ensemble learning based evaluation. The experimental results show that customer classification performance is improved when compared to other classification and ensemble methods. Also, the result shows that significant features can improve the performance of customer classification.

The proposed method generates a number of feature subsets first and builds a classifier ensemble based on those feature subsets. An individual feature set is generated by avoiding redundant features at each iteration, and the feature set is used to build a base classifier. The final decision is made by combining the result of base classifiers. That means our method can be used as a dimensionality reduction method, and also can be used as a classification method.

For generating an optimal number of significant feature subsets, we have used decision tree C4.5 in our study. Different learning methods can be used in this step and may produce different sets of features. The selection of learning method varies in different studies and needs a number of tests to select the appropriate one.

The electricity consumption diagram is in the form of time series. However, most of customer classification studies did not consider time property. The field indices based approach handles time property by summarizing the information into time intervals. However, there is still a loss of information about consumption changes over time. Therefore, we are going to consider entire dimensions for protecting the geometrical and time property of load profiles in the future study. One of the possible solutions is to apply deep learning methods.