Fluctuation Theorem of Information Exchange between Subsystems that Co-Evolve in Time
Abstract
:1. Introduction
2. Results
2.1. Theoretical Framework
2.2. Proof of Fluctuation Theorem of Information Exchange
2.3. Corollary
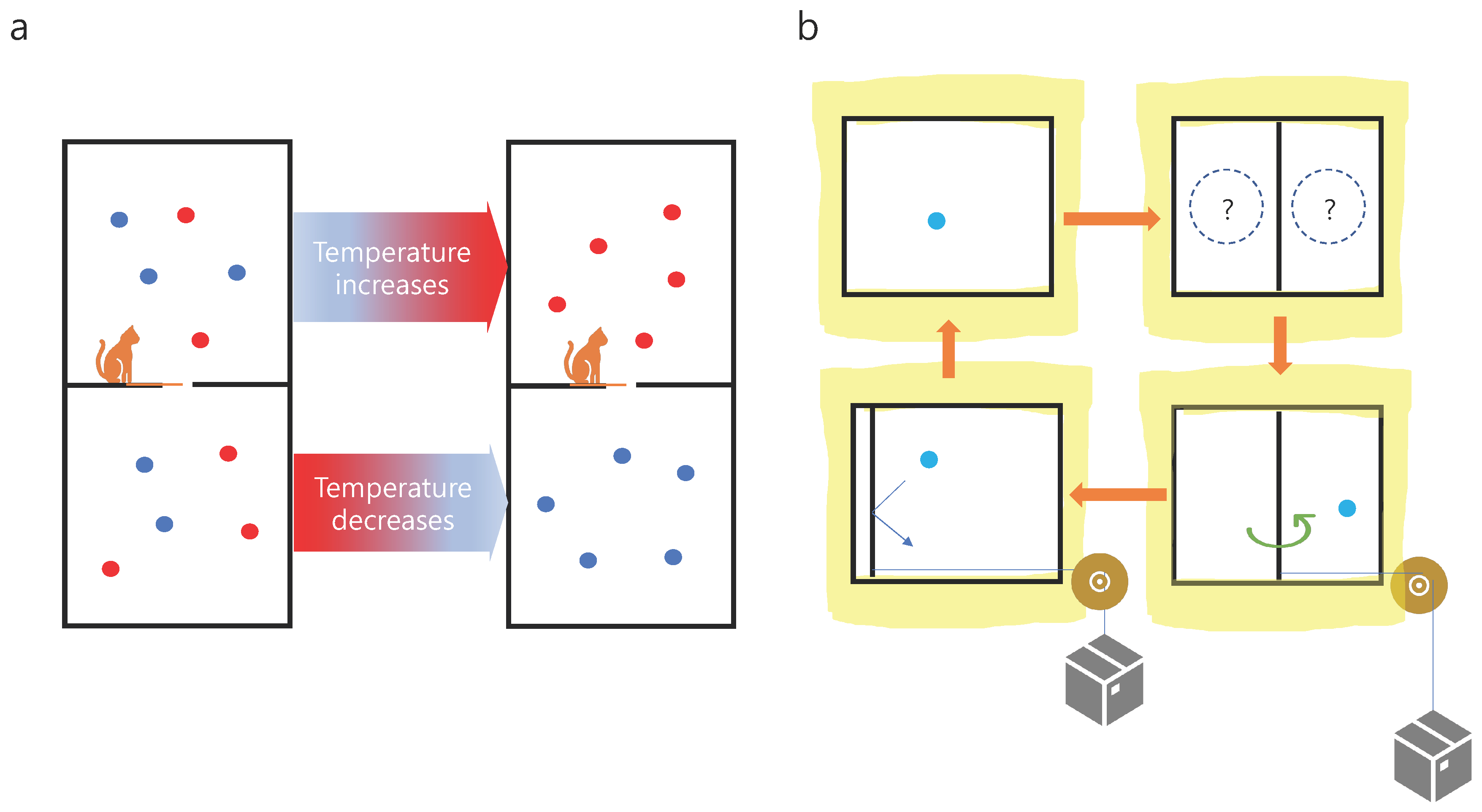
3. Examples
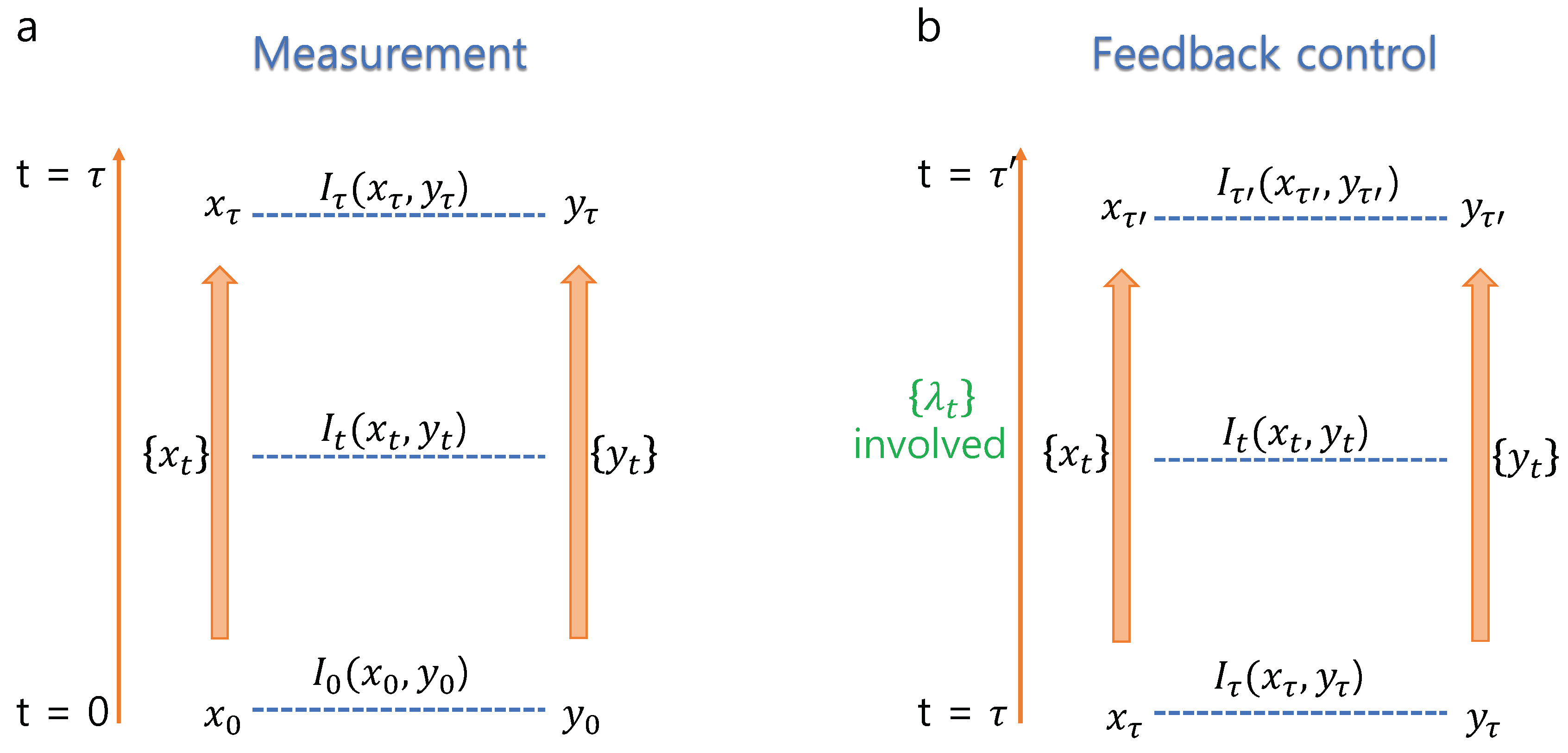
3.1. Measurement
3.2. Feedback Control
4. Conclusions
Funding
Conflicts of Interest
References
- Hartwell, L.H.; Hopfield, J.J.; Leibler, S.; Murray, A.W. From molecular to modular cell biology. Nature 1999, 402, C47. [Google Scholar] [CrossRef] [PubMed]
- Crofts, A.R. Life, information, entropy, and time: Vehicles for semantic inheritance. Complexity 2007, 13, 14–50. [Google Scholar] [CrossRef] [PubMed]
- Cheong, R.; Rhee, A.; Wang, C.J.; Nemenman, I.; Levchenko, A. Information transduction capacity of noisy biochemical signaling networks. Science 2011, 334, 354–358. [Google Scholar] [CrossRef]
- McGrath, T.; Jones, N.S.; ten Wolde, P.R.; Ouldridge, T.E. Biochemical Machines for the Interconversion of Mutual Information and Work. Phys. Rev. Lett. 2017, 118, 028101. [Google Scholar] [CrossRef] [PubMed]
- Ouldridge, T.E.; Govern, C.C.; ten Wolde, P.R. Thermodynamics of Computational Copying in Biochemical Systems. Phys. Rev. X 2017, 7, 021004. [Google Scholar] [CrossRef]
- Becker, N.B.; Mugler, A.; ten Wolde, P.R. Optimal Prediction by Cellular Signaling Networks. Phys. Rev. Lett. 2015, 115, 258103. [Google Scholar] [CrossRef] [PubMed]
- Cheng, F.; Liu, C.; Shen, B.; Zhao, Z. Investigating cellular network heterogeneity and modularity in cancer: A network entropy and unbalanced motif approach. BMC Syst. Biol. 2016, 10, 65. [Google Scholar] [CrossRef]
- Whitsett, J.A.; Guo, M.; Xu, Y.; Bao, E.L.; Wagner, M. SLICE: Determining cell differentiation and lineage based on single cell entropy. Nucleic Acids Res. 2016, 45, e54. [Google Scholar]
- Statistical Dynamics of Spatial-Order Formation by Communicating Cells. iScience 2018, 2, 27–40. [CrossRef]
- Maire, T.; Youk, H. Molecular-Level Tuning of Cellular Autonomy Controls the Collective Behaviors of Cell Populations. Cell Syst. 2015, 1, 349–360. [Google Scholar] [CrossRef]
- Mehta, P.; Schwab, D.J. Energetic costs of cellular computation. Proc. Natl. Acad. Sci. USA 2012, 109, 17978–17982. [Google Scholar] [CrossRef] [PubMed]
- Govern, C.C.; ten Wolde, P.R. Energy dissipation and noise correlations in biochemical sensing. Phys. Rev. Lett. 2014, 113, 258102. [Google Scholar] [CrossRef] [PubMed]
- Leff, H.S.; Rex, A.F. Maxwell’s Demon: Entropy, Information, Computing; Princeton University Press: Princeton, NJ, USA, 2014. [Google Scholar]
- Landauer, R. Information is physical. Phys. Today 1991, 44, 23–29. [Google Scholar] [CrossRef]
- Szilard, L. On the decrease of entropy in a thermodynamic system by the intervention of intelligent beings. Behav. Sci. 1964, 9, 301–310. [Google Scholar] [CrossRef]
- Sagawa, T.; Ueda, M. Fluctuation theorem with information exchange: Role of correlations in stochastic thermodynamics. Phys. Rev. Lett. 2012, 109, 180602. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Tsai, C.J.; Nussinov, R. A unified view of how allostery works? PLoS Comput. Biol. 2014, 10, e1003394. [Google Scholar] [CrossRef]
- Cuendet, M.A.; Weinstein, H.; LeVine, M.V. The allostery landscape: Quantifying thermodynamic couplings in biomolecular systems. J. Chem. Theory Comput. 2016, 12, 5758–5767. [Google Scholar] [CrossRef]
- Jarzynski, C. Equalities and inequalities: Irreversibility and the second law of thermodynamics at the nanoscale. Annu. Rev. Condens. Matter Phys. 2011, 2, 329–351. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef]
- Spinney, R.; Ford, I. Fluctuation Relations: A Pedagogical Overview. In Nonequilibrium Statistical Physics of Small Systems; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; pp. 3–56. [Google Scholar]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721–2726. [Google Scholar] [CrossRef]
- Seifert, U. Entropy production along a stochastic trajectory and an integral fluctuation theorem. Phys. Rev. Lett. 2005, 95, 040602. [Google Scholar] [CrossRef]
- Ponmurugan, M. Generalized detailed fluctuation theorem under nonequilibrium feedback control. Phys. Rev. E 2010, 82, 031129. [Google Scholar] [CrossRef]
- Horowitz, J.M.; Vaikuntanathan, S. Nonequilibrium detailed fluctuation theorem for repeated discrete feedback. Phys. Rev. E 2010, 82, 061120. [Google Scholar]
- Kurchan, J. Fluctuation theorem for stochastic dynamics. J. Phys. A Math. Gen. 1998, 31, 3719. [Google Scholar] [CrossRef]
- Maes, C. The fluctuation theorem as a Gibbs property. J. Stat. Phys. 1999, 95, 367–392. [Google Scholar] [CrossRef]
- Jarzynski, C. Hamiltonian derivation of a detailed fluctuation theorem. J. Stat. Phys. 2000, 98, 77–102. [Google Scholar] [CrossRef]
- Goldstein, H.; Poole, C., Jr.; Safko, J.L. Classical Mechanics, 3rd ed.; Pearson: London, UK, 2001. [Google Scholar]
- Parrondo, J.M.; Horowitz, J.M.; Sagawa, T. Thermodynamics of information. Nat. Phys. 2015, 11, 131–139. [Google Scholar] [CrossRef]
- Kawai, R.; Parrondo, J.M.R.; den Broeck, C.V. Dissipation: The phase-space perspective. Phys. Rev. Lett. 2007, 98, 080602. [Google Scholar] [CrossRef]
- Generalization of the second law for a transition between nonequilibrium states. Phys. Lett. A 2010, 375, 88–92. [CrossRef]
- Generalization of the second law for a nonequilibrium initial state. Phys. Lett. A 2010, 374, 1001–1004. [CrossRef]
- Esposito, M.; Van den Broeck, C. Second law and Landauer principle far from equilibrium. Europhys. Lett. 2011, 95, 40004. [Google Scholar] [CrossRef]
- Sagawa, T.; Ueda, M. Generalized Jarzynski equality under nonequilibrium feedback control. Phys. Rev. Lett. 2010, 104, 090602. [Google Scholar] [CrossRef] [PubMed]
- Horowitz, J.M.; Parrondo, J.M. Thermodynamic reversibility in feedback processes. Europhys. Lett. 2011, 95, 10005. [Google Scholar] [CrossRef]
| 0 (Left) | 1 (Right) | |
|---|---|---|
| 0 (Left) | 1/3 | 1/6 |
| 1 (Right) | 1/6 | 1/3 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jinwoo, L. Fluctuation Theorem of Information Exchange between Subsystems that Co-Evolve in Time. Symmetry 2019, 11, 433. https://doi.org/10.3390/sym11030433
Jinwoo L. Fluctuation Theorem of Information Exchange between Subsystems that Co-Evolve in Time. Symmetry. 2019; 11(3):433. https://doi.org/10.3390/sym11030433
Chicago/Turabian StyleJinwoo, Lee. 2019. "Fluctuation Theorem of Information Exchange between Subsystems that Co-Evolve in Time" Symmetry 11, no. 3: 433. https://doi.org/10.3390/sym11030433
APA StyleJinwoo, L. (2019). Fluctuation Theorem of Information Exchange between Subsystems that Co-Evolve in Time. Symmetry, 11(3), 433. https://doi.org/10.3390/sym11030433





