An Improved OTSU Algorithm Using Histogram Accumulation Moment for Ore Segmentation
Abstract
:1. Introduction
- (1)
- The object contrast in dark areas is improved and the shadow from stacked and adhesive ores is eliminated by using the multi-scale Retinex color restoration algorithm;
- (2)
- An improved OTSU algorithm is proposed. It reduces the error caused by image background and noise by calculating the gray-level zero-order and first-order cumulative moments closed to the selected area. The selected gray level gradually approaches the optimal threshold to avoid falling into the local optimum. This algorithm can be used in the segmentation of mineral images with unimodal or insignificant bimodal properties;
- (3)
- The validity and accuracy of the proposed algorithm is verified from the qualitative and quantitative analysis in multi-scenario ore image segmentation.
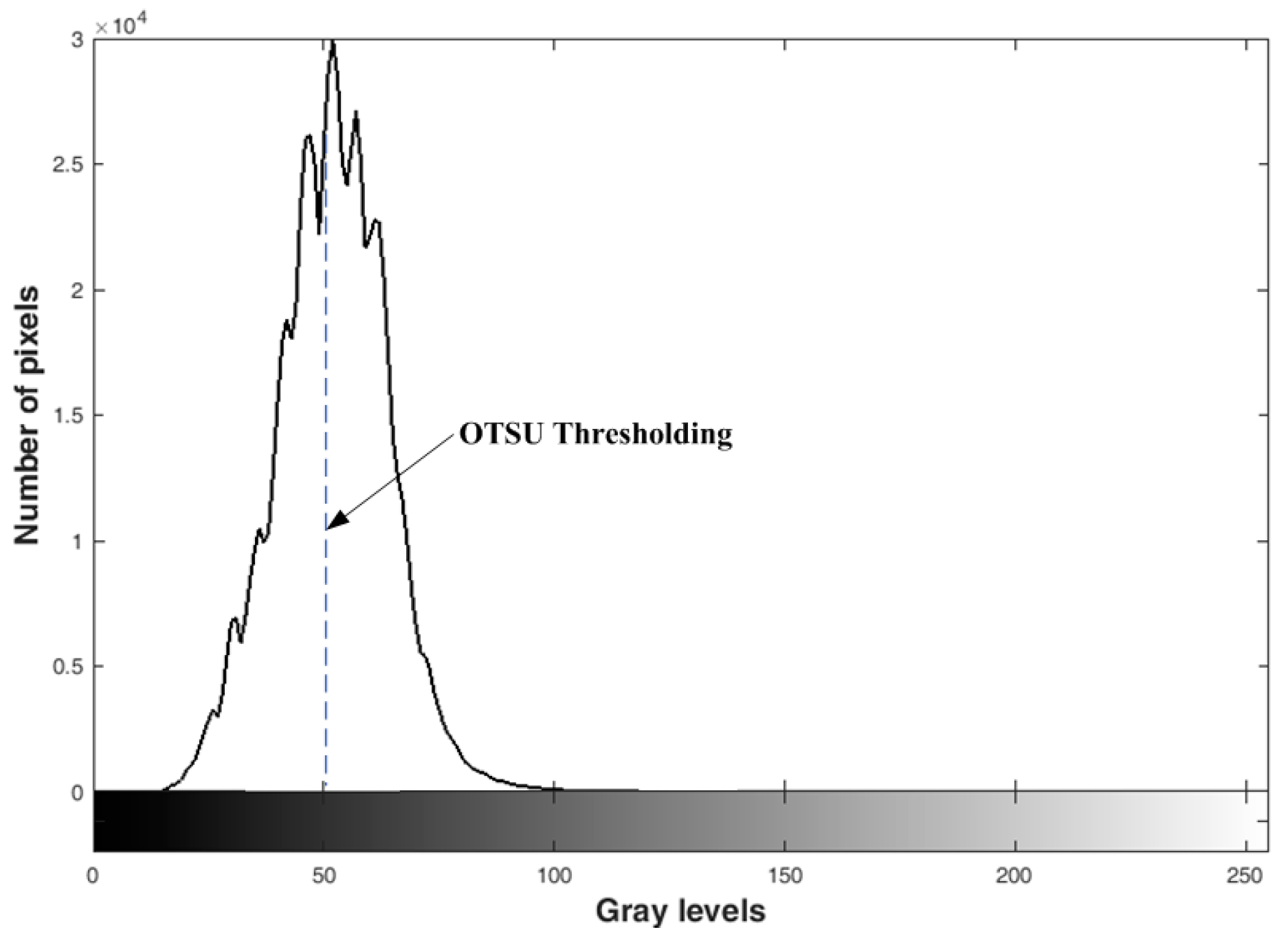
2. Problems of OTSU for Ore Segmentation
- (1)
- The ore image is affected by uneven illumination, dust and mud coverage. The noise is serious, the target edge is blurred and the contrast between the object and background is low;
- (2)
- The mineral is scattered, bulky and stacked. Due to the crushing, the ore particles with sharp edges, angular corners and complex internal texture are stacked and adhered;
- (3)
- The object and the background pixels in the image are cross-aliased, mostly resulting in unimodal or inconspicuous bimodal gray histogram distribution.
3. Improved Ore Image Segmentation Algorithm
3.1. Multiscale Retinex Color Restoration Algorithm
3.2. Improved OTSU Segmentation Based on Histogram Accumulation Moment
3.2.1. The Selection of Random Gray Value
3.2.2. Improvement of Zero-Order and First-Order Cumulative Moments
3.2.3. Selection of Optimal Threshold
3.2.4. Image Binarization
4. Experimental Results and Analysis
4.1. Qualitative Analysis
4.2. Quantitative Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, X. Beneficiation studies of tungsten ores—A review. Miner. Eng. 2018, 125, 111–119. [Google Scholar] [CrossRef]
- Leroy, S.; Pirard, E. Mineral recognition of single particles in ore slurry samples by means ofmultispectral image processing. Miner. Eng. 2019, 132, 228–237. [Google Scholar] [CrossRef]
- Charikinya, E.; Bradshaw, S.; Becker, M. Characterising and quantifying microwave induced damage in coarsesphalerite ore particles. Miner. Eng. 2015, 82, 14–24. [Google Scholar] [CrossRef]
- Pérez-Barnuevo, L.; Lévesque, S.; Bazin, C. Automated recognition of drill core textures: A geometallurgical tool formineral processing prediction. Miner. Eng. 2018, 118, 87–96. [Google Scholar] [CrossRef]
- Muter, D.; Pedersen, S.; Sorensen, H.O.; Feidenhans’l, R.; Stipp, S.L.S. Improved segmentation of X-ray tomography data from porous rocks usinga dual filtering approach. Comput. Geosci. 2012, 49, 131–139. [Google Scholar] [CrossRef]
- Chatterjee, S.; Bhattacherjee, A.; Samanta, B.; Pal, S.K. Image-based quality monitoring system of limestone ore grades. Comput. Ind. 2010, 61, 391–408. [Google Scholar] [CrossRef]
- Wang, Y.; McClung, C.; Lin, C.L.; Miller, J.D. Stereological correction of perimeter based estimates of exposed grainsurface area. Miner. Eng. 2018, 126, 64–73. [Google Scholar] [CrossRef]
- Kose, C.; Alp, I.; Ikibas, C. Statistical methods for segmentation and quantification of mineralsin ore microscopy. Miner. Eng. 2012, 30, 19–32. [Google Scholar] [CrossRef]
- Heydari, M.; Amirfattahi, R.; Nazari, B.; Rahimi, P. An industrial image processing-based approach for estimation of iron oregreen pellet size distribution. Powder Technol. 2016, 303, 260–268. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J.; Su, X.; Ding, L.; Wang, Y. Multi-scale image segmentation of coal piles on a belt based on theHessian matrix. Particuology 2013, 11, 549–555. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histogram. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Fan, H.; Xie, F.; Li, Y.; Jiang, Z.; Liu, J. Automatic segmentation of dermoscopy images using saliency combinedwith Otsu threshold. Comput. Biol. Med. 2017, 85, 75–85. [Google Scholar] [CrossRef]
- Goh, T.Y.; Basah, S.N.; Yazid, H.; Safar, M.J.A.; Saad, F.S.A. Performance analysis of image thresholding: Otsu technique. Measurement 2018, 114, 298–307. [Google Scholar] [CrossRef]
- Hua, J.; Qian, Z.; Wang, D.; Oeser, M. Influence of aggregate particles on mastic and air-voids in asphaltconcrete. Construct. Build. Mater. 2015, 93, 1–9. [Google Scholar] [CrossRef]
- Gajalakshmi, K.; Palanivel, S.; Nalini, N.J.; Saravanan, S.; Raghukandan, K. Grain size measurement in optical microstructure usingsupport vector regression. Optik 2017, 138, 320–327. [Google Scholar]
- Chi, D.L.; Song, E.; Gaudin, A.; Saltzman, W.M. Improved threshold selection for the determination of volume ofdistribution of nanoparticles administered by convection-enhanceddelivery. Comput. Med Imaging Graph. 2017, 62, 34–40. [Google Scholar] [CrossRef] [PubMed]
- Mahgoub, A.; Talab, A.; Huang, Z.; Xi, F.; HaiMing, L. Detection crack in image using Otsu method and multiple filtering in image processing techniques. Optik 2016, 127, 1030–1033. [Google Scholar]
- Malarvel, M.; Sethumadhavan, G.; Bhagi, P.C.R.; Kar, S.; Thangavel, S. An improved version of Otsu’s method for segmentation ofweld defects on X-radiography images. Optik 2017, 142, 109–118. [Google Scholar] [CrossRef]
- Yuan, X.; Wu, L.; Peng, Q. An improved Otsu method using the weighted object variance fordefect detection. Appl. Surf. Sci. 2015, 349, 472–484. [Google Scholar] [CrossRef]
- Azeroual, A.; Afdel, K. Fast Image Edge Detection based on Faber Schauder Wavelet and Otsu Threshold. Heliyon 2017, 3, e00485. [Google Scholar] [CrossRef]
- Harb, S.M.E.; Isa, N.A.M.; Salamah, S.A. Improved image magnification algorithm based on Otsu thresholding. Comput. Electr. Eng. 2015, 46, 338–355. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Liu, G.Z.; Zhu, H.; Qiu, B. Ore image thresholding using bi-neighbourhood Otsu’s approach. Electron. Lett. 2010, 46, 1666–1668. [Google Scholar] [CrossRef]
- Land, E.H.; McCann, J.J. Lightness and Retinex theory. J. Opt. Soc. Am. 1971, 61, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Dong, Q.; Pan, Z.; Zhang, W.; Duan, J.; Bai, L.; Zhang, J. Retinex theory based active contour model for segmentation of inhomogeneous images. Digit. Signal Process. 2016, 50, 43–50. [Google Scholar] [CrossRef]
- Jobson, D.J.; Rahman, Z.; Woodell, G.A. A multiscale retinex for bridging the gap between color images and the human observation of scenes. IEEE Trans. Image Process. 1997, 6, 965–976. [Google Scholar] [CrossRef]






| Data Set | OTSU | Double-Window OTSU | Our Method | |||
|---|---|---|---|---|---|---|
| Fnr | Fpr | Fnr | Fpr | Fnr | Fpr | |
| Coarse images | 0.259 | 0.057 | 0.386 | 0.063 | 0.015 | 0.008 |
| Middle image | 0.309 | 0.284 | 0.312 | 0.127 | 0.006 | 0.139 |
| Fine image | 0.587 | 0.343 | 0.363 | 0.455 | 0.285 | 0.298 |
| Detection Indicator | OTSU | Double-Window OTSU | Our Method |
|---|---|---|---|
| DR | 55.1% | 60.3% | 89.6% |
| FAR | 36.9% | 63.2% | 17.4% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, Y.; Zhang, G. An Improved OTSU Algorithm Using Histogram Accumulation Moment for Ore Segmentation. Symmetry 2019, 11, 431. https://doi.org/10.3390/sym11030431
Zhan Y, Zhang G. An Improved OTSU Algorithm Using Histogram Accumulation Moment for Ore Segmentation. Symmetry. 2019; 11(3):431. https://doi.org/10.3390/sym11030431
Chicago/Turabian StyleZhan, Yantong, and Guoying Zhang. 2019. "An Improved OTSU Algorithm Using Histogram Accumulation Moment for Ore Segmentation" Symmetry 11, no. 3: 431. https://doi.org/10.3390/sym11030431
APA StyleZhan, Y., & Zhang, G. (2019). An Improved OTSU Algorithm Using Histogram Accumulation Moment for Ore Segmentation. Symmetry, 11(3), 431. https://doi.org/10.3390/sym11030431




