A New GM(1,1) Model Based on Cubic Monotonicity-Preserving Interpolation Spline

Abstract

In the classical GM(1,1) model, an accumulated generating operation is made on the original non-negative sequence to obtain a monotone increasing 1-AGO sequence, and the forecasting model is established based on the 1-AGO sequence. A great number of scholars have improved the accuracy of grey model prediction through better developed background value and the equation for the time response. In this work, we reconstruct the background value based on a new developed monotonicity-preserving piecewise cubic interpolations spline, and thereby establish a new GM(1,1) model. Numerical examples show that the new GM(1,1) model has better prediction quality of data than the original GM(1,1) model and improves the precision of prediction in practice.

1. Introduction

Let an original non-negative and uniformly spaced sequence be

$$\begin{array}{c}\hfill X^{(0)}=\left\{x^{(0)}(1),x^{(0)}(2),\cdots ,x^{(0)}(n)\right\}.\end{array}$$

(1)

The main idea of the classical grey forecasting GM(1,1) model proposed by Deng [1,2] is to make an accumulated generating operation on the original sequence, so as to reduce the randomization of the original data and obtain an obviously monotone increasing 1-AGO sequence $X^{(1)}$. Then, establish a first-order grad forecasting differential equation on the sequence $X^{(1)}$. In addition, further use the least-square method to numerically solve the differential equation to estimate the parameters. Finally, the original data simulation and prediction are carried out by using the inverse accumulated generating operation.

The 1-AGO sequence $X^{(1)}$ is given as follows

$$\begin{array}{c}\hfill X^{(1)}=\left\{x^{(1)}(1),x^{(1)}(2),\cdots ,x^{(1)}(n)\right\},\end{array}$$

(2)

where

$$\begin{array}{c}\hfill x^{(1)}(k)=\sum _{i=0}^k{x}^{(0)}(k)=x^{(1)}(k-1)+x^{(0)}(k),k=1,2,\cdots ,n.\end{array}$$

(3)

From Equation (3), we can see that the 1-AGO sequence $X^{(1)}$ has the property of monotonicity-increasing. Suppose that $x^{(1)}(t)$ meets the following first-order grad forecasting differential equation

$$\begin{array}{c}\hfill \frac{d{x}^{(1)}(t)}{dt}+a{x}^{(1)}(t)=b,\end{array}$$

(4)

where the grey developmental coefficient a and the grey control parameter b are the parameters in the model to be estimated.

The solution of the Equation (4) with the initial condition ${\tilde{X}}^{(1)}(1)=X^{(1)}(1)$ is as follows

$$\begin{array}{c}\hfill x^{(1)}(t)=\left[x^{(1)}(1)-\frac{b}{a}\right]e^{-a(t-1)}+\frac{b}{a}.\end{array}$$

(5)

Therefore, to obtain the prediction model of the raw data sequence, we need to identify the effect of the grey development coefficient a and the grey control parameter b in Equation (4). For this purpose, we do the integral accumulation on both sides of Equation (4) for $\left[k,k+1\right],k=1,2,\cdots ,n-1$, then we can get

$$\begin{array}{c}\hfill {\int }_k^{k+1}\frac{d{x}^{(1)}(t)}{dt}dt+a{\int }_k^{k+1}{x}^{(1)}(t)dt=b,\end{array}$$

that is

$$\begin{array}{c}\hfill x^{(1)}(k+1)-x^{(1)}(k)+a{\int }_k^{k+1}{x}^{(1)}(t)dt=b,\end{array}$$

or

$$\begin{array}{c}\hfill x^{(0)}(k+1)+a{\int }_k^{k+1}{x}^{(1)}(t)dt=b.\end{array}$$

(6)

Let background value be $z^{(1)}(k+1):={\int }_k^{k+1}{x}^{(1)}(t)dt$. To calculate the background value $z^{(1)}(k+1)$, we need to integrate $x^{(1)}(t)$, which requires the values of a and b to be given in advance. However, the values of a and b need to be determined from the Equation (6). Consequently, to estimate the values of a and b, we must use some methods to estimate the background value $z^{(1)}(k+1)$. We use the piecewise linear polynomial interpolation $L(t):=\left(k+1-t\right)x^{(1)}(k)+\left(t-k\right)x^{(1)}(k+1)$ to approximate $x^{(1)}(t)$ in the classical GM(1,1) model, see [1,2], then we get the estimated background value $z^{(1)}(k+1)$ as follows

$$\begin{array}{cc}\hfill z^{(1)}(k+1)& ={\int }_k^{k+1}{x}^{(1)}(t)dt\hfill \\ & \approx {\int }_k^{k+1}L(t)dt\hfill \\ & =\frac{1}{2}\left[x^{(1)}(k)+x^{(1)}(k+1)\right].\hfill \end{array}$$

(7)

For each interval $[k,k+1]$, $k=1,2,\cdots ,n-1$, by substituting the estimated background value $z^{(1)}(k+1)$ into Equation (6) and further applying the least-square method, we estimate the values of the parameters a and b by the formula as follows

$$\begin{array}{c}\hfill \left(\begin{array}{c}a\\ b\end{array}\right)={\left(G^{T}G\right)}^{-1}{G}^{T}X,\end{array}$$

where

$$X=\left[\begin{array}{c}{x}^0(2)\\ x^0(3)\\ ⋮\\ x^0(n)\end{array}\right],G=\left(\begin{array}{cc}-z^{(1)}(2)& 1\\ -z^{(1)}(3)& 1\\ ⋮& ⋮\\ -z^{(1)}(n)& 1\end{array}\right).$$

Finally, we get the following estimated solution to the differential Equation (4) with the initial condition ${\tilde{X}}^{(1)}(1)=X^{(1)}(1)$ as follows

$$\begin{array}{c}\hfill {\tilde{x}}^{(1)}(t)=\left[x^{(1)}(1)-\frac{b}{a}\right]e^{-a\left(t-1\right)}+\frac{b}{a},k=1,2,\dots .\end{array}$$

(8)

We thus get the following grey prediction equation

$$\begin{array}{cc}\hfill {\tilde{x}}^{(0)}(k+1)& ={\tilde{x}}^{(1)}(k+1)-{\tilde{x}}^{(1)}(k),k=1,2,\dots .\hfill \end{array}$$

(9)

From (7), it can be found that the classical GM(1,1) model uses average of adjacent values to estimate the background value $z^{(1)}(k+1)$. Its geometric meaning is to use the area of straight ladder to replace the trapezoidal area which is based on the edge of exponential curve $x^{(1)}(t)$, as shown in Figure 1. This method has a shortcoming that when the 1-AGO data sequence varies greatly, the result of prediction will have large error ($\Delta \mathrm{S}$) with the exponential increasing. Thus, if we apply the classical GM(1,1) model in practice, there exist some restrictions. As pointed out in [3,4,5], the accuracy of prediction in GM(1,1) model depends on the estimation of the background value $z^{(1)}(k+1)$. In [6], Li and Dai reconstructed $x^{(1)}(t)$ by a high-order Newton interpolation polynomial. In addition, they estimated the background value $z^{(1)}(k+1)$ based on the Newton-Cores integral. However, as shown in [6], when there is a mass of data, the high-order Newton interpolation polynomial may have the Runge phenomenon and thus the truncation error may be very large. Furthermore, the numerical stability is not guaranteed when calculating the approximate value of Newton-Cores integral. In [7], Tang and Xiang estimated the background value $z^{(1)}(k+1)$ by using the piecewise quadratic interpolation polynomial to reconstruct $x^{(1)}(t)$ on the interval $[k,k+1]$. The advantage is that it has the characteristics of less computation and good numerical stability. In [8], Wang et al. used piecewise cubic interpolation spline to reconstruct $x^{(1)}(t)$ and thus got the estimated background value $z^{(1)}(k+1)$. The advantages of the given method are that it can avoid the Runge phenomenon resulted from high-order polynomial. However, the methods we mentioned above all ignore the important monotonicity-increasing feature of the curve $x^{(1)}(t)$ to be reconstructed. If the resulting reconstructed curve $x^{(1)}(t)$ loses the monotonicity-increasing feature, there will also result in a large error on the background value $z^{(1)}(k+1)$. Therefore, an accurate approximation of the reconstructed curve $x^{(1)}(t)$ is the key to enhance the estimation of the background value.

Figure 1. Prediction error source diagram of conventional GM(1,1) model.

Recently, lots of scholars proposed many methods to improve the classical GM(1,1) model. Liu and his colleagues have proposed some new methods of grey development clustering based on the multiattribute difference, which enriches the grey fixed-weight cluster theory, see [9,10,11] for example. In [12,13,14], Xie and his colleagues proposed some new grey models, including Verhulst model and the segmental corrected new information discrete GM(1,1) model. In [15], Yang and his colleagues presented a dynamic GM(1,1) model based on grey system theory and cubic spline function interpolation principle. Many scholars have put many efforts on the establishments of new grey prediction models, see for example [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31] and the references therein.

In this paper, we shall propose a monotonicity-preserving piecewise cubic interpolation spline to reconstruct the curve $x^{(1)}(t)$ and thereby give a new scheme to estimate the background value $z^{(1)}(k+1)$. The rest of this paper is structured as follows. Section 2 represents the construction of the $C^1$ monotonicity-preserving cubic interpolation splines. In Section 3, based on $C^1$ monotonicity-preserving cubic interpolation spline, a new GM(1,1) model is constructed in detail. Several numerical examples are also given. In addition, the conclusion is given in Section 4.

2. ${\mathit{C}}^{\mathbf{1}}$ Monotonicity-Preserving Piecewise Cubic Interpolation Spline

According to Equation (3), the 1-AGO sequence $X^{(1)}$ has the property of monotonicity-increasing, that is $x^{(1)}(k)\le x^{(1)}(k+1)$, $\forall k$. The fitting exponential curve $x^{(1)}(t)$ to the 1-AGO sequence $X^{(1)}$ is also monotonicity-increasing and has infinite smoothness. Therefore, we develop a $C^1$ monotonic-preserving cubic interpolation spline to interpolate the 1-AGO sequence, to reconstruct the curve $x^{(1)}(t)$.

For the discrete data $\left(k,x^{(1)}(k)\right),k=1,2,\dots ,n$, we denote $d^{(1)}\left(k\right)$ as the derivative value at node $t=k$. For $t\in \left[k,k+1\right]$, a cubic interpolation spline with local parameter ${\alpha }_k$ is constructed as follows

$$\begin{array}{cc}\hfill B(\mathrm{t})& ={\left(1-s\right)}^3{x}^{(1)}(k)+3{\left(1-s\right)}^{2}s\left[x^{(1)}(k)+\frac{d^{(1)}\left(k\right)}{{\alpha }_k}\right]\hfill \\ & +3\left(1-s\right)s^2\left[x^{(1)}(k+1)-\frac{d^{(1)}\left(k+1\right)}{{\alpha }_{k+1}}\right]+s^3{x}^{(1)}(k+1),\hfill \end{array}$$

(10)

where $s=t-k\in \left[0,1\right]$. From Equation (10), after some computations, we have

$$\left\{\begin{array}{c}B(k)=x^{(1)}\left(k\right),B(k+1)=x^{(1)}\left(k+1\right),\hfill \\ B^{\prime }(k)=\frac{3d^{(1)}\left(k\right)}{{\alpha }_k},B^{\prime }(k+1)=\frac{3d^{(1)}\left(k+1\right)}{{\alpha }_{k+1}},\hfill \end{array}\right.$$

(11)

which indicates that $B\left(k^{-}\right)=B\left(k^{+}\right),B^{\prime }\left(k^{-}\right)=B^{\prime }\left(k^{+}\right)$. This means that the cubic interpolation spline defined by Equation (10) is $C^1$ continuous for arbitrary nonzero local parameter. Here, $C^1$ continuity means that a function together with its first-order derivative function is continuous. In addition, it is of interest to note that for all ${\alpha }_k=3$, the cubic interpolation spline given in Equation (10) returns into the classic cubic Hermite interpolation spline.

In practical application, we should estimate the derivative values of the cubic interpolation spline at the nodes at first. In this paper, we calculate the derivative values by the following method

$$\left\{\begin{array}{c}{d}^{(1)}\left(1\right)=x^{(1)}\left(2\right)-x^{(1)}\left(1\right),\hfill \\ d^{(1)}\left(k\right)=\frac{1}{2}\left[x^{(1)}\left(k+1\right)-x^{(1)}\left(k-1\right)\right],k=2,3,\dots ,n-1,\hfill \\ d^{(1)}\left(n\right)=x^{(1)}\left(n\right)-x^{(1)}\left(n-1\right).\hfill \end{array}\right.$$

(12)

We shall derive sufficient conditions for the $C^1$ cubic interpolation spline preserving monotonicity. For the monotonicity-increasing 1-AGO sequence $X^{(1)}$, it is obvious that the derivative value determined by Equation (12) is non-negative, which means $d^{(1)}\left(k\right)\ge 0,\forall k$. Without loss of generality, for $t\in \left[k,k+1\right]$, direct computation gives that

$$\begin{array}{cc}\hfill B^{\prime }(t)& =3{\left(1-s\right)}^2\frac{d^{(1)}\left(k\right)}{{\alpha }_k}+s^2\frac{d^{(1)}\left(k+1\right)}{{\alpha }_{k+1}}\hfill \\ & +6\left(1-s\right)s\left\{\left[x^{(1)}\left(k+1\right)-x^{(1)}\left(k\right)\right]-\left[\frac{d^{(1)}\left(k\right)}{{\alpha }_k}+\frac{d^{(1)}\left(k+1\right)}{{\alpha }_{k+1}}\right]\right\}.\hfill \end{array}$$

Thus, we can see that the following conditions are sufficient to guarantee $R^{\prime }(t)\ge 0$

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\alpha }_k>0,{\alpha }_{k+1}>0,\hfill \\ \left[x^{(1)}\left(k+1\right)-x^{(1)}\left(k\right)\right]-\left[\frac{d^{(1)}\left(k\right)}{{\alpha }_k}+\frac{d^{(1)}\left(k+1\right)}{{\alpha }_{k+1}}\right]\hfill \\ =\left[\frac{x^{(1)}\left(k+1\right)-x^{(1)}\left(k\right)}{2}-\frac{d^{(1)}\left(k\right)}{{\alpha }_k}\right]+\left[\frac{x^{(1)}\left(k+1\right)-x^{(1)}\left(k\right)}{2}-\frac{d^{(1)}\left(k+1\right)}{{\alpha }_{k+1}}\right]\ge 0.\hfill \end{array}\right.\end{array}$$

(13)

Summarizing the above discussion, we can obtain the following sufficient conditions for $B(t)$ preserving monotonicity

$$\left\{\begin{array}{c}{\alpha }_1=max\left\{0,\frac{2d^{(1)}\left(1\right)}{x^{(1)}\left(2\right)-x^{(1)}\left(1\right)}\right\}+a_1,\hfill \\ {\alpha }_k=max\left\{0,\frac{2d^{(1)}\left(k\right)}{x^{(1)}\left(k+1\right)-x^{(1)}\left(k\right)},\frac{2d^{(1)}\left(k\right)}{x^{(1)}\left(k\right)-x^{(1)}\left(k-1\right)}\right\}+a_k,k=2,\dots ,n-1,\hfill \\ {\alpha }_n=max\left\{0,\frac{2d^{(1)}\left(n\right)}{x^{(1)}\left(n\right)-x^{(1)}\left(n-1\right)}\right\}+a_n,\hfill \end{array}\right.$$

(14)

where $a_i>0$ serves as free parameter. In practice, we recommend all $a_k=3$. If there is no special explanation below, we will take all $a_k=3$.

3. Establish New GM(1,1) Model

For the original non-negative sequence $X^{(0)}=\left\{x^{(0)}(1),x^{(0)}(2),\cdots ,x^{(0)}(n)\right\}$, we first calculate its 1-AGO sequence $X^{(1)}=\left\{x^{(1)}(1),x^{(1)}(2),\cdots ,x^{(1)}(n)\right\}$. Then for the 1-AGO sequence $X^{(1)}$, we use the sufficient conditions (14) with all the free parameters $a_k=3$ to determine a $C^1$ monotonicity-preserving piecewise cubic interpolation spline $B(t)$ to reconstruct the exponential curve $x^{(1)}(t)$. For the interval $\left[k,k+1\right]$, we estimate the background value $z^{(1)}\left(k+1\right)={\int }_k^{k+1}{x}^{(1)}\left(t\right)dt$ by the following method

$$\begin{array}{cc}\hfill z^{(1)}\left(k+1\right)& ={\int }_k^{k+1}{x}^{(1)}\left(t\right)dt\hfill \\ & \approx {\int }_k^{k+1}B\left(t\right)dt\hfill \\ & =\frac{1}{4}{x}^{(1)}(k)+\frac{1}{4}\left[x^{(1)}(k)+\frac{d^{(1)}\left(k\right)}{{\alpha }_k}\right]\hfill \\ & +\frac{1}{4}\left[x^{(1)}(k+1)-\frac{d^{(1)}\left(k+1\right)}{{\alpha }_{k+1}}\right]+\frac{1}{4}{x}^{(1)}(k+1).\hfill \end{array}$$

Then by substituting the estimated background value into the grey differential Equation (6), we further apply the following least-square method to solve Equation (6)

$$\left(\begin{array}{c}a\\ b\end{array}\right)={\left(G^{T}G\right)}^{-1}{G}^{T}X,$$

where

$$X=\left[\begin{array}{c}{x}^0(2)\\ x^0(3)\\ ⋮\\ x^0(n)\end{array}\right],G=\left(\begin{array}{cc}-z^{(1)}(2)& 1\\ -z^{(1)}(3)& 1\\ ⋮& ⋮\\ -z^{(1)}(n)& 1\end{array}\right).$$

Finally, we get the following estimated solution to the differential Equation (4) with the initial condition ${\tilde{X}}^{(1)}(1)=X^{(1)}(1)$ as follows

$${\tilde{x}}^{(1)}(t)=\left[x^{(1)}(1)-\frac{b}{a}\right]e^{-a\left(t-1\right)}+\frac{b}{a}.$$

We thus get the following grey prediction equation

$$\begin{array}{cc}\hfill {\tilde{x}}^{(0)}(k+1)& ={\tilde{x}}^{(1)}(k+1)-{\tilde{x}}^{(1)}(k)\hfill \\ & =\left(1-e^a\right)\left[x^{(1)}(1)-\frac{b}{a}\right]e^{-ak},k=1,2,\dots .\hfill \end{array}$$

(15)

We shall give several examples to show that the new GM(1,1) model based on $C^1$ monotonicity-preserving piecewise cubic interpolation spline has better predict accuracy than the classical GM(1,1) model. In the following examples, the relative error is computed by

$$\begin{array}{c}\hfill \epsilon =\frac{\left|{\overline{x}}^{(0)}(k)-x^{(0)}(k)\right|}{x^{(0)}(k)}.\end{array}$$

Example 1.

In this example, we use the exponential function $f(t)=\eta e^{\lambda t}$ in [20] to generate the original data with convexity. By letting the parameters g and k take a fixed value respectively, the original data sequence can be obtained when the parameter t takes different values. In addition, we compare the results predicted by our new GM(1,1) model with the GM(1,1) model and the method proposed in [20]. The results show that our new model achieves the best results among the three prediction models and it performs very well in predicting data with the exponential growth trend, see Table 1. On the left of Figure 2, the figure shows the 1-AGO data of Table 1 and the curves of piecewise linear interpolant, monotonic-preserving cubic interpolation spline $B(t)$ and the reconstruct exponential curve $X^{(1)}(t)$. From the right Figure 2, we can see that the interpolation spline $B(t)$ has $C^1$ continuity.

Table 1. Numerical results for Example 1.

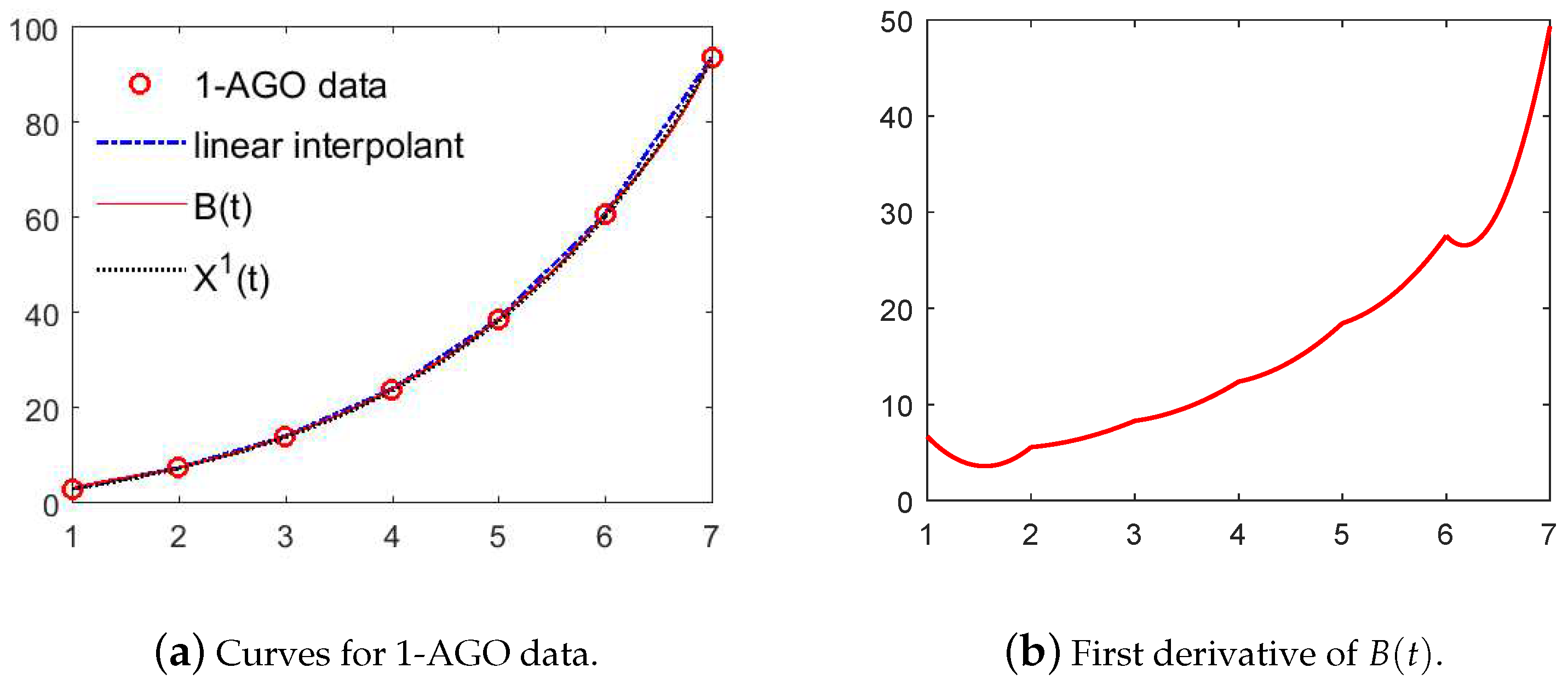
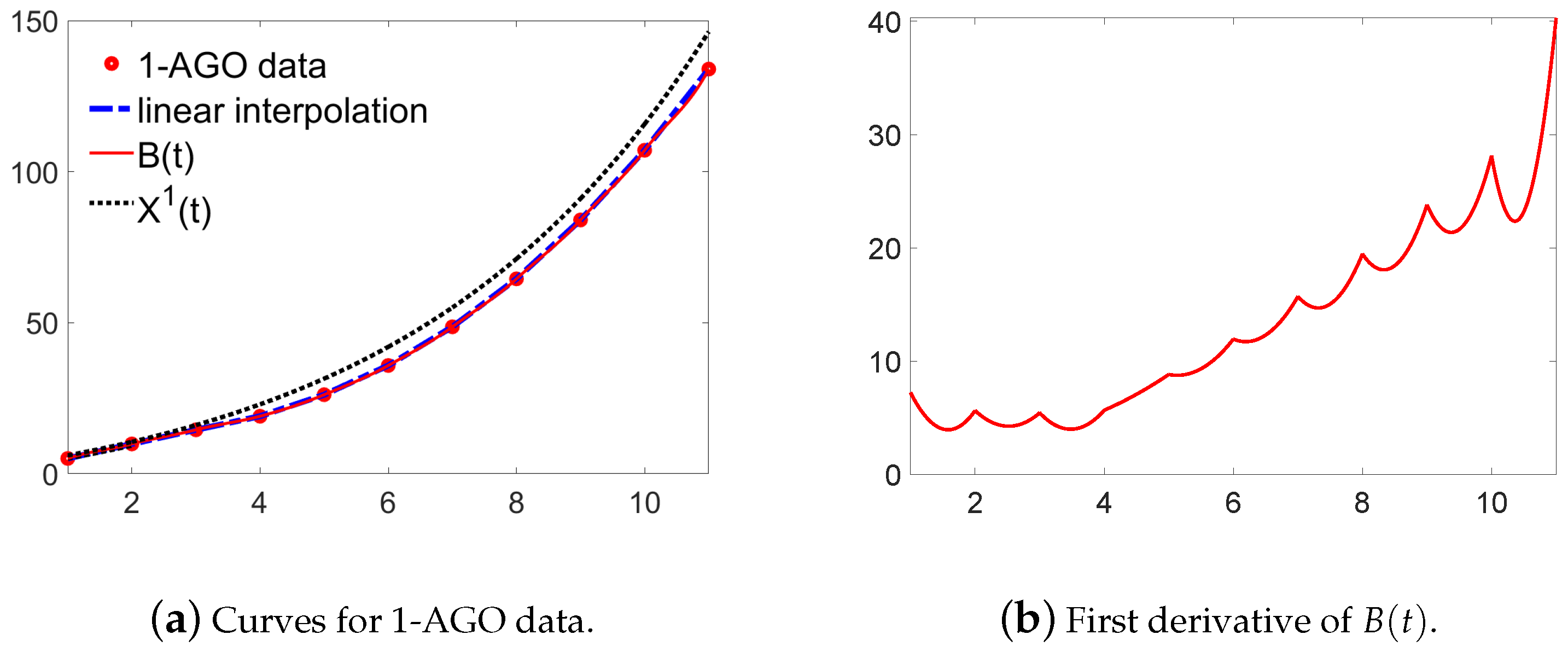
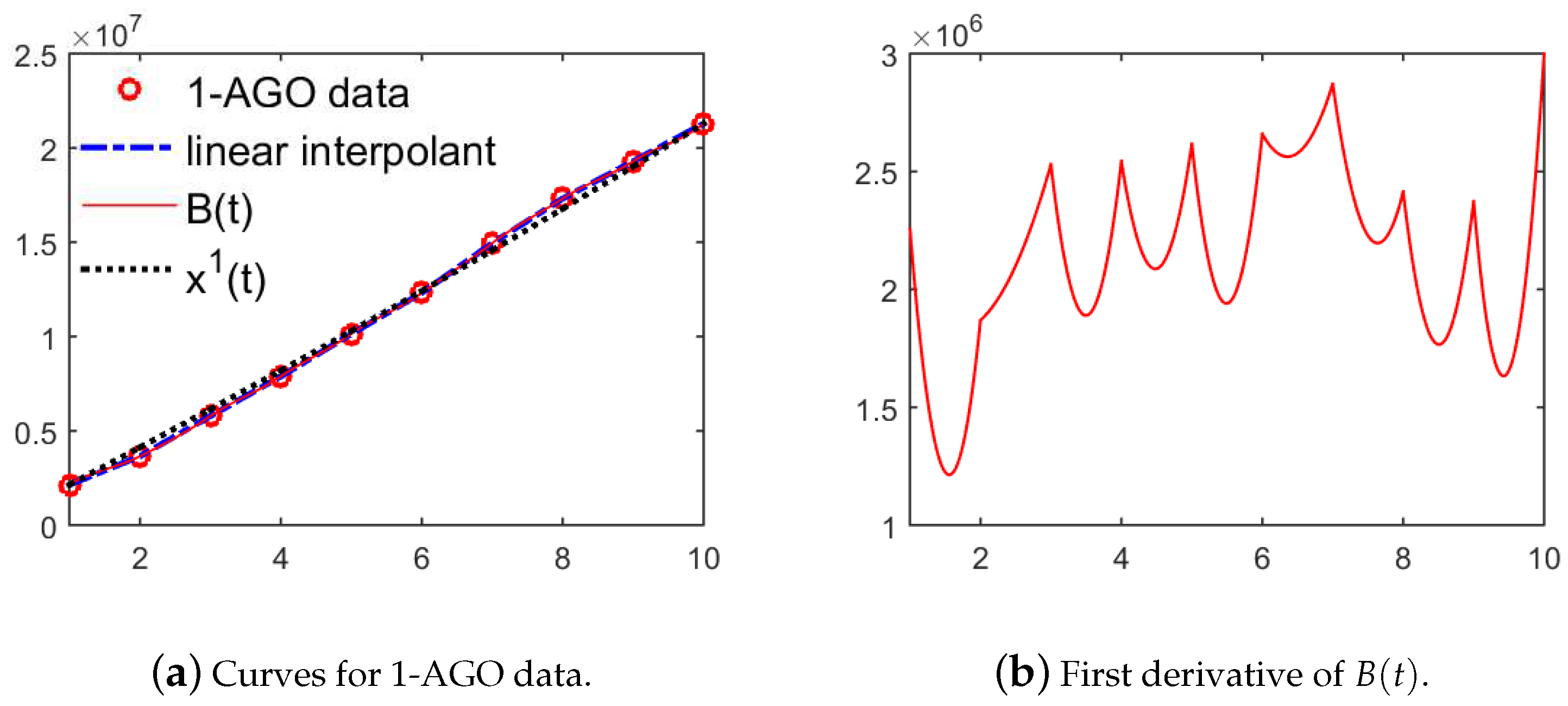
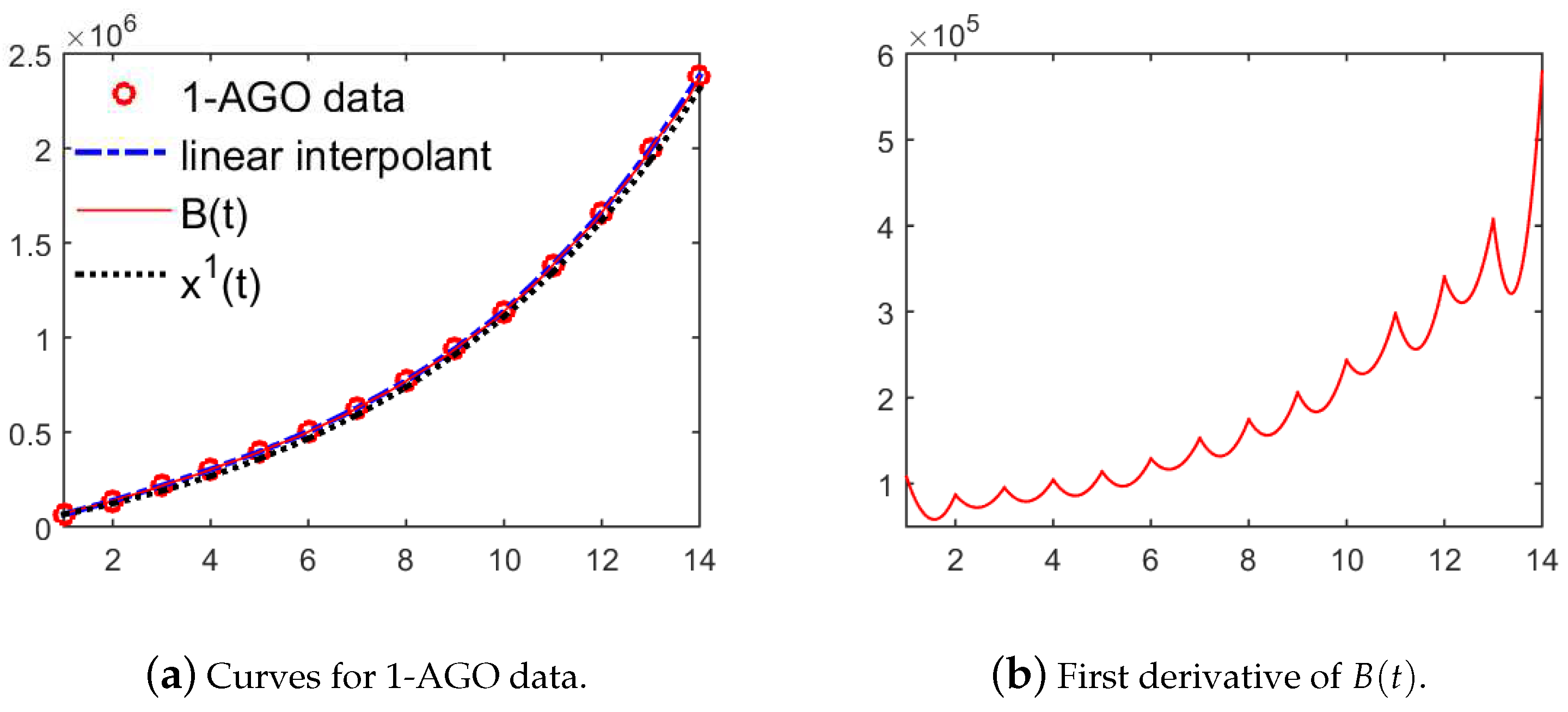
${\mathit{x}}^{(0)}$	Classical GM(1,1)		New GM(1,1)		The Model in [20]
	Prediction Data	$\mathit{\epsilon }$ (%)	Prediction Data	$\mathit{\epsilon }$ (%)	Prediction Data	$\mathit{\epsilon }$ (%)
2.9836	2.9836	0	2.9836	0	2.9836	0
4.4511	4.3804	1.5816	4.3531	2.2021	4.4561	0.1123
6.6402	6.5006	2.0903	6.5222	1.7835	6.6132	0.4066
9.9061	9.6469	2.5994	9.7720	1.3569	9.8146	0.9237
14.7781	14.3162	3.1039	14.6413	0.9344	14.5657	1.4373
22.0464	21.2454	3.6069	21.9368	0.5013	21.6168	1.9486
32.8893	31.5285	4.1065	32.8675	0.0793	32.0812	2.4570
$\overline{\epsilon }$ (%)		2.8481		1.1429		1.2143

Figure 2. Graphic results for Example 1.

Example 2.

In this example, we directly use the numerical example provided in [21]. We compare our new GM(1,1) model with the classical GM(1,1) model and the prediction models presented in [21]. The results turn out that our new GM(1,1) model prediction accuracy is significantly higher than the classical GM(1,1)model. While the method proposed in [21] performs the best in this example. The reason we suppose is that the method given in [21] simulates and predicts the sequence of exponential distribution by optimizing the background value of the grey differential equations, so that the model has better simulation and prediction accuracy. Table 2 and Figure 3 give the numerical results.

Table 2. Numerical results for Example 2.

${\mathit{x}}^{(0)}$	Classical GM(1,1)		New GM(1,1)		The Model in [21]
	Prediction Data	$\mathit{\epsilon }$ (%)	Prediction Data	$\mathit{\epsilon }$ (%)	Prediction Data	$\mathit{\epsilon }$ (%)
21.1	21.1	0	21.1	0	21.1000	0
26.6	24.4166	8.2083	24.0779	9.4816	23.3606	12.1782
36.1	35.7198	1.0531	32.5648	9.7928	35.7858	0.8704
52.3	52.2557	0.0847	50.3116	3.8018	54.8198	4.8180
80.1	76.4466	4.5611	77.7300	2.9588	83.9777	4.8411
126.8	111.8361	11.8012	120.0906	5.2913	128.6443	1.4545
196.3	163.6087	16.6537	185.5365	5.4832	197.0684	0.3914
$\overline{\epsilon }$ (%)		7.0604		6.1349		4.0923

Figure 3. Graphic results for Example 2.

Example 3.

In this example, we use the example in [8] to test the new proposed GM(1,1) model. To verify the applicability of the model to predict electricity consumption in the smart grid, we use the electricity consumption data of Jiangsu province in 2008 into the smart grid as the raw data (in KWh). The results show that the new GM(1,1) has improved prediction accuracy compared to the methods proposed in [7] and the classical GM(1,1) model. Table 3 and Figure 4 give the numerical results.

Table 3. Numerical results for Example 3.

${\mathit{x}}^{(0)}$	Classical GM(1,1)		New GM(1,1)		The Model in [7]
	Prediction Data	$\mathit{\epsilon }$ (%)	Prediction Data	$\mathit{\epsilon }$ (%)	Prediction Data	$\mathit{\epsilon }$ (%)
110,852	110,852	0	110,852	0	110,852	0
135,175	117,980	12.72	130,078	3.77	127,821	5.41
153,647	119,117	22.47	128,574	16.32	126,664	17.66
120,296	128,264	6.62	127,087	5.64	125,830	4.68
96,362	121,422	26.27	125,617	30.36	124,380	29.23
90,798	122,592	35.01	124,164	36.75	123,253	35.70
102,591	123,773	20.65	122,728	19.63	122,137	19.11
150,534	124,965	16.99	121,308	19.41	121,031	19.63
175,123	126,168	27.95	119,905	31.53	119,934	31.52
127,148	113,383	10.83	118,518	6.79	114,848	9.76
102,085	128,610	25.98	117,147	14.75	117,772	15.47
97,103	116,705	20.19	115,792	19.25	116,705	20.21
$\overline{\epsilon }$ (%)		21.73		18.56		18.91

Figure 4. Graphic results for Example 3.

Example 4.

In this example, we select the grey prediction data from [9]. This set of data is based on Chinese health statistics of people with syphilis (in millions) from 2000 to 2010. We compare the new GM(1,1) model with the classical GM(1,1) model and the model in [9]. From Table 4, we can see that our new GM(1,1) model prediction accuracy is improved compared to the classical GM(1,1) model and the model in [9]. Figure 5 gives the graphic results of this example.

Table 4. Numerical results for Example 4.

${\mathit{x}}^{(0)}$	Classical GM(1,1)		New GM(1,1)		The Model in [9]
	Prediction Data	$\mathit{\epsilon }$ (%)	Prediction Data	$\mathit{\epsilon }$ (%)	Prediction Data	$\mathit{\epsilon }$ (%)
5.08	5.08	0	5.08	0	5.08	0
4.80	3.55	26.04	4.24	11.51	3.65	23.9
4.67	4.52	3.21	5.25	12.57	4.61	1.28
4.50	5.76	28.00	5.51	22.44	5.84	29.78
7.12	7.34	3.09	8.05	13.09	7.42	4.21
9.67	9.34	3.41	9.97	3.05	9.45	2.28
12.80	11.90	7.03	12.33	3.64	12.04	5.94
15.88	15.15	4.59	15.26	3.88	15.37	3.21
19.49	19.30	0.97	18.89	3.07	19.65	0.82
23.07	24.57	6.50	23.38	1.34	24.57	8.92
26.86	31.29	16.49	28.93	7.72	31.29	19.73
$\overline{\epsilon }$ (%)		9.03		7.48		8.29

Figure 5. Graphic results for Example 4.

Example 5.

In [11], the data selected by the authors to show a downward trend is very representative, so we use this data sequence in this example. The results show that our new GM(1,1) model is still applicable to the descending sequence, and the accuracy is still slightly improved compared to the classical GM(1,1) model. While the method proposed in [11] performs the best in this example. The reason we suppose is that the method given in [11] simulates and predicts the sequence of exponential distribution by optimizing the background value of the grey differential equations, so that the model has better simulation and prediction accuracy. Table 5 and Figure 6 give the numerical results.

Table 5. Numerical results for Example 5.

${\mathit{x}}^{(0)}$	Classical GM(1,1)		New GM(1,1)		The Model in [11]
	Prediction Data	$\mathit{\epsilon }$ (%)	Prediction Data	$\mathit{\epsilon }$ (%)	Prediction Data	$\mathit{\epsilon }$ (%)
1610.71	1610.71	0	1610.71	0	1610.71	0
1245.28	1363.91	9.524	1365.22	9.632	1342.76	7.833
1347.71	1274.95	5.402	1275.75	5.340	1280.32	5.004
1382.45	1191.79	13.795	1192.14	13.766	1204.58	12.872
1018.45	1114.06	9.381	1114.01	9.383	1122.64	10.203
1014.96	1041.39	2.597	1041.00	2.566	1040.18	2.476
949.46	973.47	2.519	972.78	2.456	960.34	1.147
$\overline{\epsilon }$ (%)		6.174		6.163		5.648

Figure 6. Graphic results for Example 5.

Example 6.

In this example, we selected the relevant data from the 2012 China Statistical Yearbook in [24] to analysis of whether our GM(1,1) model can effectively predict general statistics. Thus, we only compare the prediction results of the classical GM(1,1) model with our new GM(1,1) model. The results show that our new GM(1,1) model applies to general sociological statistics, and our model performs better accuracy of prediction compared to classical GM(1,1) model. This shows that our new GM(1,1) model has the ability for further promotion and development. Table 6 and Figure 7 give the numerical results.

Table 6. Numerical results for Example 6.

${\mathit{x}}^{(0)}$	Classical GM(1,1)		New GM(1,1)
	Prediction Data	$\mathit{\epsilon }$ (%)	Prediction Data	$\mathit{\epsilon }$ (%)
64,832.05	64,832.05	0	64,832.05	0
71,847.09	57,476.77	20.001	57,308.50	20.235
78,646.30	67,165.21	14.598	67,022.83	14.779
86,293.10	78,486.76	9.046	78,383.83	9.166
93,887.95	91,716.70	2.312	91,670.62	2.362
105,557.09	107,176.71	1.534	107,209.65	1.566
125,761.85	125,242.71	0.413	125,382.70	0.301
143,143.63	146,353.96	2.243	146,636.24	2.440
168,850.20	171,023.78	1.287	171,492.46	1.565
198,739.27	199,852.01	0.560	200,562.04	0.917
245,352.80	233,539.60	4.815	234,559.18	4.400
278,541.09	272,905.57	2.023	274,319.16	1.516
334,839.41	318,907.39	4.758	320,818.83	4.187
386,086.72	372,663.28	3.477	375,200.63	2.820
$\overline{\epsilon }$ (%)		4.791		4.732

Figure 7. Graphic results for Example 6.

According to the results of the above numerical examples 1–6, the prediction accuracy of our new GM(1,1) model is improved for all the numerical examples compared to classical GM(1,1) model. In addition, our new model performs better than the methods proposed in [7,9,20]. There are different degrees of improvement for different data features. Based on the above data characteristics, we make the conclusion that the data applicable to our new GM(1, 1) model are generally with the continuously increasing feature over time. In particular, the exponential growth data can show better prediction.

4. Conclusions

By using a new developed $C^1$ monotonicity-preserving piecewise cubic interpolation spline to reconstruct the background value, we have established a new GM(1,1) model. Numerical examples show that the new GM(1,1) model can improve the forecasting quality, especially in prediction reliability and this model performs better when the original data are presented with convexity in time series. Future work will concentrate on exploring more applications of the new GM(1,1) model, such as scientific decision-making in electricity production and manufactures.