Exploiting the Symmetry of Integral Transforms for Featuring Anuran Calls
Abstract
1. Introduction
2. Materials and Methods
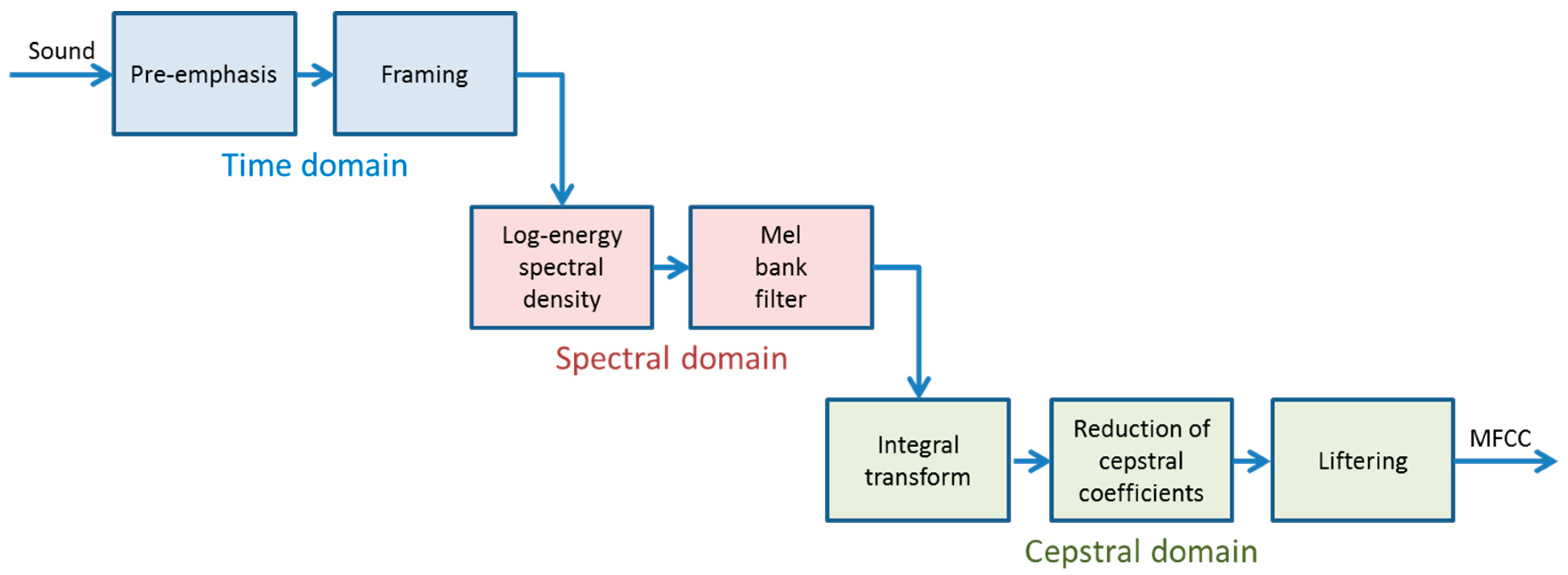
2.1. Extracting MFCC
- Pre-emphasis (time domain): The sound’s high frequencies are increased to compensate for the fact that the Signal-to-Noise Ratio (SNR) is usually lower at these frequencies.
- Framing (time domain): The samples of the full-length sound segment are split into frames of short duration ( samples, ). These frames are commonly obtained using non-rectangular overlapping windows (for instance, Hamming windows [40]). The subsequent steps are executed on the samples of each frame.
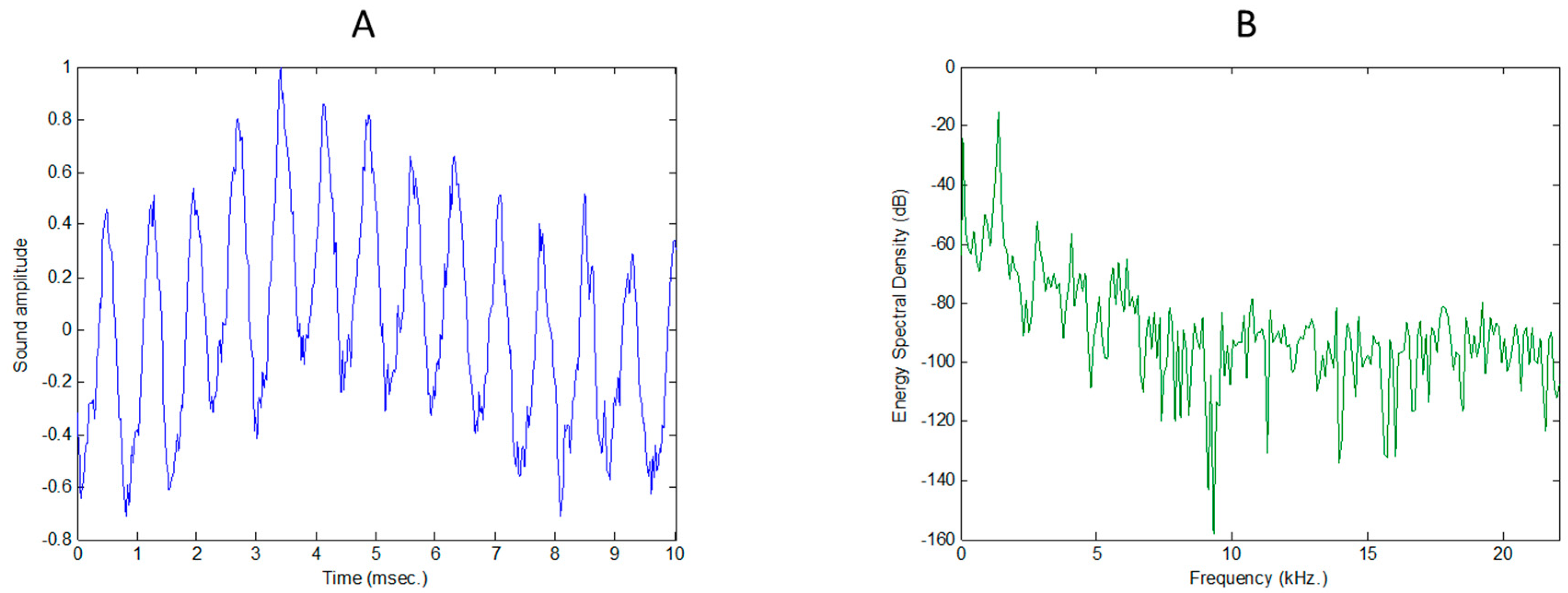
- Log-energy spectral density (spectral domain): Using the Discrete Fourier Transform (DFT) or its faster version, the Fast Fourier Transform (FFT), the samples of each frame are converted into the samples of an energy spectral density, which are usually represented in a log-scale.
- Mel bank filtering (spectral domain): The samples of each frame’s spectrum are grouped into banks of frequencies, using triangular filters centred according to the mel scale [41] and the mel Filter Bank Energy (mel-FBE) is obtained.
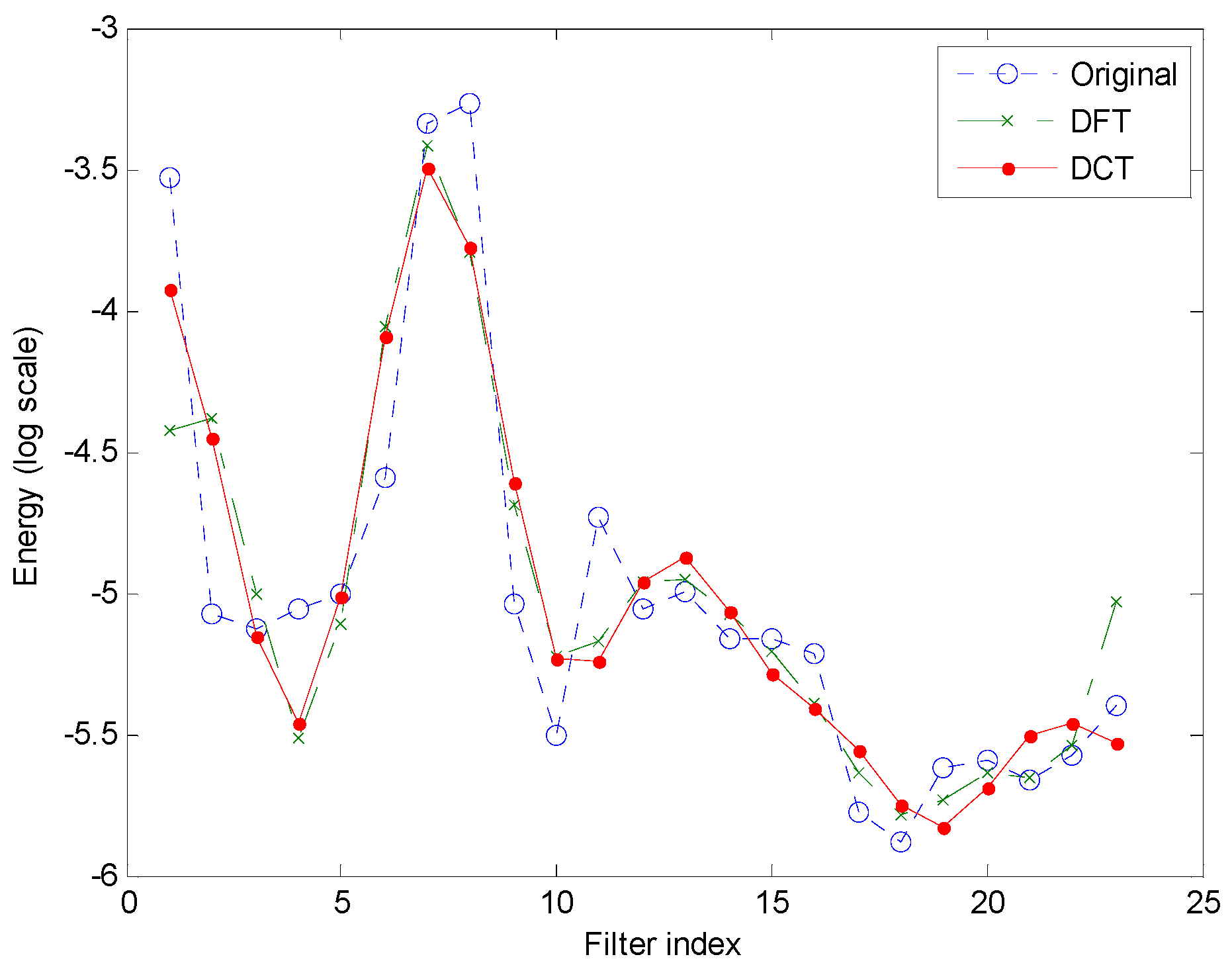
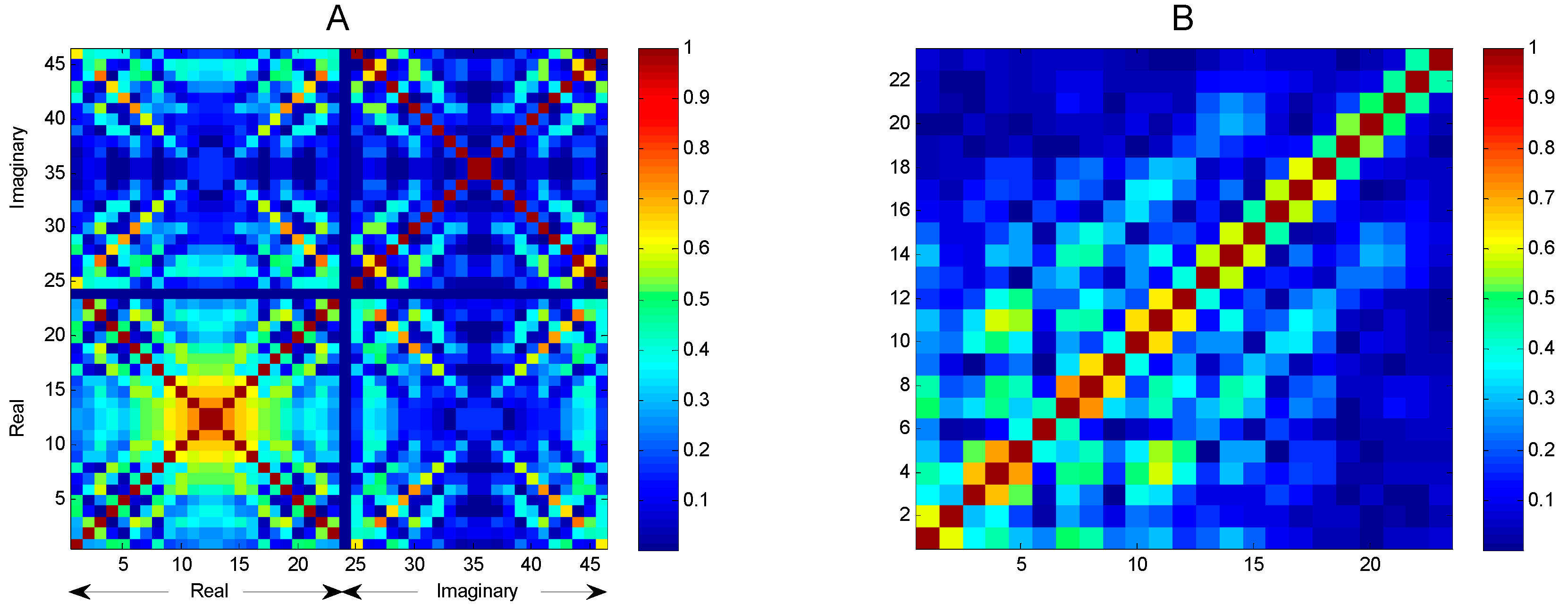
- Integral transform (cepstral domain): The samples of the mel-FBE (in the spectral domain) are converted into samples in the cepstral domain using an integral transform. In this article, it will be shown that the exploitation of the symmetry of the DFT integral transform obtained in step 3 yields a cepstral integral transform with a better performance.
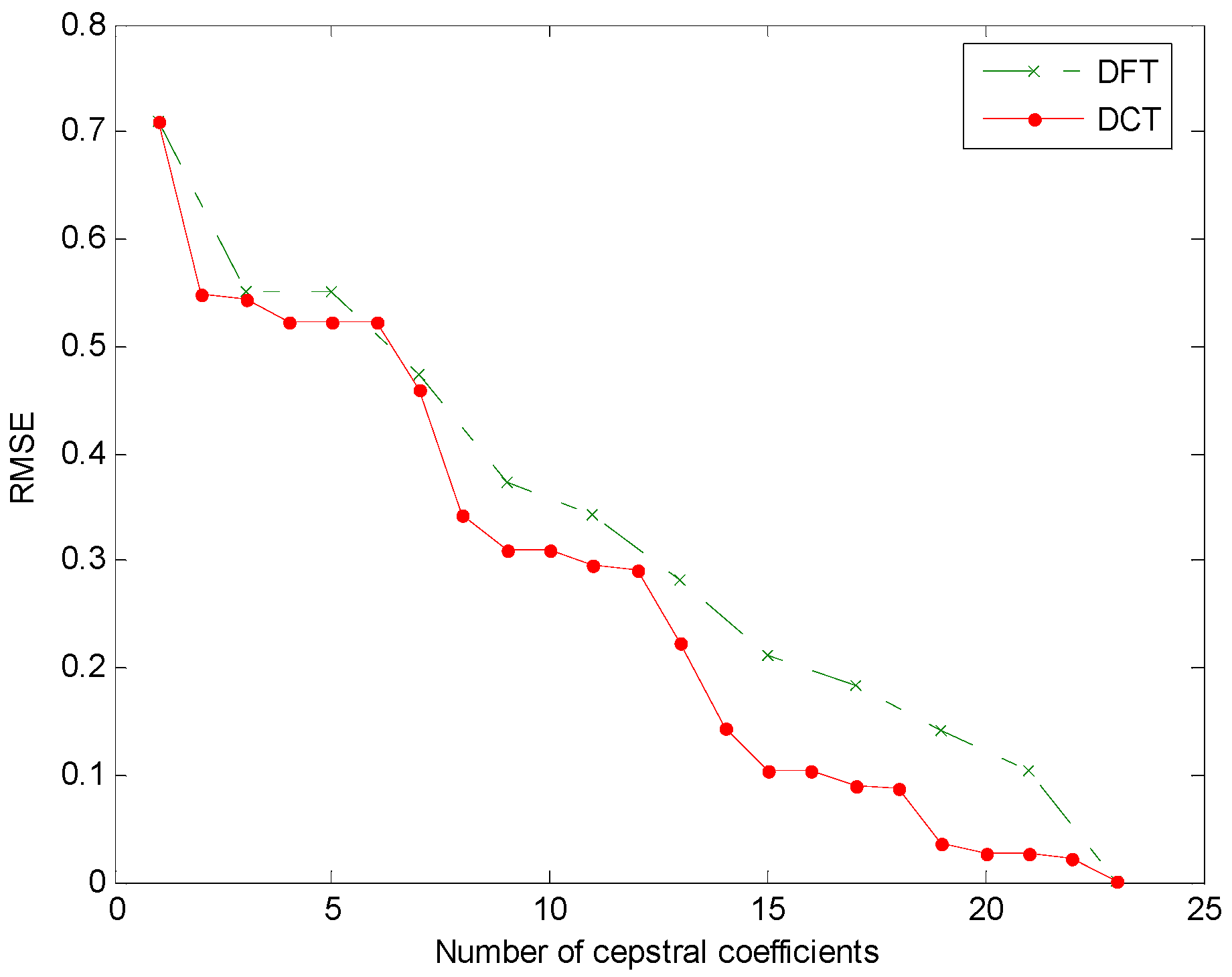
- Reduction of cepstral coefficients (cepstral domain): The samples of the cepstrum are reduced to coefficients by discarding the least significant coefficients.
- Liftering (cepstral domain): The coefficients of the cepstrum are finally liftered to compensate for the fact that high quefrency coefficients are usually much smaller than their low quefrency counterparts.
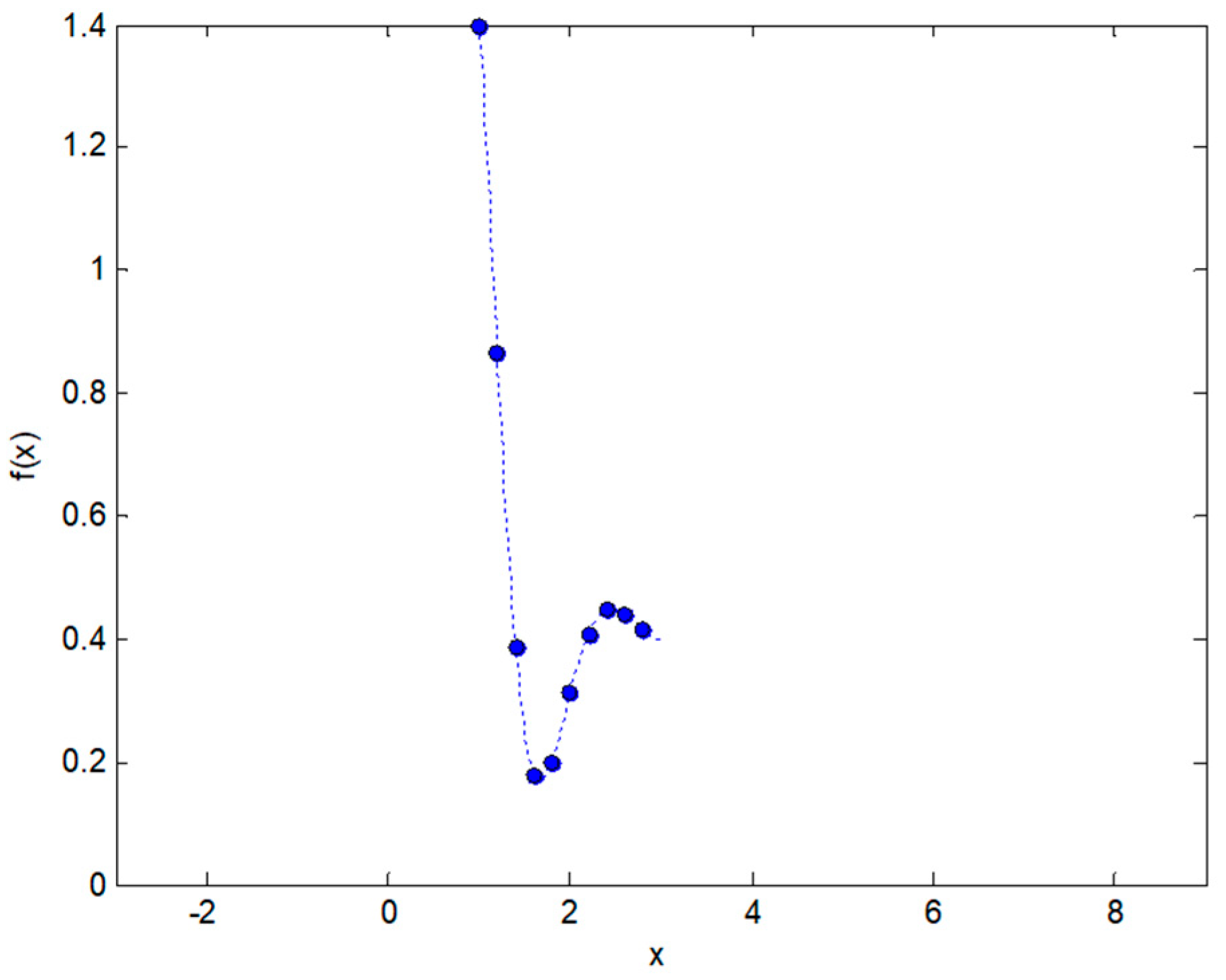
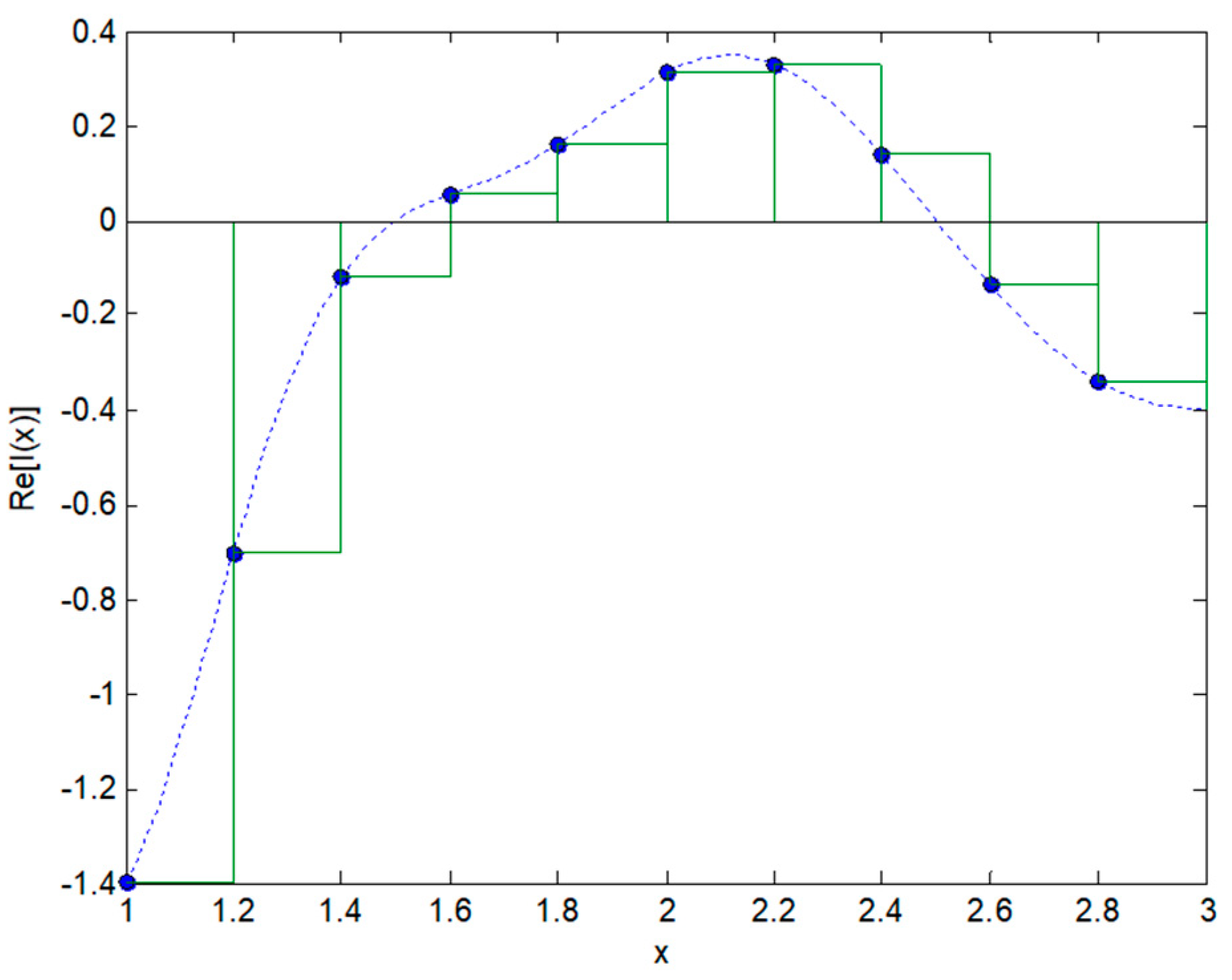
2.2. Integral Transforms of Non-Symmetric Functions
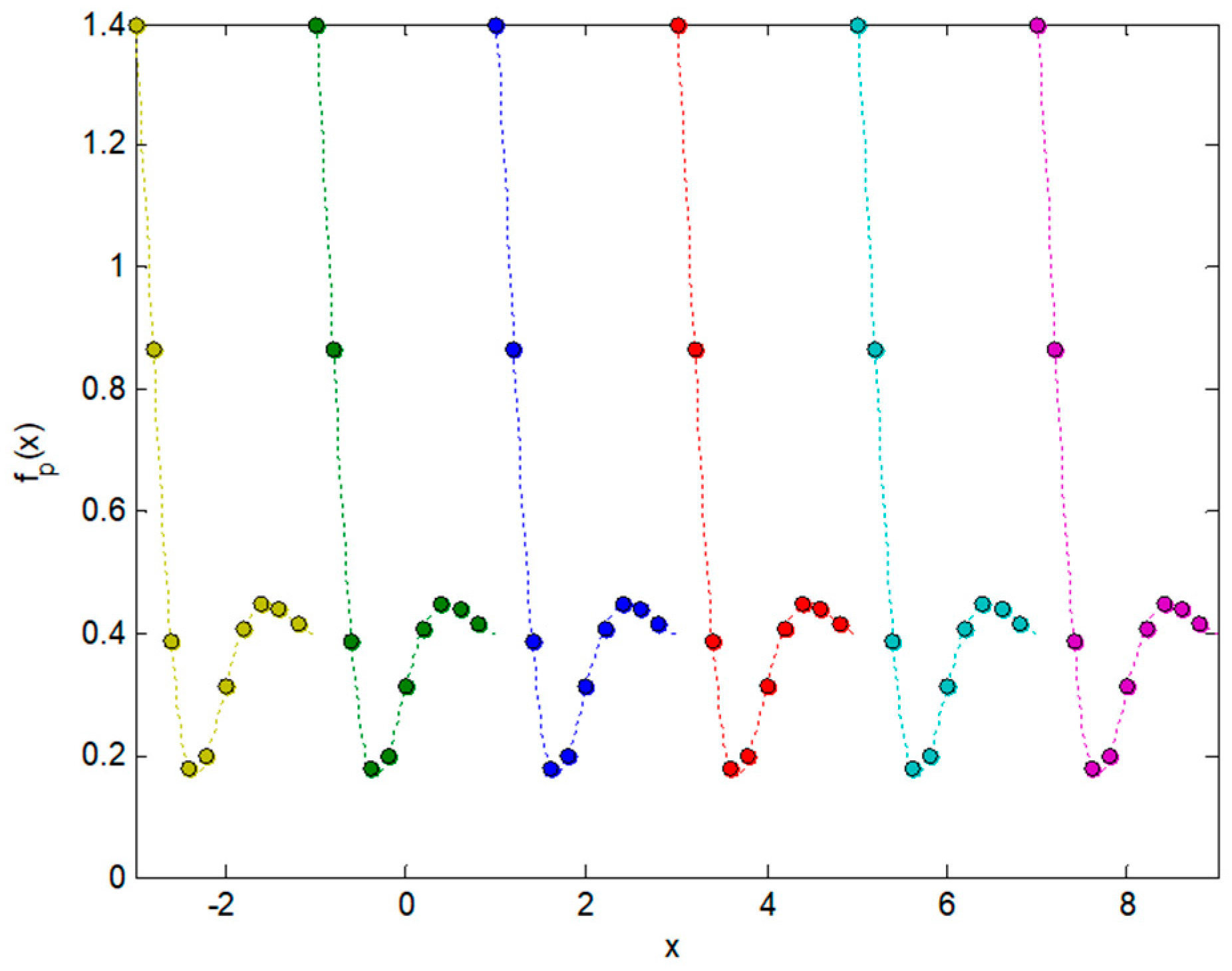
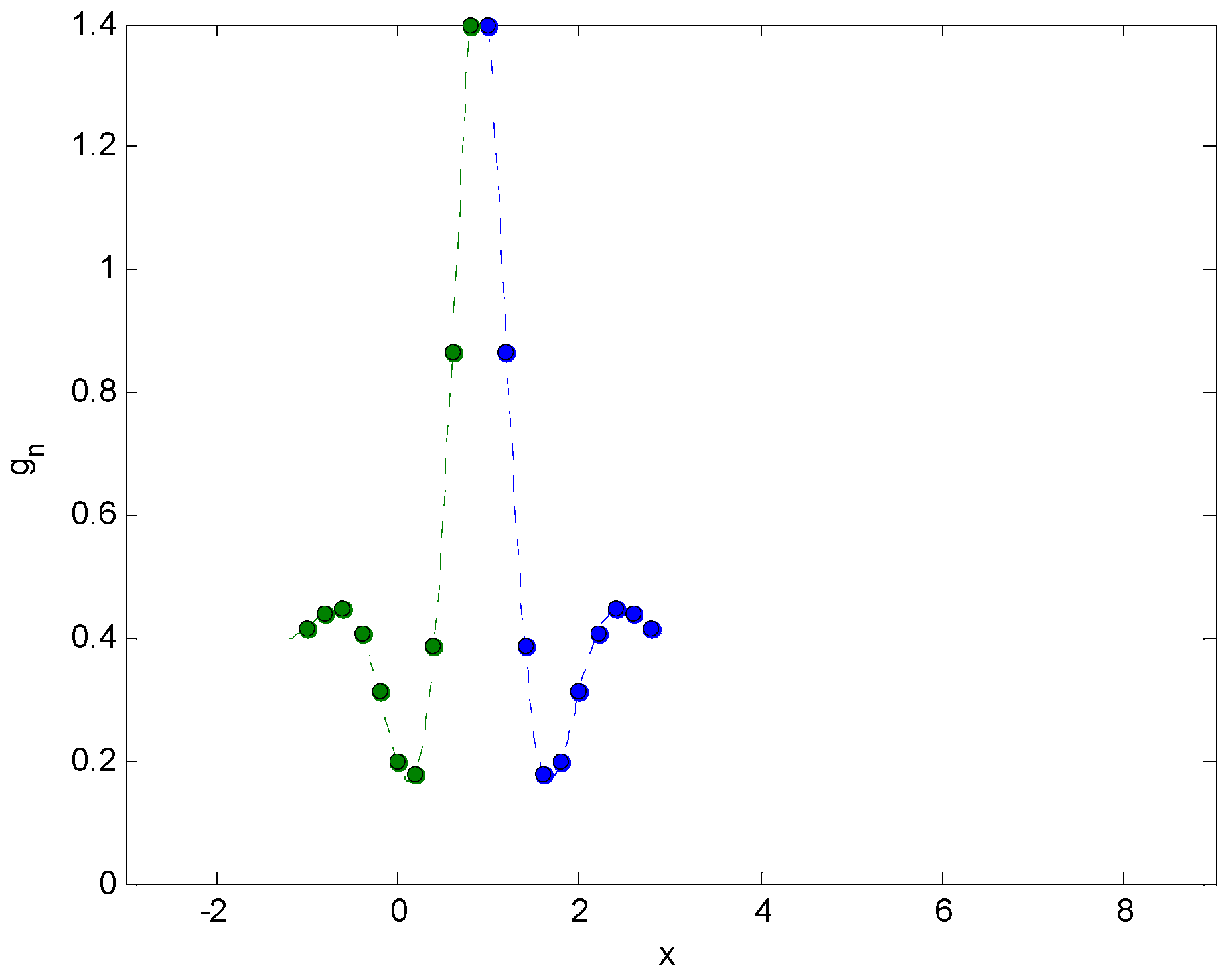
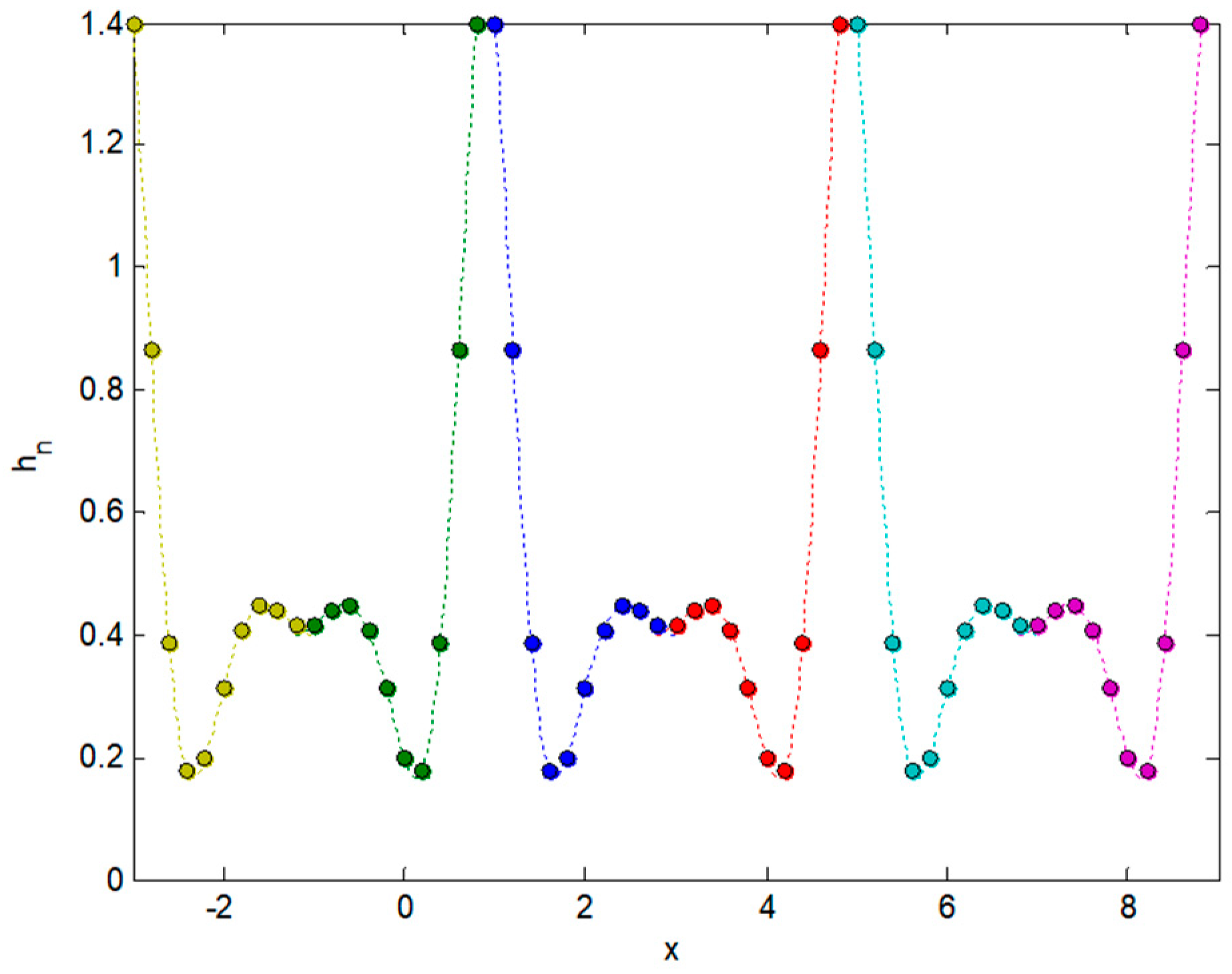
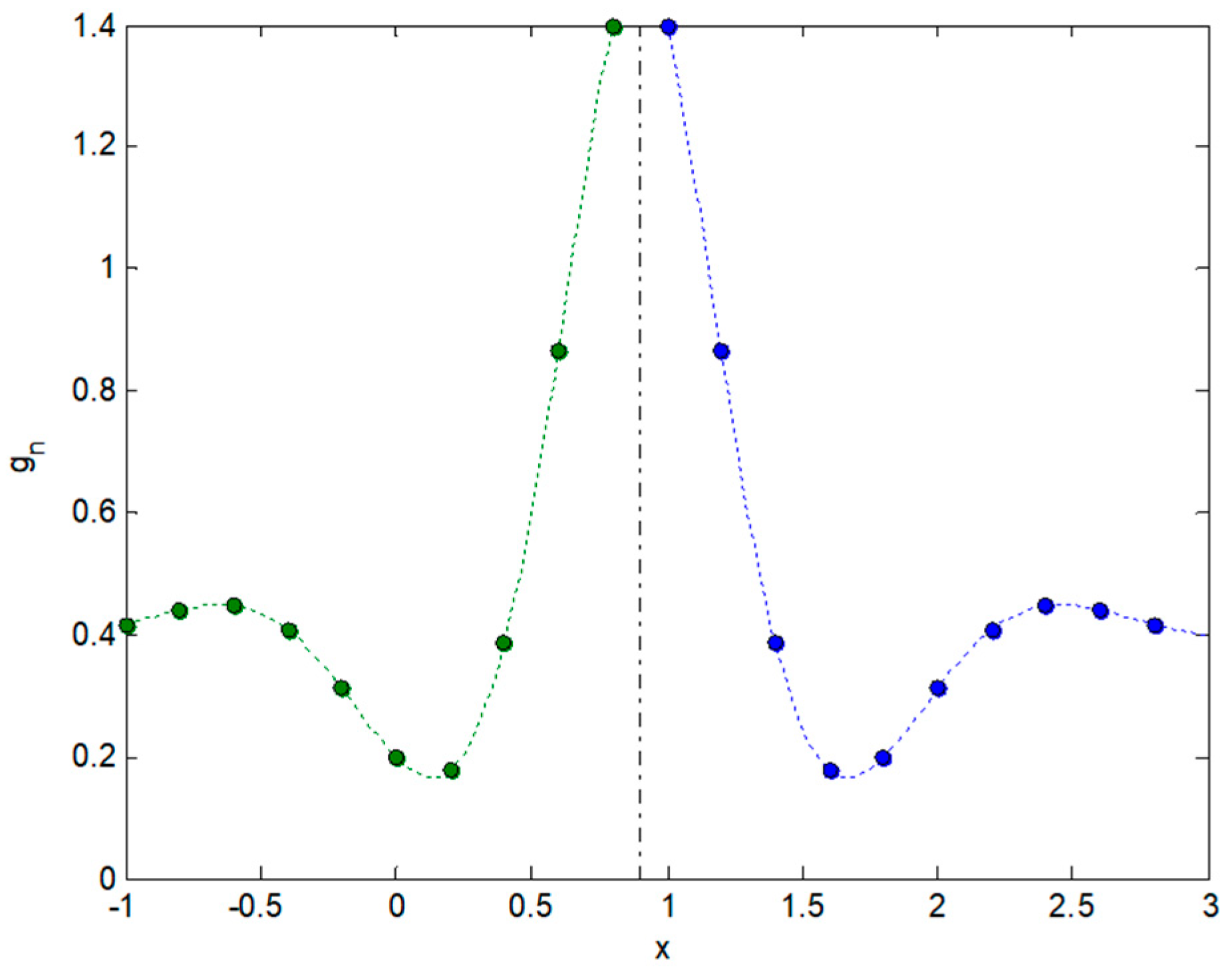
2.3. Integral Transforms of Symmetric Functions
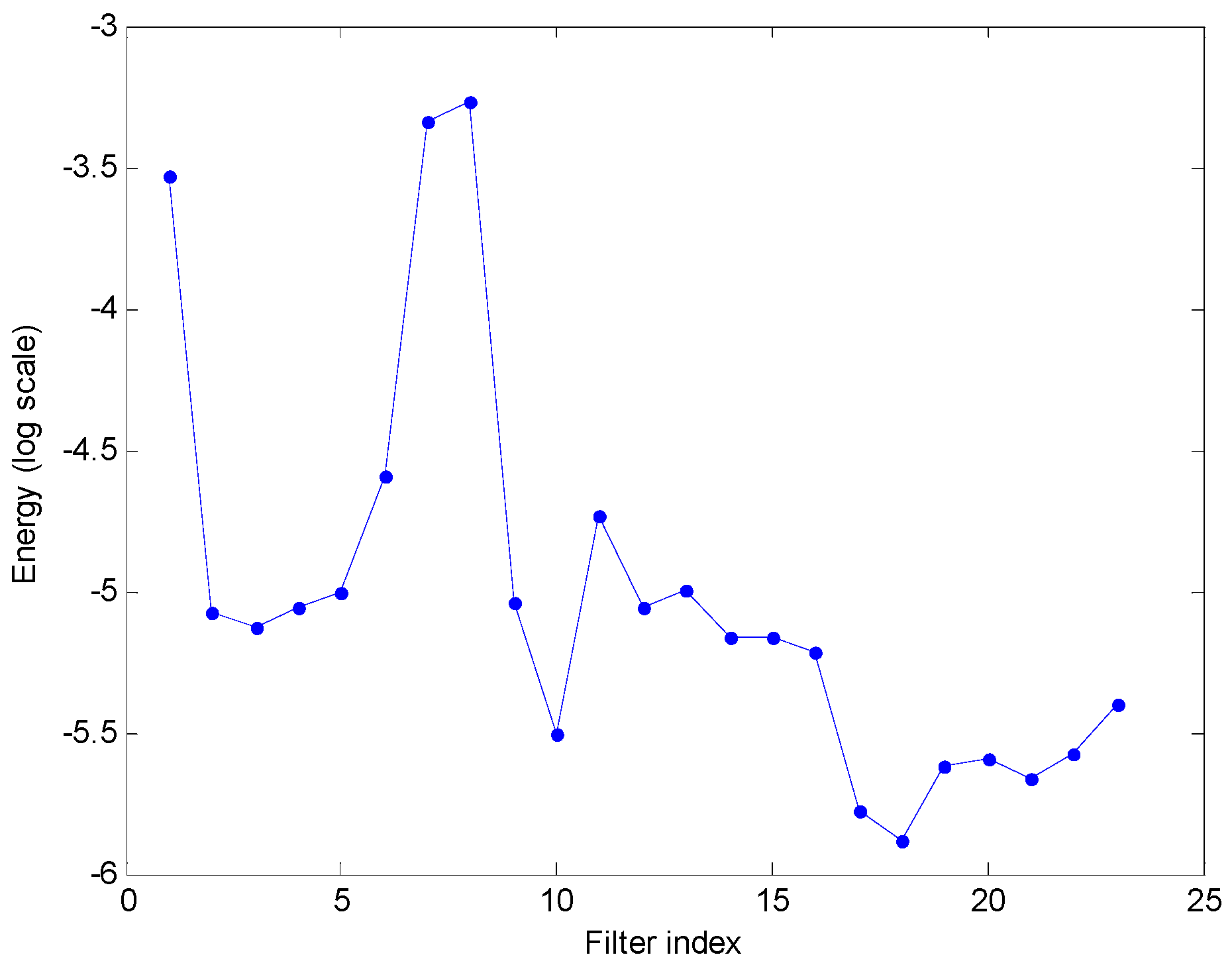
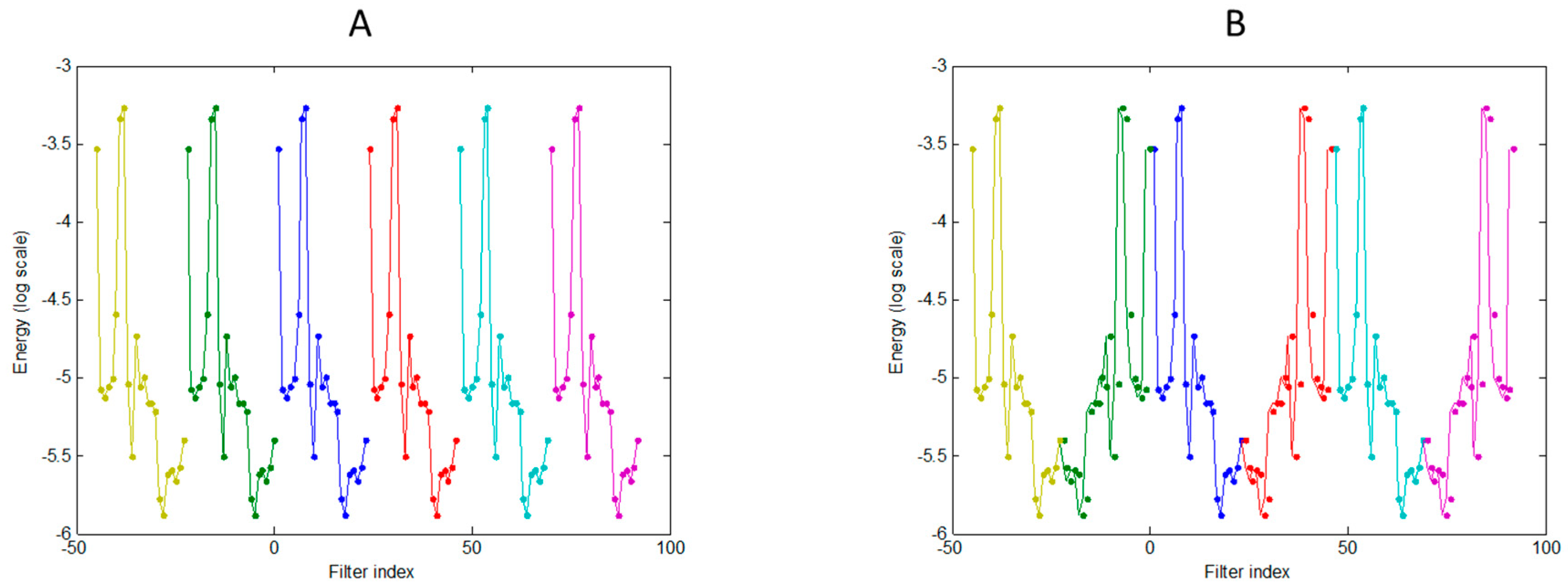
2.4. Representing Anuran Call Spectra
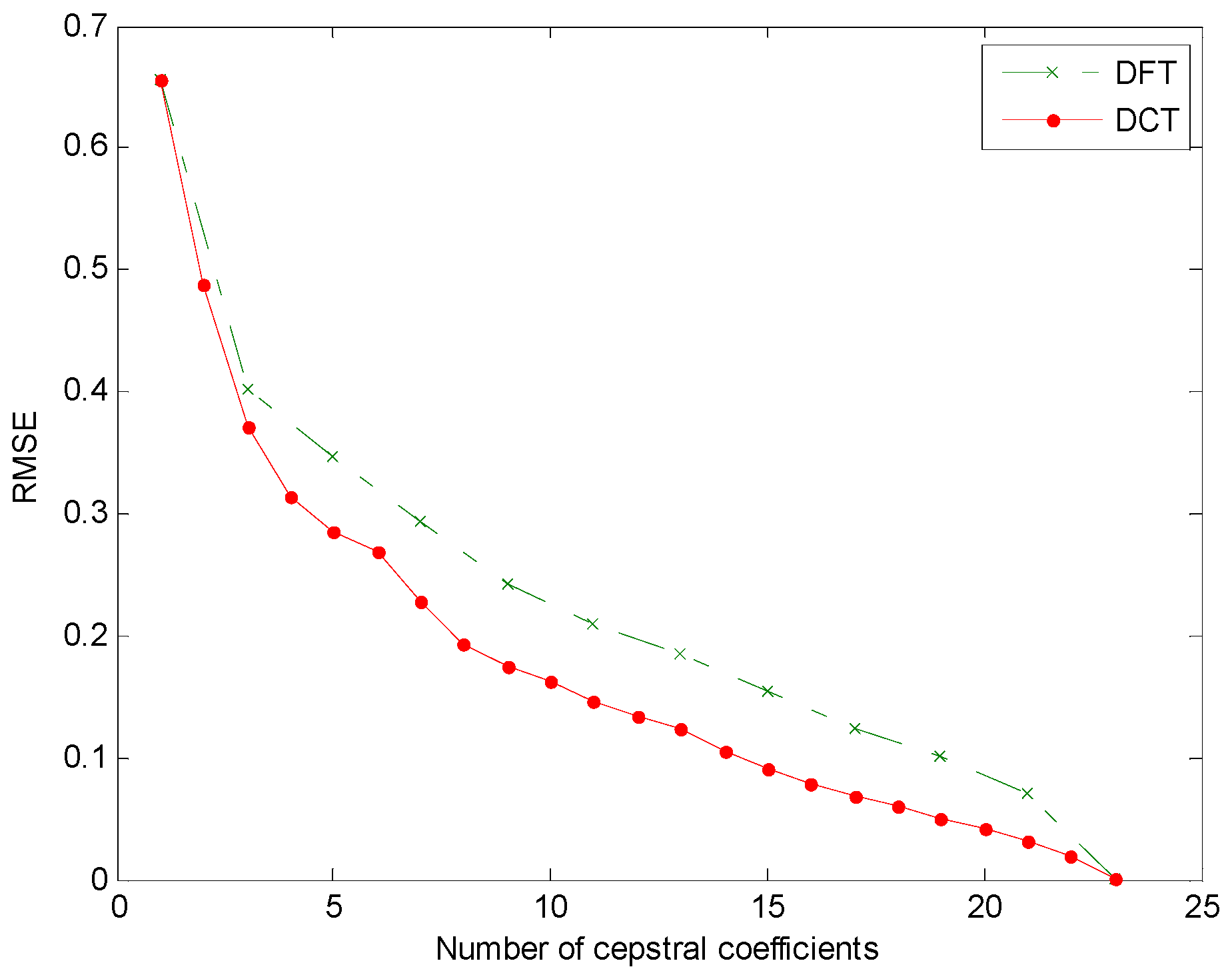
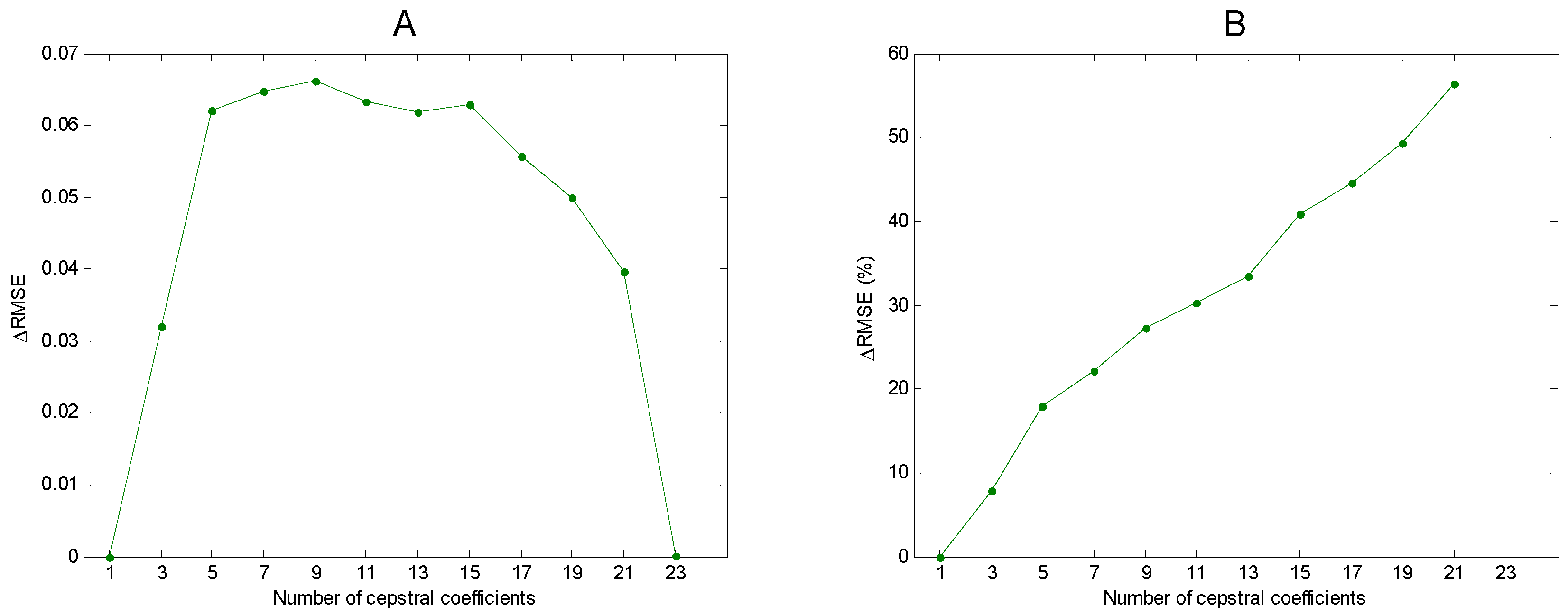
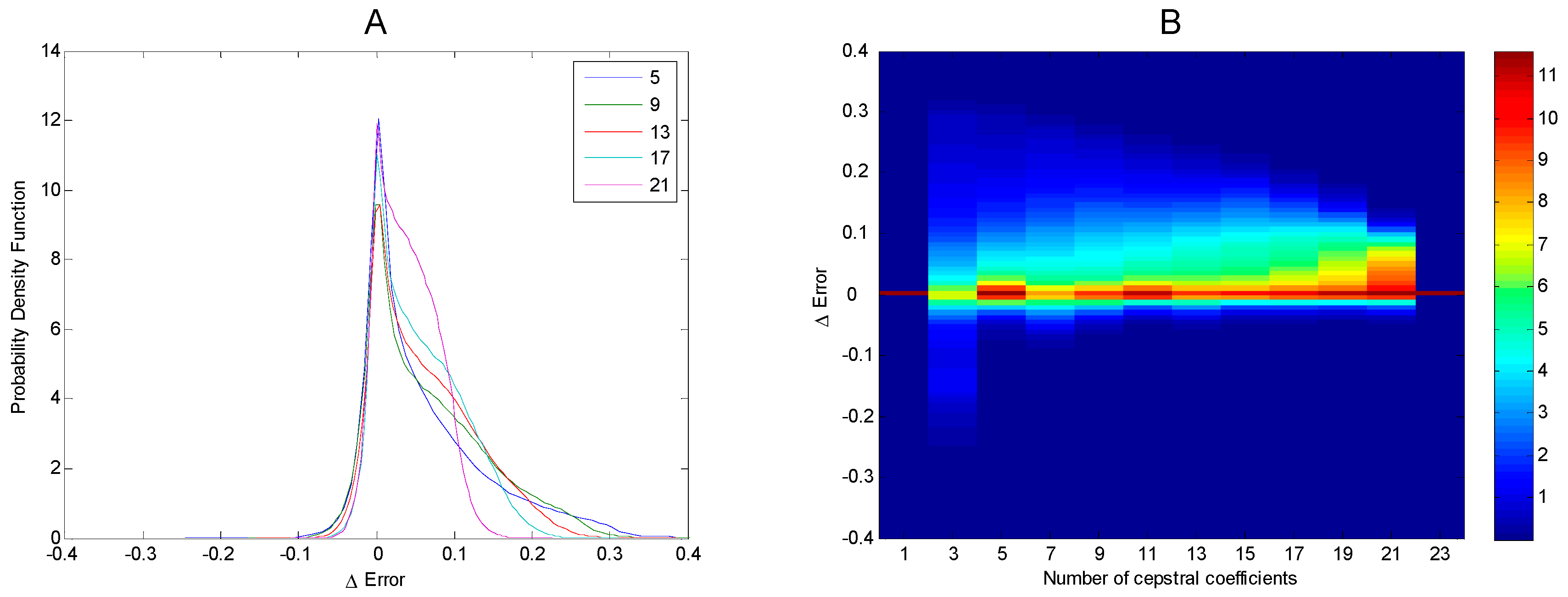
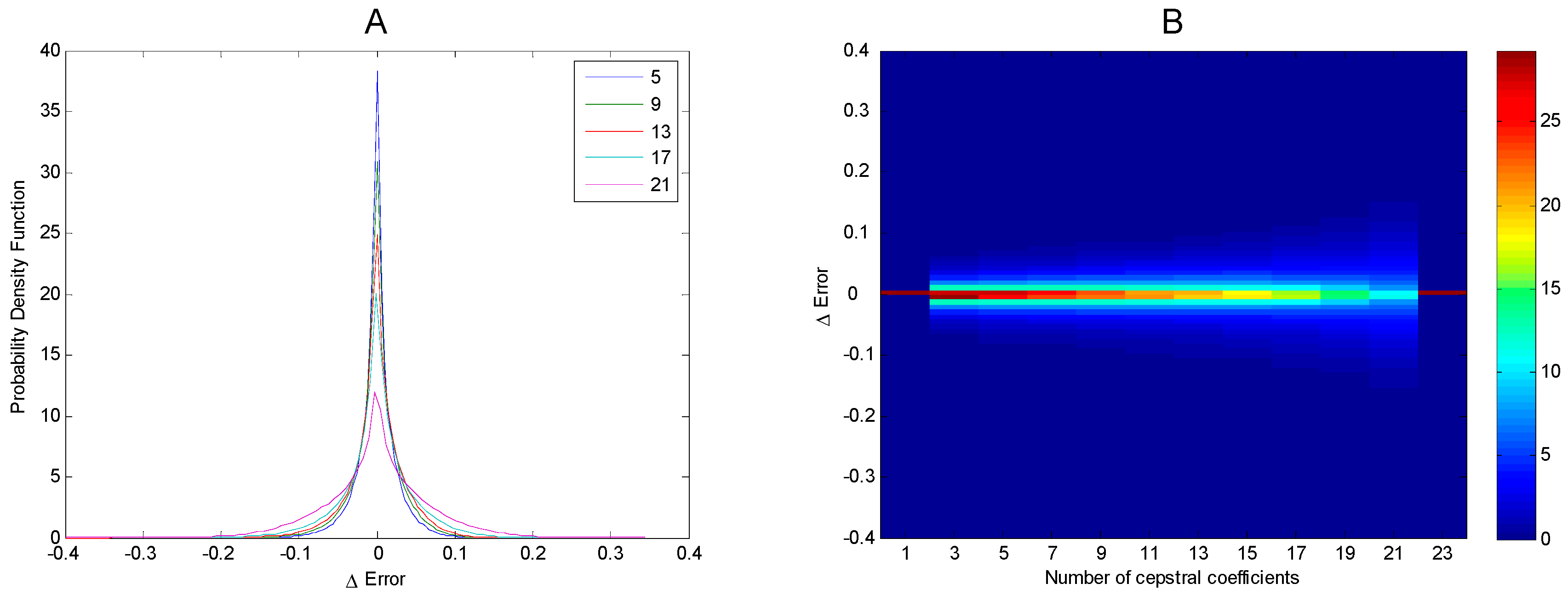
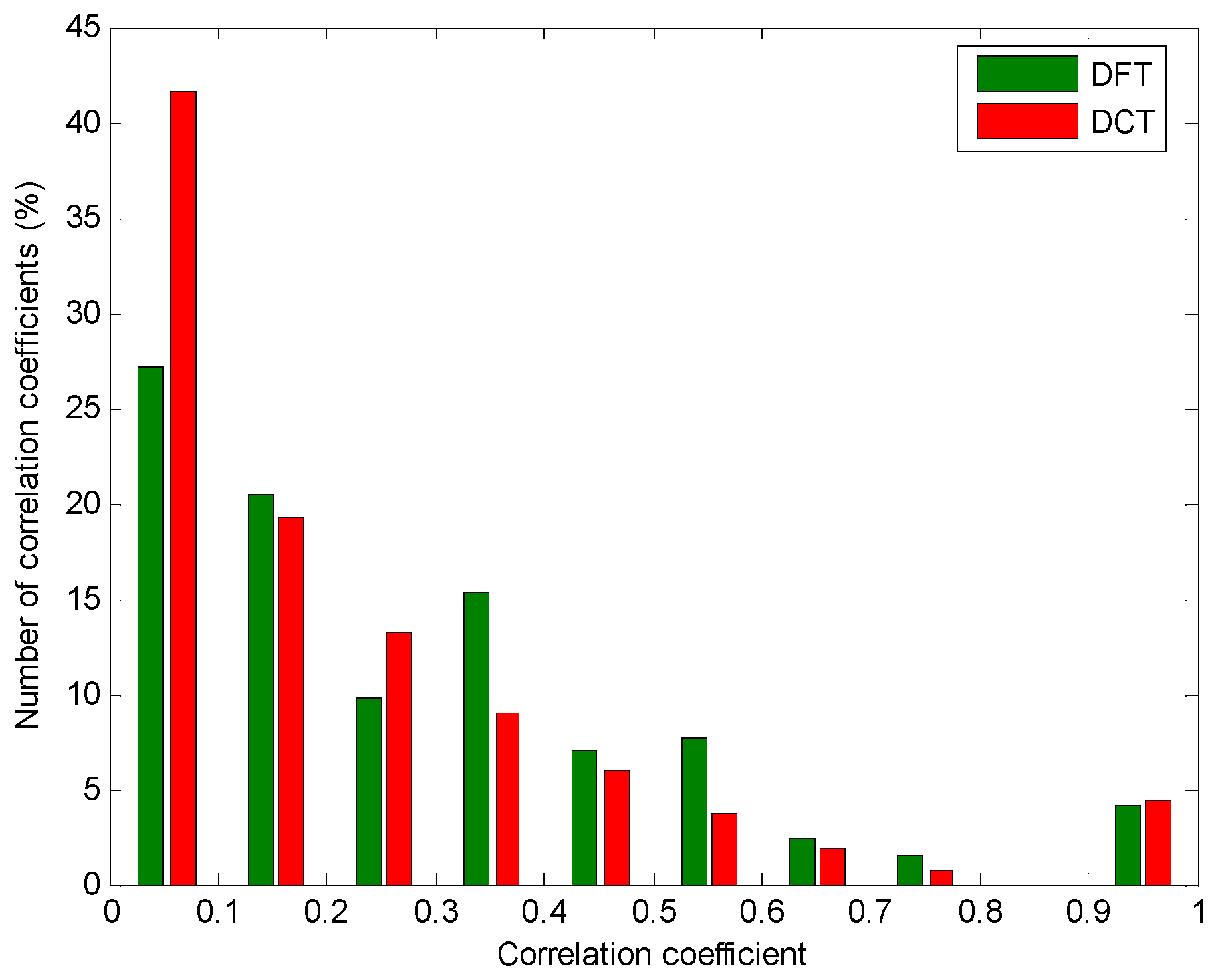
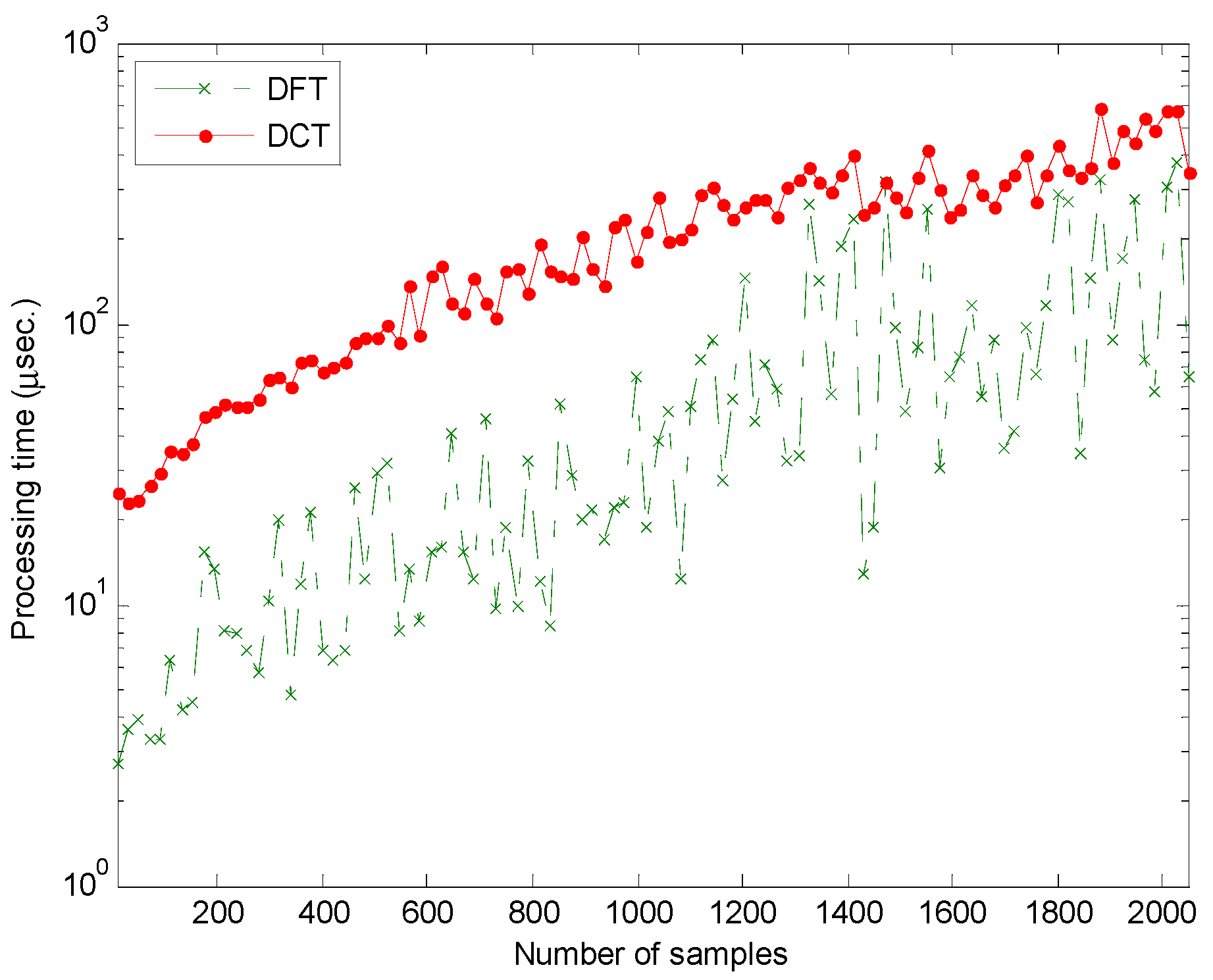
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haridas, A.V.; Marimuthu, R.; Sivakumar, V.G. A critical review and analysis on techniques of speech recognition: The road ahead. Int. J. Knowl.-Based Intell. Eng. Syst. 2018, 22, 39–57. [Google Scholar] [CrossRef]
- Gómez-García, J.A.; Moro-Velázquez, L.; Godino-Llorente, J.I. On the design of automatic voice condition analysis systems. Part II: Review of speaker recognition techniques and study on the effects of different variability factors. Biomed. Signal Process. Control 2019, 48, 128–143. [Google Scholar] [CrossRef]
- Vo, T.; Nguyen, T.; Le, C. Race Recognition Using Deep Convolutional Neural Networks. Symmetry 2018, 10, 564. [Google Scholar] [CrossRef]
- Dahake, P.P.; Shaw, K.; Malathi, P. Speaker dependent speech emotion recognition using MFCC and Support Vector Machine. In Proceedings of the 2016 International Conference on Automatic Control and Dynamic Optimization Techniques (ICACDOT), Pune, India, 9–10 September 2016; pp. 1080–1084. [Google Scholar]
- Chakraborty, S.S.; Parekh, R. Improved Musical Instrument Classification Using Cepstral Coefficients and Neural Networks. In Methodologies and Application Issues of Contemporary Computing Framework; Springer: Singapore, 2018; pp. 123–138. [Google Scholar]
- Panteli, M.; Benetos, E.; Dixon, S. A computational study on outliers in world music. PLoS ONE 2017, 12, e0189399. [Google Scholar] [CrossRef] [PubMed]
- Noda, J.J.; Sánchez-Rodríguez, D.; Travieso-González, C.M. A Methodology Based on Bioacoustic Information for Automatic Identification of Reptiles and Anurans. In Reptiles and Amphibians; IntechOpen: London, UK, 2018. [Google Scholar]
- Desai, N.P.; Lehman, C.; Munson, B.; Wilson, M. Supervised and unsupervised machine learning approaches to classifying chimpanzee vocalizations. J. Acoust. Soc. Am. 2018, 143, 1786. [Google Scholar] [CrossRef]
- Malfante, M.; Mars, J.I.; Dalla Mura, M.; Gervaise, C. Automatic fish sounds classification. J. Acoust. Soc. Am. 2018, 143, 2834–2846. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, B.; Yang, X.; Meng, Q. Heart sound identification based on MFCC and short-term energy. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 7411–7415. [Google Scholar]
- Usman, M.; Zubair, M.; Shiblee, M.; Rodrigues, P.; Jaffar, S. Probabilistic Modeling of Speech in Spectral Domain using Maximum Likelihood Estimation. Symmetry 2018, 10, 750. [Google Scholar] [CrossRef]
- Cao, J.; Cao, M.; Wang, J.; Yin, C.; Wang, D.; Vidal, P.P. Urban noise recognition with convolutional neural network. Multimed. Tools Appl. 2018. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Z.; Tan, C.; Lu, D.; Wu, B.; Su, Z.; Tang, Y. Cutting Pattern Identification for Coal Mining Shearer through Sound Signals Based on a Convolutional Neural Network. Symmetry 2018, 10, 736. [Google Scholar] [CrossRef]
- Lee, J.; Choi, H.; Park, D.; Chung, Y.; Kim, H.Y.; Yoon, S. Fault detection and diagnosis of railway point machines by sound analysis. Sensors 2016, 16, 549. [Google Scholar] [CrossRef]
- Choi, Y.; Atif, O.; Lee, J.; Park, D.; Chung, Y. Noise-Robust Sound-Event Classification System with Texture Analysis. Symmetry 2018, 10, 402. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to feature extraction. In Feature Extraction; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–25. [Google Scholar]
- Alías, F.; Socoró, J.; Sevillano, X. A review of physical and perceptual feature extraction techniques for speech, music and environmental sounds. Appl. Sci. 2016, 6, 143. [Google Scholar] [CrossRef]
- Zhang, H.; McLoughlin, I.; Song, Y. Robust sound event recognition using convolutional neural networks. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 559–563. [Google Scholar]
- Dave, N. Feature extraction methods LPC, PLP and MFCC in speech recognition. Int. J. Adv. Res. Eng. Technol. 2013, 1, 1–4. [Google Scholar]
- Paul, D.; Pal, M.; Saha, G. Spectral features for synthetic speech detection. IEEE J. Sel. Top. Signal Process. 2017, 11, 605–617. [Google Scholar] [CrossRef]
- Taebi, A.; Mansy, H.A. Analysis of seismocardiographic signals using polynomial chirplet transform and smoothed pseudo Wigner-Ville distribution. In Proceedings of the 2017 IEEE Signal Processing in Medicine and Biology Symposium (SPMB), Philadelphia, PA, USA, 2 December 2017; pp. 1–6. [Google Scholar]
- Dayou, J.; Han, N.C.; Mun, H.C.; Ahmad, A.H.; Muniandy, S.V.; Dalimin, M.N. Classification and identification of frog sound based on entropy approach. In Proceedings of the 2011 International Conference on Life Science and Technology, Mumbai, India, 7–9 January 2011; Volume 3, pp. 184–187. [Google Scholar]
- Zheng, F.; Zhang, G.; Song, Z. Comparison of different implementations of MFCC. J. Comput. Sci. Technol. 2001, 16, 582–589. [Google Scholar] [CrossRef]
- Hussain, H.; Ting, C.M.; Numan, F.; Ibrahim, M.N.; Izan, N.F.; Mohammad, M.M.; Sh-Hussain, H. Analysis of ECG biosignal recognition for client identifiction. In Proceedings of the 2017 IEEE International Conference on Signal and Image Processing Applications (ICSIPA), Kuching, Malaysia, 12–14 September 2017; pp. 15–20. [Google Scholar]
- Nickel, C.; Brandt, H.; Busch, C. Classification of Acceleration Data for Biometric Gait Recognition on Mobile Devices. Biosig 2011, 11, 57–66. [Google Scholar]
- Muheidat, F.; Tyrer, W.H.; Popescu, M. Walk Identification using a smart carpet and Mel-Frequency Cepstral Coefficient (MFCC) features. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 4249–4252. [Google Scholar]
- Negi, S.S.; Kishor, N.; Negi, R.; Uhlen, K. Event signal characterization for disturbance interpretation in power grid. In Proceedings of the 2018 First International Colloquium on Smart Grid Metrology (SmaGriMet), Split, Croatia, 24–27 April 2018; pp. 1–5. [Google Scholar]
- Xie, J.; Towsey, M.; Zhang, J.; Roe, P. Frog call classification: A survey. Artif. Int. Rev. 2018, 49, 375–391. [Google Scholar] [CrossRef]
- Colonna, J.G.; Nakamura, E.F.; Rosso, O.A. Feature evaluation for unsupervised bioacoustic signal segmentation of anuran calls. Expert Syst. Appl. 2018, 106, 107–120. [Google Scholar] [CrossRef]
- Luque, A.; Romero-Lemos, J.; Carrasco, A.; Barbancho, J. Non-sequential automatic classification of anuran sounds for the estimation of climate-change indicators. Expert Syst. Appl. 2018, 95, 248–260. [Google Scholar] [CrossRef]
- Luque, A.; Romero-Lemos, J.; Carrasco, A.; Gonzalez-Abril, L. Temporally-aware algorithms for the classification of anuran sounds. PeerJ 2018, 6, e4732. [Google Scholar] [CrossRef]
- Luque, A.; Romero-Lemos, J.; Carrasco, A.; Barbancho, J. Improving Classification Algorithms by Considering Score Series in Wireless Acoustic Sensor Networks. Sensors 2018, 18, 2465. [Google Scholar] [CrossRef] [PubMed]
- Romero, J.; Luque, A.; Carrasco, A. Anuran sound classification using MPEG-7 frame descriptors. In Proceedings of the XVII Conferencia de la Asociación Española para la Inteligencia Artificial (CAEPIA), Salamanca, Spain, 14–16 September 2016; pp. 801–810. [Google Scholar]
- Luque, A.; Gómez-Bellido, J.; Carrasco, A.; Personal, E.; Leon, C. Evaluation of the processing times in anuran sound classification. Wireless Communications and Mobile Computing 2017. [Google Scholar] [CrossRef]
- Luque, A.; Gómez-Bellido, J.; Carrasco, A.; Barbancho, J. Optimal Representation of Anuran Call Spectrum in Environmental Monitoring Systems Using Wireless Sensor Networks. Sensors 2018, 18, 1803. [Google Scholar] [CrossRef] [PubMed]
- Hershey, S.; Chaudhuri, S.; Ellis, D.P.; Gemmeke, J.F.; Jansen, A.; Moore, R.C.; Plakal, M.; Platt, D.; Saurous, R.A.; Seybold, B.; et al. CNN architectures for large-scale audio classification. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 131–135. [Google Scholar]
- Dai, W.; Dai, C.; Qu, S.; Li, J.; Das, S. Very deep convolutional neural networks for raw waveforms. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 421–425. [Google Scholar]
- Strout, J.; Rogan, B.; Seyednezhad, S.M.; Smart, K.; Bush, M.; Ribeiro, E. Anuran call classification with deep learning. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 2662–2665. [Google Scholar]
- Colonna, J.; Peet, T.; Ferreira, C.A.; Jorge, A.M.; Gomes, E.F.; Gama, J. Automatic classification of anuran sounds using convolutional neural networks. In Proceedings of the Ninth International Conference on Computer Science & Software Engineering, Porto, Portugal, 20–22 July 2016; pp. 73–78. [Google Scholar]
- Podder, P.; Khan, T.Z.; Khan, M.H.; Rahman, M.M. Comparative performance analysis of hamming, hanning and blackman window. Int. J. Comput. Appl. 2014, 96, 1–7. [Google Scholar] [CrossRef]
- O’shaughnessy, D. Speech Communication: Human and Machine, 2nd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 1999; ISBN 978-0-7803-3449-6. [Google Scholar]
- Bhatia, R. Fourier Series; American Mathematical Society: Providence, RI, USA, 2005. [Google Scholar]
- Broughton, S.A.; Bryan, K. Discrete Fourier Analysis and Wavelets: Applications to Signal and Image Processing; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Rao, K.R.; Yip, P. Discrete Cosine Transform: Algorithms, Advantages, Applications; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Tan, L.; Jiang, J. Digital Signal Processing: Fundamentals and Applications; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]


| Cepstral Transform | ACC | PRC | F1 |
|---|---|---|---|
| DFT | 94.27% | 74.46% | 77.67% |
| DCT | 94.85% | 76.76% | 78.93% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luque, A.; Gómez-Bellido, J.; Carrasco, A.; Barbancho, J. Exploiting the Symmetry of Integral Transforms for Featuring Anuran Calls. Symmetry 2019, 11, 405. https://doi.org/10.3390/sym11030405
Luque A, Gómez-Bellido J, Carrasco A, Barbancho J. Exploiting the Symmetry of Integral Transforms for Featuring Anuran Calls. Symmetry. 2019; 11(3):405. https://doi.org/10.3390/sym11030405
Chicago/Turabian StyleLuque, Amalia, Jesús Gómez-Bellido, Alejandro Carrasco, and Julio Barbancho. 2019. "Exploiting the Symmetry of Integral Transforms for Featuring Anuran Calls" Symmetry 11, no. 3: 405. https://doi.org/10.3390/sym11030405
APA StyleLuque, A., Gómez-Bellido, J., Carrasco, A., & Barbancho, J. (2019). Exploiting the Symmetry of Integral Transforms for Featuring Anuran Calls. Symmetry, 11(3), 405. https://doi.org/10.3390/sym11030405







