1. Introduction
The Klein–Gordon (KG) equation can describe various vital phenomena in chemical and physical sciences. The KG equation can be written as:
along with initial and boundary conditions:
where
,
, and
are the parameters.
The nonlinear KG equation has applications in numerous fields such as nonlinear optics, quantum mechanics, solid state physics, and in mathematical physics [
1,
2]. Various numerical techniques are employed for solving the KG equation such as the symplectic finite difference method [
3], the spectral method [
4], the meshless RBF method [
5], the finite-difference collocation method [
6], the differential quadrature method [
7], the Haar wavelet method [
8], the decomposition method [
2], the Laplace transformation and Legendre wavelets method [
9], the lattice Boltzmann method [
10], and the multiquadric quasi-interpolation method [
11].
The 2D coupled Burgers’ equations [
12,
13,
14,
15] can be written as:
with initial and boundary conditions:
where
is a real constant known as the Reynolds number.
The coupled Burgers’ equations are related to many physical problems including traffic flow, acoustic transmission, flow of a shock wave traveling in a viscous fluid, airfoil flow theory, supersonic flow, and in turbulence phenomena (see [
12,
13,
14,
15] and the references therein for details).
The 2D nonlinear regularized long wave (RLW) equation with initial and boundary conditions can be written as [
16,
17],
The regularized long wave (RLW) model equation has described many physical phenomena [
18]. So far, the existing literature contains many numerical methods used for solving the RLW equation such as finite-difference methods [
19,
20], the interpolating element-free Galerkin method [
17], the finite-element method [
21], the Fourier pseudo-spectral method [
22], and the cubic B-spline method [
23]. Furthermore, the Petrov–Galerkin method [
24] and the element-free kp-Ritz method [
25] are used for the generalized RLW equation.
Recently, meshless methods have seen broad attention for solving different kinds of PDE model areas in almost all disciplines of engineering. The meshless character is one of the most important reasons for the rising demand of such types of methods. Meshless methods reduce the complexity caused due to dimensionality to a large extent, which is faced in the carrying out of conventional methods like the finite-element and finite-difference procedures. Meshing in the case of complicated geometries is another cause for the growing demand of meshless methods. The numerical results of RBF-based algorithms have demonstrated that they are truly meshless, accurate, and easy to implement. Some interesting models can be found in [
26,
27,
28,
29,
30].
It is noted that the global meshless method (GMM), which is based on the global interpolation paradigm, has faced the problems of dense ill-conditioned matrices and finding the optimum value of the shape parameter. To avoid the limitations of the GMM, a local meshless method, which is based on local interpolation in the sub-domains, is used as a substitute to get a stable and accurate solution for the PDE models (see [
31,
32,
33,
34,
35,
36,
37]).
In the current work, the local meshless differential quadrature collocation method (LMM) based on radial basis functions (RBFs) is proposed for the numerical simulation of 1D nonlinear KG, 2D coupled Burgers’ equations, and the 2D RLW equation. The LMM is an accurate and efficient numerical technique, which requires two steps to approximate a time-dependent PDEs. Firstly, the spatial derivatives are approximated by using the RBFs, which could convert the given PDE into a system of ODEs. Then, the obtained ODEs will be solved by suitable ODE solvers.
The rest of the paper is organized as follows: the suggested numerical method is highlighted in
Section 2; the implementation of the method with different test problems is presented in
Section 3; and finally, some concluding remarks are given in
Section 4.
2. Implementation of the Numerical Method
The LMM [
26,
33] is extended to the PDE models discussed in
Section 1. The derivatives of
at the center
are approximated by the function values at a set of nodes in the neighborhood of
, where
. For the one-dimensional case,
and
, and for the two-dimensional case,
and
.
Now, for the 1D case, we have:
To find the corresponding coefficient
, radial basis function
can be substituted in Equation (
7) as follows:
where
and
in the case of multiquadric (MQ) and inverse quadratic (IQ) radial basis functions, respectively.
The matrix notation of Equation (
8) is:
where:
From Equation (
9), we obtain:
From Equations (
7) and (
10), we get:
where:
For the 2D case, the derivatives of
with respect to
x are approximated in a similar way as stated above and can be written as:
and the corresponding coefficients
can be found as follows:
Similarly, the derivatives of
with respect to
y and its corresponding coefficients
can be found as follows:
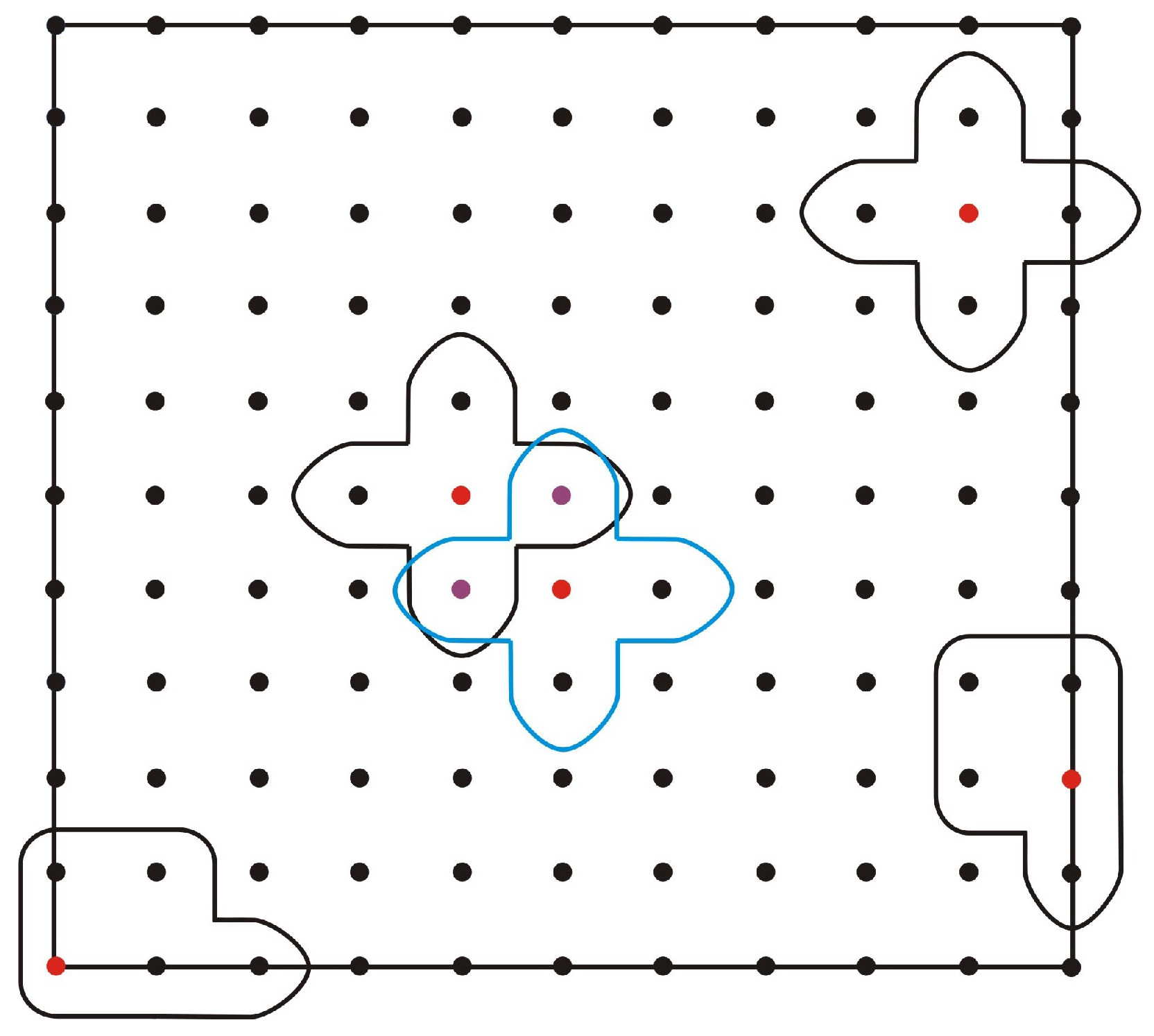
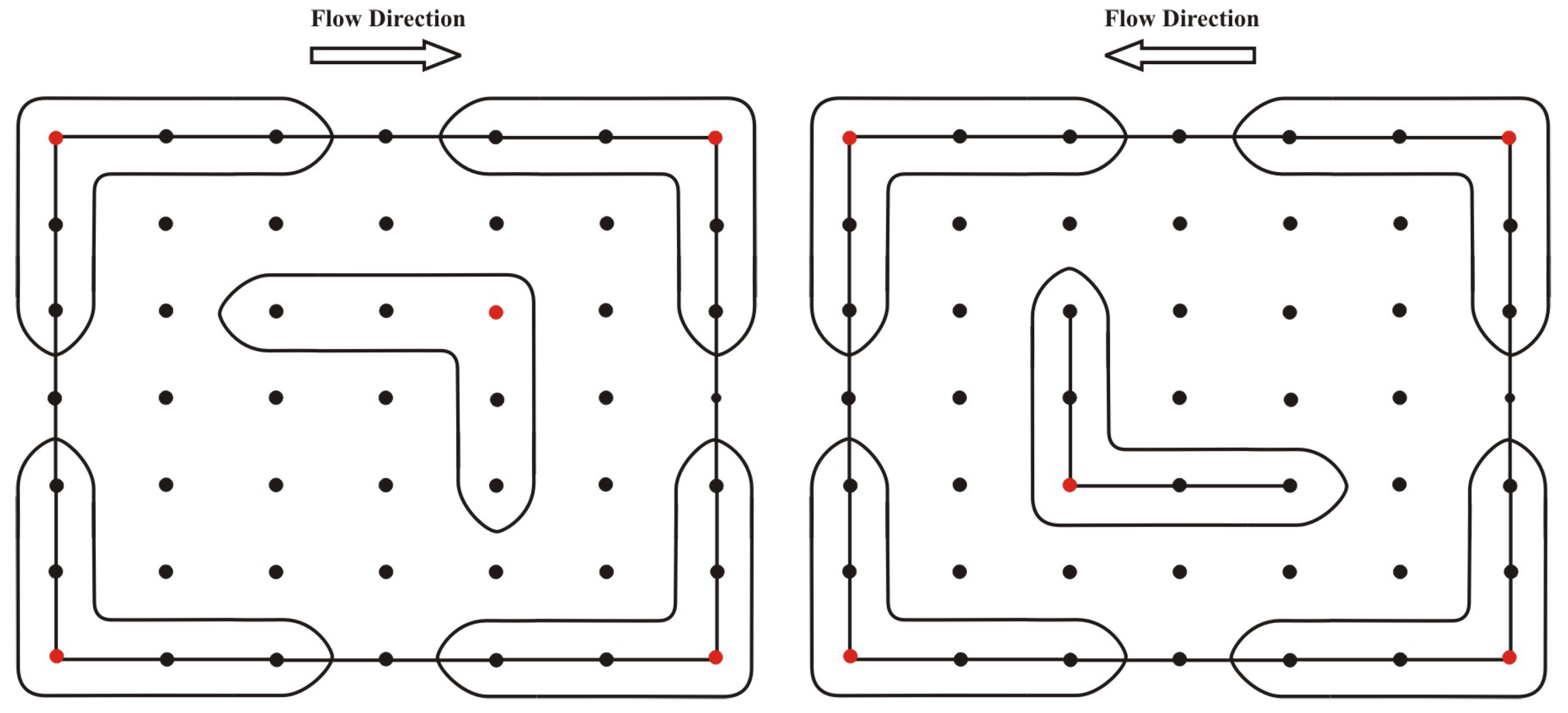
The proposed LMM is combined with a technique based on the local supported domain, called an upwind technique, in the case of convection-dominated PDE models. This technique has the ability to avoid spurious oscillatory solutions. Two types of local supported domains are used, i.e., central and upwind, as shown in
Figure 1 and
Figure 2.
2.1. Implementation of LMM for the KG Equation
Now, using the above meshless method for Equation (
1) in space, we get the second order ODE, which is reduced to the first order ODE by substituting
as follows:
with initial and boundary conditions:
Now, applying the LMM to Equation (
15):
Equations (
17) and (
18) in matrix form:
with the following corresponding initial condition:
2.2. Implementation of LMM for the 2D Model Equations
Applying the LMM to 2D model equations in space along with the prescribed boundary and initial conditions at each nodal point, we get the following form of an initial value problem:
where
represents the sparse coefficient matrix of order
(
in the 1D case and
in the 2D case).
The matrix is obtained once U and its spatial derivatives are discretized by the LMM. The vector denotes the boundary conditions of the problem, and the vector f is a vector of the corresponding initial condition of the problem. Orders of the vectors and f are , where for one- and two-dimensional PDEs, respectively.
3. Numerical Analysis
To test the accuracy and applicability of the proposed local meshless method, several problems have been considered. The proposed scheme works for any radial basis functions, but in this study, multiquadric and inverse quadratic RBFs were taken into account for spatial discretization.
The accuracy of the LMM was measured via the
,
, and
error norms, which are given as follows:
where
and
U represent the exact and approximate solutions, respectively. The following formulas were used to compute the numerical rate of convergence:
where
and
represent the numerical solutions with spatial step size
and time step size
, respectively.
The proposed LMM is truly meshless and capable of approximating the solution on both uniform and scattered nodal points. The size of the local sub-domain in the one-dimensional case was taken as three, whereas in the two-dimensional case, it was taken as five. In all numerical simulations, the multiquadric RBF with the value of the shape parameter was used for the Klein–Gordon equation, and the inverse quadric RBF with shape parameter was used for the coupled Burgers’, as well as for regularized long wave equations. The forward Euler difference formula (FEDF) was used as the time integrator throughout the numerical simulation. The central processing unit (CPU) time was calculated in seconds in all cases. All the computations were performed using MATLAB (R2012a) on a Dell PC Laptop (Windows 7, 64 bit) with an Intel (R) Core(TM)i5-240M CPU 2.50 GHz 2.5 GHs4 GB RAM.
Test Problem 1. First, consider 1D Klein–Gordon Equation (
1) with
, and the other parameters are
and
with the exact solution as given in [
2,
38].
with initial conditions:
Using the substitution
, we get:
The numerical results presented in
Table 1 were obtained by the local meshless method at coarse grids by using nodal points
, time step size
, spatial domain
, and up to final time
. The numerical results of the global meshless method of lines [
38] versus the suggested local meshless method are shown in
Table 1. It is clear from
Table 1 that the LMM gives better accuracy compared to the numerical procedures reported in [
38].
In
Table 2, the spatial convergence rate in terms of
and
error norms for the MQ radial basis function and condition number
are given for
, 21, 31, 41,
,
. It can be seen from
Table 2 that the condition number
, as well as the convergence rate both increased with the increase in the number of collocation points
N. The table also shows the second order of convergence rate of the LMM.
Table 3 shows the time convergence rate in terms of the
and
error norms for the time step sizes
,
,
,
,
, and
. The results in
Table 3 show that the FEDF has the first order convergence rate.
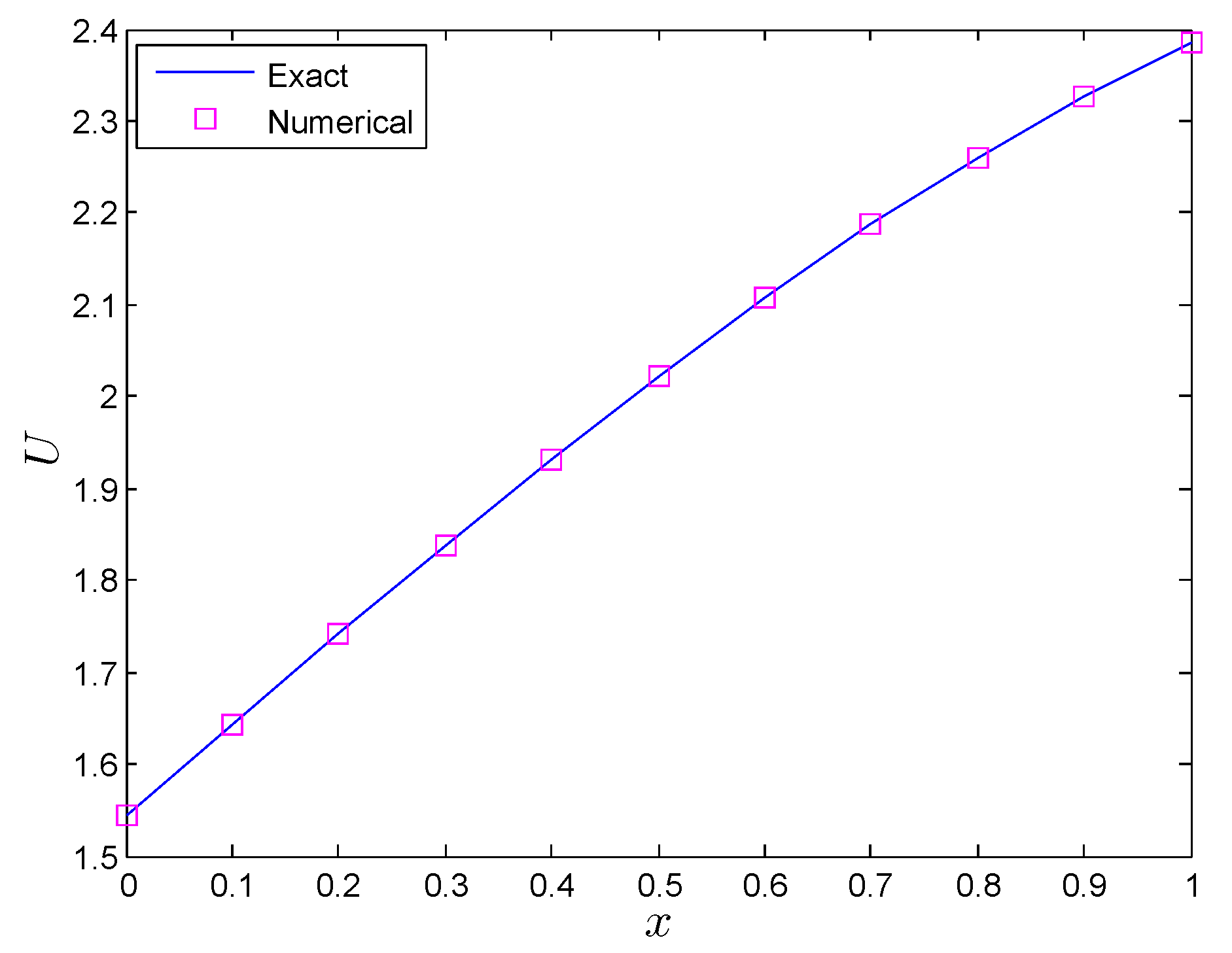
Comparisons of the exact and numerical solutions using the FEDF are plotted in
Figure 3.
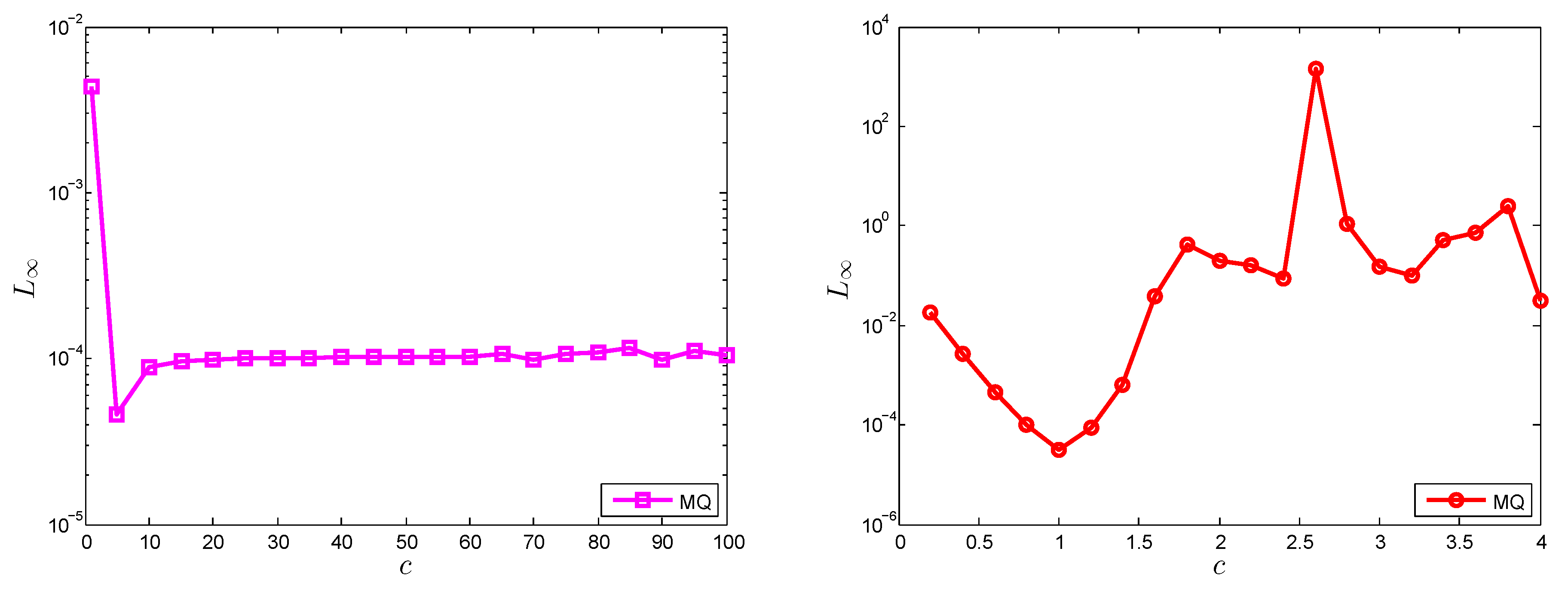
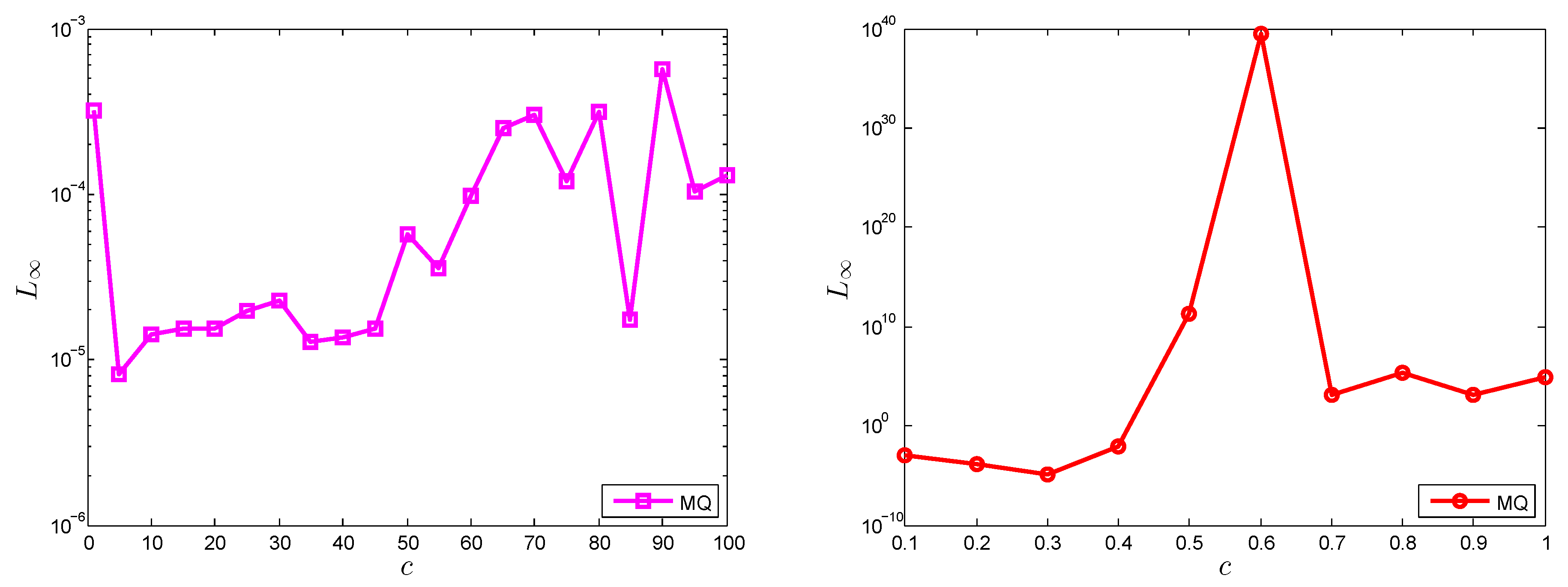
The numerical results obtained by the local and global meshless method for a long range of shape parameter value
c, with
and
, are shown in
Figure 4 for Test Problem 1. Less sensitivity to the selection of the shape parameter
c in the case of the LMM, in comparison to the GMM, can be observed from
Figure 4.
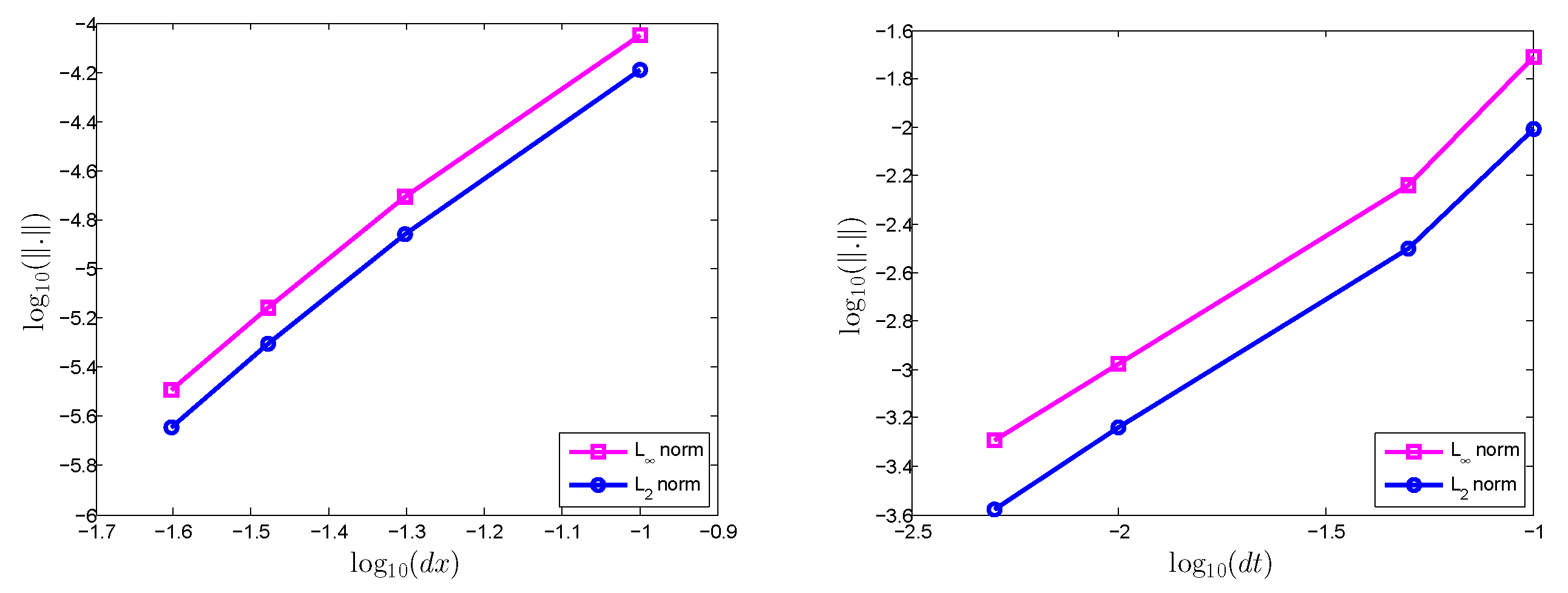
Figure 5 illustrates the convergence of the proposed method, which shows that the error decreased (
and
error norms) with the decrease of both the time step size
, as well as the distance between nodes
.
Table 2 and
Table 3 show the convergence rate corresponding to Test Problem 1. A faster spatial convergence rate as compared to the time convergence rate can easily be seen from the tables.
Test Problem 2. Consider the second test problem, by taking
,
,
, and
with the exact solution given in [
38,
39].
with initial and boundary conditions:
Using the substitution
, we get:
The results of Test Problem 2, in terms of the
error norm at various times
t, are shown in
Table 4 for spatial domain
, nodal points
, and time step size
. The results obtained by the LMM are more accurate than the results reported in [
38,
39].
In
Table 5, the condition number
and spatial convergence rate are given for
, 21, 31, 41,
, and
for Test Problem 2.
Table 5 shows that the increase in
N caused the increase in both the condition number
and convergence rate. One can observe from the table that the LMM had almost second order convergence.
Time convergence rate for Test Problem 2 is shown in
Table 6 with time step sizes
,
,
,
,
, and
. First order convergence is evident from the table.
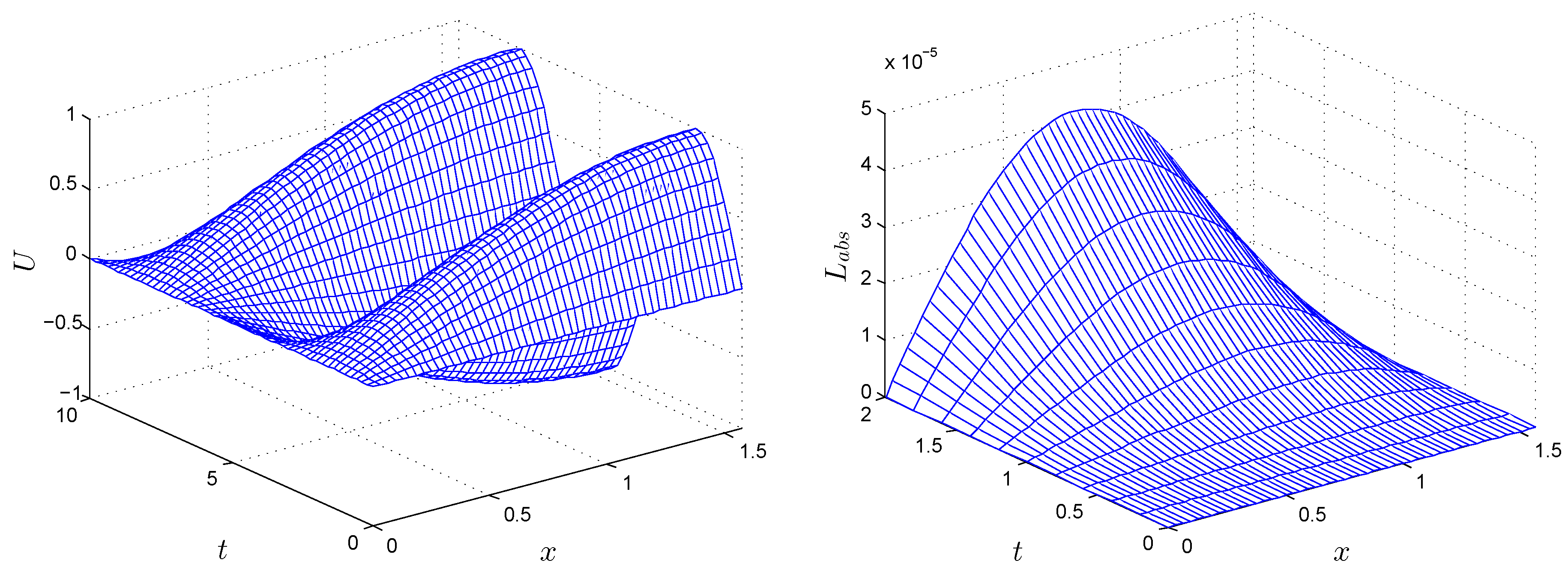
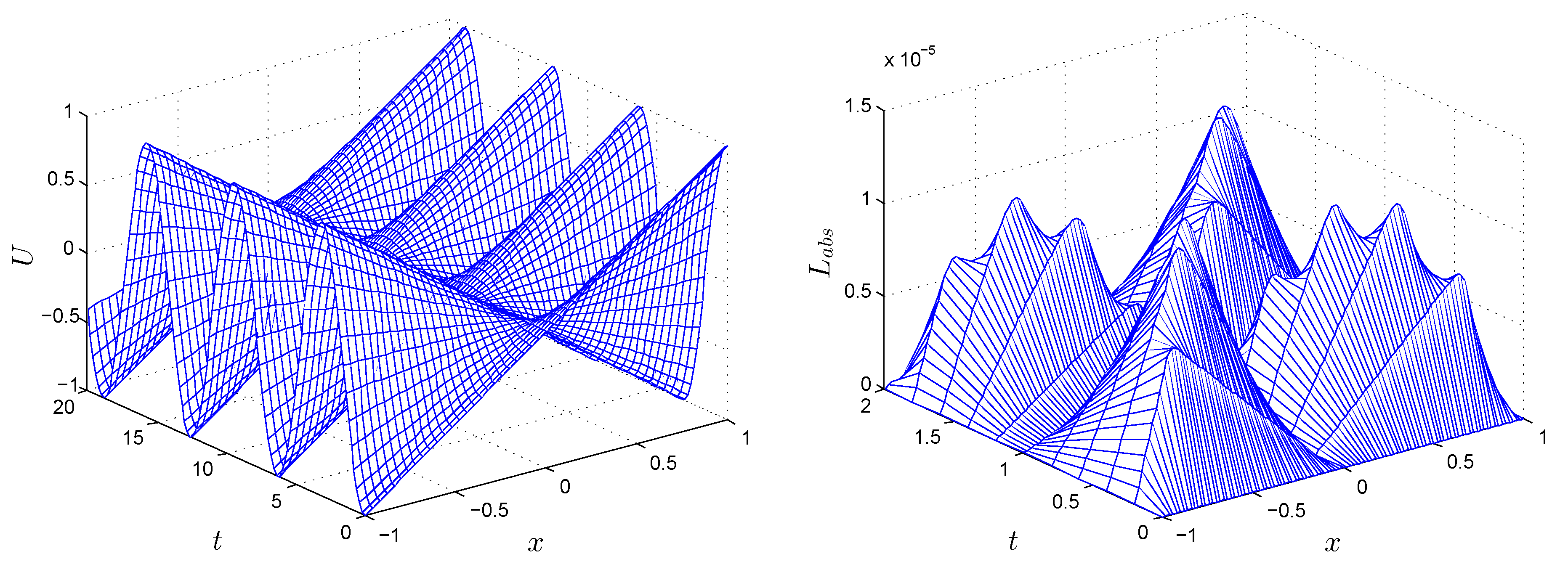
Figure 6 (left) shows the numerical solution with
,
,
at various times up to
, whereas
Figure 6 (right) shows the
error norm obtained by the FEDF for Test Problem 2.
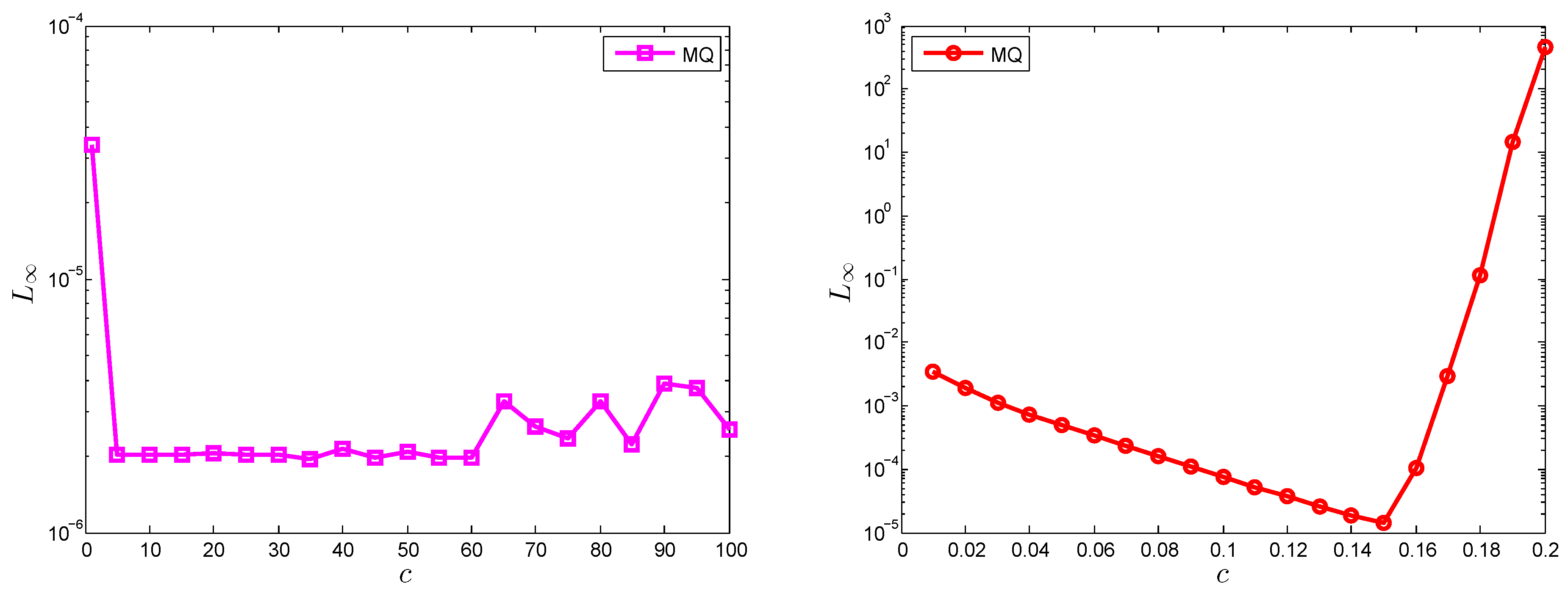
One of the drawbacks of meshless methods using shape parameter-dependent RBFs is the sensitivity of the shape parameter value. The comparison of both the local and global version of the meshless method for Test Problem 2 is shown in
Figure 7. The results were obtained for MQ RBF using
and
. It is clear from
Figure 7 that the LMM gave stable results for a long range of shape parameter value
c as compared to the GMM.
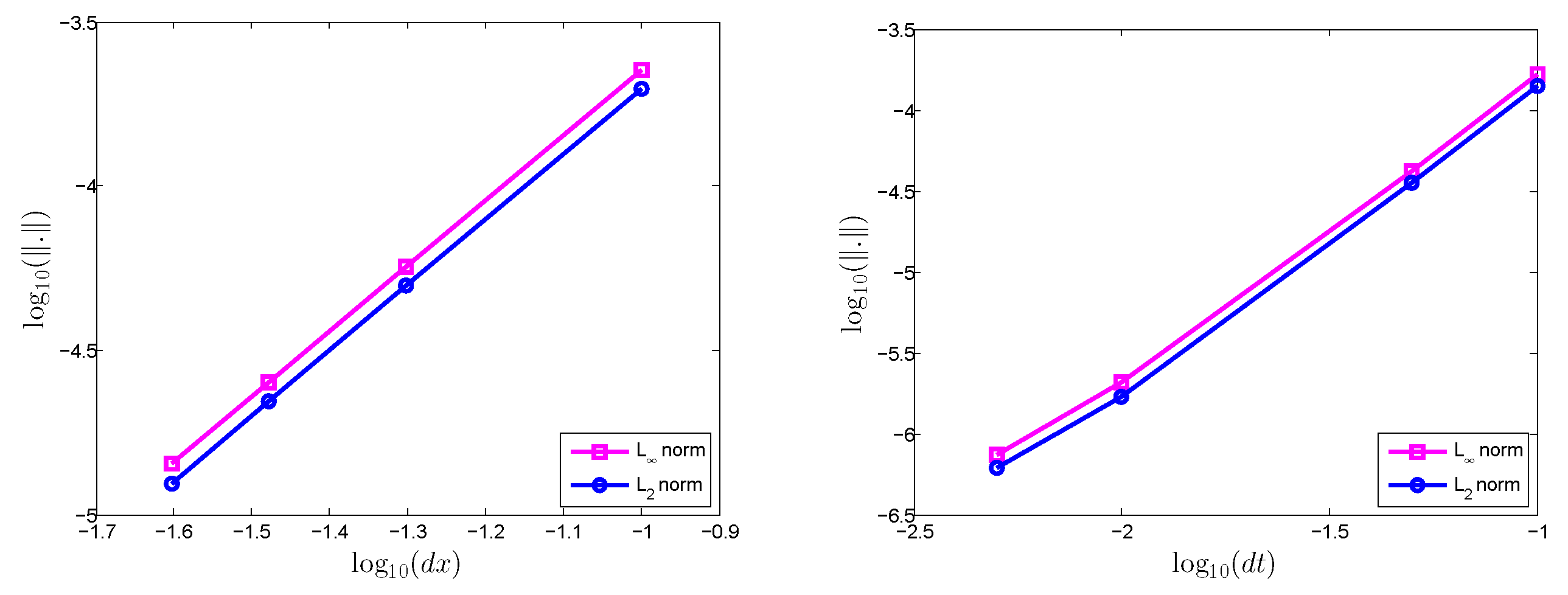
Figure 8 illustrates the convergence rate of the proposed meshless method in which one can see that the error decreased with the decrease of both the time step size
, as well as the distance between nodes
.
Table 5 and
Table 6 show the convergence rate corresponding to Test Problem 1. A faster spatial convergence rate as compared to the time convergence rate is verified in this case, as well.
Test Problem 3. In the third test problem, consider Equation (
1) with
and
,
with the exact solution given in [
38].
with initial conditions:
Using the substitution
, we get:
Numerical results for different values of
t,
,
,
are presented in
Table 7, which shows the better performance of the LMM in comparison to the results reported in [
5,
10,
11].
Figure 9 (left) shows the numerical simulation of Test Problem 3, taking
,
,
, and time up to
, and
Figure 9 (right) shows the
error norm by taking
,
,
, and
.
In
Figure 10, we compare the sensitivity of shape parameter value
c for both meshless methods, local and global. It is clear from the figure that the LMM gave stable results in the range
, but on the other hand, the GMM gave stable results only in the range
.
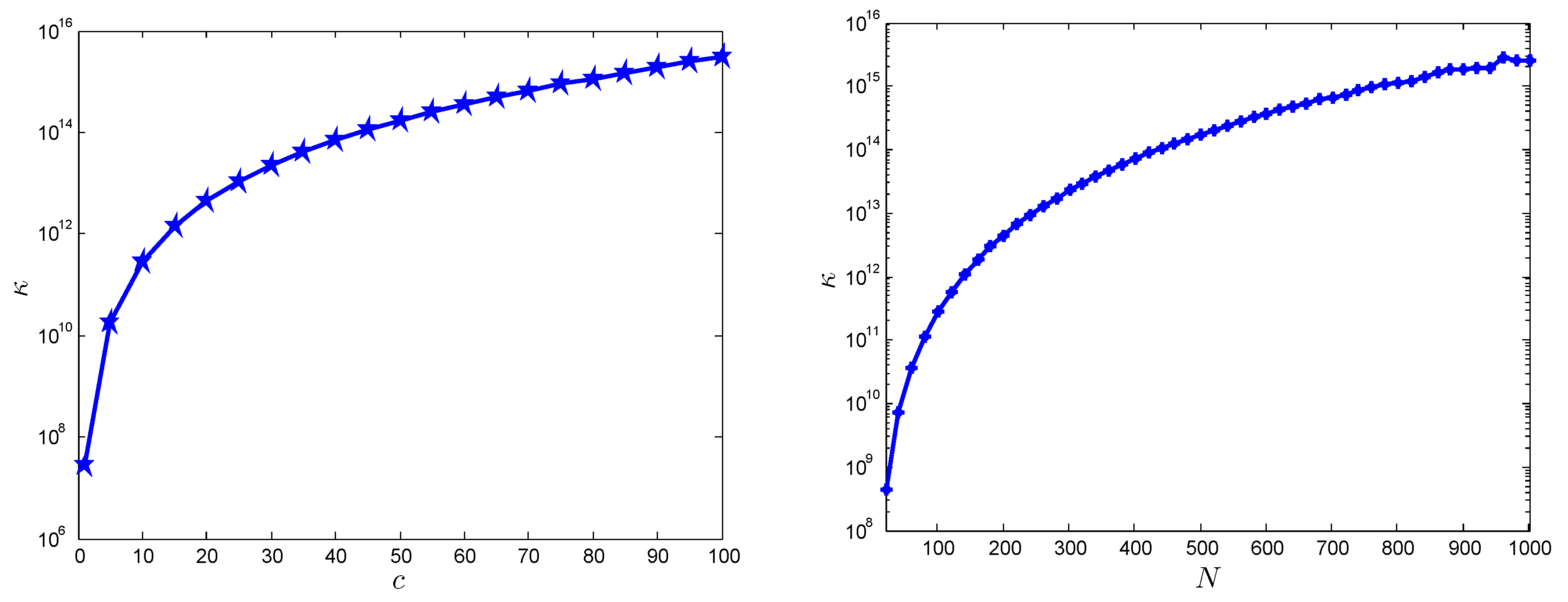
Figure 11 shows the condition number
versus shape parameter
c and number of nodal points
N, which is self explanatory.
Test Problem 4. The exact solutions for the 2D coupled Burgers’ Equation (
3) are written as [
12,
14]:
In
Table 8, the numerical results were obtained by the LMM in terms of the
error norm for Test Problem 4 using the IQ radial basis function with
. We have used different
N and
and
,
. In this table, we have compared the numerical results of the proposed Local meshless method with the local method of approximate particular solutions (LMAPS) [
15] and the local RBF-based DQmethod (LDQ) [
15]. A full agreement between the results of the LMM and the methods reported in [
15] has been observed.
In
Table 9, the performance of the LMM for Test Problem 4 is shown against the other methods [
12,
13,
14] at selected points by letting
and
,
,
. These results show the accuracy and stable performance of the LMM.
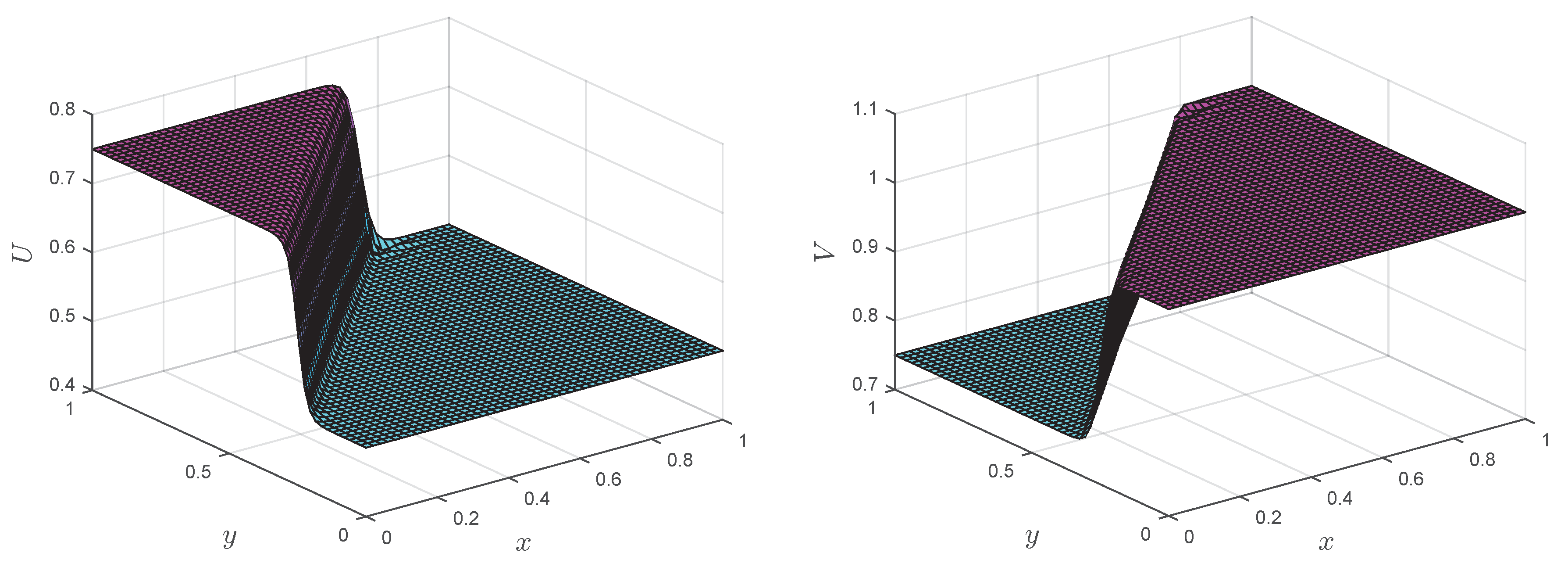
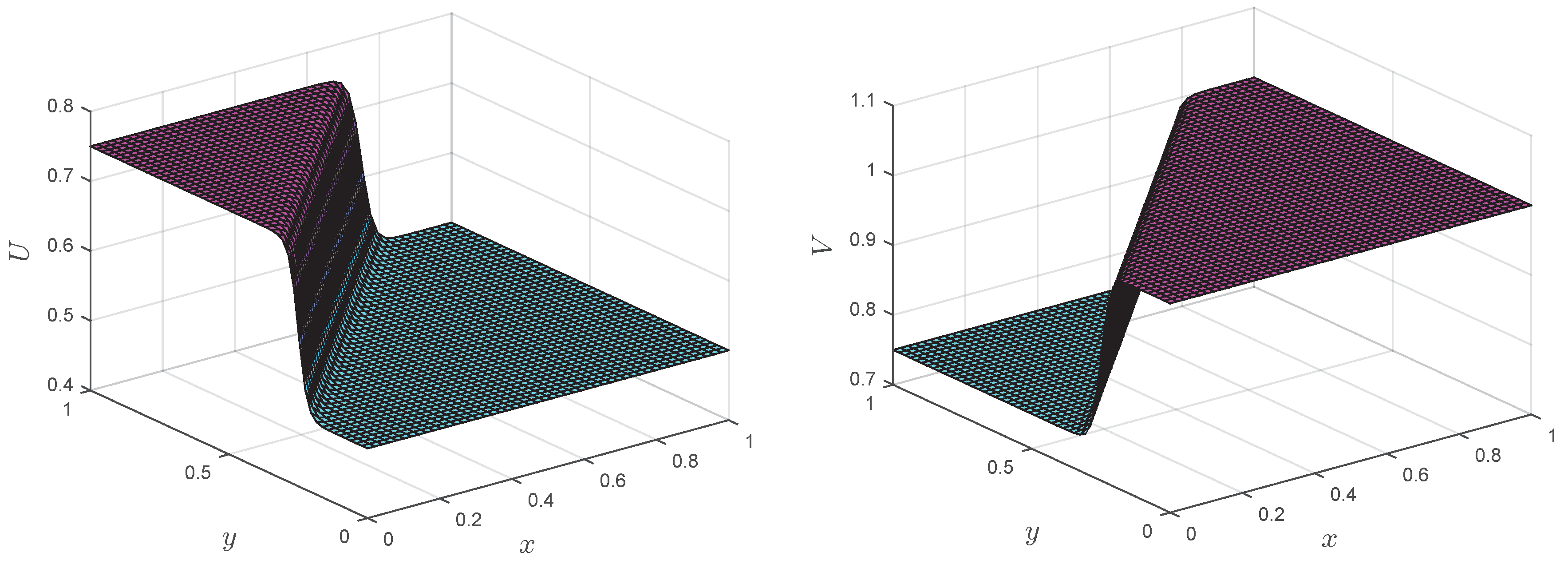
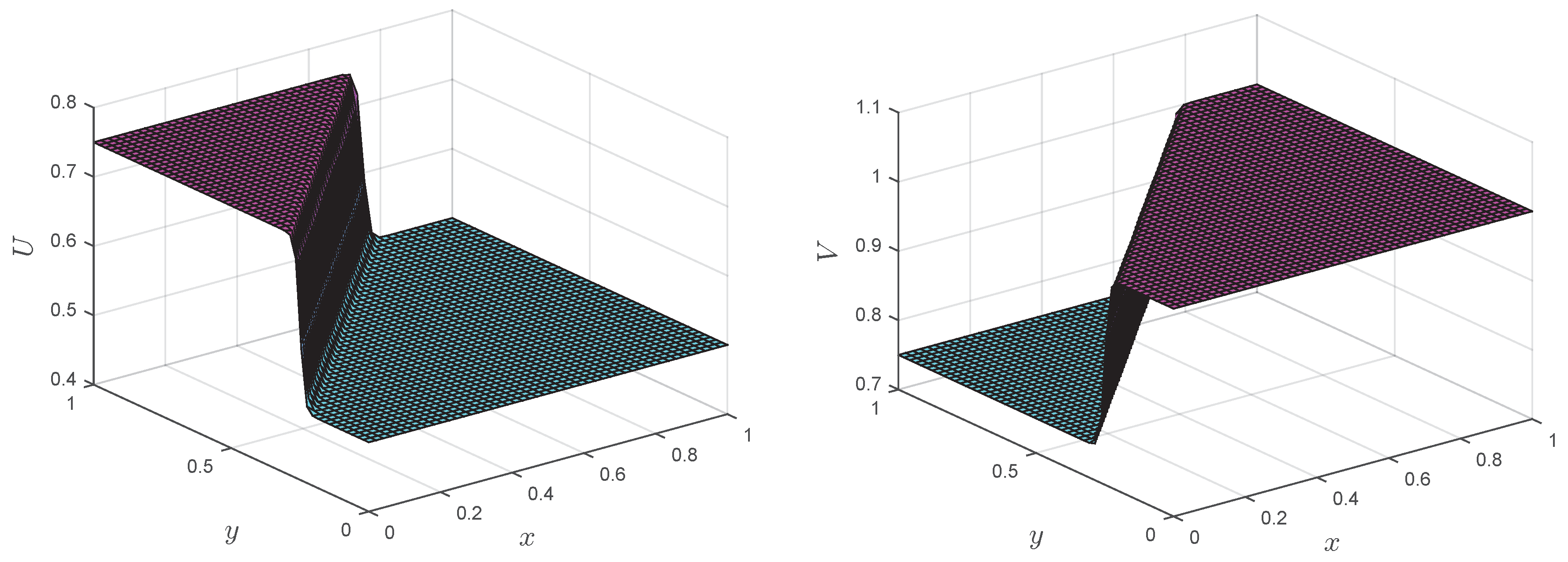
Numerical solutions of the LMM corresponding to Test Problem 4 are shown in
Figure 12,
Figure 13,
Figure 14 and
Figure 15 at different Reynolds numbers. It is clear from the figures that up to
, the proposed methods can handle the coupled Burgers’ equation, but when we increased Reynolds number, the result became unstable. In contrast, the LMM combined with the upwind technique showed stable results at
, and this phenomena can be seen in
Figure 15.
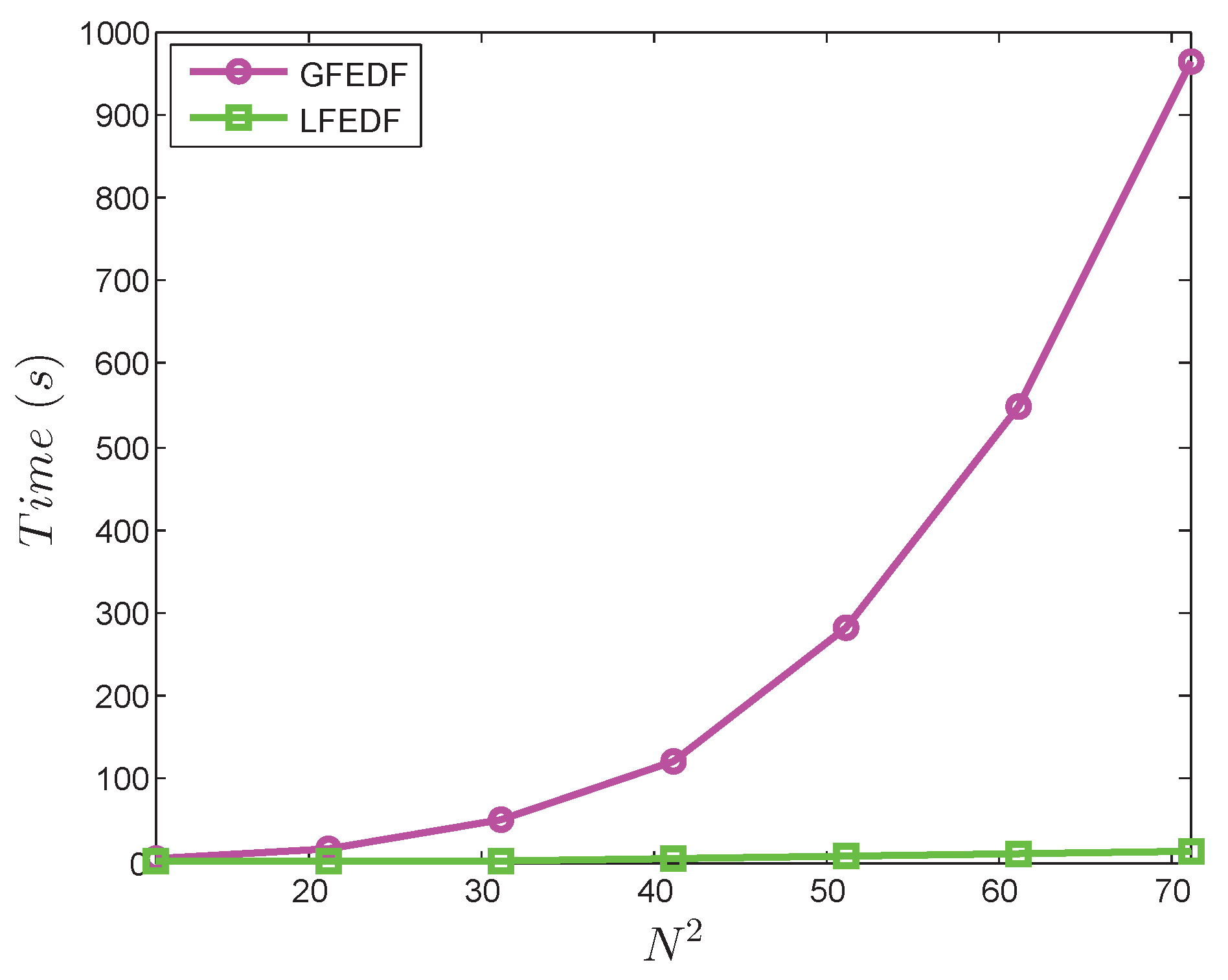
To show the computational efficiency of the LMM over the GMM, we have done a CPU time (in seconds) comparison, which is shown in
Figure 16.
Test Problem 5. Finally, consider the 2D nonlinear RLW Equation (
5) with the following exact solution:
where
and
.
The numerical results and CPU time for Test Problem 5 for
,
,
,
, and up to time
are shown in
Table 10. This table makes evident that the LMM is an accurate and efficient.
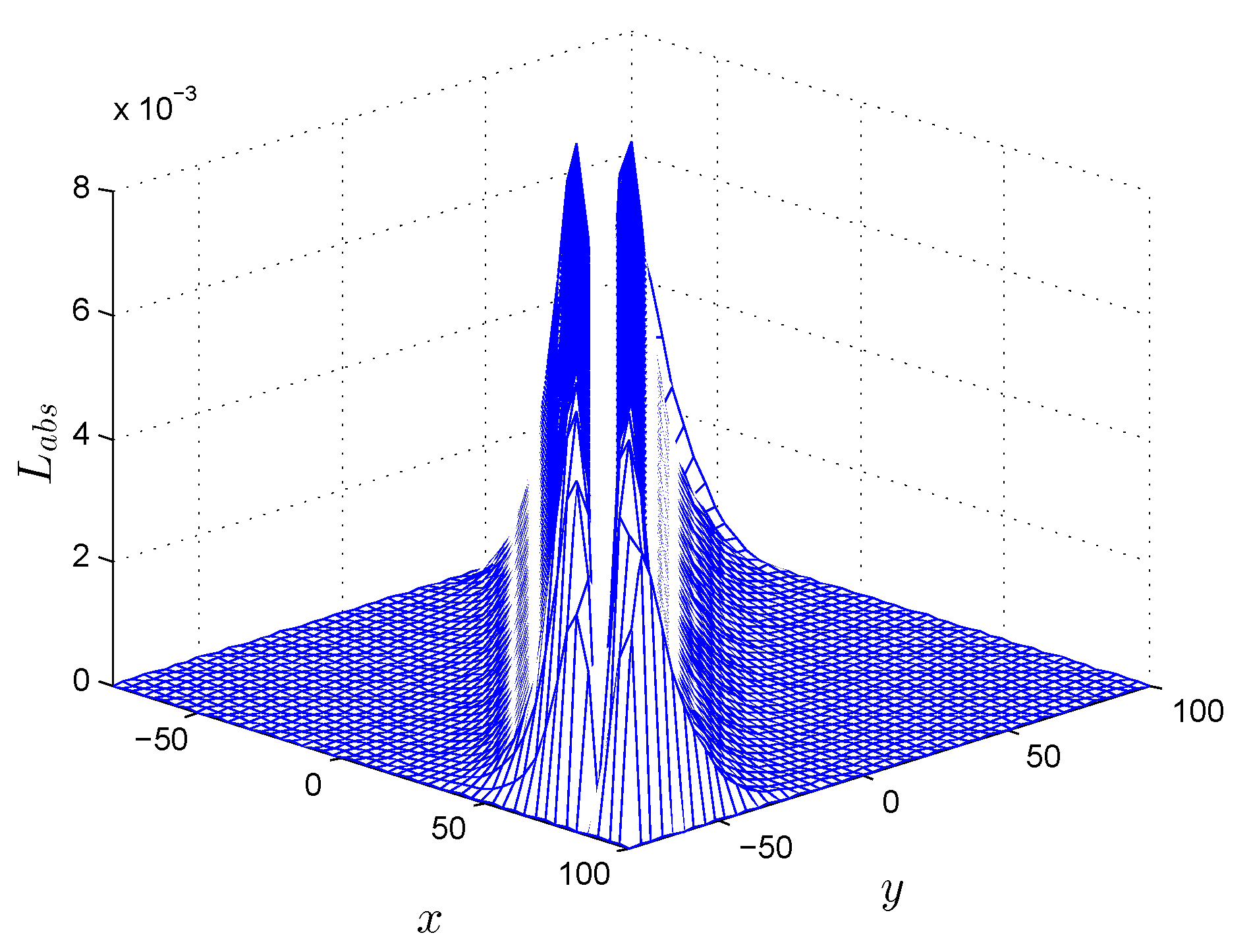
In
Figure 17, the
error is shown at
.
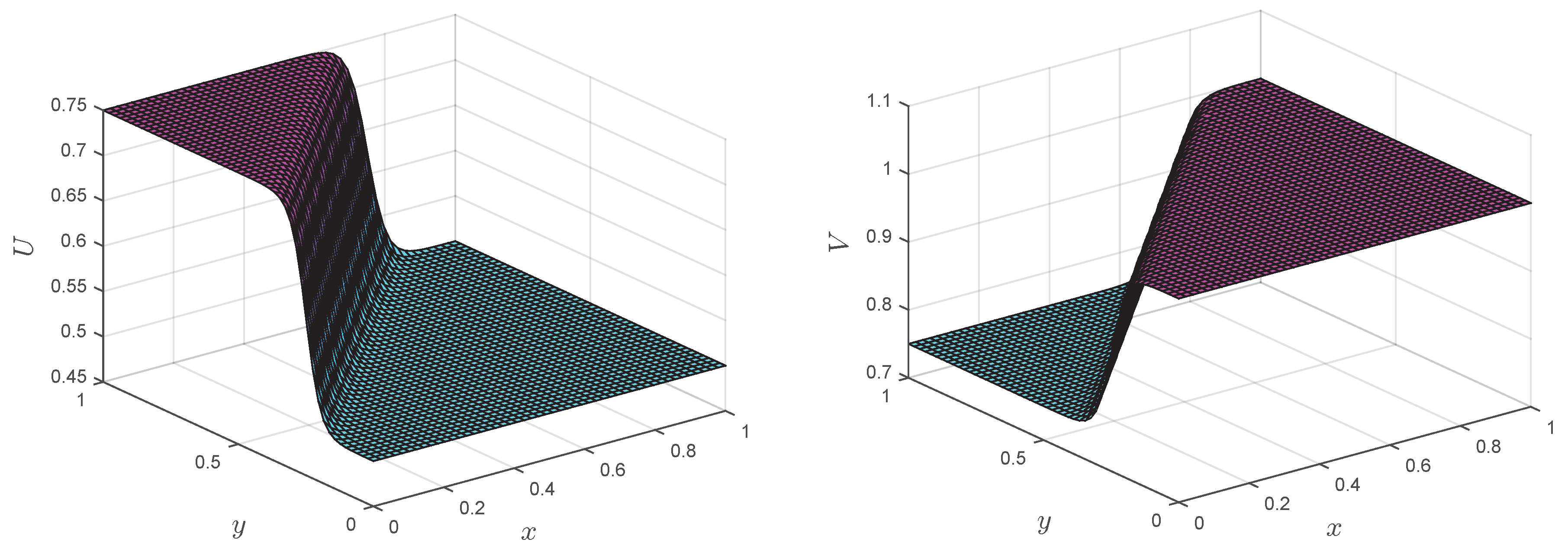
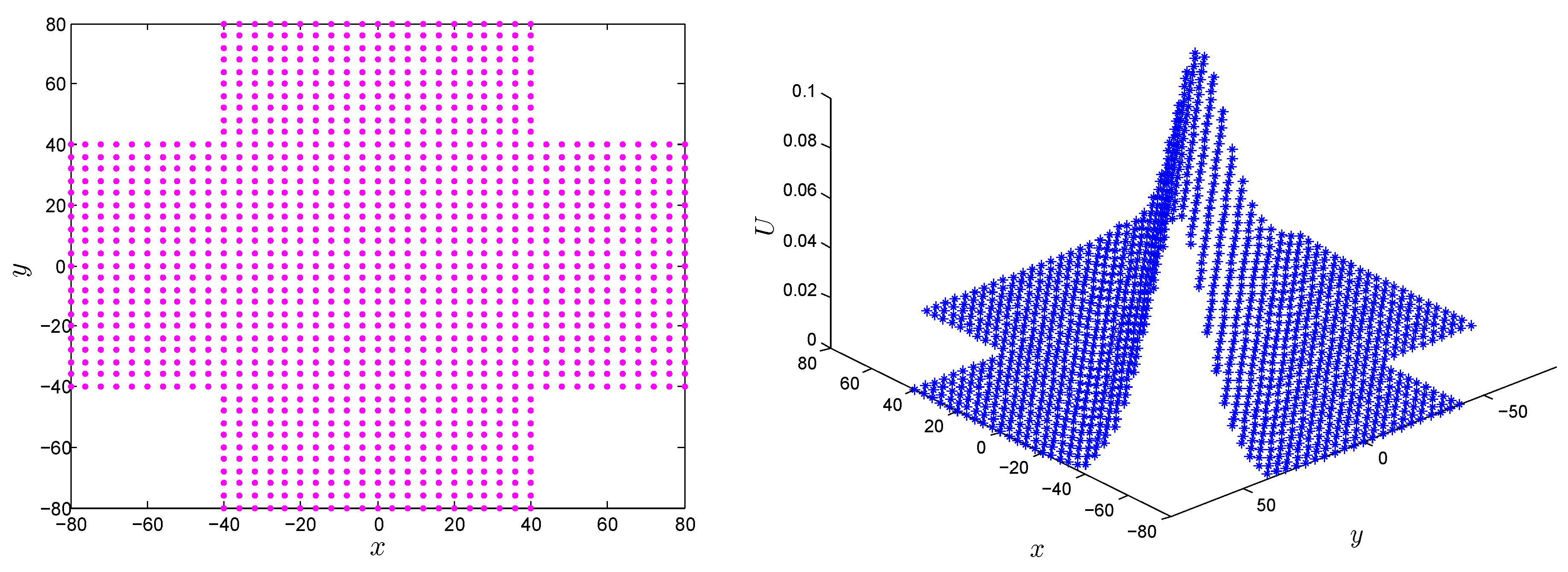
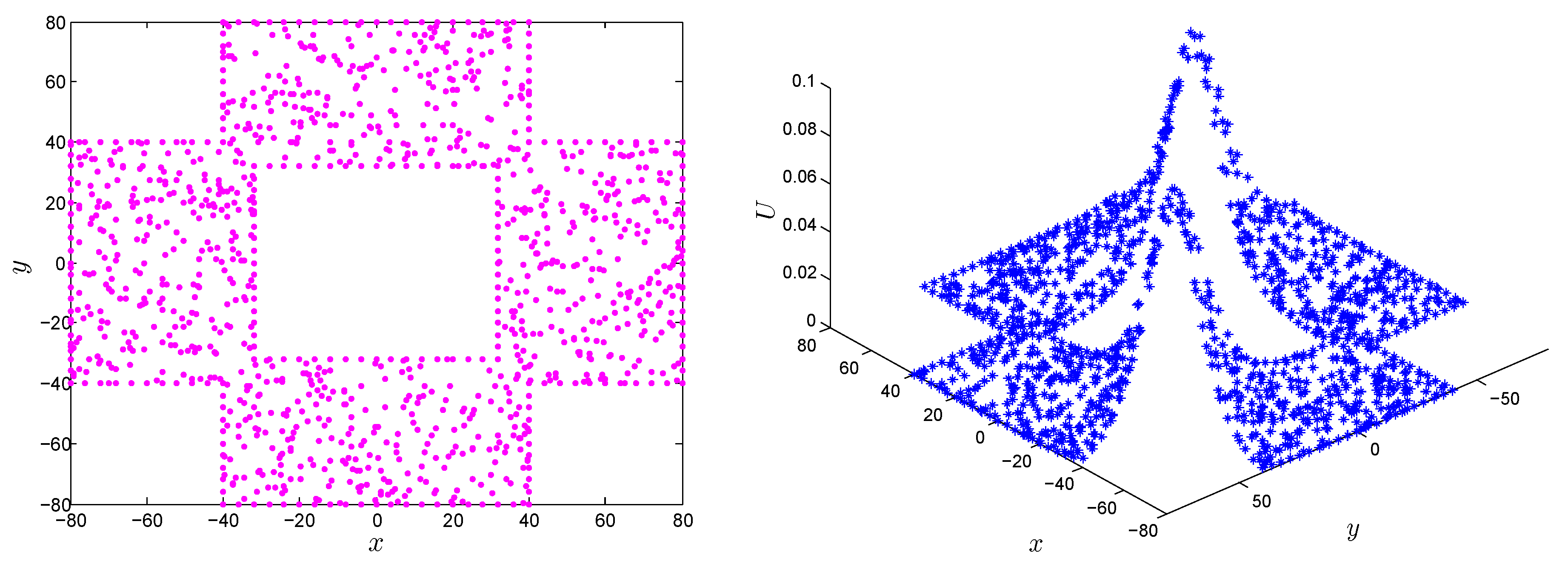
Eliminating the requirement of meshing and approximating the solution using uniform or scattered points in rectangular, as well non-rectangular domains is one of the salient features of the LMM. Numerical results of the RLW equation on non-rectangular domains are shown in
Figure 18 and
Figure 19. The
error norm of the LMM in the computational domain shown in
Figure 18 (left) and
Figure 19 (left) was
and
, respectively, at time
.