Abstract
Optimal selection of sustainable materials in construction projects can benefit several stakeholders in their respective industries with the triple bottom line (TBL) framework in a broader perspective of greater business value. Multiple criteria of social, environmental, and economic aspects should be essentially accounted for the optimal selection of materials involving the significant group of experts to avoid project failures. This paper proposes an evaluation framework for solving multi criteria decision making (MCDM) problems with incomplete weight information by extending the combinative distance assessment (CODAS) method with interval-valued intuitionistic fuzzy numbers. To compute the unknown weights of the evaluation criteria, this paper presents an optimization model based on the interval-valued intuitionistic fuzzy distance measure. In this study, we emphasize the importance of individual decision makers. To illustrate the proposed approach, an example of material selection in automotive parts industry is presented followed by a real case study of brick selection in sustainable building construction projects. The comparative study indicates the advantages of the proposed approach in comparison with the some relevant approaches. A sensitivity analysis of the proposed IVIF-CODAS method has been performed by changing the criteria weights, where the results show a high degree of stability.
1. Introduction
Selecting the right material to develop a particular product is essential for each of the organizations to survive in the competitive business sectors. One suitable material can substantially minimize the production cost and maximizes the profit. It is also needed to improve the product performance and customer satisfaction. Due to the presence of varieties types of almost similar kind of materials, the task of material selection has become one of the most challenging tasks in the real life environment [1,2,3]. Thus, the material selection process is essential in many practical industrial problems like automotive parts manufacturing, selection of robots and forklifts, designing the femoral component of cemented total hip/knee replacement, building constructions, etc. Hence, in the last few decades, several researchers have focused on this domain. This paper deals with the material selection problem with sustainability perspectives for a construction company.
The material selection problem (MSP) in the presence of imprecise and incomplete information is regarded as an important area of research where researchers try to solve ill-structured complicated real circumstances. Researchers have applied classical fuzzy set theory (CFST) to explore and solve the MSP under uncertain environment where they mainly considered the individual performance of every material. Due to the complicated and ill-structured characteristics and several practical contexts of MSP, it is necessary to adopt/use newer advanced techniques which can flexibly handle uncertain data while assessing the performance of alternative materials. In the recent years, many researchers have proposed novel methods for solving MSP under uncertainty, such as, two interval type 2 fuzzy TOPSIS method [4], interval 2-tuple linguistic model [5], and soft computing tool based on fuzzy grey relations [6]. However, only a few researchers [7] have used interval-valued intuitionistic fuzzy sets (IVIFSs) in MSP under incomplete weight information. The IVIFS theory [8] is more practical and reliable approach than CFST for handling imprecision and fuzziness in DMs’ judgments in real world decision making problems. IVIFS considers both the degree of membership and nonmembership value of a component in a given set and they can take interval values rather than exact numbers. When DMs often find it difficult to evaluate the uncertain material performance with just a single valued number using CFST, IVIFS offers more flexibility and DMs get an extra degree of freedom to evaluate the same. Hence, it has become considerably important to explore MSP under uncertainty with more efficient and appropriate mathematical approaches that use the IVIFSs for better handling of imprecise information. Due to its inherent flexible nature, recently many authors have contributed on IVIFS and applied it in decision problems. Some significant contributions of IVIFS in decision making problems are narrated below. Cheng [9] proposed a decision making method to select hotel locations using IVIFS, where the authors used IVIFS to denote the values and weights of the attributes. Wen et al. [10] introduced a new method to aggregate the IVIFNs when they are distributed all over a region. For that purpose the authors studied the interval-valued intuitionistic fuzzy definite integral and based on that they proposed interval-valued intuitionistic fuzzy definite integral (IVIFDI) operator. Rashid et al. [11] studied interval-valued knowledge measure for the IVIFSs by extending the knowledge measure of IFSs and proposed interval-valued information entropy measure for IVIFSs. Wang and Chen [12] proposed a decision making method using IVIFSs, linear programming (LP), and the extended TOPSIS method, where they used LP methodology to obtain optimal weights of attributes. Gupta et al. [13] combined extended TOPSIS and LP method to propose a multi-attribute group decision making (MAGDM) method in the context if IVIFS. Interval-valued intuitionistic fuzzy matrix (IVIFM) was used by Das et al. [14] to propose a decision making approach, where the authors assigned confident weights to the experts and then presented a decision making algorithm [15].
MSP has been recognized as an MCDM problem [7] and one has to take care of several criteria (sometimes referred as objectives) systematically, such as enactment, cost, use, mobility, transportation, availability, disposal, environmental norms, maintenance, etc., while seeking the best material [1,2,3]. The applicability of MSP in the context of MCDM to design a product/service has been explored in the literature survey segment of this paper. The availability of numerous MCDM tools has helped the DMs to identify and select the optimal choice for their MSP (refer to Section 2.2). The CODAS method is a new evaluation tool, recently proposed by Ghorabaee [16], has been proved to be efficient to deal with MCDM problems. Due to its inherent characteristics, the CODAS method possesses a systematic and simple computation procedure which is logically sound to represent the underlying principle of real life decision making problems. Thus, it has become significant to incorporate CODAS method in MSP for evaluating and ranking the alternative materials under incomplete criteria weight information and IVIFNs context.
The above-mentioned deliberations motivate us to extend the CODAS method for material selection problems (MSPs) under uncertainty. Then the extended CODAS method is used to develop a novel MCDM framework using IVIFNs under difficult situations where criteria weight are partial known or totally unknown. The projected MSP solution procedure is able to replicate both subjective judgments and objective information in practical engineering, manufacturing, and industrial problems in the context of IVIF. Finally, one illustrative example is given to examine the proposed IVIF-CODAS method for MSP followed by a real case study which is demonstrated for a sustainable building construction company. The outcomes of the proposed research framework can help DMs (engineers, manufacturers, and designers) to have an effective decision for complicated MSPs in uncertainty.
The rest of the paper is structured as follows. Section 2 offers a literature review of MSP and sustainability perspectives along with IVIFSs and MCDM. Section 3 discusses the preliminaries on IVIFSs. Next, the extended CODAS method with IVIFNs and incomplete weight information is presented in Section 4. Two illustrative examples are discussed in Section 5 to show the usefulness of the projected evaluation framework. Section 6 explains the outcomes through result comparison and sensitivity analysis while Section 7 concludes the current research work.
2. Literature survey
2.1. Material Selection in Construction Industry and Sustainability
The construction industry has been revealed as the fastest growing industry throughout the world due to the constant increase in urban population. This fastest growth has influenced the society for better economic and social movement and simultaneously has triggered the environmental pollution factors. Some researchers [17,18,19] investigated that the energy used ratio in recent infrastructures is six times more than that of the older ones, especially in United Arab Emirates (UAE). Furthermore, it was documented (https://ccap.org/assets/Success-Stories-in-Building-Energy-Efficiency_CCAP.pdf) that the construction industry consumes 40% of the world’s energy. These factors had inspired many countries to consider eco-friendly infrastructures such as buildings which gives more importance to sustainable construction rather than economic concerns [3]. Since sustainable construction has a direct impact on environment, economy, and society, the construction agencies are continuously trying to adopt it in their work cultures mainly in the form of sustainable design, structure, and material selection. This kind of changed scenario has drawn the focus of many researchers and consequently, several research works have been carried out on sustainable construction. As a pioneer of this concept, Kibert [20] stated that “Sustainable construction is the creation and responsible management of a healthy built environment based on resource efficient and ecological principles”. Among many other sustainable construction factors, sustainable material selection imparts a key role and directly effects building sustainability. Radhi [21] performed an experiment on UAE construction and found the impact of UAE construction on global warming. Elchalakani and Elgaali [22] combined the effects of recycled aggregate and recycled water and discussed the strength and durability of recycled concrete. The authors prepared a moderate strength concrete using recycled water and recycled aggregate obtained from construction wastes. Al-Hajj and Hamani [23] investigated the existing studies regarding the sources of waste and suggested some measures to reduce it. The authors noticed that the lack of awareness and poor design were the main causes of material waste. Despite the need to explore MSP in construction projects under sustainability perspectives, only a few research papers [18,24,25] are found in the literature. A more extensive literature survey can be found in [18,23]. As per our knowledge, no researcher has explored the MSP with sustainability norms in the Indian scenario. Hence, this paper attempts to fill this gap and enrich the literature of MSP in sustainable construction projects.
2.2. MSP and Various MCDMs
To find the optimal choice of MSP in construction and design engineering, one can consider diverse methodologies, such as MCDM techniques, statistical approaches, artificial intelligence, mathematical programming, and hybrid methods. Among them, MCDM tools are most widely used for MSP, since they can easily and successfully solve the evaluation problems that are complex and have multiple conflicting objectives/criteria. For example, Bahraminasab and Jahan [26] applied a comprehensive VIKOR (VIsekriterijumska optimizacija i KOmpromisno Resenje) method to find the best material for a femoral component of total knee replacement. A new framework was developed by Jahan et al. [27] for weighting of criteria in MSP. Chauhan and Vaish [28] proposed a hybrid evaluation model including entropy, VIKOR, and TOPSIS (Technique for order preference by similarity to ideal solution) methods to select the soft and hard magnetic materials. Interval 2-tuple linguistic VIKOR [3], multi-objective optimization on the basis of ratio analysis [29] (MOORA), complex proportional assessment [30] (COPRAS) are also successfully used in MSP. In recent years, Anojkumar et al. [31] used fuzzy AHP (Analytic Hierarchy Process), VIKOR and TOPSIS for MSP in the sugar industry. Furthermore, interval type 2 fuzzy TOPSIS [4], Multi-Attributive Border Approximation area Comparison [7] (MABAC), hybrid MCDM framework with DEMATEL, ANP and TOPSIS models [18], neutrosophic MULTIMOORA [32], and grey-correlation-based hybrid MCDM method [33] are notable contributions in MSP in recent times. All the authors except Xue et al. [7] have used either fuzzy sets or crisp sets.
Although many material selection methods are available in the literature, still there is a need to explore the MCDM techniques by incorporating IVIFS theory. IVIFNs remove the limitations of CFST and offer a more rational and computational flexibility to address uncertainty and ambiguity in data. IVIFS theory is receiving much interest from researchers and has been effectively used in a diverse domain of real life problems. This motives us to extend the CODAS method with IVIFNs and apply it to two real problems with incomplete criteria weight information. In this article, the readers will find a systematic and comprehensive research framework for MSP, which is capable of discoursing with the subsequent research questions: (1) what are the sustainability indicators for MSPs in construction projects in India? (2) How to set priorities of these indicators in the evaluation process? (3) Which should be the optimal choice for a sustainable alternative (here, brick) for building construction?
3. Preliminaries
This section reviews the related ideas. Interval-valued intuitionistic fuzzy set (IVIFS) [8] is a generalization of intuitionistic fuzzy set (IFS). Compared to IFS, where the values of membership and non-membership functions are exact numbers, an IVIFS has the characteristic that those values are in intervals [0, 1] instead of exact numbers. Hence, IVIFS is more suitable in uncertain situations.
Definition 1.
Letbe a universal set. An IVIFSinis expressed as
whereandare respectively the interval-valued degrees of membership and non-membership of an elementto, and the sum of upper bounds of these two interval-valued degrees is not greater than 1,. Ifandthen the IVIFSis reduced to IFS, denoted by, whereand. Hence, Atanassov’s IFS can be considered as a special case of IVIFS.
For a fixedan objectis called interval-valued intuitionistic fuzzy number (IVIFN). Letbe an IVIFN, whereand. Then the score function [34,35]ofis defined as, where. The accuracy function [34,35]ofis defined aswhere.
Xu and Jian [35] compared two IVIFNs using score and accuracy functions which is defined below.
Letandbe two IVIFNs, then
- Ifthen
- If, then
- If, then;
- If, then
Xu and Chen [36] proposed a similarity measure between two IVIFNs β1 = ([p1, q1], [r1, s1]) and β2 = ([p2, q2], [r2, s2]) defined as
Let β = ([p,q], [r,s]), β1 = ([p1,q1], [r1,s1]), β2 = ([p2,q2], [r2,s2]) be three IVIFNs and λ > 0. Some of their basic operational laws [34,37] are given below.
- (1)
- 1 − β1 = β1c = ([r1,s1], [p1,q1])
- (2)
- β1 ∩ β2 = ([min(p1,p2), min(q1,q2)], [max(r1,r2), max(s1,s2)])
- (3)
- β1 ∪ β2 = ([max(p1,p2), max(q1,q2)], [min(r1,r2), min(s1,s2)])
- (4)
- β1 + β2 = ([p1 + p2 − p1p2, q1 + q2 − q1q2], [r1r2, s1s2])
- (5)
- β1 · α2 = ([p1p2, q1q2], [r1 + r2 − r1r2, s1 + s2 − s1s2])
- (6)
- λβ = ([1 − (1 − p)λ,1 − (1 − q)λ], [rλ, sλ])
- (7)
- βλ = ([pλ, qλ], [1 − (1 − r)λ,1 − (1 − s)λ])
Definition 2.
Let βj = ([pj, qj], [rj, sj]) (j = 1,2,…,n) be a collection of IVIFNs, and w = (w1,w2,…,wn)T be their associated weight vector, with 0 ≤ wj ≤ 1 and then he interval valued intuitionistic fuzzy weighted geometric (IVIFWG) operator is defined as
Definition 3.
According to Park et al. [38] the distance measures between two IVIFSs are defined as follows:
The Hamming distanceand Euclidean distancefor the IVIFNs β1 = ([p1, q1], [r1, s1]) and β2 = ([p2, q2], [r2, s2]) are computed as:
Definition 4.
Letandbe two IVIFNs in the universe X = {x1, x2, …, xn }, then the distance measure betweenandis defined as follows:
Particularly, if λ = 1, then Equation (6) becomes the Hamming distance:
If λ = 2, then Equation (6) is degenerated to the Euclidean distance:
4. Proposed CODAS Method Using IVIFNs
This section presents an extension of the CODAS method based on IVIFS to deal with MCDM problems. Let D = {d1, d2, …, dl} be the group of decision makers, C = {c1, c2, …, cn} be the set of criteria, and A = {a1,a2,…,am} be the set of alternatives. The group of experts/decision makers D = {d1, d2, …, dl} provide their opinions regarding the criteria C = {c1, c2, …, cn} corresponding to each alternative A = {a1, a2, …, am} using linguistic terms which are presented by IVIFNs. In this algorithm, we consider that significance of individual decision makers are different and the weights of the decision makers are expressed using fuzzy membership grades. We also consider that opinions of individual decision makers about the importance of various criteria are different. A flow chart of the proposed approach is given in Figure 1.
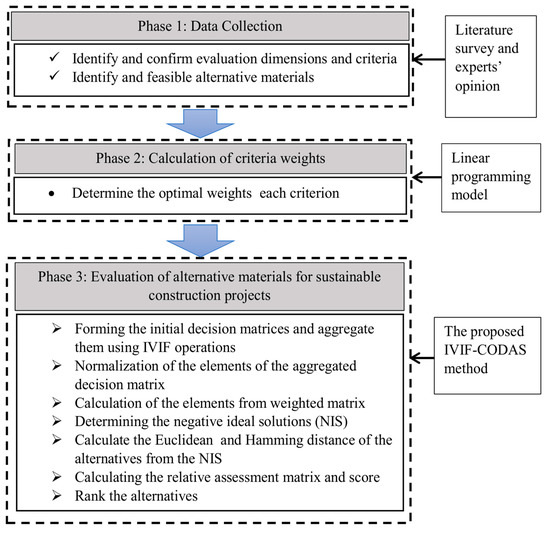
Figure 1.
Flow diagram of the proposed IVIF-CODAS.
A step wise illustration of the proposed approach is given below.
Step 1. Opinion of each expert is expressed using decision matrix given below.
Here denotes the evaluating value of th () alternative with respect to th criterion and th () decision maker which is expressed as IVIFNs.
Step 2. Interval-valued intuitionistic fuzzy weighted geometric (IVIFWG) aggregation operator is used to aggregate the opinion of individual decision makers. The aggregated/collective decision matrix is formed as
where and be the number of decision makers.
Step 3. Calculate the weights of evaluation criteria
Let be the weight vector of the criteria , , where and . The known criteria weights are divided into five basic ranking forms [39,40,41] for as given below:
- (1)
- A weak ranking: ;
- (2)
- A strict ranking: ;
- (3)
- A ranking of differences: ;
- (4)
- A ranking with multiples: ;
- (5)
- An interval form: ;
For simplicity, let H denote the set of criteria weight information given by DMs and This approach uses the known criteria weight information to define the weights of evaluation criteria.
In MSP, the significance of a criterion is determined by evaluating the performance values of the alternatives for that criterion. When the performance values of the alternatives differ a little for a particular criterion, then that criterion is considered to be less significant for choosing the best material. Similarly, when the performance values of the alternatives differ much for a particular criterion, then that criterion is considered to be much significant for choosing the best material. This observation leads to assign less weight to the less significant criteria and more weight to the much more significant criteria [42]. A criterion is said to have no significance in the material selection process when the performance values of the alternatives are same for that criteria [43].
When the criteria weight information is partially known, this paper presents an optimization model using the IVIF distance measure to compute the evaluating criteria weights. Below, we define the distance between the alternative and other alternatives corresponding to the criterion .
The overall distance measures of all the alternatives for the criterion is presented as:
Next the weighted distance function is formulated as given below.
Hence, a suitable weight vector of criteria is needed to maximize and therefore, we can present the optimization model defined below:
The optimal solution is obtained by solving the model (M − 1). We use the optimal solution as the weight vector for the evaluation criteria.
In another case, when the information concerning criteria weights is totally unknown, we can develop another model for optimization to find the optimal weights of criteria:
Lagrange’s method is used to solve the preceding Model (15) and the corresponding optimal solutions are normalized to determine the criteria weight vector.
Step 4. The collective decision matrix is normalized by determining the highest IVIFN under each criterion for all the alternatives and then performing the division operation of between the highest IVIFN and the corresponding IVIFN as given below.
where
In the above operations, and respectively represent the sets of benefit and cost criteria, and denote the normalized performance values in terms of IVIFNs.
Step 5. The weighted normalized decision matrix is determined by performing product operation between the aggregated criteria weights and the normalized performance values of the criteria corresponding to the alternatives, which is give below. It is noted that both the aggregated criteria weights and the evaluating values are expressed as IVIFNs.
where
Here the weight of th criterion is denoted by .
Step 6. The interval-valued intuitionistic fuzzy negative ideal solution is computed as
where . Here is an IVIFN for each criterion
Step 7. IVIFN-based Hamming (HD) and Euclidean distances (ED) of the alternatives from the interval-valued intuitionistic fuzzy negative ideal solution () are computed as
Step 8. The relative assessment matrix (RA) is computed as
where
where and is a threshold function defined below.
Decision maker can set the threshold parameter (). Here we consider .
Step 9. The assessment score () of each alternative is computed, which is given below.
5. Application of the IVIF--CODAS in MSPs
5.1. Illustrative Example
Here, a MSP is illustrated to show the applicability and effectiveness of the proposed IVIF-CODAS approach. We have considered an automotive parts factory in India [7], where the factory want to find the best material for the automotive instrument panel. In the selection process, a group of five experts/decision makers () evaluates four materials/alternatives () based on the values of eight evaluation criteria () and finds the suitable alternative. The structure of the problem in given in Figure 2. The linguistic assessments (using Table 1) of the alternatives given by the decision makers are shown in Table 2. This example assumes that the group of five decision makers and the set of eight criteria have their individual weights/importance. The weights of decision makers and criteria are respectively expressed using fuzzy membership grades and IVIFNs.
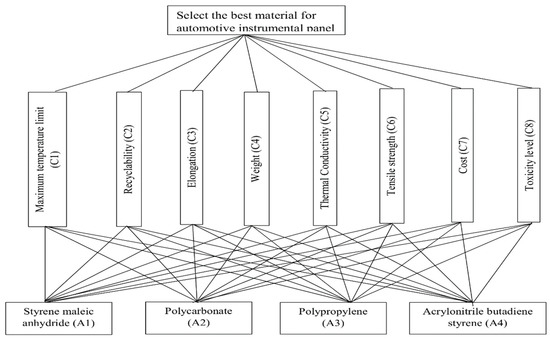
Figure 2.
Structure of material selection in automotive industry.

Table 1.
Linguistic terms and corresponding IVIFNs for evaluating materials.

Table 2.
Decision matrix with linguistic ratings.
- The collective decision matrix is shown in Table 3 which is computed by aggregating the opinions of the decision makers (DM1, DM2, …, DM5).
 Table 3. Collective decision matrix.
Table 3. Collective decision matrix. - The consensus making model [39] is used to determine the weights of the evaluation criteria. In our study, the criteria weights are unknown while the weights of experts () are known in advance. Hence, applying model () and assuming that the criteria weights are partially known as follows: . To compute the criteria priorities, Equations (16)–(18) and model (M − 1) are used to develop the linear programming model given below:
- The final criteria weights () are obtained by solving the above model and they are represented by the following weight vector .
- Weighted normalized decision matrix, shown in Table 4, is computed by finding the normalized decision matrix and then combining the criteria weights obtained in the previous step with the normalized decision matrix.
 Table 4. Weighted normalized decision matrix.
Table 4. Weighted normalized decision matrix. - Interval-valued intuitionistic fuzzy negative ideal solution for each of the criteria is shown in Table 5.
 Table 5. Negative ideal solutions.
Table 5. Negative ideal solutions. - Hamming distance and Euclidean distance of the alternatives from the Interval-valued intuitionistic fuzzy negative ideal solution is shown in Table 6.
 Table 6. Euclidean and Hamming distance matrices.
Table 6. Euclidean and Hamming distance matrices. - Relative assessment matrix, assessment scores, and rank of the alternatives are given in Table 7.
 Table 7. Assessment matrix and scores.
Table 7. Assessment matrix and scores. - Table 8 shows the ranking orders by the proposed method along with four other existing methods for result comparisons.
 Table 8. Comparison with other models.
Table 8. Comparison with other models.
5.2. A Real Case of MSP in Sustainable Construction Projects
This section presents a sustainable material selection problem for construction projects using the proposed IVIF-CODAS approach. Applicability and usefulness of the proposed model are validated through a real case study of a construction company. Initially, we sent our research proposals to 10 national builders, who are associated with construction, materials supply, and providing services mainly in India. Three out of ten companies provided positive responses to our proposal and our research team accomplished necessary groundwork on these three construction companies which are located in the “Durgapur-Asansol” division of West Bengal. We have had selected “Maha Prabhu Buiders: A national company (name changed)” for implementing our proposed research framework. The company has several operating units all over the country. The primary goal of this study is to provide wide-ranging results by incorporating the perceptions of all actors in the construction field since this research work is completely based on the decision makers’ (refer to Table 9) judgments. Therefore, we integrated some major perspectives: clients, the Construction Company, manufacturers, consultants, and material suppliers.

Table 9.
Description of experts.
The main reason for selecting “Maha Prabhu Buiders” over other two volunteering companies is because they arrange for all kind of services such as construction, consultants and architects, material suppliers, and so on. The central public works department (CPWD-2014) of India has been promoting the norms and guidelines of sustainable construction in India to increase the awareness in public, private sectors, and most importantly among the habitants. Following to the CPWD (2014) guidelines, this particular company has been striving in sustainable construction projects and most of all other activities. The general manager discussed with our team and informed the new trend in clients. The trend is not limited to embracing the concept of sustainable design of buildings but also in materials (bricks, mortar, concrete, cement, plasters, etc.). Hence, they recognized our research framework, and acknowledged the results that will classify which sustainable materials are most preferable. The consultant will endorse these results, and as a product manufacturer, the company can advertise that specific material with its sustainability indicating tags. On acceptance of the research proposal, we arranged a three-day workshop for the managing directors of the company, architects, and aforementioned clients who encourage sustainability issues in designing buildings as well as selecting materials, engineers and skilled professionals from the company. The problem goal and structure were explained to all the participants and, after several rounds of discussion, the materials selected to be evaluated are burnt clay bricks. Bricks are used substantially in almost every type of construction projects including bridges, housing, firms, hospitals, etc.
As soon as the usefulness of the proposed framework was revealed, our research team began the preliminary investigation on the sustainable alternatives of burnt clay bricks. We found there are three popular alternative bricks which are usually used in sustainable construction projects. The detailed description and characteristics of alternatives bricks can be found in Dhanjode et al. [44] and Mahendran et al. [45].
For evaluating the alternative bricks for sustainable practices, the team of experts () conducts the performance testing to decide the most suitable brick. Next, the sustainable indicators are considered as evaluation criteria which were recommended by the team of experts of the company and approved with the literature. In this concern the proposed framework is applied to find the most sustainable brick(s) based on the considered criteria of sustainable practices in construction industry. To accomplish the purpose of this assignment, a three-phase methodology was used: data collection, data aggregation using IVIFWG operator, and evaluation of bricks and selecting the most suitable brick(s) using extended IVIF-CODAS method. The decision structure of the problem is depicted in Figure 3 in which the goal of this project is located in the top level, followed by the most cited factors and criteria of sustainability. Final level of the hierarchy deals with evaluation of the alternative bricks as sustainable material for building construction.
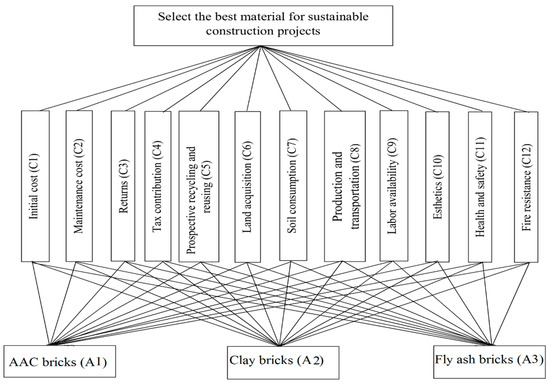
Figure 3.
Structure of sustainable material selection problem in construction industry.
In the selection process, a group of five experts () evaluates three sustainable materials/bricks () based on the values of twelve evaluation criteria () and finds the suitable material. Similar to the previous case study, the preferences of the decision makers about the materials against the criteria are given in linguistic terms as shown in Table 1. This example also assumes that the group of five decision makers and the set of twelve criteria have their individual weights/importance. The weights of decision makers and criteria are respectively expressed using fuzzy membership grades and IVIFNs. The structure of the sustainable material selection problem is given below in Figure 3.
Step 1.Data collection
After finalizing the hierarchical structure (Figure 3) of brick selection problem the required data are collected for conducting the evaluation process. For evaluating the sustainable material for construction projects, sustainability parameters are regarded as criteria in this study. In search of the most suitable sustainability parameters, we go through the present literatures available in reliable journals such as Taylor & Francis, Elsevier, MDPI, and Springer. Articles with environmental, economical, and social sustainability indicators and sustainable material selection and evaluation in the context of the construction and manufacturing projects were selected for this research work. After discussion with the relevant professionals, some criteria were selected which are given in Table 10. Next, each decision maker opined on the importance of individual criterion. Finally, the alternatives (list of bricks) were designed, which was already completed in previous steps.

Table 10.
Objectives and criteria.
Step 2.Calculation of criteria weights
Similar to previous example, according to model and Equation (14), the weight vector of the three objectives/dimensions (economic, environmental, and social) is calculated as . Likewise, the local and global criteria weights are computed and presented in Table 11.

Table 11.
Aggregated weights of sustainable material selection indicators.
Step 3.Evaluating the best sustainable material using IVIF-CODAS method
The IVIF-CODAS method is used to prioritize the optimal choice for sustainable material selection problem. We follow the step-by-step calculation mechanism is discussed in Section 4 and phase 3 in Figure 1. The mechanism includes fuzzy aggregation of individual judgments followed by normalization. The criteria weights that are obtained using Equations (11)–(16) in the second phase are lodged via Equation (20) to the normalized data yielding weighted normalized decision matrix. Next, we find the negative ideal solutions (NIS) are defined in Equation (21), which are used as criteria reference points to obtain optimal solution. The Euclidean (ED) and Hamming (HD) distances between the interval-valued intuitionistic fuzzy negative ideal solution and criteria functions in the weighted normalized decision matrix(R) are calculated using Equation (19). Finally, we determine the relative assessment matrix (RA) which is computed according to Equation (24). Now, assessment score of each alternative material is calculated taking the column sum of the RA matrix. Ultimately, the alternative/material with highest assessment score is the most desirable alternative in the material selection problem. In our problem, we find the “Fly ash bricks ()” is the optimal choice for sustainable construction projects in India.
6. Result Discussion
The goal of this section is to analyze the results of the proposed framework in order to validate its rationality and practicality. For exploring the most significant dimensions/aspects of construction projects and to avoid complexity, the sustainability indicators (criteria) were classified into 3 major aspects of sustainability. To keep it simple, we assume all three dimensions should be equally important. On contrast, each individual criterion has its own importance as a sustainable indicator for evaluating sustainable materials in construction industry. Table 11 demonstrates economic (), environmental (), and social () aspects including the corresponding criteria within them. From Table 11, it is clear that “Prospective recycling and reusing” (), “Returns” (), and “Use of local material” () are top three important criteria among the twelve sustainable indicators considered here. However, usually there are conflicting concerns on priorities of the economic and environmental factors [18]. Hence, it becomes difficult to adjust them under such conflicts. However, in the viewpoint of sustainable construction in India, our findings show that “Returns” () is the most important criterion in the economic dimension. It is quite reasonable for a company to devote its main effort to get higher returns. This fact is supported by the results we obtained by IVIFWG operator. In this cluster, the descending order of criteria is .
For the second dimension, “Prospective recycling and reusing” () occupies the most significant sustainable indicator among the four environmental factors. In this group, the descending order of criteria is as follows: . Now, to justify such order of criteria importance, some of the works in the existing literature are cited. For green practices the 3R (reduce, recycle and reuse) policy [46,47] is the most sustainable strategy for providing the promotion of environmental performance and development. Finally, “health and safety” () grips the top rank in the social dimension. Construction companies in a nation like India deals with more issues than other countries, since a large number of accidental cases as well as safety-related difficulties happen in construction. Table 11 reflects this fact that “Health and safety” () and “Fire resistance” () come first rather thinking much of “Labor availability” (), and “Esthetics” () in real life situations.
After finalizing the criteria weights, we aim to evaluate and select the most suitable brick(s) as alternative material for sustainable construction. The linguistic assessments of the three alternatives supplied by the five decision makers are shown in Table 12. The decision matrix in Table 12 is transformed to the aggregated IVIF decision matrix (Table 13) by using Equation (10). Next, the average decision matrix is normalized with the help of Equation (18) and after plugging the criteria weights the weighted normalized decision matrix (refer to Table 14) is computed. Interval-valued intuitionistic fuzzy negative ideal solution for each of the criteria is shown in Table 15. Hamming distance and Euclidean distance of the alternatives from the Interval-valued intuitionistic fuzzy negative ideal solution is shown in Table 16. Finally, Table 17 tells the overall performance scores of all the sustainable alternatives of brick, in which “Fly ash bricks” () bears the top rank with a high assessment score of . In addition, “AAC bricks” () and “Clay Bricks” () have got second and third ranks, with assessment scores and , respectively. The final ranking order of alternative bricks for sustainable construction is: . Additionally, Table 18 shows the ranking orders by the proposed method along with four other existing methods for result comparisons.

Table 12.
Decision matrix with linguistic ratings.

Table 13.
Aggregated IVIF decision matrix.

Table 14.
Weighted normalized decision matrix.

Table 15.
Negative ideal solutions.

Table 16.
Euclidean and Hamming distance matrices.

Table 17.
Assessment matrix and scores.

Table 18.
Comparison with other models.
On comparison with Clay bricks (), both of the Fly ash bricks () and AAC bricks (), which consume less energy and have better thermal insulation, are found to be stronger than conventional clay bricks. In addition to this, although Dhanjode et al. [44] argued that the Fly ash bricks and AAC brick save and carbon tax respectively compared to clay bricks to its environmental properties. However, in Indian perspectives, only a few research works are found on AAC bricks while AAC bricks have been used for the construction of several buildings. Global unavailability of the AAC bricks often arises serious concern since it increases transportation and inventory costs. Moreover, Fly ash bricks are more cost and energy saving alternative choice than other ones. Mahendran et al. [45] asserted that Fly ash brick is the most favorable choice among the building blocks in perspectives of strength, heating load, framed and load bearing buildings. The above findings have selected Fly ash brick to be the most sustainable construction material for use in this case study. When we shared our results to the relevant builders, they appreciated our task and adopted this material in their own construction business. The builders also discussed with their clients about the benefits of using this material and suggested them to use it.
6.1. Comparisons
In this section, we perform the necessary comparative analysis with a set of a few existing approaches to prove the practicality and efficiency of the proposed IVIF-CODAS method. The CODAS [16], fuzzy CODAS [48], IVIF-TOPSIS [49], IVIF-VIKOR [50] methods were modified using fuzzy and IVIF numbers. The reason behind choosing these methods is their stability and reliability in producing satisfactory solutions/results. It is essential to measure the reliability of the results attained by the proposed model for crosschecking the optimal results/alternatives. For such action in MCDM problems the most common measure is the comparison of the results produced by other stable and reliable methods [16,51].
Now, the classical CODAS needs crisp numbers as inputs. Therefore, the crisp numbers corresponding to their linguistic ratings are used to perform the CODAS algorithm. Here, the order of ranking is similar to that of the original study. On contrast, fuzzy CODAS can adopt linguistic ratings as triangular/trapezoidal fuzzy numbers. The outcome of fuzzy CODAS is also same as the ranking produced by IVIF-CODAS. Finally, IVIF-TOPSIS and IVIF-MABAC are used to solve the same material selection problem. Table 18 shows that (Fly ash bricks) occupies the first ranking in all the methods except in IVIF-VIKOR. There is a ranking swapping between (Fly ash bricks) and (AAC bricks).
From the comparative analysis, we can summarize that the results are harmonious to each other. Below we give some advantages of the proposed IVIF-CODAS method.
- (1)
- Crisp ratings is used to evaluate the classical CODAS method but this ratings often fail in real life scenario as real life problems are much uncertain. For example, the construction company may consider some criteria as highly important and to signify the importance, the corresponding rating scale need to be more flexible. This “highly important” term can be preferably expressed using as an IVIF number rather than a single crisp number . However, in this paper, we use IVIF numbers to assess the alternative bricks and criteria importance since DMs can flexibly express their opinions using IVIF numbers.
- (2)
- Compared with fuzzy CODAS, the proposed IVIF-CODAS has an advantage. Grattan-Guinness [52] argued that it is a difficult task for decision makers to represent linguistic ratings in the form of a single membership degree in classical fuzzy set theory. In response, Atanassov [53] introduced IFS as an extension of fuzzy sets. In IFS, hesitation margin is introduced as a new concept and the sum of membership and non-membership degree may be less than one. However, both in fuzzy set and IFS, the membership values are exact and crisp in nature. To present the membership and non-membership values are in intervals, Atanassov and Gargov [8] extended IFS in IVIFS. Thus, in group decision making problems the extended IVIF-CODAS method offers a better treatment in handling uncertainty in the decision making process.
- (3)
- As it is difficult to show the applicability and trustworthiness of a newly proposed method, hence it is necessary to assess it in solving several MCDM problems. Wang et al. [54] asserted a comparison which is only way to apprehend the validity of newly proposed MCDM model (here, IVIF-CODAS). To justify any proposed approach, one has to compare it with several related approaches for the same problem. Accordingly, we have presented two illustrative examples and found encouraging results that show the similarity of IVIF-CODAS to other methods. One can consider this to be one of the advantages of the novel approach that is reckoned to be applicable irrespective of its case studies.
6.2. Sensitivity Analysis
It is well known that the results of MCDM methods can be highly influenced by the weight coefficients of the evaluation criteria. Hence, a sensitivity analysis is discussed in the next two paragraphs, where we compute the final ranking of the alternative bricks by changing the criteria weights. Small variations in the rank of alternatives are noticed due to the small variations in the weight coefficients. Hence, the results of MCDM methods are analyzed by their sensitivity to these changes [55,56]. Below we present a sensitivity analysis using 10 different scenarios (Table 19). We apply the expression given in Equation (28) for changing the criteria weights.

Table 19.
Ranking for different scenarios.
Here is the percentage of change of . In this work, the sustainable material selection and criteria weights evaluation are performed by human inputs. The robustness testing of the final ranking has been conducted by considering the changed weights of the criteria. Small changes in criteria weights of the alternatives and have a negligible effect in the final ranking in the brick selection problem. The result of the performed sensitivity analyses enforce the proposal that Fly ash bricks () have the highest priority followed by AAC bricks () and Clay bricks (). The computed ranking order (Figure 4) (Fly ash bricks) (AAC bricks) (Clay bricks) can be followed in eight out of 10 scenarios. Thus, (Fly ash bricks) has been ranked as maximum number of scenarios except in scenario 5 and 10. In these two cases, there are noticeable changes (increase and or decrease) in priorities of criteria set which obviously affect the final ranking as (AAC bricks) (Fly ash bricks) (Clay bricks).
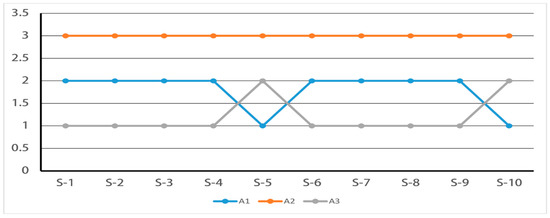
Figure 4.
Different ranking positions due to sensitivity analysis.
We find the ranking is consistent unless some noticeable changes are made in the criteria weights. The robustness of the sustainable materials has been shown by sensitivity analysis (Table 19). (Fly ash bricks) or (AAC bricks) occupies top rank in all cases and may be selected as best by the decision makers. The sensitivity analysis becomes meaningful to assess the bricks as sustainable building blocks of construction projects.
7. Conclusions
Sustainable material selection as well as suitable material selection in uncertainty for construction industry is mandatory to sustain in the competitive market and for eco-friendly environment. Since material selection is one kind of MCDM problem, an efficient MCDM method is needed to cope with the market challenges. In this study, the classical CODAS method is extended with IVIFNs known as IVIF-CODAS for comprehensive, rational, and sensible decision making and especially to handle the uncertain material selection problem. Since human reasoning capability is inherently inexact in nature, we have used linguistic terms to present the opinions of decision makers. IVIFN has been used in this study, since it uses intervals rather than exact numbers to represent the membership and non-membership functions. The comparative study shows that the proposed method is consistent and efficient in respect to the other existing methods. This ranking method will enable clients, the Construction Company, manufacturers, consultants, and material suppliers to understand central public works department norms in India and keep at parity with global standards.
Although this research article delivers numerous valuable implications, a few of the project implications are mentioned here. In any industry it is highly important to keep a balance between the cost parameters (material cost and its operating cost, etc.); hence, managers or engineers face difficulty in selecting the finest material only on the basis of its sustainability benefit. Also, the incorporation of TBL (environment, economy, and society) factors is equally difficult and needs a typical framework in material selection problem. This research work offers such a framework that aids the engineers and experts to decide the most suitable material under sustainability constraints especially in the Indian construction industries. Most research papers in the literature mainly focused on environmental concerns in the construction sector. In comparison to them this paper assists both scientific and societal contributions which contributes towards social progress along with the eco-friendly set-ups. Additionally, this study functions as a reference for researchers and practitioners working in the same field in an Indian context. As a whole, this paper helps and inspires architects, engineers, and other construction managers to respond and to decide the best sustainable material within their viable business set-up.
In future, IVIF-CODAS method can be used to solve other complex MCDM problems, like market segment evaluation and selection, project selection, supplier selection, etc.
Author Contributions
The individual contribution and responsibilities of the authors were as follows: J.R., S.D. and S.K. designed the research, collected and analyzed the data and the obtained results, performed the development of the paper. D.P. provided extensive advice throughout the study, regarding the research design, methodology, findings and revised the manuscript. All the authors have read and approved the final manuscript.
Funding
This work was supported by the Department of Science and Technology, India under the INSPIRE fellowship programme [grant no. DST/INSPIRE Fellowship/2013/544].
Acknowledgments
We wish to express our deepest appreciation to the editors and the anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jahan, A.; Edwards, K.L. A State-of-the-Art Survey on the Influence of Normalization Techniques in Ranking: Improving the Materials Selection Process in Engineering Design. Mater. Des. 2015, 65, 335–342. [Google Scholar] [CrossRef]
- Yazdani, M.; Payam, A.F. A Comparative Study on Material Selection of Microelectromechanical Systems Electrostatic Actuators Using Ashby, VIKOR and TOPSIS. Mater. Des. 2015, 65, 328–334. [Google Scholar] [CrossRef]
- Petković, D.; Madić, M.; Radovanović, M.; Gečevska, V. Application Of The Performance Selection Index Method For Solving Machining MCDM Problems. FU Mech. Eng. 2017, 15, 15–97. [Google Scholar] [CrossRef]
- Liao, T.W. Two Interval Type 2 Fuzzy TOPSIS Material Selection Methods. Mater. Des. 2015, 88, 1088–1099. [Google Scholar] [CrossRef]
- Liu, H.-C.; Liu, L.; Wu, J. Material Selection Using an Interval 2-Tuple Linguistic VIKOR Method Considering Subjective and Objective Weights. Mater. Des. 1980–2015 2013, 52, 158–167. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Vahdani, B.; Tavakkoli-Moghaddam, R.; Tajik, N. Soft Computing Based on a Fuzzy Grey Group Compromise Solution Approach with an Application to the Selection Problem of Material Handling Equipment. Int. J. Comput. Integr. Manuf. 2014, 27, 547–569. [Google Scholar] [CrossRef]
- Xue, Y.-X.; You, J.-X.; Lai, X.-D.; Liu, H.-C. An Interval-Valued Intuitionistic Fuzzy MABAC Approach for Material Selection with Incomplete Weight Information. Appl. Soft Comput. 2016, 38, 703–713. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval Valued Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Cheng, S.-H. Autocratic Multiattribute Group Decision Making for Hotel Location Selection Based on Interval-Valued Intuitionistic Fuzzy Sets. Inf. Sci. 2018, 427, 77–87. [Google Scholar] [CrossRef]
- Wen, M.; Zhao, H.; Xu, Z.; Lei, Q. Definite Integrals for Aggregating Continuous Interval-Valued Intuitionistic Fuzzy Information. Appl. Soft Comput. 2018, 70, 875–895. [Google Scholar] [CrossRef]
- Rashid, T.; Faizi, S.; Zafar, S. Distance Based Entropy Measure of Interval-Valued Intuitionistic Fuzzy Sets and Its Application in Multicriteria Decision Making. Adv. Fuzzy Syst. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Wang, C.-Y.; Chen, S.-M. Multiple Attribute Decision Making Based on Interval-Valued Intuitionistic Fuzzy Sets, Linear Programming Methodology, and the Extended TOPSIS Method. Inf. Sci. 2017, 397–398, 155–167. [Google Scholar] [CrossRef]
- Gupta, P.; Mehlawat, M.K.; Grover, N.; Pedrycz, W. Multi-Attribute Group Decision Making Based on Extended TOPSIS Method under Interval-Valued Intuitionistic Fuzzy Environment. Appl. Soft Comput. 2018, 69, 554–567. [Google Scholar] [CrossRef]
- Das, S.; Kar, S.; Pal, T. Group Decision Making Using Interval-Valued Intuitionistic Fuzzy Soft Matrix and Confident Weight of Experts. J. Artif. Intell. Soft Comput. Res. 2014, 4, 57–77. [Google Scholar] [CrossRef]
- Das, S.; Kar, M.B.; Pal, T.; Kar, S. Multiple Attribute Group Decision Making Using Interval-Valued Intuitionistic Fuzzy Soft Matrix. In Proceedings of the 2014 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Beijing, China, 7–11 July 2014; pp. 2222–2229. [Google Scholar] [CrossRef]
- Stanujkić, D.; Karabašević, D. An extension of the WASPAS method for decision-making problems with intuitionistic fuzzy numbers: A case of website evaluation. Oper. Res. Eng. Sci. Theor. Appl. 2018, 1, 29–39. [Google Scholar] [CrossRef]
- Gharzeldeen, M.N.; Beheiry, S.M. Investigating the Use of Green Design Parameters in UAE Construction Projects. Int. J. Sustain. Eng. 2015, 8, 93–101. [Google Scholar] [CrossRef]
- Popovic, M.; Kuzmanovic, M.; Savic, G. A comparative empirical study of Analytic Hierarchy Process and Conjoint analysis: Literature review. Decis. Mak. Appl. Manag. Eng. 2018, 1, 1–153. [Google Scholar] [CrossRef]
- Medineckiene, M.; Zavadskas, E.K.; Björk, F.; Turskis, Z. Multi-Criteria Decision-Making System for Sustainable Building Assessment/Certification. Arch. Civ. Mech. Eng. 2015, 15, 11–18. [Google Scholar] [CrossRef]
- Kibert, C.J. Sustainable Construction: Proceedings of the First International Conference of CIB TG 16, November 6-9, 1994, Tampa, Florida, USA; University of Florida Center: Gainesville, FL, USA, 1994. [Google Scholar]
- Radhi, H. On the Effect of Global Warming and the UAE Built Environment. In Global Warming; InTech: Vienna, Austria, 2010. [Google Scholar]
- Elchalakani, M.; Elgaali, E. Sustainable Concrete Made of Construction and Demolition Wastes Using Recycled Wastewater in the UAE. J. Adv. Concr. Technol. 2012, 10, 110–125. [Google Scholar] [CrossRef]
- Al-Hajj, A.; Hamani, K. Material Waste in the UAE Construction Industry: Main Causes and Minimization Practices. Archit. Eng. Des. Manag. 2011, 7, 221–235. [Google Scholar] [CrossRef]
- Ljungberg, L.Y. Materials Selection and Design for Development of Sustainable Products. Mater. Des. 2007, 28, 466–479. [Google Scholar] [CrossRef]
- Florez, L.; Castro-Lacouture, D. Optimization Model for Sustainable Materials Selection Using Objective and Subjective Factors. Mater. Des. 2013, 46, 310–321. [Google Scholar] [CrossRef]
- Bahraminasab, M.; Jahan, A. Material Selection for Femoral Component of Total Knee Replacement Using Comprehensive VIKOR. Mater. Des. 2011, 32, 4471–4477. [Google Scholar] [CrossRef]
- Jahan, A.; Mustapha, F.; Sapuan, S.M.; Ismail, M.Y.; Bahraminasab, M. A Framework for Weighting of Criteria in Ranking Stage of Material Selection Process. Int. J. Adv. Manuf. Technol. 2012, 58, 411–420. [Google Scholar] [CrossRef]
- Chauhan, A.; Vaish, R. Magnetic Material Selection Using Multiple Attribute Decision Making Approach. Mater. Des. 1980–2015 2012, 36, 1–5. [Google Scholar] [CrossRef]
- Karande, P.; Chakraborty, S. Application of Multi-Objective Optimization on the Basis of Ratio Analysis (MOORA) Method for Materials Selection. Mater. Des. 2012, 37, 317–324. [Google Scholar] [CrossRef]
- Maity, S.R.; Chatterjee, P.; Chakraborty, S. Cutting Tool Material Selection Using Grey Complex Proportional Assessment Method. Mater. Des. 1980–2015 2012, 36, 372–378. [Google Scholar] [CrossRef]
- Anojkumar, L.; Ilangkumaran, M.; Vignesh, M. A Decision Making Methodology for Material Selection in Sugar Industry Using Hybrid MCDM Techniques. Int. J. Mater. Prod. Technol. 2015, 51, 102–126. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Bausys, R.; Juodagalviene, B.; Garnyte-Sapranaviciene, I. Model for Residential House Element and Material Selection by Neutrosophic MULTIMOORA Method. Eng. Appl. Artif. Intell. 2017, 64, 315–324. [Google Scholar] [CrossRef]
- Tian, G.; Zhang, H.; Feng, Y.; Wang, D.; Peng, Y.; Jia, H. Green Decoration Materials Selection under Interior Environment Characteristics: A Grey-Correlation Based Hybrid MCDM Method. Renew. Sustain. Energy Rev. 2018, 81, 682–692. [Google Scholar] [CrossRef]
- Xu, Z.S. Methods for Aggregating Interval-Valued Intuitionistic Fuzzy Information and Their Application to Decision Making. Control Decis. 2007, 22, 215–219. [Google Scholar] [CrossRef]
- Xu, Z.-S.; Jian, C. Approach to Group Decision Making Based on Interval-Valued Intuitionistic Judgment Matrices. Syst. Eng.-Theory Pract. 2007, 27, 126–133. [Google Scholar] [CrossRef]
- Xu, Z.S.; Chen, J. An Overview of Distance and Similarity Measures of Intuitionistic Fuzzy Sets. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2008, 16, 529–555. [Google Scholar] [CrossRef]
- Xu, Z. A Deviation-Based Approach to Intuitionistic Fuzzy Multiple Attribute Group Decision Making. Group Decis. Negot. 2010, 19, 57–76. [Google Scholar] [CrossRef]
- Park, J.H.; Lim, K.M.; Park, J.S.; Kwun, Y.C. Distances between Interval-Valued Intuitionistic Fuzzy Sets. J. Phys. Conf. Ser. 2008, 96, 012089. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z. Soft Computing Based on Maximizing Consensus and Fuzzy TOPSIS Approach to Interval-Valued Intuitionistic Fuzzy Group Decision Making. Appl. Soft Comput. 2015, 26, 42–56. [Google Scholar] [CrossRef]
- Hashemi, H.; Bazargan, J.; Mousavi, S.M.; Vahdani, B. An Extended Compromise Ratio Model with an Application to Reservoir Flood Control Operation under an Interval-Valued Intuitionistic Fuzzy Environment. Appl. Math. Model. 2014, 38, 3495–3511. [Google Scholar] [CrossRef]
- Chen, T.-Y. Interval-Valued Intuitionistic Fuzzy QUALIFLEX Method with a Likelihood-Based Comparison Approach for Multiple Criteria Decision Analysis. Inf. Sci. 2014, 261, 149–169. [Google Scholar] [CrossRef]
- Pamučar, D.; Lukovac, V.; Božanić, D.; Komazec, N. Multi-criteria FUCOM-MAIRCA model for the evaluation of level crossings: Case study in the Republic of Serbia. Oper. Res. Eng. Sci. Theor. Appl. 2018, 1, 108–129. [Google Scholar] [CrossRef]
- Hassanpour, M. Evaluation of Iranian Wood and Cellulose Industries. Decis. Mak. Appl. Manag. Eng. 2019, 2, 13–34. [Google Scholar] [CrossRef]
- Dhanjode, C.S.; Ralegaonkar, R.V.; Dakwale, V.A. Design and Development of Sustainable Construction Strategy for Residential Buildings: A Case Study for Composite Climate. Int. J. Sustain. Constr. Eng. Technol. 2013, 4, 12–20. [Google Scholar]
- Mahendran, K.; Sivaram, T.; Shahulhameed, M.; Logaraja, R. A Comparative Study on Various Building Blocks as an Alternative to Conventional Bricks. In Proceedings of the International Conference on Emering Trends in Engineering and Management Research, Nashik, Maharastra, 23 March 2016; pp. 1097–1109. [Google Scholar]
- Benton, R. Reduce, Reuse, Recycle … and Refuse. J. Macromarket. 2015, 35, 111–122. [Google Scholar] [CrossRef]
- Hamid, Z.A.; Anuar Mohamad Kamar, K. Aspects of Off-site Manufacturing Application towards Sustainable Construction in Malaysia. Constr. Innov. 2012, 12, 4–10. [Google Scholar] [CrossRef]
- Pamucar, D.; Bozanic, D.; Lukovac, V.; Komazec, N. Normalized weighted geometric bonferroni mean operator of interval rough numbers—Application in interval rough DEMATEL-COPRAS. FU Mech. Eng. 2018, 16, 171–191. [Google Scholar] [CrossRef]
- Ashtiani, B.; Haghighirad, F.; Makui, A.; Montazer, G.A. Extension of Fuzzy TOPSIS Method Based on Interval-Valued Fuzzy Sets. Appl. Soft Comput. 2009, 9, 457–461. [Google Scholar] [CrossRef]
- Vahdani, B.; Hadipour, H.; Sadaghiani, J.S.; Amiri, M. Extension of VIKOR Method Based on Interval-Valued Fuzzy Sets. Int. J. Adv. Manuf. Technol. 2010, 47, 1231–1239. [Google Scholar] [CrossRef]
- Pamučar, D.; Petrović, I.; Ćirović, G. Modification of the Best–Worst and MABAC Methods: A Novel Approach Based on Interval-Valued Fuzzy-Rough Numbers. Expert Syst. Appl. 2018, 91, 89–106. [Google Scholar] [CrossRef]
- Grattan-Guinness, I. Fuzzy Membership Mapped onto Intervals and Many-Valued Quantities. Z. Für Math. Log. Grundlagen Math. 1976, 22, 149–160. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Wang, P.; Li, Y.; Wang, Y.-H.; Zhu, Z.-Q. A New Method Based on TOPSIS and Response Surface Method for MCDM Problems with Interval Numbers. Math. Probl. Eng. 2015, 2015, 1–11. [Google Scholar] [CrossRef]
- Debnath, A.; Roy, J.; Kar, S.; Zavadskas, E.; Antucheviciene, J. A Hybrid MCDM Approach for Strategic Project Portfolio Selection of Agro By-Products. Sustainability 2017, 9, 1302. [Google Scholar] [CrossRef]
- Chatterjee, P.; Mondal, S.; Boral, S.; Banerjee, A.; Chakraborty, S. A novel hybrid method for non-traditional machining process selection using factor relationship and Multi-Attributive Border Approximation Method. FU Mech. Eng. 2017, 15, 15–439. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).