Abstract
The main purpose of this article is two-fold: first, to justify the choice of Kirchhoff vertex conditions on a metric graph as they appear naturally as a limit of Neumann Laplacians on a family of open sets shrinking to the metric graph (“thick graphs”) in a self-contained presentation; second, to show that the metric graph example is close to a physically more realistic model where the edges have a thin, but positive thickness. The tool used is a generalization of norm resolvent convergence to the case when the underlying spaces vary. Finally, we give some hints about how to extend these convergence results to some mild non-linear operators.
1. Introduction
The study of operators on metric graphs has been an ongoing and active area of research for at least two decades. Several natural questions arise in the study of Laplacians on metric graphs: As there is some freedom in defining a self-adjoint Laplacian on a metric graph due to the vertex conditions (see, e.g., [1] and the references therein), can one justify a certain choice of such vertex conditions? Second, in a realistic physical model (a thick graph), the wires have a thickness of order , but in the metric graph model, it is simplified to : Can one justify some sort of limit of a Laplacian on the network with thickness as ?
The aim of this article is to give an answer to both questions. We show that the Neumann Laplacian on the -neighborhood of the metric graph (embedded in some ambient space ) converges to the Kirchhoff Laplacian on the metric graph. This gives answers to both questions above: First, the “natural” vertex conditions are the so-called Kirchhoff conditions; see Equations (3) and (4). Second, the limit problem is a good approximation to a realistic physical model on a thick graph as . Note that the problem significantly simplifies in the limit, as we only have to consider a system of ODEs instead of a PDE on a complicated and -dependent space. Moreover, the problem on the metric graph can often be solved explicitly.
A technical difficulty is that the Laplacian on the thick graph and on the metric graph live on different spaces. We therefore generalize the notion of norm resolvent convergence to this case; this was first done in [2]; see also the monograph [3] for a history of the problem and [4] for a recent list of references. Convergence of the (discrete) spectrum for the Neumann Laplacian on a thick graph converging to a compact metric graph has already been established by variational methods in [5,6,7].
The aim of this article is also to provide an almost self-contained presentation of the results for linear operators on thick and metric graphs to the “non-linear” community and also to give some ideas of how they can be extended to some mild non-linear operators.
2. Metric Graphs and Their Laplacians
For a detailed presentation of metric graphs and their Laplacians, we refer to [1,3] and the references therein. Let denote a metric graph given by the data , where V and E are the (at most countable) sets of vertices and edges, respectively, and where . denotes the length of the edge ; a metric edge will be the interval . The metric graph is now the disjoint union of all metric edges after identifying the endpoints with the corresponding vertices. A metric graph is a metric space using the intrinsic metric (i.e., is the length of the shortest path in between s and ). Moreover, there is a natural measure on given by the sum of the Lebesgue measures on each metric edge .
As the Hilbert space on , we choose:
where we write as family with ; moreover, denotes the Hilbert orthogonal sum with f being in it if its squared norm:
is finite. Similarly, we define for . The label “” refers to the fact that for , there is no relation between the (well-defined) values of and its derivatives at a vertex v for different . Here, denotes the set of edges that are adjacent with the vertex . Recall that functions in are continuous as we have the estimate:
Using a suitable cut-off function, we conclude the Sobolev trace estimate:
with , where denotes the evaluation of at one of the endpoints of corresponding to . In particular, we assume that:
From (1) and (2), we then conclude that the subspace:
is closed in . We denote by the common value of f at the vertex v. It follows that:
defines a closed, non-negative quadratic form in . The associated self-adjoint and non-negative operator is given by:
Here, denotes the (weak) derivative of along e towards the vertex v. The operator is sometimes referred to as the (generalized) Neumann Laplacian or Kirchhoff Laplacian (the second because of the flux condition on the derivatives). Note that for vertices of degree one, the vertex condition is just the usual Neumann boundary condition , and for vertices of degree two, we have and , i.e., the continuity of f and its derivative along v (recall that denotes the derivative towards the vertex v).
3. Thick Graphs and Their Laplacians
We assume first that the metric graph is embedded in some space () such that all edges are straight line segments in . For , denote by:
the -neighborhood of in . Here, is the mth root of the volume of the unit Euclidean ball in , i.e., , , , etc. We say that is a graph-like space or a thick graph constructed from the metric graph if there is such that:
for all (cf. Figure 1), where and are open and pairwise disjoint subsets of such that the so-called vertex and edge neighborhoods fulfil:
i.e., is isometric to the -scaled version of an open subset , is isometric with the product of an interval of length , and is a ball of radius , having m-dimensional volume one by the definition of the scaling factor . Moreover, is the sum of the lengths of the two parts of the metric edge inside the vertex neighborhood. For finite graphs, the existence of is no restriction, but for infinite graphs with an arbitrary large vertex degree, this might be a restriction on the embedding and the edge lengths. More details on spaces constructed according to a graph (so-called “graph-like spaces”) can be found in the monograph [3]; see also the references therein.
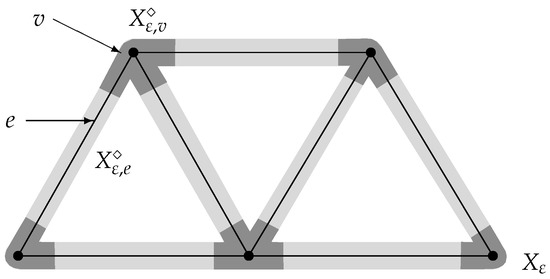
Figure 1.
The decomposition of a graph-like space of thickness of order into vertex neighborhoods (dark grey) and edge neighborhoods (light grey) according to a metric graph embedded in .
As the Hilbert space, we set . As the operator, we use the (non-negative) Neumann Laplacian defined as the self-adjoint and non-negative operator associated with the closed and non-negative quadratic form given by:
in .
In our calculations later, it is more convenient to work with edge neighborhoods that are isometric with the product of the original edge times the -scaled ball B, i.e.,
instead of the slightly shortened edge neighborhood . For , we set . We then construct as the space obtained from gluing the building blocks and such that a decomposition similar to (5) holds, now without the label . Note that is defined as an abstract flat manifold with boundary and might not be embeddable into any longer. We also call a graph-like space or thick graph. We state that the Neumann Laplacians on and are “close to each other” in Lemma 4.
Due to a decomposition of into its building blocks similar to (5) and the scaling behavior, the norm in the Hilbert space fulfills:
where and denote the restriction of u onto the -independent building blocks and . Note that with this notation, we have put all -dependencies into the norm (and later also into the quadratic form).
As the operator, we use the (negative) Neumann Laplacian defined as the self-adjoint and non-negative operator associated with the closed and non-negative quadratic form given by:
in using the scaling behavior of the building blocks. Here, denotes the derivative with respect to the longitudinal (first) variable s, and denotes the derivative with respect to the second variable .
4. Convergence of the Resolvents
How can we now compare the two Laplacians and (resp. )? The idea is first to consider the resolvents:
in , resp. , since they are bounded operators. In order to define a norm difference of these resolvents, we need a so-called identification operator:
in our situation given by
i.e., we set to zero on the vertex neighborhood and transversally constant on the edge neighborhood, together with an appropriate rescaling constant. As the identification operator in the opposite direction, we use , where an easy calculation shows that:
It is easy to see that , i.e., is an isometry.
We now compare the two resolvents, sandwiched with . Let:
What does look like? The best way to deal with it is to consider for and . We have:
where and . Note that
where is (minus) the Neumann Laplacian on B acting on the second variable . In particular, we conclude:
where we used partial integration and the fact that is a self-adjoint operator in and (as is independent of the second variable y) for the second equality and a reordering argument in the third equality. Moreover, plugging v into s means evaluation at , resp. , if v corresponds to zero, resp. ; for the longitudinal derivative, we assume , resp. if v corresponds to zero, resp. .
We now use the fact that : first note that , so that we can smuggle in a constant into the first summand, namely:
We specify in a moment. For the second summand, we use the fact that is independent of , and we have:
For the second equality, we used the fact that B at corresponds to the subset of where the edge neighborhood is attached and that the normal derivative (pointing outwards) of u vanishes on due to the Neumann conditions. For the last equality, we used the Gauss–Green formula (write ).
As , we expect that the average of u over the boundary component is close to the average of u over itself (recall that ); hence, we set:
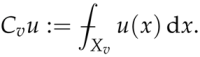
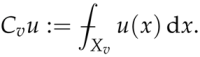
Define now:
where denotes the degree of v (i.e., the number of elements in ), then we have shown that:
Defining (with the weighted norm given by ) and , the previous equation reads as:
in operator notation, where:
and:
Let us now estimate the norms of the auxiliary operators: it also explains why we work with the weighted space :
Lemma 1.
Assume that (2) holds, then:
Proof.
From (1) and (2), for each , the fact that , and summing over , we conclude:
where . Now, the last sum equals:
hence, the second norm estimate holds. For the first one, we argue: similarly
Now,
by the spectral calculus, and the first norm estimate follows. □
More importantly, we now show that the -dependent operators have actually a norm converging to zero as :
Lemma 2.
Assume that (2) and:
hold (By some modifications in the decomposition (6) (namely, one uses for some appropriate ), one can avoid a direct upper bound on the vertex degrees, but then has to be large if is large; also, the high degree will make larger in order to have enough space to attach all the edge neighborhood; see also the discussion in ([2], Section 3.1.) for all , where is the second (first non-zero) Neumann eigenvalue of , then:
Proof.
We need the following vector-valued version of (1):
(actually, we apply (1) to for each into a line of length one at perpendicular to into , and integrate then over ). We then have:
(recall that ). Now, is the projection onto the eigenspace of the Neumann problem on of all eigenfunctions orthogonal to the constant; hence, we have:
by the variational characterization of eigenvalues. In particular, we have:
Now, letting , we have:
Moreover,
hence, .
For the second norm estimate, we have:
□
From the calculation of in (7) and Lemmas 1 and 2, we conclude:
Theorem 1.
Note that the operator norm of in leads to the error estimate , as it is dominant if .
5. Generalized Norm Resolvent Convergence
Let be a family of self-adjoint and non-negative operators () acting in an -independent Hilbert space . We say that converges in the norm resolvent sense to if:
As a consequence, operator functions of also converge in the norm, e.g., for the semigroups, we have:
Moreover, the spectra converge uniformly on bounded intervals. In particular, if all have a purely discrete spectrum, then , where denotes the kth eigenvalue ordered increasingly and repeated with respect to multiplicity.
We now want to extend these results to operators acting in different Hilbert spaces.
Definition 1.
For , let be a self-adjoint and non-negative operator acting in a Hilbert space . We say that converges to in the generalized norm resolvent sense, if there is a family of bounded operators such that:
where denotes the resolvent.
There are actually more general versions of generalized norm resolvent convergence; see, e.g., [2,3] or also [4] and the references therein. We can also specify the convergence speed as the maximum of the two norm estimates.
Moreover, almost all conclusions that hold for norm resolvent convergence are still true here, e.g., the convergence of eigenvalues or the spectrum. Moreover, if converges to in the generalized norm resolvent sense with convergence speed , then the corresponding semigroups converge, i.e., we have, e.g.,
One can even control the dependency on t ( as ); see ([4], Ex. 1.10 (ii)) for details.
As an application, we show that the corresponding solutions of the heat equations converge: denote by , resp. , the solution of
with initial data at , then we have:
i.e., the approximate solution converges to the proper solution of the more complicated problem on uniformly with respect to the initial data .
We have already shown the first norm convergence and the equality in (10) in the previous section (cf. Theorem 1); but we even have:
Theorem 2.
Proof.
It remains to show the last limit in (10). We have:
The integrand in the second sum can be estimated by:
using again the variational characterization of eigenvalues. In particular, the second sum can be estimated by . The first sum is also small, as functions with bounded energy do not concentrate at the vertex neighborhoods . The arguments to show this (actually, ) are very similar to the ones used in the proof of Lemma 2. Details can be found, e.g., in ([3], Section 6.3). □
Note that, once having proven the generalized norm resolvent convergence, with an error term of order , we can approximately solve the heat equation on as in (11): note that on a metric graph, one might even find explicit formulas for the solutions of the heat equation , at least for simple metric graphs; hence, one has automatically approximate solutions for the corresponding heat equation on the more complicated space .
Let us now come back to the original thick graph given by , where the edge neighborhoods have slightly shorter edge lengths.
We say that two operators and are asymptotically close in the generalized norm resolvent sense, if (10) holds with and replaced by . We have the following result (for the proof, see, e.g., ([3], Prp. 4.2.5):
Lemma 3.
If converges to and if and are asymptotically close, both in the generalized norm resolvent sense, then converges to in the generalized norm resolvent sense.
Now, in our concrete example with the slightly shortened edges, we have (for a proof, see ([3], Prp. 5.3.7)):
Lemma 4.
Assume that and are given as in Section 3, then and are asymptotically close in the generalized norm resolvent sense.
We then immediately conclude from Theorem 2:
6. Outlook
The author is currently working on extending this result to some mildly non-linear equations with Claudio Cacciapuoti and with Michael Hinz and Jan Simmer in two different settings. Probably, the first systematic treatment of (non-linear) partial differential operators on thin domains was given in the nice overview of Geneviéve Raugel [8], combining some abstract results with concrete examples, but to the best of our knowledge, no thick graph domain and its limit were considered there explicitly. For Neumann Laplacians on thick graphs, there were actually results about the convergence of certain non-linear problems in [9,10], but Kosugi’s papers did not contain an abstract approach using identification operators as we do.
At the conference, Jean-Guy Caputo also presented results on non-linear waves in networks and thick graphs justifying at least numerically the Kirchhoff vertex conditions; see [11,12]. There is another interesting application of the concept of generalized norm resolvent convergence: Berkolaiko et al. [13] studied the behavior of Laplacians on metric graphs if some edge lengths shrink to zero. A similar result (a compact part of the metric graph shrinks to a point) using different methods has been presented by Cacciapuoti [14] at the conference. A general convergence scheme also for some mildly non-linear equations would allow extending their analysis to non-linear problems.
We have the following type of equations in mind. Let:
for and
As the non-linearity, we think of for some and . For the the solution, we make the ansatz:
and similarly for . The non-linearity and the identification operators have to fulfil some compatibility conditions, namely has to be small in some sense. One might use an iteration procedure in order to obtain a sequence of functions converging to the solution. If in our example of thick metric graphs converging to metric graphs, then we must have .
If one wants to consider the non-linear Schrödinger equation , one faces the additional problem that the (generalized) norm resolvent convergence does not imply norm convergence of the unitary group for general initial data ; if one restricts to the range of the spectral projection for some , then there are still some operator norm estimates; see ([3], Thm. 4.2.16) for details. Nevertheless, one also has to make sure that still remains in the range of , which is probably too restrictive.
Funding
This research received no external funding.
Acknowledgments
O.P. would like to thank the organizers of the workshop “Nonlinear PDEs on Metric Graphs and Branched Networks” in Leiden/NL in August 2018 for the kind invitation. O.P. would also like to thank the organizers and the staff of the Lorentz Center for providing a beautiful atmosphere for the workshop. The author would also like to thank the anonymous referee for pointing out the nice overview article [8].
Conflicts of Interest
The author declares no conflict of interest.
References
- Berkolaiko, G.; Kuchment, P. Introduction to quantum graphs. In Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 2013. [Google Scholar]
- Post, O. Spectral convergence of quasi-one-dimensional spaces. Ann. Henri Poincaré 2006, 7, 933–973. [Google Scholar] [CrossRef]
- Post, O. Spectral analysis on graph-like spaces. In Lecture Notes in Mathematics; Springer: Berlin, Germany, 2012. [Google Scholar]
- Post, O.; Simmer, J. Quasi-unitary equivalence and generalised norm resolvent convergence. Rev. Roumaine Math. Pures Appl. 2019, 64, 2–3. [Google Scholar]
- Exner, P.; Post, O. Convergence of spectra of graph-like thin manifolds. J. Geom. Phys. 2005, 54, 77–115. [Google Scholar] [CrossRef]
- Kuchment, P.; Zeng, H. Convergence of spectra of mesoscopic systems collapsing onto a graph. J. Math. Anal. Appl. 2001, 258, 671–700. [Google Scholar] [CrossRef]
- Rubinstein, J.; Schatzman, M. Variational problems on multiply connected thin strips. I. Basic estimates and convergence of the Laplacian spectrum. Arch. Ration. Mech. Anal. 2001, 160, 271–308. [Google Scholar] [CrossRef]
- Raugel, G. Dynamics of partial differential equations on thin domains. In Dynamical Systems (Montecatini Terme, 1994); Lecture Notes in Math; Springer: Berlin, Germany, 1995; Volume 1609, pp. 208–315. [Google Scholar]
- Kosugi, S. A semilinear elliptic equation in a thin network-shaped domain. J. Math. Soc. Japan 2000, 52, 673–697. [Google Scholar] [CrossRef]
- Kosugi, S. Semilinear elliptic equations on thin network-shaped domains with variable thickness. J. Differ. Equ. 2002, 183, 165–188. [Google Scholar] [CrossRef]
- Caputo, J.G.; Dutykh, D. Nonlinear waves in networks: A simple approach using the sine-Gordon equation. Phys. Rev. E 2014, 90, 022912. [Google Scholar] [CrossRef] [PubMed]
- Caputo, J.G.; Dutykh, D.; Gleyse, D. Coupling conditions for the nonlinear shallow water equations on a network. arXiv, 2015; arXiv:1509.09082. [Google Scholar]
- Berkolaiko, G.; Latushkin, Y.; Sukhtaiev, S. Limits of quantum graph operators with shrinking edges. arXiv, 2018; arXiv:1806.00561. [Google Scholar]
- Cacciapuoti, C. Scale invariant effective Hamiltonians for a graph with a small compact core. arXiv, 2019; arXiv:1903.01898. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).