Abstract
We investigated whether semi-rigid and non-rigid π-conjugated fluorophores in the photoexcited (S1) and ground (S0) states exhibited mirror symmetry by circularly polarized luminescence (CPL) and circular dichroism (CD) spectroscopy using a range of compounds dissolved in achiral liquids. The fluorophores tested were six perylenes, six scintillators, 11 coumarins, two pyrromethene difluoroborates (BODIPYs), rhodamine B (RhB), and 4-(dicyanomethylene)-2-methyl-6-(4-dimethylaminostyryl)-4H-pyran (DCM). All the fluorophores showed negative-sign CPL signals in the ultraviolet (UV)–visible region, suggesting energetically non-equivalent and non-mirror image structures in the S1 state. The dissymmetry ratio of the CPL (glum) increased discontinuously from approximately −0.2 × 10−3 to −2.0 × 10−3, as the viscosity of the liquids increased. Among these liquids, C2-symmetrical stilbene 420 showed glum ≈ −0.5 × 10−3 at 408 nm in H2O and D2O, while, in a viscous alkanediol, the signal was amplified to glum ≈ −2.0 × 10−3. Moreover, BODIPYs, RhB, and DCM in the S0 states revealed weak (−)-sign CD signals with dissymmetry ratios (gabs) ≈ −1.4 × 10−5 at λmax/λext. The origin of the (−)-sign CPL and the (−)-sign CD signals may arise from an electroweak charge at the polyatomic level. Our CPL and CD spectral analysis could be a possible answer to the molecular parity violation hypothesis based on a weak neutral current of Z0 boson origin that could connect to the origin of biomolecular handedness.
1. Introduction
Since the mid-19th century, one of the greatest puzzles for scientists has been why life on Earth selected L-amino acids and D-sugars, because the corresponding L/D enantiomers were considered to be energetically identical [1,2,3,4,5,6,7,8,9,10,11,12,13]. Regarding other life forms that existed in the past or may exist now on exoplanets, solar planets, satellites, and comets, it is a matter of great curiosity as to whether these stereogenic centers and/or stereogenic bonds would be identical to those upon which our life is now based [14,15,16]. Living organisms can exist only in a far-from-equilibrium system allowing open flows of solar/thermal energy and low-entropy food [17]. This mystery is intimately connected to the origins of life [2,3,4,5,6,7,8,9,10,11,12,13,14] and the accelerating expansion of the universe [18,19].
In 1831, Faraday discovered that an oscillating magnetic (M) field induces an electric (E) current [20]. In 1861, Maxwell formulated this phenomenon as the theory of electromagnetism (EM) [20]. In 1845, Faraday observed a magneto-optical phenomenon, now called the “Faraday effect”, in which a light–matter (LM) interaction causes linearly polarized (LP) light to be rotated clockwise (CW) and counterclockwise (CCW) (from the observer) by passing through achiral lead-containing glass and certain liquids under the influence of a static magnetic field. In 1860, Pasteur conjectured that molecular asymmetry is a consequence of dissymmetric forces of cosmological origin [1]. Possibly, the “Faraday effect” prompted Pasteur to attempt asymmetric crystallization under the influence of a magnetic field, but the quest failed [1]. In 1894, Curie considered that magnetic and electric fields need to align co-linearly or anti-colinearly to produce optically active substances [21].
Left (l)- or right (r)-handed circularly polarized (CP) light is a physical force carrying angular momentum (±ℏ) that is a pure chiral electromagnetic (EM) force, causing mirror-symmetric LM interactions [22]. Linearly polarized (LP) light is expressed as a superposition of r- and l-CP light. LeBel in 1874 and van’t Hoff in 1894 postulated that CP light could catalyze asymmetric chemical reactions to produce chiral substances [21,23]. In 1896, Cotton, who discovered the anomalous phenomenon of circular dichroism (CD) and optical rotation dispersion (ORD) of potassium chromium (III) tartrate [24], attempted to degrade an alkaline aqueous solution of racemic copper tartrate using CP light but failed [21]. The first successful CP light-driven asymmetric synthesis, in the destruction mode, was reported by Kuhn and coworkers in 1929 and 1930, in which r- and l-CP light at 280 nm predominantly decomposed one enantiomer in racemic mixtures of 1-bromopropionic ethyl ester and azidopropionic acid dimethylamide, yielding corresponding optically active substances with small % enantioexcess (ee) values [21].
In recent years, modern photochemical reactions using unpolarized (UP) light under the influence of an intense static magnetic field afforded preferential degradation of one of two enantiomers, in which the product chirality is controllable according to the collinear or anti-collinear conditions [25]. Alternatively, CW and CCW swirling of molecular/supramolecular/polymer systems was found to result in mirror symmetry breaking (MSB) [26,27,28]; the product chirality was determined by the direction of the mechanical rotations, while no MSB happened under static conditions. The macroscopic mechano-physical rotation is assumed to impart a preferred twist direction to rotatable C–C single bonds. However, a recent experimental result suggested the occurrence of MSB even under static conditions via a thermal gradient at specific temperatures [29].
In 1927, Wigner formulated the principle of parity (P) symmetry (corresponding to mirror symmetry in chemistry), in which all interactions in nature are invariant with respect to space inversion [30]. This idea led to the categorization of seven symmetries, i.e., charge (C), P, time (T), CP, PT, CT, and CPT [31,32]. Until 1956, the seven symmetries were thought to be invariant and conserved. However, these ideas had to be partly revised because of two groundbreaking experiments: P-violated β±-decay in 1957–1959 [33,34,35,36,37,38], and CP-violated decay from a neutral K0 meson in 1964 [31,39] and neutral B0 meson in 2001 [40,41]. Without doubt, P and CP symmetries were broken at subatomic levels, although CPT symmetry was conserved. More recently, an astonishing experiment conducted by the Tokai-to-Kamioka (T2K) particle physics team investigated the possibility of CP-symmetry breaking between neutrino and antineutrino due to generation mixing between an electron-like lepton (first generation) and a muon-like lepton (second generation) [42]. The idea of generation mixing is like the mixing between S1 and triplet (T1) states of luminophores [43,44]: the S1 state involves a small fraction of the T1 state and, conversely, the T1 state is contaminated by a small fraction of the S1 state, thereby permitting the occurrence of intersystem crossing [45]. Additionally, the mixing in degenerate coupling of three anthracene dimers in a double-well (DW) was detected as quantum coherence beats from a radiation process in the S1 state at room temperature [46].
Currently, physicists concur that all events in the cosmos and material world are governed by the strong, EM, weak, and gravitational forces, known as the four fundamental physical forces [9,47]. Their relative strengths at 10−15 m are ~1:10−2:10−13:10−38, respectively [47]. However, among these fundamental physical forces, the only cosmologically dissymmetric force, causing MSB, is the weak force, which is responsible for nuclear fusion and fission reactions, while the other three forces conserve symmetry. Hence, a circularly polarized light source is a P-conserved physical source [47]. In the 1980s, physicists at Conseil Europeen pour la Recherche Nucleaire or European Organization for Nuclear Research (CERN) succeeded in the detection of charged W± bosons (80.4 GeV) and the neutral Z0 boson (91.2 GeV) [48,49,50,51]. This experiment proved that the P-conserved EM and P-violated weak forces are unified as an electroweak (EW) force with massive W± and Z0 bosons and the massless photon (γ) according to the Weinberg–Salam theory [48]. W± and Z0 bosons gain their masses from the Higgs boson (125 GeV) [48] while γ remains massless. Although W±, Z0, and γ are an equal family at high energies, Z0/γ and W± bifurcate into neutral massive/massless and charged massive bosons, respectively.
Following 50 years of theoretical and experimental development, P- and CP-symmetry breaking in particle and atomic physics is now well established [51,52,53,54,55,56,57,58,59,60]. The EW force led to the further groundbreaking predictions theoretically [61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88] and experimentally [89,90,91,92,93,94,95,96,97] that paired L/D molecules are no longer enantiomers and should behave as diastereomers. To date, several theories invoke the P-violating weak neutral current (PV-WNC) via handed electron–nucleus interactions mediated by the Z0 boson in the destabilization of one enantiomer by adding an extra energy bias (+EPV) and, conversely, stabilizing the other by subtraction (−EPV). This parity-odd energy bias is called a “parity violating energy difference” (PVED), ΔEPV, called EPV). The molecular parity violation (MPV) hypothesis definitively contradicts the accepted notion of enantiomers in the realm of modern stereochemistry and physical chemistry [98,99,100]. Molecular physicists have long argued whether P-symmetry of a molecular pair is exactly energetically equal and whether, if violated, EPV is detectable [61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88].
However, the MPV theories teach us that EPV between mirror-image molecules is very small: around 10−8–10−14 kcal∙mol−1 or 10−9–10−15 % ee [61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88]. It is, thus, likely impossible that this radical hypothesis could be experimentally proven by ordinary UV–visible, infrared, microwave, or NMR spectrometers, or by enantioseparation column chromatography. If the potential barrier (Eb) between racemic molecules in a symmetrical DW is sufficiently small, the tunneling time between the two local minima is inversely proportional to the tunneling splitting energy, ΔE± (hereafter called E±), because of even- and odd-parity eigenstates [66,72,101,102,103].
In a previous paper [104] aiming to verify the MPV hypothesis experimentally, we used circularly polarized luminescence (CPL) and CD spectroscopy in an investigation of semi-rigid and non-rigid π-conjugated luminophores in symmetrical DW/multiple-well (MW) potentials with a smaller Eb in the lowest photoexcited (S1) and ground (So) states. As we noted therein, a CPL spectropolarimeter may be regarded as a “low-energy spinning photon–molecule collider decelerator” to measure an inelastic scattering mode known as the Stokes’ shift [104], allowing for the detection of the subtle difference between l- and r-handed light speeds and the radiative lifetimes of enantiomers in the S1 state. We chose a series of luminophoric racemates, including oligofluorenes, linear and cyclic oligo-p-arylenes, binaphthyls, and fused aromatics carrying rotatable side groups. To control the Eb value in DW/MW of the luminophores in the S1 and S0 states, we used achiral solvents, including linear and branched alkanes, linear and branched alcohols, alkyl halides, linear cyclic ethers, and water (light and heavy) [104]. The solvent viscosity (η, in cP) was tunable, ranging from 0.21 to 71.0 at 20–25 °C. We observed that all the non-rigid luminophores showed negative-sign CPL signals in the UV–visible region, suggesting generation of non-mirror image structures in the S1 state. The Kuhn’s anisotropic parameter of CPL vs. photoluminescence (PL) signals (glum) of the non-rigid luminophores increased progressively but discontinuously in the range −0.2 × 10−3 to −2.0 × 10−3 as the solvent viscosity increased.
In this paper, to test the MPV hypothesis by further experiments, we investigated whether semi-rigid and non-rigid laser dyes, molecular scintillators, and other fluorophores in achiral liquids are mirror symmetrical by CPL and CD spectroscopy. Six perylenes, six scintillators, 11 coumarins, two 4,4-difluoro-4-bora-3a,4a-diaza-s-indacene derivatives (BODIPYs), rhodamine B (RhB), and 4-(dicyanomethylene)-2-methyl-6-(4-dimethylaminostyryl)-4H-pyran (DCM) were chosen. Negative-sign CPL signals were exhibited for all the fluorophores in the UV–visible region, suggesting the generation of non-mirror image structures in the S1 state. Noticeably, BODIPY, RhB, and DCM in the S0 states revealed clear (−)-sign CD signals with CD dissymmetry ratios (gabs) of approximately −1.4 × 10−5 at λext. The present comprehensive CPL/CD experimental datasets should support the long-argued MPV hypothesis regardless of PV-WNC scenarios [1].
2. Results
To validate the MPV hypothesis by CPL and CD spectroscopy, the crucial factors to choose are as follows: (i) semi-rigid and non-rigid racemic fluorophores carrying side chains allowing for rotatable freedom and/or flip-flop motional ability, (ii) fluorophores constituting only lighter atoms among the first three periods of the periodic table, and (iii) achiral liquids as solvents to continuously control the Eb value. Kasha’s rule predicts that fluorescence occurs spontaneously from the lowest S1 electronic-and-vibration coupling states (vibronic modes) associated with a significant structural reorganization at the photoexcited states via non-radiative, ro-vibrational, and translational pathways even if the fluorophores are excited at the S2 and higher Sn states [43,44].
Previously, Quack et al. [72,80,84], MacDermott and Hegstrom [83], and Bargueño [86] argued three representative cases, (i) EPV >> E±, (ii) EPV << E±, and (iii) EPV ~ E±, for several rigid, semi-rigid, and non-rigid cases of molecular chirality. Rigid enantiomers consisting of tetrahedral stereocenters cannot interfere with the E± value due to the minuteness of the EPV value. Quack et al. listed all the EPV and E± values of nearly 20 non-rigid rotamers [80,84]; the sign and magnitude of EPV in non-rigid XY–YX rotamers (X = H, D, T, Cl, and Y = O, S, Se, Te) definitively depend on the dihedral angles. The EPV and E± values depend on the nature of the rotamers; the former changes by five orders of magnitude and the latter by considerably more (25 orders of magnitude). From this, an increase in the rotational barrier height of the rotamers may be inferred. Amongst the rotamers, only T2S2 can satisfy the EPV~E± criterion (ideally EPV = E±), although radioactive T is not feasible in ordinary chemistry laboratories [82,84].
The PV-WNC model allows CPL-silent/CD-silent racemic molecular mixtures to become CPL-active/CD-active in the S0 state. This model is also applicable to racemates in the S1 state. The EPV value of luminophores can be amplified by heavier atoms (e.g., Si, Ge, Sn, Pb, Se, Te, Cl, Br, I) in periods 3–7 of the Periodic Table obeying the VSO (∝ Z2) law [69,82,84]. However, luminophores containing such heavier atoms predominantly emit phosphorescence with a very low quantum yield (QY < 0.01). Herein, we focus on fluorophores without stereogenic centers, which are utilized as laser dyes and scintillators and have a high QY (typically, 0.1–0.9). Although these dyes and scintillators consist of only lighter C, N, O, F, and S atoms, their spin–orbit interactions (ζ) are non-zero and notably large with ζ = 0.1, 0.2, 0.4, 0.7, and 1.0 kcal∙mol−1, respectively [44]. If a huge number of fluorophoric molecules (>1010–1016) in a cuvette are photoexcited simultaneously by focusing on them an incident laser beam, the faint 10−9–10−15 % ee or PVED of 10−8–10−14 kcal∙mol−1 is expected to be resonantly boosted to a level that is detectable using an ordinary CPL spectrometer during spontaneous radiation in a synchronized fashion [104].
When non-rigid enantiomers drop into one well in preference to the other in a dissymmetrical DW at the S1/S0 states by ceasing to oscillate, we postulate that the diastereomeric characteristics may accord with one of the three following scenarios [104]: (i) the fluorophore does not reveal any CPL or CD signals; (ii) the fluorophore at the S1 state does not reveal CPL signals but, at the S0 state, shows CD signals; and (iii) the fluorophore reveals CPL signals at the S1 state and CD signals at the S0 state. Detectable signals, as (+)- or (−)-sign CPL or CD, are considered to arise due to handed rotational and/or flip-flop motions.
2.1. D2h/D2 Symmetrical Perylene and C2/C1 Symmetrical Derivatives
Firstly, to ascertain the achirality of unsubstituted rigid flat π-conjugated aromatics with D2h symmetry such as the fluorophores naphthalene, anthracene, tetracene, and pyrene (see Chart 1), in the S1 and S0 states, we measured their CPL and CD spectra in the low-viscosity solvent methanol ([η] = 0.55 cP) and several other solvents, since it was pointed out that artefact-free precision measurements are serious concerns if CPL and CD spectrometers are operated using a single 50-kHz photoelastic modulator (PEM) [105,106]. We confirmed that no obvious CPL or CD signals in the corresponding PL and UV–visible spectral regions are detected by our CPL-200 [JASCO (Hachioji, Tokyo, Japan) model CPL-200]] and CD (JASCO model J-820) spectrometers [104].

Chart 1.
Chemical structures of five unsubstituted fused aromatics (naphthalene, anthracene, tetracene, pyrene, and perylene) and five perylene derivatives with substituents, 2,5,8,11-tetra-tert-butylperylene (ttBuperylene), N,N′-bis(2,6-diisopropylphenyl)-1,6,7,12-tetra-phenoxy-3,4,9,10-perylenetetracarboxylic diimide (iPrPh-PhO-perylene), N,N′-bis(2,5-di-tert-butyl-phenyl)-3,4,9,10-perylenedicarboximide (BTBPTCDI), 16,17-bis(n-octyloxy)-anthrax[9,1,2-cde]-benzo[rst]-pentaphene-5,10-dione (Violanthrone 79), and N,N′-di-n-octyl-3,4,9,10-perylenetetra-carboxylic diimide (PTCDI-C8).
Perylene has long been believed to adopt a D2h symmetrical planar and achiral framework and is postulated as one of the polyaromatic hydrocarbons (PAHs) existing in molecular clouds of the interstellar universe [107]. In actuality, the interstellar PAHs emit infrared (IR) radiation in bright HII regions, and planetary and reflection nebulae. The interstellar IR spectral radiation upon excitation of vacuum–UV and UV–visible spectral lines (for example, Lyman and Balmer series) from ionized atomic hydrogen dominate most radiation sources of the galaxy and extragalaxies [108,109]. Our fundamental question, however, pertains to whether perylene truly remains achiral in the S1 and S0 states when all the hydrogen atoms attached to the framework are considered. To address this apparently naive query, we measured the CPL and CD spectra of unsubstituted perylene and five related derivatives carrying rotatable side groups, 5,8,11-tetra-tert-butylperylene (ttBuperylene), N′-bis(2,6-diisopropylphenyl)-1,6,7,12-tetraphenoxy-3,4,9,10-perylenetetracarboxylic diimide (iPrPhPhOperylene), N,N′-bis(2,5-di-tert-butylphenyl)-3,4,9,10-perylenedicarboximide (BTBPT-CDI), 16,17-bis(n-octyloxy)-anthrax[9,1,2-cde]-benzo[rst]-pentaphene-5,10-dione (Violanthrone 79), and N,N′-dioctyl-3,4,9,10-perylenedicarboxylic diimide (PTCDI-C8) (Chart 1).
It is possible to regard unsubstituted perylene as a fused dimer of l- and r-twistable biphenyl substructures; however, if there is a twist, then perylene should no longer exhibit D2h symmetry but should exist as a mixture of D2-symmetrical l- and r-twists and/or a CS-symmetrical achiral folded framework. The structural hypothesis at the S0 state is obvious for the five cases of (a) four bulky substituents in the 1-, 6-, 7- and 12-positions of iPrPh-PhO-perylene, (b) two bulky alkoxy substituents in the 16- and 17-positions in Violanthrone 79, (c) two bulky aromatic groups in the N,N′-positions of BTBPTCDI, (d) four bulky alkyl substituents in the 2-, 5-, 8- and 11-positions of ttBuperylene, and (e) two less-bulky alkyl groups in the N,N′-positions of PTCDI-C8. This query at the S1 state is still unanswered.
Figure 1a–j display comparisons of the CPL/PL (photoluminescence) spectra of perylene and five derivatives in alcoholic solvents and chloroform at room temperature.
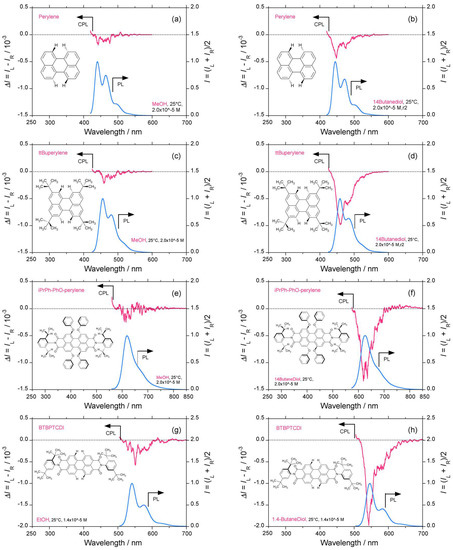
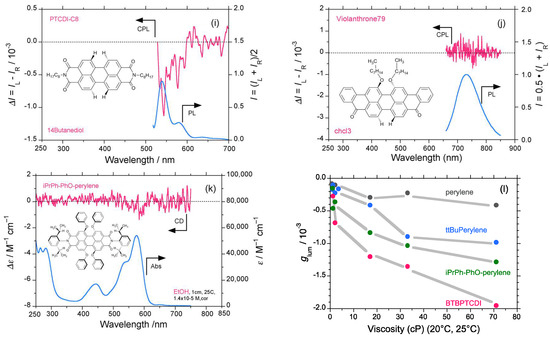
Figure 1.
Comparison of circularly polarized luminescence/photoluminescence (CPL/PL) and circular dichroism (CD)/ultraviolet (UV)–visible spectra of perylene and five derivatives in alcoholic solvents at room temperature (path length: 10 mm, cylindrical cuvette, concentration 1–2 × 10−5 M. CPL/PL spectra of perylene excited at 390 nm in (a) methanol, and (b) 1,4-butanediol. CPL/PL spectra of ttBuperylene excited at 395 nm in (c) methanol, and (d) 1,4-butanediol. CPL/PL spectra of iPrPh-PhO-perylene excited at 470 nm in (e) methanol, and (f) 1,4-butanediol. CPL/PL spectra of BTBPTCDI excited at 525 nm in (g) methanol, and (h) 1,4-butanediol. (i) CPL/PL spectra of PTCDI-C8 excited at 490 nm in 1,4-butanediol. (j) CPL/PL spectra of Violanthrone 79 excited at 625 nm in chloroform. (k) CD/UV–visible spectra of iPrPh-PhO-perylene in methanol. (l) The glum value of perylene, ttBuperylene, iPrPh-PhO-perylene, and BTBPTCDI as a function of solvent viscosity.
From Figure 1a,b, unsubstituted perylene in low-viscosity methanol (η, 0.55 cP) reveals a weak vibronic CPL signal at the corresponding PL emission at approximately 400–500 nm. The vibronic CPL band becomes more obvious, and glum reaches −0.45 × 10−3 at the first vibronic band when methanol is replaced with the more viscous 1,4-butanediol (η, 71.0 cP). The magnitude of the vibronic CPL band at the 0–0 and 0–1 peaks increases as solvent viscosity increases (Figure 1l and Figure S1a–f, Supplementary Materials). However, CD signals at the corresponding UV–visible bands cannot be distinguished due to π–π* transitions (Figure S1u, Supplementary Materials). These results imply that perylene in the S1 state temporarily adopts a chiral twisted geometry. However, the observed chirality of perylene disappears in the S0 state. Possibly, perylene in the S0 state exists as a mixture of l- and r-twisted geometries, thereby resulting in a CD-silent pair of opposite chirality twisted conformers. Photoexcited perylene may be optically active.
Research on biaryl-sensitized terbium (III) complexes showed that fluorescence lifetime enhancement in these systems is due to solvent polarity and oxygen sensitivity rather than viscosity effects [110]. Nevertheless, oxygen solubilization does not significantly influence the fluorescence quantum yield of most organic luminophores including laser dyes, but does significantly suppress phosphorescence. Solvent viscosity is, therefore, considered to be a critical factor in the fluorescence lifetimes in our systems.
In ttBuperylene, when the four hydrogen atoms in the 2-, 5-, 8- and 11-positions of the perylene framework are replaced by four bulky three-fold symmetric tert-butyl groups as rotors, (−)-sign CPL signals for the 0–0 and 0–1 peaks at approximately 450–500 nm in methanol, 1,4-butanediol, and other solvents are more clearly evident (Figure 1c–d and Figure S1g–k, Supplementary Materials). Similarly, in iPrPh-PhO-perylene, when the four isopropyl groups in the 2-, 5-, 8-, and 11-positions of the perylene framework are replaced by four two-fold symmetric sterically hindered phenoxy groups as rotors, the (−)-sign CPL signals redshift to 530–570 nm and are without doubt more obvious in methanol, 1,4-butanediol, and other solvents (Figure 1e–f and Figure S1p–t, Supplementary Materials).
Similarly, BTBPTCDI, with two sterically hindered phenyl groups in the N,N′-positions of the perylene diimide framework unambiguously exhibits (−)-sign vibronic CPL signals at approximately 550–590 nm in methanol, 1,4-butanediol, and other solvents (Figure 1g–h and Figure S1l–n, Supplementary Materials). PTCDI-C8, bearing two less bulky n-octyl groups in the N,N′-positions of the perylene diimide framework, reveals obvious (−)-sign vibronic CPL signals at approximately 540–580 nm in 1,4-butanediol and n-dodecane (Figure 1i and Figure S1o, Supplementary Materials). CPL signals for Violanthrone 79 in chloroform were not detected (Figure 1j). A faint (−)-sign CD signal for iPrPh-PhO-perylene in methanol may be seen on the order of gabs ≈ 10−6, but it is not obvious (Figure 1k). No detectable CD signals for perylene and ttBuperylene were observed (Figure S1f,g, Supplementary Materials).
Figure 1l summarizes the glum values of perylene, ttBuperylene, iPrPh-PhO-perylene, and BTBPTCDI as a function of solvent viscosity for the solvents methanol, ethanol (1.1 cP), n-propanol (2.0 cP), n-undecanol (17.0 cP), 1,3-propandiol (33.0 cP), and 1,4-butanediol (71.0 cP). We can thus conclude that the perylene and perylene diimide frameworks in the S1 state adopt a twisted geometry due to steric repulsion in the 2-, 5-, 8-, and 11-positions of the perylene framework. CPL signals of (−)-sign are apparent, and the glum value reaches a maximum of −2.0 × 10−3. Perylene, thus, does not adopt an achiral framework in the S1 state, and the same is possibly true for the S0 state.
To see the effect of twisted perylene in snapshot mode, we simulated the CD/UV–visible spectra with 0.20 eV full width at half maximum (fwhm) and electron density mapping at (c) the first first lowest unoccupied molecular orbital (1st LUMO) and (d) the first highest occupied molecular orbital (1st HOMO) for a hypothetical model of perylene twisted by 30° (Figure 2a–d). The twisted perylene clearly shows negative CD spectra at 443 nm and bisignate CD bands at approximately 300 nm. The value of gabs at 443 nm is found to be 4 × 10−4. A closed-chiral-loop current (reddish zone) (Figure 2c) is obvious for the LUMO, while the same is not true for the HOMO (Figure 2d). The closed-loop current may interfere with the one-handed chiral WNC postulated.
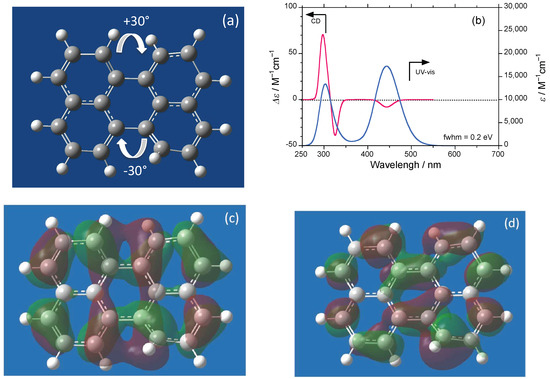
Figure 2.
(a) Hypothetical model of perylene twisted by 30°; (b) simulated CD/UV–visible spectra with 0.2 eV full width at half maximum (fwhm) and electron density mapping at (c) first lowest unoccupied molecular orbital (1st LUMO) and (d) first highest occupied molecular orbital (1st HOMO). For this time dependent density functional theory (TD-DFT) and Becke, three-parameter, Lee-Yang-Parr exchange-correlation functional (B3LYP) with 6-31G(d) basis set, Gaussian09 rev D.01 (GaussView5 package)-calculated structures, a closed-chiral-loop current (red) is obvious for the LUMO, although this is not the case for the HOMO.
2.2. Rigid Luminophores Bearing Multiple Three-Fold Symmetrical Alkyl Substituents
C2v-symmetrical pyrromethene-difluoroborate (BODIPY) and its derivatives are established as excellent emitters with a high QY and a very small Stokes’ shift (350–500 cm−1) [111,112]. Incorporation of alkyl groups into BODIPYs improves their solubility in common organic solvents. It is conceivable that certain BODIPYs carrying three-fold symmetrical alkyl groups may reveal optical activity due to handed gear motions between these alkyl groups. We, therefore, designed several C2v BODIPYs as candidates to address the question of whether the handed gear motions occur with exactly equal energies and opposite senses [113]. If the gear-like motions in CW and CCW directions at the S0 and S1 states are equally operational, CD and CPL signals will not be detectable due to mutual cancellation of the opposite chiroptical signed bands, but they will have the same absolute magnitudes. However, if the gear-like motions in the S0 and/or S1 states are occurring unidirectionally due to unequal intramolecular gear energies, this should be detectable as CD and CPL signals. Unidirectional gear-like motions drive unidirectional molecular motors.
Firstly, we tested the gear-motion behaviors of pyrromethene 597 (BODIPY 597) and pyrromethene 546 (BODIPY 546) (Chart 2), which both have five three-fold symmetry methyl groups in the 1-, 3-, 5-, 7- and 8-positions of the BODIPY frameworks. Pyrromethene 597 has two additional three-fold symmetrical tert-butyl groups in the 4,4′-positions. The tert-butyl group itself consists of three methyl groups with three-fold symmetry. Both methyl and tert-butyl groups are assumed to act as gears.

Chart 2.
Chemical structures of [[(4-tert-butyl-3,5-dimethyl-1H-pyrrol-2-yl)(4-tert-butyl-3,5-dimethyl-2H-pyrrol-2-ylidene)methyl]methane](difluoroborane) (pyrromethene 597) and [[(3,5-dimethyl-1H-pyrrol-2-yl)3,5-dimethyl-2H-pyrrol-2-ylidene]methyl]methane](difluoroborane) (pyrromethene 546).
Pyrromethene 597 (Chart 2) in methanol showed weakly vibronic CPL bands at 550–600 nm; however, in 1,4-butanediol, these were amplified significantly to glum = −1.0 × 10−3 at 562 nm (Figure 3a,d). Similarly, pyrromethene 546 (Chart 2) in methanol showed weakly vibronic CPL bands; however, in 1,4-butanediol, these bands were magnified to glum = −0.4 × 10−3 at 515 nm (Figure 3g,h). Pyrromethene 597 in n-undecanol, ethylene glycol, and other solvents showed similar vibronic CPL bands at 550–600 nm (Figure 3b,c). These (−)-sign CPL characteristics of pyrromethenes 597 and 546 depend on the nature of solvents (Figure S2a–h, Supplementary Materials).


Figure 3.
Comparison of CPL/PL and CD/UV–visible spectra of two pyrromethenes bearing rotatable alkyl groups (pyrromethene 597 and pyrromethene 546) in solution at room temperature (path length: 10 mm, cylindrical cuvette, concentration 1–3 × 10−5 M, and path length 0.1 cm and 1–3 × 10−4 M. CPL/PL spectra of pyrromethene 597 excited at 490 nm in (a) methanol, (b) n-undecanol, (c) ethylene glycol, and (d) 1,4-butanediol. CD/UV–visible spectra of pyrromethene 597 in (e) methanol, and (f) 1,4-butanediol. CPL/PL spectra of pyrromethene 546 excited at 450 nm in (g) methanol, and (h) 1,4-butanediol. CD/UV–visible spectra of pyrromethene 546 in (i) methanol, and (j) 1,4-butanediol. (k) glum value of pyrromethene 597 and pyrromethene 546 as a function of solvent viscosity. (l) Simulated CD/UV–visible spectra (fwhm = 0.20 eV) of hypothetical model of pyrromethene 597 twisted weakly by 2°, electron density mapping at (m) first LUMO and (n) first HOMO, obtained with TD-DFT, B3LYP functional with 6-31+G(d,p) basis set using Gaussian09 rev D.01 and GaussView5 package. A semi-closed-chiral-loop current (green) is seen for the HOMO, although this is not obvious for the LUMO.
More surprisingly, pyrromethene 597 in methanol revealed a clear (−)-sign CD band (Δε = 0.8 M−1∙cm−1 at 530 nm, gabs = −1.5 × 10−5), whilst the λmax of the visible band was 525 nm (Figure 3e). The Cotton CD band in viscous 1,4-butanediol showed a more intense (−)-sign CD band (Δε = 1.5 M−1∙cm−1, gabs = −3.8 × 10−5 at 527 nm), with λmax of the visible band at 525 nm (Figure 3f). Similarly, pyrromethene 546 in methanol revealed a clear (−)-sign CD band (Δε = 1.0 M−1∙cm−1 at 495 nm, gabs = −1.5 × 10−5) with λmax is 492 nm (Figure 3i). The Cotton CD band in viscous 1,4-butanediol revealed a (−)-sign CD band (Δε = 1.0 M−1∙cm−1, gabs = −1.4 × 10−5 at 496 nm) (Figure 3j). These (−)-CD characteristics are unchanged and independent of the solvent (Figure S3a–h, Supplementary Materials). These (−)-sign gabs values for the S0 state are smaller by two orders of magnitude compared to those of the corresponding (−)-sign glum values for the S1 state.
Pyrromethenes 597 and 546 (Chart 2) preferentially exhibit (−)-sign CD and CPL signals, indicating that they preferentially absorb and emit l-CP light over r-CP light. These unexpected chiroptical results imply the occurrence of handed gear-like motions between multiple alkyl rotors in the S0 and S1 states, causing a subtle distortion of the framework of the BODIPY ring. Gaussian09 simulations usng time dependent density functional theory (TD-DFT) and Becke, three-parameter, Lee-Yang-Parr exchange-correlation functional (B3LYP) with 6-31+G(d,p) basis set indicate that one of the subtly distorted pyrromethenes 597 has a negative Cotton CD band at 450 nm (Figure 3l). Its LUMO and HOMO orbitals correspond to symmetrical and anti-symmetrical electron density with respect to the C2 molecular axis (Figure 3m,n). Green- and red-colored electron density maps merely indicate the phase of the electron wavefunctions. If one assumes that a handed closed loop WNC flows only in regions of the same phase (green regions) indicated by yellow arrows, pyrromethene 597 becomes a handed chiral π-electron system at the C2 axis in the S0 state. Although a handed current flow by the yellow arrows is not obvious for the S1 state, the framework of photoexcited pyrromethene 597 may be more twisted and, thus, associated with more rapid gear motions of the seven three-fold symmetrical alkyl (methyl and tert-butyl) rotors, suggesting a potential application of UP-driven one-way alkyl rotors without chiral chemical entities detectable by CPL and CD spectroscopy.
2.3. Organic Scintillators
Spontaneous radiation produced by free electrons at the valence bands of molecules is responsible for the production of scintillation light in π-conjugated organic molecules in crystalline forms and molecularly disperse solutions [114]. Scintillation light is fluorescence from the S1 state. This scenario should obey the Jablonski diagram [43,44]. Highly emissive fluorophores with a high QY are candidates for molecular scintillators.
In fact, the Kamioka Liquid Scintillator Antineutrino Detector (KamLAND) used a molecular scintillator to detect anti-neutrinos generated geologically from the β−-decay of 238U and 232Th in the Earth’s crust, but it cannot detect anti-neutrinos from 40K due to the low energy [115,116]. Three radioactive nuclei (40K, 238U, and 232Th) are responsible for geothermal power. These radioactive atoms are considered probes of supernova explosions that followed the nucleosynthesis of heavy elements and the birth of the Earth [117].
In KamLAND, 1000 tons of liquid scintillator was composed of n-dodecane (80 vol.%), 1,2,4-trimethylbenzene (20 vol.%), and 150 kg of diphenyloxazole (PPO, Chart 3) [115,116], although it is unclear to us why n-dodecane was considered the best solvent for the liquid scintillator. Anyway, fortuitous or otherwise, based on the glum–η relationship shown above and discussed in our previous paper [104], we assume that a viscous fluid medium such as n-dodecane is crucial to magnify the efficiency of scintillation light.

Chart 3.
Chemical structures of non-rigid scintillators, 2,2″-([1,1′-biphenyl]-4.4′-diyldi-2,1-ethenediyl)bis-benzenesulfonic acid disodium salt (stilbene 420), 1,4-bis(2-methylstyryl)benzene (bis-MSB), 1,4-bis(5-phenyloxazol-2-yl)benzene (POPOP), 1,4-bis(4-methyl-5-phenyloxazol-2-yl)benzene (DMPOPOP), 2,5-bis(5-t-butyl-2-benzoxalyl)thiophene (BBOT), 2,5-bis(4-biphenylyl)thiophene (BBT), diphenyloxazole (PPO), and 1,2,4-trimethylbenzene (pseudocumene).
Non-rigid scintillators, 1,4-bis(2-methylstyryl)benzene (bis-MSB), 1,4-bis(5-phenyloxazol-2-yl)-benzene (POPOP), 1,4-bis(4-methyl-5-phenyloxazol-2-yl)benzene (DMPOPOP), 2,5-bis(5-t-butyl-2-benzoxalyl)thiophene (BBOT), 2,5-bis(4-biphenylyl)thiophene (BBT), are soluble in organic solvents, and 2,2″-([1,1′-biphenyl]-4.4′-diyldi-2,1-ethenediyl)bis-benzenesulfonic acid disodium salt (stilbene 420) is soluble in water and alcoholic solvents [118,119,120,121]. These molecular scintillators can adopt a polar C2-symmetrical conformation in the S1 and S0 states due to their rotatable main axes. However, due to multiple C–C bonds with low rotational barrier (~1.5 kcal∙mol−1) between the aromatic and trans-vinylene moieties, and due to the proximity effect of these C–H/H–C repulsions [122], those molecules cannot adopt planar structures. Thus, these molecules should exist as a mixture of many rotamers with an equal population of P- and M-twisted molecules in solution at ambient temperature.
Stilbene 420, as a trans-p-biphenylenevinylene-type oligomer, in H2O (0.96 cP) and D2O (0.96 cP) emitted (−)-sign CPL with glum = −0.5 × 10−3 at 430 nm (Figure 4a,b), possibly at the second vibronic 0–1’ band, indicating no marked isotope effect between H and D. The glum value increased to −2.0 × 10−3 at 410 nm at the first vibronic 0–0’ band when 1,4-butanediol was employed as a solvent. The glum–η relationships showed several transitions when η = 0.96–2.5 cP, 2.5-6 cP, and >22 cP (Figure 4e,f). This feature arises from 512° of rotational freedom of stilbene 420 with the five rotatable C–C bonds. From the (−)-sign in a vacuum in glum value extrapolated at η = 0.0 cP and the (−)-sign glum value in water and heavy water, water-soluble non-rigid PAHs in the interstellar universe could spontaneously favor a handed chiral and/or helical geometry that is radiating (−)-sign CP light.

Figure 4.
CPL/PL spectra of stilbene 420 (water-soluble trans-p-biphenylenevinylene-type scintillator) in (a) H2O, (b) D2O, (c) methanol, and (d) 1,4-butanediol (path length: 10 mm, cylindrical cuvette, concentration 2.5–10 × 10−5 M); (e) glum value of stilbene 420 as a function of solvent viscosity (η = 0–71 cP); (f) glum value of stilbene 420 as a function of solvent viscosity (η = 0–10 cP).
CPL/PL spectra and glum–η characteristics of bis-MSB as a trans-p-phenylenevinylene-type oligomer are similar to those of stilbene 420 (Figure 5a–f). Moreover, bis-MSB in low-viscosity solvents (n-pentane, diethyl ether, and methanol) revealed several weak but clearly detectable vibronic CPL signals with (−)-sign at 400–450 nm (Figure 5a,c and Figure S5a–p, Supplementary Materials). The CPL signals were further amplified to −0.72 × 10−3 and −0.90 × 10−3 at 400 nm when the more viscous n-undecanol and squalane were employed, respectively (Figure 5b,d). The glum value progressively and discontinuously increased when carbon numbers increased in two series of n-alkanes and n-alkanols including ethanol (Figure 5e). The glum–η characteristics showed step-like transitions with at least three plateaus between η = 5–10 cP, 10–17 cP, and >30 cP, while the glum value changed linearly in response to the η value when η = 0.22–5 cP (Figure 5f). The glum value extrapolated to η = 0 cP is −0.5 × 10−3.
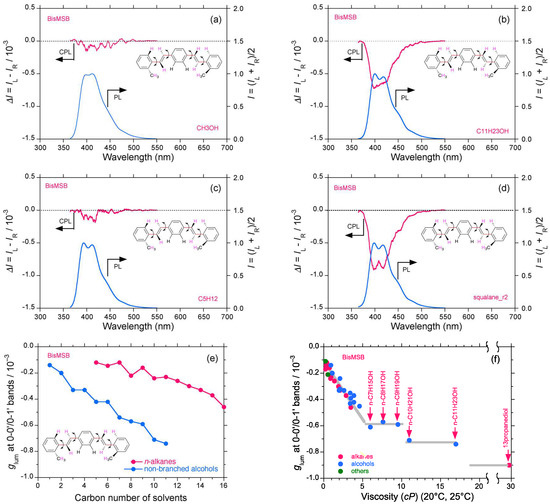
Figure 5.
CPL/PL spectra of bis-MSB (trans-p-phenylenevinylene-type scintillator) in (a) methanol, (b) n-undecanol, (c) n-pentane, and (d) squalane (path length: 10 mm, cylindrical cuvette, concentration 2.5–10 × 10−5 M); (e) glum value of bis-MSB as a function of carbon number in two series of n-alkanes and n-alkanols (including methanol and ethanol); (f) glum value of bis-MSB as a function of solvent viscosity (η = 0–30 cP).
The scintillators bis-MSB, POPOP, DMPOP, BBOT, BBT, and stilbene 420 have rotational freedom along five, four, four, four, two, and five C–C bonds, respectively, producing huge numbers of rotamers. In actuality, these π-conjugated organic scintillators do not reveal noticeable CD bands at the corresponding π–π* transitions in UV–visible regions exemplified in Figure 6e,f and Figure 7c, and Figures S4k,l and S5q,r (Supplementary Materials). However, without exception, bis-MSB, POPOP, DMPOP, BBOT, BBT, and stilbene 420 revealed intense (−)-sign CPL signals at the corresponding PL bands in various solvents (Figure 4, Figure 5, Figure 6 and Figure 7 and Figures S4a–p and S5a–p, Supplementary Materials).


Figure 6.
CPL/PL spectra of POPOP, a 1,3-oxazole ring-containing scintillator, in (a) chloroform and (c) n-hexadecane, and CD/UV–visible spectra in (e) methanol (path length: 10 mm, cylindrical cuvette, concentration 2.5–10 × 10−5 M). For comparison, CPL/PL spectra of DMPOPOP in (b) chloroform, and (d) n-dodecane, and normalized CD/UV–visible spectra in (f) methanol (path length: 10 mm, cylindrical cuvette, concentration 2.5–10 × 10−5 M).

Figure 7.
CPL/PL spectra of BBOT, a thiophene ring-containing scintillator, in (a) n-hexadecane and CD/UV–visible spectra in (c) 1,4-butanediol at room temperature. CPL/PL spectra of BBT in (b) chloroform and (d) n-hexadecane. Path length: 10 mm, cylindrical cuvette, concentration 2.5–10 × 10−5 M.
The (−)-sign CPL signals and PL spectra of POPOP in chloroform and n-hexadecane are very similar to those of DMPOPOP in chloroform and n-hexadecane (Figure 6a–d). The only difference is the luminescence wavelength; the λlum values of the CPL/PL bands at the 0-0’ band are 399 nm for POPOP and 407 nm for DMPOPOP (Figure 6a,b). Similarly, thiophene ring-containing scintillators BBOT and BBT in n-hexadecane showed (−)-sign CPL signals with glum = −0.6 × 10−3 at 428 nm (0–1’ band) and −1.0 × 10−3 at 409 nm (0–0’ band) (Figure 7a,b,d). No detectable CD signal of BBT in chloroform was confirmed (Figure 7c). This difference in glum value between BBOT and BBT should arise from the number of rotatable C–C bonds between the aromatic rings; BBOT has two, while BBT has four.
2.4. Luminophores Carrying Dialkylamino Group with Flip-Flop and/or Rotatable Motions
MacDermott and Hegstrom proposed that ammonia-type molecules (R1R2R3N with a lone pair) able to undergo flip-flop motion are well suited to test the MPV hypothesis [83] experimentally. Coumarin derivatives, DCM, and RhB [118,119,120,121], which are C1-symmetrical π-conjugated luminophores, are candidates because the frameworks of coumarin, rhodamine, 4-(dicyanomethylene)-6-styryl-4H-pyran possess dialkylamino groups, which are susceptible to flip-flop and/or rotatable motions in the S1 and S0 states. The temporal generation at the S1 state and/or persistent generation at the S0 state are detectable as CPL and/or CD signals if certain chiral geometries are indeed generated. Most researchers do not think that coumarins, DCM, and rhodamine B are optically inactive because of the lack of chiral stereocenters. Chemical structures of 11 coumarin derivatives, DCM, and rhodamine B, which all carry dialkylamino group(s) as side chains, are shown in Chart 4.

Chart 4.
Chemical structures of coumarin 6, coumarin 545, coumarin 466, coumarin 6H, coumarin 481/35, coumarin 153, coumarin 1/460, coumarin 102, coumarin 7, coumarin 30, 3,3′-carbonyl-bis(7-diethylaminocoumarin) (bis-coumarin), 4-(dicyanomethylene)-2-methyl-6-(4-dimethylaminostyryl)-4H-pyran (DCM), and rhodamine B (RhB).
Firstly, we measured the CPL/PL spectra of coumarin 6 and coumarin 545 in several solvents (Figure 8a–f and Figure S6a–j, Supplementary Materials), and, for comparison, we measured the CD/UV–visible spectra in methanol (Figure 8g,h). Coumarin 6 and coumarin 545 showed very weak green-colored (−)-sign CPL signals on the order of glum = −0.1 × 10−3 at 505 nm and 520 nm, respectively (Figure 8a,b). When 1,4-butanediol was employed as the solvent, the weak (−)-sign CPL signals increased substantially to glum = −1.2 × 10−3 at 509 nm and glum = −1.3 × 10−3 at 526 nm, respectively (Figure 8e,f). The magnitude of the (−)-sign CPL signals in n-hexadecane (η = 3.47 cP) was between those in methanol and in 1,4-butanediol (Figure 8c,d). Coumarin 6 and coumarin 545 also showed very weak (−)-sign CD signals on the order of gabs = −1.3 × 10−5 at 464 nm and gabs = −1.3 × 10−5 at 479 nm, respectively.


Figure 8.
Comparison of CPL/PL and UV–visible spectra of coumarin 6 and coumarin 545. CPL/PL spectra of coumarin 6 excited at 420 nm in (a) methanol, (c) n-hexadecane, and (e) 1,4-butanediol at room temperature. CPL/PL spectra of coumarin 545 excited at 420 nm in (b) methanol, (d) n-hexadecane, and (f) 1,4-butanediol at room temperature (path length: 10 mm, cylindrical cuvette, concentration 2.5–10 × 10−5 M. (g) CD/UV–visible spectra of coumarin 6 in methanol. (h) CD/UV–visible spectra of coumarin 545 in methanol.
These unexpected CD signals can be seen in ethanol and 1,4-butanediol. The major difference between coumarin 6 and coumarin 545 is that the former allows for free-rotation and flip-flop motions of the dialkylamino group, while, in the latter, free rotation is restricted, although the flip-flop motion is still permitted. We assume that certain flip-flop twists of the dialkylamino group commonly induce optically active conformations at the S1/S0 states of coumarin 6 and coumarin 545, giving rise to an optically active intramolecular charge transfer (ICT) state arising due to electron donation by the dialkylamino group to the electron-accepting benzothiazole ring.
Next, to clarify the effect of the benzothiazole ring, we measured the CPL/PL spectra of coumarin 466 and coumarin 6H in several solvents (Figure 9a–d and Figure S7a–f, Supplementary Materials), and, for comparison, the CD/UV–visible spectra in methanol (Figure 9e,f). Similarly, coumarin 466 and coumarin 6H showed very weak (−)-sign CPL signals on the order of glum = −0.1 × 10−3 at 457 nm and 481 nm (Figure 9a,b). In 1,4-butanediol, the (−)-sign CPL signals were enhanced to glum = −0.67 × 10−3 at 459 nm and glum = −0.53 × 10−3 at 482 nm, respectively (Figure 9c,d). These (−)- sign CPL magnitudes are half those of coumarin 6 and coumarin 545. Introduction of the benzothiazole ring appears, thus, to result in CPL signal amplification by a factor of two. Coumarin 466 and coumarin 6H also showed very weak bisignate-like CD signals although they are not obvious (Figure 9e,f). Similarly, the twisted flip-flop motion of the dialkylamino group may be crucial in inducing optically active conformations at the S1 states of coumarin 466 and coumarin 6H.

Figure 9.
Comparison of CPL/PL spectra of coumarin 466 and coumarin 6H at room temperature (path length: 10 mm, cylindrical cuvette, concentration 2.5–10 × 10−5 M. CPL/PL spectra of coumarin 466 excited at 370 nm in (a) methanol, and (c) 1,4-butanediol at room temperature. CPL/PL spectra of coumarin 6H excited at 400 nm in (b) methanol, and (d) n-hexadecane. CD/UV–visible spectra of (e) coumarin 466 and (f) coumarin 6H in methanol.
To clarify the effect of the three-fold symmetrical but electron-accepting CF3 group, we measured the CPL/PL spectra of coumarin 481/35 and coumarin 153 in several solvents (Figure 10a–f and Figure S8a–j, Supplementary Materials), and, for comparison, the CD/UV–visible spectra in methanol (Figure 10g,h). Coumarin 481/35 and coumarin 153 in methanol showed weak green-colored (−)-CPL signals at 507 nm and 527 nm, respectively (Figure 10a,b). Interestingly, these coumarins in squalane emitted blue-colored (−)-CPL signals with increased glum = −0.28 × 10−3 at 437 nm and glum = −0.39 × 10−3 at 455 nm, respectively (Figure 10c,d). In 1,4-butanediol, these (−)-CPL signals became enhanced to glum = −1.17 × 10−3 at 509 nm and glum = −0.59 × 10−3 at 527 nm, respectively (Figure 10e,f).

Figure 10.
Comparisons of CPL/PL and UV–visible spectra of coumarin 481/35 and coumarin 153 at room temperature (path length: 10 mm, cylindrical cuvette, concentration 2.5–10 × 10−5 M. CPL/PL spectra of coumarin 481/35 in (a) methanol (exited at 410 nm), (c) squalane (excited at 370 nm), and (e) 1,4-butanediol (excited at 415 nm). CPL/PL spectra of coumarin 153 in (b) methanol (excited at 435 nm), (d) squalane (excited at 385 nm), and (f) 1,4-butanediol (excited at 435 nm). CD/UV–visible spectra of (g) coumarin 481/35, and (h) coumarin 153 in methanol.
We tested the effect of the CH3 group at the peripheral position of the coumarin framework in place of the CF3 group. The CPL/PL spectra of coumarin 1/460 and coumarin 102 were recorded in several solvents (Figure 11a–d and Figure S9a–d, Supplementary Materials), and, for comparison, the CD/UV–visible spectra were recorded in methanol (Figure 11e,f). Coumarin 1/460 and coumarin 102 in methanol showed weak blue (−)-CPL signals at 450 nm and 480 nm (Figure 11a,b). In 1,4-butanediol, these increased to glum = −0.72 × 10−3 at 449 nm and −0.65 × 10−3 465 nm, respectively. The CD signals of coumarin 1/460 and coumarin 102 in methanol are not obvious (Figure 11e,f).
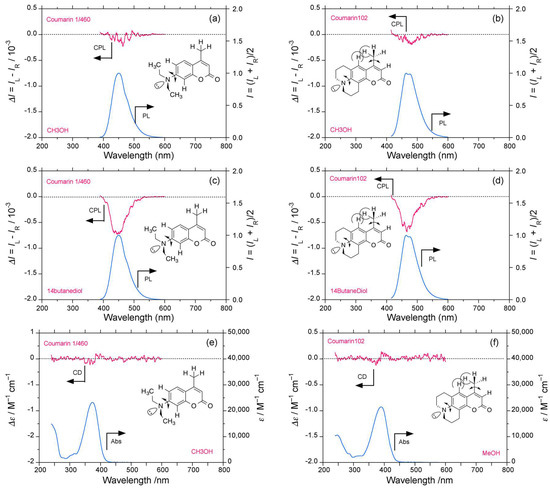
Figure 11.
Comparisons of CPL/PL and UV–visible spectra of coumarin 1/460 and coumarin 102 at room temperature (path length: 10 mm, cylindrical cuvette, concentration 2.5–10 × 10−5 M. CPL/PL spectra of coumarin 1/460 in (a) methanol (excited at 365 nm), and (c) 1,4-butanediol (excited at 365 nm). CPL/PL spectra of coumarin 102 in (b) methanol (excited at 380 nm), and (d) 1,4-butanediol (excited at 380 nm). UV–visible spectra of: (e) coumarin 1/460, and (f) coumarin 102 in methanol.
To view the effect of the N-methyl group at benzimidazole, the CPL/PL spectra of coumarin 7 and coumarin 30 were recorded in several solvents (Figure 12a–d and Figure S10a–p, Supplementary Materials). Coumarin 7 and coumarin 30 in methanol showed weak blue-green vibronic (−)-CPL signals associated with glum = −0.16 × 10−3 at 465 nm and −0.22 × 10−3 at 482 nm, respectively (Figure 12a,b). In 1,4-butanediol, these (−)-CPL signals increased to glum = −1.21 × 10−3 at 497 nm and −1.20 × 10−3 at 452 nm, respectively (Figure 12c,d). Coumarin 7 and coumarin 30 in methanol may show similar bisignate features in their CD signals, but the spectral profile of coumarin 7 is the opposite of coumarin 30 (Figure 12e,f). Although the effect of the methyl group is minimal, the presence of the benzimidazole ring markedly affects the glum values in 1,4-butanediol, when compared to coumarins 466, 6H, 481/35, 153, 1/460, and 102. The presence of benzimidazole and benzothiazole groups in coumarins with dialkylamino groups may possibly be another crucial factor in photoinduced CPL signals.

Figure 12.
Comparisons of CPL/PL and UV–visible spectra of coumarin 7 and coumarin 30 at room temperature (path length: 10 mm, cylindrical cuvette, concentration 2.5–10 × 10−5 M. CPL/PL spectra of coumarin 7 in (a) methanol (excited at 420 nm), and (c) 1,4-butanediol (excited at 420 nm). CPL/PL spectra of coumarin 30 in (b) methanol (excited at 430 nm), and (d) 1,4-butanediol (excited at 430 nm). UV–visible spectra of: (e) coumarin 7, and (f) coumarin 30 in methanol.
As candidates of photoinduced red-light CPL emitters without stereocenters, we investigated whether 4-(dicyanomethylene)-2-methyl-6-(4-dimethylaminostyryl)-4H-pyran (DCM) and rhodamine 6 in several solvents reveal CPL signals at the corresponding PL bands. DCM and rhodamine 6 are representative red-light emitters, and both bear flip-flop dialkylamino groups.
Surprisingly, DCM showed weak (−)-sign CD signals on the order of gabs = −1.3 × 10−5 at 474 nm (Figure 13f). This weak CD signal was reproducible when measured on several different occasions and unchanged in ethanol, n-propanol, and 1,4-butanediol. Although DCM showed weak (−)-CPL signals in methanol on the order of glum = −0.18 × 10−3 at 615 nm (Figure 13a), the CPL signal increased to glum = −0.95 × 10−3 at 615 nm in ethylene glycol (Figure 13c), −1.44 × 10−3 at 617 nm in 1,4-butanediol (Figure 13d), and, more surprisingly, −1.17 × 10−3 at 549 nm in the low-viscosity solvent, 1,4-dioxane (η = 1.10 cP) (Figure 13b). The CPL/PL wavelengths of DCM in 1,4-dioxane greatly blue-shifted by ca. 70 nm and showed spectral narrowing compared to the alcoholic solvents. For reasons which are unclear, ethylene glycol and 1,4-dioxane are recommended for DCM when it is used as a laser dye.

Figure 13.
Comparisons of CPL/PL spectra of 4-(dicyanomethylene)-2-methyl-6-(4-dimethyl- aminostyryl)-4H-pyran (DCM) in (a) methanol (b) 1,4-dioxane (c) ethylene glycol, (d) 1,3-propanediol, and (e) 1,4-butanediol. (f) CD/UV–visible spectra of DCM in methanol at room temperature (path length: 10 mm, cylindrical cuvette, concentration 2.5–10 × 10−5 M.
More surprisingly, RhB had a clear (−)-sign CD signal on the order of gabs = −2.0 × 10−5 at 550 nm (Figure 14f). This CD signal was reproducible when measured on several different occasions and was confirmed to be unchanged in ethanol, n-propanol, and 1,4-butanediol. Although RhB in methanol showed weak vibronic CPL signals at 572 nm (Figure 14a), it magnified abruptly to glum = −0.74 × 10−3 at 574 nm in n-C11H23OH (Figure 14c), glum = −0.72 × 10−3 at 581 nm in ethylene glycol (Figure 14d), glum = −0.83 × 10−3 at 596 nm in 1,4-dioxane (Figure 14b), and glum = −1.01 × 10−3 at 576 nm in 1,4-butanediol (Figure 14e). Similarly, ethylene glycol and 1,4-dioxane are recommended for RhB when it is used as a laser dye. Ethylene glycol and 1,4-dioxane are not the only solvents for RhB and are the key to magnified (−)-sign CPL signals in fluidic media with a higher viscosity.

Figure 14.
Comparisons of CPL/PL spectra of rhodamine B (RhB) in (a) methanol, (b) 1,4-dioxane, (c) n-undecanol, (d) ethylene glycol, and (e) 1,4-butanediol. (f) CD/UV–visible spectra in methanol at room temperature (path length: 10 mm, cylindrical cuvette, concentration 2.5–10 × 10−5 M.
Finally, we checked the CPL/PL and CD/UV–visible spectra of 3,3′-carbonylbis(7-diethylamino- coumarin) (bis-coumarin). As a result, bis-coumarin in 1,4-butanediol showed clear but broader (−)-sign CPL signals with glum = −0.65 × 10−3 at 531 nm (Figure 15a) and a clearly associated (−)-sign CD signal with gabs = −1.0 × 10−5 at 463 nm (Figure 15b).
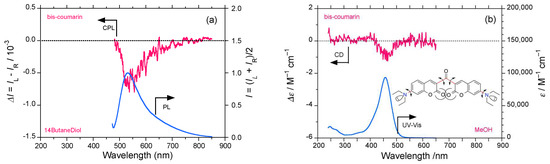
Figure 15.
(a) CPL/PL spectra of bis-coumarin excited at 430 nm in 1,4-butandiol, and (b) CD/UV–visible spectra in methanol at room temperature (path length: 10 mm, cylindrical cuvette, concentration 2.5 and 10 × 10−5 M.
As exemplified in the cases of the fused aromatic rings with substituents, BINOL derivatives [104], BODIPY, and organic scintillators shown in the sections above, the magnitudes of the (−)-sign CPL signals in a series of coumarin dyes, DCM, and RhB are greatly amplified in response to the viscosity of the solvents. The glum–η relationships for ten sets of coumarin dyes, DCM, and RhB are summarized in Figure 16a–j and Figure 17a–b. The data show that, in most cases, the absolute glum values leveled off at specific values when η > 30 cP. The leveled-off glum values are highly dependent on the nature of the substituents such as, for example, the presence or absence of benzimidazole or benzothiazole as electron-accepting groups and the position of the alkyl substituents. Moreover, in all cases, the glum values extrapolated to η = 0.0 cP are non-zero values, −0.2 × 10−3, suggesting that these luminophores should emit (−)-CPL signals under solvent-free conditions, such as in a collision-free vacuum.

Figure 16.
Comparison of glum values of (a) coumarin 6, (b) coumarin 545, (c) coumarin 466, (d) coumarin 6H, (e) coumarin 48/135, (f) coumarin 153, (g) coumarin 1/460, (h) coumarin 102, (i) coumarin 7, and (j) coumarin 30 as a function of solvent viscosity at room temperature (path length: 10 mm, cylindrical cuvette, concentration 2.5–10 × 10−5 M.
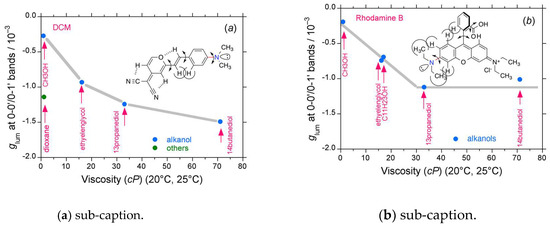
Figure 17.
Comparison of glum values of (a) DCM and (b) RhB as a function of solvent viscosity at room temperature (path length: 10 mm, cylindrical cuvette, concentration (2.5–10) × 10−5 M.
The non-zero glum values with (−)-sign extrapolated at η = 0.0 cP suggest that coumarins bearing dialkylamino group(s) with flip-flop capability adopt a handed chiral geometry preferentially by radiating (−)-sign CP light even in solvent-free, collision-free conditions. We conjecture that twisted flip-flop motions of the dialkylamino group in these luminophores may play a key role in the emergent photoinduced (−)-sign CPL signals at the S1 state with inherent handedness dictated by the PV-WNC mediated by Z0 boson.
In Figure 18, we show the CD/UV–visible spectra and HOMO–LUMO electron density of coumarin 545 optimized by Gaussian09 (DFT, B3LYP/6-31G(d) level), followed by 20 singlet states by TD-DFT calculation at the B3LYP/6-31G(d) level. Optimized coumarin 545 adopts a chiral conformation such that the dihedral angle between the benzothiazole and coumarin rings is 27.7°, and the two dihedral angles between the nitrogen atom and the two nearest carbons are 4.1° and 7.8° (Figure 18a). In fact, the chiral coumarin 545 reveals CD signals at the corresponding UV–visible bands (fwhm = 0.20 eV). The gabs value at the first Cotton band (397 nm) is calculated to be −8 × 10−5 M−1∙cm−1 (Figure 18b). From the estimated gabs value, the experimental gabs (= −1.3 × 10−5 at 479 nm) implies an enantiomeric excess (ee) of 16% in methanol. However, no CD signals are detected at the S2 state (~300 nm). The weak (−)-CD with gabs = −1.3 × 10−5 at the S1 state (~480 nm) may be interpreted as the postulated PV-WNC under a zero magnetic field.

Figure 18.
(a) Chemical structure of coumarin 545 optimized by Gaussian09 (DFT, B3LYP/6-31G(d) level) (b) Simulated CD/UV spectra with fwhm 0.20 eV, (c) 1st LUMO, and (d) 1st HOMO of coumarin 545 obtained with Gaussian09 (DFT, B3LYP/6-31G(d) level), followed by 20 singlet states by TD-DFT calculation at the B3LYP/6-31G(d) level.
The mapping of electron densities in the first LUMO and first HOMO of the optimized coumarin 545 are displayed in Figure 18c,d, respectively. The nitrogen atom in the dialkylamino group retains high electron density at both HOMO and LUMO levels. However, the phases (from green to red or vice versa) differ between HOMO and LUMO. Coumarin 545 at the S1 state may possibly adopt a more distorted geometry, simultaneously allowing a twisted flip-flop motion at the nitrogen atom.
3. Discussion
Weak interactions occur between all the six quarks and six leptons at the first., second, and third generations in the framework of elemental particle physics [47,81,123,124]. The weak interactions generate a “weak charge”, leading to a charged weak current and the weak neural current (WNC). Only left-handed particles and right-handed anti-particles carry the weak charge. The weak charge is analogous to Coulomb charges (+ and −) and Mulliken charges (δ+ and δ−) established in chemistry arising from the parity-conserving EM force. The weak charge is unique and is responsible for the basis of handedness at subatomic and atomic levels and, presumably, even at artificial molecular, oligomer, and polymer levels. The hierarchy in the handedness could be connected to the origin of biomolecular and biopolymer handedness, and beyond.
Charged left-particles and right-anti-particles can take part in the parity violating β− decay process of neutrons in the n → p + e− + anti-νe reaction. This event arises from a left-handed spinning electron (or right-handed electron from the observer) and right-handed spinning anti-neutrino (or left-handed anti-neutrino from the observer’s perspective).
According to Fermi’s theory, β− decay is the result of current–current interactions, leading to the vector (V)–axial vector (A) components of the charged weak currents. The term V is a polar vector and A is carrying angular momentum. Although the charged currents may be considered analogously to the cationic or anionic charges in molecules, no suggestion of dynamically flowing current is applied to cationic or anionic static charges. The V–A terms can generate different electric charges between p → n and e− → νe reactions, leading to the charged weak current.
Weinberg, Salam, and Glashow [47,123,124] formulated a unified theory of parity-conserving EM and parity-violating weak forces among the four fundamental physical forces based on gauge symmetry group SU(2) × U(1), while SU stands for special unitary (triplet states) and U unitary (singlet state) groups. The unified theory is popularly called the “Standard Model”, and formulates an electroweak (EW) force.
A spontaneous symmetry-breaking process with handedness is a result of three massive bosons (W+, W−, and Z0) and the massless photon (γ) [47]. The WNC is coupled with the massive neutral Z0 boson, and the EM neutral current is coupled with γ. The unified theory connects the electric charge e to the effective weak coupling gw, given by gw = e/2√2 sinθw, where θw is the Winberg’s weak mixing angle. Experimental datasets are mw (for W± bosons) = 81.0 GeV, mz (for Z0 boson) = 92.4 GeV, and sin2θw = 0. 223, because cosθw = mw/mz, while γ is kept massless.
Certainly, exchange of γ and Z0 occurs between electrons and the nucleus. The PV interaction in elemental particles can cause atomic parity violation (APV) effects as observable values in photon-induced absorption and radiation modes. Several APV theories invoked the idea that negatively charged electrons bonded to a positively charged nucleus by Coulomb force (γ) and the weak force (Z0), as illustrated in Figure 1.3 (Reference [47]) can involve three γ–γ–γ, Z0–γ–γ, and γ–γ–Z0 processes. PV potential is expressed as
where GF is Fermi’s weak coupling constant (1.16637 × 10−11 eV or 2.68971 × 10−10 kcal∙mol−1), r is the position of the electron, σ is the spin operator, me is the electron mass, c is the light speed, p = −iℏ∇ momentum operator, and δ is Dirac’s delta function. The admixing factor between the s1/2 and p1/2 states of the atom is on the order of 10−17 Z3Kr, whereby Kr is a relativistic correction factor (Kr ~ 3 for Cs and ~ 10 for Bi) [47]. The weak charge Qw is expressed as
where CVp and CVn are the coupling constants of vectoral V of proton and neutron, and N and Z are the numbers of neutrons and protons. Because 1 − 4 sin2θW = 0.116 < 1, Qw ≈ −N. In actuality, chiroptical rotation in visible and near infrared (NIR) regions due to APV effects for vapors of heavy atoms (Bi, Pb, Tl, and Cs) is always of (−)-sign, regardless of atomic mass, indicating the dominance of the −N term of Equation (2) [47].
A proton is constituted by two up quarks and one down quark, while a neutron is constituted by one up quark and two down quarks. All atoms are, thus, made of multiple up and down quarks and electrons. We radically postulate that the (−)-sign Qw value of all molecules is linearly [61] and nonlinearly amplified by huge numbers of neutrons because molecules are polyatomic and polyneutron systems constituting parity-violating atoms: unsubstituted perylene contains 20 × 6 = 120 neutrons, while pyrromethene 597 and stilbene 420 have 169 neutrons and 248 neutrons, respectively. We conjecture that enantiomeric pairs are no longer equivalent energetically, and their characteristics behave diastereomerically, owing to hundreds of neutrons within the nuclei that leads to non-mirror-symmetric LM interactions as a consequence of the (−)-sign electroweak charge.
The consistent observation of (−)-sign CPL and (−)-sign CD signals may arise from the inherent (−)-sign of Qw. If the negative-sign Qw in Equation (2) can be applied to spontaneous radiation and non-radiative processes from photoexcited non-rigid fluorophores, the CPL (and CD) signals are postulated to be commonly the same (−)–sign regardless of their chemical structures. Because the CPL signals from the observer are defined as PL(left) − PL(right), the non-rigid fluorophores in the present results and previous study [104] are primarily radiating PL(right) over PL(left) during the non-radiating reorganization process at the S1 state. Although the predicted signs in CPL and CD signals are inverted by dihedral angles of multiple C–C bonds in the non-rigid fluorophores [80], the weak (−)-charge Qw may be efficiently coupled with dipolar (δ+ and δ–) molecular structures that can adopt a significantly polar V-shape and syn-form (pseudo-C2 symmetric rotamer), and a polar rod-like shape (C1-symmetric rotamer) in the S1 and S0 states, as schematically illustrated in Chart 1, Chart 2, Chart 3 and Chart 4. The negative value Qw is additive to δ− (then, δ− − |Qw|) but is subtractive to δ+ (then, δ+ + |Qw|), then |δ− − |Qw|| ≠ |δ+ + |Qw|| for an enantiomeric pair of rotamers.
From the viewpoint of molecular dynamics, the PV-WNC force causes parity-odd rotational and/or flip-flop motions. The motions enforce (R)- and (S)-forms in the same direction (CW or CCW) that facilitates radiation with only (−)-sign CPL. However, the EM force, a parity-even, parity-conserved force, allows plural C–C bonds in the (R)-form to rotate and/or undergo flip-flop motions with CW motion and, conversely, those with the (S)-form to rotate and/or flip-flop CCW or vice versa. These motional dynamics should be mirror-symmetric. The handedness of motional dynamics by handed elemental particles can be recognized as chiral crystallization of achiral molecules: longitude polarized electrons and positrons that mirror image leptons oppositely affect an L/R preference in the crystallization of sodium chlorate and bromates in water solution [81].
In our previous paper [104], we grouped the apparent CPL and CD spectral characteristics with their signs, magnitudes, and wavelengths and associated barrier heights (Eb) in double-well and multi-well potentials into four categories as follows:
(i) Case 1. The value of Eb between rigid enantiomers is relatively high >30 kcal∙mol−1 in the S0 and S1 states. Mirror-image CD and CPL spectra are evident for the enantiomers. The parity-conserved EM force is a determining factor. Racemization rate obeys the Arrhenius equation with activation energy (Ea).
(ii) Case 2. When 10 < Eb < 30 kcal∙mol−1 at the S0 and S1 states, non-mirror-image CPL and CD spectra are often observed [15,27,90,95,120,122,125,126,127,128,129,130,131,132,133,134]. Although (+)- and (−)-signs in CPL and CD are primarily determined by atrope and point chirality, the absolute magnitudes and wavelengths at the CPL and CD bands differ considerably from each other.
(iii) Case 3. When 1 < Eb < 10 kcal∙mol−1 at the S1 and S0 states, only (−)-sign CPL and (−)-sign CD spectra should be observed. The parity-violating weak force might be a determining factor in the S1 and S0 states [104].
(iv) Case 4. When 0 < Eb < 1 kcal∙mol−1 in the S1 and S0 states, no detectable CD bands are observed, although (−)-sign CPL signals are obvious. Resonance quantum tunneling without Ea is responsible for dynamic racemization, oscillating chirality, and quantum beat [66,72,101]. The parity-violating weak force is a determining factor in the S1 state, while the parity-conserved EM force is a determining factor in the S0 state.
Moreover, regarding hidden molecular chirality, in 1970s, Mislow argued the cryptochirality of mirror-image molecules in which optical activity is non-detectable [135]. In 2006 and 2009, approaches to chemically decipher cryptochiral molecules and polymers were reported [136,137]. Additionally, with the help of CPL and CD spectroscopy, a photophysical deciphering approach was applied to the EM-originating cryptochirality of several CD-silent molecules [138,139,140,141,142].
The previous paper did not report Case 3, though we reported examples of Cases 1, 2, and 4 [104]. The present paper reports Case 3 for the first time, i.e., that pyrromethene 546, pyrromethene 597, DCM, RhB, and bis-coumarin all reveal (−)-sign CPL and (−)-sign CD spectra, even in low-viscosity solvents. EW-perturbed quantum chemistry [143], EW-perturbed photophysics and EW-perturbed photochemical reactions should be considered when open questions of unexpected L/R preference and their detectable L/R differences in non-rigid and semi-rigid artificial molecules, and supramolecules and biomolecules in the S0 and S1, Sn… states are raised.
Other plausible scenarios for the L/R preference are possible. The handedness of non-rigid molecules in an ultra-tiny % ee can be increased to ~100% ee upon photoexcitation of parity-conserved (PC) EM force-driven circularly polarized (CP) light carrying a single angular momentum (±nℏ, n = 1) in the broad range of γ-ray, X-ray, vacuum–UV, UV–visible–IR, far-IR far-THz, and cosmic microwave radiation according to certain nonlinear amplification scenarios [97,98,99,100,101,102,103,104,105,106,107,108,109], known as autocatalytic self-replication [144], sergeant-and-soldier and majority rules [145], and polymerization [146]. Parity-conserving EM force-originating macroscopic MSB was comprehensively reviewed for a large number of molecules, polymers, supramolecules, colloids, gels, and crystals [147,148,149,150]. These alternative modern scenarios provide other possible answers to the greatest mystery on the origin of homochirality on Earth.
Recently, lightning was found to be a natural particle accelerator, ubiquitously generating γ-rays. Lightning causes atmospheric photonuclear reactions. The γ-ray energy is captured by N2 molecules, followed by producing, possibly, weak force-origin handed neutrons, right-handed positrons, and left-handed neutrinos [151]. Additionally, cosmological-origin right-handed anti-ν interacting with 14N in molecular clouds in star-forming regions of supernovae and neutron stars [87,152], gravitational origin parity violation [153,154], and hydrodynamic vortex flows with the opposite handedness in the north and south hemispheres on Earth [26,27,155] are of specific interest. In recent years, vortex light (alternatively called optical spanner, spiral light, twisted light, and helical light) [156,157,158,159,160,161,162,163,164,165,166,167,168,169] was recognized as a new sort of chiral light carrying multiple orbital angular momenta (OAM) with ± lℏ, l = 1, 2, 3, 4, 5, 10… up to 200. Vortex light with l = 0 is achiral. Vortex light can generate a torque enabling the rotation of molecular droplets, polymeric solids, and metallic particles in CW or CCW directions [158,161,164]. The helical wavefront for the Laguerre–Gaussian mode of vortex light allows for sculpturing spiral relief and motifs and for rotating small objects in CCW or CW directions [156,157,158,159,160,161,162,163,164,165,166,167,168,169,170]. Like CP light–matter interactions [171,172], vortex light can discriminate between enantiomers [164], and it is possible to predominantly generate handed chiral motifs from achiral polymers [162,163,169]. Astrophysical origin vortex light [156], CP light, and right-handed solar neutrinos may, thus, be connected to the L/R preference of biomolecular substances.
Recently, astonishing findings seeking source materials connecting with the handedness of biomolecules on Earth were reported. In 2009, a National Aeronautics and Space Administration (NASA) team characterized extraterrestrial-origin glycine-embedded samples returned from comet 81P/Wild2 using liquid chromatography and spectrometry [173]. In 2016, other researchers determined glycine, phosphorus and several organic substances involving O, S, and F in specimens collected from the coma of 67P/Churyumov–Gerasimenko using a double-focusing mass spectrometer [174]. Moreover, in 2016, radio astronomers found the first astronomical-origin chiral propylene oxide and achiral n-propanol in the Sagittarius B2 star-forming region of the Milky Way galaxy, although the existence of any L/R preference remains to be elucidated [175]. Comets and interstellar materials could deliver biomolecules or their precursors and water to Earth. Although it is possible to synthesize mirror-image DNA and proteins in laboratories [176,177], it is challenging to directly detect the L/R preference, possibly associated with (−)-sign circularly polarized radiation from the observation of interstellar PAHs at the S1/S0 states in the UV–visible region [175], and rigid and non-rigid non-π-conjugated organics at the near-IR/mid-IR/far-IR/microwave regions [108,109]. It remains a great challenge and a great curiosity to provide more realistic scenarios for biomolecular handedness.
4. Materials and Methods
Instrumentation details, lists of solvents and fluorophores and their vendors, preparation of sample solutions, and chiroptical analytical data [99,104] are described below.
4.1. Instrumentation
Using a JASCO (Tokyo, Japan) J-820 spectropolarimeter, UV–visible and CD spectra were simultaneously recorded at ambient temperature using a cylindrical quartz cuvette with a path length of 10 mm. The cylindrical cuvette assured a precise CD measurement compared to the rectangular cuvettes that are often used in routine experiments. Precise CD/UV–visible spectra were obtained by using a bandwidth of 2 nm, with one or two accumulations at scanning rates of 50 or 100 nm∙min−1 with a response time of 2 s. The CD signals of the two BODIPYs and RhB were triply confirmed under the following conditions: bandwidth = 2 nm, response time = 8 s, scanning rate = 20 nm∙min−1 with four accumulations. To minimize drifts in the light source and power supply, the instrument was aged for at least 2 h prior to measurements. CPL and PL spectra were likewise collected using a JASCO CPL-200 spectrofluoropolarimeter (Hachioji, Tokyo, Japan) employing cylindrical quartz cuvettes with path lengths of 10 mm at ambient temperature. The best experiment parameters were as follows: bandwidth = 10 nm for excitation and detection; response time of PMT = 8–16 s during measurements; two to eight accumulations with scanning rate = 20–50 nm∙min−1.
4.2. Materials
4.2.1. Luminophores (vendor)
Section 1: Perylene (Tokyo Chemical Company (TCI), Tokyo, Japan), 5,8,11-tetra-tert- butylperylene (TCI), N,N′-bis(2,6-diisopropylphenyl)-1,6,7,12-tetraphenoxy-3,4,9,10-perylene-tetra-carboxylic diimide (TCI), N,N′-bis(2,5-di-tert-butylphenyl)-3,4,9,10-perylenedicarboximide (Sigma-Aldrich, St. Louis, MO, USA), 16,17-bis(n-octyloxy)-anthrax[9,1,2-cde]-benzo[rst]-pentaphene-5,10-dione (TCI), and N,N′-di-n-octyl-3,4,9,10-perylenetetracarboxylic diimide (Sigma-Aldrich) were obtained as indicated.
Section 2: Pyrromethene 546 (TCI) and pyrromethene 597 (TCI) were obtained as indicated.
Section 3: Stilbene 420 (Exciton, Tokyo Instruments Inc. (Tokyo, Japan)), bis-MSB (Exciton), POPOP (TCI), DMPOPOP (Dotite, Kumamoto, Japan), BBOT (Dotite), and BBT (TCI) were obtained as indicated.
Section 4: Coumarin 6 (TCI), coumarin 545 (TCI), coumarin 466 (TCI), coumarin 6H (Sigma- Aldrich), coumarin 481/35 (TCI), coumarin 153 (Sigma-Aldrich), coumarin 1/460 (Sigma-Aldrich), coumarin 102 (Sigma-Aldrich), coumarin 7 (Sigma-Aldrich), coumarin 30 (Sigma-Aldrich), biscoumarin) (TCI), DCM (Sigma-Aldrich), and RhB (TCI) were obtained as indicated.
4.2.2. Solvents
Vendor, viscosity in cP, and temperature in °C are provided in brackets [178,179,180,181,182,183]; in each series, entries are given in order of increasing viscosity as follows:
(1) n-Alkanes: n-pentane (FUJIFILM Wako, 0.21 (25)), n-hexane (FUJIFILM Wako, 0.30 (25)), n-heptane (Sigma-Aldrich, 0.39 (25)), n-octane (Sigma-Aldrich, 0.51 (25), n-nonane (Sigma-Aldrich, 0.71 (20)), n-decane (Sigma-Aldrich, 0.85 (25)), n-undecane (Sigma-Aldrich, 0.93 (20)), n-dodecane (Sigma-Aldrich, 1.36 (25), n-tridecane (Sigma-Aldrich, 1.88 (20)), n-tetradecane (Fluka, 2.08 (25), n-pentadecane (Sigma-Aldrich, 2.86 (20)), and n-hexadecane (Sigma-Aldrich, 3.71 (20)).
(2) Branched and cyclic alkanes: isooctane (Dotite, 0.50 (25)), cyclohexane (Dotite, 0.93 (22)), and squalane (2,6,10,15,19,23-hexamethyltetracosane) (Sigma-Aldrich, 29.50 (25)).
(3) Non-branched and n-alcohols: methanol (FUJIFILM Wako, 0.55 (25)), ethanol (FUJIFILM Wako, 1.09 (25)), n-propanol (Sigma-Aldrich, 1.96 (25)), n-butanol (FUJIFILM Wako, 2.59 (25)), n-pentanol (Sigma-Aldrich, 3.47 (25)), n-hexanol (Sigma-Aldrich, 4.59 (25)), n-heptanol (Wako, 5.97 (25)), n-octanol (Wako, 7.59 (25)), n-nonanol (Sigma-Aldrich, 9.51 (25)), n-decanol (Sigma-Aldrich, 11.50 (25)), ethylene glycol (FUJIFILM Wako, 16.1 (25), n-undecanol (Sigma-Aldrich, 16.95 (25)), 1,3-propandiol (FUJIFILM Wako, 33.0 (25)), and 1,4-butanediol (FUJIFILM Wako, 71.0 (25)).
(4) Branched alcohols: isopropanol (Dotite, 2.07 (25), isobutanol (Sigma-Aldrich, 3.38 (25)), and isopentanol (Sigma-Aldrich, 3.86 (25)).
(5) Chlorinated hydrocarbons: dichloromethane (Dotite, 0.41 (25)) and chloroform (Dotite, 0.55 (25)).
(6) Other solvents: diethyl ether (FUJIFILM Wako, 0.22 (25)), acetone (FUJIFILM Wako, 0.31 (25), acetonitrile (FUJIFILM Wako, 0.34 (25)), tetrahydrofuran (Dotite, 0.46 (25)), benzene (FUJIFILM Wako, 0.60 (25)), water (Wako, 1.00 (20)), 1,4-dioxane (Dotite, 1.10 (25)), anisole (TCI, 1.09 (25)), heavy water (Wako, 1.25 (20)), and sulfolane (TCI, 10.10 (25)).
4.3. Preparation of Sample Solutions
Firstly, a representative stock solution (10−3 M) of luminophore dissolved in spectroscopic grade CHCl3 (Dotite, Kumamoto, Japan) was prepared. For RhB and stilbene 420, ethanol was used as the stock solution solvent. A small quantity of the stock solution was added to the desired liquid (1.9–2.1 mL) in the cylindrical quartz cuvette using a microsyringe. The CD/UV–visible and CPL/PL spectra were then recorded. Oxygen was not purged from the solvents or solutions in CPL and CD measurements since it does not significantly influence the fluorescence quantum yield of most organic luminophores.
4.4. Chiroptical Analysis
The dissymmetry factor of the circular polarization at the S0 state (gabs) was evaluated as gabs = (εL − εR)/(1/2(εL+εR)), where εL and εR are the extinction coefficients for l- and r-CP light, respectively [99]. The dissymmetry factor of the circular polarization at the S1 state (glum) was evaluated as glum = (IL − IR)/(1/2(IL + IR)), where IL and IR are the intensities of the signals for l- and r-CP light respectively, under the incident UP light [99]. The parameter gabs was experimentally determined using the expression Δε/ε = (ellipticity (in mdeg)/32980)/absorbance at the CD extremum, similar to the parameter glum, calculated as ΔI/I = (ellipticity (in mdeg)/(32980/ln10))/total PL intensity (in volts) at the CPL extremum.
5. Conclusions
We tested whether or not semi-rigid and non-rigid π-conjugated fluorophores in the S1 and S0 states in a series of achiral liquids with η ranging from 0.22 cP to 71.0 cP are optically inactive and have mirror symmetry as measured by CPL and CD spectroscopy. The fluorophores included six perylenes with and without substituents, two BODIPYs, six scintillators, RhB, DCM, and 11 coumarins. Perylenes were models of interstellar small and large PAHs radiating IR spectra of bright HII regions, planetary nebulae, and reflection nebulae. Without exception, all the non-rigid fluorophoric enantiomers, and possibly also the highly twisted perylene derivatives, showed (−)-sign CPL signals radiating from the vibronic photoexcited state in support of the molecular parity-violating hypothesis based on the Z0 boson origin PV-weak neutral current mechanism. The fluorophore emission intensities increased progressively and discontinuously to approximately –0.2 × 10−3 and −2.0) × 10−3 as a function of the solvent viscosity. Of specific interest was the detection of weak but clear CD signals with gabs values of −1.4 × 10−5 at λmax/λext for two pyrromethene derivatives, RhB, DCM, and bis-coumarin at the S0 states. The results of the present CPL and CD spectral characteristics should provide a possible answer to the parity violation hypothesis at the molecular level based on a handed weak neutral current mediated by the Z0 boson. The present comprehensive and previous experimental datasets [104] led us to address the “Ozma problem” posed by Gardner [1]. The query was how we can correctly communicate the left-and-right issue to intellectually advanced alien lifeforms. Our answer is that, when an unpolarized UV light source is applied to excite semi-rigid and non-rigid π-conjugated luminophores, we define (−)-sign CPL signals from the observer as “right” without exception.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-8994/11/3/363/s1.
Author Contributions
M.F. and J.R.K. have long discussed searching for experimental verification of the MPV hypothesis over 20 years. M.F. designed the application of CPL/CD spectroscopy to test the MPV hypothesis of the π-conjugated luminophores. M.F. and S.A. measured and analyzed CPL and CD datasets. M.F. and J.R.K. cowrote the manuscript. Requests for all original and processed CPL/CD datasets (saved in several file formats JASCO ##.jws, their converted ##.txt, followed by processed data using KaleidaGraph (mac, ver 4.53) ##.qpc, and ##.qda) should be sent to M.F. (fujikim@ms.naist.jp).
Funding
This work was supported by Grants-in-Aid for Scientific Research (16H04155 (FY2016-2018), 23651092 (FY2014-2016), 22350052 (FY2010-2013), 16655046 (FY2003-2005)), the Sekisui Chemical Foundation (FY2009), and the NAIST Foundation (FY2009).
Acknowledgments
Firstly, we owe a debt of gratitude to Reiko Kuroda (Tokyo Science University) for giving us the opportunity to disclose our hitherto unpublished CPL/CD spectroscopic datasets accumulated at NTT Basic Research Laboratory (Tokai, Musashino and Atsugi) and NAIST over 25 years to test the MPV hypothesis. Great inspiration for this work came from her book written in Japanese and titled “Seimei-Sekai-No-Hi-Taishosei” (Broken Symmetry in the Biological World—Why Nature Loves Imbalance) (Chuko-Shinsho, Tokyo, Japan, 1992). This intuitive book prompted M.F. to officially start an in-house research project titled “Study on Artificial Helix—Quest for the Possibility of Parity Nonconservation (PNC) of Helical Polymers and Organic Substances” at NTT Basic Research Laboratory (proposed on 19 May 1994 and 20 September 1995). We are grateful to the Kento Okoshi (Chitose Institute of Science and Technology), Eiji Yashima (Nagoya University), Yoshio Okamoto (Nagoya University), Yosef Scolnik (Weizmann Institute of Science), the late Meir Shinitzky (Weizmann Institute of Science), Victor Borovkov (South-Central University for Nationalities), Katsuya Inoue (Hiroshima University), Ullrich Scherf (Bergische Universität Wuppertal), Kazuo Yamaguchi (Kanagawa University), Daisuke Uemura (Kanagawa University), Masakatsu Matsumoto (Kanagawa University), Nobuhiro Kihara (Kanagawa University), Takayoshi Kawasaki (Tokuyama Corporation), Anubhav Saxena (Pidilite Industries, India), Tohru Asahi (Waseda University), Kenso Soai (Tokyo Science of University), Tamaki Nakano (Hokkaido University), Kenji Monde (Hokkaido University), Yoshitane Imai (Kindai University), and Mikiharu Kamachi (Osaka University). M.F. is also grateful to his colleagues at NTT Basic Research Laboratory, Kyozaburo Takeda (Waseda University), Hiroyuki Teramae (Jousai University), Kazuaki Furukawa (Meisei University), Keisuke Ebata, Tsutomu Horiuchi (Institute of Technology), Hiroaki Takayanagi (Tokyo Science University), Kei-ichi Torimitsu (Tohoku University), Nobuo Matsumoto (Shonan Institute of Technology), Masao Morita (Tohoku University), Osamu Niwa (Saitama Institute of Technology), Noriyuki Hatakenaka (Hiroshima University), Seiji Toyota (NTT group), Hisao Tabei, Hiromi Takigawa-Tamoto, Masaie Fujino (National Institute of Technology, Gunma College), and Hiroaki Isaka (NTT group). Also, M.F., as a principal investigator of a JST-CREST program (FY 1998–2003), is grateful to his intuitive mentors, Hideki Sakurai (Tohoku University), Toyoki Kunitake (Kyushu University), Masaki Hasegawa (the University of Tokyo), Shinji Murai (Osaka University), Hiizu Iawamura (University of Tokyo), Shigeyuki Kimura (National institute for Research in Inorganic Materials), the late Kenji Koga (University of Tokyo), Tadashi Imaki (Mitsubishi Chemical Corporation), the late Katsuhiko Kuroda (Mitsubishi Chemical Corporation), the late Akio Teramoto (Osaka University), Takahiro Sato (Osaka University), Masashi Kunitake (Kumamoto University), Junji Watanabe (Tokyo Institute of Technology), Hiroshi Nakashima (NTT Basic Research Laboratory), Hong-Zhi Tang (University of Michigan), Masao Motonaga, Zhong-Biao Zhang (Tianjin Normal University), and his colleagues. Also, M.F. is grateful to his students at NAIST (since FY 2002), Masaaki Ishikawa, Fumiko Ichiyanagi, Yoshihiro Kimura, Yoshifumi Kawagoe, Yoko Nakano, Takashi Mori, Woojung Chung, Ayako Nakao, Kana Yoshida, Makoto Taguchi, Yuri Donguri, Nozomu Suzuki, Keisuku Yoshida, Yuka Kato, Shosei Yoshimoto, Duong Thi Sang, Sibo Guo, Yota Katsurada, Hiroki Kamite, Ai Yokokura, Toshiki Nagai, Nor Azura Abdul Rahim, Jalilah Binti Abd Jalil, Shun Okazaki, Nanami Ogata, and Asuka Okubo for critical comments and constructive discussion on the MPV hypothesis and our radical ideas. M.F. learned about the unique nature of vortex light from Masahiro Katoh (Institute for Molecular Science (IMS)), Masaki Fujimoto (IMS), Daisuke Tadokoro (Kyoto University), and Takashiro Akitsu (Tokyo University of Science). Most of all, students at NAIST and several visiting researchers and students recognized the inherent imbalance in chiroptical properties (sign, magnitude, and wavelength) of the non-rigid luminophores using our CPL-200 spectrophotometer even after precision maintenance by a JASCO engineer, including replacement and tuning of the high-pressure Xe light source, power supply, concave/flat mirror sets, and two focused lenses. We are thankful to Takashi Takakuwa (JASCO), Yoshirou Kondo (JASCO), Hiroshi Kiyonaga (JASCO), and Koushi Nagamori (JASCO) for their technical advice for many years, and particular thanks are due to Nobuyuki Sakayanagi (JASCO), who designed the original CPL-200 spectrophotometer and released the first commercial model to M.F.’s lab in March 1999. Also, thanks are given to Yasuo Nakanishi (JASCO Engineering Co.), who continuously maintained the instrument in top condition with a high S/N ratio and wavelength calibration. Without such care and maintenance of the spectrophotometers, we could not test the MPV hypothesis.
Conflicts of Interest
The authors have no competing interests or other interests that might be perceived to influence the results and/or discussion reported in this article.
References
- Gardner, M. The New Ambidextrous Universe—Symmetry and Asymmetry from Mirror Reflections to Superstrings; 3rd ed.; Freeman: New York, NY, USA, 1990; ISBN 9780486442440. [Google Scholar]
- Miller, S.L. A Production of Amino Acids under Possible Primitive Earth Conditions. Science 1953, 117, 528–529. [Google Scholar] [CrossRef] [PubMed]
- Hanafusa, H.; Akabori, S. Polymerization of Aminoacetonitrile. Bull. Chem. Soc. Jpn. 1959, 32, 626–630. [Google Scholar] [CrossRef]
- Harada, K.; Fox, S.W. Thermal Synthesis of Natural Amino-Acids from a Postulated Primitive Terrestrial Atmosphere. Nature 1964, 201, 335–336. [Google Scholar] [CrossRef] [PubMed]
- Seckbach, J.; Chela-Flores, J.; Owen, T.; Raulin, F. (Eds.) Life in the Universe: From the Miller Experiment to the Search for Life on other Worlds; Kluwer: Dordrecht, Germany, 2004; ISBN 1-4020-2371-5. [Google Scholar]
- Breslow, R. A Likely Possible Origin of Homochirality in Amino Acids and Sugars on Prebiotic Earth. Tetrahedron Lett. 2011, 52, 2028–2032. [Google Scholar] [CrossRef]
- Mason, S.F. Chemical Evolution: Origin of the Elements, Molecules, and Living Systems; Oxford University Press: New York, NY, USA, 1991; ISBN 0-19-855272-6. [Google Scholar]
- Wagnière, G.H. On Chirality and the Universal Asymmetry: Reflections on Image and Mirror Image; Wiley-VCH: Zülich, Switzerland, 2007; ISBN 978-3-90639-038-3. [Google Scholar]
- Guijarro, A.; Yus, M. Origin of Chirality in the Molecules of Life: A Revision from Awareness to the Current Theories and Perspectives of this Unsolved Problem; RSC Publishing: Cambridge, UK, 2008; ISBN 978-0-85404-156-5. [Google Scholar]
- Rauchfuss, H. Chemical Evolution and the Origin of Life; Mitchell, T.N., Translator; Springer: Berlin, Germany, 2008; ISBN 978-3-540-78822-5. [Google Scholar]
- Soai, K. (Ed.) Amplification of Chirality; Springer: Berlin, Germany, 2008; ISBN 978-3-540-77868-4. [Google Scholar]
- Meierhenrich, U. Amino Acids and the Asymmetry of Life; Springer: Berlin, Germany, 2010; ISBN 978-3-540-76885-2. [Google Scholar]
- Boyd, R. Stardust, Supernovae and the Molecules of Life: Might We All Be Aliens? Springer: New York, NY, USA, 2012; ISBN 978-1-4614-1331-8. [Google Scholar]
- MacDermott, A.J. The Ascent of Parity-Violation: Exochirality in the Solar System and Beyond. Enantiomer 2000, 5, 153–168. [Google Scholar] [PubMed]
- Fujiki, M.; Yoshida, K.; Suzuki, N.; Rahim, N.A.A.; Jalil, J.A. Tempo-Spatial Chirogenesis. Limonene-Induced Mirror Symmetry Breaking of Si–Si Bond Polymers During Aggregation in Chiral Fluidic Media. J. Photochem. Photobiol. A Chem. 2016, 331, 120–129. [Google Scholar] [CrossRef]
- Schwieterman, E.W.; Kiang, N.Y.; Parenteau, M.N.; Harman, C.E.; DasSarma, S.; Fisher, T.M.; Arney, G.N.; Hartnett, H.E.; Reinhard, C.T.; Olson, S.L.; et al. Exoplanet Biosignatures: A Review of Remotely Detectable Signs of Life. Astrobiology 2018, 18, 663–708. [Google Scholar] [CrossRef] [PubMed]
- Schrodinger, E. What Is Life? With Mind and Matter and Autobiographical Sketches; Reprint Version; Cambridge University Press: Cambridge, UK, 2012; ISBN 1107683653. [Google Scholar]
- Freedman, R.; Geller, R.; Kaufmann, W.J. Universe, 10th ed.; Freeman, W.H., Ed.; W.H. Freeman and Company, Now an Imprint of Macmillan Higher Education, a Division of Macmillan Publishers: London, UK, 2015; ISBN 1319042384. [Google Scholar]
- Accelerating Expansion of the Universe. Available online: https://en.wikipedia.org/wiki/Accelerating_expansion_of_the_universe (accessed on 11 November 2018).
- Forbes, N.; Mahon, B. Faraday, Maxwell, and the Electromagnetic Field: How Two Men Revolutionized Physics; Prometheus Books: Amherst, NY, USA, 2014; ISBN 9781616149420. [Google Scholar]
- Lennartson, A. Appendix. Absolute Asymmetric Synthesis 1874–2009. In Absolute Asymmetric Synthesis; University of Gothenburg: Gothenburg, Sweden, 2011; pp. 59–74. ISBN 978-91-628-7836-8. [Google Scholar]
- Beth, R.A. Mechanical Detection and Measurement of the Angular Momentum of Light. Phys. Rev. 1936, 50, 115–125. [Google Scholar] [CrossRef]
- Inoue, Y. Asymmetric Photochemical Reactions in Solution. Chem. Rev. 1992, 92, 741–770. [Google Scholar] [CrossRef]
- Laur, P. The First Decades After the Discovery of CD and ORD by Aimé Cotton in 1895. In Comprehensive Chiroptical Spectroscopy: Applications in Stereochemical Analysis of Synthetic Compounds, Natural Products, and Biomolecules; Berova, N., Polavarapu, P.L., Nakanishi, K., Woody, R.W., Eds.; Wiley: Hoboken, NJ, USA, 2000; Volume 2, Chapter 1; pp. 1–35. [Google Scholar] [CrossRef]
- Rikken, G.L.J.A.; Raupach, E. Enantioselective Magnetochiral Photochemistry. Nature 2000, 405, 932–935. [Google Scholar] [CrossRef] [PubMed]
- Ribó, J.M.; Blanco, C.; Crusats, J.; El-Hachemi, Z.; Hochberg, D.; Moyano, A. Absolute Asymmetric Synthesis in Enantioselective Autocatalytic Reaction Networks: Theoretical Games, Speculations on Chemical Evolution and Perhaps A Synthetic Option. Chem. Eur. J. 2014, 20, 17250–17271. [Google Scholar] [CrossRef]
- Okano, K.; Taguchi, M.; Fujiki, M.; Yamashita, T. Circularly Polarized Luminescence of Rhodamine B in a Supramolecular Chiral Medium Formed by a Vortex Flow. Angew. Chem. Int. Ed. 2011, 50, 12474–12477. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Li, Y.; Yan, F.; Liu, C.; Sang, Y.; Tian, F.; Feng, Q.; Duan, P.; Zhang, L.; Shi, X.; et al. Control Over the Emerging Chirality in Supramolecular Gels and Solutions by Chiral Microvortices in Milliseconds. Nat. Commun. 2018, 9, 2599. [Google Scholar] [CrossRef]
- Mineo, P.; Villari, V.; Scamporrino, E.; Micali, N. New Evidence about the Spontaneous Symmetry Breaking: Action of an Asymmetric Weak Heat Source. J. Phys. Chem. B 2015, 119, 12345–12353. [Google Scholar] [CrossRef] [PubMed]
- Eugene Wigner. Available online: https://en.wikipedia.org/wiki/Eugene_Wigner (accessed on 17 November 2018).
- Wigner, E.P. Violation of Symmetry in Physics. Sci. Am. 1965, 213, 28–36. [Google Scholar] [CrossRef]
- Gross, D.J. Symmetry in Physics: Wigner’s Legacy. Phys. Today 1995, 48, 46–50. [Google Scholar] [CrossRef]
- Lee, T.D.; Yang, C.N. Question of Parity Conservation in Weak Interactions. Phys. Rev. 1956, 104, 254–258. [Google Scholar] [CrossRef]
- Wu, C.S.; Ambler, E.; Hayword, R.W.; Hoppes, D.D.; Hudson, R.P. Experimental Test of Parity Conservation on Beta Decay. Phys. Rev. 1957, 105, 1413–1415. [Google Scholar] [CrossRef]
- Schopper, H. Circular Polarization of γ-Rays: Further Proof for Parity Failure in β Decay. Philos. Mag. 1957, 2, 710–713. [Google Scholar] [CrossRef]
- Goldhaber, M.; Grodzins, L.; Sunyar, A. Helicity of Neutrinos. Phys. Rev. 1958, 109, 1015–1017. [Google Scholar] [CrossRef]
- Fagg, L.W.; Hanna, S.S. Polarization Measurements on Nuclear Gamma Rays. Rev. Mod. Phys. 1959, 31, 711–758. [Google Scholar] [CrossRef]
- Wu, C.S. Parity Experiments in Beta Decay. Rev. Mod. Phys. 1959, 31, 783–790. [Google Scholar] [CrossRef]
- Christenson, J.H.; Cronin, J.W.; Fitch, V.L.; Turlay, R. Evidence for the 2π Decay of the K20 Meson. Phys. Rev. Lett. 1964, 13, 138–140. [Google Scholar] [CrossRef]
- Aubert, B.; et al. [BABAR Collaboration] Observation of CP Violation in the B0 Meson System. Phys. Rev. Lett. 2001, 87, 091801. [Google Scholar] [CrossRef] [PubMed]
- Abe, K.; et al. [Belle Collaboration] Observation of Large CP Violation in the Neutral B Meson System. Phys. Rev. Lett. 2001, 87, 091802. [Google Scholar] [CrossRef] [PubMed]
- Abe, K.; et al. [T2K Collaboration] Combined Analysis of Neutrino and Antineutrino Oscillations at T2K. Phys. Rev. Lett. 2017, 118, 151801. [Google Scholar] [CrossRef] [PubMed]
- Calvert, J.G.; Pitts, J.N., Jr. Photochemistry, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1966; Chapter 4-2D Selection rule; pp. 258–260. ISBN 0471130907. [Google Scholar]
- Turro, N.J. Modern Molecular Photochemistry; University Science Books: Sausalito, CA, USA, 1991; Chapter 5.6 State Mixing: Breakdown of the Single Orbital Configuration and Pure Multiplicity Approximations; pp. 96–103. ISBN 0935702717. [Google Scholar]
- Görling, C.; Jalviste, E.; Ohta, N.; Ottinger, C. Lifetime Measurements of the Collision-Free Slow Fluorescence from Glyoxal S1/T1 Gateway Levels in a Beam. J. Phys. Chem. A 1998, 102, 10620–10629. [Google Scholar] [CrossRef]
- Yamazaki, I.; Aratani, N.; Akimoto, S.; Yamazaki, T.; Osuka, A. Observation of Quantum Coherence for Recurrence Motion of Exciton in Anthracene Dimers in Solution. J. Am. Chem. Soc. 2003, 125, 7192–7193. [Google Scholar] [CrossRef]
- Latal, H. Parity Violation in Atomic Physics. In Chirality—From Weak Bosons to the α-Helix; Janoschek, R., Ed.; Springer: Berlin, Germany, 1991; pp. 1–17. ISBN 978-3-642-76569. [Google Scholar]
- Van der Meer, S. Stochastic Cooling and the Accumulation of Antiprotons. Rev. Mod. Phys. 1985, 57, 689–698. [Google Scholar] [CrossRef]
- Rubbia, C. Experimental Observation of the Intermediate Vector Bosons W+, W– and Z0. Rev. Mod. Phys. 1985, 57, 699–722. [Google Scholar] [CrossRef]
- Walgate, R. What Will Come After the Z0? Nature 1983, 303, 473. [Google Scholar] [CrossRef]
- Bouchiat, M.A.; Bouchiat, C.C. Weak Neutral Currents in Atomic Physics. Phys. Lett. B 1974, 48, 111–114. [Google Scholar] [CrossRef]
- Baied, P.E.G.; Brimcombe, M.W.S.M.; Roberts, G.J.; Sandars, P.G.H.; Soreide, D.C.; Fortson, E.N.; Lewis, L.L.; Lindahl, E.G.; Soreide, D.C. Search for Parity Non-Conserving Optical Rotation in Atomic Bismuth. Nature 1976, 264, 528–529. [Google Scholar] [CrossRef]
- Forte, M.; Heckel, B.R.; Ramsey, N.F.; Green, K.; Greene, G.L.; Byrne, J.; Pendlebury, J.M. First measurement of parity-nonconserving neutron-spin rotation: The tin isotopes. Phys. Rev. Lett. 1980, 45, 2088–2091. [Google Scholar] [CrossRef]
- Bucksbaum, P.H.; Commins, E.D.; Hunter, L.R. Observations of Parity Non-Conservation in Atomic Thallium. Phys. Rev. D 1981, 24, 1134–1148. [Google Scholar] [CrossRef]
- Emmons, T.P.; Reeves, J.M.; Fortson, E.N. Parity-Non-Conserving Optical Rotation in Atomic Lead. Phys. Rev. Lett. 1983, 51, 2089–2091. [Google Scholar] [CrossRef]
- Bouchiat, M.-A.; Pottier, L. Optical Experiments and Weak Interactions. Science 1986, 234, 1203–1210. [Google Scholar] [CrossRef]
- Bouchiat, M.A.; Bouchiat, C.C. Parity Violation in Atoms. Rep. Prog. Phys. 1997, 60, 1351–1396. [Google Scholar] [CrossRef]
- Wood, C.S.; Bennett, S.C.; Cho, D.; Masterson, B.P.; Roberts, J.L.; Tanner, C.E.; Wieman, C.E. Measurement of Parity Nonconservation and an Anapole Moment in Cesium. Science 1997, 275, 1759–1763. [Google Scholar] [CrossRef]
- Mitchell, G.E.; Bowman, J.D.; Penttilä, S.I.; Sharapov, E.I. Parity Violation in Compound Nuclei: Experimental Methods and Recent Results. Phys. Rep. 2001, 354, 157–241. [Google Scholar] [CrossRef]
- Guéna, J.; Lintz, M.; Bouchiat, M.-A. Atomic Parity Violation: Principles, Recent Results, Present Motivations. Mod. Phys. Lett. A 2005, 20, 375–390. [Google Scholar] [CrossRef]
- Yamagata, Y. A Hypothesis for the Asymmetric Appearance of Biomolecules on Earth. J. Theor. Biol. 1966, 11, 495–498. [Google Scholar] [CrossRef]
- Rein, D.W. Some Remarks on Parity Violating Effects of Intramolecular Interactions. J. Mol. Evol. 1974, 4, 15–22. [Google Scholar] [CrossRef]
- Letokhov, V.S. On Difference of Energy Levels of Left and Right Molecules Due to Weak Interactions. Phys. Lett. A 1975, 53, 275–276. [Google Scholar] [CrossRef]
- Zel’Dovich, Ya. B.; Saakyan, D.B.; Sobel’Man, I.I. Energy Difference between Right-Hand and Left-Hand Molecules due to Parity Nonconservation in Weak Interactions of Electrons with Nuclei. JETP Lett. 1977, 25, 94–97. [Google Scholar]
- Keszthelyi, L. Origin of the Asymmetry of Biomolecules and Weak Interaction. Orig. Life 1977, 8, 299–340. [Google Scholar] [CrossRef]
- Harris, R.A.; Stodolsky, L. Quantum Beats in Optical Activity and Weak Interactions. Phys. Lett. B 1978, 78, 313–317. [Google Scholar] [CrossRef]
- Hegstrom, R.A.; Rein, D.W.; Sandars, P.G.H. Calculation of the Parity Nonconserving Energy Difference between Mirror-Image Molecules. J. Chem. Phys. 1980, 73, 2329–2341. [Google Scholar] [CrossRef]
- Mason, S.F.; Tranter, G.E. Energy Inequivalence of Peptide Enantiomers from Parity Non-Conservation. Chem. Commun. 1983, 117–119. [Google Scholar] [CrossRef]
- Mason, S.F.; Tranter, G.E. The Parity-Violating Energy Difference between Enantiomeric Molecules. Mol. Phys. 1984, 53, 1091–1111. [Google Scholar] [CrossRef]
- Barron, L.D. Symmetry and molecular chirality. Chem. Soc. Rev. 1986, 15, 189–223. [Google Scholar] [CrossRef]
- Kondepudi, D. Parity Violations and the Origin of Bimolecular Handedness. In Entropy, Information and Evolution: New Perspective on Physical and Biological Evolution; Weber, B.H., Depew, D.J., Smith, J.D., Eds.; MIT Press: Cambridge, MA, USA, 1988; ISBN 0262731681. [Google Scholar]
- Quack, M. Structure and Dynamics of Chiral Molecules. Angew. Chem. Int. Ed. 1989, 28, 571–586. [Google Scholar] [CrossRef]
- Hegstrom, R.A.; Kondepudi, D.K. The Handedness of the Universe. Sci. Am. 1990, 262, 108–115. [Google Scholar] [CrossRef]
- Salam, A. The Role of Chirality in the Origin of Life. J. Mol. Evol. 1991, 33, 105–113. [Google Scholar] [CrossRef]
- Macdermott, A.J. Electroweak Enantioselection and the Origin of Life. Orig. Life Evol. Biosph. 1995, 25, 191–199. [Google Scholar] [CrossRef]
- Kikuchi, O.; Kiyonaga, H. Parity-Energy Shift of Helical n-Alkanes. J. Mol. Struct. (Theochem.) 1994, 312, 271–274. [Google Scholar] [CrossRef]
- Avetisov, V.; Goldanskii, V. Mirror Symmetry-Breaking at the Molecular Level. Proc. Natl. Acad. Sci. USA 1996, 93, 11435–11442. [Google Scholar] [CrossRef]
- Bonner, W.A. Enantioselective Autocatalysis. IV. Implications for Parity Violation Effects. Orig. Life Evol. Biosph. 1996, 26, 27–45. [Google Scholar] [CrossRef]
- Szabó-Nagy, A.; Keszthelyi, L. Demonstration of the Parity-Violating Energy Difference between Enantiomers. Proc. Natl. Acad. Sci. USA 1999, 96, 4252–4255. [Google Scholar] [CrossRef]
- Gottselig, M.; Luckhaus, D.; Quack, M.; Stohner, J.; Willeke, M. Mode Selective Stereomutation and Parity Violation in Disulfane Isotopomers H2S2, D2S2, T2S2. Helv. Chim. Acta 2001, 84, 1846–1861. [Google Scholar] [CrossRef]
- Compton, R.N.; Pagni, R.M. The Chirality of Biomolecules. Adv. At. Mol. Opt. Phys. 2002, 48, 219–261. [Google Scholar] [CrossRef]
- Schwerdtfeger, P.; Gierlich, J.; Bollwein, T. Large Parity-Violation Effects in Heavy-Metal-Containing Chiral Compounds. Angew. Chem. Int. Ed. 2003, 42, 1293–1296. [Google Scholar] [CrossRef]
- MacDermott, A.J.; Hegstrom, R.A. A Proposed Experiment to Measure the Parity-Violating Energy Difference between Enantiomers from the Optical Rotation of Chiral Ammonia-Like “Cat” Molecules. Chem. Phys. 2004, 305, 55–68. [Google Scholar] [CrossRef]
- Quack, M.; Stohner, J.; Willeke, M. High-Resolution Spectroscopic Studies and Theory of Parity Violation in Chiral Molecules. Annu. Rev. Phys. Chem. 2008, 59, 741–769. [Google Scholar] [CrossRef]
- Bargueño, P.; Gonzalo, I.; de Tudela, R.P. Detection of Parity Violation in Chiral Molecules by External Tuning of Electroweak Optical Activity. Phys. Rev. A 2009, 80, 012110. [Google Scholar] [CrossRef]
- Dorta-Urra, A.; Peñate-Rodríguez, H.C.; Bargueño, P.; Rojas-Lorenzo, G.; Miret-Artés, S. Dissipative Geometric Phase and Decoherence in Parity-Violating Chiral Molecules. J. Chem. Phys. 2012, 136, 174505. [Google Scholar] [CrossRef]
- Famiano, M.A.; Boyd, R.N.; Kajino, T.; Onaka, T.; Mo, Y. Amino Acid Chiral Selection via Weak Interactions in Stellar Environments: Implications for the Origin of Life. Sci. Rep. 2018, 8, 8833. [Google Scholar] [CrossRef]
- Daussy, Ch.; Marrel, T.; Amy-Klein, A.; Nguyen, C.T.; Bordé, C.J.; Chardonnet, C. Limit on the Parity Nonconserving Energy Difference between the Enantiomers of a Chiral Molecule by Laser Spectroscopy. Phys. Rev. Lett. 1999, 83, 1554–1557. [Google Scholar] [CrossRef]
- Wang, W.; Yi, F.; Ni, Y.; Zhao, Z.; Jin, X.; Tang, Y. Parity Violation of Electroweak Force in Phase Transitions of Single Crystals of D- and L-Alanine and Valine. J. Biol. Phys. 2000, 26, 51–65. [Google Scholar] [CrossRef]
- Fujiki, M. Experimental Tests of Parity Violation at Helical Polysilylene Level. Macromol. Rapid Commun. 2001, 22, 669–674. [Google Scholar] [CrossRef]
- Pagni, R.M.; Compton, R.N. Asymmetric Synthesis of Optically Active Sodium Chlorate and Bromate Crystals. Cryst. Growth Des. 2002, 2, 249–253. [Google Scholar] [CrossRef]
- Scolnik, T.; Portnaya, I.; Cogan, U.; Tal, S.; Haimovitz, R.; Fridkin, M.; Elitzur, A.C.; Deamer, D.W.; Shinitzky, M. Subtle Differences in Structural Transitions between Poly-L- and Poly-D-Amino Acids of Equal Length in Water. Phys. Chem. Chem. Phys. 2006, 8, 333–339. [Google Scholar] [CrossRef]
- Kodona, E.K.; Alexopoulos, C.; Panou-Pomonis, E.; Pomonis, P.J. Chirality and Helix Stability of Polyglutamic Acid Enantiomers. J. Colloid Interface Sci. 2008, 319, 72–80. [Google Scholar] [CrossRef]
- Darquié, B.; Stoeffler, C.; Shelkovnikov, A.; Daussy, C.; Amy-Klein, A.; Chardonnet, C.; Zrig, S.; Guy, L.; Crassous, J.; Soulard, P. Progress Toward the First Observation of Parity Violation in Chiral Molecules by High-Resolution Laser Spectroscopy. Chirality 2010, 22, 870–884. [Google Scholar] [CrossRef]
- Fujiki, M. Mirror Symmetry Breaking in Helical Polysilanes: Preference between Left and Right of Chemical and Physical Origin. Symmetry 2010, 2, 1625–1652. [Google Scholar] [CrossRef]
- Albert, S.; Arn, F.; Bolotova, I.; Chen, Z.; Fábri, C.; Grassi, G.; Lerch, P.; Quack, M.; Seyfang, G.; Wokaun, A.; et al. Synchrotron-Based Highest Resolution Terahertz Spectroscopy of the ν24 Band System of 1,2-Dithiine (C4H4S2): A Candidate for Measuring the Parity Violating Energy Difference between Enantiomers of Chiral Molecules. J. Phys. Chem. Lett. 2016, 7, 3847–3853. [Google Scholar] [CrossRef]
- Kozlova, S.G.; Gabuda, S.P. Thermal Properties of Zn2(C8H4O4)2·C6H12N2 Metal-Organic Framework Compound and Mirror Symmetry Violation of Dabco Molecules. Sci. Rep. 2017, 7, 11505. [Google Scholar] [CrossRef]
- Lightner, D.A.; Gurst, J.E. Organic Conformational Analysis and Stereochemistry from Circular Dichroism Spectroscopy; Wiley-VCH: Weinheim, Germany, 2000; ISBN 978-0-471-35405-5. [Google Scholar]
- Eliel, E.L.; Wilen, S.H. Stereochemistry of Organic Compounds, 1st ed.; Wiley-Interscience: Hoboken, NJ, USA, 1994; ISBN 9780471016700. [Google Scholar]
- Anslyn, E.V.; Dougherty, D.A. Modern Physical Organic Chemistry; University Science: Mill Valley, CA, USA, 2005; ISBN 9781891389313. [Google Scholar]
- Hund, F. Symmetriecharaktere yon Termen bei Systemen mit Gleichen Partikeln in der Quantenmechanik. Z. Phys. 1927, 43, 788–803. [Google Scholar] [CrossRef]
- Bell, R.P. The Tunnel Effect in Chemistry; Chapman and Hall: London, UK, 1980; ISBN 0-412-21340-0. [Google Scholar]
- Laane, J. Vibrational Potential Energy Surfaces in Electronic Excited States. In Frontiers of Molecular Spectroscopy; Laane, J., Ed.; Elsevier: New York, NY, USA, 2009; Chapter 4; pp. 63–132. ISBN 978-0-444-53175-9. [Google Scholar]
- Fujiki, M.; Koe, J.R.; Mori, T.; Kimura, Y. Questions of Mirror Symmetry at the Photoexcited and Ground States of Non-Rigid Luminophores Raised by Circularly Polarized Luminescence and Circular Dichroism Spectroscopy: Part 1. Oligofluorenes, Oligophenylenes, Binaphthyls and Fused Aromatics. Molecules 2018, 23, 2606. [Google Scholar] [CrossRef]
- Shindo, Y.; Nakagawa, M. On the Artifacts in Circularly Polarized Emission Spectroscopy. Appl. Spectrosc. 1985, 39, 32–38. [Google Scholar] [CrossRef]
- Blok, P.M.L.; Dekkers, H.P.J.M. Measurement of the Circular Polarization of the Luminescence of Photoselected Samples under Artifact-free Conditions. Appl. Spectrosc. 1990, 44, 305–309. [Google Scholar] [CrossRef]
- Kaur, S. A Review on Electronic Spectroscopy of Perylene. Master’s Thesis, San Jose State University, San Jose, CA, USA, 1999. Available online: http://scholarworks.sjsu.edu/etd_theses/1879 (accessed on 1 February 2019).
- Allamandola, L.J.; Tielens, A.G.G.M.; Barker, J.R. Interstellar Polycyclic Aromatic Hydrocarbons—The Infrared Emission Bands, the Excitation/Emission Mechanism, and the Astrophysical Implications. Astrophys. J. Suppl. Ser. 1989, 71, 733–775. [Google Scholar] [CrossRef]
- Tielens, A.G.G.M. Interstellar Polycyclic Aromatic Hydrocarbon Molecules. Annu. Rev. Astron. Astrophys. 2008, 46, 289–337. [Google Scholar] [CrossRef]
- Walter, E.R.H.; Williams, J.A.G.; Parker, D. Solvent polarity and oxygen sensitivity, rather than viscosity, determine lifetimes of biaryl-sensitised terbium luminescence. Chem. Commun. 2017, 53, 13344–133347. [Google Scholar] [CrossRef]
- Arbeloa, F.L.; Bañuelos, J.; Martínez, V.; Arbeloa, T.; López Arbeloa, I. Structural, Photophysical and Lasing Properties of Pyrromethene Dyes. Int. Rev. Phys. Chem. 2005, 24, 339–374. [Google Scholar] [CrossRef]
- Cerdán, L.; García-Moreno, S.; Costela, A.; García-Moreno, I.; de la Moya, A.S. Circularly Polarized Laser Emission Induced in Isotropic and Achiral Dye Systems. Sci. Rep. 2016, 6, 28740. [Google Scholar] [CrossRef]
- Ebata, K.; Inada, T.; Kabuto, C.; Sakurai, H. Hexakis(fluorodimethylsilyl)benzene, Hexakis(methoxy-dimethylsilyl)benzene, and Related Compounds. Novel Neutral Pentacoordinate Structures for Silicon and Merry-Go-Round Degenerate Fluorine Migration. J. Am. Chem. Soc. 1994, 116, 3595–3596. [Google Scholar] [CrossRef]
- Organic Scintillators Energy. Available online: https://en.wikipedia.org/wiki/Scintillator#Organic_scintillators (accessed on 13 October 2018).
- Araki, T.; Enomoto, S.; Furuno, K.; Gando, Y.; Ichimura, K.; Ikeda, H.; Inoue, K.; Kishimoto, Y.; Koga, M.; Koseki, Y.; et al. Experimental Investigation of Geologically Produced Antineutrinos with KamLAND. Nature 2005, 436, 499–503. [Google Scholar] [CrossRef]
- KamLAND. Available online: https://en.wikipedia.org/wiki/Kamioka_Liquid_Scintillator_Antineutrino_Detector (accessed on 7 November 2018).
- Nucleosynthesis Reactions. Available online: https://en.wikipedia.org/wiki/Nucleosynthesis (accessed on 7 November 2018).
- Jones, G., II; Jackson, W.R.; Choi, C.Y.; Bergmark, W.R. Solvent Effects on Emission Yield and Lifetime for Coumarin Laser Dyes. Requirements for a Rotatory Decay Mechanism. J. Phys. Chem. 1985, 89, 294–300. [Google Scholar] [CrossRef]
- Weber, M.J. Handbook of Laser Wavelengths; CRC Press: Boca Raton, FL, USA, 1998; ISBN 0849335086. [Google Scholar]
- Birks, J.B. The Theory and Practice of Scintillation Counting; Elsevier: Amsterdam, The Netherlands, 1964; ISBN 978-0-08-010472-0. [Google Scholar]
- Duarte, F.J. (Ed.) Tunable Lasers Handbook (Optics and Photonics); Academic Press: Cambridge, MA, USA, 1995; ISBN 012222695X. [Google Scholar]
- Fujiki, M.; Jalilah, A.J.; Suzuki, N.; Taguchi, M.; Zhang, W.; Abdellatif, M.M.; Nomura, K. Chiral Optofluidics: Gigantic Circularly Polarized Light Enhancement of All-trans-poly(9,9-di-n-octylfluorene-2,7-vinylene) during Mirror-symmetry-breaking Aggregation by Optically Tuning Fluidic Media. RSC Adv. 2012, 2, 6663–6671. [Google Scholar] [CrossRef]
- Weinberg Angle. Available online: https://en.wikipedia.org/wiki/Weinberg_angle (accessed on 2 October 2018).
- Electroweak Interaction. Available online: https://en.wikipedia.org/wiki/Electroweak_interaction (accessed on 30 October 2018).
- Nakashima, H.; Koe, J.R.; Torimitsu, K.; Fujiki, M. Transfer and Amplification of Chiral Molecular Information to Polysilylene Aggregates. J. Am. Chem. Soc. 2001, 123, 4847–4848. [Google Scholar] [CrossRef] [PubMed]
- Fujiki, M. Mirror Symmetry Breaking of Silicon Polymers—From Weak Bosons to Artificial Helix. Chem. Rec. 2009, 9, 271–298. [Google Scholar] [CrossRef] [PubMed]
- Nakano, Y.; Fujiki, M. Circularly Polarized Light Enhancement by Helical Polysilane Aggregates Suspension in Organic Optofluids. Macromolecules 2011, 44, 7511–7519. [Google Scholar] [CrossRef]
- Fujiki, M.; Yoshida, K.; Suzuki, N.; Zhang, J.; Zhang, W.; Zhu, X. Mirror Symmetry Breaking and Restoration within μm-sized Polymer Particles in Optofluidic Media by Pumping Circularly Polarised Light. RSC Adv. 2013, 3, 5213–5219. [Google Scholar] [CrossRef]
- Fujiki, M.; Kawagoe, Y.; Nakano, Y.; Nakao, A. Mirror-Symmetry-Breaking in Poly[(9,9-di-n-octylfluorenyl-2,7-diyl)-alt-biphenyl] (PF8P2) is Susceptible to Terpene Chirality, Achiral Solvents and Mechanical Stirring. Molecules 2013, 18, 7035–7057. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Suzuki, N.; Liu, J.; Matsuda, T.; Rahim, N.A.A.; Zhang, W.; Fujiki, M.; Zhang, Z.; Zhou, N.; Zhu, X. Limonene Induced Chiroptical Generation and Inversion during Aggregation of Achiral Polyfluorene Analogs: Structure-Dependence and Mechanism. Polym. Chem. 2014, 5, 5920–5927. [Google Scholar] [CrossRef]
- Fujiki, M.; Donguri, Y.; Zhao, Y.; Nakao, A.; Suzuki, N.; Yoshida, K.; Zhang, W. Photon Magic: Chiroptical Polarisation, Depolarisation, Inversion, Retention and Switching of Non-Photochromic Light-Emitting Polymers in Optofluidic Medium. Polym. Chem. 2015, 6, 1627–1638. [Google Scholar] [CrossRef]
- Nakano, Y.; Ichiyanagi, F.; Naito, M.; Yang, Y.; Fujiki, M. Chiroptical Generation and Inversion During the Mirror-Symmetry-Breaking Aggregation of Dialkylpolysilanes due to Limonene Chirality. Chem. Commun. 2012, 48, 6636–6638. [Google Scholar] [CrossRef]
- Duong, T.S.; Fujiki, M. The Origin of Bisignate Circularly Polarized Luminescence (CPL) Spectra from Chiral Polymer Aggregates and Molecular Camphor: Anti-kasha’s Rule Revealed by CPL Excitation (CPLE) Spectra. Polym. Chem. 2017, 8, 4673–4679. [Google Scholar] [CrossRef]
- Jalilah, A.J.; Asanoma, F.; Fujiki, M. Unveiling Controlled Breaking of the Mirror Symmetry of Eu(fod)3 with α-/β-Pinene and BINAP by Circularly Polarised Luminescence (CPL), CPL Excitation, and 19F-/31P{1H}-NMR Spectra and Mulliken Charges. Inorg. Chem. Front. 2018, 5, 2718–2733. [Google Scholar] [CrossRef]
- Mislow, K. Absolute Asymmetric Synthesis: A Commentary. Collect. Czech. Chem. Commun. 2003, 68, 849–864. [Google Scholar] [CrossRef]
- Kawasaki, T.; Tanaka, H.; Tsutsumi, T.; Kasahara, T.; Sato, I.; Soai, K.J. Chiral discrimination of cryptochiral saturated quaternary and tertiary hydrocarbons by asymmetric autocatalysis. Am. Chem. Soc. 2006, 128, 6032–6033. [Google Scholar] [CrossRef]
- Kawasaki, T.; Hohberger, C.; Araki, Y.; Hatase, K.; Beckerle, K.; Okuda, J.; Soai, K. Discrimination of Cryptochirality in Chiral Isotactic Polystyrene by Asymmetric Autocatalysis. Chem. Commun. 2009, 5621–5623. [Google Scholar] [CrossRef]
- Amako, T.; Nakabayashi, K.; Suzuki, N.; Guo, S.; Rahim, N.A.A.; Harada, T.; Fujiki, M.; Imai, Y. Pyrene Magic: Chiroptical Enciphering and Deciphering 1,3-Dioxolane Bearing Two Wirepullings to Drive Two Remote Pyrenes. Chem. Commun. 2015, 51, 8237–8240. [Google Scholar] [CrossRef]
- Nakanishi, S.; Nakabayashi, K.; Mizusawa, T.; Suzuki, N.; Guo, S.; Fujiki, M.; Imai, Y. Cryptochiral Binaphthyl–Bipyrene Luminophores Linked with Alkylene Esters: Intense Circularly Polarised Luminescence, But Ultraweak Circular Dichroism. RSC Adv. 2016, 6, 99172–99176. [Google Scholar] [CrossRef]
- Nakabayashi, K.; Kitamura, S.; Suzuki, N.; Guo, S.; Fujiki, M.; Imai, Y. Non-Classically Controlled Signs in a Circularly Polarised Luminescent Molecular Puppet: The Importance of the Wire Structure Connecting Binaphthyl and Two Pyrenes. Eur. J. Org. Chem. 2016, 64–69. [Google Scholar] [CrossRef]
- Hara, N.; Yanai, M.; Kaji, D.; Shizuma, M.; Tajima, N.; Fujiki, M.; Imai, Y. A Pivotal Biaryl Rotamer Bearing Two Floppy Pyrenes that Exhibits Cryptochiral Characteristics in the Ground State. ChemistrySelect 2018, 3, 9970–9973. [Google Scholar] [CrossRef]
- Maeda, K.; Hirose, D.; Okoshi, N.; Shimomura, K.; Wada, Y.; Ikai, T.; Kanoh, S.; Yashima, E. Direct Detection of Hardly Detectable Hidden Chirality of Hydrocarbons and Deuterated Isotopomers by a Helical Polyacetylene through Chiral Amplification and Memory. J. Am. Chem. Soc. 2018, 140, 3270–3276. [Google Scholar] [CrossRef]
- Bakasov, A.; Ha, T.-K.; Quack, M. Ab Initio Calculation of Molecular Energies including Parity Violating Interactions. J. Chem. Phys. 1998, 109, 7263–7285. [Google Scholar] [CrossRef]
- Soai, K.; Kawasaki, T. Asymmetric Autocatalysis with Amplification of Chirality. Top. Curr. Chem. 2008, 284, 1–33. [Google Scholar] [CrossRef]
- Green, M.M.; Jain, V. Homochirality in Life: Two Equal Runners, One Tripped. Orig. Life Evol. Biosph. 2010, 40, 111–118. [Google Scholar] [CrossRef] [PubMed]
- Sandars, P.G.H. A Toy Model for the Generation of Homochirality During Polymerization. Orig. Life Evol. Biosph. 2003, 33, 575–587. [Google Scholar] [CrossRef] [PubMed]
- Viedma, C. Selective Chiral Symmetry Breaking during Crystallization: Parity Violation or Cryptochiral Environment in Control? Cryst. Growth Des. 2007, 7, 553–556. [Google Scholar] [CrossRef]
- McLaughlin, D.T.; Nguyen, T.P.T.; Mengnjo, L.; Bian, C.; Leung, Y.H.; Goodfellow, E.; Ramrup, P.; Woo, S.; Cuccia, L.A. Viedma Ripening of Conglomerate Crystals of Achiral Molecules Monitored Using Solid-State Circular Dichroism. Cryst. Growth Des. 2014, 14, 1067–1076. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, L.; Wang, T. Supramolecular Chirality in Self-Assembled Systems. Chem. Rev. 2015, 115, 7304–7397. [Google Scholar] [CrossRef]
- Yashima, E.; Ousaka, N.; Taura, D.; Shimomura, K.; Ikai, T.; Maeda, K. Supramolecular Helical Systems: Helical Assemblies of Small Molecules, Foldamers, and Polymers with Chiral Amplification and Their Functions. Chem. Rev. 2016, 22, 13752–13990. [Google Scholar] [CrossRef]
- Enoto, T.; Wada, Y.; Furuta, Y.; Nakazawa, K.; Yuasa, T.; Okuda, K.; Makishima, K.; Sato, M.; Sato, Y.; Nakano, T.; et al. Photonuclear Reactions Triggered by Lightning Discharge. Nature 2017, 551, 481–484. [Google Scholar] [CrossRef]
- Bargueño, P.; de Tudela, R.P. The Role of Supernova Neutrinos on Molecular Homochirality. Orig. Life Evol. Biosph. 2007, 37, 253–257. [Google Scholar] [CrossRef]
- Alexander, S.; Marcianò, A.; Smolin, L. Gravitational Origin of the Weak Interaction’s Chirality. Phys. Rev. D 2014, 89, 065017. [Google Scholar] [CrossRef]
- Bargueño, P. Gravitational Origin Parity Violation. Chirality 2015, 27, 375–381. [Google Scholar] [CrossRef]
- Ribó, J.M.; Crusats, J.; Sagúes, F.; Claret, J.; Rubires, R. Chiral Sign Induction by Vortices During the Formation of Mesophases in Stirred Solutions. Science 2001, 292, 2063–2066. [Google Scholar] [CrossRef]
- Tamburini, F.; Thidé, B.; Molina-Terriza, G.; Gabriele Anzolin, G. Twisting of Light Around Rotating Black Holes. Nat. Phys. 2011, 7, 195–197. [Google Scholar] [CrossRef]
- Higurashi, E.; Ohguchi, O.; Tamamura, T.; Ukita, H.; Sawada, R. Optically Induced Rotation of Dissymmetrically Shaped Fluorinated Polyimide Micro-Objects in Optical Traps. J. Appl. Phys. 1997, 82, 2773–2779. [Google Scholar] [CrossRef]
- Simpson, N.B.; Dholakia, K.; Allen, L.; Padgett, M.J. Mechanical Equivalence of Spin and Orbital Angular Momentum of Light: An Optical Spanner. Opt. Lett. 1997, 22, 52–54. [Google Scholar] [CrossRef]
- Friese, M.E.J.; Rubinsztein-Dunlop, H.; Gold, J.; Hagberg, P.; Hanstorp, D. Optically Driven Micromachine Elements. Appl. Phys. Lett. 2001, 78, 547–549. [Google Scholar] [CrossRef]
- Curtis, J.E.; Koss, B.A.; Grier, D.G. Dynamic Holographic Optical Tweezers. Opt. Commun. 2002, 207, 169–175. [Google Scholar] [CrossRef]
- Brasselet, E.; Murazawa, N.; Misawa, H.; Juodkazis, S. Optical Vortices from Liquid Crystal Droplets. Phys. Rev. Lett. 2009, 103, 103903. [Google Scholar] [CrossRef]
- Ambrosio, A.; Marrucci, L.; Borbone, F.; Roviello, A.; Maddalena, P. Light-Induced Spiral Mass Transport in Azo-Polymer Films Under Vortex-Beam Illumination. Nat. Commun. 2012, 3, 989. [Google Scholar] [CrossRef]
- Watabe, M.; Juman, G.; Miyamoto, K.; Omatsu, T. Light Induced Conch-Shaped Relief in An Azo-Polymer Film. Sci. Rep. 2014, 4, 4281. [Google Scholar] [CrossRef]
- Brullot, W.; Vanbel, M.K.; Swusten, T.; Verbiest, T. Resolving Enantiomers Using the Optical Angular Momentum of Twisted Light. Sci. Adv. 2016, 2, e1501349. [Google Scholar] [CrossRef]
- Shen, Z.; Su, L.; Yuan, X.-C.; Shen, Y.-C. Trapping and Rotating of a Metallic Particle Trimer with Optical Vortex. Appl. Phys. Lett. 2016, 109, 241901. [Google Scholar] [CrossRef]
- Katoh, M.; Fujimoto, M.; Mirian, N.S.; Konomi, T.; Taira, Y.; Kaneyasu, T.; Kuroda, K.; Miyamoto, A.; Miyamoto, K.; Sasaki, S. Helical Phase Structure of Radiation from an Electron in Circular Motion. Sci Rep. 2017, 7, 6130. [Google Scholar] [CrossRef]
- Taira, Y.; Masahiro Katoh, M. Gamma-Ray Vortices Emitted from Nonlinear Inverse Thomson Scattering of a Two-Wavelength Laser Beam. Phys. Rev. A 2018, 98, 052130. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, J.; Jiao, X.-Q.; Sun, K.; Shen, W.-G.; Qiao, L.-F.; Tang, H.; Lin, X.-F.; Jin, X.-M. Mapping Twisted Light into and Out of a Photonic Chip. Phys. Rev. Lett. 2018, 121, 233602. [Google Scholar] [CrossRef]
- Samlan, C.T.; Suna, R.R.; Naik, D.N.; Viswanathan, N.K. Spin-orbit Beams for Optical Chirality Measurement. Appl. Phys. Lett. 2018, 112, 031101. [Google Scholar] [CrossRef]
- Torrres, J.P.; Torner, L. (Eds.) Twisted photons: Applications of Light with Orbital Angular Momentum; Wiley-VCH: Weinheim, Germany, 2011; ISBN 3527635378. [Google Scholar]
- Inoue, Y.; Ramamurthy, V. (Eds.) Chiral Photochemistry: Molecular and Supramolecular Photochemistry; CRC Press: Tokyo, Japan, 2004; ISBN 9780824757106. [Google Scholar]
- Fujiki, M. Creation and Controlling Asymmetric Small Molecules, Polymers, Colloids, and Small Objects Endowed with Polarized Light and Spin Polarized Particles. Kobunshi Ronbunshu 2017, 74, 114–133. [Google Scholar] [CrossRef]
- Elsila, J.E.; Glavin, D.P.; Dworkin, J.P. Cometary Glycine Detected in Samples Returned by Stardust. Meteorit. Planet. Sci. 2009, 44, 1323–1330. [Google Scholar] [CrossRef]
- Altwegg, K.; Balsiger, H.; Bar-Nun, A.; Berthelier, Je.; Bieler, A.; Bochsler, P.; Briois, C.; Calmonte, U.; Combi, M.R.; Cottin, H.; et al. Prebiotic Chemicals—Amino Acid and Phosphorus—In the Coma of Comet 67P/Churyumov-Gerasimenko. Sci. Adv. 2016, 2, e1600285. [Google Scholar] [CrossRef]
- McGuire, B.A.; Carroll, B.P.; Loomis, R.A.; Finneran, I.A.; Jewell, R.P.; Remijan, A.J.; Blake, G.A. Discovery of the Interstellar Chiral Molecule Propylene Oxide (CH3CHCH2O). Science 2016, 352, 1449–1452. [Google Scholar] [CrossRef]
- Urata, H.; Shinohara, K.; Ogura, E.; Uweda, Y.; Akagi, M. Mirror-image DNA. J. Am. Chem. Soc. 1991, 113, 8174–8175. [Google Scholar] [CrossRef]
- Zawadzke, L.E.; Berg, J.M. A Racemic Protein. J. Am. Chem. Soc. 1992, 114, 4002–4003. [Google Scholar] [CrossRef]
- Riddick, J.A.; Bunger, W.B.; Sakano, T.K. Organic Solvents: Physical Properties and Methods of Purification, 4th ed.; John Wiley & Sons: New York, NY, USA, 1986; ISBN 0-471-08467-0. [Google Scholar]
- Lide, D.R. Handbook of Organic Solvents; CRC Press: Boca Raton, FL, USA, 1994; ISBN 0849389305. [Google Scholar]
- Viswanath, D.S.; Ghosh, T.; Prasad, D.H.L.; Dutt, N.V.K.; Rani, K.Y. Viscosity of Liquids; Theory, Estimation, Experiment and Data; Springer: Berlin, Germany, 2007; ISBN 9048173787. [Google Scholar]
- Properties of Organic Solvents. Available online: http://murov.info/orgsolvents.htm (accessed on 12 June 2018).
- Hardy, R.C.; Cottington, R.L. Viscosity of Deuterium Oxide and Water in the Range 5°C to 125 °C. J. Res. Natl. Bureau Stand. 1949, 42, 573–578. [Google Scholar] [CrossRef]
- Cho, C.H.; Urquidi, J.; Singh, S.; Robinson, G.W. Thermal Offset Viscosities of Liquid H2O, D2O, and T2O. J. Phys. Chem. B 1999, 103, 1991–1994. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).