Optimizing MSE for Clustering with Balanced Size Constraints
Abstract
:1. Introduction
2. Related Work
2.1. Soft Constraints
2.2. Hard Constraints
3. Balanced Clustering Algorithm
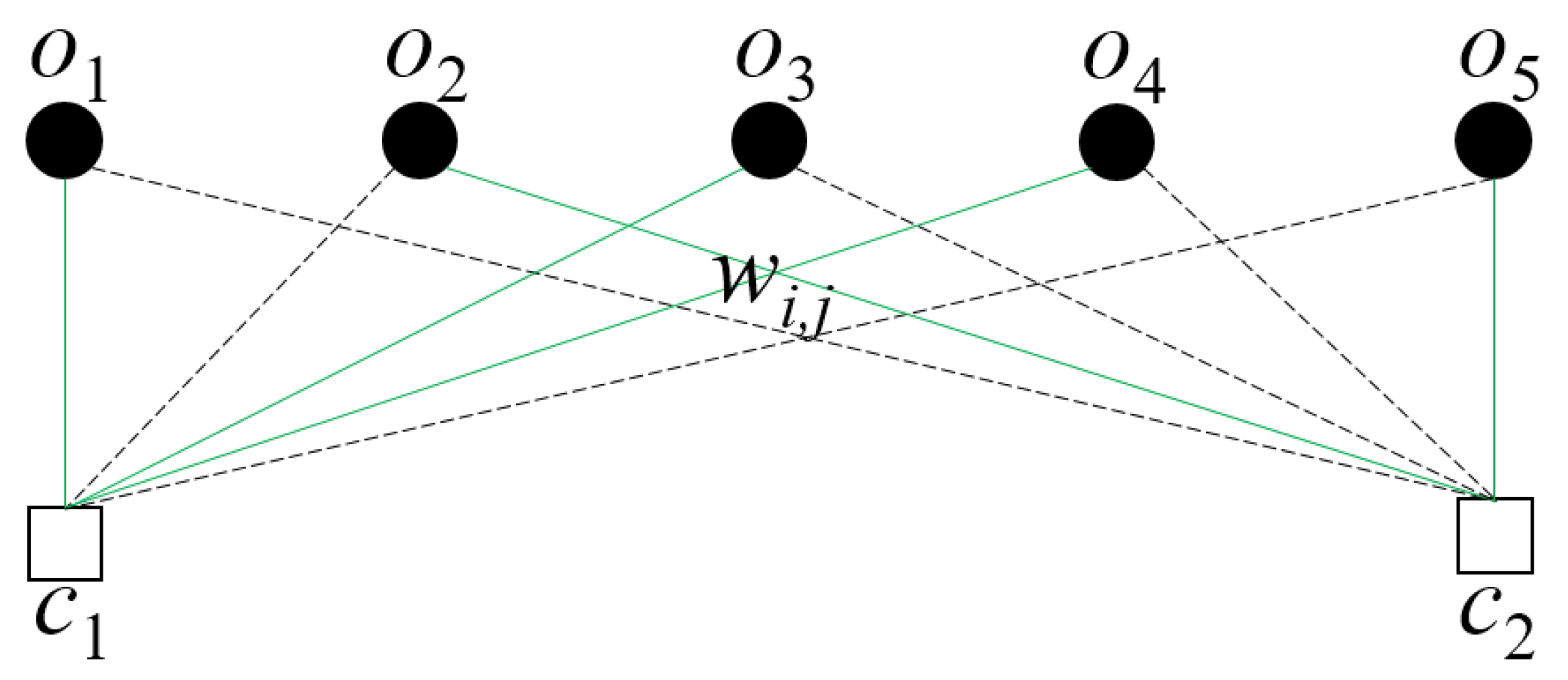
3.1. Problem Formulation
3.2. Proposed Solution
| Algorithm 1 Clustering with balanced size constraints |
| Input: Observations , number of clusters k Output: Labels of the observations.
|
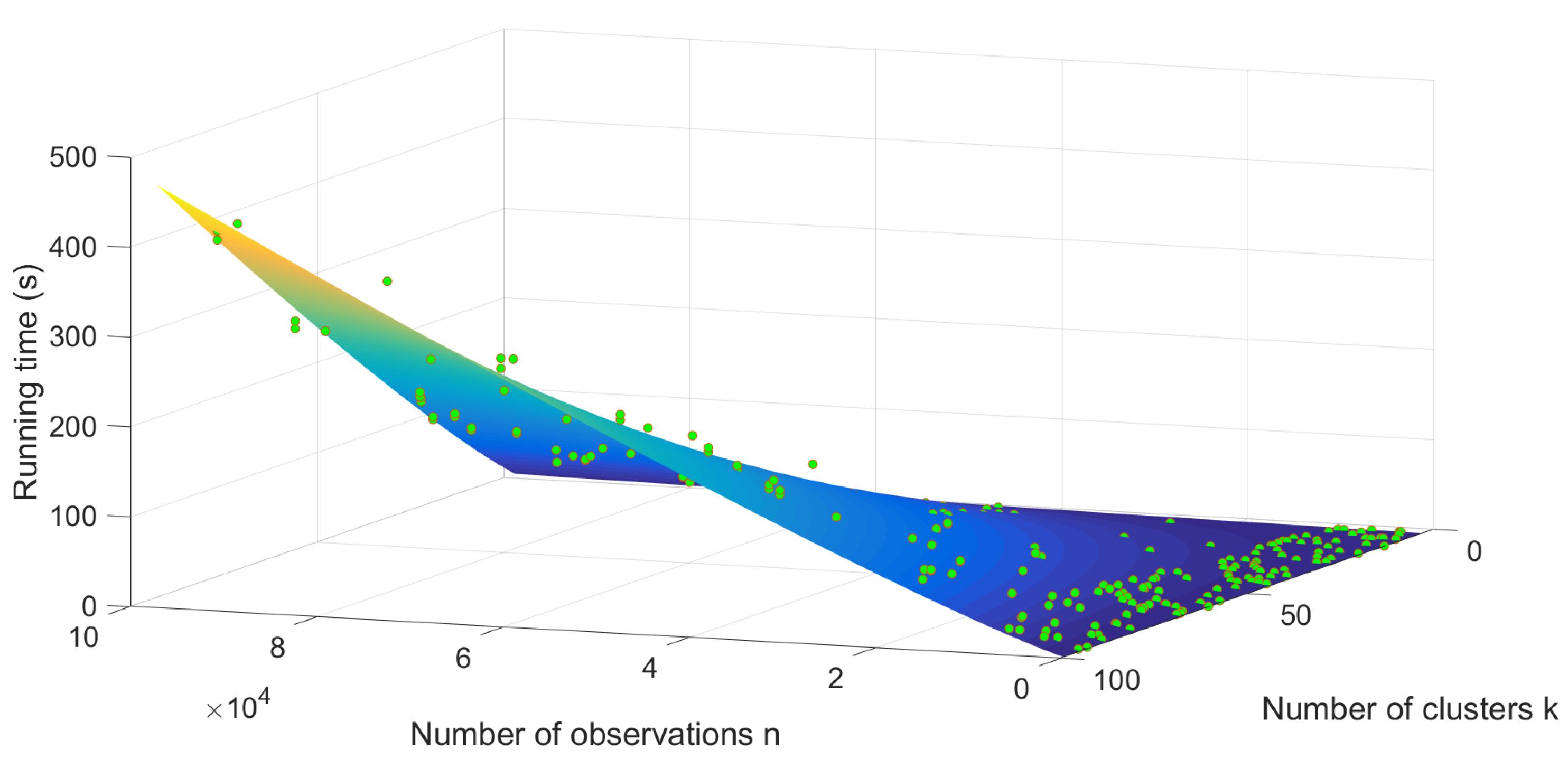
3.3. Time Complexity
4. Experiments
4.1. Experimental Settings
4.2. Experimental Results
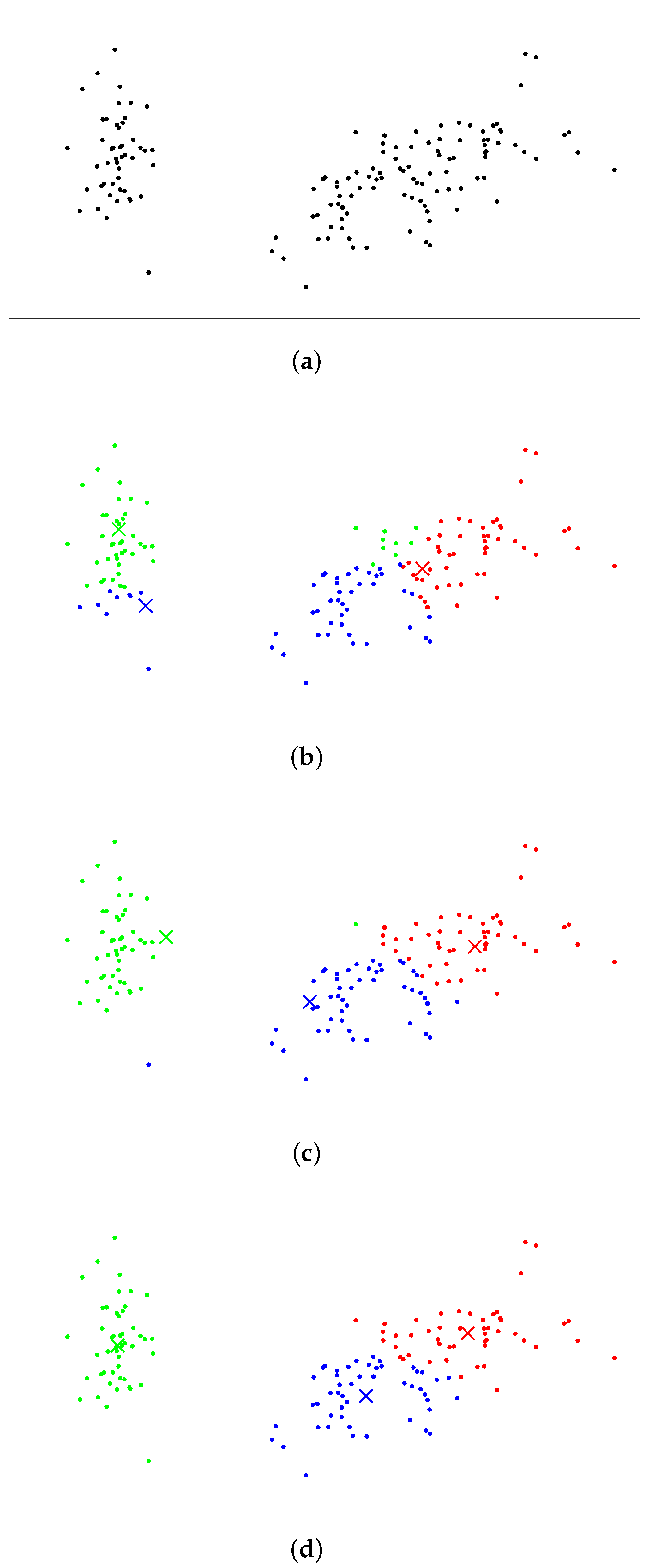
4.2.1. Balanced Assignment
4.2.2. Balanced Clustering
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, R.; Wunsch, D.C. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Padmanabhan, B. Segmenting customer transactions using a pattern-based clustering approach. In Proceedings of the International Conference on Data Mining, Melbourne, FL, USA, 19–22 November 2003; pp. 411–418. [Google Scholar]
- Liao, Y.; Qi, H.; Li, W. Load-Balanced Clustering Algorithm with Distributed Self-Organization for Wireless Sensor Networks. IEEE Sens. J. 2013, 13, 1498–1506. [Google Scholar] [CrossRef]
- Hagen, L.; Kahng, A. Fast spectral methods for ratio cut partitioning and clustering. In Proceedings of the IEEE International Conference on Computer-Aided Design, Santa Clara, CA, USA, 11–14 November 1991; pp. 10–13. [Google Scholar]
- Issal, C.; Ebbesson, M. Document Clustering. IEEE Swarm Intel. Symp. 2010, 38, 185–191. [Google Scholar]
- Dengel, A.; Althoff, T.; Ulges, A. Balanced Clustering for Content-Based Image Browsing. Gi-Informatiktage 2008, 27–30. [Google Scholar]
- Banerjee, A.; Ghosh, J. Frequency-sensitive competitive learning for scalable balanced clustering on high-dimensional hyperspheres. IEEE Trans. Neural Netw. 2004, 15, 702–719. [Google Scholar] [CrossRef] [PubMed]
- Koberstein, A. Progress in the dual simplex algorithm for solving large scale LP problems: techniques for a fast and stable implementation. Comput. Optim. Appl. 2008, 41, 185–204. [Google Scholar] [CrossRef]
- Malinen, M.I.; Fränti, P. Balanced k-means for Clustering. In Proceedings of the Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition (SSPR), Joensuu, Finland, 20–22 August 2014; pp. 32–41. [Google Scholar]
- Mardia, K.V.; Kent, J.T.; Bibby, J.M. Multivariate analysis. Math. Gazette 1979, 37, 123–131. [Google Scholar]
- Grossi, V.; Romei, A.; Turini, F. Survey on using constraints in data mining. Data Mining Knowl. Discov. 2017, 31, 424–464. [Google Scholar] [CrossRef]
- Banerjee, A.; Ghosh, J. Scalable Clustering Algorithms with Balancing Constraints. Data Mining Knowl. Discov. 2006, 13, 365–395. [Google Scholar] [CrossRef]
- Luxburg, U.V. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Ji, X. Size Regularized Cut for Data Clustering. In Proceedings of the Advances in Neural Information Processing Systems 18, Vancouver, BC, Canada, 5–8 December 2005; pp. 211–218. [Google Scholar]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 22, 888–905. [Google Scholar]
- Kawahara, Y.; Nagano, K.; Okamoto, Y. Submodular fractional programming for balanced clustering. Pattern Recognit. Lett. 2011, 32, 235–243. [Google Scholar] [CrossRef]
- Chang, X.; Nie, F.; Ma, Z.; Yang, Y. Balanced k-means and Min-Cut Clustering. arXiv. 2014. Available online: https://arxiv.org/abs/1411.6235 (accessed on 5 March 2019).
- Zhu, S.; Wang, D.; Li, T. Data clustering with size constraints. Knowl.-Based Syst. 2010, 23, 883–889. [Google Scholar] [CrossRef]
- He, R.; Xu, W.; Sun, J.; Zu, B. Balanced k-means Algorithm for Partitioning Areas in Large-Scale Vehicle Routing Problem. In Proceedings of the International Symposium on Intelligent Information Technology Application, Nanchang, China, 21–22 November 2009; pp. 87–90. [Google Scholar]
- Tai, C.L.; Wang, C.S. Balanced k-means. In Intelligent Information and Database Systems; Nguyen, N.T., Tojo, S., Nguyen, L.M., Trawiński, B., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 75–82. [Google Scholar]
- Bennett, K.; Bradley, P.; Demiriz, A. Constrained k-Means Clustering; Technical Report; Microsoft Research: Redmond, WA, USA, 2000. [Google Scholar]
- Yuepeng, S.; Min, L.; Cheng, W. A Modified k-means Algorithm for Clustering Problem with Balancing Constraints. In Proceedings of the International Conference on Measuring Technology and Mechatronics Automation, Shanghai, China, 6–7 January 2011; pp. 127–130. [Google Scholar]
- Ganganath, N.; Cheng, C.T.; Chi, K.T. Data Clustering with Cluster Size Constraints Using a Modified k-means Algorithm. In Proceedings of the International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery, Shanghai, China, 13–15 October 2014; pp. 158–161. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the Eighteenth ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Papadimitriou, C.H.; Steiglitz, K. Combinatorial Optimization: Algorithms and Complexity; Prentice Hall: Mineola, NY, USA, 1998. [Google Scholar]
- Schrijver, A. Theory of Linear and Integer Programming; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1986. [Google Scholar]
- Spielman, D.A.; Teng, S. Smoothed analysis of algorithms: why the simplex algorithm usually takes polynomial time. J. ACM 2004, 51, 385–463. [Google Scholar] [CrossRef]
- Borgwardt, K.H. The Simplex Method: A Probabilistic Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Fang, S.C.; Puthenpura, S. Linear Optimization and Extensions: Theory and Algorithms; Prentice-Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Dheeru, D.; Taniskidou, E.K. UCI Machine Learning Repository; University of California: Irvine, CA, USA, 2019. [Google Scholar]
| Category | Data | Size | Dimension |
|---|---|---|---|
| Random | R1 | 200 | 2 |
| R2 | 600 | 2 | |
| R3 | 1000 | 2 | |
| R4 | 2000 | 2 | |
| R5 | 5000 | 2 | |
| Real | Iris | 150 | 4 |
| Wine | 178 | 14 | |
| Thyroid | 215 | 5 | |
| Hill Valley (HV) | 606 | 100 | |
| Anuran Calls Subset (ACS) | 1500 | 22 |
| Data | K | Cost Ours/BK | Time Ours/BK |
|---|---|---|---|
| R1 | 3 | 2.87/2.88 | 0.37/0.21 |
| 9 | 1.11/1.12 | 0.02/0.11 | |
| 21 | 4.76/5.10 | 0.03/0.1 | |
| 45 | 2.52/3.17 | 0.03/0.13 | |
| 93 | 9.23/13.25 | 0.07/0.11 | |
| R2 | 3 | 1.15/1.15 | 0.02/14.54 |
| 9 | 4.22/4.25 | 0.03/3.19 | |
| 21 | 1.84/1.9 | 0.05/1.94 | |
| 45 | 8.01/8.66 | 0.09/1.35 | |
| 93 | 3.66/4.6 | 0.17/1.26 | |
| R3 | 3 | 1.6/1.6 | 0.05/84.7 |
| 9 | 5.92/5.94 | 0.04/14.95 | |
| 21 | 2.55/2.6 | 0.08/6.77 | |
| 45 | 1.7/1.77 | 0.18/6.01 | |
| 93 | 5.92/6.4 | 0.41/4.58 | |
| R4 | 3 | 2.86/2.86 | 0.14/1081.9 |
| 9 | 1.23/1.23 | 0.12/151.8 | |
| 21 | 6.53/6.58 | 0.2/79.91 | |
| 45 | 4.27/4.38 | 0.47/48.86 | |
| 93 | 1.4/1.48 | 1.19/29.07 | |
| R5 | 3 | 6.81/6.81 | 0.68/59946 |
| 9 | 2.93/2.93 | 0.43/7582.1 | |
| 21 | 1.52/1.53 | 0.75/2618.4 | |
| 45 | 6.82/6.85 | 1.78/786.55 | |
| 93 | 4.67/4.76 | 4.91/620.3 |
| Data | K | Cost Ours/BK | Time Ours/BK |
|---|---|---|---|
| Iris | 3 | 4.95/4.95 | 0.01/0.08 |
| 9 | 2.28/2.34 | 0.02/0.06 | |
| 21 | 1.31/1.45 | 0.03/0.07 | |
| 45 | 5.11/8.85 | 0.03/0.07 | |
| 93 | 1.16/3.92 | 0.05/0.06 | |
| Wine | 3 | 5.12/5.13 | 0.02/0.13 |
| 9 | 3.74/3.75 | 0.02/0.1 | |
| 21 | 2.45/2.54 | 0.04/0.1 | |
| 45 | 1.68/1.71 | 0.04/0.15 | |
| 93 | 8.62/10 | 0.06/0.08 | |
| Thyroid | 3 | 1.31/1.32 | 0.02/0.43 |
| 9 | 8.75/8.86 | 0.02/0.17 | |
| 21 | 4.79/4.91 | 0.03/0.16 | |
| 45 | 2.31/2.73 | 0.04/0.15 | |
| 93 | 1.03/1.3 | 0.07/0.13 | |
| HV | 3 | 2.77/2.77 | 0.02/3.57 |
| 9 | 1.4/1.41 | 0.04/2.78 | |
| 21 | 1.15/1.2 | 0.07/2.72 | |
| 45 | 3.66/4.01 | 0.11/3.9 | |
| 93 | 1.63/1.89 | 0.22/4.27 | |
| ACS | 3 | 1.31/1.31 | 0.04/198.75 |
| 9 | 654.78/656.54 | 0.08/36.16 | |
| 21 | 478.67/482 | 0.13/32.07 | |
| 45 | 299.23/307.21 | 0.25/41.05 | |
| 93 | 212.48/221.01 | 0.7/64.48 |
| Data | K | MSE Ours/BK /BSCK | Time Ours/BK /BSCK | Iterations Ours/BK |
|---|---|---|---|---|
| R1 | 3 | 629.81/630.97/794.71 | 0.2/0.57/0.06 | 5.6/6.3 |
| 9 | 168.88/169.1/440.24 | 0.11/0.53/0.03 | 5/6.1 | |
| 21 | 71.7/74.71/791.17 | 0.17/0.58/0.04 | 4.4/5.7 | |
| 45 | 28.13/31.9/711.57 | 0.24/0.51/0.06 | 3.2/4.8 | |
| 93 | 9.93/12.64/669.44 | 0.36/0.35/0.12 | 2/3 | |
| R2 | 3 | 645.78/645.78/721.07 | 0.13/5.69/0.03 | 4.1/5.1 |
| 9 | 183.54/180.61/382.93 | 0.83/12.73/0.06 | 11.3/16 | |
| 21 | 78.29/78.48/422.43 | 1.06/7.42/0.13 | 6.7/8.3 | |
| 45 | 34.06/34.68/492.25 | 1.81/7.74/0.29 | 5.5/7.6 | |
| 93 | 14.86/15.71/594.6 | 3.62/7.88/0.65 | 5.1/6.5 | |
| R3 | 3 | 635.91/636.01/710.53 | 1.24/62.07/0.06 | 9.7/10.3 |
| 9 | 190.61/190.67/382.46 | 1.64/26.72/0.13 | 7.4/8.8 | |
| 21 | 78.08/78.17/416.13 | 2.93/30.18/0.31 | 8.1/11.2 | |
| 45 | 35.26/35.6/437.29 | 7.62/34.15/0.75 | 10.4/9.6 | |
| 93 | 15.9/16.28/459.43 | 13.2/40.71/1.66 | 8.3/9.2 | |
| R4 | 3 | 664.25/664.3/807.32 | 2.32/783.43/0.21 | 9/9.5 |
| 9 | 190.78/190.86/343.39 | 4.68/223.61/0.55 | 15.1/12.9 | |
| 21 | 79.59/79.8/376.08 | 4.81/210.67/1.27 | 15.2/14.2 | |
| 45 | 34.82/34.92/360.01 | 8.5/272.93/2.89 | 16.6/17 | |
| 93 | 16.65/16.76/443.89 | 15.01/318.73/7.83 | 13.6/13.2 | |
| R5 | 3 | 664.54/664.58/800.04 | 22.32/67500/0.37 | 12.8/11.8 |
| 9 | 184.39/184.40/283.19 | 7.88/1900/0.42 | 7.9/7.7 | |
| 21 | 79.84/79.84/252.66 | 49.95/3100/1.37 | 17.7/20 | |
| 45 | 36.53/36.45/366.76 | 90.64/5100/5.38 | 26.3/30.2 | |
| 93 | 17.32/17.37/327.91 | 88.69/5100/22.95 | 19.7/20.9 |
| Data | K | MSE Ours/BK /BSCK | Time Ours/BK /BSCK | Iterations Ours/BK |
|---|---|---|---|---|
| Iris | 3 | 9.35/9.35/23.5 | 0.03/0.15/0.01 | 1.6/2.6 |
| 9 | 4.08/4.2/28.3 | 0.11/0.36/0.02 | 6.2/6.1 | |
| 21 | 2.18/2.32/25.4 | 0.15/0.37/0.03 | 5.2/5.9 | |
| 45 | 1.09/1.26/26.6 | 0.17/0.29/0.04 | 3/4.1 | |
| 93 | 6.07/19.4/212 | 0.18/0.41/0.09 | 1/4.9 | |
| Wine | 3 | 1.25/1.25/1.36 | 0.03/0.17/0.01 | 1/2.2 |
| 9 | 9.14/9.10/18.4 ) | 0.11/0.6/0.02 | 5.5/7.6 | |
| 21 | 6.77/6.83/18.6 | 0.16/0.42/0.03 | 4.6/4.8 | |
| 45 | 4.66/4.72/18.6 | 0.16/0.3/0.05 | 2/2.7 | |
| 93 | 3.23/3.18/14 | 0.33/0.33/0.11 | 1.9/3.1 | |
| Thyroid | 3 | 3.46/3.47/11.9 | 0.1/2.71/0.02 | 6.2/7.6 |
| 9 | 1.88/1.89/16 | 0.12/1.48/0.02 | 5.3/7.6 | |
| 21 | 9.15/9.46/106 | 0.24/1.16/0.04 | 6.1/6.4 | |
| 45 | 3.97/4.35/86 | 0.31/1.02/0.07 | 3.6/4.8 | |
| 93 | 1.94/2.35/55.3 | 0.48/0.81/0.13 | 2.5/4.4 | |
| HV | 3 | 2.75/2.75/24.89 | 0.21/13.56/0.11 | 2/2 |
| 9 | 8.44/8.5/349.29 | 0.12/8.16/0.06 | 2/2.3 | |
| 21 | 2.04/2.18/359.52 | 0.25/12.49/0.12 | 3.4/3.1 | |
| 45 | 6.59/6.98/3203.1 | 0.65/20.54/0.25 | 4.3/4.4 | |
| 93 | 2.43/2.94/2449.2 | 1.57/32.64/0.54 | 4.9/5.3 | |
| ACS | 3 | 0.31/0.31/0.51 | 0.35/1008.9/0.07 | 7/7 |
| 9 | 0.14/0.14/0.47 | 1.11/268.08/0.14 | 12.2/11.3 | |
| 21 | 0.08/0.08/0.54 | 2.9/259.55/0.42 | 17.6/13.6 | |
| 45 | 0.06/0.06/0.54 | 4.56/287.23/1 | 14.6/14.7 | |
| 93 | 0.04/0.05/0.54 | 9.71/265.17/3.27 | 11/12 |
| Data | K | MSE C.V. Ours/BK /BSCK | Time C.V. Ours/BK /BSCK | Iterations C.V. Ours/BK |
|---|---|---|---|---|
| R1 | 3 | 0.03/0.03/0.07 | 1.57/0.77/2.43 | 0.95/0.8 |
| 9 | 0.04/0.04/0.39 | 0.49/0.55/0.59 | 0.57/0.53 | |
| 21 | 0.04/0.05/0.24 | 0.28/0.38/0.28 | 0.33/0.41 | |
| 45 | 0.08/0.07/0.12 | 0.22/0.27/0.04 | 0.29/0.27 | |
| 93 | 0.1/0.11/0.18 | 0.03/0.11/0.05 | 0/0.16 | |
| R2 | 3 | 0.03/0.03/0.05 | 0.76/0.63/0.07 | 0.94/0.75 |
| 9 | 0.06/0.04/0.33 | 0.63/0.78/0.03 | 0.68/0.77 | |
| 21 | 0.03/0.02/0.17 | 0.36/0.24/0.03 | 0.42/0.23 | |
| 45 | 0.05/0.03/0.13 | 0.24/0.4/0.05 | 0.27/0.47 | |
| 93 | 0.03/0.03/0.11 | 0.23/0.28/0.05 | 0.28/0.29 | |
| R3 | 3 | 0/0/0.04 | 0.29/0.29/0.05 | 0.32/0.3 |
| 9 | 0.03/0.03/0.11 | 0.78/0.62/0.04 | 0.87/0.61 | |
| 21 | 0.02/0.02/0.17 | 0.41/0.53/0.05 | 0.47/0.55 | |
| 45 | 0.03/0.01/0.23 | 0.21/0.19/0.08 | 0.23/0.16 | |
| 93 | 0.02/0.02/0.1 | 0.38/0.21/0.05 | 0.43/0.26 | |
| R4 | 3 | 0.01/0.01/0.04 | 1.52/1.51/0.05 | 1.55/1.52 |
| 9 | 0/0/0.11 | 0.78/0.95/0.05 | 0.82/0.88 | |
| 21 | 0.01/0.01/0.21 | 0.58/0.41/0.05 | 0.59/0.43 | |
| 45 | 0.03/0.03/0.19 | 0.4/0.32/0.07 | 0.38/0.34 | |
| 93 | 0.01/0.01/0.17 | 0.22/0.24/0.05 | 0.23/0.3 | |
| R5 | 3 | 0.01/0.01/0.04 | 0.98/1.07/1 | 0.99/1.12 |
| 9 | 0.01/0.01/0.11 | 0.45/0.34/0.35 | 0.45/0.4 | |
| 21 | 0.01/0.01/0.16 | 0.52/0.57/0.29 | 0.51/0.52 | |
| 45 | 0.02/0.01/0.22 | 0.35/0.23/0.27 | 0.33/0.23 | |
| 93 | 0.01/0.01/0.21 | 0.14/0.24/0.22 | 0.14/0.25 |
| Data | K | MSE C.V. Ours/BK /BSCK | Time C.V. Ours/BK /BSCK | Iterations C.V. Ours/BK |
|---|---|---|---|---|
| Iris | 3 | 0/0/0.89 | 0.37/0.7/0.07 | 0.6/0.37 |
| 9 | 0.03/0.04/0.33 | 0.51/0.44/0.06 | 0.6/0.45 | |
| 21 | 0.03/0.07/0.26 | 0.24/0.25/0.05 | 0.31/0.27 | |
| 45 | 0.07/0.17/0.18 | 0.2/0.17/0.04 | 0.27/0.18 | |
| 93 | 0.4/0.09/0.12 | 0.02/0.17/0.03 | 0/0.2 | |
| Wine | 3 | 0/0/0.02 | 0.03/0.22/0.11 | 0/0.19 |
| 9 | 0.03/0.02/0.15 | 0.29/0.35/0.05 | 0.36/0.33 | |
| 21 | 0.03/0.02/0.18 | 0.36/0.24/0.09 | 0.45/0.26 | |
| 45 | 0.04/0.03/0.13 | 0.24/0.22/0.03 | 0.33/0.31 | |
| 93 | 0.07/0.05/0.09 | 0.32/0.13/0.11 | 0.39/0.1 | |
| Thyroid | 3 | 0/0/0.37 | 0.07/0.09/0.05 | 0.07/0.07 |
| 9 | 0.09/0.09/0.18 | 0.31/0.35/0.06 | 0.37/0.27 | |
| 21 | 0.01/0.01/0.2 | 0.24/0.13/0.06 | 0.25/0.13 | |
| 45 | 0.03/0.03/0.12 | 0.11/0.11/0.13 | 0.14/0.13 | |
| 93 | 0.07/0.08/0.06 | 0.21/0.12/0.04 | 0.28/0.29 | |
| HV | 3 | 0/0/0.06 | 2.61/0.02/2.37 | 0/0 |
| 9 | 0/0.01/0.25 | 1.08/0.07/0.35 | 0/0.21 | |
| 21 | 0/0.03/0.16 | 0.15/0.08/0.11 | 0.15/0.1 | |
| 45 | 0/0.04/0.1 | 0.19/0.09/0.12 | 0.11/0.12 | |
| 93 | 0.06/0.09/0.02 | 0.07/0.06/0.11 | 0.12/0.13 | |
| ACS | 3 | 0/0/0.04 | 0.96/0.03/0.98 | 0/0 |
| 9 | 0.02/0.02/0.28 | 0.4/0.33/0.25 | 0.43/0.48 | |
| 21 | 0.01/0.01/0.21 | 0.3/0.29/0.24 | 0.31/0.26 | |
| 45 | 0.01/0.02/0.19 | 0.2/0.3/0.19 | 0.19/0.31 | |
| 93 | 0.01/0.01/0.04 | 0.15/0.15/0.08 | 0.15/0.19 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, W.; Yang, Y.; Zeng, L.; Zhan, Y. Optimizing MSE for Clustering with Balanced Size Constraints. Symmetry 2019, 11, 338. https://doi.org/10.3390/sym11030338
Tang W, Yang Y, Zeng L, Zhan Y. Optimizing MSE for Clustering with Balanced Size Constraints. Symmetry. 2019; 11(3):338. https://doi.org/10.3390/sym11030338
Chicago/Turabian StyleTang, Wei, Yang Yang, Lanling Zeng, and Yongzhao Zhan. 2019. "Optimizing MSE for Clustering with Balanced Size Constraints" Symmetry 11, no. 3: 338. https://doi.org/10.3390/sym11030338
APA StyleTang, W., Yang, Y., Zeng, L., & Zhan, Y. (2019). Optimizing MSE for Clustering with Balanced Size Constraints. Symmetry, 11(3), 338. https://doi.org/10.3390/sym11030338




