Algebraic Construction of a Strongly Consistent, Permutationally Symmetric and Conservative Difference Scheme for 3D Steady Stokes Flow †
Abstract
:1. Introduction
2. Algorithmic Generation of the Difference Scheme for Stokes Flow
3. Consistency Analysis
4. Modified Stokes Flow
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Blinkov, Y.A.; Gerdt, V.P.; Lyakhov, D.A.; Michels, D.L. A Strongly Consistent Finite Difference Scheme for Steady Stokes Flow and its Modified Equations. In Computer Algebra in Scientific Computing, Proceedings of the 20th International Workshop on Computer Algebra in Scientific Computing, Lille, France, 17–21 September 2018; Gerdt, V.P., Koepff, W., Seiler, W.M., Vorozhtsov, E.V., Eds.; Springer: Cham, Switzerland, 2018; pp. 67–81. [Google Scholar]
- Milne-Tompson, L.M. Theoretical Hydrodynamics, 5th ed.; Macmillan Education LTD: Houndmills, UK, 1968. [Google Scholar]
- Kohr, M.; Pop, I. Viscous Incompressible Flow for Low Reynolds Numbers, Advances in Boundary Elements; WIT Press: Southampton, UK, 2004; Volume 16. [Google Scholar]
- Koren, B.; Abgral, R.; Bochev, P.; Frank, J. Physics—Compatible numerical methods. J. Comput. Phys. B 2014, 257, 1039–1526. [Google Scholar] [CrossRef]
- Strikwerda, J.C. Finite Difference Schemes and Partial Differential Equations, 2nd ed.; SIAM: Philadelphia, PA, USA, 2004. [Google Scholar]
- Gerdt, V.P.; Robertz, D. Consistency of finite difference approximations for linear PDE systems and its algorithmic verification. In Proceedings of the 2010 International Symposium on Symbolic and Algebraic Computation; Watt, S.M., Ed.; The Association for Computing Machinery: New York, NY, USA, 2010; pp. 53–59. [Google Scholar]
- Gerdt, V.P. Consistency analysis of finite difference approximations to PDE Systems. In Mathematical Modelling and Computational Science, Proceedings of International Conference on Mathematical Moddeling and Computational Physics, Stará Lesná, Slovakia, 4–8 July 2011; Adam, G., Buša, J., Hnatič, M., Eds.; Springer: Berlin, Germany, 2012; pp. 28–42. [Google Scholar]
- Levin, A. Difference Algebra. Algebra and Applications; Springer: New York, NY, USA, 2008; Volume 8. [Google Scholar]
- Seiler, W.M. Involution: The Formal Theory of Differential Equations and its Applications in Computer Algebra. Algorithms and Computation in Mathematics; Springer: Heidelberg, Germany, 2010; Volume 24. [Google Scholar]
- Gerdt, V.P.; Blinkov, Y.A.; Mozzhilkin, V.V. Gröbner Bases and Generation of Difference Schemes for Partial Differential Equations. SIGMA 2006, 2, 051. [Google Scholar] [CrossRef]
- Amodio, P.; Blinkov, Y.A.; Gerdt, V.P.; La Scala, R. On Consistency of Finite Difference Approximations to the Navier–Stokes Equations. In Computer Algebra in Scientific Computing, Proceedings of the 15th International Workshop on Computer Algebra in Scientific Computing, Berlin, Germany, 9–13 September 2013; Gerdt, V.P., Koepff, W., Mayr, E.W., Vorozhtsov, E.V., Eds.; Springer: Cham, Switzerland, 2013; pp. 46–60. [Google Scholar]
- Amodio, P.; Blinkov, Y.A.; Gerdt, V.P.; La Scala, R. Algebraic construction and numerical behavior of a new s-consistent difference scheme for the 2D Navier–Stokes equations. Appl. Math. Comput. 2017, 314, 408–421. [Google Scholar] [CrossRef]
- Gerdt, V.P. Involutive algorithms for computing Gröbner Bases. In Computational Commutative and Non-Commutative Algebraic Geometry, Proceedings of the NATO Advanced Research Workshop on Computational Commutative and Non-Commutative Algebraic Geometry, Chisinau, Moldova, 6–11 June 2004; Cojocaru, S., Pfister, G., Ufnarovski, V., Eds.; IOS Press: Amsterdam, The Netherlands, 2004; pp. 199–225. [Google Scholar]
- Blinkov, Y.A.; Cid, C.F.; Gerdt, V.P.; Plesken, W.; Robertz, D. The MAPLE Package Janet: II. Linear Partial Differential Equations. In Computer Algebra in Scientific Computing, Proceedings of the 6th International Workshop on Computer Algebra in Scientific Computing, Passau, Germany, 20–26 September 2003; Ganzha, V.G., Mayr, E.W., Vorozhtsov, E.V., Eds.; Technische Universität: München, Germany, 2003; pp. 41–54. [Google Scholar]
- Gerdt, V.P.; Robertz, D. Computation of difference Gröbner bases. Comput. Sc. J. Moldova 2012, 20, 203–226. [Google Scholar]
- Shokin, Y.I. The Method of Differential Approximation; Springer-Verlag: Berlin, Germany, 1983. [Google Scholar]
- Ganzha, V.G.; Vorozhtsov, E.V. Computer-aided Analysis of Difference Schemes for Partial Differential Equations; John Wiley & Sons. Inc.: New York, NY, USA, 1996. [Google Scholar]
- Moin, P. Fundamentals of Engineering Numerical Analysis, 2nd ed.; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Adams, W.W.; Loustanau, P. Introduction to Gröbner Bases. Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 1994; Volume 3. [Google Scholar]
- Petersson, N.A. Stability of Pressure Boundary Conditions for Stokes and Navier–Stokes Equations. J. Comput. Phys. 2001, 172, 40–70. [Google Scholar] [CrossRef]
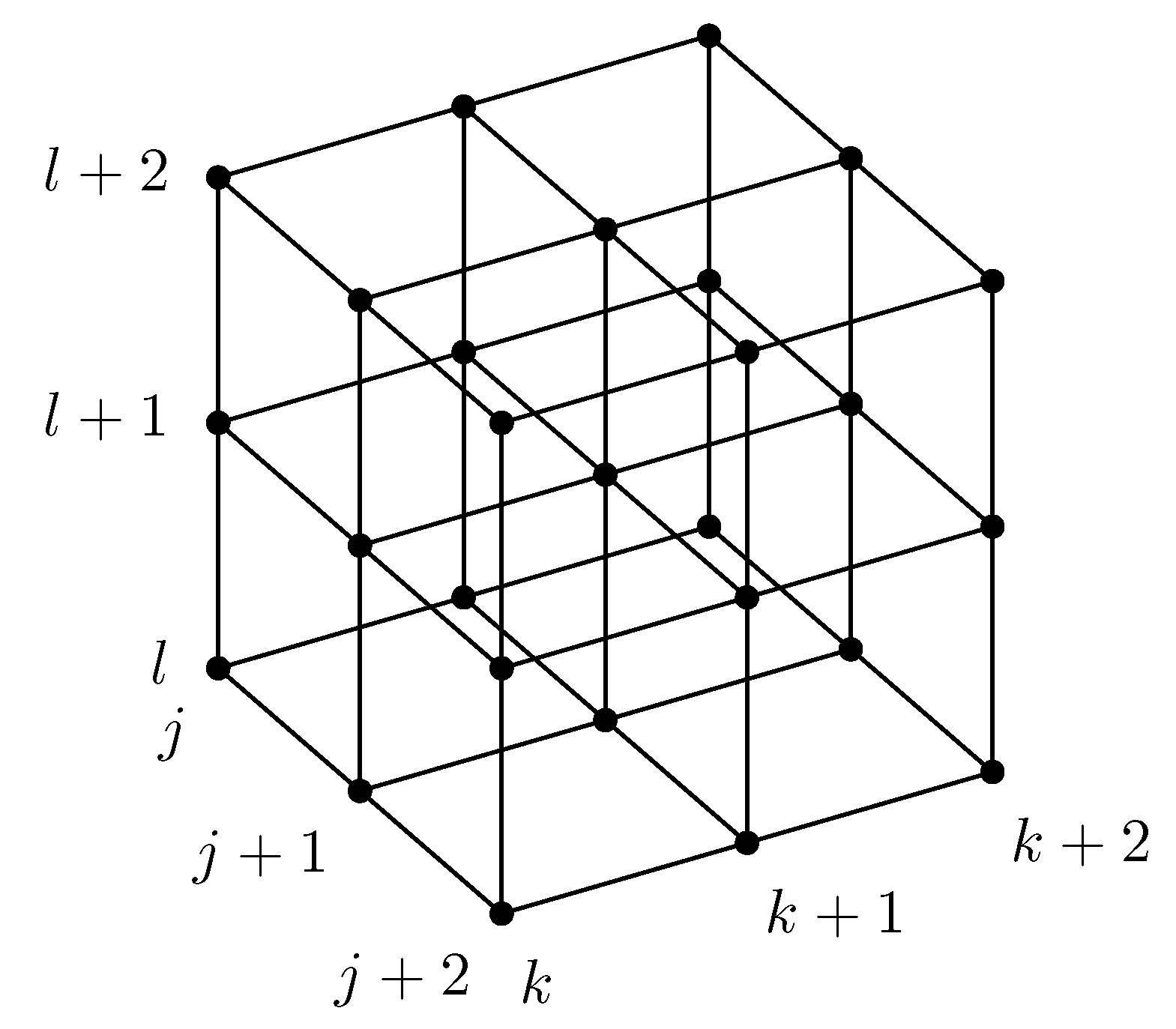
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Gerdt, V.P.; Blinkov, Y.A. Algebraic Construction of a Strongly Consistent, Permutationally Symmetric and Conservative Difference Scheme for 3D Steady Stokes Flow. Symmetry 2019, 11, 269. https://doi.org/10.3390/sym11020269
Zhang X, Gerdt VP, Blinkov YA. Algebraic Construction of a Strongly Consistent, Permutationally Symmetric and Conservative Difference Scheme for 3D Steady Stokes Flow. Symmetry. 2019; 11(2):269. https://doi.org/10.3390/sym11020269
Chicago/Turabian StyleZhang, Xiaojing, Vladimir P. Gerdt, and Yury A. Blinkov. 2019. "Algebraic Construction of a Strongly Consistent, Permutationally Symmetric and Conservative Difference Scheme for 3D Steady Stokes Flow" Symmetry 11, no. 2: 269. https://doi.org/10.3390/sym11020269
APA StyleZhang, X., Gerdt, V. P., & Blinkov, Y. A. (2019). Algebraic Construction of a Strongly Consistent, Permutationally Symmetric and Conservative Difference Scheme for 3D Steady Stokes Flow. Symmetry, 11(2), 269. https://doi.org/10.3390/sym11020269




