A Robust and Automatic Method for the Best Symmetry Plane Detection of Craniofacial Skeletons
Abstract
1. Introduction
2. Related Works
- -
- Cephalometric methods
- -
- Morphometric methods
- -
- ICP-based methods
2.1. Cephalometric Methods
- -
- -
- of best fit passing through a selection of midline landmarks [31].
2.2. Morphometric Methods
2.3. ICP-Based Methods
- -
- -
- -
- the final solution is strictly affected by the initial one;
- -
- the function to be minimized likewise considers all the points of the model, including local defectiveness, such as holes or bony prominences, that should not be considered in the evaluation of symmetry plane of the skull.
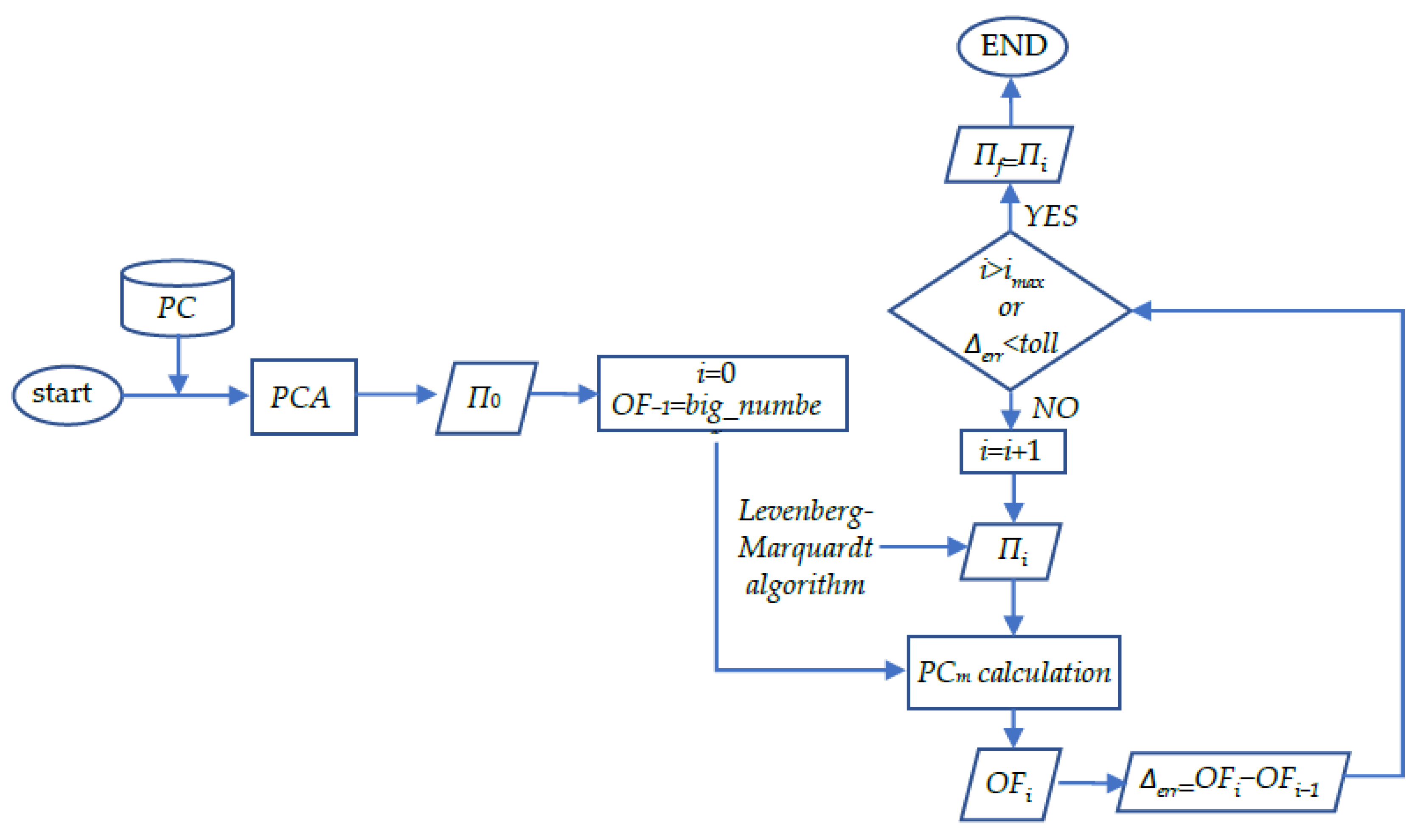
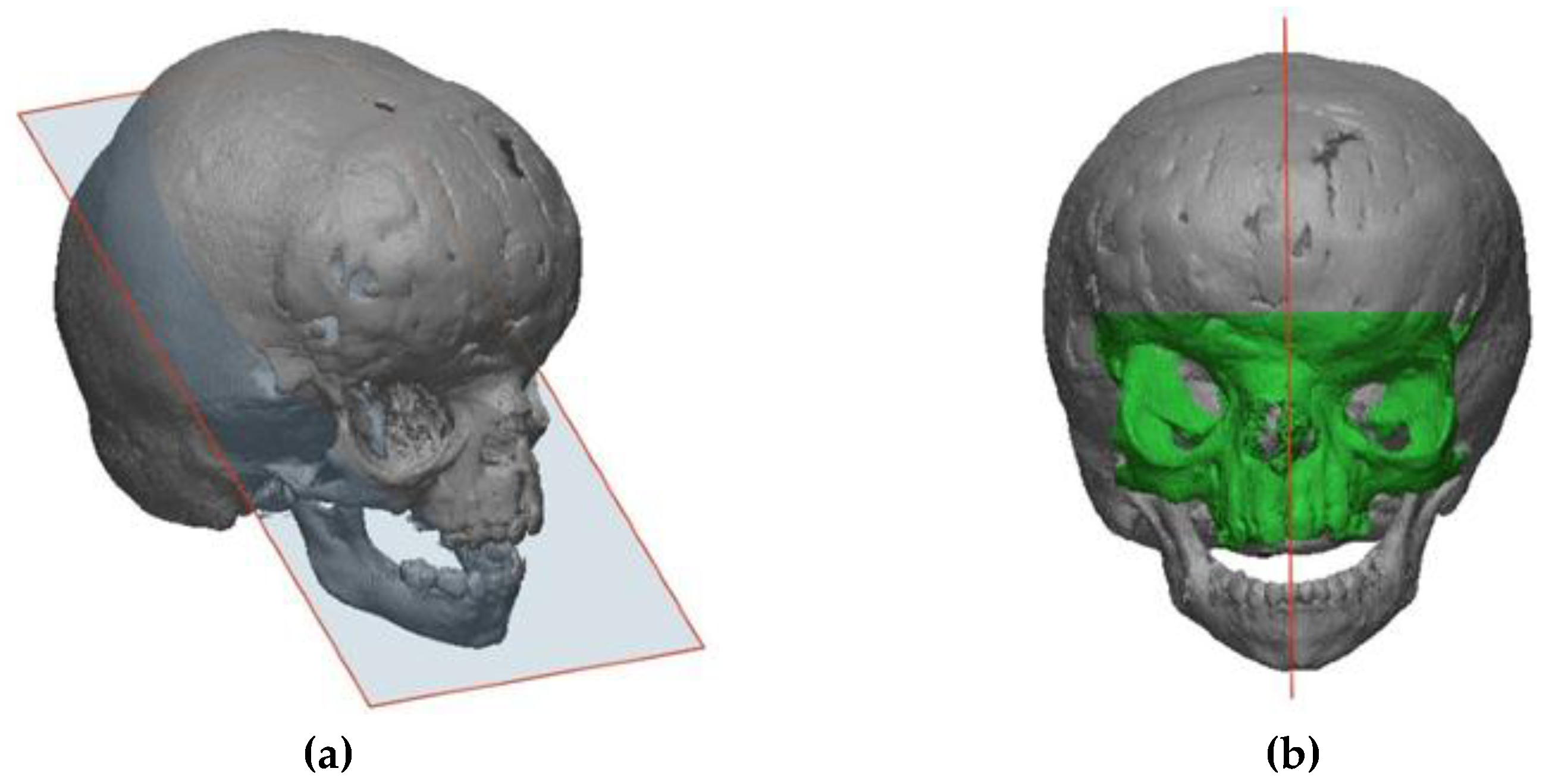
3. The Mirroring and Weighted Approach
3.1. The Published Method
- -
- n is the number of points of the source point cloud (PC);
- -
- pj is the j-th point belonging to PC;
- -
- TS(PCm,i) is the tessellated surface of the mirrored data at i-th iteration (PCm,i);
- -
- dHauss(pj,TS(PCm,i)) is the Hausdorff distance between pj and TS(PCm,i);
- -
- wi,j is the weight associated to pj at i-th iteration.
- -
- di,j is the distance between pj and the symmetry plane Πi (at the i-th iteration).
- -
- σs and σr define, respectively, the distance and the radius values for which the weight is the 36.79% of its maximum value [38].
3.2. Main Limitations and Proposed Improvements
- -
- the acquisition quality is not affected by the distance from the symmetry plane;
- -
- the most symmetrical areas may be those that are farthest from the symmetry plane;
- -
- the weight ws,i,j proves to be not only useless but also negatively affecting the results.
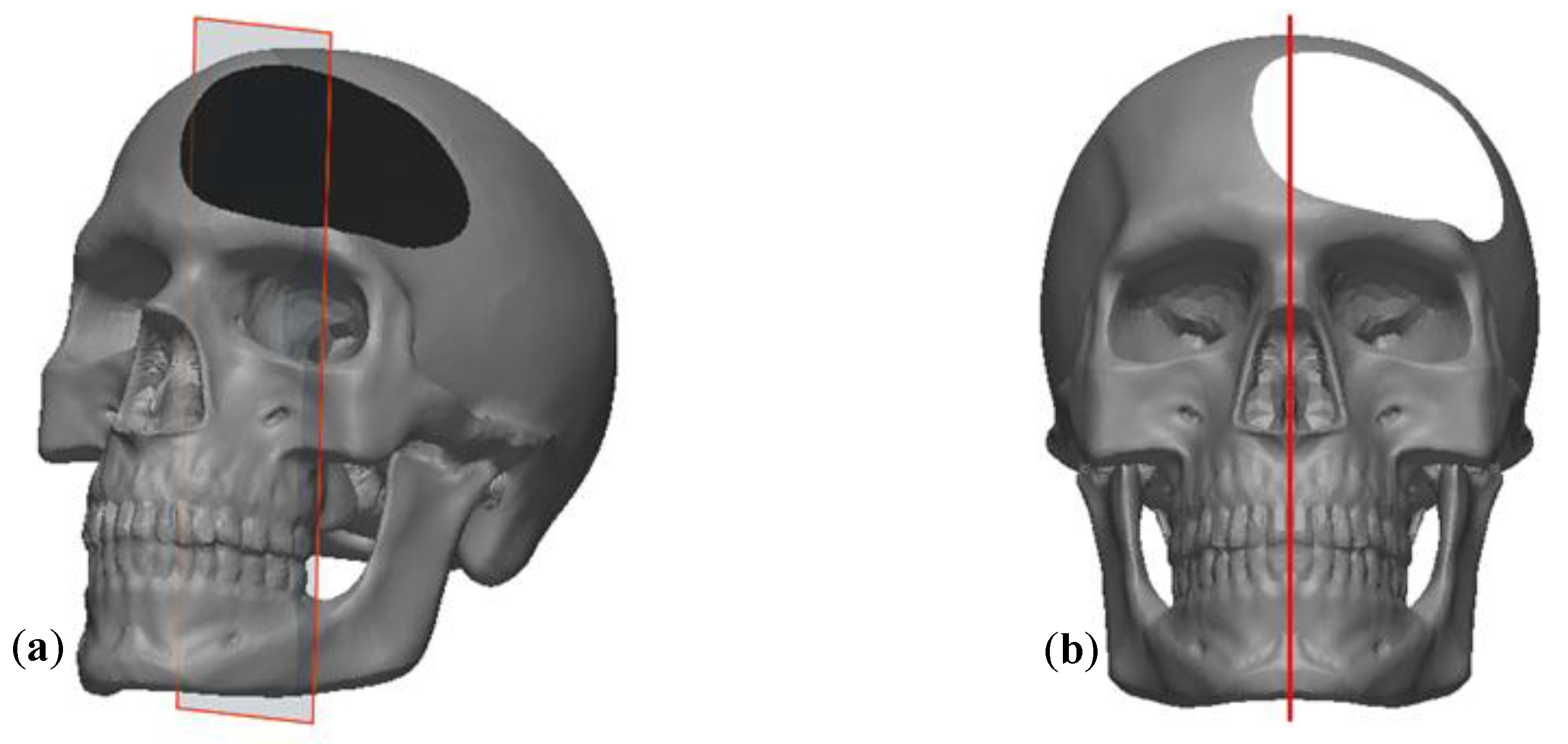
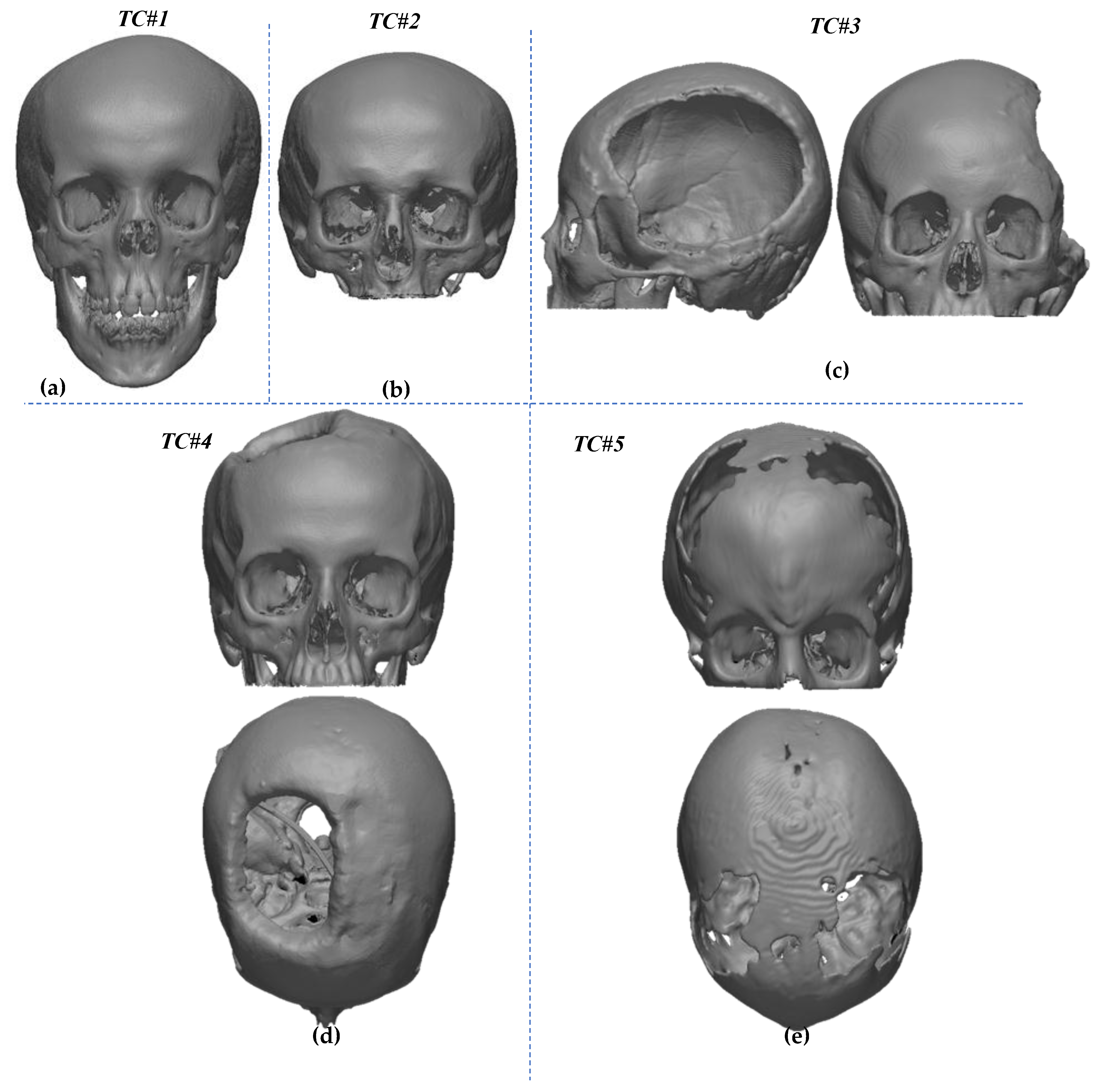
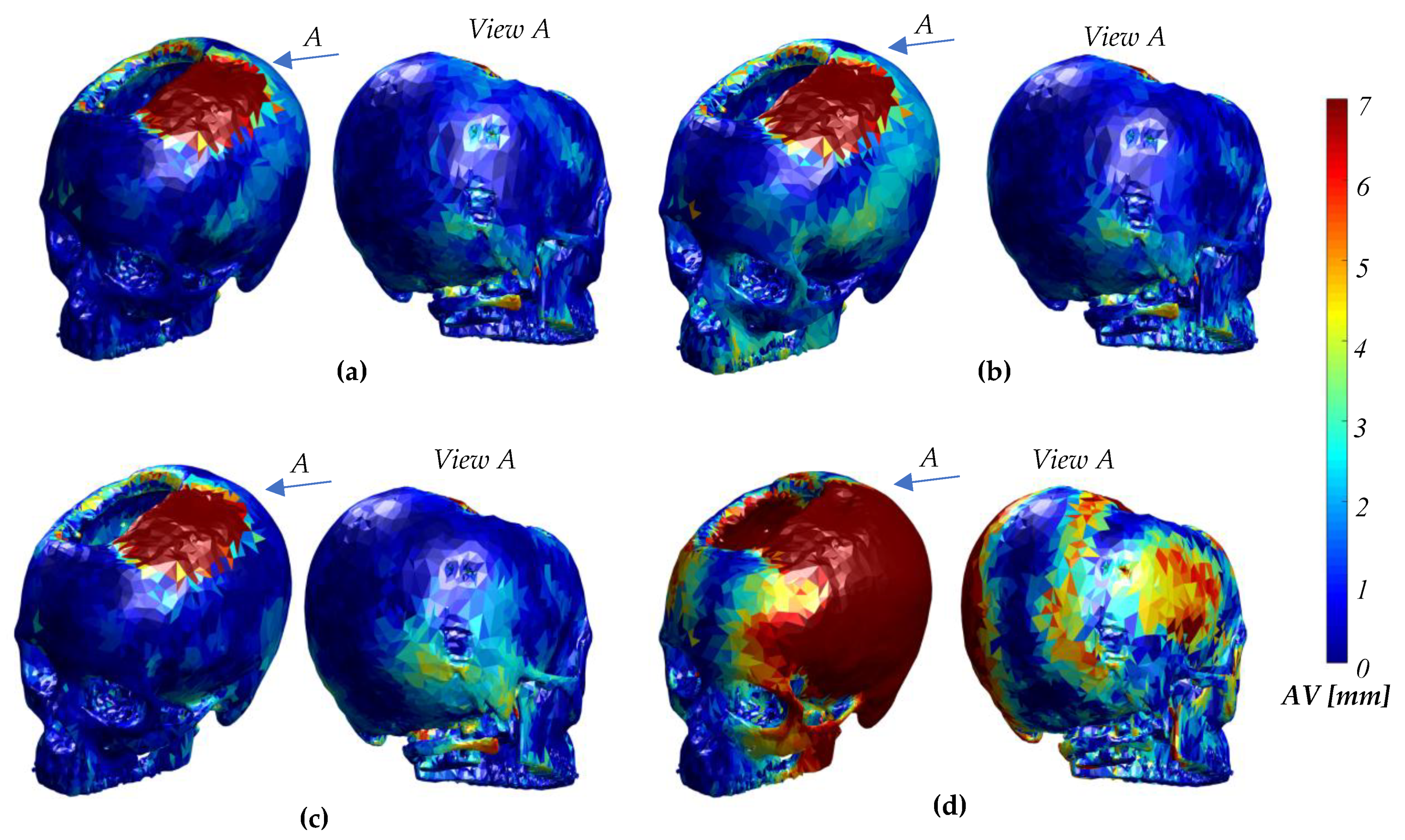
4. Experiments and Results
- -
- TC#1 and TC#2 are two healthy real skulls (Figure 6a,b), to demonstrate the reliability of each method in real cases. For TC#2 an incomplete skull model has been chosen because, commonly, the TC images acquisition addresses only the region of interest to reduce the irradiation risks.
- -
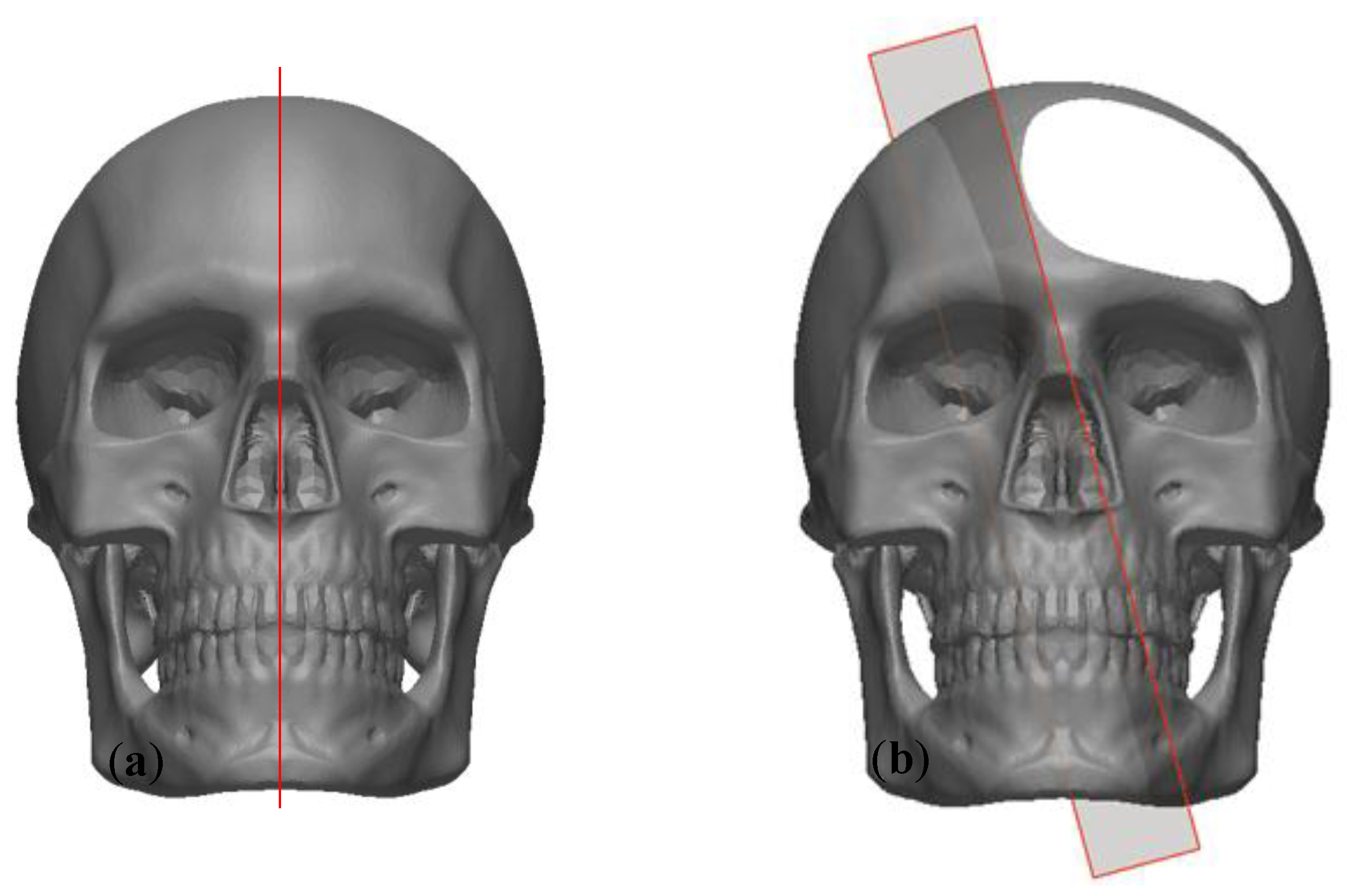
- TC#3, TC#4 and TC#5 are real skulls, each with a large defect (so, large asymmetry) (Figure 6c–e), to demonstrate the reliability and the robustness of the new method compared with the other approaches. These three case studies include one unilateral defect, one bilateral defect and one defect crossing the MSP.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gangestad, S.W.; Thornhill, R.; Yeo, R.A. Facial attractiveness, developmental stability, and fluctuating asymmetry. Ethol. Sociobiol. 1994, 15, 73–85. [Google Scholar] [CrossRef]
- Grammar, K.; Thornhill, R. Human facial attractiveness and sexual selection: The role of averageness and symmetry. J. Comp. Psychol. 1994, 108, 233–242. [Google Scholar] [CrossRef]
- Penton-Voak, I.S.; Jones, B.C.; Little, A.C.; Baker, S.; Tiddeman, B.; Burt, D.M.; Perrett, D.I. Symmetry, sexual dimorphism in facial proportions and male facial attractiveness. Proc. Biol. Sci. 2001, 268, 1617–1623. [Google Scholar] [CrossRef]
- Mealey, L.; Bridgstock, R.; Townsend, G.C. Symmetry and perceived facial attractiveness: A monozygotic co-twin comparison. J. Pers. Soc. Psychol. 1999, 76, 151–158. [Google Scholar] [CrossRef]
- Rhodes, G.; Proffitt, F.; Grady, J.M.; Sumich, A. Facial symmetry and the perception of beauty. Psychon. Bull. Rev. 1998, 5, 659–669. [Google Scholar] [CrossRef]
- Rhodes, G.; Yoshikawa, S.; Clark, A.; Lee, K.; McKay, R.; Akamatsu, S. Attractiveness of facial averageness and symmetry in non-western cultures: In search of biologically based standards of beauty. Perception 2001, 30, 611–625. [Google Scholar] [CrossRef]
- Rhodes, G.; Yoshikawa, S.; Palermo, R.; Simmons, L.W.; Peters, M.; Lee, K.; Halberstadt, J.; Crawford, J.R. Perceived health contributes to the attractiveness of facial symmetry, averageness, and sexual dimorphism. Perception 2007, 36, 1244–1252. [Google Scholar] [CrossRef]
- Rhodes, G.; Zebrowitz, L.A.; Clark, A.; Kalick, S.M.; Hightower, A.; McKay, R. Do facial averageness and symmetry signal health? Evol. Hum. Behav. 2001, 22, 31–46. [Google Scholar] [CrossRef]
- Thornhill, R.; Gangestad, S.W. Human facial beauty: Averageness, symmetry, and parasite resistance. Hum. Nat. 1993, 4, 237–269. [Google Scholar] [CrossRef]
- Apthorp, D.; Bell, J. Symmetry is less than meets the eye. Curr. Biol. 2015, 25, 267–268. [Google Scholar] [CrossRef] [PubMed]
- Perrett, D.I.; May, K.A.; Yoshikawa, S. Facial shape and judgments of female attractiveness. Nature 1994, 368, 239–242. [Google Scholar] [CrossRef]
- Cheney, E.A. Dentofacial asymmetries and their clinical significance. Am. J. Orthod. 1961, 47, 814–829. [Google Scholar] [CrossRef]
- Pirttiniemi, P.; Kantomaa, T.; Lahtela, P. Relationship between craniofacial and condyle path asymmetry in unilateral cross-bite patients. Eur. J. Orthod. 1990, 12, 408–413. [Google Scholar] [CrossRef]
- Meyer-Marcotty, P.; Alpers, G.W.; Gerdes, A.B.M.; Stellzig-Eisenhauer, A. Impact of facial asymmetry in visual perception: A 3-dimensional data analysis. Am. J. Orthod. Dentofac. Orthop. 2010, 137, 168.e1–168.e8. [Google Scholar] [CrossRef]
- Swennen, G.R.; Mollemans, W.; Schutyser, F. Three-dimensional treatment planning of orthognathic surgery in the era of virtual imaging. J. Oral Maxillofac. Surg. 2009, 67, 2080–2092. [Google Scholar] [CrossRef]
- Proffit, W.R.; Turvey, T.A. Dentofacial asymmetry. In Surgical Orthodontic Treatment; Proffit, W.R., White, R.P., Jr., Eds.; Mosby Inc.: Maryland Heights, MO, USA, 1991; pp. 483–549. [Google Scholar]
- Hwang, H.S.; Hwang, C.H.; Lee, K.H.; Kang, B.C. Maxillofacial 3-dimensional image analysis for the diagnosis of facial asymmetry. Am. J. Orthod. Dentofac. Orthop. 2006, 130, 779–785. [Google Scholar] [CrossRef]
- Yàñez-Vico, R.M.; Iglesias-Linares, A.; Torres-Lagares, D.; Gurierrez-Perez, J.L.; Solano-Reina, E. Three-dimensional evaluation of craniofacial asymmetry: An analysis using computed tomography. Clin. Oral Investig. 2010, 15, 729–736. [Google Scholar] [CrossRef]
- Tuncer, B.B.; Atac, M.S.; Yuksel, S. A case report comparing 3-D evaluation in the diagnosis and treatment planning of hemimandibular hyperplasia with conventional radiography. J. Craniomaxillofac. Surg. 2009, 37, 312–319. [Google Scholar] [CrossRef]
- Baek, S.H.; Cho, I.S.; Chang, Y.I.; Kim, M.J. Skeletodental factors affecting chin point deviation in female patients with class III malocclusion and facial asymmetry: A three-dimensional analysis using computed tomography. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. Endod. 2007, 104, 628–639. [Google Scholar] [CrossRef]
- Kwon, T.G.; Park, H.S.; Ryoo, H.M.; Lee, S.H. A comparison of craniofacial morphology in patients with and without facial asymmetry—A three-dimensional analysis with computed tomography. Int. J. Oral Maxillofa. Surg. 2006, 5, 43–48. [Google Scholar] [CrossRef]
- Buonamici, F.; Furferi, R.; Genitori, L.; Governi, L.; Marzola, A.; Mussa, F.; Volpe, Y. Reverse engineering techniques for virtual reconstruction of defective skulls: An overview of existing approaches. Comput-Aided Des. Appl. 2018, 16, 103–112. [Google Scholar] [CrossRef]
- Willing, R.T.; Roumeliotis, G.; Jenkyn, T.R.; Yazdani, A. Development and evaluation of a semi-automatic technique for determining the bilateral symmetry plane of the facial skeleton. Med. Eng. Phys. 2013, 35, 1843–1849. [Google Scholar] [CrossRef]
- Damstra, J.; Fourie, Z.; De Wit, M.; Ren, Y. A three-dimensional comparison of a morphometric and conventional cephalometric midsagittal planes for craniofacial asymmetry. Clin. Oral Investig. 2012, 16, 285–294. [Google Scholar] [CrossRef]
- De Momi, E.; Chapuis, J.; Pappas, I.; Ferrigno, G.; Hallermann, W.; Schramm, A.; Caversaccio, M. Automatic extraction of the mid-facial plane for cranio-maxillofacial surgery planning. Int. J. Oral Maxillofac. Surg. 2006, 35, 636–642. [Google Scholar] [CrossRef]
- Zhang, L.; Razdan, A.; Farin, G.; Femiani, J.; Bae, M.; Lockwood, C. 3D face authentication and recognition based on bilateral symmetry analysis. Vis. Comput. 2006, 22, 43–55. [Google Scholar] [CrossRef]
- Bartalucci, C.; Furferi, R.; Governi, L.; Volpe, Y. A Survey of Methods for Symmetry Detection on 3D High Point Density Models in Biomedicine. Symmetry 2018, 10, 263. [Google Scholar] [CrossRef]
- Di Angelo, L.; Di Stefano, P. A Computational Method for Bilateral Symmetry Recognition in Asymmetrically Scanned Human Faces. Comput-Aided Des. Appl. 2014, 11, 275–283. [Google Scholar] [CrossRef]
- Gupta, A.; Kharbanda, O.P.; Balachandran, R.; Sardana, V.; Kalra, S.; Chaurasia, S.; Sardana, H.K. Precision of manual landmark identification between as-received and oriented volume-rendered cone-beam computed tomography images. Am. J. Orthod. Dentofac. Orthop. 2017, 151, 118–131. [Google Scholar] [CrossRef]
- Kim, T.Y.; Baik, J.S.; Park, J.Y.; Chae, H.S.; Huh, K.H.; Choi, S.C. Determination of midsagittal plane for evaluation of facial asymmetry using three-dimensional computed tomography. Imaging Sci. Dent. 2011, 41, 79–84. [Google Scholar] [CrossRef]
- Green, M.N.; Bloom, J.M.; Kulbersh, R. A simple and accurate craniofacial midsagittal plane definition. Am. J. Orthod. Dentofac. Orthop. 2017, 152, 355–363. [Google Scholar] [CrossRef]
- Cavalcanti, M.G.; Vannier, M.W. Quantitative analysis of spiral computed tomography for craniofacial clinical applications. Dentomaxillofac. Radiol. 1998, 27, 344–350. [Google Scholar] [CrossRef]
- Gupta, A.; Kharbanda, O.P.; Sardana, V.; Balachandran, R.; Sardana, H.K. A knowledge-based algorithm for automatic detection of cephalometric landmarks on CBCT images. Int. J. Comput. Assisted Radiol. Surg. 2015, 10, 1737–1752. [Google Scholar] [CrossRef]
- Yoon, K.W.; Yoon, S.J.; Kang, B.C.; Kim, Y.H.; Kook, M.S.; Lee, J.S.; Palomo, J.M. Deviation of landmarks in accordance with methods of establishing reference planes in three-dimensional facial CT evaluation. Imaging Sci. Dent. 2014, 44, 207–212. [Google Scholar] [CrossRef]
- Pan, G.; Wu, Z. 3D face recognition from range data. Int. J. Image Graph. 2005, 5, 573–593. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A Method for Registration of 3-D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Leclerc, Y.G. Constructing simple stable descriptions for image partitioning. Int. J. Comput. Vis. 1989, 3, 73–102. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks (ICNN), Perth, Australia, 27 November–1 December 1995. [Google Scholar] [CrossRef]
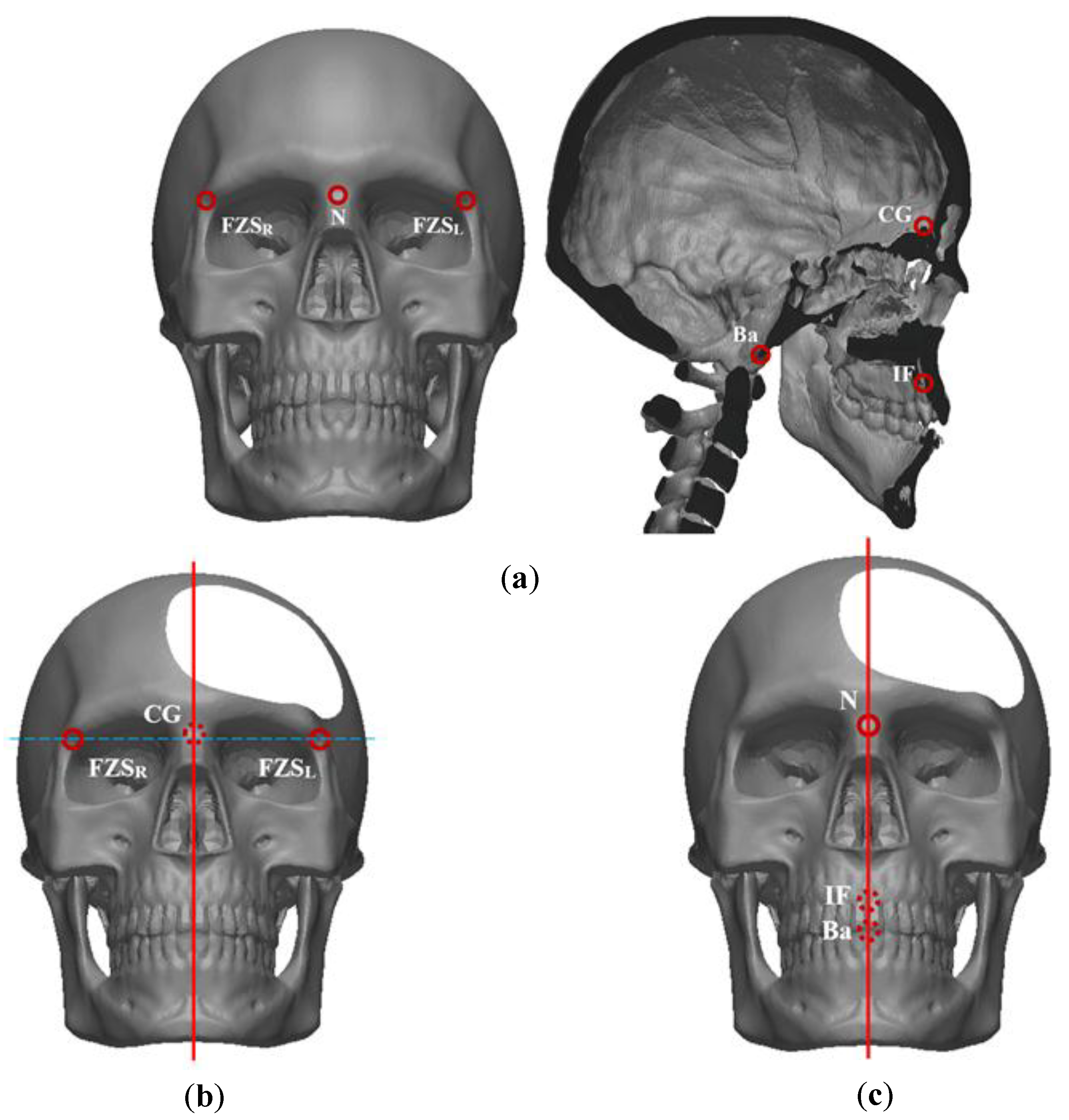
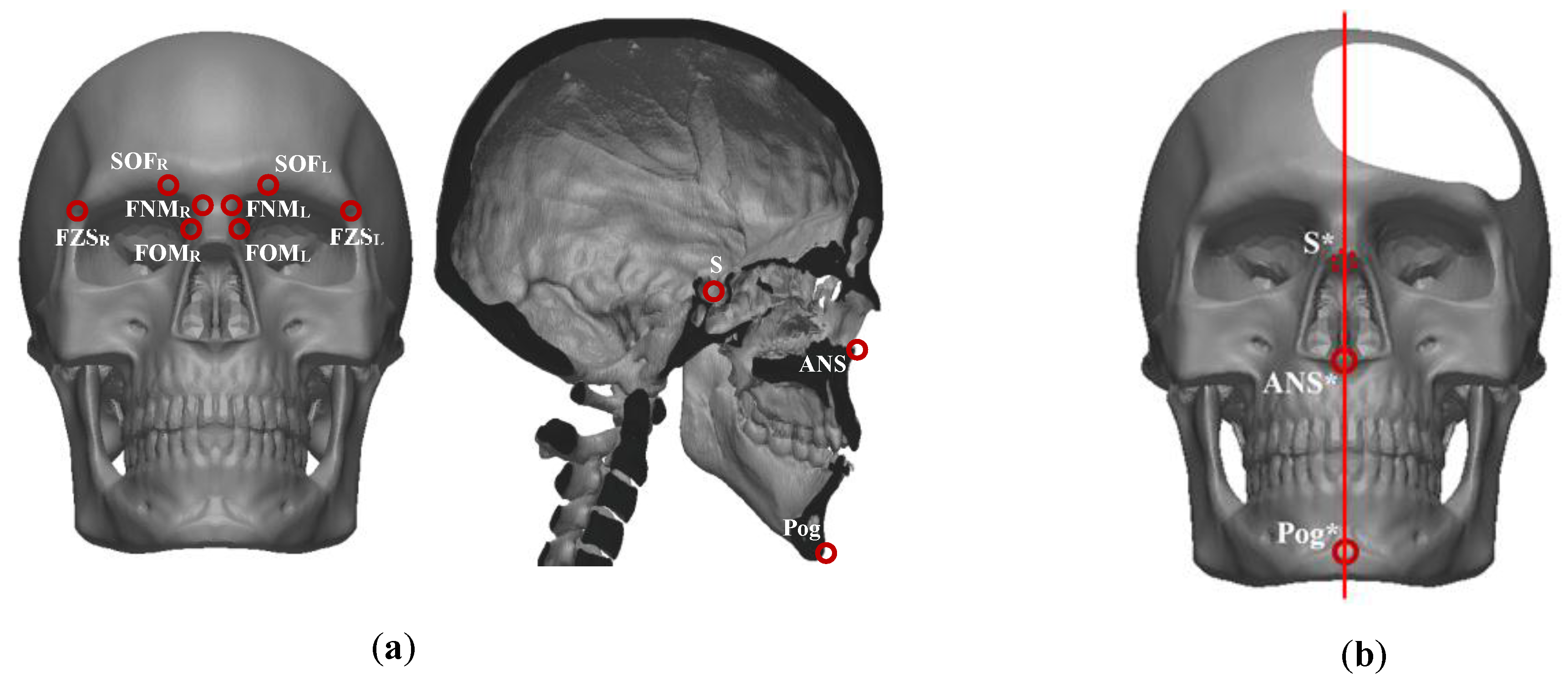
| Landmark | Abbr | Definition |
|---|---|---|
| Basion | Ba | The most anterior point on the margin of the foramen magnum in the mid-sagittal plane |
| Nasion | N | Most anterior point of the frontonasal suture in the mid-sagittal plane |
| Crista Galli | CG | Most superior point of the Crista Galli |
| Incisive Foramen | IF | The midpoint of the Incisive Foramen |
| Frontozygomatic Suture | FZS | The most medial and anterior point of left (FZSL) or right (FZSR) frontozygomatic suture at the level of the lateral orbital rim |
| Supraorbital Foramen | SOF | The midpoint of supraorbital foramen |
| Fontorbitomaxillare | FOM | Lateral point of the frontomaxillary suture on the medial margin of the orbit |
| Frontonasomaxillare | FNM | The intersection of the nasomaxillary, frontomaxillary, and frontonasal sutures |
| Sella | S | Center of the sella turcica |
| Pogonion | Pog | Most anterior point of the bony chin in the median plane |
| Anterior Nasal Spine | ANS | Most anterior point midpoint of the anterior nasal spine of the maxilla |
| Test Cases | MWR-Method | Mpm-Method | Cplm1-Method | CPLM2-METHOD |
|---|---|---|---|---|
| TC#1 | 0.95 | 1.02 | 0.98 | 0.97 |
| TC#2 | 0.66 | 1.09 | 0.72 | 0.73 |
| TC#3 | 0.78 | 0.88 | 1.01 | 1.01 |
| TC#4 | 0.76 | 0.88 | 0.80 | 1.48 |
| TC#5 | 1.30 | 1.56 | 1.59 | -- |
| Test Cases | MWR-Method | Mpm-Method | Cplm1-Method | Cplm2-Method |
|---|---|---|---|---|
| TC#1 | 0.95 | 1.02 | 0.98 | 0.97 |
| TC#2 | 0.66 | 1.09 | 0.72 | 0.73 |
| TC#3 | 0.78 | 0.88 | 1.01 | 1.01 |
| TC#4 | 0.76 | 0.88 | 0.80 | 1.48 |
| TC#5 | 1.30 | 1.56 | 1.59 | -- |
| TC#6 | 1.11 | 1.33 | 1.43 | 1.21 |
| TC#7 | 0.75 | 0.81 | 0.88 | 1.24 |
| TC#8 | 0.63 | 0.72 | 0.76 | 0.75 |
| TC#9 | 0.65 | 0.80 | 0.75 | 0.76 |
| TC#10 | 1.02 | 1.13 | 1.18 | 1.27 |
| TC#11 | 1.26 | 1.52 | 1.38 | 1.55 |
| TC#12 | 0.87 | 1.24 | 1.25 | 1.20 |
| TC#13 | 1.04 | 1.11 | 1.42 | 1.39 |
| TC#14 | 0.76 | 0.84 | 0.86 | 1.10 |
| TC#15 | 0.89 | 1.07 | 1.21 | 1.20 |
| TC#16 | 0.69 | 0.92 | 0.90 | 0.98 |
| TC#17 | 1.18 | 1.40 | 1.24 | 1.37 |
| TC#18 | 0.70 | 0.85 | 0.97 | 0.92 |
| TC#19 | 1.23 | 1.39 | 1.56 | 1.55 |
| TC#20 | 0.84 | 1.09 | 0.93 | 0.92 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Angelo, L.; Di Stefano, P.; Governi, L.; Marzola, A.; Volpe, Y. A Robust and Automatic Method for the Best Symmetry Plane Detection of Craniofacial Skeletons. Symmetry 2019, 11, 245. https://doi.org/10.3390/sym11020245
Di Angelo L, Di Stefano P, Governi L, Marzola A, Volpe Y. A Robust and Automatic Method for the Best Symmetry Plane Detection of Craniofacial Skeletons. Symmetry. 2019; 11(2):245. https://doi.org/10.3390/sym11020245
Chicago/Turabian StyleDi Angelo, Luca, Paolo Di Stefano, Lapo Governi, Antonio Marzola, and Yary Volpe. 2019. "A Robust and Automatic Method for the Best Symmetry Plane Detection of Craniofacial Skeletons" Symmetry 11, no. 2: 245. https://doi.org/10.3390/sym11020245
APA StyleDi Angelo, L., Di Stefano, P., Governi, L., Marzola, A., & Volpe, Y. (2019). A Robust and Automatic Method for the Best Symmetry Plane Detection of Craniofacial Skeletons. Symmetry, 11(2), 245. https://doi.org/10.3390/sym11020245







