An Analytical Numerical Method for Solving Fuzzy Fractional Volterra Integro-Differential Equations
Abstract
:1. Introduction
2. Overview of Fuzzy Calculus and Fuzzy Fractional Calculus
- is fuzzy convex, that is,for all,
- is normal, that is,for which.
- is upper-semi continuous, that is,for any
- is the support of, andis compact, wheredenotes the closure of a subset.
- is a bounded non-decreasing left continuous for each, and right continuous at.
- is a bounded non-increasing left continuous for eachand right continuous at.
- , for each.
- The H-differencesexist, for eachsufficiently tends to 0 and
- The H-differencesexist, for eachsufficiently tends to 0 and.
- Ifis (1)-differentiable on, thenandare two differentiable functions on, and
- Ifis (2)-differentiable on, thenandare two differentiable functions on, and
3. Formulation of Fuzzy Fractional Volterra IDEs
- Step 1: Solve the system (4) and (5) for and .
- Step 2: Ensure that and are valid level sets on or on a partial interval in.
- Step 3: Construct a -differentiable solution whose -cut representation is .
- Step 1: Solve the system (6) and (7) for and .
- Step 2: Ensure that and are valid level sets on or on a partial interval in.
- Step 3: Construct a -differentiable solution whose -cut representation is .
4. Description of the FRPS Technique
5. Applications and Simulations
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Zhang, H.; Liao, X.; Yu, J. Fuzzy modeling and synchronization of hyperchaotic systems. Chaos Solitons Fractals 2005, 26, 835–843. [Google Scholar] [CrossRef]
- El Naschie, M.S. From experimental quantum optics to quantum gravity via a fuzzy Kähler manifold. Chaos Solitons Fractals 2005, 25, 969–977. [Google Scholar] [CrossRef]
- Diamond, P. Time-dependent differential inclusions, cocycle attractors and fuzzy differential equations. IEEE Trans. Fuzzy Syst. 1999, 7, 734–740. [Google Scholar] [CrossRef]
- Feng, G.; Chen, G. Adaptive control of discrete time chaotic systems: a fuzzy control approach. Chaos Solitons Fractals 2005, 23, 459–467. [Google Scholar] [CrossRef]
- Priyadharsini, S.; Parthiban, V.; Manivannan, A. Solution of fractional integro-differential system with fuzzy initial condition. Int. J. Pure Appl. Math. 2016, 106, 107–112. [Google Scholar]
- Shabestari, M.R.; Ezzati, R.; Allahviranloo, T. Numerical solution of fuzzy fractional integro-differential equation via two-dimensional Legendre wavelet method. J. Intell. Fuzzy Syst. 2018, 34, 2453–2465. [Google Scholar] [CrossRef]
- Padmapriya, V.; Kaliyappan, M.; Parthiban, V. Solution of Fuzzy Fractional Integro-Differential Equations Using A Domian Decomposition Method. J. Inform. Math. Sci. 2017, 9, 501–507. [Google Scholar]
- Matinfar, M.; Ghanbari, M.; Nuraei, R. Numerical solution of linear fuzzy Volterra integro-differential equations by variational iteration method. J. Intell. Fuzzy Syst. 2013, 24, 575–586. [Google Scholar]
- Gumah, G.; Moaddy, K.; Al-Smadi, M.; Hashim, I. Solutions to uncertain Volterra integral equations by fitted reproducing kernel Hilbert space method. J. Funct. Spaces 2016, 2016, 2920463. [Google Scholar] [CrossRef]
- Alikhani, R.; Bahrami, F. Global solutions for nonlinear fuzzy fractional integral and integrodifferential equations. Commun. Nonlinear Sci. Numer. Siml. 2013, 18, 2007–2017. [Google Scholar] [CrossRef]
- Saadeh, R.; Al-Smadi, M.; Gumah, G.; Khalil, H.; Khan, R.A. Numerical Investigation for Solving Two-Point Fuzzy Boundary Value Problems by Reproducing Kernel Approach. Appl. Math. Inf. Sci. 2016, 10, 1–13. [Google Scholar] [CrossRef]
- Gumah, G.N.; Naser, M.F.M.; Al-Smadi, M.; Al-Omari, S.K. Application of reproducing kernel Hilbert space method for solving second-order fuzzy Volterra integro-differential equations. Adv. Diff. Equ. 2018, 2018, 475. [Google Scholar] [CrossRef]
- Salahshour, S.; Allahviranloo, T.; Abbasbandy, S. Solving fuzzy fractional differential equations by fuzzy Laplace transforms. Commun. Nonlinear Sci. Numer. Siml. 2012, 17, 1372–1381. [Google Scholar] [CrossRef]
- Abu Arqub, O.; Momani, S.; Al-Mezel, S.; Kutbi, M. Existence, uniqueness, and characterization theorems for nonlinear fuzzy integrodifferential equations of Volterra type. Math. Probl. Eng. 2015, 2015, 835891. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Abu Arqub, O. Computational algorithm for solving fredholm time-fractional partial integrodifferential equations of dirichlet functions type with error estimates. Appl. Math. Comput. 2019, 342, 280–294. [Google Scholar] [CrossRef]
- Abu Arqub, O.; Odibat, Z.; Al-Smadi, M. Numerical solutions of time-fractional partial integrodifferential equations of Robin functions types in Hilbert space with error bounds and error estimates. Nonlinear Dyn. 2018, 94, 1819–1834. [Google Scholar] [CrossRef]
- Abu Arqub, O.; Al-Smadi, M. Numerical algorithm for solving time-fractional partial integrodifferential equations subject to initial and Dirichlet boundary conditions. Num. Methods Partial Diff. Equ. 2018, 34, 1577–1597. [Google Scholar] [CrossRef]
- Abu Arqub, O.; Al-Smadi, M. Numerical algorithm for solving two-point, second-order periodic boundary value problems for mixed integro-differential equations. Appl. Math. Comput. 2014, 243, 911–922. [Google Scholar] [CrossRef]
- Abu Arqub, O. Series solution of fuzzy differential equations under strongly generalized differentiability. J. Adv. Res. Appl. Math. 2013, 5, 31–52. [Google Scholar] [CrossRef]
- Moaddy, K.; Al-Smadi, M.; Hashim, I. A novel representation of the exact solution for differential algebraic equations system using residual power-series method. Discrete Dyn. Nat. Soc. 2015, 2015, 205207. [Google Scholar] [CrossRef]
- El-Ajou, A.; Abu Arqub, O.; Momani, S.; Baleanu, D.; Alsaedi, A. A novel expansion iterative method for solving linear partial differential equations of fractional order. Int. J. Appl. Math. Comput. 2015, 257, 119–133. [Google Scholar] [CrossRef]
- Elajou, A.; Abu Arqub, O.; Zhour, Z.A. New Results on Fractional Power Series: Theory and Applications. Entropy 2013, 12, 5305–5323. [Google Scholar] [CrossRef]
- Komashynska, I.; Al-Smadi, M.; Abu Arqub, O.; Momani, S. An efficient analytical method for solving singular initial value problems of nonlinear systems. Appl. Math. Inf. Sci. 2016, 10, 647–656. [Google Scholar] [CrossRef]
- Komashynska, I.; Al-Smadi, M.; Ateiwi, A.; Al-Obaidy, S. Approximate analytical solution by residual power series method for system of Fredholm integral equations. Appl. Math. Inf. Sci. 2016, 10, 1–11. [Google Scholar] [CrossRef]
- El-Ajou, A.; Abu Arqub, O.; Al-Smadi, M. A general form of the generalized Taylor’s formula with some applications. Appl. Math. Comput. 2015, 256, 851–859. [Google Scholar] [CrossRef]
- Alaroud, M.; Al-Smadi, M.; Ahmad, R.R.; Din, S.K.U. Computational optimization of residual power series algorithm for certain classes of fuzzy fractional differential equations. Int. J. Differ. Equ. 2018, 2018, 8686502. [Google Scholar] [CrossRef]
- Moaddy, K.; Al-Smadi, M.; Abu Arqub, O.; Hashim, I. Analytic-numeric treatment for handling system of second-order, three-point BVPs. In Proceedings of the AIP Conference, Seoul, Korea, 23–27 May 2017; Volume 1830, p. 020025. [Google Scholar]
- Kaleva, O. Fuzzy differential equations. Fuzzy Sets Syst. 1987, 24, 301–317. [Google Scholar] [CrossRef]
- Goetschel, J.R.; Voxman, W. Elementary fuzzy calculus. Fuzzy Sets Syst. 1986, 18, 31–43. [Google Scholar] [CrossRef]
- Puri, M.L.; Ralescu, D.A. Differentials of fuzzy functions. J. Math. Anal. Appl. 1983, 91, 552–558. [Google Scholar] [CrossRef]
- Bede, B.; Gal, S.G. Generalizations of the differentiability of fuzzy-number-valued functions with applications to fuzzy differential equations. Fuzzy Sets Syst. 2005, 151, 581–599. [Google Scholar] [CrossRef]
- Moaddy, K.; Freihat, A.; Al-Smadi, M.; Abuteen, E.; Hashim, I. Numerical investigation for handling fractional-order Rabinovich–Fabrikant model using the multistep approach. Soft Comput. 2018, 22, 773–782. [Google Scholar] [CrossRef]
- Chalco-Cano, Y.; Roman-Flores, H. On new solutions of fuzzy differential equations. Chaos Solitons Fractals 2008, 38, 112–119. [Google Scholar] [CrossRef]
- Salahshour, S.; Allahviranloo, T.; Abbasbandy, S.; Baleanu, D. Existence and uniqueness results for fractional differential equations with uncertainty. Adv. Differ. Equ. 2012, 1, 112. [Google Scholar] [CrossRef]
- Ali, M.R. Approximate solutions for fuzzy Volterra integrodifferential equations. J. Abst. Comput. Math. 2018, 3, 11–22. [Google Scholar]
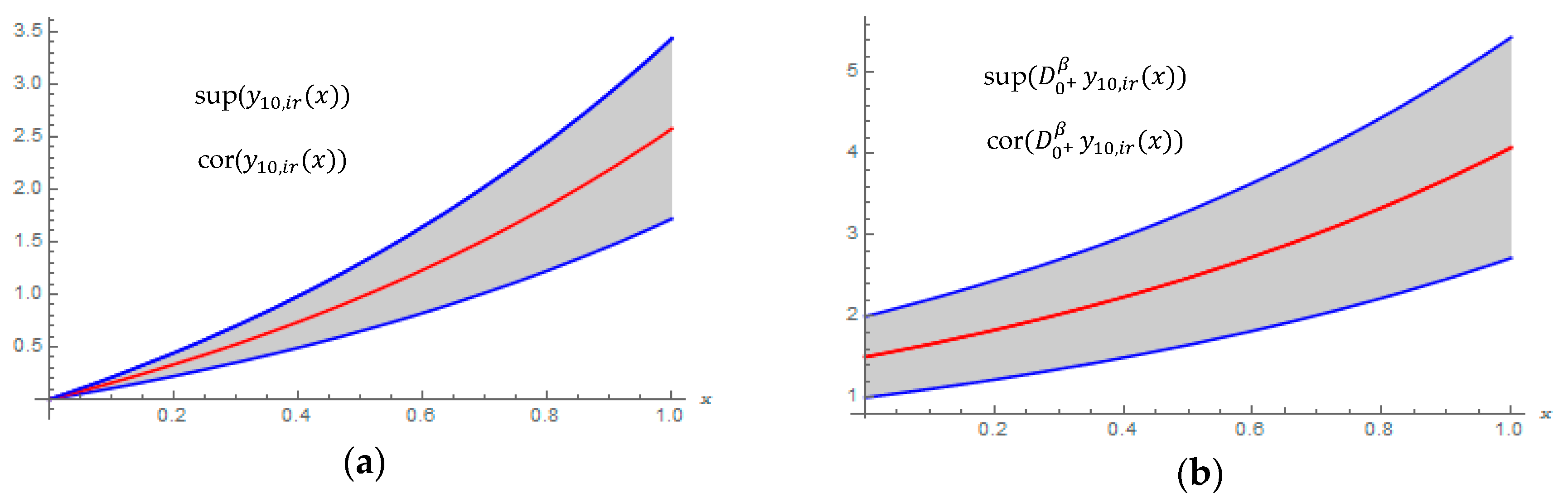
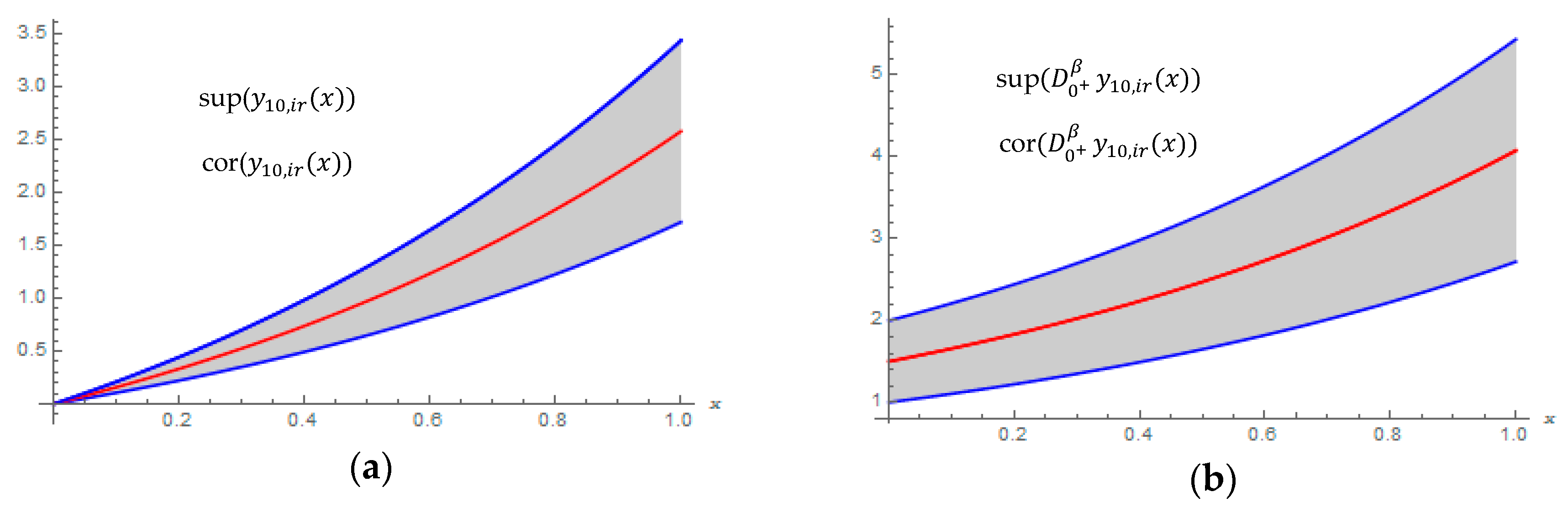
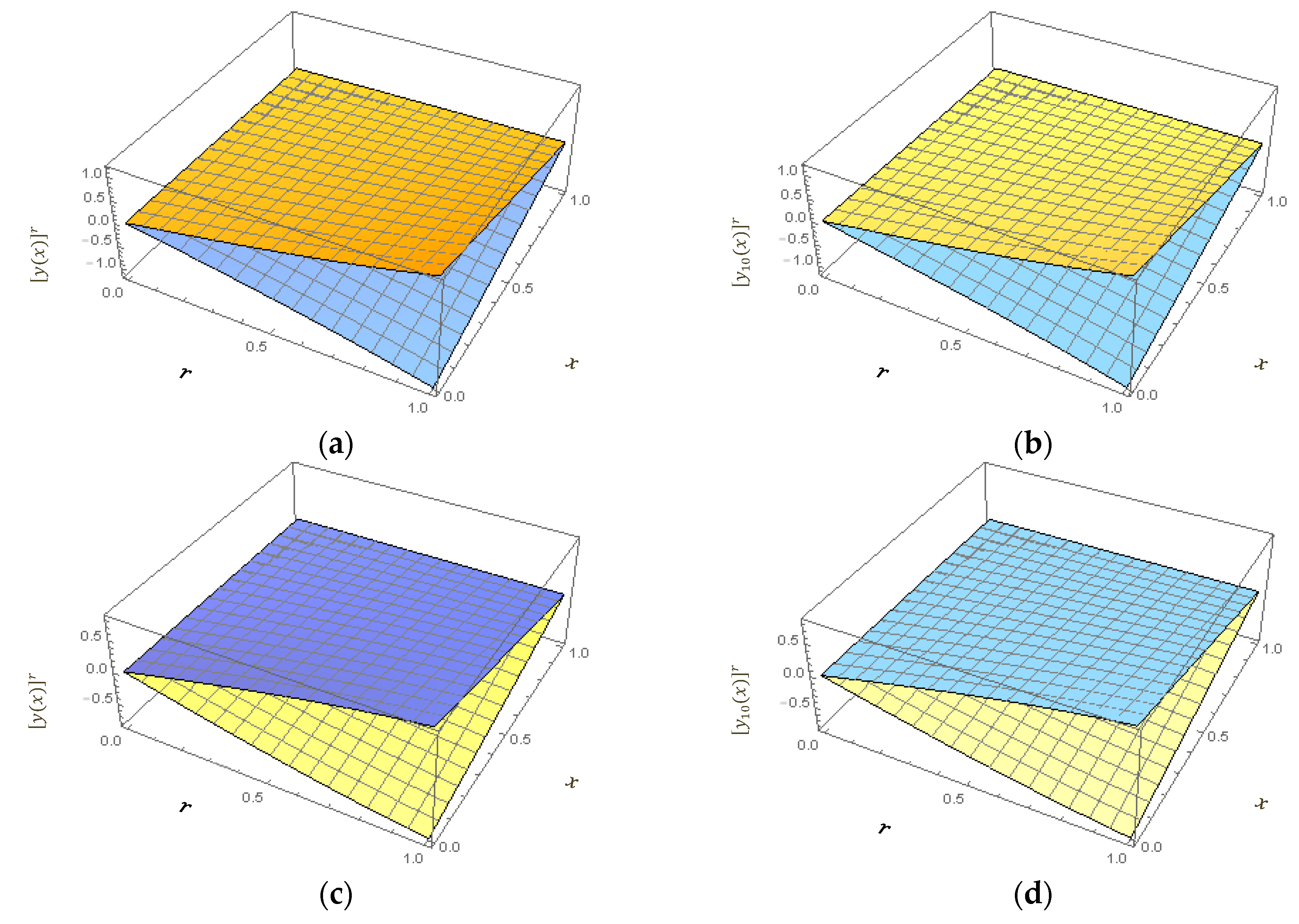
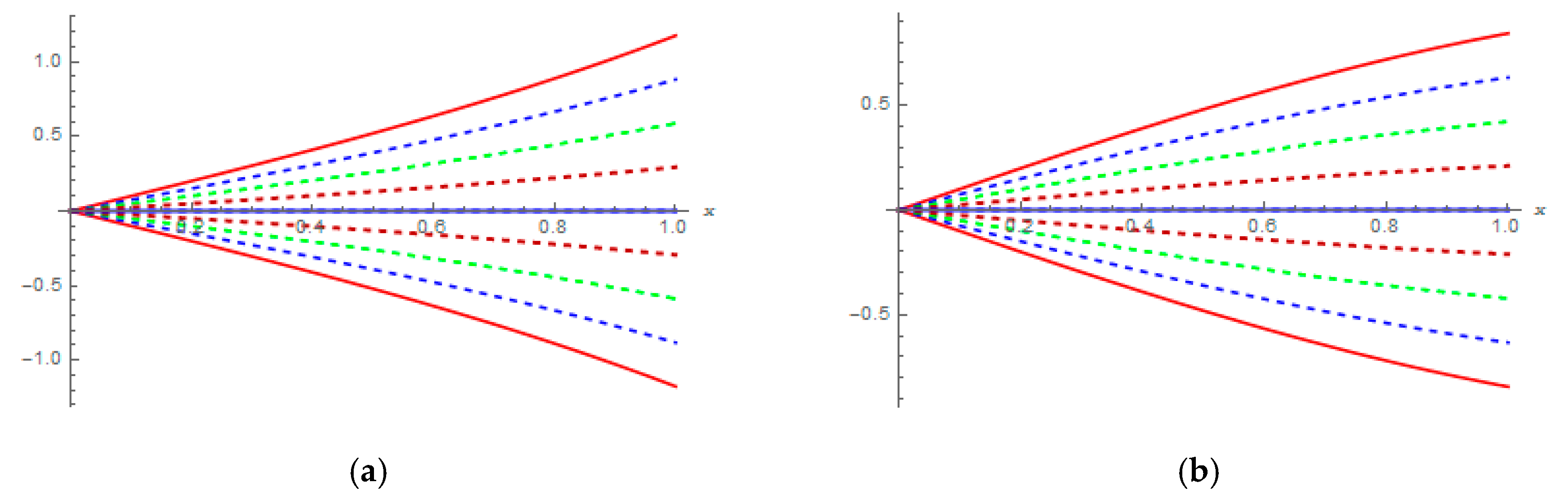
| 7th-FRPS Approximated Solutions | |
|---|---|
| 7th-FRPS Approximated Solutions | |
|---|---|
| FRPS Method | HW Method | |
| FRPS Method | HW Method | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alaroud, M.; Al-Smadi, M.; Rozita Ahmad, R.; Salma Din, U.K. An Analytical Numerical Method for Solving Fuzzy Fractional Volterra Integro-Differential Equations. Symmetry 2019, 11, 205. https://doi.org/10.3390/sym11020205
Alaroud M, Al-Smadi M, Rozita Ahmad R, Salma Din UK. An Analytical Numerical Method for Solving Fuzzy Fractional Volterra Integro-Differential Equations. Symmetry. 2019; 11(2):205. https://doi.org/10.3390/sym11020205
Chicago/Turabian StyleAlaroud, Mohammad, Mohammed Al-Smadi, Rokiah Rozita Ahmad, and Ummul Khair Salma Din. 2019. "An Analytical Numerical Method for Solving Fuzzy Fractional Volterra Integro-Differential Equations" Symmetry 11, no. 2: 205. https://doi.org/10.3390/sym11020205
APA StyleAlaroud, M., Al-Smadi, M., Rozita Ahmad, R., & Salma Din, U. K. (2019). An Analytical Numerical Method for Solving Fuzzy Fractional Volterra Integro-Differential Equations. Symmetry, 11(2), 205. https://doi.org/10.3390/sym11020205





