A New Flexible Sigmoidal Growth Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Model
2.2. Parameter Estimation
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Accessibility
References
- Vermeij, M. Early life-history dynamics of Caribbean coral species on artificial substratum: The importance of competition, growth and variation in life-history strategy. Coral Reefs 2006, 25, 59–71. [Google Scholar] [CrossRef]
- Zhao, D.; Borders, B.; Wilson, M. Individual-tree diameter growth and mortality models for bottomland mixed-species hardwood stands in the lower Mississippi alluvial valley. For. Ecol. Manag. 2004, 199, 307–322. [Google Scholar] [CrossRef]
- Lhotka, J.M.; Loewenstein, E.F. An individual-tree diameter growth model for managed uneven-aged oak-shortleaf pine stands in the ozark Highlands of Missouri, USA. For. Ecol. Manag. 2011, 261, 770–778. [Google Scholar] [CrossRef]
- Holland, E.P.; Pech, R.P.; Ruscoe, W.A.; Parkes, J.P.; Nugent, G.; Duncan, R.P. Thresholds in plant–herbivore interactions: Predicting plant mortality due to herbivore browse damage. Oecologia 2013, 172, 751–766. [Google Scholar] [CrossRef]
- Scogings, P.F.; Hjältén, J.; Skarpe, C.; Hattas, D.; Zobolo, A.; Dziba, L.; Rooke, T. Nutrient and secondary metabolite concentrations in a savanna are independently affected by large herbivores and shoot growth rate. Plant Ecol. 2014, 215, 73–82. [Google Scholar] [CrossRef]
- Zeide, B. Analysis of growth equations. For. Sci. 1993, 39, 594–616. [Google Scholar] [CrossRef]
- Archontoulis, S.V.; Miguez, F.E. Nonlinear regression models and applications in agricultural research. Agron. J. 2015, 107, 786–798. [Google Scholar] [CrossRef]
- Ratkowsky, D.; Olley, J.; McMeekin, T.; Ball, A. Relationship between temperature and growth rate of bacterial cultures. J. Bacteriol. 1982, 149, 1–5. [Google Scholar]
- Ratkowsky, D.; Lowry, R.; McMeekin, T.; Stokes, A.; Chandler, R. Model for bacterial culture growth rate throughout the entire biokinetic temperature range. J. Bacteriol. 1983, 154, 1222–1226. [Google Scholar]
- Briere, J.-F.; Pracros, P.; Le Roux, A.-Y.; Pierre, J.-S. A novel rate model of temperature-dependent development for arthropods. Environ. Entomol. 1999, 28, 22–29. [Google Scholar] [CrossRef]
- Lactin, D.J.; Holliday, N.; Johnson, D.; Craigen, R. Improved rate model of temperature-dependent development by arthropods. Environ. Entomol 1995, 24, 68–75. [Google Scholar] [CrossRef]
- Miguez, F.E.; Villamil, M.B.; Long, S.P.; Bollero, G.A. Meta-analysis of the effects of management factors on miscanthus× giganteus growth and biomass production. Agric. For. Meteorol. 2008, 148, 1280–1292. [Google Scholar] [CrossRef]
- Sebens, K.P. The ecology of indeterminate growth in animals. Annu. Rev. Ecol. Syst. 1987, 371–407. [Google Scholar] [CrossRef]
- Paine, C.; Marthews, T.R.; Vogt, D.R.; Purves, D.; Rees, M.; Hector, A.; Turnbull, L.A. How to fit nonlinear plant growth models and calculate growth rates: An update for ecologists. Methods Ecol. Evol. 2012, 3, 245–256. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for ontogenetic growth. Nature 2001, 413, 628–631. [Google Scholar] [CrossRef]
- Brown, J.H.; West, G.B. Scaling in Biology; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–126. [Google Scholar] [CrossRef]
- Verhulst, P. La loi d’accroissement de la population. Nouv. Mem. Acad. R. Soc. Belle-Lettr. Bruxelles 1845, 18, 1. [Google Scholar]
- Ricklefs, R.E. Patterns of growth in birds. Ibis 1968, 110, 419–451. [Google Scholar] [CrossRef]
- Gompertz, B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos. Trans. R. Soc. Lond. 1825, 115, 513–583. [Google Scholar] [CrossRef]
- Martin, T.L.; Huey, R.B. Why “suboptimal” is optimal: Jensen’s inequality and ectotherm thermal preferences. Am. Nat. 2008, 171, E102–E118. [Google Scholar] [CrossRef]
- Richards, F. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–301. [Google Scholar] [CrossRef]
- Causton, D. A computer program for fitting the richards function. Biometrics 1969, 25, 401–409. [Google Scholar] [CrossRef]
- France, J.; Thornley, J.H. Mathematical Models in Agriculture; Butterworths: London, UK, 1984. [Google Scholar]
- Brisbin, I.L.; Collins, C.T.; White, G.C.; McCallum, D.A. A new paradigm for the analysis and interpretation of growth data: The shape of things to come. Auk 1987, 552–554. [Google Scholar] [CrossRef]
- Glazier, D.S. Separating the respiration rates of embryos and brooding females of Daphnia magna: Implications for the cost of brooding and the allometry of metabolic rate. Limnol. Oceanogr. 1991, 36, 354–361. [Google Scholar] [CrossRef]
- Vincenzi, S.; Mangel, M.; Crivelli, A.J.; Munch, S.; Skaug, H.J. Determining individual variation in growth and its implication for life-history and population processes using the empirical bayes method. PLoS Comput. Biol. 2014, 10, e1003828. [Google Scholar] [CrossRef]
- Shelton, A.O.; Mangel, M. Estimating von bertalanffy parameters with individual and environmental variations in growth. J. Biol. Dyn. 2012, 6, 3–30. [Google Scholar] [CrossRef]
- Pardo, S.A.; Cooper, A.B.; Dulvy, N.K. Avoiding fishy growth curves. Methods Ecol. Evol. 2013, 4, 353–360. [Google Scholar] [CrossRef]
- Oswald, S.A.; Nisbet, I.C.; Chiaradia, A.; Arnold, J.M. FlexParamCurve: R package for flexible fitting of nonlinear parametric curves. Methods Ecol. Evol. 2012, 3, 1073–1077. [Google Scholar] [CrossRef]
- Kahm, M.; Hasenbrink, G.; Lichtenberg-Fraté, H.; Ludwig, J.; Kschischo, M. Grofit: Fitting biological growth curves with R. J. Stat. Softw. 2010, 33, 1–21. [Google Scholar] [CrossRef]
- R Development Core Team. A Language and Environment for Statistical Computing. Vienna, Austria, 2014. Available online: http://www.R-project.org (accessed on 13 December 2018).
- Horst, R.; Pardalos, P.M. Handbook of Global Optimization; Kluwer Academic Publishers, Springer Science & Business Media: Berlin, Germany, 2013; Volume 2. [Google Scholar]
- Brun, F.; Wallach, D.; Makowski, D.; Jones, J.W. Working with Dynamic Crop Models: Evaluation, Analysis, Parameterization, and Applications; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Vesterstrøm, J.; Thomsen, R. A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems. In Proceedings of the 2004 Congress on Evolutionary Computation, CEC2004, Portland, OR, USA, 19–23 June 2004. [Google Scholar]
- Feoktistov, V. Differential Evolution; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Rocca, P.; Oliveri, G.; Massa, A. Differential evolution as applied to electromagnetics. IEEE Antennas Propag. Mag. 2011, 53, 38–49. [Google Scholar] [CrossRef]
- Sharpe, P.J.H.; DeMichele, D.W. Reaction kinetics of poikilotherm development. J. Theor. Biol. 1977, 64, 649–670. [Google Scholar] [CrossRef]
- Shi, P.; Ge, F. A comparison of different thermal performance functions describing temperature-dependent development rates. J. Therm. Biol. 2010, 35, 225–231. [Google Scholar] [CrossRef]
- Shi, P.J.; Chen, L.; Hui, C.; Grissino-Mayer, H.D. Capture the time when plants reach their maximum body size by using the beta sigmoid growth equation. Ecol. Model. 2016, 320, 177–181. [Google Scholar] [CrossRef]
- Watterson, I.G. Calculation of probability density functions for temperature and precipitation change under global warming. J. Geophys. Res. 2008, 113, D12106. [Google Scholar] [CrossRef]
- Yin, X.; Kropff, M.J.; McLaren, G.; Visperas, R.M. A nonlinear model for cropdevelopment as a function of temperature. Agric. For. Meteorol. 1995, 77, 1–16. [Google Scholar] [CrossRef]
- Mullen, K.; Ardia, D.; Gil, D.L.; Windover, D.; Cline, J. DEoptim: An R package for global optimization by differential evolution. J. Stat.Softw. 2011, 40, 1–26. [Google Scholar] [CrossRef]
- Aho, K.; Derryberry, D.; Peterson, T. Model selection for ecologists: The worldviews of AIC and BIC. Ecology 2014, 95, 631–636. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar]
- Shi, P.-J.; Men, X.-Y.; Sandhu, H.S.; Chakraborty, A.; Li, B.-L.; Ou-Yang, F.; Sun, Y.-C.; Ge, F. The “general” ontogenetic growth model is inapplicable to crop growth. Ecol. Model. 2013, 266, 1–9. [Google Scholar] [CrossRef]
- Woolfenden, G.E. Growth and survival of young florida scrub jays. Wilson Bull. 1978, 90, 1–18. [Google Scholar]
- Ritter, L.V. Growth of nestling scrub jays in California. J. Field Ornithol. 1984, 48–53. [Google Scholar]
- Goshu, A.T.; Koya, P.R. Derivation of inflection points of nonlinear regression curves—Implications to statistics. Am. J. Theor. Appl. Stat. 2013, 2, 268–272. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. The origin of universal scaling laws in biology. Scal. Biol. 2000, 87–112. [Google Scholar] [CrossRef]
- Brody, S.; Procter, R. Relation between Basal Metabolism and Mature Body Weight in Different Species of Mammals and Birds; University of Missouri Agricultural Experiment Station Research Bulletin: Columbia, MO, USA, 1932; Volume 116, pp. 89–101. [Google Scholar]
- Kleiber, M. Body size and metabolism. ENE 1932, 1, E9. [Google Scholar] [CrossRef]
- Smil, V. Laying down the law. Nature 2000, 403, 597. [Google Scholar] [CrossRef]
- Enquist, B.J.; Brown, J.H.; West, G.B. Allometric scaling of plant energetics and population density. Nature 1998, 395, 163–165. [Google Scholar] [CrossRef]
- Bokma, F. Evidence against universal metabolic allometry. Funct. Ecol. 2004, 18, 184–187. [Google Scholar] [CrossRef]
- Glazier, D.S. Beyond the ‘3/4-power law’: Variation in the intra-and interspecific scaling of metabolic rate in animals. Biol. Rev. 2005, 80, 611–662. [Google Scholar] [CrossRef]
- Glazier, D.S. The 3/4-power law is not universal: Evolution of isometric, ontogenetic metabolic scaling in pelagic animals. BioScience 2006, 56, 325–332. [Google Scholar] [CrossRef]
- Glazier, D.S. A unifying explanation for diverse metabolic scaling in animals and plants. Biol. Rev. 2010, 85, 111–138. [Google Scholar] [CrossRef]
- Thornley, J.H.; France, J. An open-ended logistic-based growth function. Ecol. Model. 2005, 184, 257–261. [Google Scholar] [CrossRef]
- Kozusko, F.; Bourdeau, M. The trans-gompertz function: An alternative to the logistic growth function with faster growth. Acta Biotheor. 2015, 63, 397–405. [Google Scholar] [CrossRef]
- Spiess, A.-N.; Neumeyer, N. An evaluation of R squared as an inadequate measure for nonlinear models in pharmacological and biochemical research: A Monte Carlo approach. BMC Pharmacol. 2010, 10, 6. [Google Scholar] [CrossRef]
- Angilletta, M.J., Jr.; Niewiarowski, P.H.; Navas, C.A. The evolution of thermal physiology in ectotherms. J. Therm. Biol. 2002, 27, 249–268. [Google Scholar] [CrossRef]
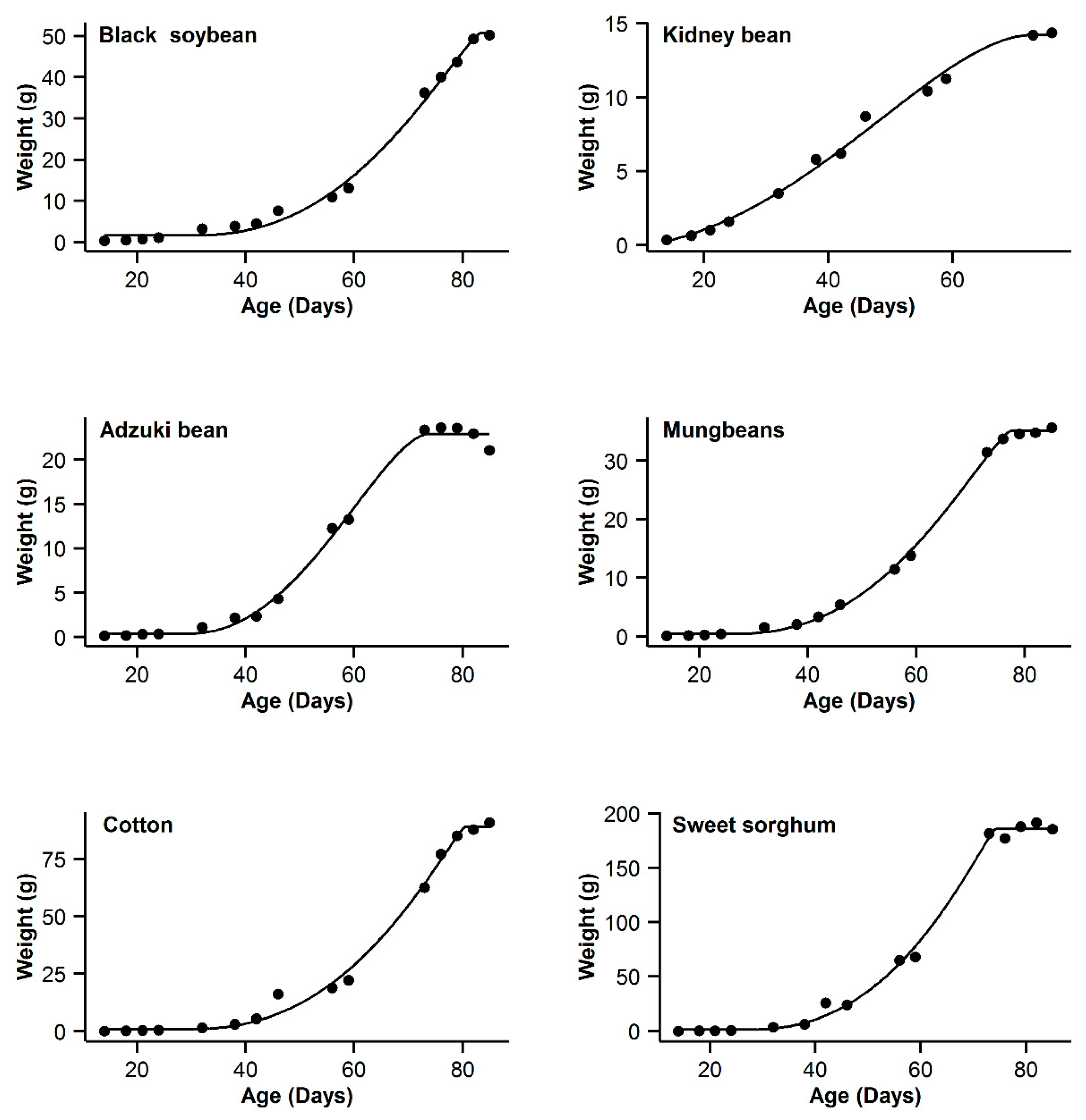
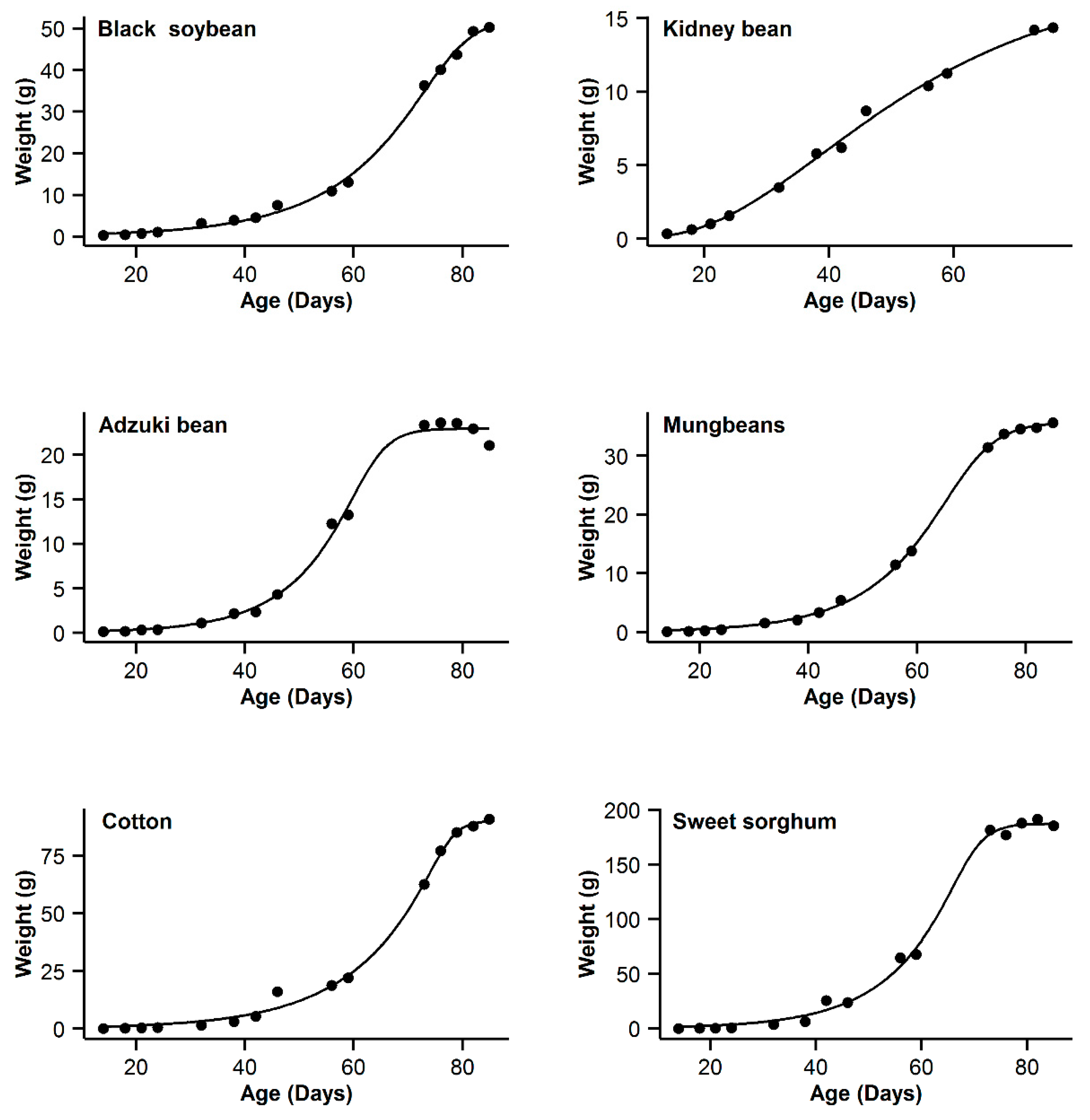
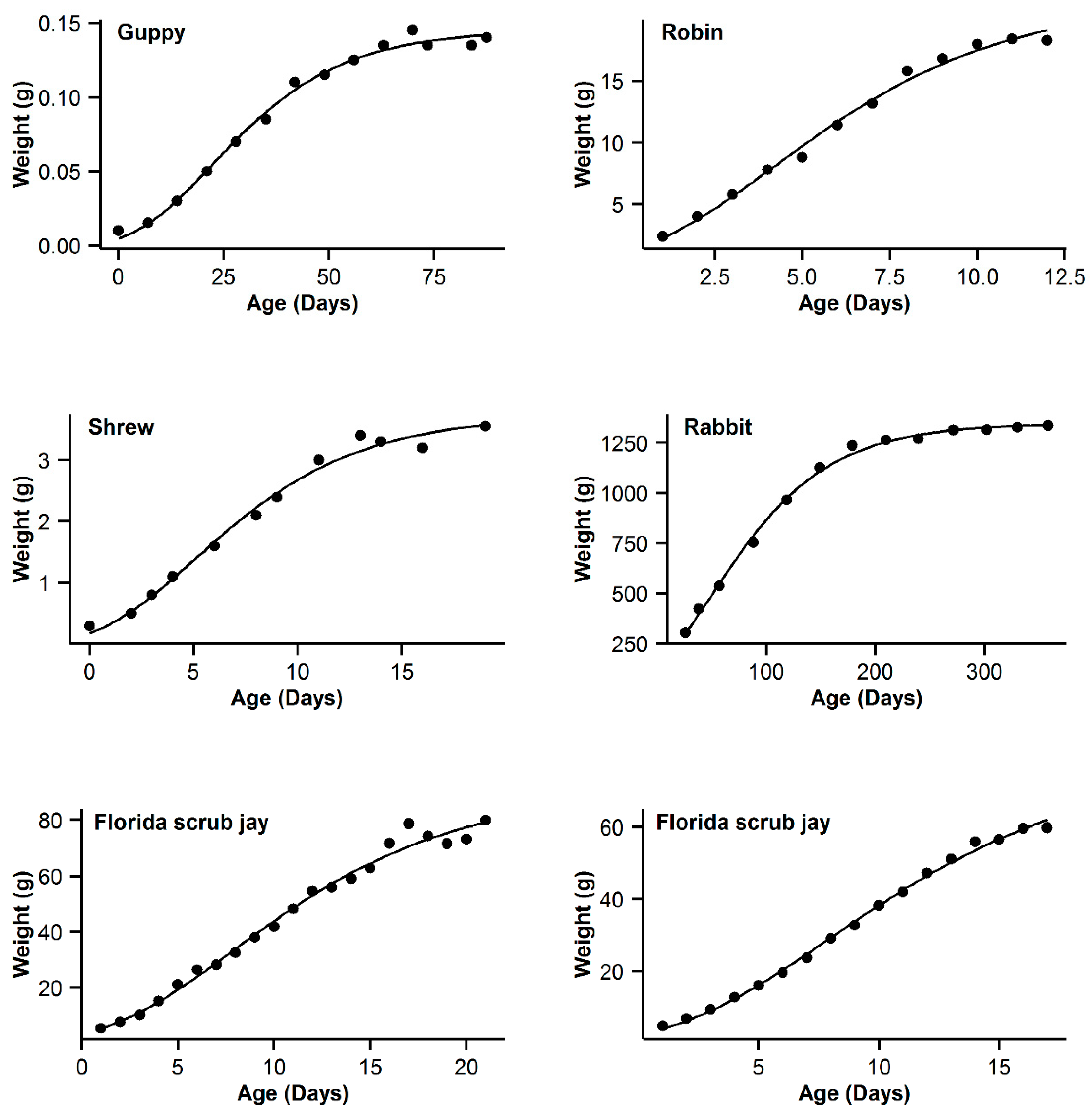
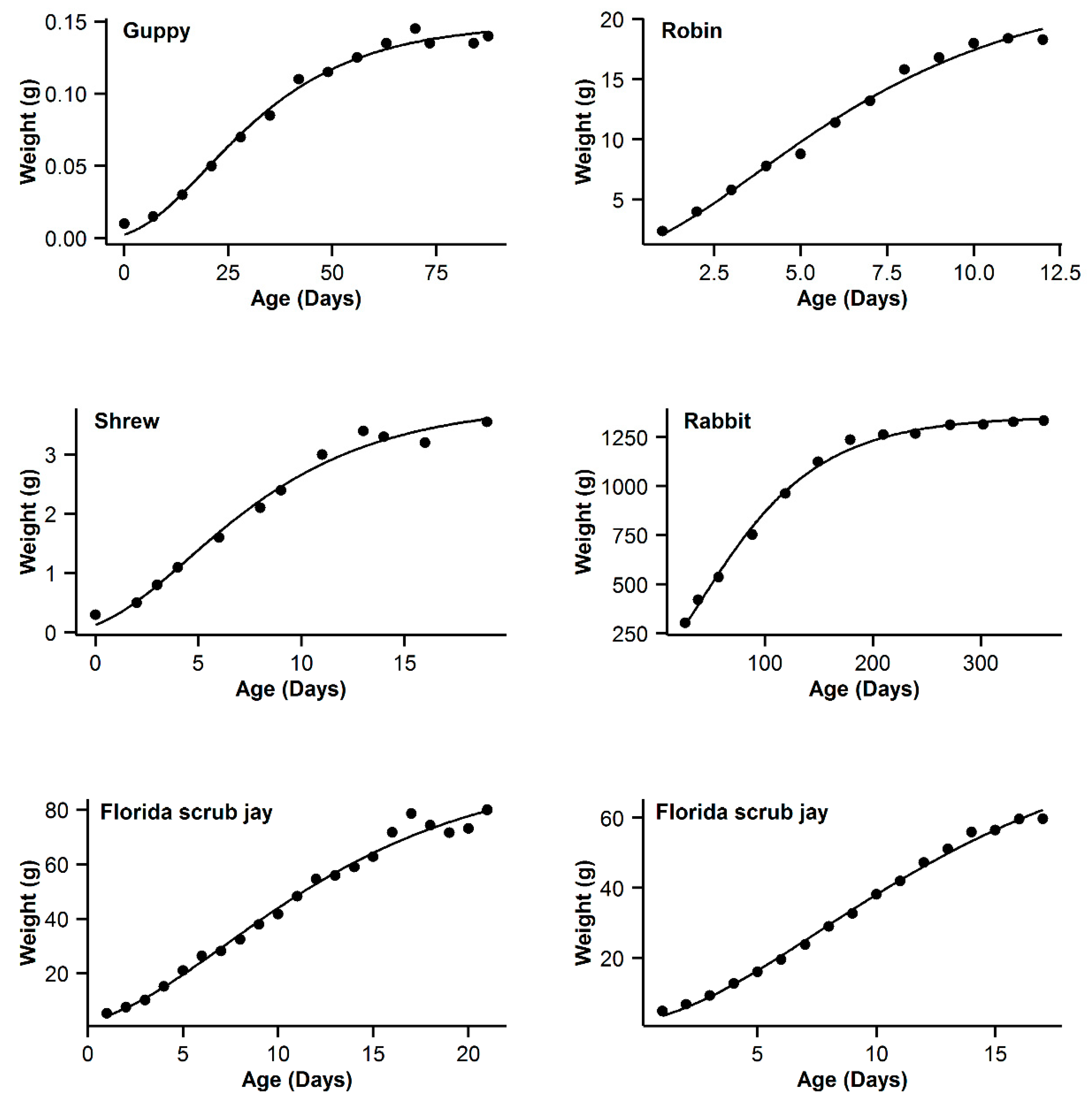
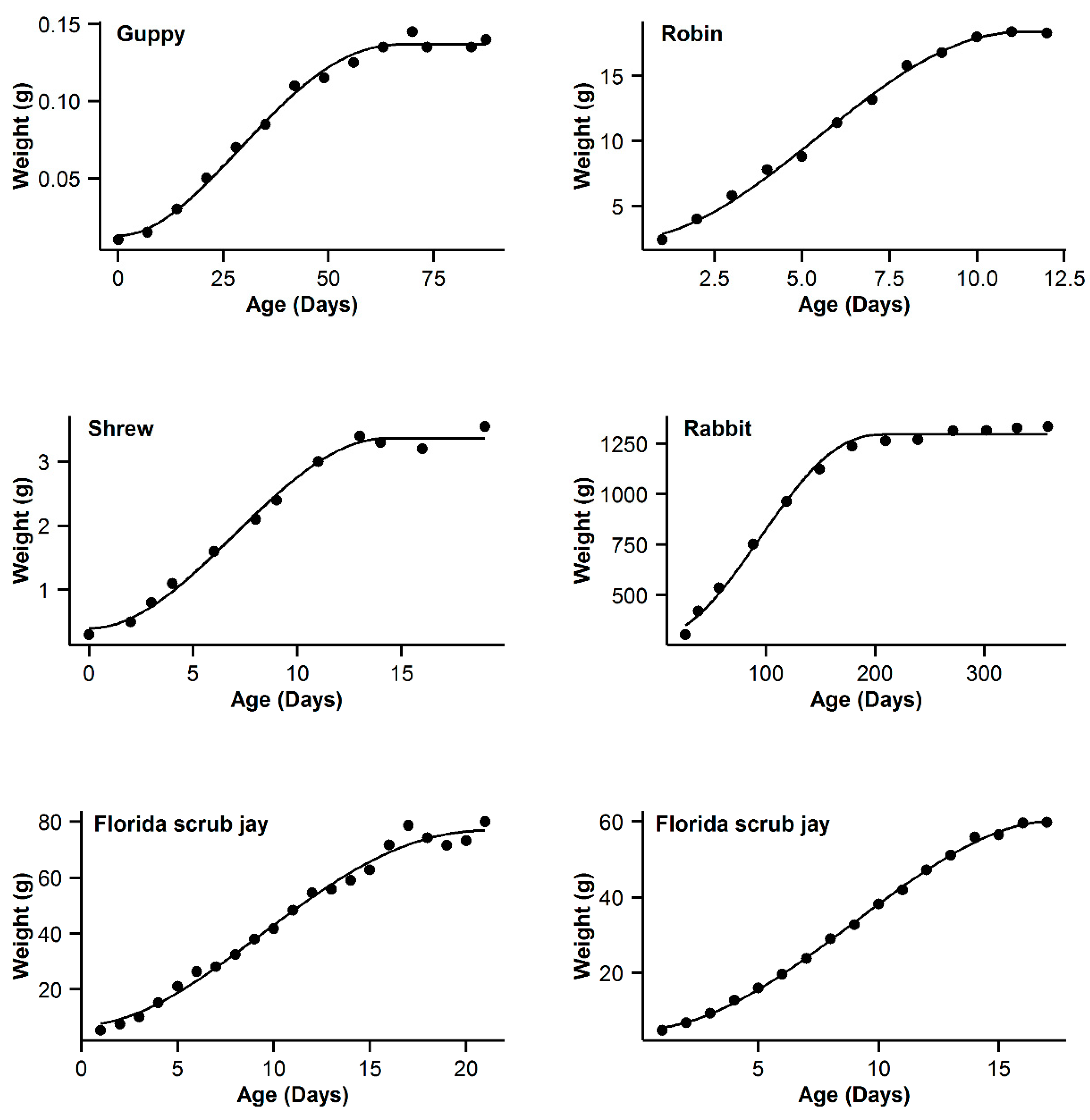
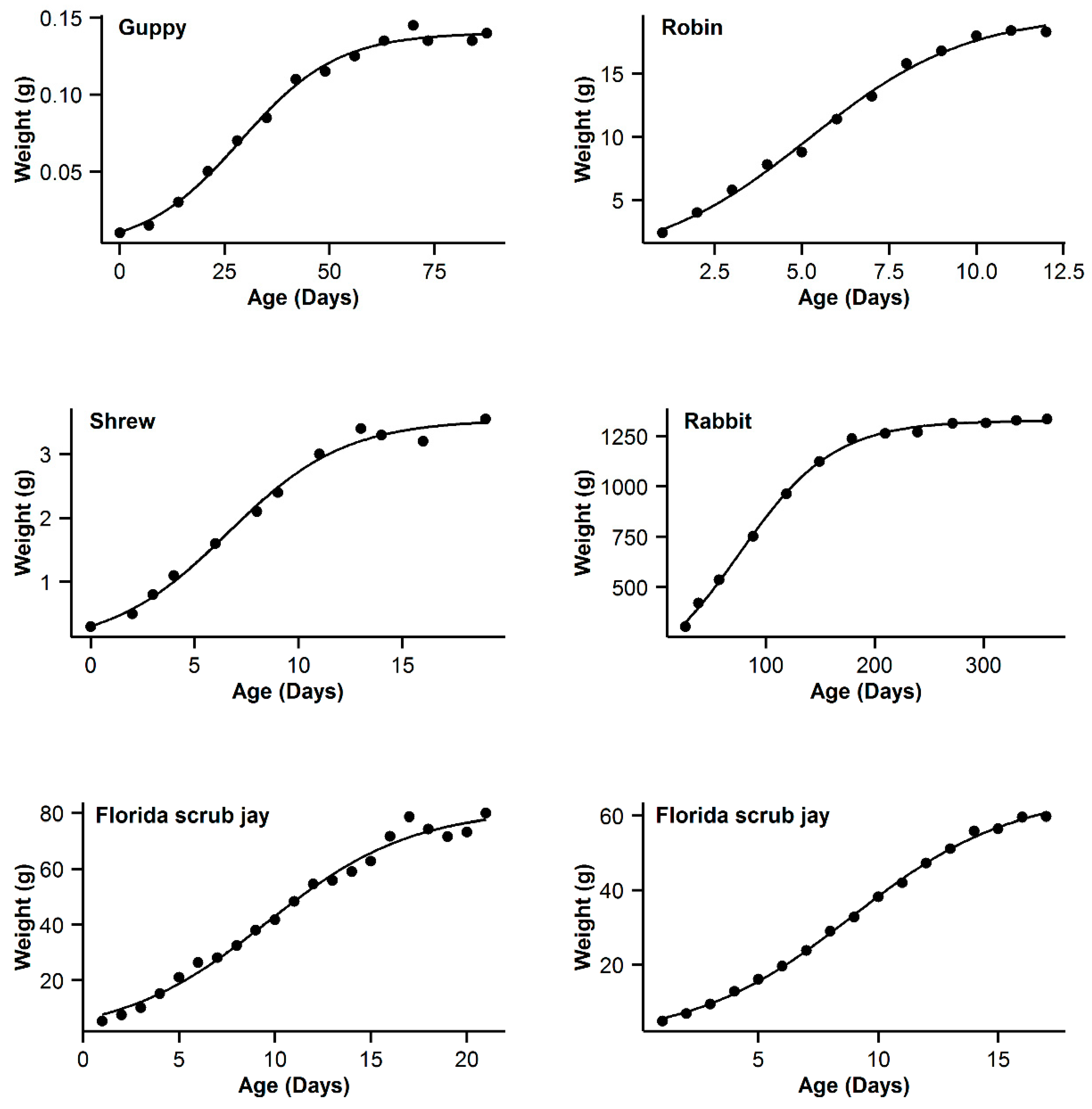

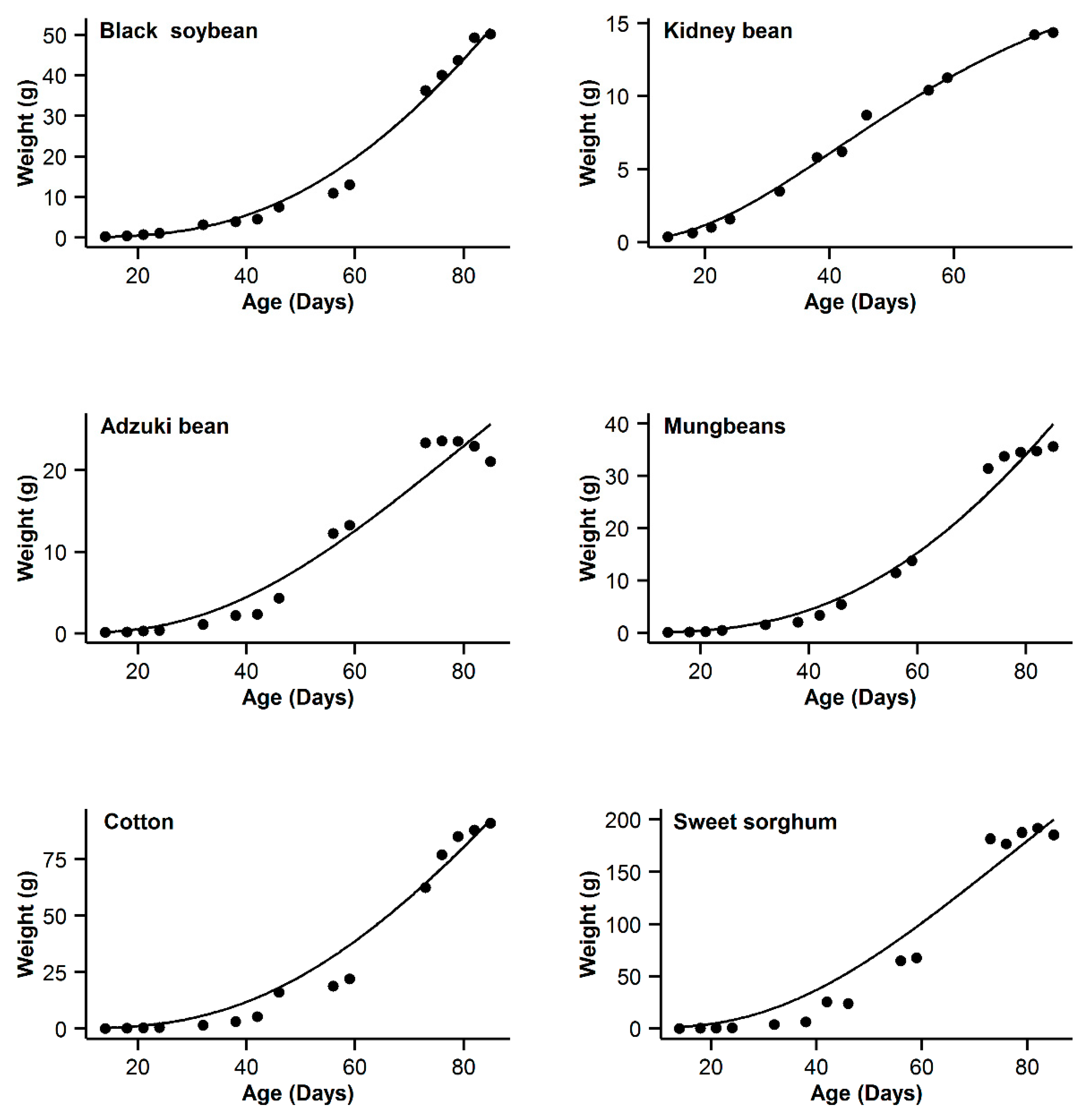
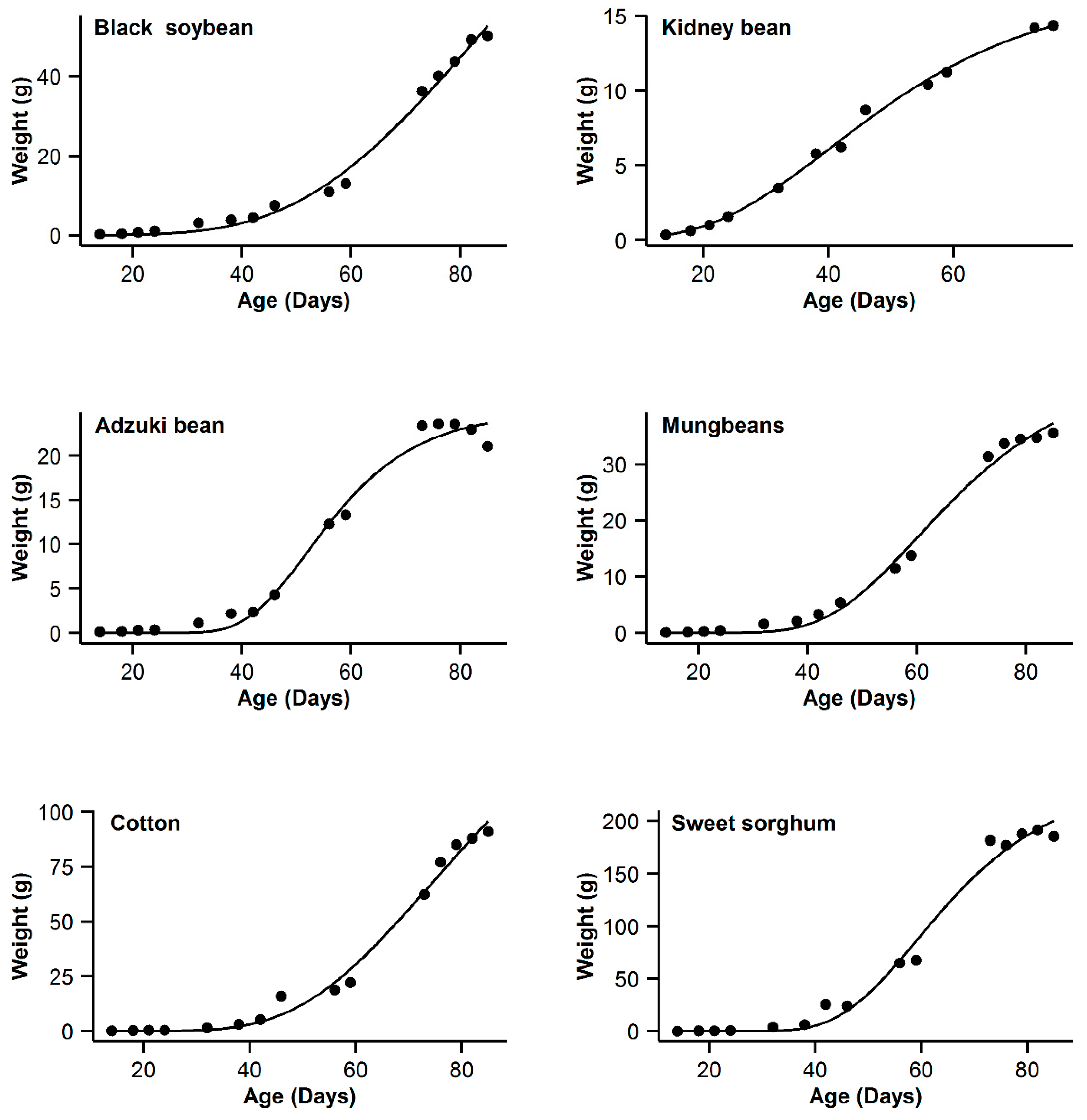
| Model | Parameter | Lower Bound | Upper Bound |
|---|---|---|---|
| a | 1.00 × 10−9 | 1.00 × 10−3 | |
| b | 0 | 5 | |
| NSG | 0 | 300 | |
| m | −200 | 200 | |
| n | 0 | 500 | |
| 0 | 500 | ||
| Richards | k | 0 | 1 |
| 0 | 500 | ||
| v | 0 | 1 | |
| 0 | 500 | ||
| Logistic | k | 0 | 1 |
| 0 | 500 | ||
| 0 | 500 | ||
| Gompertz | k | 0 | 1 |
| 0 | 500 | ||
| 0 | 500 | ||
| OGM | 0 | 1 | |
| a | 0 | 1 |
| Code | Models Name | NSG | Logistic | Gompertz | Richards | OGM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Species | R2 | AIC | ΔAIC | R2 | AIC | ΔAIC | R2 | AIC | ΔAIC | R2 | AIC | ΔAIC | R2 | AIC | ΔAIC | |
| 1 | Black soybean | 0.995 | 18.77 | 15.63 | 0.996 | 11.14 | 8 | 0.993 | 20.91 | 17.77 | 0.998 | 3.14 | 0 | 0.985 | 31.04 | 27.9 |
| 2 | Kidney bean | 0.993 | −11.08 | 10.48 | 0.991 | −11.89 | 9.67 | 0.996 | −21.56 | 0 | 0.996 | −20.24 | 1.32 | 0.995 | −17.94 | 3.62 |
| 3 | Adzuki bean | 0.995 | −1.55 | 0.3 | 0.992 | 1.65 | 3.5 | 0.987 | 9.18 | 11.03 | 0.995 | −1.85 | 0 | 0.953 | 28.95 | 30.8 |
| 4 | Mung bean | 0.998 | −11.75 | 11.5 | 0.998 | −4.21 | 19.04 | 0.993 | 12.88 | 36.13 | 0.999 | −23.25 | 0 | 0.978 | 29.21 | 52.46 |
| 5 | Cotton | 0.994 | 40.29 | 9.64 | 0.993 | 37.98 | 7.33 | 0.99 | 44.77 | 14.12 | 0.996 | 30.65 | 0 | 0.966 | 62.58 | 31.93 |
| 6 | Sweet sorghum | 0.996 | 58.22 | 3.31 | 0.993 | 63.47 | 8.56 | 0.986 | 73.23 | 18.32 | 0.996 | 54.91 | 0 | 0.949 | 93.06 | 38.15 |
| 7 | Guppy | 0.993 | −16.84 | 5.89 | 0.994 | −22.73 | 0 | 0.993 | −19.8 | 2.93 | 0.995 | −21.54 | 1.19 | 0.991 | −16.28 | 6.45 |
| 8 | Robin | 0.997 | −16.61 | 0.47 | 0.995 | −17.08 | 0 | 0.992 | −11.29 | 5.79 | 0.99 | −5.85 | 5.44 | 0.991 | −9.26 | 7.82 |
| 9 | Shrew | 0.992 | −44.98 | 3.76 | 0.992 | −48.74 | 0 | 0.989 | −44.68 | 4.06 | 0.992 | −46.96 | 1.78 | 0.987 | −42.53 | 6.21 |
| 10 | Rabbit | 0.994 | −22.52 | 22.03 | 0.998 | −44.55 | 0 | 0.997 | −36.5 | 8.05 | 0.998 | −42.57 | 1.98 | 0.996 | −32.82 | 11.73 |
| 11 | Florida scrub jay | 0.989 | 50.13 | 3.51 | 0.988 | 47.39 | 0.77 | 0.989 | 46.62 | 0 | 0.989 | 48.21 | 1.59 | 0.988 | 47.63 | 1.01 |
| 12 | Western scrub jay | 0.999 | −10.43 | 0 | 0.999 | −8.05 | 2.38 | 0.997 | 5.09 | 15.52 | 0.999 | −5.92 | 4.51 | 0.996 | 11.03 | 21.46 |
| Species | NSG | Richards | Logistic | Gompertz | OGM | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | m | n | k | v | k | k | a | ||||||||||
| Black soybean | 3.24 × 10−4 | 4.79 | 50.76 | 30.36 | 83.23 | 52.77 | 0.25 | 72.76 | 3.58 | 67.31 | 0.09 | 72.14 | 147.76 | 0.03 | 86.00 | 510.94 | 1.00 × 10−25 | 0.19 |
| Kidney bean | 6.77 × 10−6 | 1.23 | 14.20 | −26.41 | 72.41 | 17.75 | 0.04 | 39.00 | −0.20 | 14.80 | 0.10 | 44.60 | 16.79 | 0.05 | 40.33 | 20.07 | 1.03 × 10−24 | 0.29 |
| Adzuki bean | 7.64 × 10−5 | 1.49 | 22.91 | 29.55 | 73.55 | 22.94 | 0.35 | 59.72 | 3.67 | 23.59 | 0.15 | 55.99 | 24.93 | 0.09 | 52.03 | 67.98 | 2.43 × 10−24 | 0.21 |
| Mung bean | 2.44 × 10−4 | 3.96 | 35.10 | 26.54 | 77.34 | 35.28 | 0.28 | 65.34 | 3.32 | 38.43 | 0.13 | 62.40 | 46.57 | 0.06 | 60.23 | 305.78 | 5.72 × 10−24 | 0.18 |
| Cotton | 8.40 × 10−4 | 8.91 | 88.95 | 29.86 | 80.31 | 90.05 | 0.54 | 74.05 | 7.52 | 111.70 | 0.11 | 69.94 | 180.64 | 0.04 | 73.99 | 521.88 | 1.00 × 10−25 | 0.24 |
| Sweet sorghum | 2.33 × 10−3 | 11.02 | 185.78 | 27.48 | 74.06 | 186.95 | 0.43 | 65.45 | 4.71 | 201.58 | 0.14 | 61.72 | 236.38 | 0.07 | 59.17 | 524.10 | 1.05 × 10−24 | 0.35 |
| Guppy | 1.37 × 10−7 | 0.66 | 13.68 | −246.67 | 68.91 | 14.15 | 0.08 | 26.84 | 0.64 | 14.02 | 0.09 | 28.80 | 14.56 | 0.06 | 22.02 | 14.82 | 0.26 | 0.38 |
| Robin | 7.90 × 10−4 | 0.86 | 18.38 | −59.23 | 11.30 | 24.11 | 0.19 | 3.88 | −0.27 | 19.75 | 0.44 | 5.20 | 21.79 | 0.26 | 4.17 | 22.87 | 0.89 | 1.87 |
| Shrew | 8.18 × 10−5 | 0.82 | 3.37 | −40.70 | 14.47 | 3.50 | 0.41 | 6.98 | 1.37 | 3.54 | 0.36 | 6.60 | 3.74 | 0.22 | 5.04 | 3.85 | 0.13 | 1.05 |
| Rabbit | 5.17 × 10−5 | 0.61 | 12.95 | −20.15 | 21.01 | 13.27 | 0.23 | 7.44 | 0.96 | 13.26 | 0.23 | 7.51 | 13.47 | 0.17 | 5.07 | 13.55 | 1.06 | 1.15 |
| Florida scrub jay | 1.11 × 10−4 | 0.72 | 76.97 | −141.30 | 21.55 | 86.55 | 0.19 | 8.57 | 0.32 | 81.51 | 0.26 | 9.57 | 90.91 | 0.15 | 7.91 | 96.25 | 2.30 | 1.54 |
| Western scrub jay | 3.18 × 10−4 | 1.07 | 59.99 | −226.33 | 17.12 | 67.06 | 0.28 | 8.76 | 0.83 | 65.99 | 0.30 | 8.91 | 78.65 | 0.16 | 7.93 | 87.04 | 1.76 | 1.47 |
| Species | Observed (g) | NSG | Richards | Logistic | Gompertz | OGM |
|---|---|---|---|---|---|---|
| Black soybean | 50.20 | 1.01 | 1.05 | 1.34 | 2.94 | 10.18 |
| Kidney bean | 14.35 | 0.99 | 1.24 | 1.03 | 1.17 | 1.40 |
| Adzuki bean | 23.60 | 0.97 | 0.97 | 1.00 | 1.06 | 2.88 |
| Mung bean | 35.60 | 0.99 | 0.99 | 1.08 | 1.31 | 8.59 |
| Cotton | 90.80 | 0.98 | 0.99 | 1.23 | 1.99 | 5.75 |
| Sweet sorghum | 191.50 | 0.97 | 0.98 | 1.05 | 1.23 | 2.74 |
| Guppy | 0.15 | 0.94 | 0.98 | 0.97 | 1.00 | 1.02 |
| Robin | 18.40 | 1.00 | 1.31 | 1.07 | 1.18 | 1.24 |
| Shrew | 3.55 | 0.95 | 0.99 | 1.00 | 1.05 | 1.08 |
| Rabbit | 1335.00 | 0.97 | 0.99 | 0.99 | 1.01 | 1.01 |
| Florida scrub jay | 80.00 | 0.96 | 1.08 | 1.02 | 1.14 | 1.20 |
| Western scrub jay | 59.75 | 1.00 | 1.12 | 1.10 | 1.32 | 1.46 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, L.; Shi, P.-J.; Li, L.; Chen, G. A New Flexible Sigmoidal Growth Model. Symmetry 2019, 11, 204. https://doi.org/10.3390/sym11020204
Cao L, Shi P-J, Li L, Chen G. A New Flexible Sigmoidal Growth Model. Symmetry. 2019; 11(2):204. https://doi.org/10.3390/sym11020204
Chicago/Turabian StyleCao, Liying, Pei-Jian Shi, Lin Li, and Guifen Chen. 2019. "A New Flexible Sigmoidal Growth Model" Symmetry 11, no. 2: 204. https://doi.org/10.3390/sym11020204
APA StyleCao, L., Shi, P.-J., Li, L., & Chen, G. (2019). A New Flexible Sigmoidal Growth Model. Symmetry, 11(2), 204. https://doi.org/10.3390/sym11020204






