Clustering Mixed Data Based on Density Peaks and Stacked Denoising Autoencoders
Abstract
:1. Introduction
- (1)
- (2)
- (1)
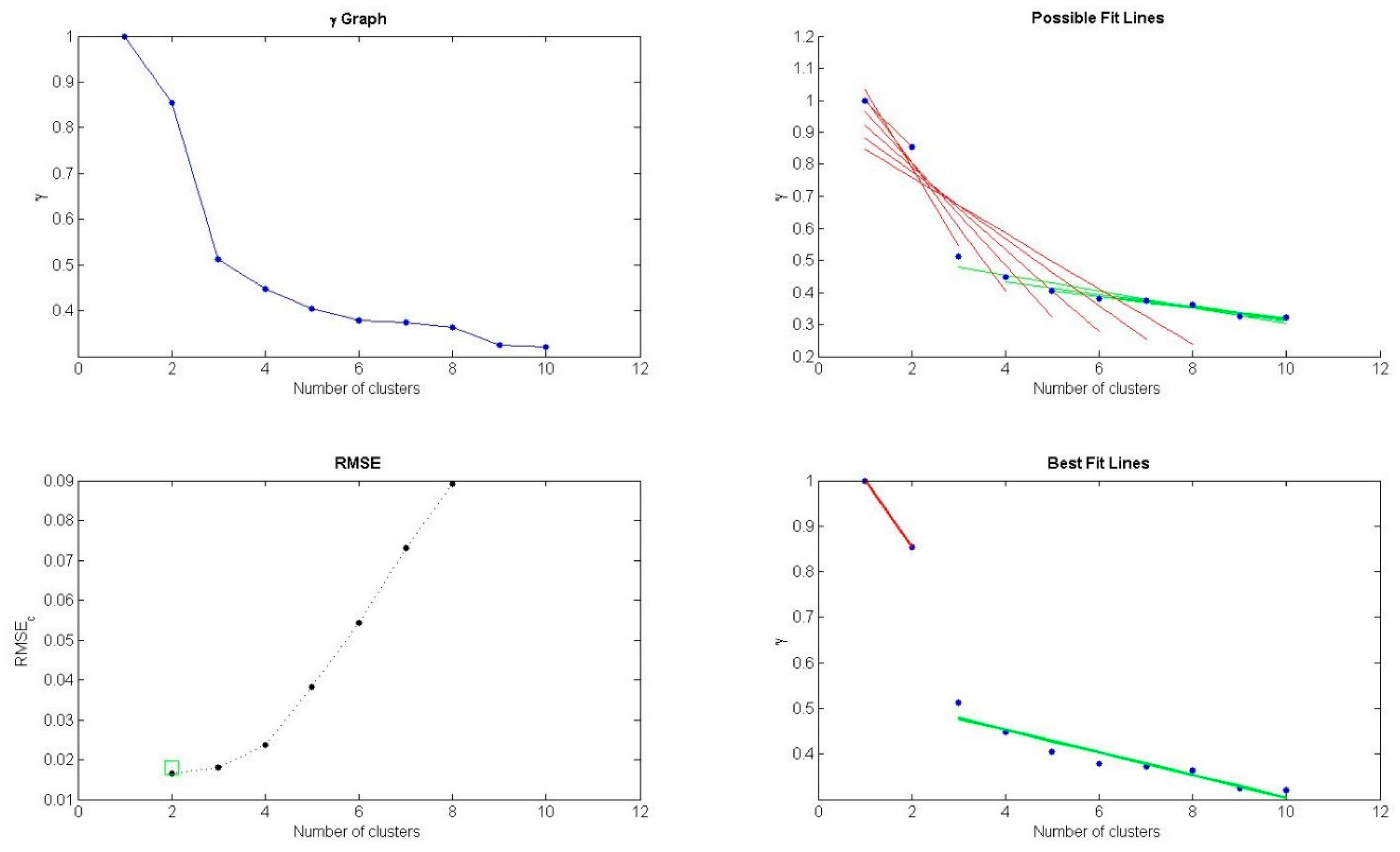
- The DPC algorithm is improved by employing L-method to determine the number of cluster centers automatically, which overcomes the drawback of selecting the number of cluster centers by decision graph manually in DPC-based algorithms.
- (2)
- Based on numeralization of categorical attributes by the one-hot encoding technique, we propose a framework for clustering mixed data by integrating stacked denoising autoencoders and density peaks clustering algorithm, which can utilize the robust feature representations learned from SDAE to enhance the clustering quality and be also suitable for clustering data with nonspherical distribution based on density peaks clustering algorithm.
- (3)
- By conducting experiments on six datasets from UCI machine learning repository, we observed that our proposed clustering algorithm outperforms three baseline algorithms in terms of clustering accuracy and rand index, which also demonstrates that stacked denoising autoencoders can be applied to clustering small sample datasets effectively besides clustering large scale datasets.
2. Related Works
2.1. Clustering Approaches to Mixed Data
2.2. Clustering Algorithm Based on Deep Learning
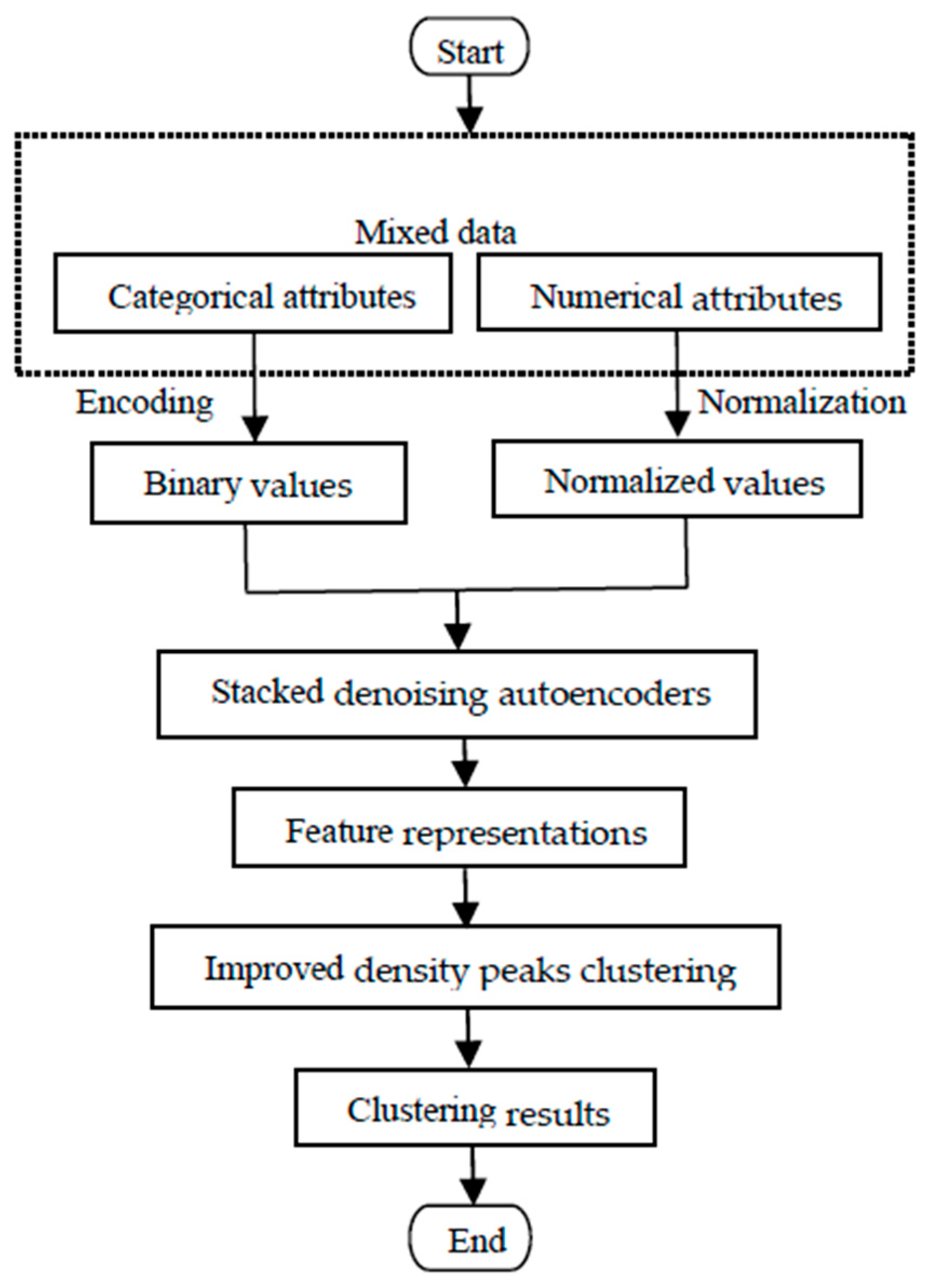
3. Methodology
3.1. Data Prepocessing
3.1.1. Encoding of Categorical Attributes
3.1.2. Normalization of Numerical Attributes
3.2. Feature Extraction by Stacked Denoising Autoencoders
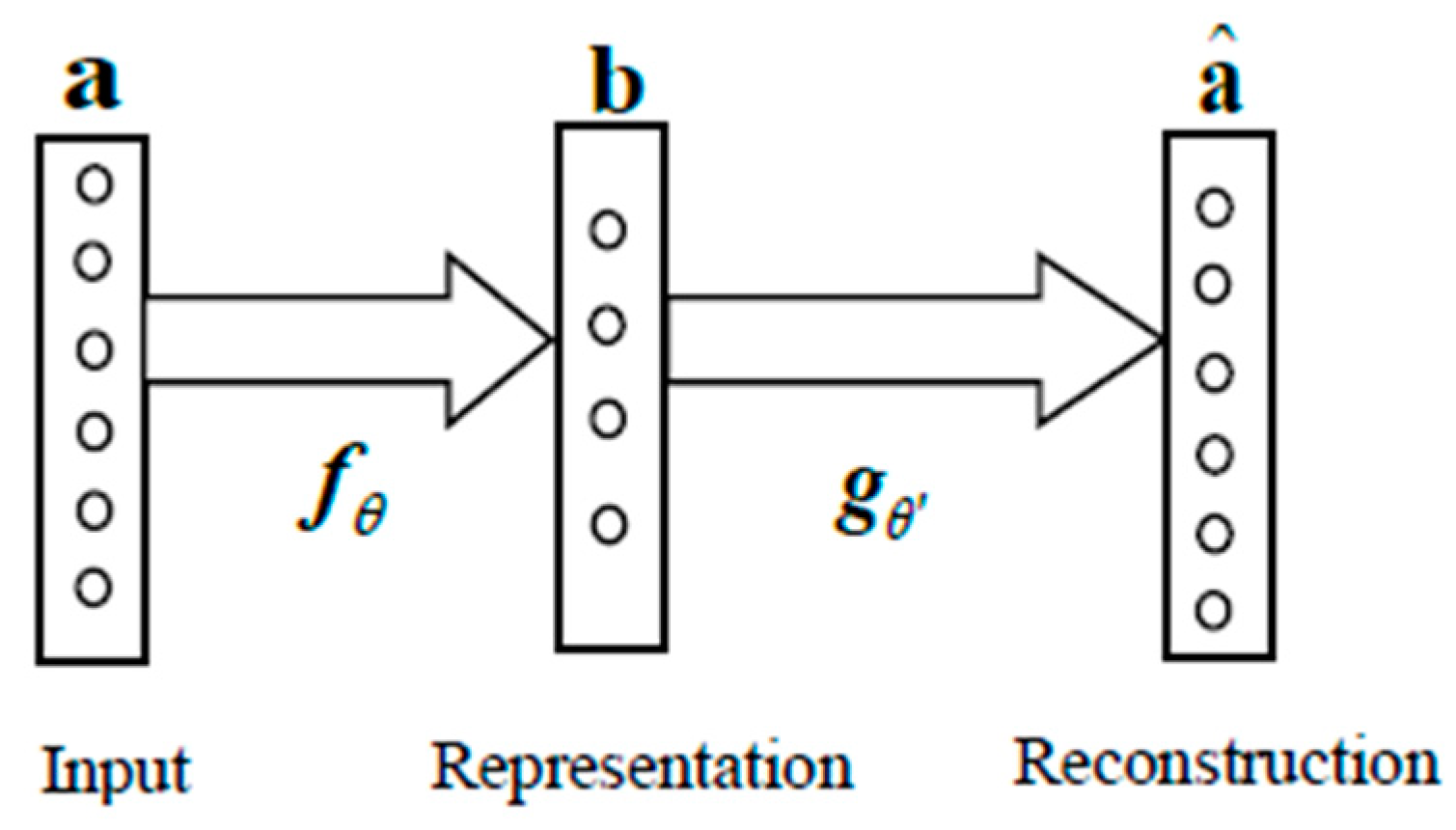
3.2.1. AutoEncoder (AE)
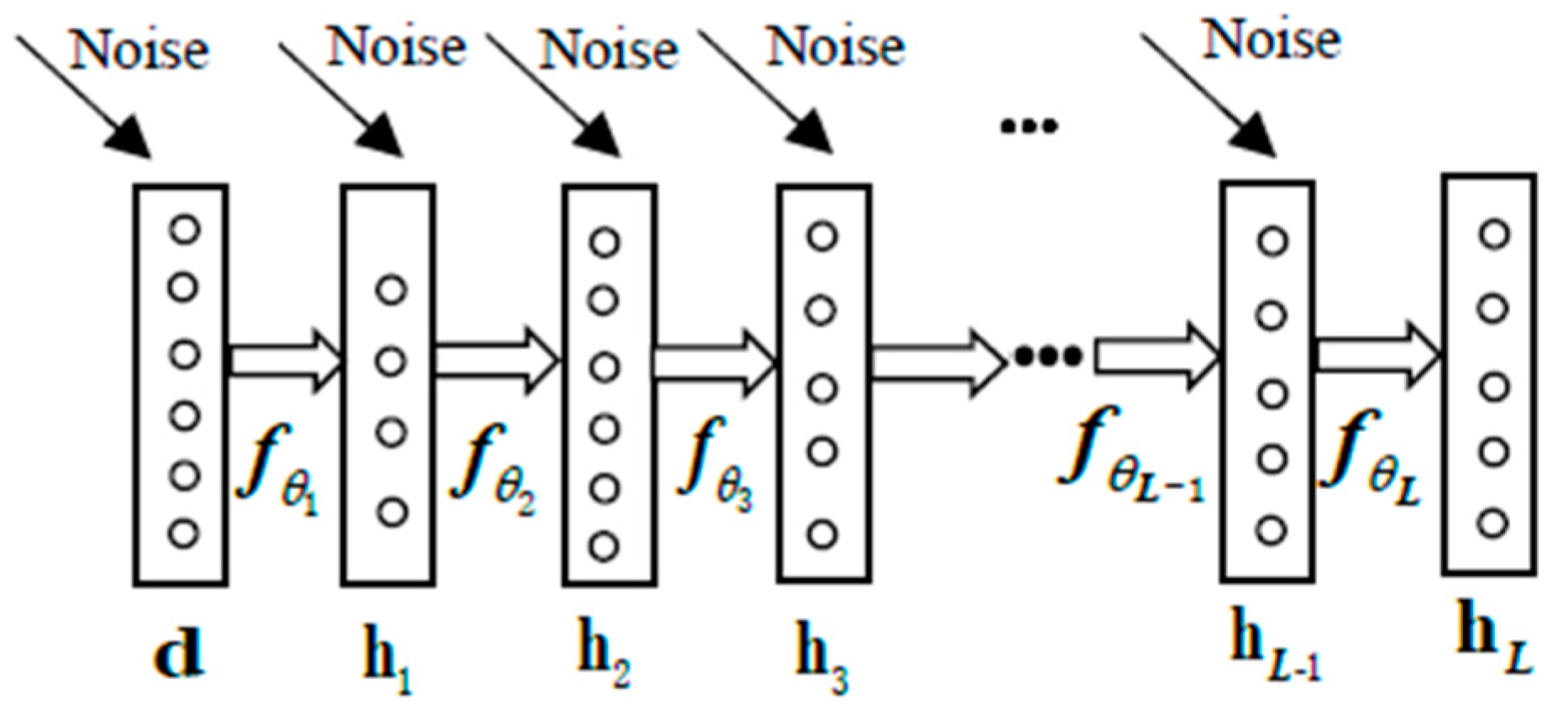
3.2.2. Stacked Denoising Autoencoders (SDAE)
3.2.3. Feature Construction for Clustering
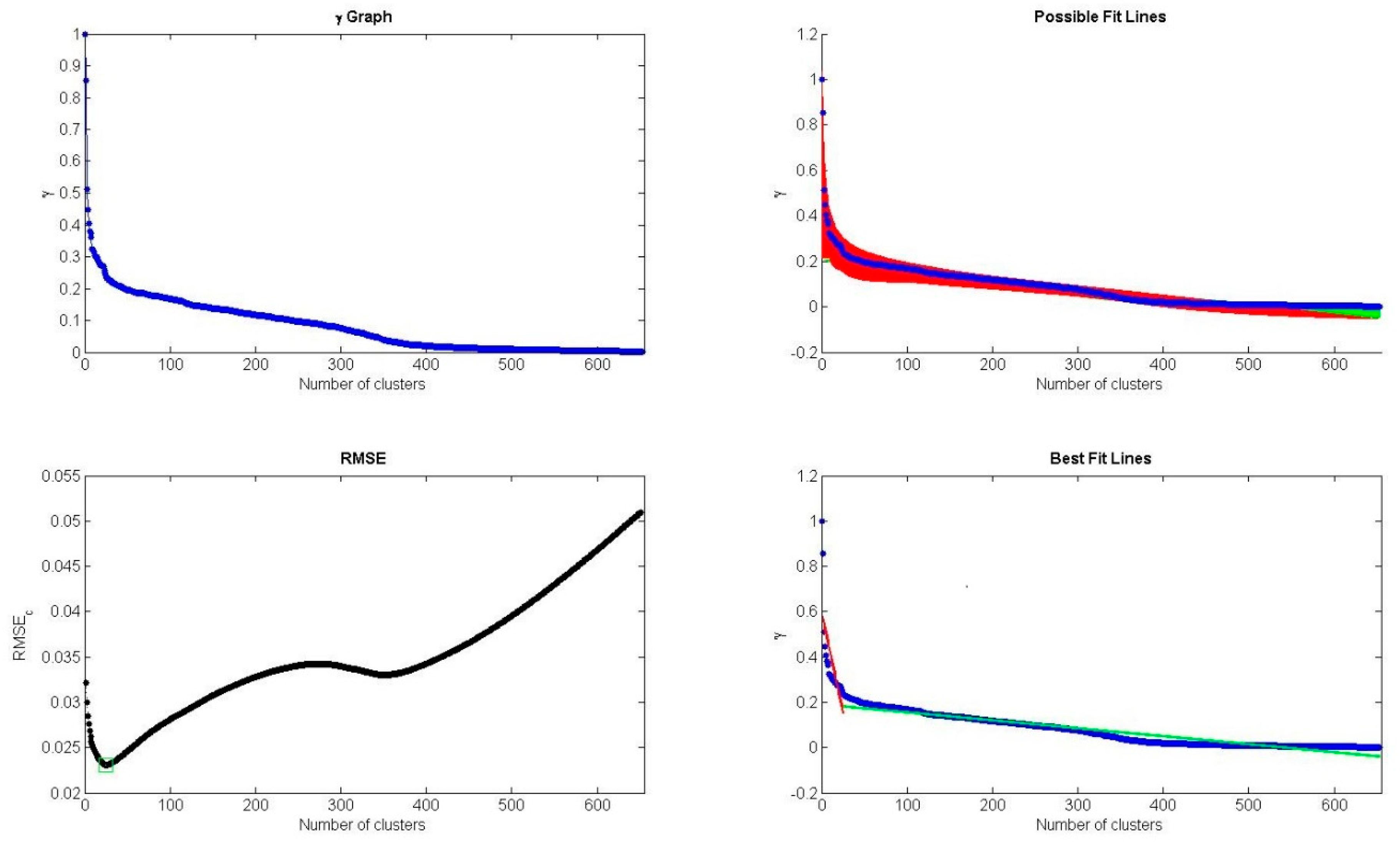
3.3. Density Peak Clustering and Its Improvement
3.4. Algorithm Summarization and Time Complexity Analysis
| Algorithm 1. DPC-SDAE algorithm | |
| Inputs: | mixed dataset consisting of N data objects, the initial value of encoding parameters and decoding parameters , and cutoff distance |
| Outputs: | cluster label vector |
| Steps: 1. | Transform categorical attributes into a binary matrix by one-hot encoding. |
| 2. | Normalize numerical attributes by (2) and concatenate with the binary matrix to obtain a matrix . |
| 3. | Input to SDAE with the initial value of and to extract clustering features and construct a normalized feature matrix |
| 4. | Calculate distances between objects based on by (8). |
| 5. | Calculate and normalize the local densities of data objects based on cutoff distance by (9) and (11). |
| 6. | Calculate and normalize the relative distances of data objects by (10) and (12). |
| 7. | Calculate by (13) and sort data objects by in descending order. |
| 8. | Determine the number of clusters with L-method and select data objects with larger as cluster centers. |
| 9. | Assign each remaining data object a cluster label as the same as its nearest cluster center. |
| 10. | Return the cluster label vector |
4. Results and Discussion
4.1. Datasets
4.2. Evaluation Indexes
4.3. Clustering Results and Analysis
4.4. Discussion on Hyperparameters in DPC-SDAE Algorithm
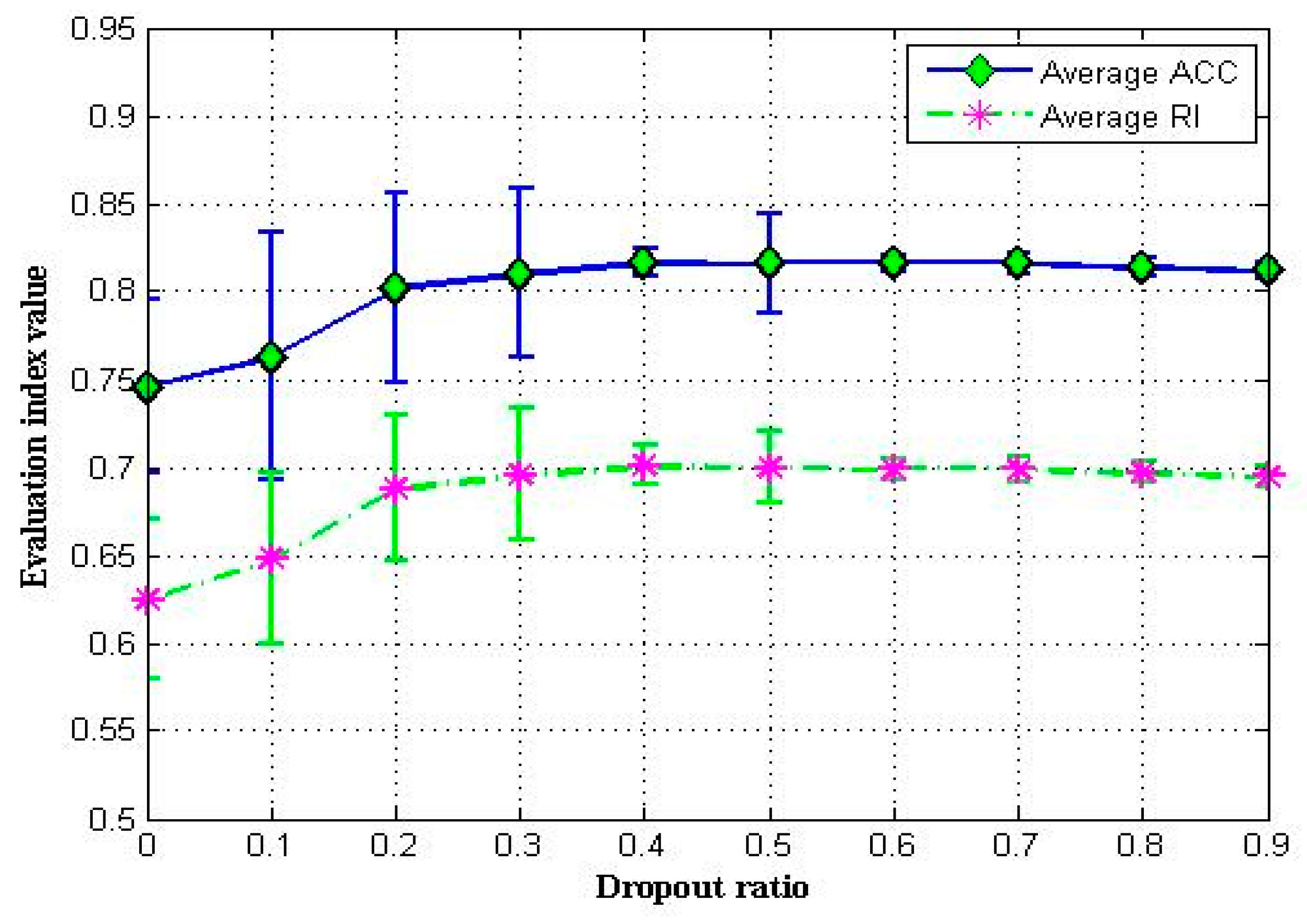
4.4.1. Dropout Ratio
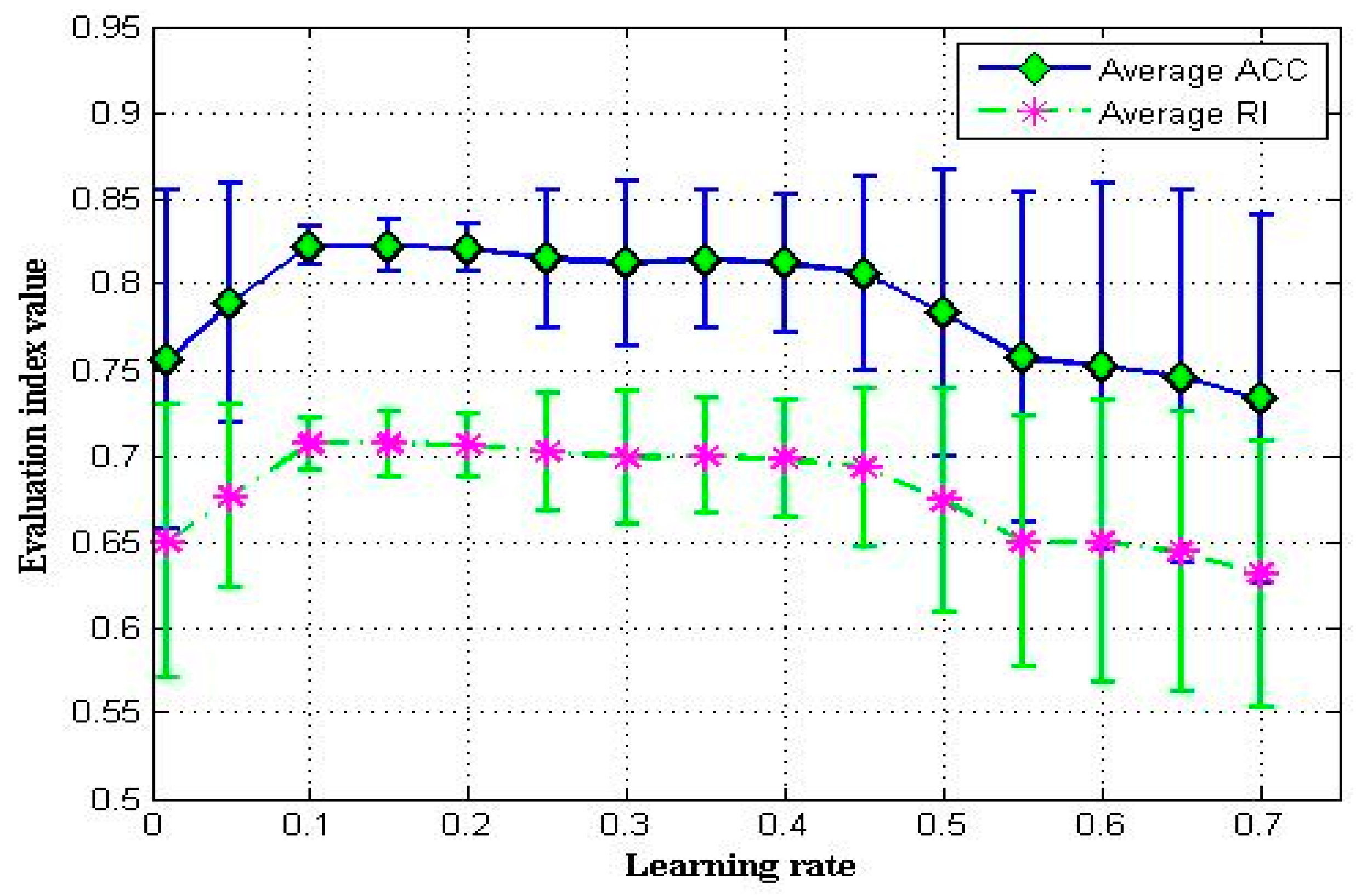
4.4.2. Learning Rate
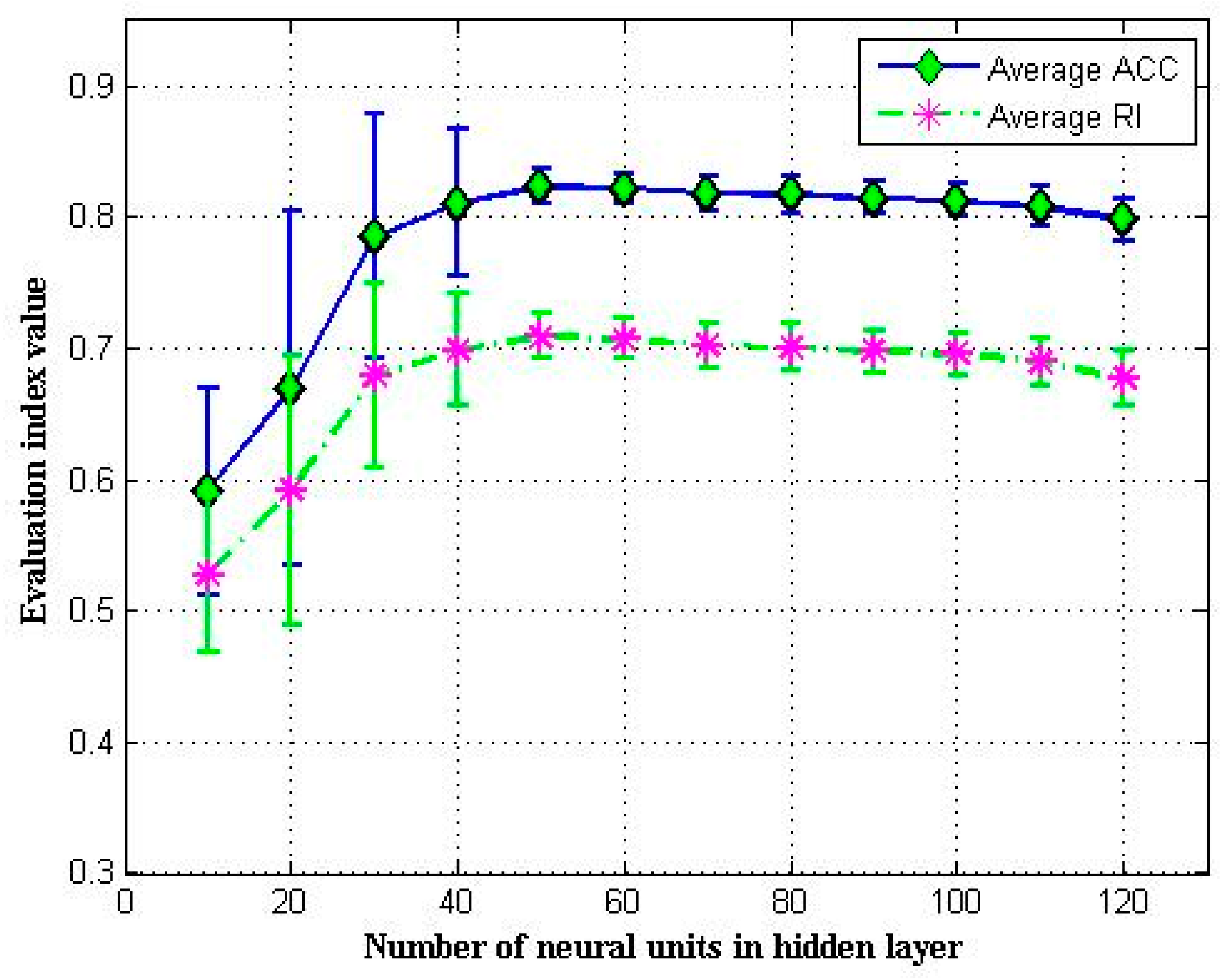
4.4.3. Number of Neural Units in Hidden Layer
4.4.4. Neighbor Ratio
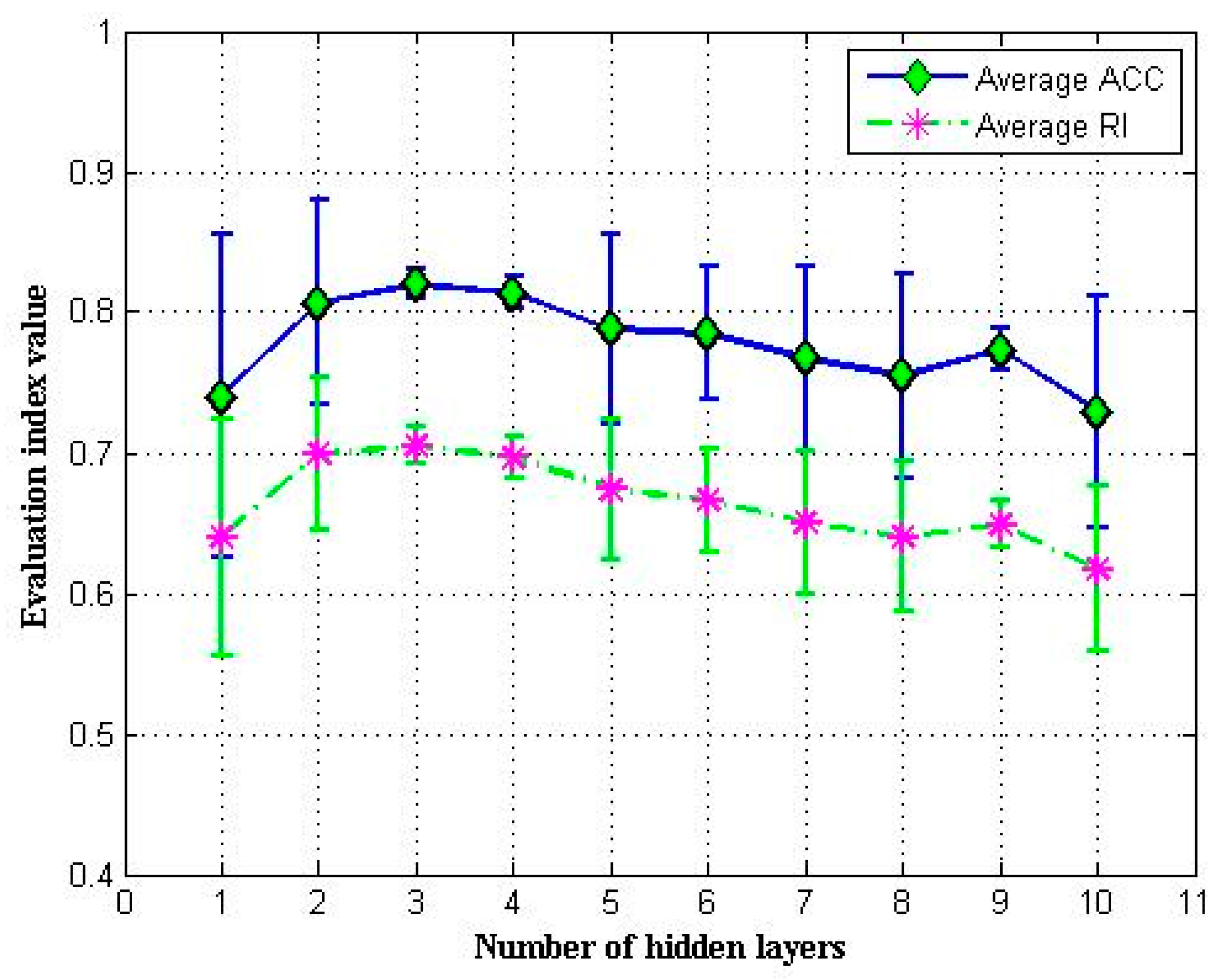
4.4.5. Number of Hidden Layers
4.5. Discussion on the Generalization of the Results
4.6. Discussion on the Methodological and Practical Implications
4.7. Discussion on the Limitations of DPC-SDAE
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ushakov, A.; Klimentova, X.; Vasilyev, I. Bi-level and Bi-objective p-Median Type Problems for Integrative Clustering: Application to Analysis of Cancer Gene-Expression and Drug-Response Data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 15, 46–59. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Chen, G. Fuzzy soft subspace clustering method for gene co-expression network analysis. Int. J. Mach. Learn. Cybern. 2017, 8, 1157–1165. [Google Scholar] [CrossRef]
- Subudhi, S.; Panigrahi, S. A hybrid mobile call fraud detection model using optimized fuzzy C-means clustering and group method of data handling-based network. Vietnam J. Comput. Sci. 2018, 5, 205–217. [Google Scholar] [CrossRef]
- Han, C.Y. Improved SLIC imagine segmentation algorithm based on K-means. Clust. Comput. 2017, 20, 1017–1023. [Google Scholar] [CrossRef]
- Ahmadi, P.; Gholampour, I.; Tabandeh, M. Cluster-based sparse topical coding for topic mining and document clustering. Adv. Data Anal. Classif. 2018, 12, 537–558. [Google Scholar] [CrossRef]
- Sutanto, T.; Nayak, R. Fine-grained document clustering via ranking and its application to social media analytics. Soc. Netw. Anal. Min. 2018, 8, 1–19. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1965; Volume 1, pp. 281–297. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining(KDD’96), Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Donath, W.E.; Hoffman, A.J. Lower Bounds for the Partitioning of Graphs. IBM J. Res. Dev. 1973, 17, 420–425. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, X.; Liu, X.; Wang, C.; Li, Z. A spectral clustering method with semantic interpretation based on axiomatic fuzzy set theory. Appl. Soft Comput. 2018, 64, 59–74. [Google Scholar] [CrossRef]
- Bianchi, G.; Bruni, R.; Reale, A.; Sforzi, F. A min-cut approach to functional regionalization, with a case study of the Italian local labour market areas. Optim. Lett. 2016, 10, 955–973. [Google Scholar] [CrossRef]
- Huang, Z. Clustering Large Data Sets with Mixed Numeric and Categorical Values. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD’97), Singapore, 22–23 February 1997; pp. 21–34. [Google Scholar]
- Cheung, Y.M.; Jia, H. Categorical-and-numerical-attribute data clustering based on a unified similarity metric without knowing cluster number. Pattern Recognit. 2013, 46, 2228–2238. [Google Scholar] [CrossRef]
- Ding, S.; Du, M.; Sun, T.; Xu, X.; Xue, Y. An entropy-based density peaks clustering algorithm for mixed type data employing fuzzy neighborhood. Knowl. Based Syst. 2017, 133, 294–313. [Google Scholar] [CrossRef]
- Ralambondrainy, H. A conceptual version of the K-means algorithm. Pattern Recognit. Lett. 1995, 16, 1147–1157. [Google Scholar] [CrossRef]
- He, Z.; Xu, X.; Deng, S. Scalable algorithms for clustering large datasets with mixed type attributes. Int. J. Intell. Syst. 2010, 20, 1077–1089. [Google Scholar] [CrossRef]
- Huang, Z. A Fast Clustering Algorithm to Cluster Very Large Categorical Data Sets in Data Mining. In Proceedings of the the SIGMOD Workshop on Research Issues on Data Mining and Knowledge Discovery (DMKD’97), Tucson, AZ, USA, 11 May 1997. [Google Scholar]
- Ji, J.; Pang, W.; Zhou, C.; Han, X.; Wang, Z. A fuzzy k-prototype clustering algorithm for mixed numeric and categorical data. Knowl. Based Syst. 2012, 30, 129–135. [Google Scholar] [CrossRef]
- Chatzis, S.P. A fuzzy c-means-type algorithm for clustering of data with mixed numeric and categorical attributes employing a probabilistic dissimilarity functional. Exp. Syst. Appl. 2011, 38, 8684–8689. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [PubMed]
- Du, M.; Ding, S.; Xue, Y. A novel density peaks clustering algorithm for mixed data. Pattern Recognit. Lett. 2017, 97, 46–53. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, B.; Huang, D.; Shen, L. Clustering Mixed Data by Fast Search and Find of Density Peaks. Math. Probl. Eng. 2017, 2017, 5060842. [Google Scholar] [CrossRef]
- Xie, J.; Girshick, R.; Farhadi, A. Unsupervised Deep Embedding for Clustering Analysis. In Proceedings of the 33nd International Conference on Machine Learning (ICML 2016), New York, NY, USA, 19–24 June 2016; pp. 478–487. [Google Scholar]
- Li, F.; Qiao, H.; Zhang, B. Discriminatively boosted image clustering with fully convolutional auto-encoders. Pattern Recognit. 2018, 83, 161–173. [Google Scholar] [CrossRef]
- Chen, G. Deep Learning with Nonparametric Clustering. Available online: http://arxiv.org/abs/1501.03084 (accessed on 13 January 2015).
- Hsu, C.C.; Huang, Y.P. Incremental clustering of mixed data based on distance hierarchy. Expert Syst. Appl. 2008, 35, 1177–1185. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Q.; Chen, Z.; Marsic, I.; Kumar, V.; Jiang, G.; Zhang, J. From Categorical to Numerical: Multiple Transitive Distance Learning and Embedding. In Proceedings of the 2015 SIAM International Conference on Data Mining (SIAM 2015), Vancouver, BC, Canada, 30 April–2 May 2015; pp. 46–54. [Google Scholar]
- David, G.; Averbuch, A. SpectralCAT: Categorical spectral clustering of numerical and nominal data. Pattern Recognit. 2012, 45, 416–433. [Google Scholar] [CrossRef]
- Jia, H.; Cheung, Y.M. Subspace Clustering of Categorical and Numerical Data with an Unknown Number of Clusters. IEEE Trans. Neural. Netw. Learn. Syst. 2018, 29, 3308–3325. [Google Scholar] [PubMed]
- Zheng, Z.; Gong, M.; Ma, J.; Jiao, L.; Wu, Q. Unsupervised evolutionary clustering algorithm for mixed type data. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC 2010), Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Liu, X.; Yang, Q.; He, L. A novel DBSCAN with entropy and probability for mixed data. Clust. Comput. 2017, 20, 1313. [Google Scholar] [CrossRef]
- Behzadi, S.; Ibrahim, M.A.; Plant, C. Parameter Free Mixed-Type Density-Based Clustering. In Proceedings of the 29th International Conference Database and Expert Systems Applications (DEXA 2018), Regensburg, Germany, 3–6 September 2018; pp. 19–34. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Hsu, C.; Lin, C. CNN-Based Joint Clustering and Representation Learning with Feature Drift Compensation for Large-Scale Image Data. IEEE Trans. Multimed. 2018, 20, 421–429. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. Available online: http://arxiv.org/abs/1312.6114 (accessed on 1 May 2014).
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS’14), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Jiang, Z.; Zheng, Y.; Tan, H.; Tang, B.; Zhou, H. Variational Deep Embedding: An Unsupervised and Generative Approach to Clustering. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence (IJCAI 2017), Melbourne, Australia, 19–25 August 2017; pp. 1965–1972. [Google Scholar]
- Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems 29 (NIPS’16), Barcelona, Spain, 5–10 December 2016; pp. 2172–2180. [Google Scholar]
- Lam, D.; Wei, M.Z.; Wunsch, D. Clustering Data of Mixed Categorical and Numerical Type with Unsupervised Feature Learning. IEEE Access 2015, 3, 1605–1613. [Google Scholar] [CrossRef]
- Bu, F. A High-Order Clustering Algorithm Based on Dropout Deep Learning for Heterogeneous Data in Cyber-Physical-Social Systems. IEEE Access 2018, 6, 11687–11693. [Google Scholar] [CrossRef]
- Aljalbout, E.; Golkov, V.; Siddiqui, Y.; Cremers, D. Clustering with Deep Learning: Taxonomy and New Methods. Available online: http://arxiv.org/abs/1801.07648 (accessed on 13 September 2018).
- Min, E.; Guo, X.; Liu, Q.; Zhang, G.; Cui, J.; Long, J. A Survey of Clustering with Deep Learning: From the Perspective of Network Architecture. IEEE Access 2018, 6, 39501–39514. [Google Scholar] [CrossRef]
- Zhang, W.; Du, T.; Wang, J. Deep Learning over Multi-field Categorical Data: A Case Study on User Response Prediction. In Proceedings of the European Conference on Information Retrieval (ECIR 2016), Padua, Italy, 20–23 March 2016; pp. 45–57. [Google Scholar]
- Bengio, Y.; Lamblin, P.; Dan, P.; Larochelle, H. Greedy layer-wise training of deep networks. In Proceedings of the Advances in Neural Information Processing Systems 19 (NIPS’06), Vancouver, BC, Canada, 4–7 December 2006; pp. 153–160. [Google Scholar]
- Ranzato, M.A.; Poultney, C.S.; Chopra, S.; LeCun, Y. Efficient Learning of Sparse Representations with an Energy-Based Model. In Proceedings of the Advances in Neural Information Processing Systems 19 (NIPS’06), Vancouver, BC, Canada, 4–7 December 2006; pp. 1137–1144. [Google Scholar]
- Luo, S.; Zhu, L.; Althoefer, K.; Liu, H. Knock-Knock: Acoustic object recognition by using stacked denoising autoencoders. Neurocomputing 2017, 267, 18–24. [Google Scholar] [CrossRef]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. J. Mach. Learn. Res. 2011, 12, 257–269. [Google Scholar]
- Rumelhart, E.D.; Hinton, E.G.; Williams, J.R. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Shelhamer, E.; Long, J.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar] [CrossRef] [PubMed]
- Bie, R.; Mehmood, R.; Ruan, S.S.; Sun, Y.C.; Dawood, H. Adaptive fuzzy clustering by fast search and find of density peaks. Personal Ubiquitous Comput. 2016, 20, 785–793. [Google Scholar] [CrossRef]
- Salvador, S.; Chan, P. Determining the number of clusters/segments in hierarchical clustering/segmentation algorithms. In Proceedings of the 2004 IEEE 16th International Conference on Tools with Artificial Intelligence (ICTAI 2004), Boca Raton, FL, USA, 15–17 November 2004; pp. 576–584. [Google Scholar]
- Zagouras, A.; Inman, R.H.; Coimbra, C.F.M. On the determination of coherent solar microclimates for utility planning and operations. Sol. Energy 2014, 102, 173–188. [Google Scholar] [CrossRef]
- Dua, D.; Taniskidou, E.K. UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml (accessed on 5 January 2019).
- Qian, Y.; Li, F.; Liang, J.; Liu, B.; Dang, C. Space Structure and Clustering of Categorical Data. IEEE Trans. Neural Netw. Learn. Syst. 2017, 27, 2047–2059. [Google Scholar] [CrossRef]
- Rand, W.M. Objective Criteria for the Evaluation of Clustering Methods. J. Am. Stat. Assoc. 1971, 66, 846–850. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. 1955, 2, 83–97. [Google Scholar] [CrossRef]


| Dataset | N | Mc | Mr | C |
|---|---|---|---|---|
| Iris | 150 | 0 | 4 | 3 |
| Vote | 435-203 | 16 | 0 | 2 |
| Credit | 690-37 | 9 | 6 | 2 |
| Abalone | 4177-9 | 1 | 7 | 21 |
| Dermatology | 366-8 | 33 | 1 | 6 |
| Adult_10000 | 10000 | 8 | 6 | 2 |
| Dataset | DPC-SDAE | k-prototypes | OCIL | DPC-M |
|---|---|---|---|---|
| Iris | 0.899 ± 0.078 | 0.793 ± 0.146 | 0.806 ± 0.094 | 0.860 |
| Vote | 0.891 ± 0.005 | 0.866 ± 0.004 | 0.887 ± 0.001 | 0.867 |
| Credit | 0.820 ± 0.010 | 0.748 ± 0.090 | 0.798 ± 0.101 | 0.809 |
| Abalone | 0.199 ± 0.009 | 0.165 ± 0.006 | 0.169 ± 0.007 | 0.194 |
| Dermatology | 0.806 ± 0.056 | 0.589 ± 0.079 | 0.680 ± 0.097 | 0.683 |
| Adult_10000 | 0.716 ± 0.004 | 0.650 ± 0.047 | 0.709 ± 0.006 | 0.715 |
| Dataset | DPC-SDAE | k-prototypes | OCIL | DPC-M |
|---|---|---|---|---|
| Iris | 0.894 ± 0.049 | 0.828 ± 0.072 | 0.832 ± 0.041 | 0.852 |
| Vote | 0.806 ± 0.008 | 0.767 ± 0.005 | 0.804 ± 0.002 | 0.797 |
| Credit | 0.705 ± 0.013 | 0.638 ± 0.066 | 0.673 ± 0.071 | 0.690 |
| Abalone | 0.812 ± 0.012 | 0.754 ± 0.004 | 0.778 ± 0.005 | 0.799 |
| Dermatology | 0.933 ± 0.017 | 0.821 ± 0.051 | 0.856 ± 0.046 | 0.865 |
| Adult_10000 | 0.593 ± 0.003 | 0.549 ± 0.023 | 0.589 ± 0.004 | 0.592 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, B.; Han, L.; Gou, Z.; Yang, Y.; Chen, S. Clustering Mixed Data Based on Density Peaks and Stacked Denoising Autoencoders. Symmetry 2019, 11, 163. https://doi.org/10.3390/sym11020163
Duan B, Han L, Gou Z, Yang Y, Chen S. Clustering Mixed Data Based on Density Peaks and Stacked Denoising Autoencoders. Symmetry. 2019; 11(2):163. https://doi.org/10.3390/sym11020163
Chicago/Turabian StyleDuan, Baobin, Lixin Han, Zhinan Gou, Yi Yang, and Shuangshuang Chen. 2019. "Clustering Mixed Data Based on Density Peaks and Stacked Denoising Autoencoders" Symmetry 11, no. 2: 163. https://doi.org/10.3390/sym11020163
APA StyleDuan, B., Han, L., Gou, Z., Yang, Y., & Chen, S. (2019). Clustering Mixed Data Based on Density Peaks and Stacked Denoising Autoencoders. Symmetry, 11(2), 163. https://doi.org/10.3390/sym11020163





