1. Introduction
With the increase in car ownership, traffic accidents, environmental pollution and oil shortage etc., are getting worse [
1]. To solve these problems, advanced driver assistance systems (ADAS) and battery electric vehicles (BEVs) are two important vehicle technologies [
2,
3]. Integrating these two advanced technologies, vehicles can achieve better driving safety, driving convenience and environmental friendliness.
To improve driving safety, driving convenience, etc., ADAS have been developed in recent decades [
4]. Among various ADAS technologies, adaptive cruise control (ACC) is one of the most widely used assistance system. The first ACC system has been on market since 1995 in Japan, in Europe since 1998, and in America since 2000. The first generation of ACC systems was mainly applied in high-end vehicles. Nowadays, the ACC system are available in vehicles ranging from high-end to mid-range vehicles [
5]. With the development of new energy vehicles, the application of ACC systems has gradually evolved from traditional fuel vehicles to BEVs. As driving and braking for BEVs can be realized by the motor, the control of BEVs is relatively easy, so there is more room for the optimization of ACC strategies in BEVs. The ACC is an extension of traditional cruise control, and the distance control system is integrated on the basis of the traditional cruise system. Therefore, both the cruise control function and the following function can be achieved [
6]. When there is no vehicle in front of the vehicle with the ACC function (henceforth referred to as the own vehicle), the own vehicle is in a state of speed control. When a vehicle (henceforth referred to as the front vehicle) appears in front of the own vehicle, the own vehicle is in a state of distance control, and the driving process of distance control will be referred to as the car-following process in this paper. During the car-following process, the own vehicle can ensure safety by tracking the velocity of the front vehicle or keeping an expected spacing [
7].
The battery is used as a power source, and the motor is used to provide the driving force for the BEV, so there are different dynamic characteristics and energy limitations compared with fuel vehicles [
8,
9,
10]. For the different dynamic characteristics, the acceleration characteristics and deceleration characteristics of BEVs are different from those of fuel vehicles [
8,
9]. In addition, the acceleration, desired acceleration, and the change rate of acceleration (jerk) can reflect the acceleration characteristics and deceleration characteristics. These variables are referred to as acceleration-related variables in this paper. So acceleration-related variables are extremely important in the study of performance optimization for BEVs. For energy limitations, the energy density of batteries for BEV is lower than for conventional diesel and gasoline, which limits the distance traveled by BEVs on a full charge [
10]. In addition, BEVs are charged for a long time, which places higher demands on the distance traveled by a BEV in one charge. Therefore, it is necessary to improve the energy economy of BEVs.
To achieve the optimization for multiple objectives of the ACC system, an effective control algorithm is necessary. There are some control algorithms for solving the multi-objective optimization, including sliding mode control, particle swarm optimization, and genetic algorithm [
11,
12,
13]. However, the model predictive control (MPC) algorithm is one of the most effective methods for solving the multi-objective optimization problem [
14]. The advantages of the MPC algorithm for multi-objective optimization can be summarized as follows: predictive control for multi-objective optimization is based on a model, so the process of modelling is convenient; multiple objectives can be integrated into an MPC framework, which can be easily handled by the designer; the multiple objectives are optimized in a method of online receding horizon optimization, which can compensate for errors due to inaccuracies in modelling [
15,
16,
17,
18].
Some studies related to performance optimization of ACC system for BEV have been carried out in MPC frameworks. In [
10], an efficient cruise control was proposed to improve the driving range of the vehicle, where the speed reference for the own vehicle was obtained based on upcoming traffic signals, while safety was guaranteed by maintaining a safe minimum spacing between two vehicles. Energy efficiency control was achieved based on a variety of traffic information to increase the driving range in [
19]. Safety was ensured by maintaining a suitable spacing between the front vehicle and the own vehicle. In [
20], an ACC control strategy was designed for semi-autonomous vehicles, and the potential field method was applied to the upper controller based on MPC, and the optimization for torque was considered in the lower controller. In [
21], energy consumption was reduced with terrain information based on the motor efficiency to increase the traveling distance. In addition, velocity was selected as the variable to be optimized in order to reduce the energy consumption. In [
22], to minimize energy consumption and maximize recovery, an eco-adaptive cruise control was proposed in consideration of safety and comfort. In [
23], Schwickart et al. proposed an eco-cruise controller to minimize energy consumption, and a compromise between energy consumption and speed-reference tracking was achieved.
From the above analysis, various objectives, including safety, tracking, comfort and energy economy, have been considered in research on ACC for BEV. Most research has focused on comfort and energy economy. In order to achieve better comfort and energy economy, BEVs should be in a steady driving state. In addition, the amplitude of fluctuation of the acceleration-related variables should be as small as possible in order for safety to be guaranteed. Therefore, control strategies for good comfort and energy economy usually come with strict constraints on acceleration-related variables, resulting in a slow acceleration response for the own vehicle. However, it also makes the own vehicle unable to perform high-jerk operations when the necessary driving or brake torque is required. This makes it difficult for the own vehicle to respond quickly to changes in the movement of the front vehicle, limiting the tracking performance. Better tracking would decrease the comfort and energy economy, and worse tracking would result in frequent cut ins. In addition, the improvement of tracking and the improvement comfort and energy economy are in conflict. Because the BEVs have different dynamic characteristics and energy limitations compared with traditional fuel vehicles, it is important to achieve a good compromise among the different control objectives.
Real-time changes in the motion states of the own vehicle and the front vehicle result in time-varying driving conditions. The MPC with constant weights does not adapt well to real-time changes in driving conditions, and cannot effectively solve the conflict between the improvement of tracking and the improvement of comfort and energy economy. Therefore, real-time weight adjustment is considered in this paper. The relative velocity is able to reflect the motion states of the two vehicles and the driving conditions, and is also related with the spacing error and velocity of the front vehicle. Therefore, the relative velocity is selected as the main variable in the strategy for weight adjustment to improve tracking. To reduce the computational complexity, the weight matrix is in symmetric form along the diagonal of the matrix, and the strategy of weight adjustment is designed as a simple mathematical formula based on the relationship between relative velocity and different weights.
In this paper, ACC is studied for BEV for the car-following process. In addition, multiple objectives, including safety, tracking, comfort and energy economy are optimized in the car-following process. The acceleration-related variables are important in the research of ACC for BEV, so the acceleration-related variables are fully considered in the modeling and control strategies for ACC systems in this paper. The contribution of this paper is that the weight adjustment strategy is proposed to improve the tracking performance, in which some weights in MPC can be adjusted according to the relative velocity of two vehicles in real time. The conflict described above can be effectively solved through the strategy for the weight adjustment.
2. Model for BEV
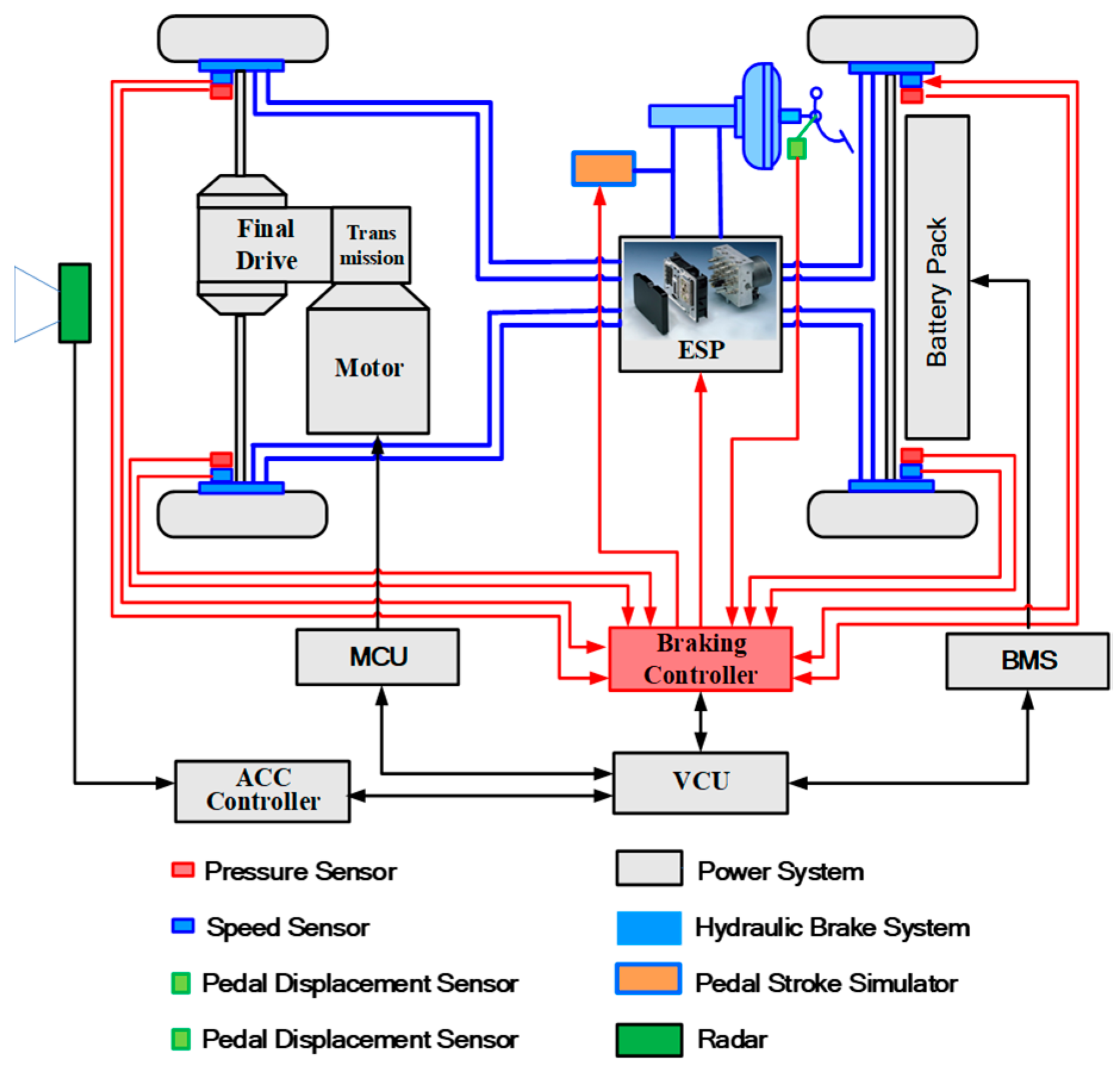
In this paper, a front-wheel-drive BEV was selected as the object in order to establish the BEV model. A diagram of the structure of the BEV is shown in
Figure 1. The lithium battery and permanent magnet synchronous motor are two important components of the BEV.
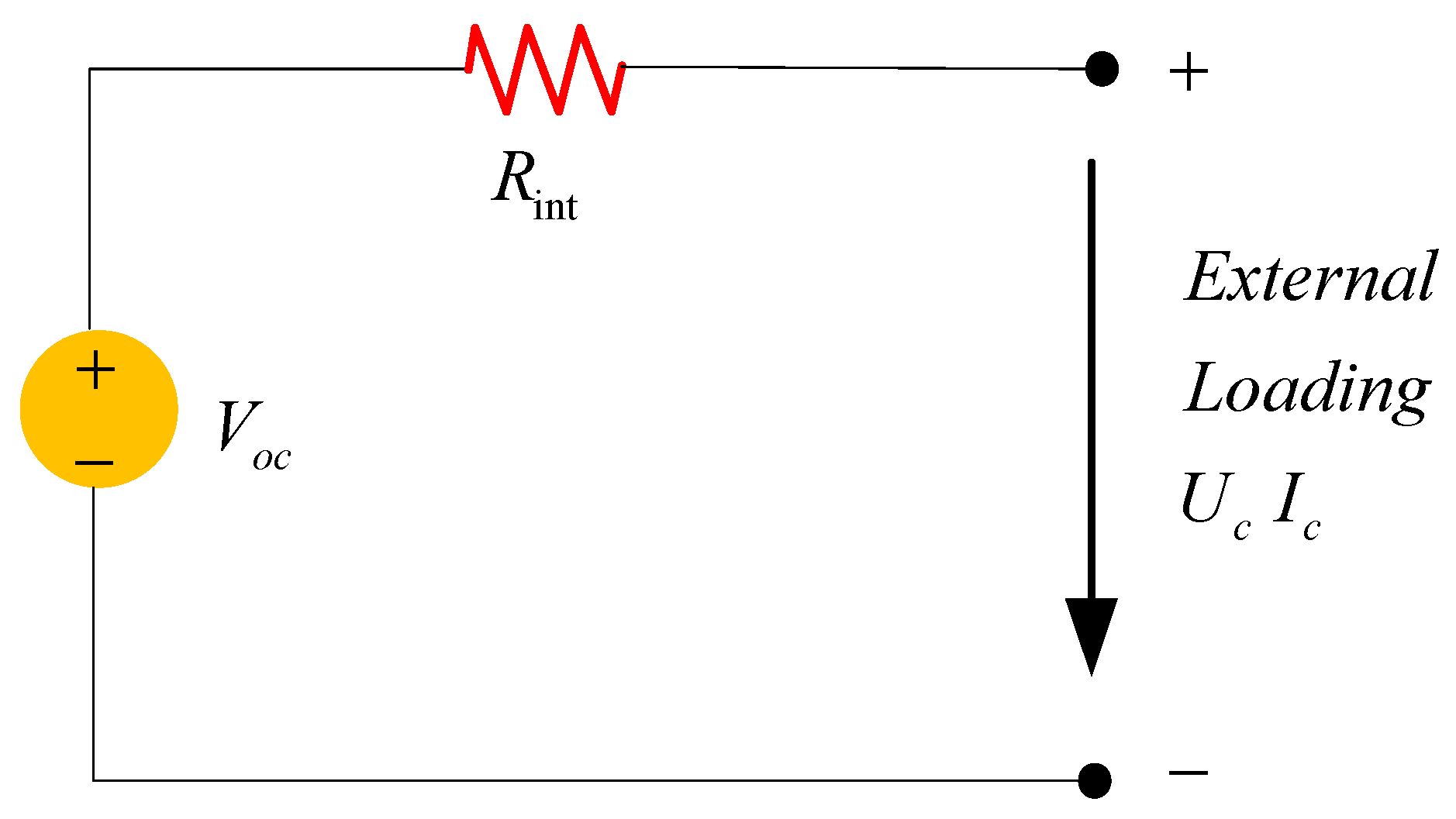
The vehicle model was designed in the CarSim software, but the complete powertrain model of the BEV is not included in Carsim, so external models of the motor and battery were added. An internal resistance model was adopted for the battery component [
24] as in
Figure 2, wherein, the
Voc and
Rint are the open circuit voltage and battery internal resistance, respectively, and the
Uc and
Ic are the voltage and current of external load. The efficiency of the battery related to the internal resistance of the battery is considered in the battery model. The efficiency of the motor related to the speed and torque of the motor is considered in the motor model [
24,
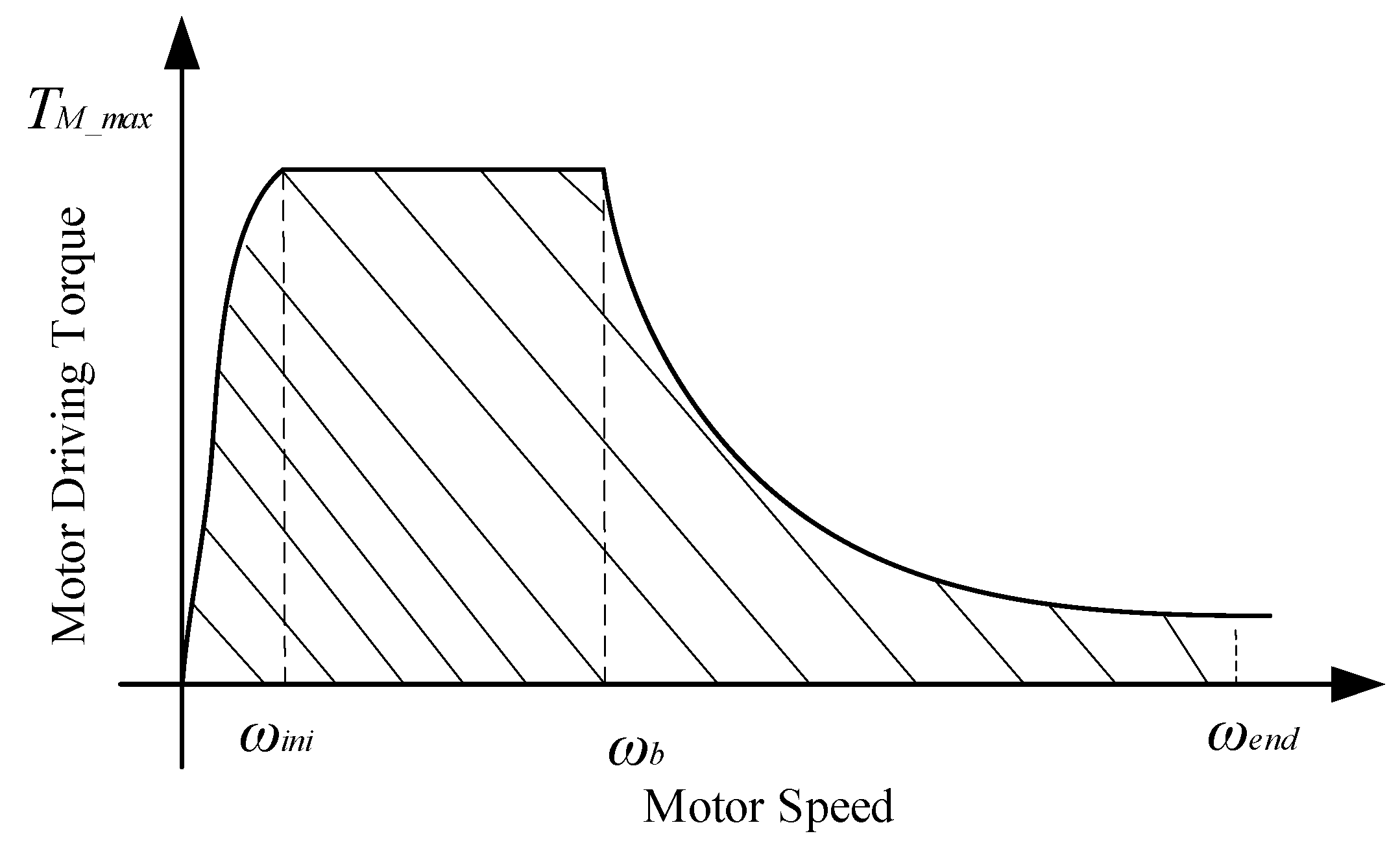
25]. The maximum torque and speed characteristics for the motor are shown in
Figure 3. The maximum torque and speed characteristics are defined as follows:
where
TM_max is the maximum driving torque,
PM_max is the peak power of the motor,
fm(
ωm) is the correction for the motor torque related to the motor efficiency,
ωm is the angular velocity of the motor,
ωini is the minimum speed for constant torque control,
ωb is the base speed, and
ωend is the highest speed. The main parameters for the BEV model are listed in
Table 1.
3. Proposed ACC System
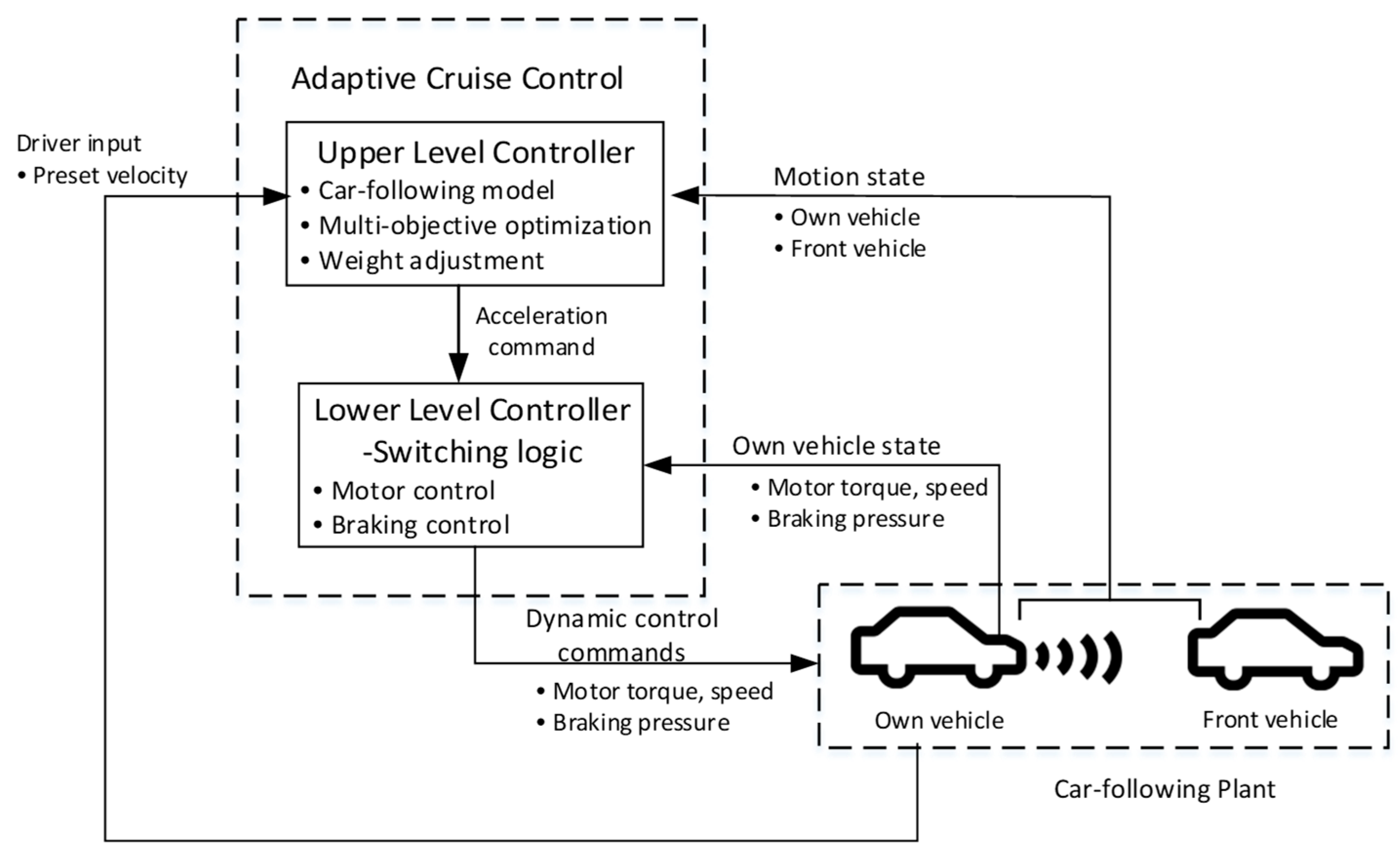
The ACC system in this paper adopts a hierarchical structure comprising an upper controller and a lower controller [
26]. In addition, the upper controller is used as a decision layer, and the lower controller is used as a control layer. A diagram of the hierarchical control structure is presented in
Figure 4. The focus of this paper is on the upper controller.
When there is no vehicle in front of the own vehicle, the own vehicle is in the speed control mode, and the own vehicle drives at a speed preset by the driver. When there is a vehicle in front of the own vehicle, the own vehicle is in distance control mode. The distance control process is also referred to as the car-following process. The upper controller for the car-following process includes a car-following model, a multi-objective optimization algorithm, and a weight adjustment strategy. The upper controller calculates the optimized acceleration to act on the lower controller on the basis of the motion state of the own vehicle and the front vehicle. The lower controller includes a mode switching strategy, a motor drive control strategy, an ESC-based brake control strategy, and so on. The lower controller tracks the control command of the acceleration from the upper controller, and produces the brake pressure and motor torque signals that will act on the own vehicle.
4. Car-Following Model
To design the upper controller, the car-following model needs to first be established. In this paper, the car-following model is based on the longitudinal motion relationship of the front vehicle and the own vehicle.
The spacing ∆
s and relative velocity
vrel at moment
k are defined as follows:
where the
sf and
s are the distance of the front vehicle and the own vehicle, respectively, and
vf and
v are the speeds of the front vehicle and the own vehicle, respectively.
At moment
k+1, the distances of the front vehicle and the own vehicle are defined as follows:
where
af and
a are the acceleration of the front vehicle and the own vehicle, respectively, and
Ts is the sampling time.
At moment
k+1, the velocity of the front vehicle and the own vehicle are defined as follows:
At moment
k+1, the spacing and relative velocity are defined as follows:
Combining Equations (2)–(5) and (8), Equation (10) can be obtained:
Combining Equations (3), (6), (7) and (9), Equation (11) can be obtained:
When the upper controller for the ACC system is designed, due to the foundation of the lower controller, it can be assumed that the actual acceleration of the own vehicle
a and the control command for acceleration (also called expected acceleration)
u satisfy the following relationship [
15,
27,
28]:
where
u is the control command for acceleration,
τ is the time constant of the lower controller.
The rate of change of acceleration is also called jerk, and the jerk at moment
k can be defined as follows:
At moment
k + 1, the jerk can be defined as follows:
Combining Equations (12) and (14), Equation (15) can be obtained:
State vectors contain the spacing, the speed of the own vehicle, the relative velocity, the acceleration of the own vehicle, and the jerk of the own vehicle, and they are defined as:
The disturbance is the acceleration of the front vehicle, and it can be defined as:
Combining Equations (7), (10)–(12) and (15), the car-following model in the longitudinal direction is defined as follows:
where
5. Multi-Objective Optimization Algorithm
In the multi-objective optimized upper controller, the control objectives enable the own vehicle to guarantee safety, tracking, comfort and energy economy in the car-following process. To achieve these control objectives, the multiple objectives are analyzed based on the car-following model. The multiple objectives are transformed into the corresponding system constraints and performance indicators. In addition, the optimization for multiple objectives during the driving process is finally transformed into a constrained optimization proposition.
∆
sdes is the expected spacing obtained from the constant time headway (CTH) spacing policy,
δ is the difference between the real spacing and the expected spacing, and ∆
sdes and
δ at moment
k can be defined as follows:
where
d0 is the fixed distance between the two vehicles when the vehicle speed is low and zero,
th is the time headway.
To ensure the tracking in the car-following process, the error of spacing and relative velocity should be as small as possible. The ACC system should regulate the actual spacing to the expected spacing calculated by the spacing strategy, and the ACC system should regulate its velocity to the velocity of the front vehicle.
To improve the comfort during the car-following process, the range of fluctuation for acceleration and jerk should be minimized:
From the above analysis, the spacing error, relative velocity, acceleration of the own vehicle and jerk of the own vehicle are chosen as the performance vector, and the performance vector is defined as follows:
The following relationship can be established between the performance vector and the state variable:
where
During the car-following process, a smooth system response is preferred. To smooth the response, the exponential decay function is introduced as a reference trajectory for the performance vector.
The coefficient for the spacing error in the reference trajectory is defined in Equation (25), and other coefficients can be defined in a similar way.
where
δr is the reference trajectory for the error of spacing, and
α is the time constant of the reference trajectory for the spacing error.
The system response is smoothed as follows:
where the
ρδ,
ρvrel,
ρa and
ρj are the coefficients in the reference trajectory, and
ρδ is the coefficient of the spacing error, and
ρvrel is the coefficient of relative velocity,
ρa is the coefficient for the acceleration of the own vehicle, and
ρj is the coefficient for the jerk of the own vehicle. The reference trajectory matrix is in symmetrical form along the diagonal of the matrix in order to reduce the complexity of the calculation.
The values of these coefficients are between 0 and 1. Along the reference trajectory, the performance vector smoothly approaches zero, rather than directly approaching zero.
As for energy economy, this is related to acceleration. In addition, acceleration is determined by the acceleration control command. Therefore, the acceleration control command is selected as the performance index for energy economy [
29]. To improve the energy economy, the fluctuation range for the control command should be minimized:
No matter what control algorithm is used, safety is the primary objective of an ACC system. Although we can guarantee a safe expected spacing through the spacing strategy, collision is likely to occur before reaching the expected spacing. Therefore, for the purpose of ensuring the safety of the two vehicles throughout the driving process, the actual vehicle spacing must be constrained as follows:
where
dc is the minimum safe spacing between two vehicles.
Taking into account the limitations with respect to the vehicle’s own capacity, the velocity, acceleration, jerk and acceleration command of the own vehicle need to be constrained. The constraints can be defined as follows:
Because of the advantages of MPC in achieving multi-objective optimization [
29,
30,
31], the MPC is applied to the multi-objective optimization of the ACC system. In addition, considering the different objectives in Equations (21), (22) and (27) and the reference trajectory in Equation (26), the discretized objective function based on MPC theory can be obtained in symmetrical form:
where
yp(
k +
i|
k) is the prediction of the performance vector for the moment
k +
i at the moment
k,
p is the predictive horizon,
m is the control horizon,
Q and
R are the weight matrices, and
u(
k +
i) is the control command at moment
k +
i.
The objective function in Equation (30) combined with the constraints in Equations (28) and (29) can be transformed into an optimization problem that can be solved through quadratic programming [
32,
33,
34].
6. Strategy for Weight Adjustment
In the car-following process, the motion states of the own vehicle and the front vehicle change with respect to time, resulting in the variation of driving conditions in real time. The MPC with constant weights does not adapt well to changes in driving conditions, which limits the performance of the ACC systems. Therefore, a strategy for weight adjustment is proposed in the MPC framework to promote the improvement of tracking performance. In addition, the conflict between the improvement of tracking and the improvement of comfort and energy economy can be effectively solved.
The
Q is in symmetrical form along the diagonal; the symmetric form can be applied to reduce computational complexity, and can be defined as:
R in the objective function can be defined as:
where the
wδ(
k),
wvrel(
k),
wa(
k) and
wj(
k) in the
Q matrix are the weights corresponding to the spacing error, relative velocity, and acceleration and jerk of the own vehicle at moment
k,
wu(
k) in the
R matrix is the weight corresponding to the control command of the acceleration at moment
k.
There are five weights (wδ, wvrel, wa, wj and wu) in the objective function, but only four weights (wδ, wvrel, wa and wj) are considered in the strategy for weight adjustment. The reason for this is that a constant value for wu can ensure good performances for the controller in a series of trial and error operations, and there is no need to adjust the weight wu in real time.
Constant weights are also referred to as initial weights, and are considered as the basis of strategy for the weight adjustment. The initial weights wδ(0), wvrel(0), wa(0), wj(0) and wu(0), corresponding to wδ(k), wvrel(k), wa(k), wj(k) and wu(k) obtained from a series of trial-and-error operations, are 1, 10, 1, 1 and 1, respectively. Moreover, the safety, tracking, comfort and energy economy are also considered in the selection of the initial weights.
To reduce the complexity of the weight adjustment, adjustable weights can be divided into two categories. One of these is the relative velocity, and while the other corresponds to the spacing error, acceleration, and jerk of the own vehicle. In the MPC with constant weights, the ratio of the two kinds of the weight is 10, which is also referred to as the initial ratio.
When vrel < 0, the spacing between the two vehicles decreases gradually. The greater the absolute value of relative velocity, the faster the spacing between the two vehicles decreases. If the own vehicle is in this state for a long time, there will be a collision between the own vehicle and the front vehicle. Therefore, the velocity of the own vehicle should be adjusted as soon as possible to be close to the velocity of the front vehicle. The weight for the relative velocity should be bigger, and the weights of spacing error, acceleration and jerk should be smaller, so as to regulate the velocity of the own vehicle at close to the velocity of the front vehicle. The corresponding ratio is greater (>10). The greater the absolute value of the relative velocity, the bigger the change in weights relative to the initial weights and the bigger the change in ratio relative to the initial ratio.
When vrel > 0, the spacing between the two vehicles increases gradually. In addition, the greater the absolute value of the relative velocity, the faster the spacing between the two vehicles increases. If the vehicle is in this state for a long time, the spacing between the two vehicles will increase, and greater spacing will result in worse tracking for the expected spacing. Therefore, the spacing between the two vehicles should be adjusted as soon as possible to be close to the expected spacing. The weights of error of spacing, acceleration and jerk should be bigger, the weight for the relative velocity should be smaller, in order to regulate the spacing to be close to the expected spacing. The corresponding ratio is smaller (<10). The greater the absolute value of the relative velocity, the bigger the change in weight relative to the initial weight, and the bigger the change in ratio relative to the initial ratio.
From the above analysis, the weights in the
Q matrix should be adjusted according to relative velocity. The relationship between the relative velocity and the weights are listed in
Table 2.
Therefore, in this paper, relative velocity is selected as the main variable in the weight adjustment strategy to improve tracking while ensuring the other control objectives. In addition, the weights in
Q at moment
k are defined in mathematical form as follows:
where
When vrel(k) < 0, wvrel(k) is adjusted to increase, and wδ(k), wa(k) and wj(k) are adjusted to decrease; when vrel(k) > 0, wvrel(k) is adjusted to decrease, and wδ(k), wa(k) and wj(k) are adjusted to increase. In the definition of weights, the nvrel(k − 1) is the normalization function changing the range for vrel(k) from (−∞, +∞) to (−1,1), and r(k) is used to make the sum of all adjustable weight coefficients equal to 1. The driving condition of vrel = 0 is also considered in Equation (33), and the ratio in this driving condition is 10, and the weights in this driving condition are 1/13, 10/13, 1/13 and 1/13, respectively.
7. Simulation Experiment and Discussion
7.1. Method
The purpose of this subsection is to describe a method of performance evaluation for ACC systems. Two different ACC systems are compared for three different scenarios, one is the ACC system with weight adjustment (MPC_ADJ), and the other is the ACC system with constant weight (MPC_CON). The difference between the two ACC systems is that some weights in MPC_ADJ can be adjusted in real time, while the weights in MPC_CON are constant and equal to the corresponding initial weights.
The minimum safe spacing is an important indicator for evaluating safety during the driving process. When the spacing is greater than the minimum safe spacing, the driving process is considered to be safe. In [
35], a method of root mean square estimate (RMSE) of velocity error was used to evaluate the tracking of velocity. In this paper, the RMSEs of the spacing error and relative velocity throughout the entire simulation process were used to evaluate tracking of the expected spacing and velocity of the front vehicle. In addition, the RMSEs for the spacing error and relative velocity are defined in Equations (36) and (37). With respect to comfort, the maximum absolute value for jerk was used as the comfort criterion [
36]. Energy economy is evaluated on the basis of the rate of SOC change and distance.
where
n is the total number of summation, and
δ(
i) and
vrel(
i) are the spacing error and relative velocity at moment
i.
The three scenarios are as follows: (1) the speed of the front vehicle changes; (2) cut in; and (3) hard brake. The settings for the three simulated scenarios can be found in
Table 3, where ∆
s_
ini is the initial vehicle spacing,
vrel_
ini is the initial relative velocity,
v_ini and
vf_
ini are the initial speed for the own vehicle and the front vehicle, respectively, and
a_
amp is the amplitude of acceleration for the front vehicle. The parameters of the optimization algorithm are shown in
Table 4. The control strategies were designed in the Matlab/Simulink, and verified through co-simulation in Carsim.
7.2. Scenario 1
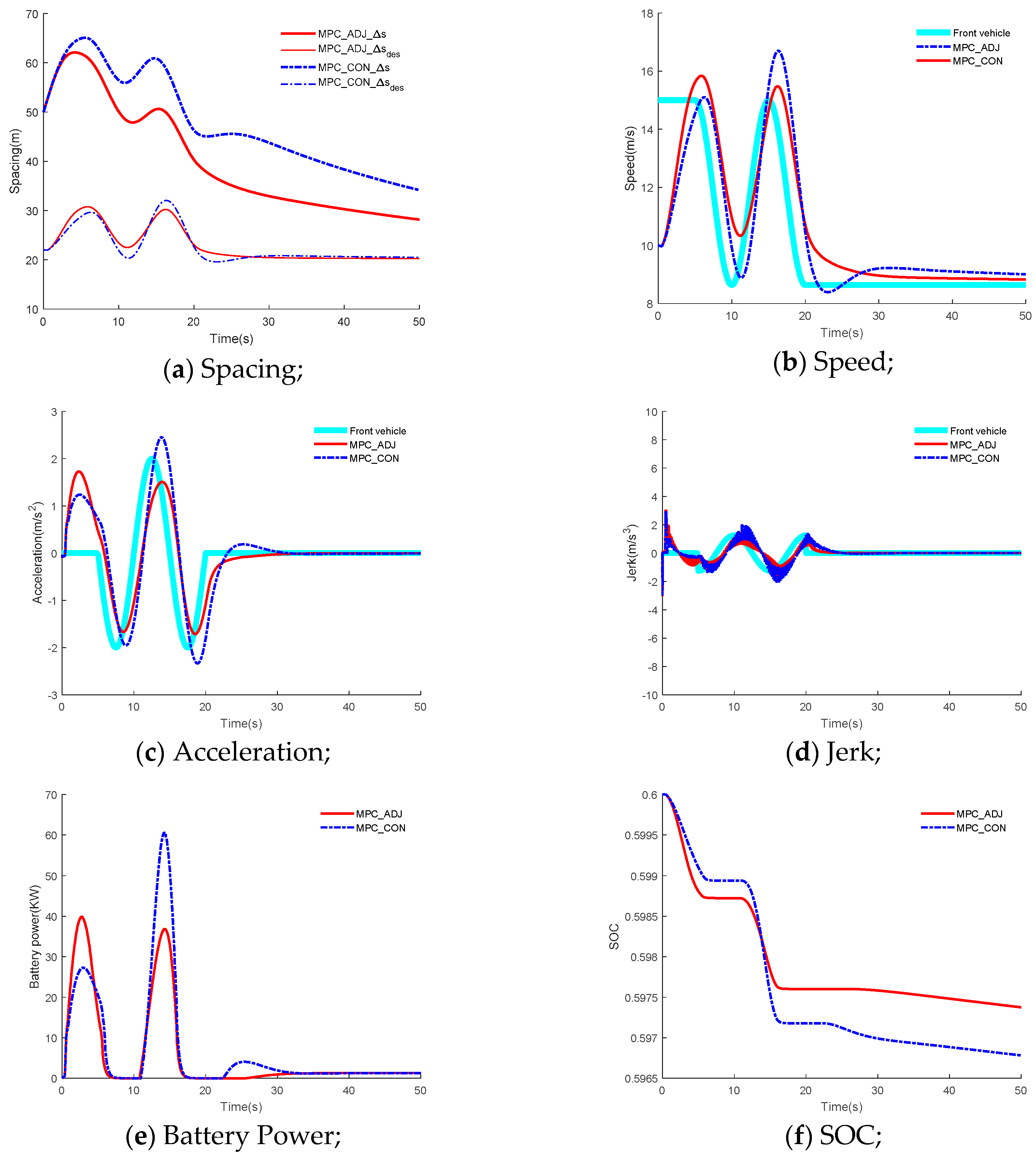
In scenario 1, the speed of the front vehicle changes. This scenario examines the speed adjustment and tracking capability of the own vehicle when the speed of the front vehicle changes in a single lane. The simulation results for scenario 1 are shown in
Figure 5. From
Figure 5a, it can be seen that the spacing in the two ACC systems is larger than 5 m, so the safety is ensured in both MPC_ADJ and MPC_CON. The RMSEs of the spacing error for MPC_CON and MPC_ADJ are 26.04 m and 19.02 m, respectively, and the tracking improvement for the expected spacing is 26.27% with respect to MPC_CON. In addition, the RMSEs of the relative velocity for MPC_CON and MPC_ADJ are 1.66 m/s and 1.54 m/s, respectively, and the improvement of tracking for the velocity of the front vehicle is 7.23% compared to the MPC_CON. The tracking performance for the expected spacing and velocity of the front vehicle is improved. This is because the weight adjustment strategy is applied for MPC_ADJ, and the weights can be adjusted to adapt to different driving conditions. From
Figure 5b,c, it can be seen that the range of speed and acceleration fluctation in MPC_ADJ is larger than in MPC_CON before 10 s; this is because when the
vrel > 0, greater weights are applied for spacing errors, and the own vehicle adjusts in response to speed, acceleration and jerk in order to reduce spacing error.
In
Figure 5d, the maximum absolute values for jerk in the two ACC systems are less than 3 m/s
3, which is the maximum value accepted by passengers. Therefore, comfort is ensured in both MPC_ADJ and MPC_CON. From
Figure 5e, the peak values of battery power are greater in the MPC_ADJ before 10 s, and after 10 s, the peak values of battery power are smaller in MPC_ADJ. From
Figure 5f, the change of SOC in MPC_ADJ is smaller than MPC_CON. In addition, the rate of SOC change and the distance for MPC_ADJ and MPC_CON are 0.0049 km
−1 and 0.0061 km
−1, the improvement of the index of the energy economy is 19.66%. The reasons for the improvement in energy economy include the facts that the weight adjustment strategy is adopted in MPC_ADJ, and a good compromise between fast response and the reduction of system response fluctuation is achieved in MPC_ADJ. From
Figure 5g,h, the peak values for the brake pressure and driving torque in MPC_ADJ are smaller throughout most of the simulation time. The smaller peak values of brake pressure correspond to less kinetic waste, and the smaller peak values of driving torque for the motor correspond to lower energy consumption. Therefore, the energy economy is improved.
From the above analysis, because the MPC_ADJ adopts the weight adjustment strategy, the ACC system is able to adapt to different driving conditions. In addition, a good compromise between rast response and reduced system response fluctuation is achieved in MPC_ADJ. Therefore, in scenario 1, based on achieving safety, tracking and comfort, the MPC_ADJ achieves a better performance in terms of energy economy compared with MPC_CON.
7.3. Scenario 2
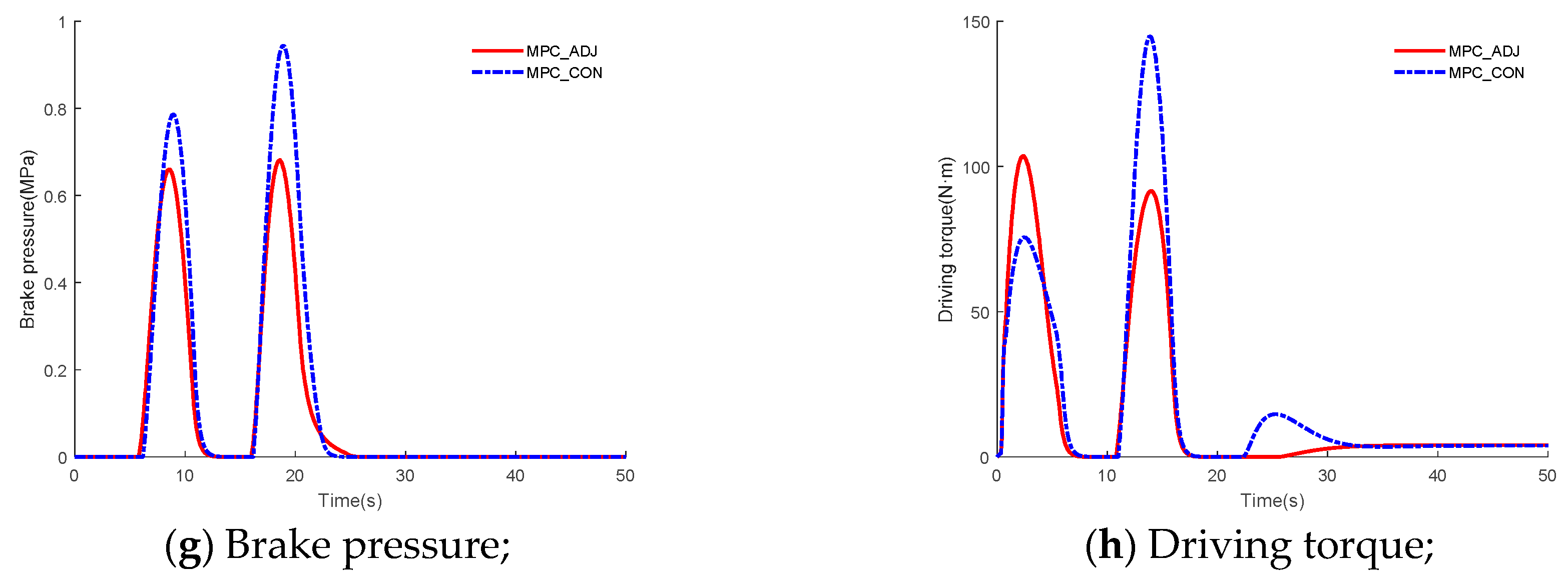
In the cut in scenario, during the driving process of the own vehicle, the front vehicle of the adjacent lane suddenly changes lane, and the front vehicle is inserted in front of the own vehicle. The simulation results in scenario 2 are shown in
Figure 6. From
Figure 6a, it can be seen that both ACC systems take effective braking measures to avoid collision after the front vehicle performs a cut-in operation. In addition, the spacing is larger than 5 m in MPC_ADJ and MPC _CON, so safety is guaranteed in both ACC systems. The RMSEs of the spacing error for MPC_ CON and MPC_ADJ are 6.35 m and 5.80 m, respectively, and the improvement of tracking for the expected spacing is 8.66% compared to the MPC_CON. In addition, the RMSEs of the relative velocity for MPC_CON and MPC_ADJ are 1.43 m/s and 1.39 m/s, respectively, and the improvement of tracking for the velocity of the front vehicle is 2.8% with respect to the MPC_CON. The tracking performance for the expected spacing and velocity of the front vehicle are improved. This is because the weight adjustment strategy is applied in MPC_ADJ, and the weights can be adjusted to adapt to different driving conditions. From
Figure 6b,c, it can be seen that the fluctuation range of speed and acceleration in MPC_ADJ is smaller than in MPC_CON after 15 s. This is because when
vrel > 0, the greater weight is applied for spacing error, acceleration and jerk, and the vehicle adjusts in response to the speed, acceleration and jerk in orer to reduce the spacing error.
From
Figure 6d, it can be seen that the maximum absolute values for jerk in the two ACC systems are less than 3 m/s
3, which is the maximum jerk for ordinary passengers. Therefore, comfort is ensured in both ACC systems. From
Figure 6e, the peak values of the battery power are smaller for MPC_ADJ throughout the entire simulation period. However, in MPC_CON, the maximal peak values of the battery power are 53.69 KW. From
Figure 6f, the change in SOC is smaller in MPC_ADJ. In addition, the rates of the SOC change and distance for the MPC_ADJ and MPC_CON are 0.0028 km
−1 and 0.0039 km
−1, respectively, and the improvement of the energy economy index is 28.84%. The reason for the improvement in energy economy in the cut in scenario is that the weight adjustment strategy is adopted in order to improve the tracking performance in MPC_ ADJ. In addition, a good compromise between fast response and reduction of system response fluctuation is achieved. In
Figure 6g,h, the peak values of the brake pressure and driving torque are smaller in MPC_ADJ compared to the MPC_CON. For the entire simulation time, smaller peak values of the brake pressure are able to reduce loss of kinetic energy during the braking process, and smaller driving torque is able to reduce energy consumption during the driving process.
In summary, because the MPC_ADJ adopts the weight adjustment strategy, the ACC system can adapt well to different driving conditions. In addition, a good compromise between fast response and the reduction of system response fluctuation is achieved in MPC_ADJ. Therefore, in the cut in scenario, based on ensuring the other control objectives, MPC_ADJ achieves better tracking performance compared with MPC_CON. While the tracking is improved, the energy economy is also improved.
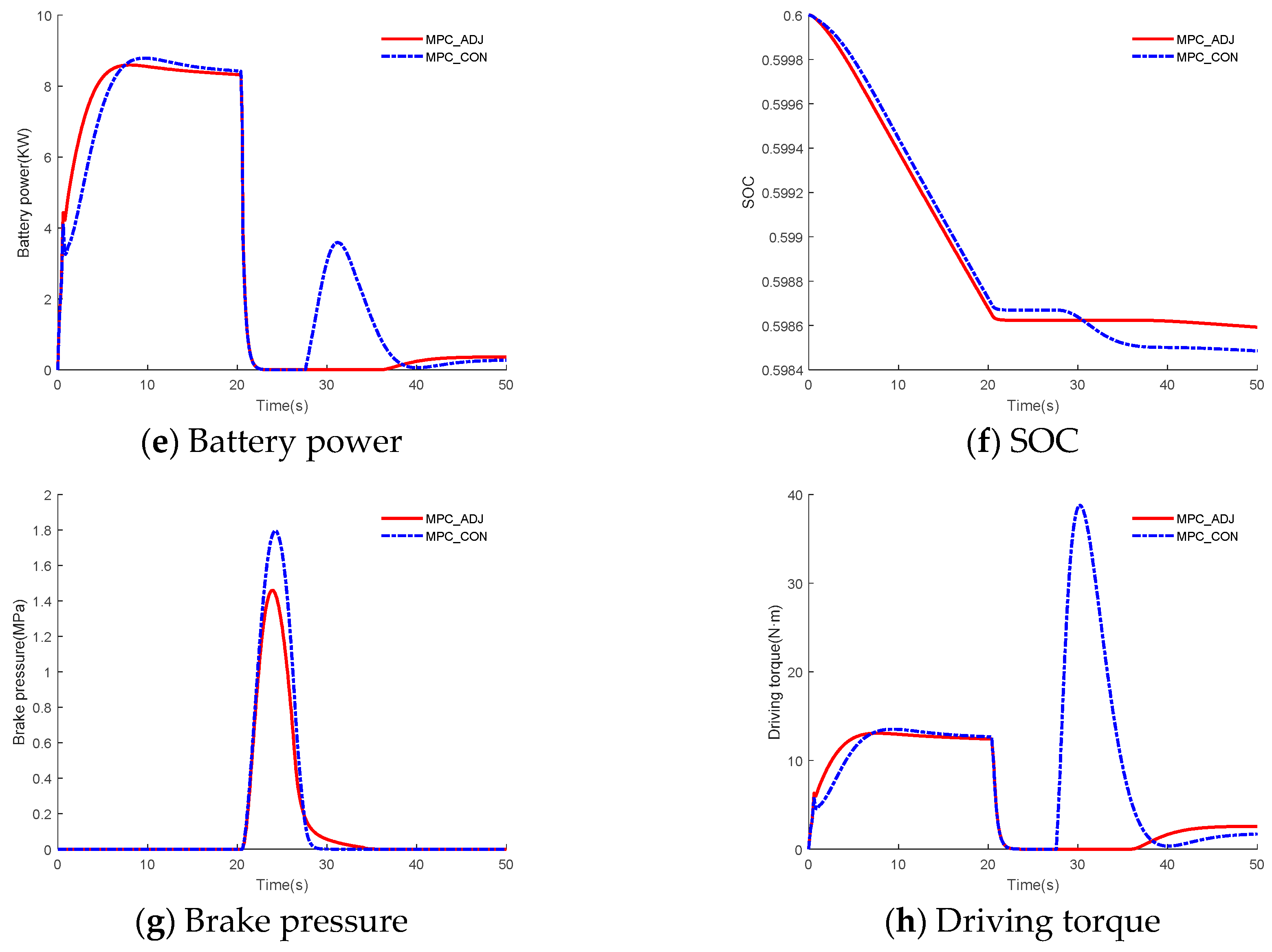
7.4. Scenario 3
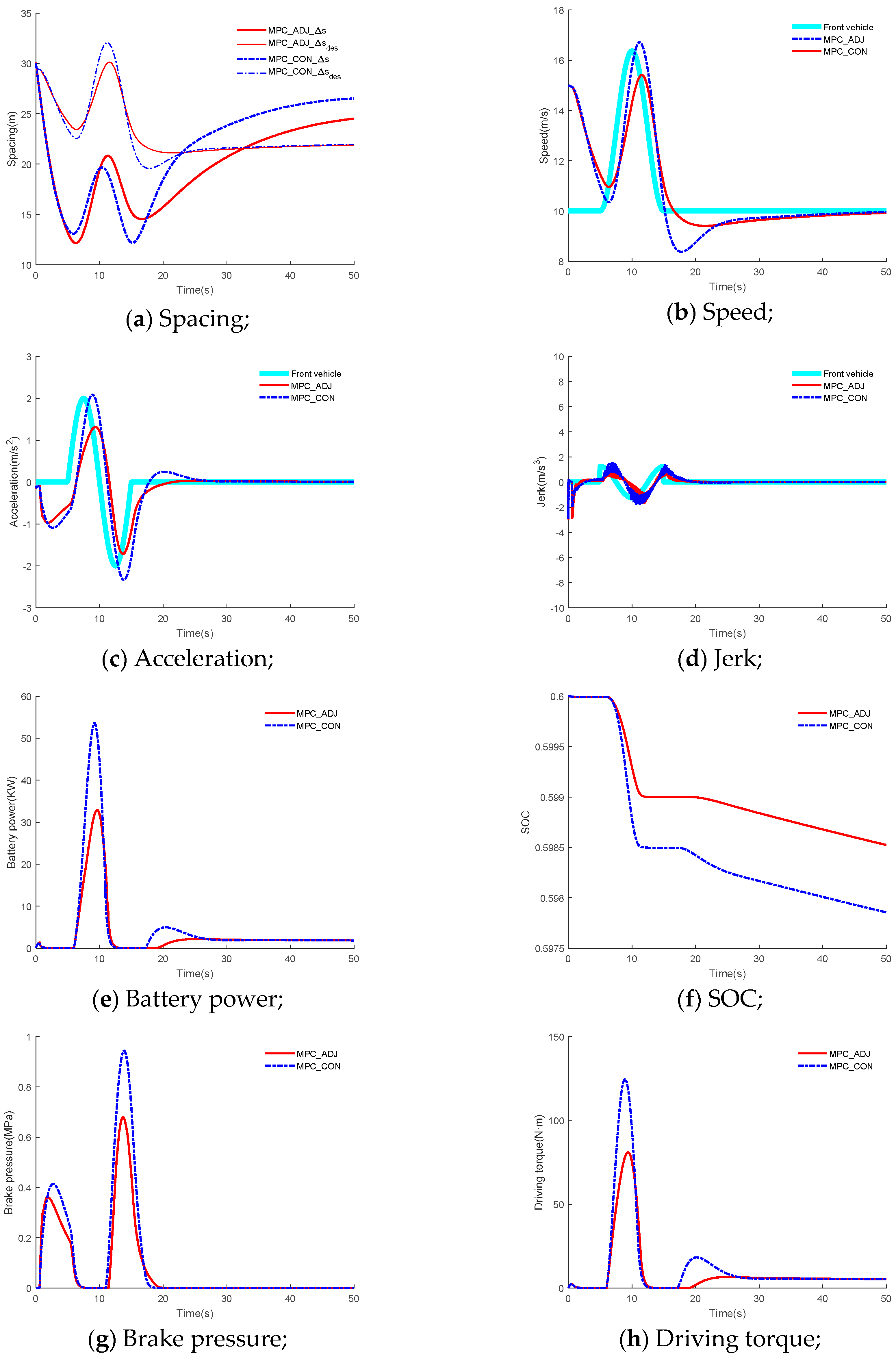
The scenario hard brake scenario investigates a situation in which the two vehicles are close together, the front vehicle suddenly brakes violently, and the own vehicle takes effective measures to avoid collision. Therefore, the hard brake scenario can effectively reflect the safety of the ACC system. The simulation results in scenario 3 are shown in
Figure 7. From
Figure 7a, at 20 s, the front vehicle suddenly brakes violently, and both ACC systems engage emergency braking to avoid collision. The spacing is larger than 5 m throughout the simulation process in the two ACC systems. Therefore, the safety of the two ACC systems is ensured. The RMSE of the spacing error for MPC_CON and MPC_ ADJ is 22.27 m and 12.16 m, respectively, and the improvement of tracking for the expected spacing is 45.40% with respect to the MPC_CON. In addition, the RMSE of the relative velocity for MPC_CON and MPC_ADJ is 1.21 m/s and 1.19 m/s, respectively, and the improvement of tracking for the velocity of the front vehicle is 1.65% with respect to MPC_CON. The tracking performance for the expected spacing and velocity of the front vehicle are improved. This is because the weight adjustment strategy is applied in MPC_ADJ, and the weights can be adjusted to adapt to different driving conditions. From
Figure 7b, it can be seen that the relative velocity of MPC_ADJ is lower than MPC_ CON after 30 s. This is because when
vrel < 0, the greater weight is applied to relative velocity in MPC_ ADJ. The vehicle adjusts the speed, acceleration and jerk responses in order to obtain better tracking for the velocity of the front vehicle.
From
Figure 7d, the maximum absolute values for jerk for the passengers and driver in the two ACC systems were less than 3 m/s
3. Therefore, comfort is ensured in both ACC systems. From
Figure 7e, the peak values of the battery power are smaller in MPC_ADJ throughout the entire simulation process. From
Figure 7f, the change of the SOC is smaller in MPC_ADJ. The rates of the SOC change and distance in MPC_ADJ and MPC_CON are 0.0024 km
−1 and 0.0026 km
−1, respectively, and the improvement of the energy economy index is 8.65%. This is because the weight adjustment strategy is adopted in MPC_ADJ, a good compromise is made betwen fast response and reduction of the fluctuation range for the various responses. In
Figure 7g,h, the peak values of the brake pressure and driving torque are smaller in MPC_ ADJ compared to the MPC_CON. Throughout the entire simulation time, the smaller peak values of the brake pressure are able to reduce the loss of kinetic energy during the braking process, and smaller peak values of driving torque can reduce the energy consumption during the driving process. The improvement of the index for energy economy in hard braking is less than in the first two scenarios. This is because the safety is the most important performance metric in the hard brake scenario; other performance metrics are temporarily ignored.
From the above analysis, because the MPC_ADJ adopts the weight adjustment strategy, the ACC system is able to adapt well to different driving conditions. In addition, a good compromise is achieved between fast responses and the reduction of the system response fluctuation in MPC_ADJ. Therefore, in the hard brake scenario, based on guaranteeing the other control objectives, MPC_ADJ is able to achieve a better tracking performance compared with MPC_CON. While the tracking is improved, the energy economy is also improved.
8. Conclusions
In this paper, multiple objectives are optimized in an MPC framework for BEVs during the car-following process. In addition, the weights in MPC can be adjusted on the basis of relative velocity in order to improve the tracking. The ACC system with weight adjustment was evaluated in simulation experiments for three representative scenarios. Based on ensuring other control objectives, the MPC_ADJ was able to obtain a better tracking performance than the MPC_CON. While tracking was improved, energy economy was also improved by using MPC_ADJ. The results of the experiment show that the strategy for weight adjustment was effective. In addition, a good compromise between the fast responses and the reduction of system response fluctuation is achieved using MPC_ADJ. In the future, new methods such as machine learning will be used to determine the weights for the weight adjustment strategy.