1. Introduction
Even when atoms are located in a vacuum, monopoles are induced due to the perturbations of fluctuating quantum fields and various radiative phenomena take place. In the 1970s, it was discovered that a uniformly accelerated particle detector in interaction with the vacuum massless scalar field acts as if it were immersed in a thermal bath at the temperature
with
a being the atomic proper acceleration, and this is the so-called Fulling–Davies–Unruh (FDU) effect [
1,
2,
3,
4]. In sharp contrast with the case of a static atom in interaction with the vacuum fields, a peculiar phenomenon—spontaneous excitation—occurs for an accelerated atom. It has been well understood that the spontaneous excitation occurs because the balance between the contributions of vacuum fluctuations and the contribution of atomic radiation reaction, which cancel off completely for an inertial atom, breaks up for a non-inertial atom [
5,
6].
Ever since the pioneering works on the FDU effect [
1,
2,
3], effects of non-inertial motion on the transition processes of a single atom in interaction with various kinds of quantum fields and their relationships with the FDU effect have been extensively studied [
7,
8,
9,
10,
11,
12,
13,
14]. Similar investigations have also been done to more general cases of non-inertial multi-atoms in interaction with diverse quantum fields [
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27].
In recent years, the interaction between a non-inertial two-atom system and the vacuum fields in various backgrounds have attracted much attention. On the one hand, it has been discovered that the radiative properties such as the resonance interatomic potential of two atoms in the two maximally entangled states [the symmetric/antisymmetric entangled state] are characterized by peculiar characters. They are never perturbed by the vacuum fluctuations, but are wholly caused by the atomic radiation reaction; and the resonance interatomic potential of two atoms in the maximally entangled state and in synchronized uniform acceleration is affected by nonthermal effects [
21,
22,
27], which is in sharp contrast with the energy shift of a single uniformly accelerated atom [
5,
7,
8,
9,
10,
11,
12,
13,
14,
28,
29]. On the other hand, a two-atom system is one of the simplest systems frequently exploited to study quantum entanglement, which is a central concept of quantum physics and a key property in quantum communication [
30,
31] and teleportation [
32]. In the past decades, the entanglement dynamics of a two-atom system in non-inertial motions have been extensively investigated [
33,
34,
35,
36,
37,
38,
39,
40], and, very recently, by calculating the expectation value of the rate of change of energy of a two-atom system in terms of the contributions of field fluctuations and atomic radiation reaction, the generation and degradation of entanglement in various spacetime backgrounds have also been discussed [
17,
19,
20,
24].
Many aforementioned research works on the interaction between non-inertial atoms and the fields deal with the interactions in unbounded spacetimes. However, in a more realistic model, the effects of boundaries should be also considered as they may result in important modifications. In Ref. [
41], the authors studied the disentanglement of two static and initially entangled atoms coupled individually to two spatially separated cavities. In the framework of open systems, Yu et al. studied the entanglement dynamics of two independent uniformly accelerated atoms in interaction with the vacuum scalar field and vacuum electromagnetic field near a reflecting plane boundary [
34,
40]. Very recently, by calculating the rates of transition of a static two-atom system that is interacting with the vacuum massless scalar field near boundaries, Arias et al. showed that the rates of transition of such a two-atom system can be enhanced or inhibited, depending on the specific entangled state and the separation between the two atoms [
18]. As the change of energy of the two-atom system is closely related with the transition processes, this route directly shows how the transitions of the two-atom system lead to the degradation and the generation of entanglement.
In this paper, we use the method exploited in Ref. [
18] to calculate the response rate of two synchronously uniformly accelerated atoms in the symmetric/antisymmetric entangled state and in interaction with the vacuum massless scalar field near a perfectly reflecting boundary and in a cavity, respectively. We are concerned with the acceleration and boundary effects on the transition processes of the two-atom system. We show that, in both cases, both the upward transition and the downward transition can occur, which is in sharp contrast with the findings of Arias et al. [
18] that for a static two-atom system only the downward transition can happen; and thermal-like effects that never exist in the case of two static atoms alters the transition processes of the two-atom system. We also show with analytical and numerical results how the non-inertial motion and the presence of boundaries modify the transition processes of the two-atom system. Our results on the rates of transition may also be helpful for the interpretation of disentanglement of the uniformly accelerated two-atom system.
The paper is organized as follows. In
Section 2, we introduce the general formalism of the transition probability and the response functions of a two-atom system in interaction with the vacuum massless scalar field. In
Section 3 and
Section 4, by using the formalism introduced in
Section 2, we calculate and discuss the response of the two-atom system in the symmetric/antisymmetric entangled state and in uniform acceleration near a perfectly reflecting boundary and in a cavity respectively. Finally we give a summary in
Section 5. Throughout the paper, we exploit units that
.
2. Response of The Two-Atom System Coupled to The Vacuum Massless Scalar Field
We assume that two identical atoms labeled by A and B are moving synchronously along stationary trajectories in a vacuum with massless scalar field fluctuations, thus the interatomic separation is constant and the proper times of the two atoms can be represented by the same . We denote the trajectories of the two atoms in the laboratory frame by and . The two atoms are modeled as point-like systems with two internal energy levels, and , thus the two-atom system is characterized by three eigenstates with energies . Correspondingly, we label them by with . We suppose that the two-atom system is initially prepared in one of the three eigenstates, , and we denote the initial state of the “atoms+field" system by .
In the instantaneously inertial frame, the Hamiltonian describing the atom-field interaction is given by
where
is the coupling constant which is assumed to be very small,
is the field operator, and
is the monopole operator for a single atom. Hereafter,
and
represent the ground state and the excited state of a single atom.
As a result of the atoms-field interaction, transitions may happen for the two-atom system. According to the time-dependent perturbation theory in the first-order approximation, the transition amplitude for the “atoms+field” system to transit from the initial state
to a final state
is
thus the probability of the transition is given by the squared modulus of this amplitude. Using the relation that
where
is the free Hamiltonian of a single atom, and summing the probability over all the possible states of the field, we obtain the transition probability for the two-atom system:
where
, and
and
are the response functions defined as
with the subscripts
being the labels
A or
B, and
being the positive frequency Wightmann function of the scalar field.
The response functions per unit proper time can be easily deduced from Equation (
5) to be
where
, and then the rate of transition of the two-atom system from the initial state
to a final state
follows:
The above two equations show that the rate of transition of the two-atom system is dependent on the initial state and the trajectories of the atoms.
In the following two sections, we use the formalism introduced above to study the rates of transition of a two-atom system in uniform acceleration and in interaction with the vacuum massless scalar field in two cases: near a perfectly reflecting boundary and in a cavity. We suppose that the two atoms are initially prepared in one of the maximally entangled states, i.e., the symmetric/antisymmetric entangled states,
Obviously, the energy of the two-atom system in these states is zero. We aim to show how the non-inertial motion of the atoms and the presence of boundaries affect the transition processes of the two-atom system.
3. Rates of Transition of a Uniformly Accelerated Two-Atom System Near a Perfectly Reflecting Boundary
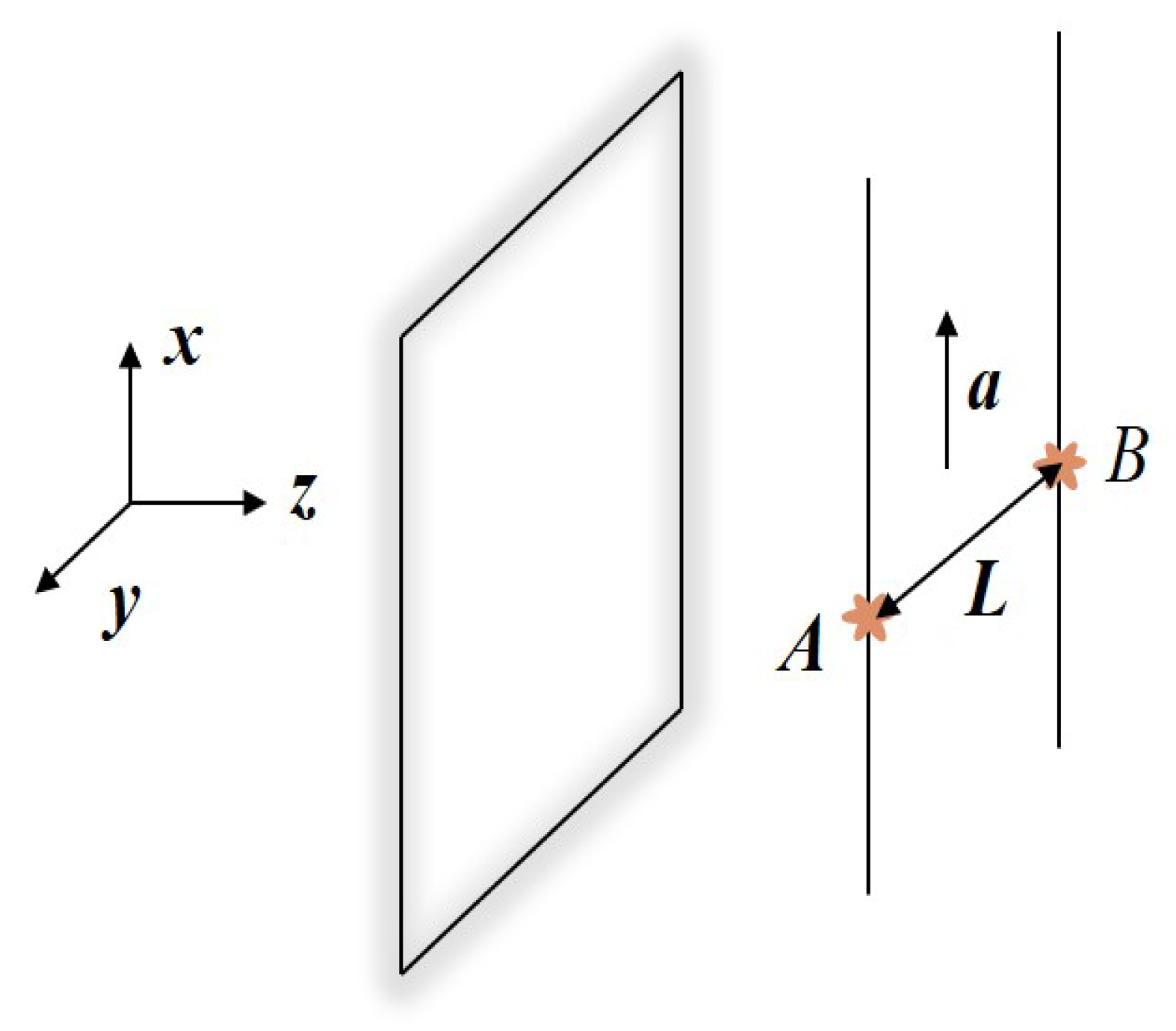
We firstly consider the rates of transition of a uniformly accelerated two-atom system prepared in the symmetric/antisymmetric entangled state and in interaction with the vacuum massless scalar field near a perfectly reflecting boundary. As shown in
Figure 1, we suppose that the two atoms are moving synchronously with their proper acceleration parallel to the boundary. In the laboratory frame, we choose the Cartesian coordinates such that the mirror is fixed at
, and the atomic trajectories, in terms of the atomic proper time
, can be depicted by
in which
are constants, and
denotes the constant interatomic separation. The proper acceleration for atoms moving along such trajectories is
a.
We assume that the massless scalar field satisfies the Dirichlet boundary condition, i.e.,
, then for any two points
and
,
where
. The first term on the right of the above equation is identical to the positive Wightmann function of the massless scalar field in an unbounded space, and the second term appears as a result of the presence of the boundary.
Combining the atomic trajectories, Equations (10) and (11), with the above expression, we obtain
where
. Substituting Equation (
13) into Equations (7) and (8), we can express the rate of the transition,
, as
with
for
, and
for
.
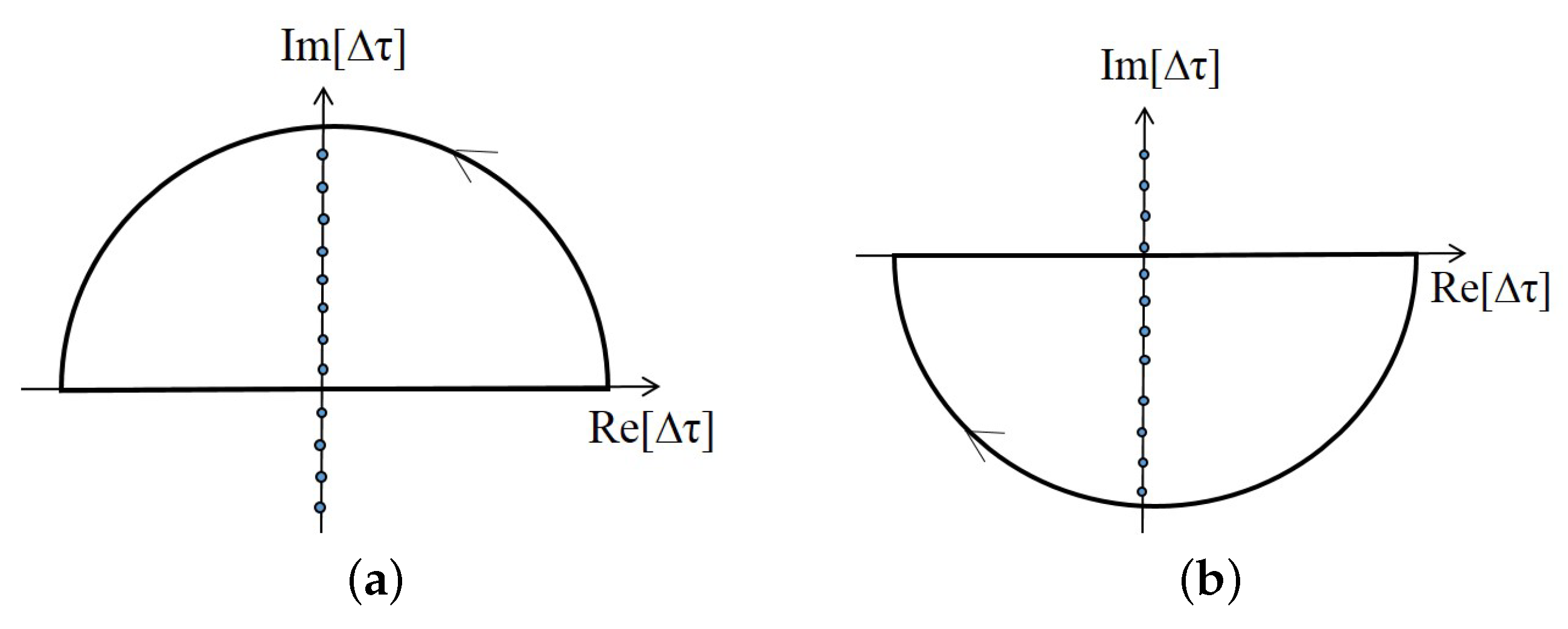
Doing the above integrations by the technique of contour integration and the residue theorem, as shown in the
Appendix A, and using the expression of the monopole moment operator, Equation (
2), we can simplify Equation (
14) to be
where we have defined
with
,
is the step function defined as
and the “∓” corresponds to the symmetric/antisymmetric entangled state, respectively. This result, Equation (
17), shows that two transition processes can occur for the two-atom system in the symmetric/antisymmetric entangled state and in uniform acceleration: the downward transition
[or equivalently
] and the upward transition
[or equivalently
], as in both cases
. Concretely, the rate for the downward transition is
and the rate for the upward transition is
In each of the two equations, there are two terms which are dependent on both atoms and are characterized by “±” or “∓”. They originate from the interference effect of the radiative fields of the two entangled atoms. Obviously, the interference effects in this case are mediated by the atomic non-inertial motion.
When
, the above downward transition rate reduces to
and the upward transition rate vanishes,
indicating that only the downward transition
can occur for an inertial two-atom system. Here it is worth pointing out that if we choose the perpendicular alignment of the two atoms with respect to the boundary, the transition rates for the static two-atom system, Equations (22) and (23), are consistent with those derived in Ref. [
18], except for a factor
in the coefficients, which can be understood to have been incorporated in the coupling constant in Ref. [
18].
The comparison of the rates of transition of the uniformly accelerated two-atom system [Equations (20) and (21)] with their counterparts in the case of an inertial two-atom system [Equations (22) and (23)], shows that the atomic non-inertial motion not only alters the downward transition rate, but also intrigues the upward transition .
At the end of this section, we show the effects of the atomic non-inertial motion and the presence of the boundary on the rates of transition of the two-atom system with some figures. We take the two atoms prepared in the symmetric entangled state
and with their constant separation
parallel to the boundary for example. This interatomic separation corresponds to
m for atoms with transition frequency
. For the downward transition
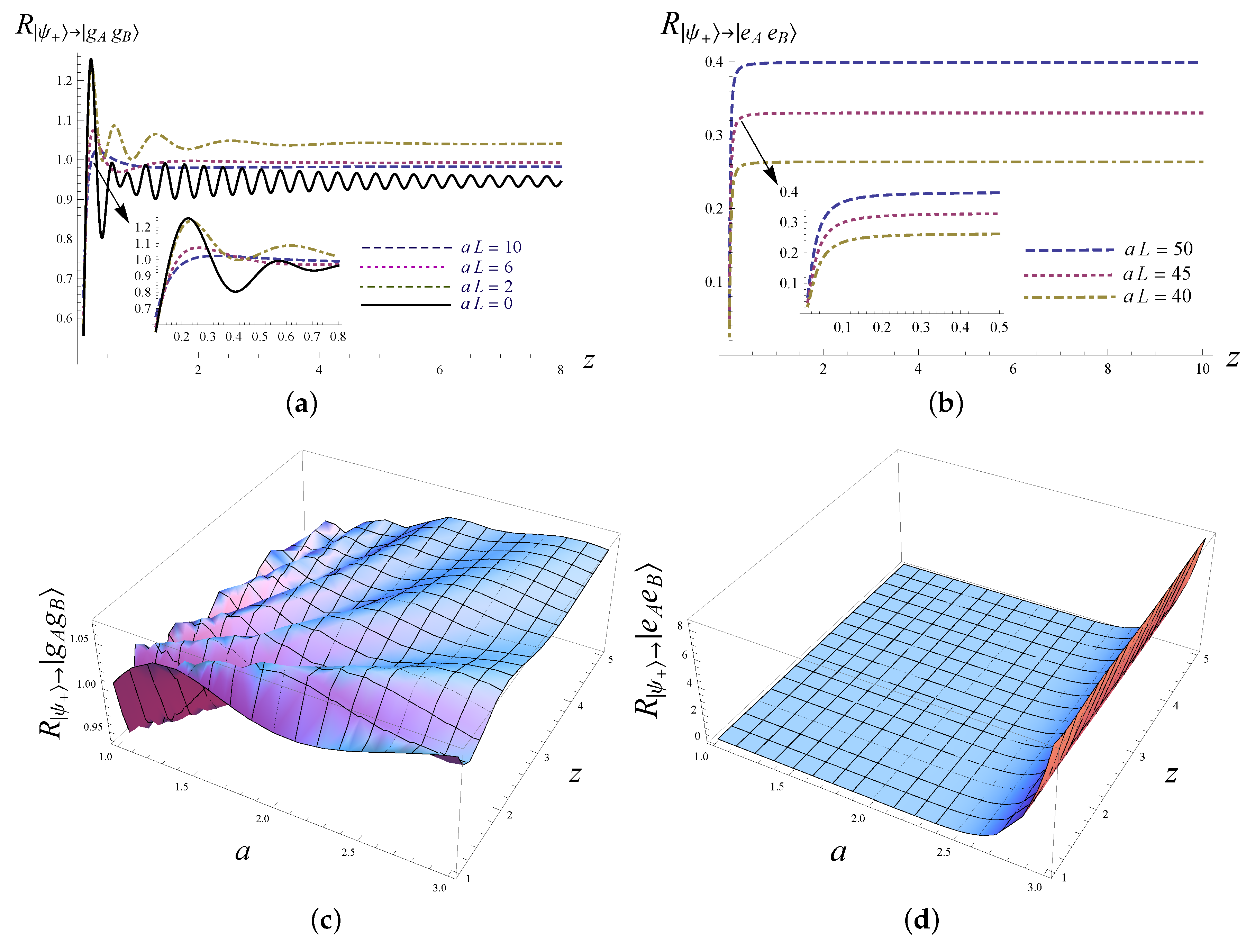
,
Figure 2a shows that, when the atomic trajectories are very close to the boundary, the downward transition rate can be larger than, smaller than, and even equal to its counterpart of two static atoms, depending on the value of the atoms-boundary separations. With the increase of the atoms-boundary separation, the downward transition rate gradually approaches the value of its counterpart in a free space, and this change is more rapid for atoms with larger acceleration.
Figure 2b shows that the upward transition rate of the two-atom system in uniform acceleration is always different from zero, which is in sharp contrast to that of a static two-atom system. When the atomic trajectories are very close to the boundary, of
m for example, this upward transition rate increases quickly with increasing atoms-boundary separations; however, beyond that region, it quickly reaches the value of its counterpart in a free space.
Figure 2c shows that for the two-atom system in the symmetric entangled state and with their trajectories very close to the boundary, the downward transition rate exhibits an oscillatory behavior with the atoms-boundary separations, and the larger is the acceleration, the less severe is the oscillation. However, as shown in
Figure 2d, the upward transition rate does not oscillate obviously with the atoms-boundary separations.
4. Rates of Transition of The Two-Atom System in Uniform Acceleration in A Cavity
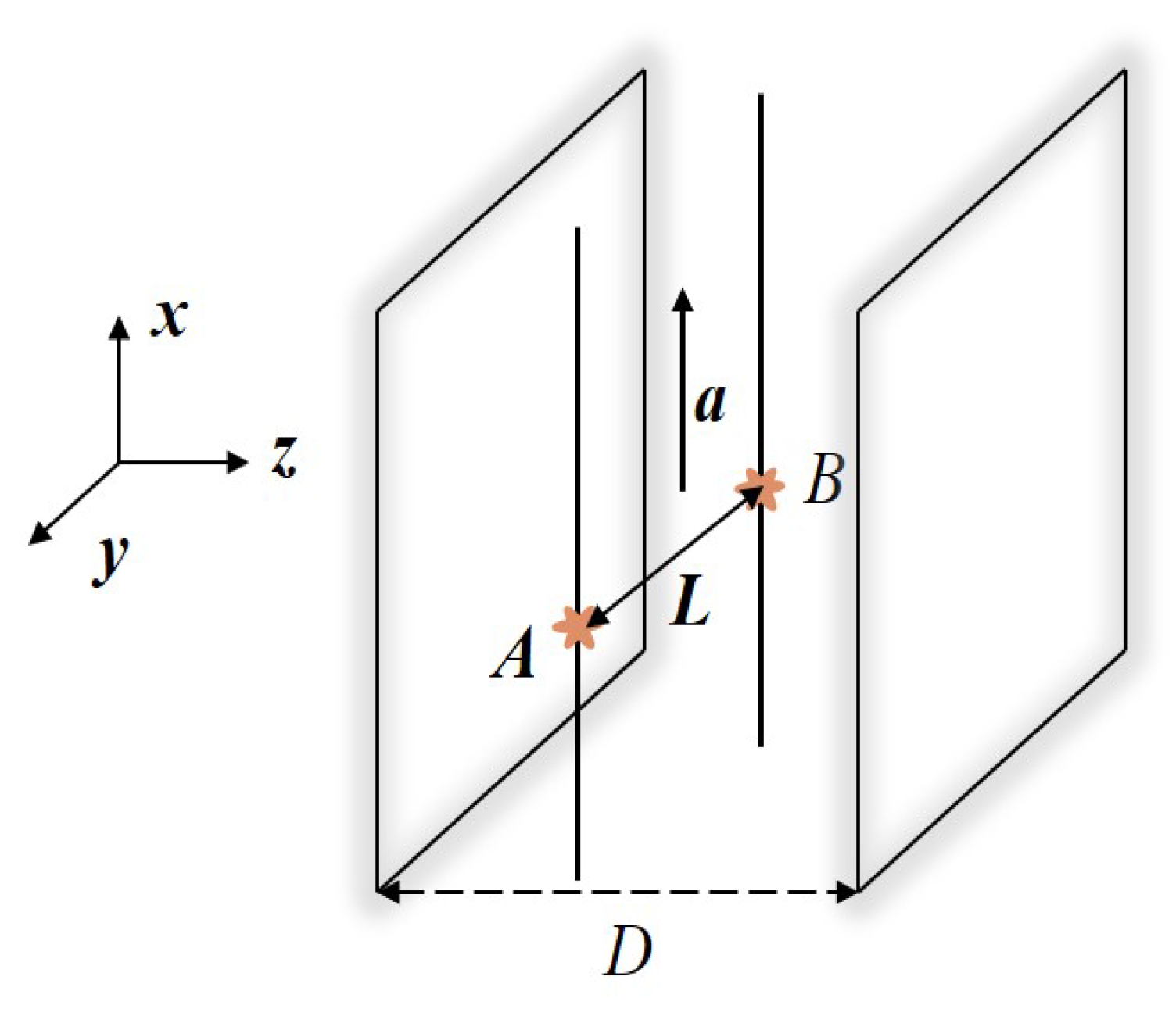
In this section, we consider that the two atoms with constant separation
L and correlated by the symmetric/antisymmetric entangled state are in synchronized uniform acceleration in a cavity, which is constructed by two perfectly reflecting mirrors with separation
D. We choose the coordinates such that the two mirrors are fixed at
and
, respectively. The trajectories of the two atoms with respect to the cavity is plotted in
Figure 3.
For simplicity, we suppose that the interatomic separation is parallel to the mirrors; then, the atomic trajectories are given by
in which
z is a constant and
.
Similar to in the previous section, we suppose that the scalar field satisfies the Dirichlet boundary condition, i.e.,
, then by the use of the positive Wightmann function of the massless scalar field near a perfectly reflecting boundary, Equation (
12), and the method of images, we can write the positive Wightmann function of the vacuum massless scalar field confined in the cavity to be
For the two atoms moving along the trajectories described by Equations (24) and (25), the above expression can be further simplified to be
for
, and
for
.
Substituting Equations (27) and (28) into Equations (7) and (8), we derive the following rates of transition of the two-atom system in the cavity:
with
for
, and
for
.
Following similar procedures as done in the previous section [the integrations in Equations (29)–(31) are similar to those listed out in the
Appendix A], i.e., doing the integrations with the technique of contour integration and using the residue theorem, we can further simplify the above rates of transition, Equation (
29), into,
where we define
For the definition of the function
, see Equation (
18).
Equation (
32) shows that, similar to in the case of two atoms synchronously uniformly accelerated near a perfectly reflecting boundary, two transition processes, i.e. the downward transition
and the upward transition
, take place for the two-atom system uniformly accelerated in the cavity and correlated by the symmetric/antisymmetric entangled state. However, in the present case, these rates of transition are modulated by the atomic acceleration
a, the interatomic separation
L, the width of the cavity
D, and the relative position of the two-atom system with respect to the cavity
z. Concretely, the rate for the downward transition is
and the rate for the upward transition is
When
, the downward transition rate reduces to
with
Similar to the result in the previous case [two atoms uniformly accelerated near a perfectly reflecting boundary], the upward transition rate vanishes, .
When
while
, it is easy to check that only the
terms in Equation (
39) are important, and thus Equation (
39) reduces to Equation (
22), which is the rate of transition of a static two-atom system located near a perfectly reflecting boundary.
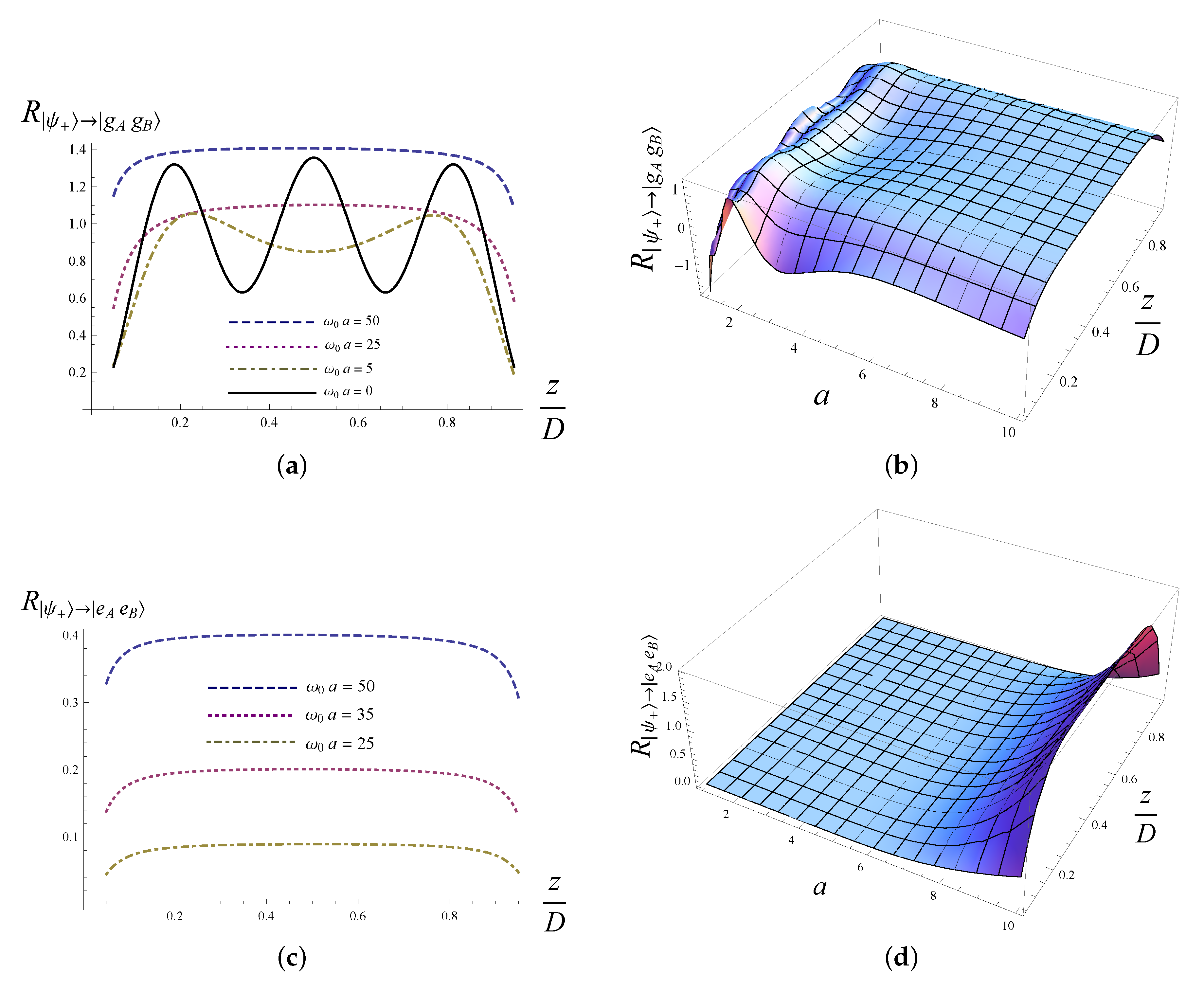
As Equations (37) and (38) are rather lengthy, we plot some figures to show how the atomic non-inertial motion and the relative positions of the atoms with respect to the cavity affect the rates of transition of the two-atom system. As shown in
Figure 4a, the downward transition rate
of a static two-atom system in the symmetric entangled state exhibit an oscillatory behavior with the separation between the atoms and the boundary fixed at
; however, this oscillation becomes less severe when the atoms are accelerated; and the oscillation can even be smoothed out when the atomic acceleration is very high [see
Figure 4b].
Figure 4a,c shows that, for relatively high acceleration and for the width of the cavity chosen to be
, which corresponds to
m for an atom with transition frequency
s
, the upward transition rate is almost constant except when the atomic trajectories are very close to one of the boundaries.
Figure 4d shows that the upward transition rate is larger for the two-atom system with higher acceleration. The atomic non-inertial motion and the presence of the cavity also have similar effects on the rates of transition of the two-atom system in the antisymmetric entangled state.
At the end of this section, we give some remarks on the results obtained in
Section 3 and
Section 4. Firstly, as a result of the non-inertial motion, both the downward transition and the upward transition happen for the two-atom system. Secondly, similar to the rates of transition of a static atom immersed in a thermal bath with the FDU temperature
[
4], the rates of transition of the uniformly accelerated two-atom system in vacuum [see Equations (20), (21), (37) and (38)] are characterized by the Plank factor
. This character of the transition rates of the uniformly accelerated two-atom system is in sharp contrast to those of its other radiative properties, such as the resonance interatomic potential, for which the revisions of the effects of uniform acceleration are never characterized by such a factor [
21,
22]. Thirdly, for the two cases of atoms accelerated near a boundary and accelerated in a cavity, both the upward transition and the downward transition result in the breakup of the maximally entangled states, and the ratio between the rates of the two processes is determined by the atomic transition frequency,
, and the atomic proper acceleration,
a:
When , this ratio approaches zero and it means that the disentanglement caused by the upward-transition is negligible, while, if , this ratio approaches unity and it indicates that the disentanglement caused by the upward transition and that caused by the downward transition become equally important.
5. Summary
In this paper, by using the time-dependent perturbation theory, we study the response and rates of transitions of a uniformly accelerated two-atom system prepared in the symmetric/antisymmetric entangled state and in interaction with the vacuum massless scalar field near a perfectly reflecting boundary and in a cavity, respectively.
We show that, as a result of the atomic non-inertial motion, both the downward transition and the upward transition take place for the two-atom system. This conclusion is in sharp contrast to that in the case of two static atoms, as the upward transition never happens for a static two-atom system. Besides, similar to the rates of transition of a static atom immersed in a thermal bath with the FDU temperature, both the downward transition rate and the upward transition rate of the uniformly accelerated two-atom system are characterized by the factor , as in sharp contrast to the other radiative properties of the two-atom system, such as the resonance interatomic energy, for which the revisions of the effects of uniform acceleration are not characterized by such a factor. For two atoms uniformly accelerated near a perfectly reflecting boundary, the rates of transition are closely dependent on the atoms-boundary separations, the atomic acceleration, and the interatomic separation. For two atoms uniformly accelerated in a cavity, the rates of transition are crucially dependent on the relative positions of the atoms with respect to the cavity, the atomic acceleration, the interatomic separation, and the width of the cavity. Our results show that the atomic non-inertial motion and the presence of boundaries can be effectively manipulated to control and modulate the transition processes of the two-atom system in the symmetric/antisymmetric entangled state. The roles the upward-transition and the downward transition play in the disentanglement of the two-atom system are also discussed.