Nonparametric Tensor Completion Based on Gradient Descent and Nonconvex Penalty
Abstract
1. Introduction
- Unlike existing methods, our method has no parameters and is easily manipulated.
- In each iteration, we use tensor matricization and SVD to approximate the gradient descent direction, so the entries outside the observation range can also be updated.
- Considering the symmetry of every dimension of a universal tensor, we select the optimal gradient tensor via scaled latent nuclear norm in each iteration.
- We design the formula of iteration step-size elaborately, which makes our iteration able to achieve a higher convergence speed and a lower error.
2. Background Knowledge
2.1. Symbols and Formulas
- is the nuclear norm of matrix , where is the ith singular value of .
- represents a D-dimensional tensor, where is the size of each dimension.
- is the inner product of two tensors and of the same dimension, where and are the elements in and , respectively.
- is the Frobenius norm of .
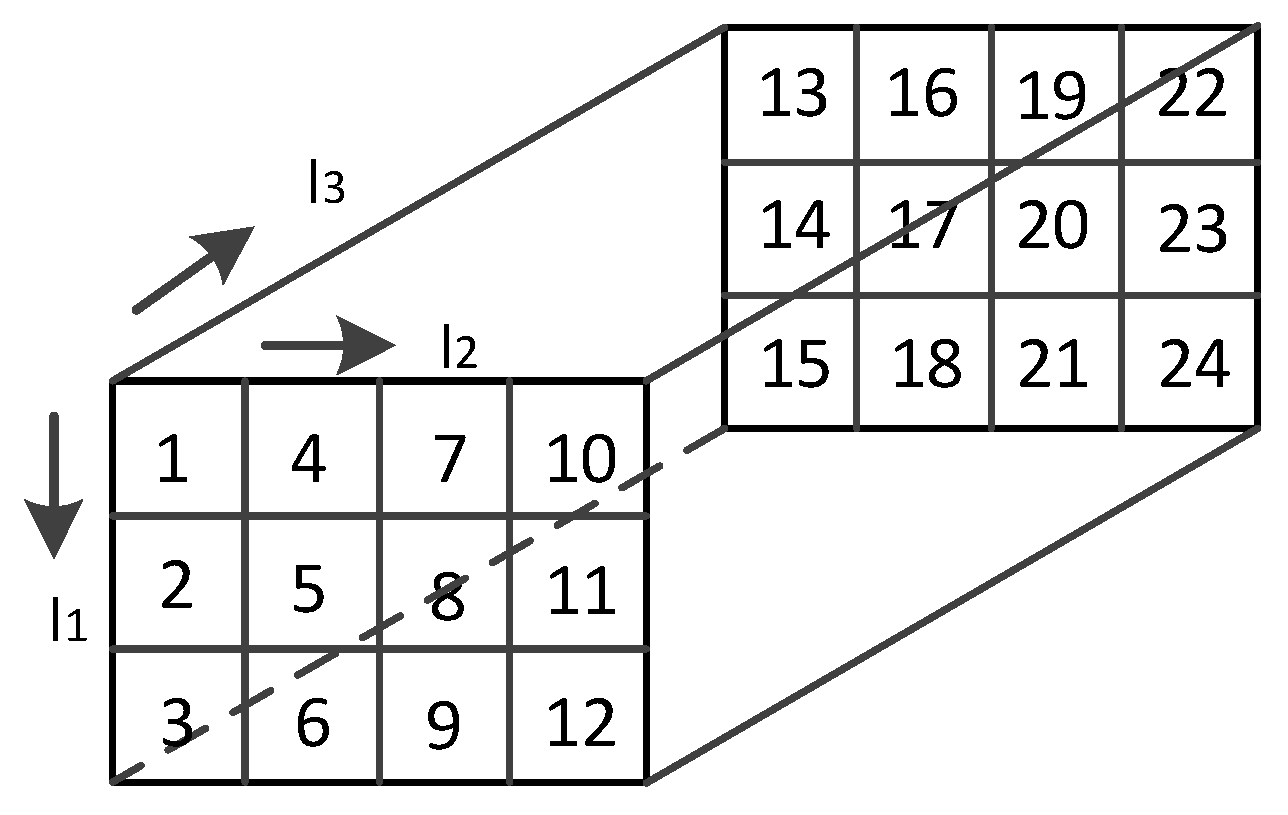
- represents the mode-d matricization of , i.e., , .
- represents the mode-d tensorization of , i.e., .
2.2. Related Algorithms
3. Nonparametric Tensor Completion
3.1. Problem Description
3.2. Iterative Calculation Based on Gradient Descent
3.3. Proof of Iterative Convergence
3.4. Selection of the Unfolding Direction
3.5. Design of the Iteration Step-Size
- In the gradient descent method, is the fastest descent direction, and we use the maximum singular value (and corresponding singular vectors) of its unfolding matrix to calculate it approximately. If the maximum singular value is very large, we may ignore some larger singular values, and the approximation of the fastest descent direction may be unsatisfactory. Therefore, we should adopt a small step-size to avoid excessive errors. Conversely, if the maximum singular value is very small, the approximation may be more accurate, and we can adopt a large step-size. In other words, the larger the maximum singular value is, the smaller the step-size.
- In the gradient descent method, will become increasingly smaller during the iterative process; thus, the maximum singular value of each iteration presents a downtrend as a whole. Then, according to Point 1, the step-size should show an upward trend during the iterative process. However, the traditional approach and some related approaches [29,30] all make the step-size increasingly smaller during the iterative process, which does not meet our requirements.
- The step-size can also be viewed as a penalty for the singular value. In matrix completion, the nonconvex function is used to penalize the singular value and achieves a better effect than the direct use of the nuclear norm [31,32]. Reference [32] penalizes the singular value by the function for matrix completion and does not introduce additional parameters.
3.6. Optimization of Calculation
3.7. Analysis of Time Complexity
4. Experiments
4.1. Performance Comparison
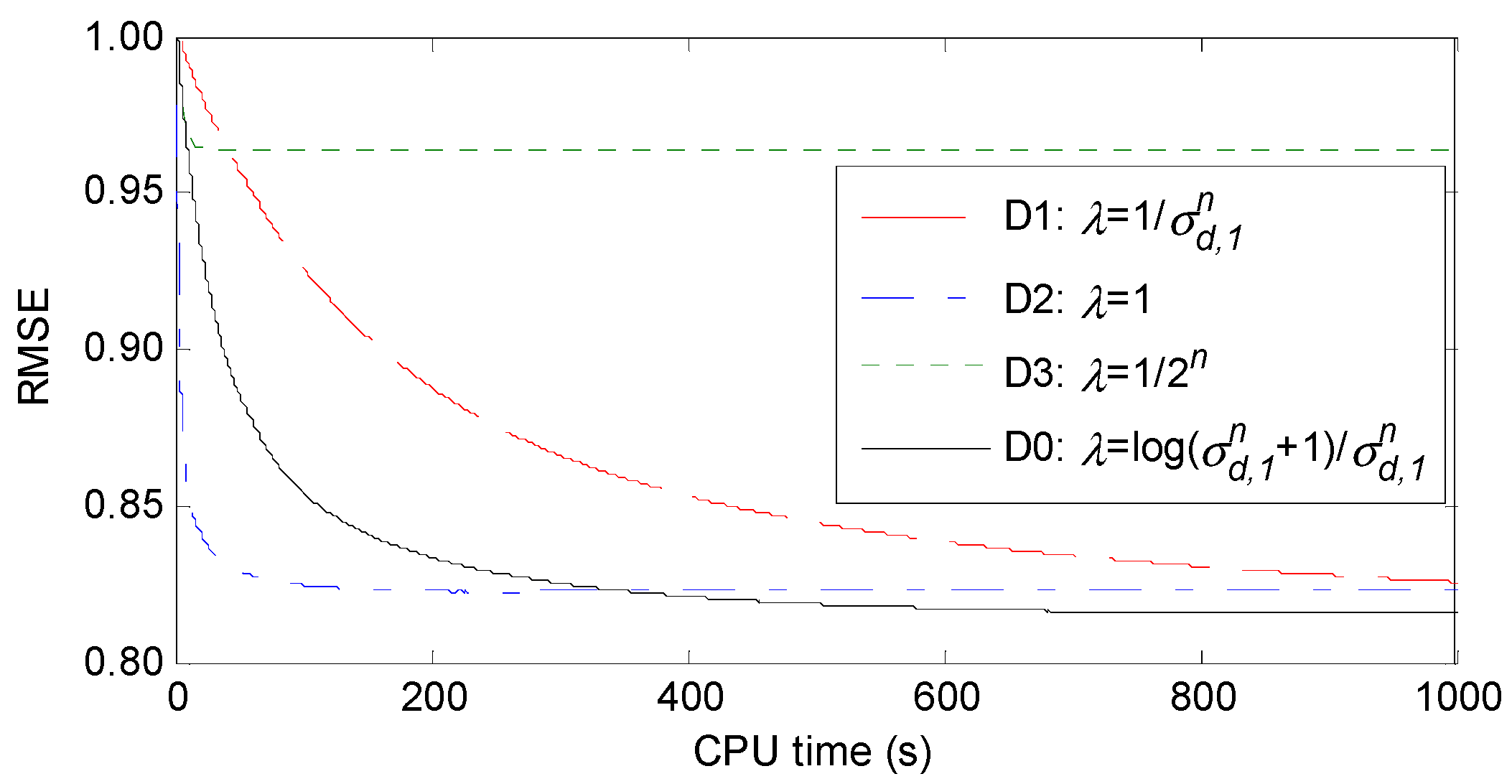
4.2. Effectiveness of Our Step-Size Design
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hu, Y.; Zhang, D.; Ye, J.; Li, X.; He, X. Fast and accurate matrix completion via truncated nuclear norm regularization. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2117–2130. [Google Scholar] [CrossRef] [PubMed]
- Symeonidis, P. ClustHOSVD: Item recommendation by combining semantically enhanced tag clustering with tensor HOSVD. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 1240–1251. [Google Scholar] [CrossRef]
- Shlezinger, N.; Dabora, R.; Eldar, Y.C. Using mutual information for designing the measurement matrix in phase retrieval problems. In Proceedings of the IEEE International Symposium on Information Theory, Aachen, Germany, 25–30 June 2017; pp. 2343–2347. [Google Scholar]
- Li, S.; Shao, M.; Fu, Y. Multi-view low-rank analysis with applications to outlier detection. ACM Trans. Knowl. Discov. Data 2018, 12, 32. [Google Scholar] [CrossRef]
- Cheng, M.; Jing, L.; Ng, M.K. Tensor-based low-dimensional representation learning for multi-view clustering. IEEE Trans. Image Process. 2019, 28, 2399–2414. [Google Scholar] [CrossRef]
- Zhao, G.; Tu, B.; Fei, H.; Li, N.; Yang, X. Spatial-spectral classification of hyperspectral image via group tensor decomposition. Neurocomputing 2018, 316, 68–77. [Google Scholar] [CrossRef]
- Cichocki, A.; Phan, A.H.; Zhao, Q.B.; Lee, N.; Oseledets, I.; Sugiyama, M.; Mandic, D.P. Tensor networks for dimensionality reduction and large-scale optimizations part 2 applications and future perspectives. Found. Trends Mach. Learn. 2017, 9, 431–673. [Google Scholar] [CrossRef]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Wen, Z.; Yin, W.; Zhang, Y. Solving a low-rank factorization model for matrix completion by a nonlinear successive over-relaxation algorithm. Math. Program. Comput. 2012, 4, 333–361. [Google Scholar] [CrossRef]
- Rahmani, M.; Atia, G.K. High dimensional low rank plus sparse matrix decomposition. IEEE Trans. Signal Process. 2017, 65, 2004–2019. [Google Scholar] [CrossRef]
- Kilmer, M.E.; Martin, C.D. Factorization strategies for third-order tensors. Linear Algebra Appl. 2011, 435, 641–658. [Google Scholar] [CrossRef]
- Kilmer, M.E.; Braman, K.; Hao, N.; Hoover, R.C. Third-order tensors as operators on matrices: A theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 2013, 34, 148–172. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, M.; Luo, D.; Ding, C.; Chakravarthy, S. Low-order tensor decompositions for social tagging recommendation. In Proceedings of the 4th ACM international conference on Web search and data mining, Hong Kong, China, 9–12 February 2011; pp. 695–704. [Google Scholar]
- Lee, H.; Yoo, J.; Choi, S. Semi-supervised nonnegative matrix factorization. IEEE Signal Process. Lett. 2009, 17, 4–7. [Google Scholar]
- Yuan, M.; Zhang, C.H. On tensor completion via nuclear norm minimization. Found. Comput. Math. 2016, 16, 1031–1068. [Google Scholar] [CrossRef]
- Nimishakavi, M.; Jawanpuria, P.; Mishra, B. A dual framework for low-rank tensor completion. In Proceedings of the 32nd Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Kasai, H.; Mishra, B. Low-rank tensor completion: A Riemannian manifold preconditioning approach. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1012–1021. [Google Scholar]
- Kressner, D.; Steinlechner, M.; Vandereycken, B. Low-rank tensor completion by Riemannian optimization. BIT Numer. Math. 2014, 54, 447–468. [Google Scholar] [CrossRef]
- Xu, Y.; Hao, R.; Yin, W.; Su, Z. Parallel matrix factorization for low-rank tensor completion. Inverse Probl. Imaging 2015, 9, 601–624. [Google Scholar] [CrossRef]
- Yu, W.; Zhang, H.; He, X.; Chen, X.; Xiong, L.; Qin, Z. Aesthetic-based clothing recommendation. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 649–658. [Google Scholar]
- Halko, N.; Martinsson, P.G.; Tropp, J.A. Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions. SIAM Rev. 2011, 53, 217–288. [Google Scholar] [CrossRef]
- Ji, T.Y.; Huang, T.Z.; Zhao, X.L.; Ma, T.H.; Deng, L.J. A non-convex tensor rank approximation for tensor completion. Appl. Math. Model. 2017, 48, 410–422. [Google Scholar] [CrossRef]
- Derksen, H. On the nuclear norm and the singular value decomposition of tensor. Found. Comput. Math. 2016, 16, 779–811. [Google Scholar] [CrossRef]
- Yao, Q.; Kwok, J.T. Accelerated and inexact soft-impute for large-scale matrix and tensor completion. IEEE Trans. Knowl. Data Eng. 2019, 31, 1665–1679. [Google Scholar] [CrossRef]
- Liu, J.; Musialski, P.; Wonka, P.; Ye, J.P. Tensor completion for estimating missing values in visual data. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 208–220. [Google Scholar] [CrossRef]
- Wimalawarne, K.; Sugiyama, M.; Tomioka, R. Multitask learning meets tensor factorization: Task imputation via convex optimization. In Proceedings of the International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2825–2833. [Google Scholar]
- Tomioka, R.; Suzuki, T. Convex tensor decomposition via structured schatten norm regularization. In Proceedings of the 26th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 1331–1339. [Google Scholar]
- Guo, X.; Yao, Q.; Kwok, J.T. Efficient sparse low-rank tensor completion using the Frank-Wolfe algorithm. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 1948–1954. [Google Scholar]
- Lu, S.; Hong, M.; Wang, Z. A nonconvex splitting method for symmetric nonnegative matrix factorization: Convergence analysis and optimality. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing, New Orleans, LA, USA, 5–9 March 2017; pp. 2572–2576. [Google Scholar]
- Kuang, D.; Yun, S.; Park, H. SymNMF: Nonnegative low-rank approximation of a similarity matrix for graph clustering. J. Glob. Optim. 2015, 62, 545–574. [Google Scholar] [CrossRef]
- Oh, T.H.; Matsushita, Y.; Tai, Y.W.; Kweon, I.S. Fast randomized singular value thresholding for nuclear norm minimization. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 4484–4493. [Google Scholar]
- Nie, F.; Hu, Z.; Li, X. Matrix completion based on non-convex low-rank approximation. IEEE Trans. Image Process. 2019, 28, 2378–2388. [Google Scholar] [CrossRef] [PubMed]
- Yokota, T.; Zhao, Q.; Cichocki, A. Smooth PARAFAC decomposition for tensor completion. IEEE Trans. Signal Process. 2016, 64, 5423–5436. [Google Scholar] [CrossRef]
- Lee, J.; Choi, D.; Sael, L. CTD: Fast, accurate, and interpretable method for static and dynamic tensor decompositions. PLoS ONE 2018, 13, e0200579. [Google Scholar] [CrossRef]
- Harper, F.M.; Konstan, J.A. The movielens datasets: History and context. ACM Trans. Interact. Intell. Syst. 2016, 5, 19. [Google Scholar] [CrossRef]

| Methods | Mountain | Rice | Stockton | |||
|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| NTC | 0.224 | 0.136 | 0.258 | 0.176 | 0.502 | 0.360 |
| SPC | 0.307 | 0.224 | 0.647 | 0.541 | 0.664 | 0.520 |
| TR-LS | 0.266 | 0.169 | 0.265 | 0.176 | 0.462 | 0.319 |
| Rprecon | 0.281 | 0.180 | 0.296 | 0.208 | 0.504 | 0.353 |
| GeomCG | 0.402 | 0.291 | 0.304 | 0.210 | 0.568 | 0.402 |
| FFW | 0.241 | 0.150 | 0.272 | 0.188 | 0.520 | 0.376 |
| CTD-S | 0.843 | 0.713 | 0.867 | 0.730 | 0.915 | 0.782 |
| Methods | Mountain | Rice | Stockton | |||
|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| NTC | 0.190 | 0.129 | 0.218 | 0.145 | 0.458 | 0.324 |
| SPC | 0.254 | 0.162 | 0.537 | 0.439 | 0.515 | 0.367 |
| TR-LS | 0.236 | 0.149 | 0.220 | 0.147 | 0.433 | 0.291 |
| Rprecon | 0.237 | 0.145 | 0.290 | 0.204 | 0.476 | 0.332 |
| GeomCG | 0.238 | 0.146 | 0.290 | 0.204 | 0.513 | 0.363 |
| FFW | 0.211 | 0.132 | 0.239 | 0.162 | 0.481 | 0.344 |
| CTD-S | 0.748 | 0.628 | 0.759 | 0.635 | 0.858 | 0.725 |
| Name | Size | Number of Entries | Number of Known Entries |
|---|---|---|---|
| 300T | 300 × 4667 × 19 | 26,601,900 | 66,887 |
| 2400T | 2400 × 11,292 × 19 | 514,915,200 | 611,198 |
| 4000T | 4000 × 13,370 × 19 | 1,016,120,000 | 1,028,536 |
| Methods | 300T | 2400T | 4000T | |||
|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| NTC | 0.919 | 0.726 | 0.853 | 0.654 | 0.843 | 0.647 |
| SPC | 0.962 | 0.776 | 0.996 | 0.795 | —— | —— |
| TR-LS | 0.936 | 0.742 | 0.858 | 0.651 | 0.851 | 0.654 |
| Rprecon | 0.963 | 0.738 | 0.870 | 0.657 | 0.856 | 0.647 |
| GeomCG | 0.944 | 0.735 | 0.870 | 0.661 | 0.854 | 0.641 |
| FFW | 0.915 | 0.721 | 0.860 | 0.768 | 0.858 | 0.662 |
| CTD-S | 0.987 | 0.806 | 0.969 | 0.663 | 0.974 | 0.773 |
| Methods | 300T | 2400T | 4000T | |||
|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| NTC | 0.926 | 0.724 | 0.877 | 0.677 | 0.860 | 0.663 |
| SPC | 0.968 | 0.768 | 0.998 | 0.798 | —— | —— |
| TR-LS | 0.934 | 0.735 | 0.971 | 0.763 | 0.867 | 0.670 |
| Rprecon | 0.970 | 0.738 | 0.887 | 0.664 | 0.872 | 0.657 |
| GeomCG | 0.975 | 0.772 | 0.886 | 0.672 | 0.872 | 0.659 |
| FFW | 0.926 | 0.728 | 0.882 | 0.684 | 0.881 | 0.684 |
| CTD-S | 0.993 | 0.803 | 0.979 | 0.778 | 0.987 | 0.786 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, K.; Xiong, Z. Nonparametric Tensor Completion Based on Gradient Descent and Nonconvex Penalty. Symmetry 2019, 11, 1512. https://doi.org/10.3390/sym11121512
Xu K, Xiong Z. Nonparametric Tensor Completion Based on Gradient Descent and Nonconvex Penalty. Symmetry. 2019; 11(12):1512. https://doi.org/10.3390/sym11121512
Chicago/Turabian StyleXu, Kai, and Zhi Xiong. 2019. "Nonparametric Tensor Completion Based on Gradient Descent and Nonconvex Penalty" Symmetry 11, no. 12: 1512. https://doi.org/10.3390/sym11121512
APA StyleXu, K., & Xiong, Z. (2019). Nonparametric Tensor Completion Based on Gradient Descent and Nonconvex Penalty. Symmetry, 11(12), 1512. https://doi.org/10.3390/sym11121512





