Abstract
Cross-efficiency evaluation approaches and common set of weights (CSW) approaches have long been suggested as two of the more important and effective methods for the ranking of decision making units (DMUs) in data envelopment analysis (DEA). The former emphasizes the flexibility of evaluation and its weights are asymmetric, while the latter focuses on the standardization of evaluation and its weights are symmetrical. As a compromise between these two approaches, this paper proposes a cross-efficiency evaluation method that is based on two types of flexible evaluation criteria balanced on interval weights. The evaluation criteria can be regarded as macro policy—or means of regulation—according to the industry’s current situation. Unlike current cross-efficiency evaluation methods, which tend to choose the set of weights for peer evaluation based on certain preferences, the cross-efficiency evaluation method based on evaluation criterion determines one set of input and output weights for each DMU. This is done by minimizing the difference between the weights of the DMU and the evaluation criteria, thus ensuring that the cross-evaluation of all DMUs for evaluating peers is as consistent as possible. This method also eliminates prejudice and arbitrariness from peer evaluations. As a result, the proposed cross-efficiency evaluation method not only looks for non-zero weights, but also ranks efficient DMUs completely. The proposed DEA model can be further extended to seek a common set of weights for all DMUs. Numerical examples are provided to illustrate the applications of the cross-efficiency evaluation method based on evaluation criterion in DEA ranking.
1. Introduction
Data envelopment analysis (DEA) is a practical methodology originally proposed by Charnes et al. [1]. Since that time, DEA has been widely studied and applied all over the world, and the method has been further developed and expanded by many scholars. In recent years, the outstanding studies in DEA can be found in the literature [2,3,4,5,6,7,8]. DEA is used to evaluate the performance of a group of decision making units (DMUs) using multiple inputs to produce multiple outputs. DEA method requires each decision-making unit to evaluate its efficiency and assign the most favorable weight to itself. In addition, efficiency is the optimistic efficiency of DMU, which should not be greater than 1. If the efficiency value of the decision unit is equal to 1, the DMU is called a DEA efficient DMU. Otherwise, DMU is considered to be a non DEA efficient DMU.
The traditional DEA method has two major drawbacks. The first is a lack of discrimination, and the second is the existence of unrealistic weights. The DEA method allows each DMU to evaluate its efficiency with the most favorable weights. In this way, more than one DMU is often evaluated as DEA efficient, and these DMUs cannot be further distinguished. Therefore, the lack of discrimination is one of the main defects of the DEA method. This also leads to another important problem. The input and output that is beneficial to a particular DMU will be weighted heavily, while the input and output that is unfavorable to the DMU will be weighted lightly, or even ignored. As a result, weighting for self-assessment can sometimes be unrealistic.
Studies to overcome the weakness of DEA’s discrimination power are grouped into two trends. One remedy is the cross-efficiency method suggested by Sexton et al. [9], which introduces a secondary goal. The most commonly used methods include the benevolent and aggressive cross-efficiency assessment proposed by Doyle and Green [10], both of which are calculated using the weights that are benevolent or aggressive to peers. Wang & Chin [11] proposed a neutral cross-efficiency evaluation method, in which the attitude of decision makers is neutral and there is no need to make a choice between benevolent and aggressive formulas. Liang et al. [12] put forward the game cross-efficiency evaluation method. Using the idea of game, each DMU is regarded as an independent player, and bargains between the optimistic efficiency. In addition, Jahanshahloo et al. [13] proposed symmetrical weight distribution technology. This technique rewards the DMU with symmetrical selection weights. Wu et al. [6] proposed a DEA model with balanced weight. The second goal is to reduce the number of zero weights and the large differences in weighted data. Ruiz [14] proposed the cross-efficiency evaluation of direction distance function for fractional programming. Cook and Zhu [15] proposed a unit invariant multiplicative DEA model, which can directly obtain the maximum and unique cross-efficiency scores of each DMU. Wu [7] proposed to use the target recognition model as a means to obtain the reachable targets of all DMUs. Several secondary objective models are proposed for weight selection. These models consider the expected and unexpected cross-efficiency goals of all DMUs. Other cross-efficiency evaluation methods are discussed in Wu and Chu [8], Oral et al. [16], Oukil [17], Carrillo [18], and Shi et al. [19].
Another remedy is the common set of weights (CSW) approach in DEA, which was first suggested by Cook et al. [20]. This method utilizes the idea of common weights to measure the relative efficiency of highway maintenance patrols. Years later, this study was further developed by Jahanshahloo et al. [21], Kao & Hung [22], and Liu & Peng [23]. In more recent studies, Amir et al. [24] proposes a novel TCO-based model in which a common set of weights imprecise DEA (CSW-IDEA) is used to address the managerial and technical issues of handling weighting schemes and imprecise data. Hossein et al. [25] suggests a novel method for determining the CSWs in a multi-period DEA. The CSWs problem is formulated as a multi-objective fractional programming problem. Then, a multi-period form of the problem is formulated, and the mean efficiency of the DMUs is maximized, while their efficiency variances are minimized. The CSW approaches have been developed to find a common set of weights for all DMUs, in order to overcome the shortcomings of the weights flexibility method, where each DMU can take its own most desirable weight.
From the literature review above, all the cross-efficiency evaluation methods are formulated so that each DMU chooses one set of weights determined by the CCR model (self-evaluation model proposed by Charnes, Cooper and Rhodes) that has alternate optima solutions. When a DMU evaluates its peers, the DMU selects one set of ideal weights from alternative weights by means of the quadratic optimization of the target function from various angles. In other words, cross-evaluation is an evaluation method, which determines a set of weights for each DMU, in order to rate itself and its peers in consideration of the diversity of DMUs. The common weight evaluation method, which determines a common set of weights as the common evaluation criteria, is used to evaluate each DMU, without considering the flexibility of the DMUs, and belongs to a non-differentiating evaluation method.
In terms of practical applications, differences between homogeneous DMUs still exist, such as scale, history, culture, and region. Common weight evaluation is obviously unfair, because this method does not take into account the differences of the DMUs. However, there are also shortcomings in cross-evaluation, such as the fact that each DMU excessively enlarges the weights of its own superiority indicators and ignores the importance of input–output indicators, thus forming unrealistic and subjective evaluation conclusions. The combination of the two methods discussed above is more meaningful. That is, each DMU can take its own desirable weight, which is obtained under the constraints of an objective criterion. Therefore, we propose the cross-evaluation method based on evaluation criteria in this paper.
In this paper, we propose a series of DEA models for cross-efficiency evaluation based on evaluation criteria. The evaluation criteria may be formed based on the overall situation of the industry, or the performance of some representative enterprises. Accordingly, two evaluation criteria are proposed, which are balanced on the interval weights of input–output variables. One is based on the eclectic decision-making method, which takes the aggregation of the minimum of upper limit of interval weights and maximum of lower limit of interval weights. The harmonic coefficient is introduced into the eclectic decision-making method to increase the flexibility of evaluation criteria. The other is based on weighted mathematical expectation. Because the importance of each DMU is different in cross-evaluation, we introduce the parameter into the evaluation criteria as a weight that reflects the position of a DMU. Mathematical expectations are weighted and added by to form the evaluation criteria. Then, the proposed method based on an evaluation criterion determines one set of input and output weights for each DMU. This is done by minimizing the deviations of input and output weights for peer evaluation from a standard criterion. In this way, aside from reducing zero weights, the weights for peer-evaluation (which are closer and more concentrated) are more realistic to peers.
The rest of the paper is organized as follows. Section 2 describes the cross-efficiency evaluations, mainly including aggressive and benevolent formulations. The evaluation criterion balanced on interval weights is developed in Section 3. The DEA models for cross-efficiency evaluation based on evaluation criteria are extended in Section 4. Numerical examples are demonstrated in Section 5. Conclusions are offered in Section 6.
2. The Efficiency Evaluation
Suppose there are n DMUs to be evaluated against m inputs and s outputs. Denote by () and () the input and output values of DMUj (), whose efficiencies are defined as follows. Consider a DMU, say, DMUk, , whose efficiency relative to the other DMUs can be measured by the following CCR model (Charnes et al. [1]):
which aims to find a set of input and output weights that are most favourable to DMUk. The Charnes and Cooper transformation can be equivalently transformed into the linear program (LP) below for the solution:
Let () and () be the optimal solution to the above model. Then, is referred to as the CCR-efficiency of DMUk, which is the best relative efficiency that DMUk can achieve, and reflects the self-evaluated efficiency of DMUk. As such, is referred to as a cross-efficiency of DMUj and reflects the peer evaluation of DMUk to DMUj ().
Model (2) is solved n times, with a different DMU being solved each time. As a result, n DMUs will have n sets of input and output weights, and each DMU will have (n − 1) cross-efficiency, plus a CCR-efficiency, which together form a cross-efficiency matrix. The average cross-efficiency for DMUk is (), where () are the CCR-efficiencies of the n DMUs, that is, .
Note that model (2) may have multiple optimal solutions. If the input and output weights are not unique, the use of cross efficiency evaluation will be destroyed. In order to solve this problem, a remedy proposed by Sexton et al. [9] is to introduce a secondary goal, one which optimizes the input and output weights while maintaining the CCR-efficiency determined by model (2). Doyle and green [10] proposed the most commonly used secondary goals, as follows:
and
Model (3) is called the aggressive formula of cross-efficiency evaluation, which aims to minimize the cross-efficiency of peers in some way. Instead, model (4) is called the benevolence formula for cross-efficiency evaluation. To some extent, the model improves the cross-efficiency of other EMUs. These two models optimize input and output weights in two different ways. Therefore, there is no guarantee that they can lead to the same efficiency ranking or conclusion of N DMUs.
In addition, other secondary goals or models are mentioned in the DEA literature. For interested readers, please refer to Sexton et al. [9], Liang et al. [12], Wang et al. [26,27], and Jahanshahloo et al. [13]. These secondary goals focus on how to uniquely determine input and output weights. In the next section, we focus on the diversity of input and output weights, and develop some alternative DEA models to minimize the weights differences used to evaluate peers. This enables cros-efficiency to be evaluated with more reasonable input and output weights.
3. Evaluation Criteria Balanced on Interval Weights of N DMUs
From our perspective, when a DMU is given an opportunity to unilaterally decide upon a set of input and output weights for evaluating peers, in addition to being as favourable as possible to itself, the DMU tends have specific preferences when choosing the set of weights. This preferential choice of weights leads to an unfair and arbitrary situation for peers. Therefore, we need to establish some evaluation criteria to ensure the relative consistency of cross-evaluation for peers by eliminating prejudice. That is, we not only look for non-zero weights, but we also seek to ensure that weights for evaluating peers are as close as possible by taking a certain evaluation criterion as a reference point. That means we seek to minimize the difference between the weights of each DMU and the evaluation criteria. Two evaluation criteria are proposed as follows:
3.1. The DEA Modes of Interval Weights
For a DMU, we get a set of maximum weights from among the alternate optima in the CCR model by maximizing the weight of each variable (including input and output variables). By contrast, a set of minimum weights is obtained by minimizing the weight of each variable. Consider an efficient DMU, say, DMUk. The maximum attainable value of or of the DMUk can be obtained by solving the following LP model:
where are a type of Boolean and . When , the optimization goal is , and when , the optimization goal is . Let () and () be the maximum attainable value (upper bound) obtained by the above model. To obtain the minimum attainable value (lower boundary) of and , one simply changes the objective function to minimizing , and () and () is obtained as the minimum attainable value. For (and ) of a DMUk, this method leads to an interval weight , and then n DMUs lead to n interval weights for , and interval weights of for the same thing.
3.2. Evaluation Criteria Based on the Eclectic Decision-Making Method
There are multiple methods in the criteria for evaluating peers based on the interval weights. The optimistic decision method would consider the upper limit of the interval weights as a peer evaluation criterion. The pessimistic decision method can also take the lower limit as a peer evaluation criterion. However, the decision makers cannot be absolutely optimistic or pessimistic; they are more likely to be between the two. Therefore, the eclectic decision-making method is introduced as peer evaluation criteria. We can use to express the minimum of the upper limit, and to denote the maximum value of the lower limit. Both and reflect the idea of the eclectic decision-making method, and their formula is as follows:
To make the evaluation criteria more realistic and flexible in terms of weights, a harmonic coefficient, namely , is introduced to combine and . That is, the parameter displays a preference for , and is introduced as a damping coefficient reflecting the preference for . Then, we use the to express the evaluation criterion of n DMUs in . The same procedures are used in , where is denoted as the evaluation criterion. In this way, one set of weights (, ) (as shown in Formula (6a) and (6b)) is obtained as an evaluation criterion, which in turn is a balance between the maximum and the minimum attainable values of n DMUs in and . This ensures the evaluation criterion meets a variety of application requirements. This is the first evaluation criterion, which is based on the eclectic decision-making method, or ECED for short:
3.3. Evaluation Criterion Based on Weighted Mathematical Expectation
If we denote the optimal solution of the above model (5) by for corresponding DMUj , then solving model (5) n times would lead to n sets of optimal solutions available for n DMUs, which in turn would form an interval weight matrix (IWM). An IWM is shown as follows:
In practical applications, it is unfair and subjective to use the upper or lower bounds of the interval weight by the criterion for peer evaluating. Rather, an application should consider the level that most DMUs can reach. However, we cannot obtain sufficient knowledge of the weight distribution information in the interval. The term probability distribution refers to the probability rule used to express the value of random variables. We may assume that the weights satisfy one or other forms of probability distribution (such as normal distribution or uniform distribution). The mathematical expectation of probability distribution can best represent the interval weight used as a criterion for peer evaluating when that weight obeys the probability distribution. According to the central limit theorem, the random variables approximately obey the normal distribution when the sample size is large enough. Supposing that weights satisfy the standard normal distribution in this paper, the mathematical expectation matrix-based interval weight matrix (IWM) is as follows:
where is the mathematical expectation of the interval weights , and is the mathematical expectation of interval weights . Where
For DMUj, and may not be a real weight, and this represents the compromise decision for the decision-makers, as an objective evaluation criterion. There are n sets of mathematical expectations representing the evaluation criteria for n DMUs. As the importance of each DMU is different in cross-evaluation, let be the weight of DMUj, which embodies the position of DMUj. Therefore, the evaluation criterion based on weighted mathematical expectation (ECWME) is calculated as follows:
where
4. DEA Models for Cross-Efficiency Evaluation Based on Evaluation Criteria
It is well known that each DMU personally chooses the profile of weights to be used in the cross-efficiency evaluation. Therefore, the DMU’s choice is often prejudiced. One DMU’s attitude towards its peers may be aggressive, benevolent, indifferent, or something else. Those prejudicial attitudes of DMUs to peers need to be avoided in many applications. This is why the weights that are chosen by each DMU for peer evaluations should be based on an evaluation criterion, as stated in part 3. We propose a method that makes a selection between alternate optima of CCR. This is done by, to the greatest extent possible, reducing the degree of deviation of weights for peer evaluation from the evaluation criteria. In other words, our purpose is to look for the profiles of DMU weights that are closest to the evaluation criterion. To do this, a nonlinear programming model is proposed as follows:
where are obtained from Formula (6a) and (6b) or Formula (7a) and (7b), which is the evaluation criterion for the evaluating peers. Also, are the variables that need to be solved. The above model needs to be solved n times, one time for each DMU. The purpose of the model is to minimize the deviation of input and output weights from the evaluation criterion. In other words, each DMU obtains one set of weights that is favorable to that DMU and is also as close to the evaluation criterion of the evaluating peers as possible.
Model (8) is a form of nonlinear programming. To make this nonlinear model (8) become capable of linear programming, we introduce the new decision variables , and we add , to the set of constraints. Thus, we minimize the linear objective function .
If we denote the optimal solution of model (9) by for the corresponding DMUk, then the cross-efficiency of a given DMUj with the profile of weights provided by DMUk will be obtained as follows:
Therefore, the cross-efficiency score of DMUj is the average of these cross-efficiencies:
Besides cross-evaluation, the weights solved by model (9) are similar to their evaluation criteria derived from formulae (67). The weights are relatively concentrated, and their coefficient of variation is small, which can further be extended to be a common set of weights (CSW) based on evaluation criteria for all DMUs. The extended CSW deviates little from the cross weights solved by model (9), which are easily accepted by each DMU.
Let , solved by model (9), be the optimal weights of efficient DMUk, and let , solved by model (2), be the optimal weights of inefficient DMUt. Suppose there are efficient DMUs and inefficient DMUs. The CSW based on evaluation criteria is obtained as follows:
We consider the inefficient DMU and efficient DMU separately, because, in the case of low efficiency DMU, the weights’ distribution provided by the proposed method is the only optimal solution to the weights in the CCR model. This same train of thought can be seen in Nuria Ramón (2011). This paper, however, differs from the idea proposed in Nuria Ramón (2011). The cross-evaluation proposed in this paper allows for the inefficient DMUs that keep the weights in the CCR model. For efficient DMUs, the weights for evaluating peers are obtained by minimizing deviation from the evaluation criterion, rather than reducing the differences between the weights of any two DMUs. In addition, the model proposed by Nuria Ramón needs to be solved times, and this approach is not suitable for a large number of DMUs. The measure of our approach is different. We focus attention on the deviation of input and output weights from the evaluation criterion. The model in this paper only needs to be solved n times and needs to be more practical.
5. Numerical Examples
Example 1.

In this section, we provide one numerical example to illustrate the proposed methods detailed above. We consider the numerical examples with the data presented in Table 1. The case of seven academic departments in a university is presented in Table 1, with three inputs and three outputs.

Table 1.
Data and efficiency of Example 1.
- Input 1: Total number of academic staff (x1)
- Input 2: Academic staff salaries in thousands of pounds (x2)
- Input 3: Support staff salaries in thousands of pounds (x3)
- Output 1: Total number of undergraduate students (y1)
- Output 2: Total number of postgraduate students (y2)
- Output 3: Total number of research papers (y3)
For a DMU, the minimum output and input weights can be obtained by solving model (5). The result is taken as the upper bound of the interval weights (UBIW). The maximum output and input weights can also be obtained by solving model (5). This result is taken as the lower bound of the interval weights (LBIW). Therefore, each DMU will get a set of interval weights, as shown in Table 2.

Table 2.
Weights of decision-making units (DMUs), solved by model (5).
Firstly, the cross-evaluation efficiency is discussed, based on eclectic decision-making evaluation criterion (ECED). The UBIW and LBIW are obtained by Formulaes (6a) and (6b), as shown in the first and second row of Table 3. To make sure the evaluation criteria fall into the interval weights of all DMUs (as much as possible), the ECED is calculated with α = 0.5, as can be seen in the last row of Table 3. Each DMU attempts to obtain a set of weights that is as close (or as similar as possible) to the cross-evaluation criterion. This is done by minimizing deviation from the cross-evaluation criterion. When the evaluation criterion is the ECED, the cross-evaluation weights of each DMU solved by model (9) are shown in Table 4.

Table 3.
Eclectic decision-making evaluation criterion (ECED) of all DMUs. UBIW, upper bound of the interval weights; LBIW, lower bound of the interval weights.

Table 4.
Cross evaluation weights of each DMU, solved by model (9), based on the ECED.
Secondly, another criterion is proposed, which is based on weighted mathematical expectation. There is a mathematical expectation regarding the arbitrary weight interval. Then, n sets of mathematical expectations are computed from Table 2 for n DMUs. These are seen in the second to seventh lines in Table 5. In order to be comparable to the evaluation criterion based on eclectic decision-making (ECED), we assume that each DMU has the same status, that is, . Then, the evaluation criterion based on weighted mathematical expectation is shown in the last line of Table 5. In Table 6, we show the weights for peer evaluation as solved by model (9) for the seven academic departments, which are based on the ECWME.

Table 5.
Expectation of each DMU and the evaluation criterion based on weighted mathematical expectation (ECWME) of all DMUs.

Table 6.
Evaluation weights of each DMU solved by model (9), based on the ECWME.
When comparing Table 4 and Table 6, we can see that the weights of DMU4 have not changed. This is because DMU4, which is an inefficient DMU, retains the weights in the CCR model in the cross-evaluation of this paper. In the coming section, we illustrate how the performance of the proposed approach is better than the classic cross-efficiency evaluation method in reducing zero weights. In Table 7, we show the weights solved by DEA model (2); that is, the CCR model. Cross-evaluation weights under the proposed method are limited by the constraints of the criteria, so the weights in Table 6 fluctuate around the evaluation criteria. The weights of the CCR model have no restriction of evaluation criteria. Each DMU only considers whether the weights are favourable or not, and does not need to consider the reality of the weights. So a large number of zero-value weights often appear in Table 7, which is easy to find by comparing Table 6 and Table 7. In Table 8 and Table 9, we show the weights solved by aggressive and benevolent cross evaluation. It is particularly noticeable that the number of zero weights is sharply reduced in the proposed ECED and ECWME-based approach when comparing Table 4, Table 6, Table 7, Table 8 and Table 9.

Table 7.
Weights of each DMU solved by CCR model.

Table 8.
Weights of each DMU solved by benevolent cross evaluation.

Table 9.
Weights of each DMU solved by aggressive cross evaluation.
The cross-efficiency scores and the rankings based on all the methods mentioned in this paper are provided in Table 10. We find that the proposed ECED and ECWME-based method has more discrimination power than CCR-efficiency, and basically provides different ranking with benevolent and aggressive cross-evaluation. This indicates that the proposed approaches in this paper represent a new method, one which can achieve effective ranking for DMUs. In addition, cross-efficiency scores and the rankings of the proposed approach based on ECED are shown in Table 11 when harmonic coefficient α = 0.2, α = 0.5, and α = 0.8. The proposed approach’s economic meaning is that each DMU has its own inputs and outputs, which are different from others. This leads to different DMU rankings under different evaluation criteria. This may become a macro policy whose value is high or low, according to the evaluation need, by adjusting α = 0.2, 0.5, or any value between 0 and 1.

Table 10.
Cross-efficiency scores and rankings based on all the methods mentioned in this paper.

Table 11.
Scores and rankings based on ECED when α = 0.2, α = 0.5, and α = 0.8.
Evaluation criteria are often formulated according to the present industry, which is not the integration of all enterprises, but the embodiment of some representative enterprises. That is, each DMU has a different role in the formation of evaluation criteria. Therefore, we consider two ECWME situations in this example, when p1 = p2 = p3 = p4 = p5 = p6 = p7 and 3p1 = 2 p2 = 6p3 = 6p4 = 6 p5 = 6 p6 = 6 p7. The cross-efficiency scores and rankings based on ECWME under the two combinations of p are shown in Table 12.

Table 12.
Scores and rankings based on ECWME using two combinations of p.
The coefficient of variation (CV) of the weights of each variable is computed and compared with the CCR model. The proposed approach is based on ECED and ECWME, and the result can be seen in Table 13. As can be seen, the mean of CV of the weights provided by the proposed approach is smaller than that of the weights provided by the CCR model. Also, the proposed ECWME-based approach is smaller than the proposed approach based on ECED. The CV of weights based on ECED and ECWME changes in line with changes in coefficient α and combinations of p.

Table 13.
Coefficient of variation (CV) of multiple methods.
Obviously, the CV of the weights of the two methods is very small in any case. This means that the weights of each DMU are very similar. These similar weights are further extended to be CSW, under which the score and rank based on ECED and ECWME are shown in Table 14. From the results shown in Table 14, the CSW in any case can be used to achieve the effective ranking of DMUs, and the rankings are different from each other.

Table 14.
Score and rank under the common set of weights (CSW) based on ECED and ECWME.
Example 2:
In order to illustrate the rationality and feasibility of the method, data pertaining to 27 innovative machinery manufacturing enterprises in Fujian Province in 2015 are collected and evaluated in terms of four inputs and four outputs, which are defined below:
- x1: R&D (research and development) personnel (ratio of R&D personnel to total personnel);
- x2: Total expenditure on scientific and technological activities in the current year (in increments of $10,000);
- x3: Total expenditure on R&D of enterprises (in increments of $10,000);
- x4: Number of senior technicians and technicians at the end of the year (persons);
- y1: Sales revenue of new products (services or processes) of enterprises in this year (in increments of 10,000 yuan);
- y2: Added value of enterprises in this year (in increments of 10,000 yuan);
- y3: Total profits realized by enterprises in this year (in increments of 10,000 yuan);
- y4: Total labor productivity of enterprises in this year (in increments of 10,000 yuan/person).
The letters in the enterprise number are the initials of the name of the area in which the enterprise is located. For example, “PT” in “PT 1” stands for Pu Tian City of Fujian Province.
The application example involves 27 innovative machinery manufacturing enterprises in Fujian Province, located in different cities in Fujian Province. The CCR-efficiency of each enterprise is shown in last column of Table 15. According to CCR-efficiency, 12 out of the 27 sampled enterprises are DEA effective. The interval weights of these 12 DEA-effective enterprises are obtained by solving model (5), as shown in Table A1 of the Appendix A. On the basis of the interval weights (Table A1 of the Appendix A), 10 ECEDs are denoted by A, B, C, D, E, F, G, H, I, and J, when the values of α were 1, 0.9, 0.8, 0.7, 0.6, 0.5, 0.3, 0.2, and 0.1, respectively. With any decrease of α, the value of ECED increases gradually. That is, the ECED is the minimum of the 10 evaluation criteria when α = 1 and the highest evaluation criteria when α = 0.1. The 10 ECED are shown in Table A2 of the Appendix A. For the 27 enterprises, if they are evaluated in a non-differentiated way (such as using the common weight evaluation method), then it is not conducive to encouraging enterprises in different regions to carry out innovative activities according to local conditions. However, evaluating these enterprises in a differentiated way (such as using the traditional cross-efficiency evaluation method) allows each enterprise to avoid its own weaknesses and emphasize its own advantages. In this case, the evaluation results will inevitably be unfair. Therefore, differentiated evaluation under evaluation criteria is carried out for these 27 enterprises, that is, cross-efficiency evaluation under the 10 criteria (Table A2 of the Appendix A). The comparison of the evaluation results is shown in Figure 1 and Figure 2.

Table 15.
Application example.

Figure 1.
Comparison of cross-efficiency scores of 27 machinery manufacturing enterprises based on 10 evaluation criteria based on eclectic decision-making (ECED). DMU, decision-making unit.
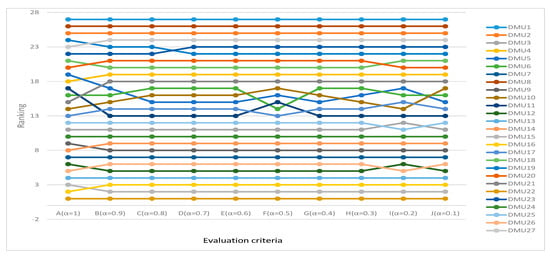
Figure 2.
Comparison of rankings of 27 machinery manufacturing enterprises based on 10 ECED.
We can see in Figure 1 that the degree of cross-efficiency of the 27 enterprises varies under different criteria, that is, the cross-efficiency of 27 enterprises is generally higher under the evaluation criterion (minimum criterion) when α = 1, and lower under the evaluation criterion (highest criterion) when α = 0.1. This result shows that the evaluation criteria have a supervisory and regulatory effect on the cross-efficiency of enterprises. When the evaluation criteria are lower, the weights space available for enterprises is larger, and the enterprises can select more favorable weights for themselves. Therefore, the cross-efficiency is generally higher. Conversely, when the weights space is smaller, the cross-efficiency is smaller. This conclusion is consistent with the application. The lower the evaluation criteria, the higher the performance of the enterprises will be.
According to Figure 2, the evaluation criteria also have an impact on the rankings of the 27 enterprises, and the rankings under almost every criterion are different. At the same time, the ranking of the 27 enterprises under different criteria has not changed to any significant degree. In particular, the ranking of the top enterprises and the bottom enterprises is relatively stable. This result shows that the rankings obtained under the proposed method can basically reflect the basic strength of enterprises.
By introducing the parameter p, the ECWME above takes into account the importance of DMUs in the criterion formulation. In order to highlight the changing regularity of cross-efficiency under different ECWME, we try to simplify the evaluation criteria. That is, one evaluation criterion only considers the importance of one DEA-effective enterprise. Therefore, the weighted mathematical expectation of 12 DEA-effective enterprises forms 12 evaluation criteria by adjusting the parameter p (see Table A3 of the Appendix A). Also, 12 ECWMEs are shown in Table A4 of the Appendix A. The cross-efficiency comparison chart of the 27 sampled machinery manufacturing enterprises based on 12 ECWME is shown in Figure 3, and the ranking comparison chart is shown in Figure 4. In Figure 3, the cross-efficiency of each DMU changes to different degrees under different standards, but the trend is basically the same. This shows that the evaluation criteria have a regulatory effect on the cross-efficiency. However, their decisive effect on the cross efficiency is the enterprise’s own performance. In addition, in Figure 3, when DMU-14 is used as the evaluation criterion, the cross efficiency of each DMU is higher. Combined with DMU-14 (see Appendix A Table A4 for bid winning), its value is lower than other evaluation criteria; it can be seen that the lower the evaluation criterion, the higher the cross efficiency of the evaluated DMU. In Figure 4, we use red dots to mark the ranking of 12 DEA-effective enterprises under 12 ECWMEs (see Table A4 of the Appendix A). For example, a small red dot is used to mark the ranking of a DEA-effective enterprise denoted as DMU5 under ECWME, denoted as DMU-5. This only considers the importance of DMU5. From the red dot distribution in Figure 4, it is not difficult to find that the ranking of DMU5 under ECWME DMU-5 is higher than the ranking under other criteria. The conclusion is also valid for other DEA-efficient enterprises, such as DMU6, DMU7, DMU11, and so on. This conclusion is reached because the weights for the enterprises (DMU5, DMU6, DMU7, DMU11, and so on) to be selected are subject to less conditional constraints (under ECWME, such as DMU-5, DMU-6, DMU-7, DMU-11, and so on) in cross-evaluation. That is, there is more weights room for the enterprises to choose, and each enterprise can obtain more conducive weights for themselves. This result is also consistent with the actual application. That is, the enterprise that is used as the evaluation criterion has more advantages in the comprehensive evaluation. Of course, few evaluation criteria in practical application only consider the importance of a certain enterprise. Often, some mainstream enterprises or representative enterprises are taken as evaluation criteria, in order to enhance the objectivity of the evaluation results and avoid the issue of evaluation subjectivity.
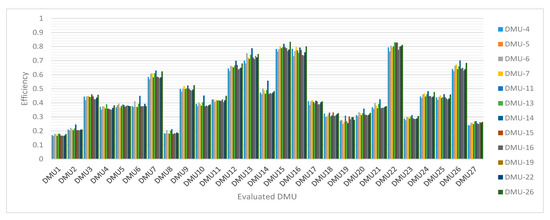
Figure 3.
Comparison of cross-efficiency scores of 27 machinery manufacturing enterprises based on 12 ECWMEs.
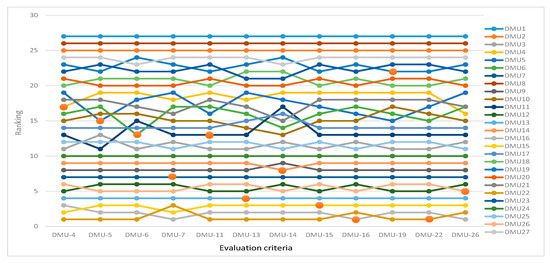
Figure 4.
Comparison of rankings of 27 machinery manufacturing enterprises, based on 12 ECWMEs.
From the analysis of the results of these examples, we can see that, firstly, the level of evaluation criteria will affect the ranking of an enterprise’s performance. Low criteria will help to implement enterprise incentive policies, and high criteria will help to macro-control enterprises. Secondly, enterprises ranked higher when considered by evaluation criteria. Taking multiple enterprises as evaluation criteria is conducive to setting up market benchmarks, and taking the vast majority of enterprises as evaluation criteria is conducive to creating a fair and free competitive market environment.
6. Conclusions
Cross-efficiency evaluation is an important method for ranking DMUs. Existing DEA models for cross-efficiency evaluation tend to choose the set of weights for peer evaluating using subjective attitudes, without an objective evaluation criterion as a reference point for peer evaluation. This makes it difficult for the DM to make a subjective DEA ranking.
To resolve these problems, we have proposed in this paper a cross-efficiency evaluation method based on evaluation criterion balanced on interval weights. The DEA model determines one set of weights for each DMU to evaluate its peers. This is done by minimizing the distance from the CCR-weights of the DMU to the evaluation criteria, which is balanced on interval weights. The criteria standard is different from the original intention of the evaluation, and the corresponding ranking based on cross-efficiency evaluation is also different. On the basis of the interval weights, this paper proposes two types of flexible evaluation criteria. One is based on the evaluation criteria that, in turn, are based on the eclectic decision-making method. Also, changing the harmonic coefficient can be done to adjust the evaluation criteria. The other criterion is based on the evaluation criteria of mathematical expectation, taking into account the importance of each DMU in the standard formulation by introducing the parameter P. As a result, the cross-efficiencies computed using this method are more objective and flexible, thus meeting the requirements of macro regulation. We have also extended the DEA model and proposed a cross-weight evaluation, which seeks a common set of weights for all DMUs. This method’s usefulness has been illustrated with numerical examples.
From the results of the illustrative example, it is particularly noticeable that the number of zero weights is sharply reduced and using cross-evaluation weights is more objective. This method avoids the situation where decision-makers try, for some purpose, to choose weights that are too subjective. In addition, the proposed approach can lead to different DMU rankings under different evaluation criteria and has more discrimination power than the CCR-efficiency method. The cross-evaluation criteria in the manuscript can be regarded as a means of macro-control, which is derived from the real market situation, and which is applied to macro-control market trends at the same time. Under the market environment, whether an industry or a chain enterprise, there should be established industry evaluation criteria or enterprise management objectives, and performance evaluation can be carried out by reference to the evaluation criteria or management objectives. This paper effectively solves these two problems. Firstly, the two evaluation criteria proposed in this paper provide feasible means and methods for industry criteria or enterprise management objectives; then, the cross-evaluation method based on evaluation criteria provides methods and theoretical support for performance evaluation, taking industry criteria or enterprise management objectives as references. Therefore, the proposed approach can be effectively applied to different evaluation problems, such as enterprise performance evaluation, school management, and the macro-control of banks. This work has several limitations that should be improved in future research. Firstly, the proposed approach assumes that DMUs are homogeneous, which limits the method’s application scope. Secondly, the criteria for macro-control should be based on a large sample, but this paper uses a small sample. Therefore, readers interested in this research can expand the approach by combining DEA and statistical methods that consider the heterogeneity of decision-making units (DMUs).
Author Contributions
Conceptualization, H.S. and Y.W.; methodology, H.S.; software, H.S.; validation, H.S., Y.W. and X.Z.; formal analysis, H.S.; investigation, H.S.; resources, H.S.; data curation, H.S.; writing—original draft preparation, H.S.; writing—review and editing, H.S.; visualization, H.S.; supervision, H.S.; project administration, H.S.; funding acquisition, Y.W.
Funding
This work was supported by the National Natural Science Foundation of China (No. 71801048, 71801050, and 71371053), Natural Science Foundation of Fujian Province (No. 2018J01650), and Youth Foundation of Education Department of Fujian Province (JAT170634).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Weights of 12 efficient machinery manufacturing enterprises.
Table A1.
Weights of 12 efficient machinery manufacturing enterprises.
| DMU | v1 | v2 | v3 | v4 | u1 | u2 | u3 | u4 |
|---|---|---|---|---|---|---|---|---|
| DMU4 | (0, 0.0824) | (0, 0.0058) | (0.029, 0.082) | (0, 0.55915) | (0, 0.0003) | (0, 0.0032) | (0, 0.00185) | (0, 0.4348) |
| DMU5 | (0, 0.4453) | (0, 12.676) | (0, 0.0157) | (0, 0.55335) | (0, 0.0016) | (0, 0.0083) | (0, 0.04655) | (0, 1.35135) |
| DMU6 | (0, 0.2795) | (0.013,0.027) | (0, 0.0125) | (0, 0.01635) | (0, 0.0003) | (0, 0.0018) | (0.0048, 0.00665) | (0, 0.3408) |
| DMU7 | (1.116, 1.40) | (0, 0.0016) | (0.008, 0.016) | (0, 0.0995) | (0.0005, 0.0008) | (0, 0.00115) | (0, 0.0008) | (0.982, 1.263) |
| DMU11 | (0, 0.38425) | (0, 0.0086) | (0, 0.0084) | (0.076, 2.424) | (0, 0.00075) | (0.0005, 0.0012) | (0, 0.0092) | (0, 0.5782) |
| DMU13 | (0, 0.5) | (0, 0.04005) | (0, 0.0094) | (0, 0.30675) | (0, 0.0004) | (0, 0.00295) | (0, 0.01035) | (0, 0.5804) |
| DMU14 | (0.332, 0.507) | (0, 0.0023) | (0, 0.0025) | (0, 0.00485) | (0, 0.0002) | (0, 0.0004) | (0, 0.00135) | (0.276, 0.404) |
| DMU15 | (0, 0.30715) | (0, 0.0053) | (0, 0.0054) | (0, 0.56935) | (0, 0.00035) | (0, 0.0006) | (0, 0.0022) | (0, 0.2597) |
| DMU16 | (0, 0.4337) | (0, 0.025) | (0, 0.0248) | (0, 1.04525) | (0, 0.0009) | (0, 0.003) | (0, 0.00775) | (0.072, 0.439) |
| DMU19 | (0, 0.27505) | (0, 0.0182) | (0, 0.0182) | (19.93, 20.03) | (0, 0.00175) | (0, 0.0138) | (0, 0.0641) | (0, 1.515) |
| DMU22 | (0, 0.9381) | (0, 0.0149) | (0, 0.12195) | (0, 1.235) | (0, 0.0009) | (0, 0.01005) | (0, 0.00505) | (0, 1.465) |
| DMU26 | (0.444, 0.687) | (0, 0.003) | (0, 0.003) | (0, 0.1071) | (0, 0.0003) | (0, 0.0009) | (0, 0.002) | (0, 0.418) |

Table A2.
Eclectic decision-making evaluation criterion (ECED) under different values of parameter α.
Table A2.
Eclectic decision-making evaluation criterion (ECED) under different values of parameter α.
| ECED | v1 | v2 | v3 | v4 | u1 | u2 | u3 | u4 |
|---|---|---|---|---|---|---|---|---|
| A (α = 1) | 0.1648 | 0.0032 | 0.0054 | 0.0097 | 0.0004 | 0.0008 | 0.0016 | 0.5194 |
| B (α = 0.9) | 0.2599 | 0.01288 | 0.00779 | 2.01145 | 0.00041 | 0.00077 | 0.00192 | 0.56565 |
| C (α = 0.8) | 0.355 | 0.02256 | 0.01018 | 4.0132 | 0.00042 | 0.00074 | 0.00224 | 0.6119 |
| D (α = 0.7) | 0.4501 | 0.03224 | 0.01257 | 6.01495 | 0.00043 | 0.00071 | 0.00256 | 0.65815 |
| E (α = 0.6) | 0.5452 | 0.04192 | 0.01496 | 8.0167 | 0.00044 | 0.00068 | 0.00288 | 0.7044 |
| F (α = 0.5) | 0.6403 | 0.0516 | 0.01735 | 10.01845 | 0.00045 | 0.00065 | 0.0032 | 0.75065 |
| G (α = 0.4) | 0.7354 | 0.06128 | 0.01974 | 12.0202 | 0.00046 | 0.00062 | 0.00352 | 0.7969 |
| H (α = 0.3) | 0.8305 | 0.07096 | 0.02213 | 14.02195 | 0.00047 | 0.00059 | 0.00384 | 0.84315 |
| I (α = 0.2) | 0.9256 | 0.08064 | 0.02452 | 16.0237 | 0.00048 | 0.00056 | 0.00416 | 0.8894 |
| J (α = 0.1) | 1.0207 | 0.09032 | 0.02691 | 18.02545 | 0.00049 | 0.00053 | 0.00448 | 0.93565 |

Table A3.
Combinations of p-value.
Table A3.
Combinations of p-value.
| Evaluation Criterion | p4 | p5 | p6 | p7 | p11 | p13 | p14 | p15 | p16 | p19 | p22 | p26 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DMU-4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU-5 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU-6 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU-7 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU-11 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU-13 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU-14 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| DMU-15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| DMU-16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| DMU-19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| DMU-22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| DMU-26 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |

Table A4.
Under different combinations of p in Table A3.
Table A4.
Under different combinations of p in Table A3.
| ECWME | v1 | v2 | v3 | v4 | u1 | u2 | u3 | u4 |
|---|---|---|---|---|---|---|---|---|
| DMU-4 | 0.0824 | 0.0058 | 0.08205 | 0.55915 | 0.0003 | 0.0032 | 0.00185 | 0.4348 |
| DMU-5 | 0.4453 | 12.6763 | 0.0157 | 0.55335 | 0.0016 | 0.0083 | 0.04655 | 1.35135 |
| DMU-6 | 0.2795 | 0.0274 | 0.0125 | 0.01635 | 0.0003 | 0.0018 | 0.00665 | 0.3408 |
| DMU-7 | 1.39955 | 0.0016 | 0.01605 | 0.0995 | 0.0008 | 0.00115 | 0.0008 | 1.26305 |
| DMU-11 | 0.38425 | 0.0086 | 0.0084 | 2.42355 | 0.00075 | 0.0012 | 0.0092 | 0.5782 |
| DMU-13 | 0.5 | 0.04005 | 0.0094 | 0.30675 | 0.0004 | 0.00295 | 0.01035 | 0.58035 |
| DMU-14 | 0.50725 | 0.0023 | 0.0025 | 0.00485 | 0.0002 | 0.0004 | 0.00135 | 0.4041 |
| DMU-15 | 0.30715 | 0.0053 | 0.0054 | 0.56935 | 0.00035 | 0.0006 | 0.0022 | 0.2597 |
| DMU-16 | 0.4337 | 0.025 | 0.0248 | 1.04525 | 0.0009 | 0.003 | 0.00775 | 0.4391 |
| DMU-19 | 0.27505 | 0.0182 | 0.0182 | 20.0272 | 0.00175 | 0.01375 | 0.0641 | 1.51515 |
| DMU-22 | 0.9381 | 0.01485 | 0.12195 | 1.23525 | 0.0009 | 0.01005 | 0.00505 | 1.4647 |
| DMU-26 | 0.6865 | 0.003 | 0.00305 | 0.1071 | 0.0003 | 0.0009 | 0.002 | 0.41845 |
References
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Banker, R.D.; Podinovski, V.V. Novel theory and methodology developments in data envelopment analysis. Ann. Oper. Res. 2017, 250, 1–3. [Google Scholar] [CrossRef]
- Hatami-Marbini, A.; Agrell, P.J.; Fukuyama, H.; Gholami, K.; Khoshnevis, P. The role of multiplier bounds in fuzzy data envelopment analysis. Ann. Oper. Res. 2017, 250, 249–276. [Google Scholar] [CrossRef]
- Wei, G.; Chen, J.; Wang, J. Stochastic efficiency analysis with a reliability consideration. Omega 2014, 48, 1–9. [Google Scholar] [CrossRef]
- Wei, G.; Wang, J. A comparative study of robust efficiency analysis and data envelopment analysis with imprecise data. Expert Syst. Appl. 2017, 81, 28–38. [Google Scholar] [CrossRef]
- Wu, J.; Sun, J.; Liang, L. Cross efficiency evaluation method based on weight-balanced data envelopment analysis model. Comput. Ind. Eng. 2012, 63, 513–519. [Google Scholar] [CrossRef]
- Wu, J.; Chu, J.; Sun, J.; Zhu, Q.; Liang, L. Extended secondary goal models for weights selection in DEA cross-efficiency evaluation. Comput. Ind. Eng. 2016, 93, 143–151. [Google Scholar] [CrossRef]
- Wu, J.; Chu, J.; Sun, J.; Zhu, Q. DEA cross-efficiency evaluation based on Pareto improvement. Eur. J. Oper. Res. 2016, 248, 571–579. [Google Scholar] [CrossRef]
- Sexton, T.R.; Silkman, R.H.; Hogan, A.J. Data envelopment analysis: Critique and extensions. New Dir. Program Eval. 1986, 32, 73–105. [Google Scholar] [CrossRef]
- Doyle, J.; Green, R. Efficiency and cross-efficiency in DEA: Derivations, meanings and uses. J. Oper. Res. Soc. 1994, 45, 567–578. [Google Scholar] [CrossRef]
- Wang, Y.M.; Chin, K.S. A neutral DEA model for cross-efficiency evaluation and its extension. Expert Syst. Appl. 2010, 37, 3666–3675. [Google Scholar] [CrossRef]
- Liang, L.; Wu, J.; Zhu, C.J. The DEA game cross-efficiency model and its Nash equilibrium. Oper. Res. 2008, 56, 1278–1288. [Google Scholar] [CrossRef]
- Jahanshahloo, G.R.; Lotfi, F.H.; Jafari, Y.; Maddahi, R. Selecting symmetric weights as a secondary goal in DEA cross-efficiency evaluation. Appl. Math. Model. 2011, 35, 544–549. [Google Scholar] [CrossRef]
- Ruiz, J.L. Cross-efficiency evaluation with directional distance functions. Eur. J. Oper. Res. 2013, 228, 181–189. [Google Scholar] [CrossRef]
- Cook, W.D.; Zhu, J. DEA Cobb–Douglas frontier and cross-efficiency. J. Oper. Res. Soc. 2014, 65, 265–268. [Google Scholar] [CrossRef]
- Oral, M.; Amin, G.R.; Oukil, A. Cross-efficiency in DEA: A maximum resonated appreciative model. Measurement 2015, 63, 159–167. [Google Scholar] [CrossRef]
- Oukil, A. Ranking via composite weighting schemes under a DEA cross-evaluation framework. Comput. Ind. Eng. 2018, 117, 217–224. [Google Scholar] [CrossRef]
- Carrillo, M.; Jorge, J.M. An alternative neutral approach for cross-efficiency evaluation. Comput. Ind. Eng. 2018, 120, 137–245. [Google Scholar] [CrossRef]
- Shi, H.; Wang, Y.; Chen, L. Neutral cross-efficiency evaluation regarding an ideal frontier and anti-ideal frontier as evaluation criteria. Comput. Ind. Eng. 2019, 132, 385–394. [Google Scholar] [CrossRef]
- Cook, W.D.; Roll, Y.; Kazakov, A. A DEA model for measuring the relative efficiencies of highway maintenance patrols. Inf. Syst. Oper. Res. 1990, 28, 113–124. [Google Scholar]
- Jahanshahloo, G.R.; Memariani, A.; Hosseinzadeh Lotfi, F.; Rezai, H.Z. A note on some of DEA models and finding efficiency and complete ranking using common set of weights. Appl. Math. Comput. 2005, 166, 265–281. [Google Scholar] [CrossRef]
- Kao, C.; Hung, H.T. Data envelopment analysis with common weights: The compromise solution approach. J. Oper. Res. Soc. 2005, 56, 1196–1203. [Google Scholar] [CrossRef]
- Liu, F.H.F.; Peng, H.H. Ranking of units on the DEA frontier with common weights. Comput. Oper. Res. 2008, 35, 1624–1637. [Google Scholar] [CrossRef]
- Amir, S.; Franco, V.; Paolo, B.; Wout, D.; Daniele, V. Reliable estimation of suppliers’ total cost of ownership: An imprecise data envelopment analysis model with common weights. Omega 2019, in press. [Google Scholar]
- Hossein, R.H.S.; Hannan, A.M.; Madjid, T.; Sadat, H.S. A novel common set of weights method for multi-period efficiency measurement using mean-variance criteria. Measurement 2018, 129, 569–581. [Google Scholar]
- Wang, Y.M.; Chin, K.S.; Jiang, P. Weight determination in the cross-efficiency evaluation. Comput. Ind. Eng. 2011, 61, 497–502. [Google Scholar] [CrossRef]
- Wang, Y.M.; Chin, K.S.; Luo, Y. Cross-efficiency evaluation based on ideal and anti-ideal decision making units. Expert Syst. Appl. 2011, 38, 10312–10319. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).