Multi-Attribute Decision-Making Based on m-Polar Fuzzy Hamacher Aggregation Operators

Abstract

In this paper, we introduce certain aggregation operators, namely, the m-polar fuzzy (mF) Hamacher weighted average operator, mF Hamacher ordered weighted average (mFHOWA) operator, mF Hamacher hybrid average (mFHHA) operator, mF Hamacher weighted geometric (mFHWG) operator, mF Hamacher weighted ordered geometric operator, and mF Hamacher hybrid geometric (mFHHG) operator. We discuss some properties of these operators, inclusive of their ability to implement both symmetric and asymmetric treatments of the items. We develop an algorithmic model to solve multi-attribute decision-making (MADM) problems in mF environment using mF Hamacher weighted average operator (mFHWA) and mFHWG operators. They can compensate for the possible asymmetric roles of the attributes that describe the problem. In the end, to prove the validity and feasibility of the proposed work, we give applications for selecting the most affected country regarding human trafficking, selecting health care waste treatment methods and selecting the best company for investment. We also solve practical MADM problems by using ELECTRE-I method, and give a comparative analysis.

1. Introduction

Multi-attribute decision-making (MADM) plays an efficient role in different domains, ranging from engineering to social sciences. MADM approaches identify how attribute information is to be processed to compute a suitable alternative or to rank the alternatives for supporting decision-making. It has been broadly applied in different domains, including engineering technology [1], operation research [2], and management science [3]. To solve decision-making problems having uncertainty, Atanassov [4] introduced the idea of intuitionistic fuzzy sets (IFSs) which involve both membership and non-membership functions, an efficient generalization of fuzzy sets [5] which characterize only membership function.

Aggregation operators (AOs) play a key role in combining information into a single datum and solving MADM issues. For instance, Yager [6] proposed weighted AOs. Xu [7] introduced some novel AOs based on intuitionistic fuzzy sets. Xu and Yager [8] gave some novel geometric AOs with some practical applications in MADM. From the information analysis of an alternative, it is easy to see that there is another property that is its counterpart for each property of the alternative. With this viewpoint, Zhang [9,10] initiated the concept of bipolar fuzzy (BF) sets. The membership degree of BF sets enlarged from $[0,1]$ to $[-1,0]\times [0,1]$. In a BF set, there are two membership parts, positive and negative memberships which belong to the intervals $[0,1]$ and $[-1,0]$, respectively. BF sets have a wide range of applications in many research domains, including medicine science [11] and decision analysis [12]. Wei et al. [13] presented some hesitant BF weighted arithmetic and geometric AOs. Xu and Wei [14] developed dual hesitant BF arithmetic and geometric AOs. Garg [15] utilized linguistic prioritized AOs to develop a MADM method under a single-valued neutrosophic environment. Beg and Rashi [16] proposed a intuitionistic hesitant fuzzy set model for group decision-making. Grzegorzewski [17] discussed the separability of fuzzy relations. Alcantud et al. [18] take advantage of the theoretical foundations of aggregation operators to produce the first procedure for the aggregation of infinitely many intuitionistic fuzzy sets, which they use to make decisions in an intertemporal framework (i.e., with decisions that spread over an indefinitely long number of periods).

AOs are an important topic today and are attracting a great deal of attention. Hamacher t-conorm and t-norm [19] are the algebraic and Einstein t-conorm and t-norm [20] expanded variants, respectively. Based on Hamacher operations, AOs play an efficient role in solving different MADM problems. Liu [21] used Hamacher operations to develop AOs for interval-valued intuitionistic fuzzy sets environment. Many MADM models have been developed using bipolar fuzzy numbers, t-norms, and t-conorms, for instance, Wei et al. [22] proposed some BF Hamacher arithmetic and geometric operators and investigated their basic properties. Gao et al. [23] introduced dual hesitant BF Hamacher prioritized weighted average and geometric operators. Due to the existence of multi-polar information in many real situations, the concept of m-polar fuzzy (mF) sets was introduced by Chen et al. [24] as an extension of BF sets. Khameneh and Kilucman developed certain mF soft weighted AOs. We observe that almost all AOs used BF numbers, intuitionistic fuzzy numbers, Pythagorean fuzzy numbers, or mF numbers without using Hamacher operations. Akram et al. [25,26,27,28,29,30,31] introduced several decision-making techniques. In this research article, our main focus is how to apply Hamacher operators to aggregate the mF information. For further terminologies which are not discussed in the paper, the readers are referred to [32,33,34,35,36,37,38,39,40,41,42,43,44].

The motivation of this article is described as follows:

• The assessment of the best alternative in an mF environment is a very difficult MADM problem and has several imprecise factors. In the present MADM techniques, assessment data is simply portrayed by fuzzy and BF numbers which may prompt data mutilation.
• As a prevalent set, mF numbers demonstrates extraordinary execution in providing multi-polar vague, reliable, and inexact assessment information. Therefore, mF numbers might be the best way for the evaluation of alternatives using information having multi-polarity.
• Taking into account that Hamacher AOs are a straight forward, however ground-breaking, approach for solving decision-making issues, this article, in general, aims to define Hamacher AOs in the mF context to tackle difficult problems of choice.
• Hamacher AOs make the decision results more precise and exact when applied to real-life MADM based on the mF environment.
• The proposed operators overcome the limitations of previously existing operators.

Thus, an mF decision-making approach based on Hamacher AOs is proposed to choose the ideal alternative. The proposed method has three main benefits compared to other strategies. First, the method presented uses mF numbers, which can more accurately explain the problems having multiple attributes. Secondly, the proposed method is more efficient and versatile by using only one parameter. Thirdly, it is very important and significant to use Hamacher AOs for mF numbers and to solve practical problems by applying them. The proposed technique is more suitable in tackling complex realistic issues like the selection of the best health care waste treatment methods.

The main contributions of this article are:

• The concept of Hamacher AOs is extended to mF environment. Some fundamental properties are discussed. These operators are more flexible and can be taken as the generalization of algebraic and Einstein operators.
• An algorithm is developed to handle complex realistic problems with multi-polar data.
• Lastly, the strengths and characteristics of these operators are illustrated by comparison analysis.

The remainder of this paper is organized as follows: In Section 2, we recall some basic notions and then introduce certain Hamacher weighted averaging operators, namely mF Hamacher weighted average (mFHWA), mF Hamacher ordered weighted average (mFHOWA), and mF Hamacher hybrid average (mFHHA) operators. In this section, we also developed some Hamacher weighted geometric operators, namely mF Hamacher weighted geometric (mFHWG), mFHOWG, and mF Hamacher hybrid geometric (mFHHG) operators. In Section 3, we provide mathematical modeling of proposed operators to solve real-life MADM problems. In Section 4, we solve three practical MADM problems by using the proposed operators and ELECTRE-I method. In Section 5, we give a comparison analysis. In Section 6, we give conclusion and future directions.

2. mF Hamacher Aggregation Operators

Definition 1

([24]). An mF set over a universe $\mathcal{U}$ is a function $\xi :\mathcal{U}\to {[0,1]}^m$. The membership of each object is represented by $\xi \left(u\right)=(p_1\circ \xi \left(u\right),p_2\circ \xi \left(u\right),\dots ,p_m\circ \xi \left(u\right))$ where $p_r\circ \xi :{[0,1]}^m\to [0,1]$ is the r-th projection mapping.

Let $\widehat{\xi }=(p_1\circ \xi ,\dots ,p_m\circ \xi )$ be an mF number, where $p_r\circ \xi \in [0,1]$ for each $r=1,2,\dots ,m$.

Definition 2.

The score function S of an mF number $\widehat{\xi }=(p_1\circ \xi ,\dots ,p_m\circ \xi )$ is formulated as

$$S\left(\widehat{\xi }\right)={\displaystyle \frac{1}{m}}\left(\sum _{r=1}^m(p_r\circ \xi )\right),S\left(\widehat{\xi }\right)\in [0,1].$$

Definition 3.

The accuracy function H of an mF number $\widehat{\xi }=(p_1\circ \xi ,\dots ,p_m\circ \xi )$ is given by

$$H\left(\widehat{\xi }\right)={\displaystyle \frac{1}{m}}\left(\sum _{r=1}^m{(-1)}^r(p_r\circ \xi -1)\right),H\left(\widehat{\xi }\right)\in [-1,1].$$

Clearly, for an arbitrary mF number $\widehat{\xi }$, $S\left(\widehat{\xi }\right)\in [0,1].$

Definition 4.

Let ${\widehat{\xi }}_1=(p_1\circ {\xi }_1,\dots ,p_m\circ {\xi }_1)$, and ${\widehat{\xi }}_2=(p_1\circ {\xi }_2,\dots ,p_m\circ {\xi }_2)$ be two mF numbers. Then

1.

${\widehat{\xi }}_1<{\widehat{\xi }}_2$, if $S\left({\widehat{\xi }}_1\right)<S\left({\widehat{\xi }}_2\right)$.

2.

${\widehat{\xi }}_1>{\widehat{\xi }}_2$, if $S\left({\widehat{\xi }}_1\right)>S\left({\widehat{\xi }}_2\right)$.

3.

${\widehat{\xi }}_1={\widehat{\xi }}_2$, If $S\left({\widehat{\xi }}_1\right)=S\left({\widehat{\xi }}_2\right)$ and $H\left({\widehat{\xi }}_1\right)=H\left({\widehat{\xi }}_2\right)$.

4.

${\widehat{\xi }}_1<{\widehat{\xi }}_2$, if $S\left({\widehat{\xi }}_1\right)=S\left({\widehat{\xi }}_2\right)$, but $H\left({\widehat{\xi }}_1\right)<H\left({\widehat{\xi }}_2\right)$.

5.

${\widehat{\xi }}_1>{\widehat{\xi }}_2$, if $S\left({\widehat{\xi }}_1\right)=S\left({\widehat{\xi }}_2\right)$, but $H\left({\widehat{\xi }}_1\right)>H\left({\widehat{\xi }}_2\right)$.

Now we describe some fundamental operations on mF numbers as follows:

• ${\widehat{\xi }}_1⊞{\widehat{\xi }}_2=\left(p_1\circ {\xi }_1+p_1\circ {\xi }_2-p_1\circ {\xi }_1.p_1\circ {\xi }_2,\dots ,p_m\circ {\xi }_1+p_m\circ {\xi }_2-p_m\circ {\xi }_1.p_m\circ {\xi }_2\right)$,
• ${\widehat{\xi }}_1⊠{\widehat{\xi }}_2=\left(p_1\circ {\xi }_1.p_1\circ {\xi }_2,\dots ,p_m\circ {\xi }_1.p_m\circ {\xi }_2\right)$,
• $\alpha \widehat{\xi }=\left(1-{(1-p_1\circ \xi )}^{\alpha },\dots ,1-{(1-p_m\circ \xi )}^{\alpha }\right),\alpha >0$,
• ${\left(\widehat{\xi }\right)}^{\alpha }=\left({(p_1\circ \xi )}^{\alpha },\dots ,{(p_m\circ \xi )}^{\alpha }\right),\alpha >0,$
• ${\widehat{\xi }}^c=\left(1-p_1\circ \xi ,\dots ,1-p_m\circ \xi \right),$
• ${\widehat{\xi }}_1\subseteq {\widehat{\xi }}_2,$ if and only if $p_1\circ {\xi }_1\le p_1\circ {\xi }_2,\dots ,p_m\circ {\xi }_1\le p_m\circ {\xi }_2,$
• ${\widehat{\xi }}_1\cup {\widehat{\xi }}_2=\left(max(p_1\circ {\xi }_1,p_1\circ {\xi }_2),\dots ,max(p_m\circ {\xi }_1,p_m\circ {\xi }_2)\right),$
• ${\widehat{\xi }}_1\cap {\widehat{\xi }}_2=\left(min(p_1\circ {\xi }_1,p_1\circ {\xi }_2),\dots ,min(p_m\circ {\xi }_1,p_m\circ {\xi }_2)\right).$

Theorem 1.

Let ${\widehat{\xi }}_1=(p_1\circ {\xi }_1,\dots ,p_m\circ {\xi }_1\left(u\right))$ and ${\widehat{\xi }}_2=(p_1\circ {\xi }_2,\dots ,p_m\circ {\xi }_2)$ be two mF numbers, $\alpha ,{\alpha }_1,{\alpha }_2>0,$ then

1.

${\widehat{\xi }}_1⊞{\widehat{\xi }}_2={\widehat{\xi }}_2⊞{\widehat{\xi }}_1$,

2.

${\widehat{\xi }}_1⊠{\widehat{\xi }}_2={\widehat{\xi }}_2⊠{\widehat{\xi }}_1$,

3.

$\alpha ({\widehat{\xi }}_1⊞{\widehat{\xi }}_2)=\alpha \left({\widehat{\xi }}_1\right)⊞\alpha \left({\widehat{\xi }}_2\right)$,

4.

${({\widehat{\xi }}_1⊠{\widehat{\xi }}_2)}^{\alpha }={\left({\widehat{\xi }}_1\right)}^{\alpha }⊠{\left({\widehat{\xi }}_2\right)}^{\alpha }$,

5.

${\alpha }_1{\widehat{\xi }}_1⊞{\alpha }_2{\widehat{\xi }}_1=({\alpha }_1+{\alpha }_2){\widehat{\xi }}_1$,

6.

${\left({\widehat{\xi }}_1\right)}^{{\alpha }_1}⊠{\left({\widehat{\xi }}_2\right)}^{{\alpha }_2}={\left({\widehat{\xi }}_1\right)}^{{\alpha }_1+{\alpha }_2},$

7.

${\left({\left({\widehat{\xi }}_1\right)}^{{\alpha }_1}\right)}^{{\alpha }_2}={\left({\widehat{\xi }}_1\right)}^{{\alpha }_1{\alpha }_2}.$

Proof. 

Straightforward. □

2.1. Hamacher Operations of mF Numbers

Hamacher [19] introduced an extension of t-norm and t-conorm. Hamacher product ⊗ and Hamacher sum ⊕ are respectively t-norm and t-conorm, which are given as follows, for all $l,t\in [0,1]$.

$$\begin{array}{cc}\hfill \mathcal{T}(l,t)& =l\otimes t={\displaystyle \frac{lt}{\lambda +(1-\lambda )(l+t-lt)}},\lambda >0.\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\mathcal{T}}^{*}(l,t)& =l\oplus t={\displaystyle \frac{l+t-lt-(1-\lambda )lt}{1-(1-\lambda )lt}},\lambda >0.\hfill \end{array}$$

(2)

In particular, when $\lambda =1$ in Equations (1) and (2), we get algebraic t-norm and t-conorm, respectively.

$$\begin{array}{cc}\hfill \mathcal{T}(l,t)& =l\otimes t=lt,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\mathcal{T}}^{*}(l,t)& =l\oplus t=l+t-lt,\hfill \end{array}$$

(4)

and when $\lambda =2$ in Equations (1) and (2), we obtain Einstein t-norm and t-conorm, respectively, as follows:

$$\begin{array}{cc}\hfill \mathcal{T}(l,t)& =l\otimes t={\displaystyle \frac{lt}{1+(1-l)(1-t)}},\lambda >0.\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\mathcal{T}}^{*}(l,t)& =l\oplus t={\displaystyle \frac{l+t}{1+lt}},\lambda >0.\hfill \end{array}$$

(6)

With the help of Hamacher operations defined in [22,38] for bipolar fuzzy numbers, we now present the Hamacher operations for mF numbers. Let $\widehat{{\xi }_1}=(p_1\circ {\xi }_1,\dots ,p_m\circ {\xi }_1),\widehat{{\xi }_2}=(p_1\circ {\xi }_2,\dots ,p_m\circ {\xi }_2)$ and $\widehat{\xi }=(p_1\circ \xi ,\dots ,p_m\circ \xi )$ be mF numbers. We define the following basic Hamacher operations for mF numbers with $\lambda >0$.

• ${\widehat{\xi }}_1\oplus {\widehat{\xi }}_2=\left({\displaystyle \frac{p_1\circ {\xi }_1+p_1\circ {\xi }_2-p_1\circ {\xi }_1.p_1\circ {\xi }_2-(1-\lambda )p_1\circ {\xi }_1.p_1\circ {\xi }_2}{1-(1-\lambda )p_1\circ {\xi }_1.p_1\circ {\xi }_2}},\dots ,{\displaystyle \frac{p_m\circ {\xi }_1+p_m\circ {\xi }_2-p_m\circ {\xi }_1.p_m\circ {\xi }_2-(1-\lambda )p_m\circ {\xi }_1.p_m\circ {\xi }_2}{1-(1-\lambda )p_m\circ {\xi }_1.p_m\circ {\xi }_2}}\right)$
• ${\widehat{\xi }}_1\otimes {\widehat{\xi }}_2=\left({\displaystyle \frac{p_1\circ {\xi }_1.p_1\circ {\xi }_2}{\lambda +(1-\lambda )(p_1\circ {\xi }_1+p_1\circ {\xi }_2-p_1\circ {\xi }_1.p_1\circ {\xi }_2)}},\dots ,{\displaystyle \frac{p_m\circ {\xi }_1.p_m\circ {\xi }_2}{\lambda +(1-\lambda )(p_m\circ {\xi }_1+p_m\circ {\xi }_2-p_m\circ {\xi }_1.p_m\circ {\xi }_2)}}\right)$
• $\alpha \widehat{\xi }=\left({\displaystyle \frac{{(1+(\lambda -1)p_1\circ \xi )}^{\alpha }-{(1-p_1\circ \xi )}^{\alpha }}{{(1+(\lambda -1)p_1\circ \xi )}^{\alpha }+(\lambda -1){(1-p_1\circ \xi )}^{\alpha }}},\dots ,{\displaystyle \frac{{(1+(\lambda -1)p_m\circ \xi )}^{\alpha }-{(1-p_m\circ \xi )}^{\alpha }}{{(1+(\lambda -1)p_m\circ \xi )}^{\alpha }+(\lambda -1){(1-p_m\circ \xi )}^{\alpha }}}\right),\alpha >0$
• ${\left(\widehat{\xi }\right)}^{\alpha }=\left({\displaystyle \frac{\lambda {(p_1\circ \xi )}^{\alpha }}{{(1+(\lambda -1)(1-p_1\circ \xi ))}^{\alpha }+(\lambda -1){(p_1\circ \xi )}^{\alpha }}},\dots ,{\displaystyle \frac{\lambda {(p_m\circ \xi )}^{\alpha }}{{(1+(\lambda -1)(1-p_m\circ \xi ))}^{\alpha }+(\lambda -1){(p_m\circ \xi )}^{\alpha }}}\right),\alpha >0.$

2.2. mF Hamacher Arithmetic Aggregation Operators

We propose mF Hamacher arithmetic aggregation operators as follows:

Definition 5.

Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of mF numbers where ‘j’ varies from 1 to n. Then, an mF Hamacher weighted average (mFHWA) operator is a mapping from ${\widehat{\xi }}^n$ to $\widehat{\xi }$, which is defined as

$$\begin{array}{c}\hfill mFHW{A}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨁}}\left({\theta }_j{\widehat{\xi }}_j\right)\end{array}$$

(7)

where $\theta ={({\theta }_1,{\theta }_2,\dots ,{\theta }_n)}^T$ represents the weight vector of ${\widehat{\xi }}_j,$ for each ‘j’ varies from 1 to n, with ${\theta }_j>0$ and ${\displaystyle \sum _{j=1}^n}{\theta }_j=1$.

Theorem 2.

Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of mF numbers where ‘j’ varies from 1 to n. The accumulated value of these mF numbers using the mFHWA operator is also an mF numbers, which is given as

$$\begin{array}{cc}\hfill mFHW{A}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})& =\underset{j=1}{\overset{n}{⨁}}\left({\theta }_j{\widehat{\xi }}_j\right),\hfill \\ \hfill & =({\displaystyle \frac{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_1\circ {\xi }_j\right)}^{{\theta }_j}-{\prod }_{j=1}^n{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_1\circ {\xi }_j\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^n{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_m\circ {\xi }_j\right)}^{{\theta }_j}-{\prod }_{j=1}^n{\left(1-p_m\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_m\circ {\xi }_j\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^n{\left(1-p_m\circ {\xi }_j\right)}^{{\theta }_j}}}).\hfill \end{array}$$

(8)

Proof. 

We use the mathematical induction technique to prove it.

Case 1.

When $n=1$ from Equation (8), we get

$$\begin{array}{cc}\hfill mFHW{A}_{\theta }(\widehat{{\xi }_1},,\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})& ={\theta }_1{\widehat{\xi }}_1={\widehat{\xi }}_1,(\mathrm{since}{\theta }_1=1)\hfill \\ \hfill & =({\displaystyle \frac{1+(\lambda -1)p_1\circ {\xi }_1-(1-p_1\circ {\xi }_1)}{(1+(\lambda -1)p_1\circ {\xi }_1)+(\lambda -1)(1-p_1\circ {\xi }_1)}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{1+(\lambda -1)p_m\circ {\xi }_1-(1-p_m\circ {\xi }_1)}{(1+(\lambda -1)p_m\circ {\xi }_1)+(\lambda -1)(1-p_m\circ {\xi }_1)}}).\hfill \end{array}$$

Thus, for $n=1$ Equation (8) holds.

Case 2.

We now suppose that Equation (8) holds for $n=s$, where $s\in \mathbb{N}$ (set of natural numbers), then we get

$$\begin{array}{cc}\hfill mFHW{A}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_s})& =\underset{j=1}{\overset{s}{⨁}}\left({\theta }_j{\widehat{\xi }}_j\right),\hfill \\ \hfill & =({\displaystyle \frac{{\prod }_{j=1}^s{\left(1+(\lambda -1)p_1\circ {\xi }_j\right)}^{{\theta }_j}-{\prod }_{j=1}^s{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^s{\left(1+(\lambda -1)p_1\circ {\xi }_j\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^s{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^s{\left(1+(\lambda -1)p_m\circ {\xi }_j\right)}^{{\theta }_j}-{\prod }_{j=1}^s{\left(1-p_m\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^s{\left(1+(\lambda -1)p_m\circ {\xi }_j\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^s{\left(1-p_m\circ {\xi }_j\right)}^{{\theta }_j}}}).\hfill \end{array}$$

(9)

For $n=s+1$,

$$\begin{array}{cc}\hfill mFHW{A}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_s},{\widehat{\xi }}_{s+1})=& \underset{j=1}{\overset{s}{⨁}}\left({\theta }_j{\widehat{\xi }}_j\right)\oplus \left({\theta }_{s+1}{\widehat{\xi }}_{s+1}\right),\hfill \\ \hfill =& ({\displaystyle \frac{{\prod }_{j=1}^s{\left(1+(\lambda -1)p_1\circ {\xi }_j\right)}^{{\theta }_j}-{\prod }_{j=1}^s{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^s{\left(1+(\lambda -1)p_1\circ {\xi }_j\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^s{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^s{\left(1+(\lambda -1)p_m\circ {\xi }_j\right)}^{{\theta }_j}-{\prod }_{j=1}^s{\left(1-p_m\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^s{\left(1+(\lambda -1)p_m\circ {\xi }_j\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^s{\left(1-p_m\circ {\xi }_j\right)}^{{\theta }_j}}})\oplus \hfill \\ \hfill & ({\displaystyle \frac{{(1+(\lambda -1)p_1\circ {\xi }_{s+1})}^{{\theta }_{s+1}}-{(1-p_1\circ {\xi }_{s+1})}^{{\theta }_{s+1}}}{{(1+(\lambda -1)p_1\circ {\xi }_{s+1})}^{{\theta }_{s+1}}+(\lambda -1){(1-p_1\circ {\xi }_{s+1})}^{{\theta }_{s+1}}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{(1+(\lambda -1)p_m\circ {\xi }_{s+1})}^{{\theta }_{s+1}}-{(1-p_m\circ {\xi }_{s+1})}^{{\theta }_{s+1}}}{{(1+(\lambda -1)p_m\circ {\xi }_{s+1})}^{{\theta }_{s+1}}+(\lambda -1){(1-p_m\circ {\xi }_{s+1})}^{{\theta }_{s+1}}}})\hfill \end{array}$$

$$\begin{array}{cc}\hfill =& ({\displaystyle \frac{{\prod }_{j=1}^{s+1}{\left(1+(\lambda -1)p_1\circ {\xi }_j\right)}^{{\theta }_j}-{\prod }_{j=1}^{s+1}{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^{s+1}{\left(1+(\lambda -1)p_1\circ {\xi }_j\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^{s+1}{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^{s+1}{\left(1+(\lambda -1)p_m\circ {\xi }_j\right)}^{{\theta }_j}-{\prod }_{j=1}^{s+1}{\left(1-p_m\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^{s+1}{\left(1+(\lambda -1)p_m\circ {\xi }_j\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^{s+1}{\left(1-p_m\circ {\xi }_j\right)}^{{\theta }_j}}}).\hfill \end{array}$$

Therefore, Equation (8) holds for $n=s+1$. Thus, we conclude that Equation (8) holds for any $n\in \mathbb{N}$. □

Example 1.

Let ${\widehat{\xi }}_1=(0.2,0.5,0.7,0.3),{\widehat{\xi }}_2=(0.8,0.6,0.6,0.4)$ and ${\widehat{\xi }}_3=(0.1,0.2,0.4,0.5)$ be 4F numbers with a weight vector $\theta ={(0.3,0.5,0.2)}^T$ for these 4F numbers. Then, for $\lambda =3$,

$$\begin{array}{cc}\hfill & mFHW{A}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\widehat{{\xi }_3})=\underset{j=1}{\overset{3}{⨁}}\left({\theta }_j{\widehat{\xi }}_j\right)\hfill \\ \hfill & =({\displaystyle \frac{{\prod }_{j=1}^3{\left(1+(\lambda -1)p_1\circ {\xi }_j\right)}^{{\theta }_j}-{\prod }_{j=1}^3{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^3{\left(1+(\lambda -1)p_1\circ {\xi }_j\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^3{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^3{\left(1+(\lambda -1)p_4\circ {\xi }_j\right)}^{{\theta }_j}-{\prod }_{j=1}^3{\left(1-p_4\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^3{\left(1+(\lambda -1)p_4\circ {\xi }_j\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^3{\left(1-p_4\circ {\xi }_j\right)}^{{\theta }_j}}})\hfill \\ \hfill & =({\displaystyle \frac{{\left(1+\left(2\right)0.2\right)}^{0.3}\times {\left(1+\left(2\right)0.8\right)}^{0.5}\times {\left(1+\left(2\right)0.1\right)}^{0.2}-{\left(1-0.2\right)}^{0.3}\times {\left(1-0.8\right)}^{0.5}\times {\left(1-0.1\right)}^{0.2}}{{\left(1+\left(2\right)0.2\right)}^{0.3}\times {\left(1+\left(2\right)0.8\right)}^{0.5}\times {\left(1+\left(2\right)0.1\right)}^{0.2}+\left(2\right)\left({\left(1-0.2\right)}^{0.3}\times {\left(1-0.8\right)}^{0.5}\times {\left(1-0.1\right)}^{0.2}\right)}},\hfill \\ \hfill & {\displaystyle \frac{{\left(1+\left(2\right)0.5\right)}^{0.3}\times {\left(1+\left(2\right)0.6\right)}^{0.5}\times {\left(1+\left(2\right)0.2\right)}^{0.2}-{\left(1-0.5\right)}^{0.3}\times {\left(1-0.6\right)}^{0.5}\times {\left(1-0.2\right)}^{0.2}}{{\left(1+\left(2\right)0.5\right)}^{0.3}\times {\left(1+\left(2\right)0.6\right)}^{0.5}\times {\left(1+\left(2\right)0.2\right)}^{0.2}+\left(2\right)\left({\left(1-0.5\right)}^{0.3}\times {\left(1-0.6\right)}^{0.5}\times {\left(1-0.2\right)}^{0.2}\right)}},\hfill \\ \hfill & {\displaystyle \frac{{\left(1+\left(2\right)0.7\right)}^{0.3}\times {\left(1+\left(2\right)0.6\right)}^{0.5}\times {\left(1+\left(2\right)0.4\right)}^{0.2}-{\left(1-0.7\right)}^{0.3}\times {\left(1-0.6\right)}^{0.5}\times {\left(1-0.4\right)}^{0.2}}{{\left(1+\left(2\right)0.7\right)}^{0.3}\times {\left(1+\left(2\right)0.6\right)}^{0.5}\times {\left(1+\left(2\right)0.4\right)}^{0.2}+\left(2\right)\left({\left(1-0.7\right)}^{0.3}\times {\left(1-0.6\right)}^{0.5}\times {\left(1-0.4\right)}^{0.2}\right)}},\hfill \\ \hfill & {\displaystyle \frac{{\left(1+\left(2\right)0.3\right)}^{0.3}\times {\left(1+\left(2\right)0.4\right)}^{0.5}\times {\left(1+\left(2\right)0.5\right)}^{0.2}-{\left(1-0.3\right)}^{0.3}\times {\left(1-0.4\right)}^{0.5}\times {\left(1-0.5\right)}^{0.2}}{{\left(1+\left(2\right)0.3\right)}^{0.3}\times {\left(1+\left(2\right)0.4\right)}^{0.5}\times {\left(1+\left(2\right)0.5\right)}^{0.2}+\left(2\right)\left({\left(1-0.3\right)}^{0.3}\times {\left(1-0.4\right)}^{0.5}\times {\left(1-0.5\right)}^{0.2}\right)}})\hfill \\ \hfill & =(0.5397,0.4980,0.5974,0.3913).\hfill \end{array}$$

We now give two particular cases of the mFHWA operator.

• When $\lambda =1$, mFHWA operator reduces into mF weighted averaging (mFWA) operator as below:

  $$\begin{array}{cc}\hfill & mFW{A}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨁}}\left({\theta }_j{\widehat{\xi }}_j\right)\hfill \\ \hfill & =\left(1-\prod _{j=1}^n{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j},1-\prod _{j=1}^n{\left(1-p_2\circ {\xi }_j\right)}^{{\theta }_j},\dots ,1-\prod _{j=1}^n{\left(1-p_m\circ {\xi }_j\right)}^{{\theta }_j}\right).\hfill \end{array}$$

  (10)
• When $\lambda =2$, mFHWA operator reduces into mF Einstein weighted averaging (mFEWA) operator as below:

  $$\begin{array}{cc}\hfill & mFEW{A}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨁}}\left({\theta }_j{\widehat{\xi }}_j\right)\hfill \\ \hfill & =({\displaystyle \frac{{\prod }_{j=1}^n{\left(1+p_1\circ {\xi }_j\right)}^{{\theta }_j}-{\prod }_{j=1}^n{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^n{\left(1+p_1\circ {\xi }_j\right)}^{{\theta }_j}+{\prod }_{j=1}^n{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^n{\left(1+p_m\circ {\xi }_j\right)}^{{\theta }_j}-{\prod }_{j=1}^n{\left(1-p_m\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^n{\left(1+p_m\circ {\xi }_j\right)}^{{\theta }_j}+{\prod }_{j=1}^n{\left(1-p_m\circ {\xi }_j\right)}^{{\theta }_j}}}).\hfill \end{array}$$

  (11)

Theorem 3

(Idempotency Property). Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j),$ be a family of ‘n’ mF numbers. If all these mF numbers are same, in other words, ${\widehat{\xi }}_j=\widehat{\xi },\forall j=1,2,\dots ,n$, then

$$\begin{array}{c}\hfill mFHW{A}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\widehat{\xi }.\end{array}$$

(12)

Proof. 

Since ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)=\widehat{\xi },$ where ‘j’ varies from 1 to $n.$. Then, from Equation (8), we get

$$\begin{array}{cc}\hfill mFHW{A}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})& =\underset{j=1}{\overset{n}{⨁}}\left({\theta }_j{\widehat{\xi }}_j\right),\hfill \\ \hfill & =({\displaystyle \frac{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_1\circ {\xi }_j\right)}^{{\theta }_j}-{\prod }_{j=1}^n{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_1\circ {\xi }_j\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^n{\left(1-p_1\circ {\xi }_j\right)}^{{\theta }_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_m\circ {\xi }_j\right)}^{{\theta }_j}-{\prod }_{j=1}^n{\left(1-p_m\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_m\circ {\xi }_j\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^n{\left(1-p_m\circ {\xi }_j\right)}^{{\theta }_j}}})\hfill \\ \hfill & =({\displaystyle \frac{{(1+(\lambda -1)p_1\circ \xi )}^{\theta }-{(1-p_1\circ \xi )}^{\theta }}{{(1+(\lambda -1)p_1\circ \xi )}^{\theta }+(\lambda -1){(1-p_1\circ \xi )}^{\theta }}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{(1+(\lambda -1)p_m\circ \xi )}^{\theta }-{(1-p_m\circ \xi )}^{\theta }}{{(1+(\lambda -1)p_m\circ \xi )}^{\theta }+(\lambda -1){(1-p_m\circ \xi )}^{\theta }}})\hfill \\ \hfill & =(p_1\circ \xi ,p_2\circ \xi ,\dots ,p_m\circ \xi ),\mathrm{for}\lambda =1\hfill \\ \hfill & =\widehat{\xi }.\hfill \end{array}$$

Hence, $mFHW{A}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\widehat{\xi }$ holds if ${\widehat{\xi }}_j=\widehat{\xi },$$\forall j=1,2,\dots ,n$.  □

The following properties, namely, boundedness and monotonicity, can be easily followed by Definition 5. So, we omit their proofs.

Theorem 4

(Boundedness Property). Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j),$ be a family of ‘n’ mF numbers, ${\widehat{\xi }}^{-}={\bigcap }_{j=1}^n\left({\xi }_j\right)$ and ${\widehat{\xi }}^{+}={\bigcup }_{j=1}^n\left({\xi }_j\right)$, then

$$\begin{array}{c}\hfill {\widehat{\xi }}^{-}\le mFHW{A}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})\le {\widehat{\xi }}^{+}.\end{array}$$

(13)

Theorem 5

(Monotonicity Property). Let ${\widehat{\xi }}_j$ and $\widehat{{\xi }_j^{\prime }}j=1,2,\dots ,n$ be two families of mF numbers. If ${\widehat{\xi }}_j\le \widehat{{\xi }_j^{\prime }}$, then

$$\begin{array}{c}\hfill mFHW{A}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})\le mFHW{A}_{\theta }(\widehat{{\xi }_1^{\prime }},\widehat{{\xi }_2^{\prime }},\dots ,\widehat{{\xi }_n^{\prime }}).\end{array}$$

(14)

We now propose mF Hamacher ordered weighted average operator.

Definition 6.

Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of mF numbers where ‘j’ varies from 1 to n. An mF Hamacher ordered weighted average (mFHOWA) operator is a mapping mFHOWA: ${\widehat{\xi }}^n\to \widehat{\xi }$ with weight vector $w={(w_1,w_2,\dots ,w_n)}^T$ where $w_j\in (0,1]$ and $\sum _{j=1}^n{w}_j=1$. Thus,

$$\begin{array}{c}\hfill mFHOW{A}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨁}}\left(w_j{\widehat{\xi }}_{\sigma \left(j\right)}\right)\end{array}$$

(15)

where $\left(\sigma \right(1),\sigma (2),\dots ,\sigma (n\left)\right)$ is the permutation of the indices $j=1,2,\dots ,n$, for which ${\widehat{\xi }}_{\sigma (j-1)}\ge {\widehat{\xi }}_{\sigma \left(j\right)}$, ∀ $j=1,2,\dots ,n$.

Theorem 6.

Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of ‘n’ mF numbers. The accumulated value of these mF numbers using the mFHOWA operator is also an mF numbers, which is given by

$$\begin{array}{cc}\hfill mFHOW{A}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})& =\underset{j=1}{\overset{n}{⨁}}\left(w_j{\widehat{\xi }}_{\sigma \left(j\right)}\right)\hfill \\ \hfill & =({\displaystyle \frac{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}-{\prod }_{j=1}^n{\left(1-p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}+(\lambda -1){\prod }_{j=1}^n{\left(1-p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}-{\prod }_{j=1}^n{\left(1-p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}+(\lambda -1){\prod }_{j=1}^n{\left(1-p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}}).\hfill \end{array}$$

(16)

Proof. 

Its proof follows directly by similar arguments as used in Theorem 2.  □

Example 2.

Let ${\widehat{\xi }}_1=(0.3,0.6,0.4,0.7),{\widehat{\xi }}_2=(0.2,0.5,0.3,0.6)$, and ${\widehat{\xi }}_3=(0.7,0.6,0.7,0.8)$ be 4F numbers with a weight vector $w={(0.4,0.3,0.3)}^T$ for these 4F numbers. Then, scores and aggregated values of mF numbers for $\lambda =3$ can be computed as below:

$$\begin{array}{cc}\hfill S\left({\widehat{\xi }}_1\right)& ={\displaystyle \frac{0.3+0.6+0.4+0.7}{4}}=0.5,S\left({\widehat{\xi }}_2\right)={\displaystyle \frac{0.2+0.5+0.3+0.6}{4}}=0.4,\hfill \\ \hfill S\left({\widehat{\xi }}_3\right)& ={\displaystyle \frac{0.7+0.6+0.7+0.8}{4}}=0.7.\hfill \end{array}$$

Since, $S\left({\widehat{\xi }}_3\right)>S\left({\widehat{\xi }}_1\right)>S\left({\widehat{\xi }}_2\right)$, thus

$$\begin{array}{cc}\hfill {\widehat{\xi }}_{\sigma \left(1\right)}& ={\widehat{\xi }}_3=(0.7,0.6,0.7,0.8),{\widehat{\xi }}_{\sigma \left(2\right)}={\widehat{\xi }}_1=(0.3,0.6,0.4,0.7),\hfill \\ \hfill {\widehat{\xi }}_{\sigma \left(3\right)}& ={\widehat{\xi }}_2=(0.2,0.5,0.3,0.6).\hfill \end{array}$$

Then, from Theorem 6,

$$\begin{array}{cc}\hfill & mFHOW{A}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\widehat{{\xi }_3})=\underset{j=1}{\overset{3}{⨁}}\left(w_j{\widehat{\xi }}_{\sigma \left(j\right)}\right)\hfill \\ \hfill & =({\displaystyle \frac{{\prod }_{j=1}^3{\left(1+(\lambda -1)p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}-{\prod }_{j=1}^3{\left(1-p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^3{\left(1+(\lambda -1)p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}+(\lambda -1){\prod }_{j=1}^3{\left(1-p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^3{\left(1+(\lambda -1)p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}-{\prod }_{j=1}^3{\left(1-p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^3{\left(1+(\lambda -1)p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}+(\lambda -1){\prod }_{j=1}^3{\left(1-p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}})\hfill \\ \hfill & =({\displaystyle \frac{{\left(1+\left(2\right)0.7\right)}^{0.4}\times {\left(1+\left(2\right)0.3\right)}^{0.3}\times {\left(1+\left(2\right)0.2\right)}^{0.3}-{\left(1-0.7\right)}^{0.4}\times {\left(1-0.3\right)}^{0.3}\times {\left(1-0.2\right)}^{0.3}}{{\left(1+\left(2\right)0.7\right)}^{0.4}\times {\left(1+\left(2\right)0.3\right)}^{0.3}\times {\left(1+\left(2\right)0.2\right)}^{0.3}+\left(2\right)\left({\left(1-0.7\right)}^{0.4}\times {\left(1-0.3\right)}^{0.3}\times {\left(1-0.2\right)}^{0.3}\right)}},\hfill \\ \hfill & {\displaystyle \frac{{\left(1+\left(2\right)0.6\right)}^{0.4}\times {\left(1+\left(2\right)0.6\right)}^{0.3}\times {\left(1+\left(2\right)0.5\right)}^{0.3}-{\left(1-0.6\right)}^{0.4}\times {\left(1-0.6\right)}^{0.3}\times {\left(1-0.5\right)}^{0.3}}{{\left(1+\left(2\right)0.6\right)}^{0.4}\times {\left(1+\left(2\right)0.6\right)}^{0.3}\times {\left(1+\left(2\right)0.5\right)}^{0.3}+\left(2\right)\left({\left(1-0.6\right)}^{0.4}\times {\left(1-0.6\right)}^{0.3}\times {\left(1-0.5\right)}^{0.3}\right)}},\hfill \\ \hfill & {\displaystyle \frac{{\left(1+\left(2\right)0.7\right)}^{0.4}\times {\left(1+\left(2\right)0.4\right)}^{0.3}\times {\left(1+\left(2\right)0.3\right)}^{0.3}-{\left(1-0.7\right)}^{0.4}\times {\left(1-0.4\right)}^{0.3}\times {\left(1-0.3\right)}^{0.3}}{{\left(1+\left(2\right)0.7\right)}^{0.4}\times {\left(1+\left(2\right)0.4\right)}^{0.3}\times {\left(1+\left(2\right)0.3\right)}^{0.3}+\left(2\right)\left({\left(1-0.7\right)}^{0.4}\times {\left(1-0.4\right)}^{0.3}\times {\left(1-0.3\right)}^{0.3}\right)}},\hfill \\ \hfill & {\displaystyle \frac{{\left(1+\left(2\right)0.8\right)}^{0.4}\times {\left(1+\left(2\right)0.7\right)}^{0.3}\times {\left(1+\left(2\right)0.6\right)}^{0.3}-{\left(1-0.8\right)}^{0.4}\times {\left(1-0.7\right)}^{0.3}\times {\left(1-0.6\right)}^{0.3}}{{\left(1+\left(2\right)0.8\right)}^{0.4}\times {\left(1+\left(2\right)0.7\right)}^{0.3}\times {\left(1+\left(2\right)0.6\right)}^{0.3}+\left(2\right)\left({\left(1-0.8\right)}^{0.4}\times {\left(1-0.7\right)}^{0.3}\times {\left(1-0.6\right)}^{0.3}\right)}})\hfill \\ \hfill & =(0.4528,0.5714,0.5077,0.7192).\hfill \end{array}$$

In the following, we give two particular cases of mFHOWA operator.

• When $\lambda =1$, mFHOWA operator converted into mF ordered weighted averaging (mFOWA) operator as below:

  $$\begin{array}{cc}\hfill & mFOW{A}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨁}}\left(w_j{\widehat{\xi }}_{\sigma \left(j\right)}\right)\hfill \\ \hfill & =\left(1-\prod _{j=1}^n{\left(1-p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j},1-\prod _{j=1}^n{\left(1-p_2\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j},\dots ,1-\prod _{j=1}^n{\left(1-p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}\right).\hfill \end{array}$$

  (17)
• When $\lambda =2$, mFHOWA operator reduces into mF Einstein ordered weighted averaging (mFEOWA) operator as below:

  $$\begin{array}{cc}\hfill & mFEOW{A}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨁}}\left(w_j{\widehat{\xi }}_{\sigma \left(j\right)}\right)\hfill \\ \hfill & =({\displaystyle \frac{{\prod }_{j=1}^n{\left(1+p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}-{\prod }_{j=1}^n{\left(1-p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}+{\prod }_{j=1}^n{\left(1-p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^n{\left(1+p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}-{\prod }_{j=1}^n{\left(1-p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}+{\prod }_{j=1}^n{\left(1-p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}}).\hfill \end{array}$$

  (18)

Theorem 7

(Idempotency Property). Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of ‘n’ mF numbers. If all these mF numbers are same, i.e., ${\widehat{\xi }}_j=\widehat{\xi },\forall j=1,2,\dots ,n$, then

$$\begin{array}{c}\hfill mFHOW{A}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\widehat{\xi }.\end{array}$$

(19)

Proof. 

Since ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)=\widehat{\xi },$ where ‘j’ varies from 1 to n. Then, from Equation (16), we obtain

$$\begin{array}{cc}\hfill mFHOW{A}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})& =\underset{j=1}{\overset{n}{⨁}}\left(w_j{\widehat{\xi }}_{\sigma \left(j\right)}\right),\hfill \\ \hfill & =({\displaystyle \frac{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}-{\prod }_{j=1}^n{\left(1-p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}+(\lambda -1){\prod }_{j=1}^n{\left(1-p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}-{\prod }_{j=1}^n{\left(1-p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}+(\lambda -1){\prod }_{j=1}^n{\left(1-p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}})\hfill \\ \hfill & =({\displaystyle \frac{{(1+(\lambda -1)p_1\circ \xi )}^w-{(1-p_1\circ \xi )}^w}{{(1+(\lambda -1)p_1\circ \xi )}^w+(\lambda -1){(1-p_1\circ \xi )}^w}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{(1+(\lambda -1)p_m\circ \xi )}^w-{(1-p_m\circ \xi )}^w}{{(1+(\lambda -1)p_m\circ \xi )}^w+(\lambda -1){(1-p_m\circ \xi )}^w}})\hfill \\ \hfill & =(p_1\circ \xi ,p_2\circ \xi ,\dots ,p_m\circ \xi ),\mathrm{for}\lambda =1\hfill \\ \hfill & =\widehat{\xi }.\hfill \end{array}$$

Hence, $mFHOW{A}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\widehat{\xi }$ holds if ${\widehat{\xi }}_j=\widehat{\xi },$ ∀$j=1,2,\dots ,n$. □

Theorem 8

(Boundedness Property). Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,p_2\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of ‘n’ mF numbers, ${\widehat{\xi }}^{-}={\bigcap }_{j=1}^n\left({\xi }_j\right)$ and ${\widehat{\xi }}^{+}={\bigcup }_{j=1}^n\left({\xi }_j\right)$, then

$$\begin{array}{c}\hfill {\widehat{\xi }}^{-}\le mFHOW{A}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})\le {\widehat{\xi }}^{+}.\end{array}$$

(20)

Theorem 9

(Monotonicity Property). Let ${\widehat{\xi }}_j$ and $\widehat{{\xi }_j^{\prime }}$ be two families of mF numbers where ‘j’ varies from 1 to n. If ${\widehat{\xi }}_j\le \widehat{{\xi }_j^{\prime }}$, then

$$\begin{array}{c}\hfill mFHOW{A}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})\le mFHOW{A}_w(\widehat{{\xi }_1^{\prime }},\widehat{{\xi }_2^{\prime }},\dots ,\widehat{{\xi }_n^{\prime }}).\end{array}$$

(21)

Theorem 10

(Commutativity Property). Let ${\widehat{\xi }}_j$ and $\widehat{{\xi }_j^{\prime }}j=1,2,\dots ,n$ be two families of mF numbers, then

$$\begin{array}{c}\hfill mFHOW{A}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=mFHOW{A}_w(\widehat{{\xi }_1^{\prime }},\widehat{{\xi }_2^{\prime }},\dots ,\widehat{{\xi }_n^{\prime }})\end{array}$$

(22)

where $\widehat{{\xi }_j^{\prime }}$ is an arbitrary permutation of $\widehat{{\xi }_j}$.

In Definitions 5 and 6, we observe that mFHWA operator and mFHOWA operator weight mF numbers and ordered arrangement of mF numbers, respectively. We now propose another operator, namely, mF Hamacher hybrid averaging operator, which combines the qualities of mFHWA operator and mFHOWA operator.

Definition 7.

Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,p_2\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of mF numbers where ‘j’ varies from 1 to n. An mF Hamacher hybrid averaging (mFHHA) operator is given as below:

$$\begin{array}{c}\hfill mFHH{A}_{w,\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨁}}\left(w_j{\tilde{\widehat{\xi }}}_{\sigma \left(j\right)}\right),\end{array}$$

(23)

where $w={(w_1,w_2,\dots ,w_n)}^T$ is the associated-weight vector of the mF numbers $\widehat{{\xi }_j}$, where ‘j’ varies from 1 to n, $w_j\in (0,1],{\displaystyle \sum _{j=1}^n}{w}_j=1$, ${\tilde{\widehat{\xi }}}_{\sigma \left(j\right)}$ is the jth biggest mF numbers, ${\tilde{\widehat{\xi }}}_{\sigma \left(j\right)}=\left(n{\theta }_j\right)\widehat{{\xi }_j},(j=1,2,\dots ,n)$, $\theta =({\theta }_1,{\theta }_2,\dots ,{\theta }_n)$ is the weight vector, with ${\theta }_j\in [0,1],{\displaystyle \sum _{j=1}^n}{\theta }_j=1$ and n serves as the balancing coefficient.

Note that if $w=(\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n})$, then mFHHA operator degenerates into mFHWA operator. When $\theta =(\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n})$, then mFHHA operator degenerates into mFHOWA operator. Therefore, mFHHA operator is an extension of the operators, mFHWA and mFHOWA, which explains the degrees and ordered arrangements of the given mF values.

Theorem 11.

Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,p_2\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of ‘n’ mF numbers. The accumulated value of these mF numbers using the mFHHA operator is also an mF numbers, which is given by

$$\begin{array}{cc}\hfill mFHH{A}_{w,\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})& =\underset{j=1}{\overset{n}{⨁}}\left(w_j{\tilde{\widehat{\xi }}}_{\sigma \left(j\right)}\right)\hfill \\ \hfill & =({\displaystyle \frac{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}-{\prod }_{j=1}^n{\left(1-p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}+(\lambda -1){\prod }_{j=1}^n{\left(1-p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}-{\prod }_{j=1}^n{\left(1-p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}+(\lambda -1){\prod }_{j=1}^n{\left(1-p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}}).\hfill \end{array}$$

(24)

Proof. 

Its proof follows immediately by similar arguments used in Theorem 2. □

We give two particular cases of mFHHA operator as below:

• When $\lambda =1$, mFHHA operator converted into mF hybrid averaging (mFHA) operator as below:

  $$\begin{array}{cc}\hfill & {mFHA}_{w,\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨁}}\left(w_j{\tilde{\widehat{\xi }}}_{\sigma \left(j\right)}\right)\hfill \\ \hfill & =\left(1-\prod _{j=1}^n{\left(p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j},1-\prod _{j=1}^n{\left(p_2\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j},\dots ,1-\prod _{j=1}^n{\left(p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}\right).\hfill \end{array}$$

  (25)
• When $\lambda =2$, mFHHA operator converted into mF Einstein hybrid averaging (mFEHA) operator as below:

  $$\begin{array}{cc}\hfill & mFEH{A}_{w,\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨁}}\left(w_j{\tilde{\widehat{\xi }}}_{\sigma \left(j\right)}\right)\hfill \\ \hfill & =({\displaystyle \frac{{\prod }_{j=1}^n{\left(1+p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}-{\prod }_{j=1}^n{\left(1-p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}+{\prod }_{j=1}^n{\left(1-p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^n{\left(1+p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}-{\prod }_{j=1}^n{\left(1-p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}+{\prod }_{j=1}^n{\left(1-p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}}).\hfill \end{array}$$

  (26)

Example 3.

Let ${\widehat{\xi }}_1=(0.8,0.2,0.6),{\widehat{\xi }}_2=(0.7,0.4,0.6)$ and ${\widehat{\xi }}_3=(0.5,0.6,0.7)$ be 3F numbers with an associated-weight vector $w={(0.4,0.4,0.2)}^T$ for these 3F numbers and a weight vector $\theta ={(0.3,0.2,0.5)}^T$. Then, from Definition 7, for $\lambda =3$

$$\begin{array}{cc}\hfill {\tilde{\widehat{\xi }}}_1& =({\displaystyle \frac{{\left(1+(\lambda -1)p_1\circ {\xi }_1\right)}^{n{w}_1}-{\left(1-p_1\circ {\xi }_1\right)}^{n{w}_1}}{{\left(1+(\lambda -1)p_1\circ {\xi }_1\right)}^{n{w}_1}+(\lambda -1){\left(1-p_1\circ {\xi }_1\right)}^{n{w}_1}}},{\displaystyle \frac{{\left(1+(\lambda -1)p_2\circ {\xi }_1\right)}^{n{w}_1}-{\left(1-p_2\circ {\xi }_1\right)}^{n{w}_1}}{{\left(1+(\lambda -1)p_2\circ {\xi }_1\right)}^{n{w}_1}+(\lambda -1){\left(1-p_2\circ {\xi }_1\right)}^{n{w}_1}}},\hfill \\ \hfill & {\displaystyle \frac{{\left(1+(\lambda -1)p_3\circ {\xi }_1\right)}^{n{w}_1}-{\left(1-p_3\circ {\xi }_1\right)}^{n{w}_1}}{{\left(1+(\lambda -1)p_3\circ {\xi }_1\right)}^{n{w}_1}+(\lambda -1){\left(1-p_3\circ {\xi }_1\right)}^{n{w}_1}}}),\hfill \\ \hfill & =({\displaystyle \frac{{\left(1+2\left(0.8\right)\right)}^{3\left(0.3\right)}-{\left(1-0.8\right)}^{3\left(0.3\right)}}{{\left(1+2\left(0.8\right)\right)}^{3\left(0.3\right)}+2{\left(1-0.8\right)}^{3\left(0.3\right)}}},{\displaystyle \frac{{\left(1+2\left(0.2\right)\right)}^{3\left(0.3\right)}-{\left(1-0.2\right)}^{3\left(0.3\right)}}{{\left(1+2\left(0.2\right)\right)}^{3\left(0.3\right)}+2{\left(1-0.2\right)}^{3\left(0.3\right)}}},\hfill \\ \hfill & {\displaystyle \frac{{\left(1+2\left(0.6\right)\right)}^{3\left(0.3\right)}-{\left(1-0.6\right)}^{3\left(0.3\right)}}{{\left(1+2\left(0.6\right)\right)}^{3\left(0.3\right)}+2{\left(1-0.6\right)}^{3\left(0.5\right)}}}),\hfill \\ \hfill & =(0.7512,0.1792,0.5481).\hfill \end{array}$$

Similarly,

$$\begin{array}{cc}\hfill {\tilde{\widehat{\xi }}}_2& =({\displaystyle \frac{{\left(1+2\left(0.7\right)\right)}^{3\left(0.2\right)}-{\left(1-0.7\right)}^{3\left(0.2\right)}}{{\left(1+2\left(0.7\right)\right)}^{3\left(0.2\right)}+2{\left(1-0.7\right)}^{3\left(0.2\right)}}},{\displaystyle \frac{{\left(1+2\left(0.4\right)\right)}^{3\left(0.2\right)}-{\left(1-0.4\right)}^{3\left(0.2\right)}}{{\left(1+2\left(0.4\right)\right)}^{3\left(0.2\right)}+2{\left(1-0.4\right)}^{3\left(0.2\right)}}},\hfill \\ \hfill & {\displaystyle \frac{{\left(1+2\left(0.6\right)\right)}^{3\left(0.2\right)}-{\left(1-0.6\right)}^{3\left(0.2\right)}}{{\left(1+2\left(0.6\right)\right)}^{3\left(0.2\right)}+2{\left(1-0.6\right)}^{3\left(0.2\right)}}}),\hfill \\ \hfill & =(0.4528,0.2373,0.3725),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\tilde{\widehat{\xi }}}_3& =({\displaystyle \frac{{\left(1+2\left(0.5\right)\right)}^{3\left(0.5\right)}-{\left(1-0.5\right)}^{3\left(0.5\right)}}{{\left(1+2\left(0.5\right)\right)}^{3\left(0.3\right)}+2{\left(1-0.5\right)}^{3\left(0.5\right)}}},{\displaystyle \frac{{\left(1+2\left(0.6\right)\right)}^{3\left(0.5\right)}-{\left(1-0.6\right)}^{3\left(0.5\right)}}{{\left(1+2\left(0.6\right)\right)}^{3\left(0.5\right)}+2{\left(1-0.6\right)}^{3\left(0.5\right)}}},\hfill \\ \hfill & {\displaystyle \frac{{\left(1+2\left(0.7\right)\right)}^{3\left(0.5\right)}-{\left(1-0.7\right)}^{3\left(0.5\right)}}{{\left(1+2\left(0.7\right)\right)}^{3\left(0.5\right)}+2{\left(1-0.7\right)}^{3\left(0.5\right)}}}),\hfill \\ \hfill & =(0.7000,0.7986,0.8782).\hfill \end{array}$$

Then, scores and aggregated values of mF numbers for $\lambda =3$ can be computed as below:

$$\begin{array}{cc}\hfill S\left({\tilde{\widehat{\xi }}}_1\right)& ={\displaystyle \frac{0.7512+0.1792+0.5481}{3}}=0.4928,S\left({\tilde{\widehat{\xi }}}_2\right)={\displaystyle \frac{0.4528+0.2373+0.3725}{3}}=0.3542,\hfill \\ \hfill S\left({\tilde{\widehat{\xi }}}_3\right)& ={\displaystyle \frac{0.7000+0.7986+0.8782}{3}}=0.7923.\hfill \end{array}$$

Since, $S\left({\tilde{\widehat{\xi }}}_3\right)>S\left({\tilde{\widehat{\xi }}}_1\right)>S\left({\tilde{\widehat{\xi }}}_2\right)$, thus

$$\begin{array}{cc}\hfill {\tilde{\widehat{\xi }}}_{\sigma \left(1\right)}& ={\tilde{\widehat{\xi }}}_3=(0.7000,0.7986,0.8782),{\tilde{\widehat{\xi }}}_{\sigma \left(2\right)}={\tilde{\widehat{\xi }}}_1=(0.7512,0.1792,0.5481),\hfill \\ \hfill {\tilde{\widehat{\xi }}}_{\sigma \left(3\right)}& ={\tilde{\widehat{\xi }}}_2=(0.4528,0.2373,0.3725).\hfill \end{array}$$

Then, from Theorem 11,

$$\begin{array}{cc}\hfill & {mFHHA}_{w,\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\widehat{{\xi }_3})=\underset{j=1}{\overset{3}{⨁}}\left(w_j{\widehat{\xi }}_{\sigma \left(j\right)}\right)\hfill \\ \hfill & =({\displaystyle \frac{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}-{\prod }_{j=1}^n{\left(1-p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}+(\lambda -1){\prod }_{j=1}^n{\left(1-p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}-{\prod }_{j=1}^n{\left(1-p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}+(\lambda -1){\prod }_{j=1}^n{\left(1-p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}})\hfill \\ \hfill & =({\displaystyle \frac{{\left(1+\left(2\right)0.7000\right)}^{0.4}\times {\left(1+\left(2\right)0.7512\right)}^{0.4}\times {\left(1+\left(2\right)0.4528\right)}^{0.2}-{\left(1-0.7000\right)}^{0.4}\times {\left(1-0.7512\right)}^{0.4}\times {\left(1-0.4528\right)}^{0.2}}{{\left(1+\left(2\right)0.7000\right)}^{0.4}\times {\left(1+\left(2\right)0.7512\right)}^{0.4}\times {\left(1+\left(2\right)0.4528\right)}^{0.2}+\left(2\right)\left({\left(1-0.7000\right)}^{0.4}\times {\left(1-0.7512\right)}^{0.4}\times {\left(1-0.4528\right)}^{0.2}\right)}},\hfill \\ \hfill & {\displaystyle \frac{{\left(1+\left(2\right)0.7986\right)}^{0.4}\times {\left(1+\left(2\right)0.1792\right)}^{0.4}\times {\left(1+\left(2\right)0.2373\right)}^{0.2}-{\left(1-0.7986\right)}^{0.4}\times {\left(1-0.1792\right)}^{0.4}\times {\left(1-0.2373\right)}^{0.2}}{{\left(1+\left(2\right)0.7986\right)}^{0.4}\times {\left(1+\left(2\right)0.1792\right)}^{0.4}\times {\left(1+\left(2\right)0.2373\right)}^{0.2}+\left(2\right)\left({\left(1-0.7986\right)}^{0.4}\times {\left(1-0.1792\right)}^{0.4}\times {\left(1-0.2373\right)}^{0.2}\right)}},\hfill \\ \hfill & {\displaystyle \frac{{\left(1+\left(2\right)0.8782\right)}^{0.4}\times {\left(1+\left(2\right)0.5481\right)}^{0.4}\times {\left(1+\left(2\right)0.3725\right)}^{0.2}-{\left(1-0.8782\right)}^{0.4}\times {\left(1-0.5481\right)}^{0.4}\times {\left(1-0.3725\right)}^{0.2}}{{\left(1+\left(2\right)0.8782\right)}^{0.4}\times {\left(1+\left(2\right)0.5481\right)}^{0.4}\times {\left(1+\left(2\right)0.3725\right)}^{0.2}+\left(2\right)\left({\left(1-0.8782\right)}^{0.4}\times {\left(1-0.5481\right)}^{0.4}\times {\left(1-0.3725\right)}^{0.2}\right)}})\hfill \\ \hfill & =(0.6817,0.4899,0.6968).\hfill \end{array}$$

2.3. mF Hamacher Geometric Aggregation Operators

We now proposes different types of Hamacher geometric aggregation operators with mF numbers, namely, mFHWG operator, mFHOWG operator, and mFHHG operator.

Definition 8.

Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of mF numbers where ‘j’ varies from 1 to n. An mFHWG operator of is a function mFHWG: ${\widehat{\xi }}^n\to \widehat{\xi }$, which is defined as follows:

$$\begin{array}{c}\hfill mFHW{G}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨂}}{\left({\widehat{\xi }}_j\right)}^{{\theta }_j}\end{array}$$

(27)

where $\theta ={({\theta }_1,{\theta }_2,\dots ,{\theta }_n)}^T$ denotes the weight vector, with ${\theta }_j\in (0,1],{\displaystyle \sum _{j=1}^n}{\theta }_j=1$.

Theorem 12.

Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of ‘n’ mF numbers. The accumulated value of these mF numbers using the mFHWG operator is also an mF numbers, which is given as

$$\begin{array}{cc}\hfill mFHW{G}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})& =\underset{j=1}{\overset{n}{⨂}}{\left({\widehat{\xi }}_j\right)}^{{\theta }_j},\hfill \\ \hfill & =({\displaystyle \frac{\lambda {\prod }_{j=1}^n{\left(p_1\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)(1-p_1\circ {\xi }_j)\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^n{\left(p_1\circ {\xi }_j\right)}^{{\theta }_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{\lambda {\prod }_{j=1}^n{\left(p_m\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)(1-p_m\circ {\xi }_j)\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^n{\left(p_m\circ {\xi }_j\right)}^{{\theta }_j}}}).\hfill \end{array}$$

(28)

Proof. 

It can be easily followed using mathematical induction. □

Example 4.

Let ${\widehat{\xi }}_1=(0.5,0.7,0.4),{\widehat{\xi }}_2=(0.8,0.5,0.4)$ and ${\widehat{\xi }}_3=(0.3,0.4,0.5)$ be 3F numbers with a weight vector $\theta ={(0.3,0.6,0.1)}^T$ for these 3F numbers. Then, for $\lambda =3$,

$$\begin{array}{cc}\hfill & mFHW{G}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\widehat{{\xi }_3})=\underset{j=1}{\overset{3}{⨂}}{\left({\widehat{\xi }}_j\right)}^{{\theta }_j},\hfill \\ \hfill & =({\displaystyle \frac{\lambda {\prod }_{j=1}^3{\left(p_1\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^3{\left(1+(\lambda -1)(1-p_1\circ {\xi }_j)\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^3{\left(p_1\circ {\xi }_j\right)}^{{\theta }_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{\lambda {\prod }_{j=1}^3{\left(p_3\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^3{\left(1+(\lambda -1)(1-p_3\circ {\xi }_j)\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^3{\left(p_3\circ {\xi }_j\right)}^{{\theta }_j}}})\hfill \\ \hfill & =({\displaystyle \frac{\left(3{\left(0.5\right)}^{0.3}{\left(0.8\right)}^{0.6}{\left(0.3\right)}^{0.1}\right)}{{\left(1+2(1-0.5)\right)}^{0.3}\times {\left(1+2(1-0.8)\right)}^{0.6}\times {\left(1+2(1-0.3)\right)}^{0.1}+\left(2\right)\left({\left(0.5\right)}^{0.3}{\left(0.8\right)}^{0.6}{\left(0.3\right)}^{0.1}\right)}},\hfill \\ \hfill & {\displaystyle \frac{\left(3{\left(0.7\right)}^{0.3}{\left(0.5\right)}^{0.6}{\left(0.4\right)}^{0.1}\right)}{{\left(1+2(1-0.7)\right)}^{0.3}\times {\left(1+2(1-0.5)\right)}^{0.6}\times {\left(1+2(1-0.4)\right)}^{0.1}+\left(2\right)\left({\left(0.7\right)}^{0.3}{\left(0.5\right)}^{0.6}{\left(0.4\right)}^{0.1}\right)}},\hfill \\ \hfill & {\displaystyle \frac{\left(3{\left(0.4\right)}^{0.3}{\left(0.4\right)}^{0.6}{\left(0.5\right)}^{0.1}\right)}{{\left(1+2(1-0.4)\right)}^{0.3}\times {\left(1+2(1-0.4)\right)}^{0.6}\times {\left(1+2(1-0.5)\right)}^{0.1}+\left(2\right)\left({\left(0.4\right)}^{0.3}{\left(0.4\right)}^{0.6}{\left(0.5\right)}^{0.1}\right)}})\hfill \\ \hfill & =(0.6507,0.5463,0.4094).\hfill \end{array}$$

Theorem 13

(Idempotency Property). Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of ‘n’ mF numbers. If all these mF numbers are same, i.e., ${\widehat{\xi }}_j=\widehat{\xi },\forall j=1,2,\dots ,n$, then

$$\begin{array}{c}\hfill mFHW{G}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\widehat{\xi }.\end{array}$$

(29)

Theorem 14

(Boundedness Property). Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of ‘n’ mF numbers, ${\widehat{\xi }}^{-}={\bigcap }_{j=1}^n\left({\xi }_j\right)$ and ${\widehat{\xi }}^{+}={\bigcup }_{j=1}^n\left({\xi }_j\right)$, then

$$\begin{array}{c}\hfill {\widehat{\xi }}^{-}\le mFHW{G}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})\le {\widehat{\xi }}^{+}.\end{array}$$

(30)

Theorem 15

(Monotonicity Property). Let ${\widehat{\xi }}_j$ and $\widehat{{\xi }_j^{\prime }},(j=1,2,\dots ,n)$ be two families of mF numbers. If ${\widehat{\xi }}_j\le \widehat{{\xi }_j^{\prime }}$, then

$$\begin{array}{c}\hfill mFHW{G}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})\le mFHW{G}_{\theta }(\widehat{{\xi }_1^{\prime }},\widehat{{\xi }_2^{\prime }},\dots ,\widehat{{\xi }_n^{\prime }}).\end{array}$$

(31)

We give two particular cases of mFHWG operator.

• When $\lambda =1$, mFHWG operator converted into mF weighted geometric (mFWG) operator as below:

  $$\begin{array}{cc}\hfill & mFW{G}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨂}}{\left({\widehat{\xi }}_j\right)}^{{\theta }_j}\hfill \\ \hfill & =\left(\prod _{j=1}^n{\left(p_1\circ {\xi }_j\right)}^{{\theta }_j},\prod _{j=1}^n{\left(p_2\circ {\xi }_j\right)}^{{\theta }_j},\dots ,\prod _{j=1}^n{\left(p_m\circ {\xi }_j\right)}^{{\theta }_j}\right).\hfill \end{array}$$

  (32)
• When $\lambda =2$, mFHWG operator reduces into mF Einstein weighted geometric (mFEWG) operator as below:

  $$\begin{array}{cc}\hfill & mFEW{G}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨂}}{\left({\widehat{\xi }}_j\right)}^{{\theta }_j}\hfill \\ \hfill & =\left({\displaystyle \frac{2{\prod }_{j=1}^n{\left(p_1\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^n{\left(2-p_1\circ {\xi }_j)\right)}^{{\theta }_j}+{\prod }_{j=1}^n{\left(p_1\circ {\xi }_j\right)}^{{\theta }_j}}},\dots ,{\displaystyle \frac{2{\prod }_{j=1}^n{\left(p_m\circ {\xi }_j\right)}^{{\theta }_j}}{{\prod }_{j=1}^n{\left(2-p_m\circ {\xi }_j)\right)}^{{\theta }_j}+{\prod }_{j=1}^n{\left(p_m\circ {\xi }_j\right)}^{{\theta }_j}}}\right).\hfill \end{array}$$

  (33)

We now propose mFHOWG operator.

Definition 9.

Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,p_2\circ {\xi }_j,\dots ,p_m\circ {\xi }_j),j=1,2,\dots ,n$ be a family of mF numbers. An mFHOWG operator is a mapping mFHOWG: ${\widehat{\xi }}^n\to \widehat{\xi }$ with weight vector $w=(w_1,w_2,\dots ,w_n)$, for which $w_j>0$ and ${\displaystyle \sum _{j=1}^n}{w}_j=1$. Thus,

$$\begin{array}{c}\hfill mFHOW{G}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨂}}\left(w_j{\widehat{\xi }}_{\sigma \left(j\right)}\right)\end{array}$$

(34)

where $\left(\sigma \right(1),\sigma (2),\dots ,\sigma (n\left)\right)$ is the permutation of the indices ‘j’ varies from 1 to n, for which ${\widehat{\xi }}_{\sigma (j-1)}\ge {\widehat{\xi }}_{\sigma \left(j\right)}$, ∀$j=1,2,\dots ,n$.

Theorem 16.

Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of ‘n’ mF numbers. The accumulated value of these mF numbers using the mFHOWG operator is also an mF numbers, which is given by

$$\begin{array}{cc}\hfill mFHOW{G}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})& =\underset{j=1}{\overset{n}{⨂}}{\left({\widehat{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}\hfill \\ \hfill & =({\displaystyle \frac{\lambda {\prod }_{j=1}^n{\left(p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)(1-p_1\circ {\xi }_{\sigma \left(j\right)})\right)}^{w_j}+(\lambda -1){\prod }_{j=1}^n{\left(p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{\lambda {\prod }_{j=1}^n{\left(p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)(1-p_m\circ {\xi }_{\sigma \left(j\right)})\right)}^{w_j}+(\lambda -1){\prod }_{j=1}^n{\left(p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}}).\hfill \end{array}$$

(35)

Example 5.

Let ${\widehat{\xi }}_1=(0.5,0.6,0.8),{\widehat{\xi }}_2=(0.3,0.5,0.6)$ and ${\widehat{\xi }}_3=(0.6,0.7,0.8)$ be 3F numbers with a weight vector $w={(0.2,0.5,0.3)}^T$ for these 3F numbers. Then, scores and aggregated values of mF numbers for $\lambda =3$ can be computed as below:

$$\begin{array}{cc}\hfill S\left({\widehat{\xi }}_1\right)& ={\displaystyle \frac{0.5+0.6+0.8}{3}}=0.6333,S\left({\widehat{\xi }}_2\right)={\displaystyle \frac{0.3+0.5+0.6}{3}}=0.4667,\hfill \\ \hfill S\left({\widehat{\xi }}_3\right)& ={\displaystyle \frac{0.6+0.7+0.8}{3}}=0.7.\hfill \end{array}$$

Since, $S\left({\widehat{\xi }}_3\right)>S\left({\widehat{\xi }}_1\right)>S\left({\widehat{\xi }}_2\right)$, thus

$$\begin{array}{cc}\hfill {\widehat{\xi }}_{\sigma \left(1\right)}& ={\widehat{\xi }}_3=(0.6,0.7,0.8),{\widehat{\xi }}_{\sigma \left(2\right)}={\widehat{\xi }}_1=(0.5,0.6,0.8),\hfill \\ \hfill {\widehat{\xi }}_{\sigma \left(3\right)}& ={\widehat{\xi }}_2=(0.3,0.5,0.6).\hfill \end{array}$$

Then, from Theorem 16,

$$\begin{array}{cc}\hfill & mFHOW{G}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\widehat{{\xi }_3})=\underset{j=1}{\overset{3}{⨂}}{\left({\widehat{\xi }}_{\sigma \left(j\right)}\right)}^{{\theta }_j},\hfill \\ \hfill & =({\displaystyle \frac{\lambda {\prod }_{j=1}^3{\left(p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{{\theta }_j}}{{\prod }_{j=1}^3{\left(1+(\lambda -1)(1-p_1\circ {\xi }_{\sigma \left(j\right)})\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^3{\left(p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{{\theta }_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{\lambda {\prod }_{j=1}^3{\left(p_3\circ {\xi }_{\sigma \left(j\right)}\right)}^{{\theta }_j}}{{\prod }_{j=1}^3{\left(1+(\lambda -1)(1-p_3\circ {\xi }_{\sigma \left(j\right)})\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^3{\left(p_3\circ {\xi }_{\sigma \left(j\right)}\right)}^{{\theta }_j}}})\hfill \\ \hfill & =({\displaystyle \frac{3\left({\left(0.6\right)}^{0.2}{\left(0.5\right)}^{0.5}{\left(0.3\right)}^{0.3}\right)}{{\left(1+2(1-0.6)\right)}^{0.2}\times {\left(1+2(1-0.5)\right)}^{0.5}\times {\left(1+2(1-0.3)\right)}^{0.3}+2\left({\left(0.6\right)}^{0.2}{\left(0.5\right)}^{0.5}{\left(0.3\right)}^{0.3}\right)}},\hfill \\ \hfill & {\displaystyle \frac{3\left({\left(0.7\right)}^{0.2}{\left(0.6\right)}^{0.5}{\left(0.5\right)}^{0.3}\right)}{{\left(1+2(1-0.7)\right)}^{0.2}\times {\left(1+2(1-0.6)\right)}^{0.5}\times {\left(1+2(1-0.5)\right)}^{0.3}+2\left({\left(0.7\right)}^{0.2}{\left(0.6\right)}^{0.5}{\left(0.5\right)}^{0.3}\right)}},\hfill \\ \hfill & {\displaystyle \frac{3\left({\left(0.8\right)}^{0.2}{\left(0.8\right)}^{0.5}{\left(0.6\right)}^{0.3}\right)}{{\left(1+2(1-0.8)\right)}^{0.2}\times {\left(1+2(1-0.8)\right)}^{0.5}\times {\left(1+2(1-0.6)\right)}^{0.3}+2\left({\left(0.8\right)}^{0.2}{\left(0.8\right)}^{0.5}{\left(0.6\right)}^{0.3}\right)}})\hfill \\ \hfill & =(0.4512,0.5885,0.7394).\hfill \end{array}$$

We give two particular cases of mFHOWG operator.

• When $\lambda =1$, mFHOWG operator reduces into mF ordered weighted geometric (mFOWG) operator as

  $$\begin{array}{cc}\hfill & mFOW{G}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨂}}{\left({\widehat{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}\hfill \\ \hfill & =\left(\prod _{j=1}^n{\left(p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j},\prod _{j=1}^n{\left(p_2\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j},\dots ,\prod _{j=1}^n{\left(p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}\right).\hfill \end{array}$$

  (36)
• When $\lambda =2$, mFHOWG operator reduces into mF Einstein ordered weighted geometric (mFEOWG) operator as below:

  $$\begin{array}{cc}\hfill mFEOW{G}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})& =\underset{j=1}{\overset{n}{⨂}}{\left({\widehat{\xi }}_j\right)}^{w_j}\hfill \\ \hfill & =({\displaystyle \frac{2{\prod }_{j=1}^n{\left(p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(2-p_1\circ {\xi }_{\sigma \left(j\right)})\right)}^{w_j}+{\prod }_{j=1}^n{\left(p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{2{\prod }_{j=1}^n{\left(p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(2-p_m\circ {\xi }_{\sigma \left(j\right)})\right)}^{w_j}+{\prod }_{j=1}^n{\left(p_m\circ {\xi }_{\sigma \left(j\right)}\right)}^{w_j}}}).\hfill \end{array}$$

  (37)

For the mFHOWG operator, the following properties can be easily shown.

Theorem 17

(Idempotency Property). Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of ‘n’ mF numbers. If all these mF numbers are same, in other words, ${\widehat{\xi }}_j=\widehat{\xi },\forall j=1,2,\dots ,n$, then

$$\begin{array}{c}\hfill mFHOW{G}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\widehat{\xi }.\end{array}$$

(38)

Theorem 18

(Boundedness Property). Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of mF ‘n’ numbers, ${\widehat{\xi }}^{-}={\bigcap }_{j=1}^n({\widehat{\xi }}_1,{\widehat{\xi }}_2,\dots ,{\widehat{\xi }}_n)$ and ${\widehat{\xi }}^{+}={\bigcup }_{j=1}^n({\widehat{\xi }}_1,{\widehat{\xi }}_2,\dots ,{\widehat{\xi }}_n)$, then

$$\begin{array}{c}\hfill {\widehat{\xi }}^{-}\le mFHOW{G}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})\le {\widehat{\xi }}^{+}.\end{array}$$

(39)

Theorem 19

(Monotonicity Property). Let ${\widehat{\xi }}_j$ and $\widehat{{\xi }_j^{\prime }},(j=1,2,\dots ,n)$ be two families of mF numbers. If ${\widehat{\xi }}_j\le \widehat{{\xi }_j^{\prime }}$, then

$$\begin{array}{c}\hfill mFHOW{G}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})\le mFHOW{G}_w(\widehat{{\xi }_1^{\prime }},\widehat{{\xi }_2^{\prime }},\dots ,\widehat{{\xi }_n^{\prime }}).\end{array}$$

(40)

Theorem 20

(Commutativity Property). Let ${\widehat{\xi }}_j$ and $\widehat{{\xi }_j^{\prime }}j=1,2,\dots ,n$ be two families of mF numbers. If ${\widehat{\xi }}_j\le \widehat{{\xi }_j^{\prime }}$, then

$$\begin{array}{c}\hfill mFHOW{G}_w(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=mFHOW{G}_w(\widehat{{\xi }_1^{\prime }},\widehat{{\xi }_2^{\prime }},\dots ,\widehat{{\xi }_n^{\prime }}),\end{array}$$

(41)

where $\widehat{{\xi }_j^{\prime }}$ is any permutation of $\widehat{{\xi }_j},j=1,2,\dots ,n$.

In Definitions 5 and 6, we observe that mFHWG operator and mFHOWG operator weight mF numbers and their ordered arrangement, respectively. We now propose another operator, namely, mF Hamacher hybrid averaging operator, which combine the features of these operators.

Definition 10.

Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,p_2\circ {\xi }_j,\dots ,p_m\circ {\xi }_j)$ be a family of mF numbers where ‘j’ varies from 1 to n. An mF Hamacher hybrid geometric (mFHHG) operator is given as below:

$$\begin{array}{c}\hfill mFHH{G}_{w,\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨂}}{\left({\tilde{\widehat{\xi }}}_{\sigma \left(j\right)}\right)}^{w_j},\end{array}$$

(42)

where $\left(\sigma \right(1),\sigma (2),\dots ,\sigma (n\left)\right)$ is the permutation of $(1,2,\dots ,n)$, for which ${\widehat{\xi }}_{\sigma (j-1)}\ge {\widehat{\xi }}_{\sigma \left(j\right)}$, ∀$j=1,2,\dots ,n$ and $w={(w_1,w_2,\dots ,w_n)}^T$ is the associated-weight vector of the mF numbers $(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})$, $w_j\in (0,1],{\displaystyle \sum _{j=1}^n}{w}_j=1$. ${\tilde{\widehat{\xi }}}_{\sigma \left(j\right)}$ is the jth biggest mF numbers, ${\tilde{\widehat{\xi }}}_{\sigma \left(j\right)}=\left(n{\theta }_j\right)\widehat{{\xi }_j},(j=1,2,\dots ,n)$, $\theta ={({\theta }_1,{\theta }_2,\dots ,{\theta }_n)}^T$ represents the weight vector, with ${\theta }_j>0,{\displaystyle \sum _{j=1}^n}{\theta }_j=1$ and n serves as the balancing coefficient.

Theorem 21.

Let ${\widehat{\xi }}_j=(p_1\circ {\xi }_j,p_2\circ {\xi }_j,\dots ,p_m\circ {\xi }_j),j=1,2,\dots ,n$ be a family of mF numbers. The accumulated value of these mF numbers using the mFHHG operator is also an mF numbers, which is given by

$$\begin{array}{cc}\hfill mFHH{G}_{w,\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})& =\underset{j=1}{\overset{n}{⨂}}{\left({\tilde{\widehat{\xi }}}_{\sigma \left(j\right)}\right)}^{w_j}\hfill \\ \hfill & =({\displaystyle \frac{\lambda {\prod }_{j=1}^n{\left(p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)(1-p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)})\right)}^{w_j}+(\lambda -1){\prod }_{j=1}^n{\left(p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{\lambda {\prod }_{j=1}^n{\left(p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)(1-p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)})\right)}^{w_j}+(\lambda -1){\prod }_{j=1}^n{\left(p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}}).\hfill \end{array}$$

(43)

Proof. 

It can be easily proved by mathematical induction technique. □

Example 6.

Let ${\widehat{\xi }}_1=(0.5,0.4,0.7),{\widehat{\xi }}_2=(0.8,0.5,0.7)$ and ${\widehat{\xi }}_3=(0.7,0.7,0.8)$ be 3F numbers with an associated-weight vector $w={(0.3,0.4,0.3)}^T$ for these 3F numbers and a weight vector $\theta ={(0.3,0.5,0.2)}^T$. Then, from Definition 7, for $\lambda =3$

$$\begin{array}{cc}\hfill {\tilde{\widehat{\xi }}}_1& =({\displaystyle \frac{\lambda {\left(p_1\circ {\xi }_1\right)}^{n{\theta }_1}}{{\left(1+(\lambda -1)(1-p_1\circ {\xi }_1)\right)}^{n{\theta }_1}+(\lambda -1){\left(p_1\circ {\xi }_1\right)}^{n{\theta }_1}}},\hfill \\ & {\displaystyle \frac{\lambda {\left(p_2\circ {\xi }_1\right)}^{n{\theta }_1}}{{\left(1+(\lambda -1)(1-p_2\circ {\xi }_1)\right)}^{n{\theta }_1}+(\lambda -1){\left(p_2\circ {\xi }_1\right)}^{n{\theta }_1}}},\hfill \\ \hfill & {\displaystyle \frac{\lambda {\left(p_3\circ {\xi }_1\right)}^{n{\theta }_1}}{{\left(1+(\lambda -1)(1-p_3\circ {\xi }_1)\right)}^{n{\theta }_1}+(\lambda -1){\left(p_3\circ {\xi }_1\right)}^{n{\theta }_1}}}),\hfill \\ \hfill & =({\displaystyle \frac{3{\left(0.5\right)}^{3\left(0.3\right)}}{{\left(1+2(1-0.5)\right)}^{3\left(0.3\right)}+2{\left(0.5\right)}^{3\left(0.3\right)}}},{\displaystyle \frac{3{\left(0.8\right)}^{3\left(0.3\right)}}{{\left(1+2(1-0.8)\right)}^{3\left(0.3\right)}+2{\left(0.8\right)}^{3\left(0.3\right)}}},\hfill \\ \hfill & {\displaystyle \frac{3{\left(0.6\right)}^{3\left(0.3\right)}}{{\left(1+2(1-0.6)\right)}^{3\left(0.3\right)}+2{\left(0.6\right)}^{3\left(0.3\right)}}}),\hfill \\ \hfill & =(0.5472,0.8208,0.6399).\hfill \end{array}$$

Similarly,

$$\begin{array}{cc}\hfill {\tilde{\widehat{\xi }}}_2& =({\displaystyle \frac{3{\left(0.4\right)}^{3\left(0.5\right)}}{{\left(1+2(1-0.4)\right)}^{3\left(0.5\right)}+2{\left(0.4\right)}^{3\left(0.5\right)}}},{\displaystyle \frac{3{\left(0.5\right)}^{3\left(0.5\right)}}{{\left(1+2(1-0.5)\right)}^{3\left(0.5\right)}+2{\left(0.5\right)}^{3\left(0.5\right)}}},\hfill \\ \hfill & {\displaystyle \frac{3{\left(0.7\right)}^{3\left(0.5\right)}}{{\left(1+2(1-0.7)\right)}^{3\left(0.5\right)}+2{\left(0.7\right)}^{3\left(0.5\right)}}}),\hfill \\ \hfill & =(0.2014,0.3000,0.5499),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\tilde{\widehat{\xi }}}_3& =({\displaystyle \frac{3{\left(0.7\right)}^{3\left(0.2\right)}}{{\left(1+2(1-0.7)\right)}^{3\left(0.2\right)}+2{\left(0.7\right)}^{3\left(0.2\right)}}},{\displaystyle \frac{3{\left(0.7\right)}^{3\left(0.2\right)}}{{\left(1+2(1-0.7)\right)}^{3\left(0.2\right)}+2{\left(0.7\right)}^{3\left(0.2\right)}}},\hfill \\ \hfill & {\displaystyle \frac{3{\left(0.8\right)}^{3\left(0.2\right)}}{{\left(1+2(1-0.8)\right)}^{3\left(0.2\right)}+2{\left(0.8\right)}^{3\left(0.2\right)}}}),\hfill \\ \hfill & =(0.8237,0.8237,0.8826).\hfill \end{array}$$

Then, scores and aggregated values of mF numbers for $\lambda =3$ can be computed as below:

$$\begin{array}{cc}\hfill S\left({\tilde{\widehat{\xi }}}_1\right)& ={\displaystyle \frac{0.5472+0.8208+0.6399}{3}}=0.6692,S\left({\tilde{\widehat{\xi }}}_2\right)={\displaystyle \frac{0.2014+0.3000+0.5499}{3}}=0.3504,\hfill \\ \hfill S\left({\tilde{\widehat{\xi }}}_3\right)& ={\displaystyle \frac{0.8237+0.8237+0.8826}{3}}=0.8433.\hfill \end{array}$$

Since, $S\left({\tilde{\widehat{\xi }}}_3\right)>S\left({\tilde{\widehat{\xi }}}_1\right)>S\left({\tilde{\widehat{\xi }}}_2\right)$, thus

$$\begin{array}{cc}\hfill {\tilde{\widehat{\xi }}}_{\sigma \left(1\right)}& ={\tilde{\widehat{\xi }}}_3=(0.8237,0.8237,0.8826),{\tilde{\widehat{\xi }}}_{\sigma \left(2\right)}={\tilde{\widehat{\xi }}}_1=(0.5472,0.8208,0.6399),\hfill \\ \hfill {\tilde{\widehat{\xi }}}_{\sigma \left(3\right)}& ={\tilde{\widehat{\xi }}}_2=(0.2014,0.3000,0.5499).\hfill \end{array}$$

Then, from Theorem 16,

$$\begin{array}{cc}\hfill & mFHOW{G}_{\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\widehat{{\xi }_3})=\underset{j=1}{\overset{3}{⨂}}{\left({\widehat{\xi }}_{\sigma \left(j\right)}\right)}^{{\theta }_j},\hfill \\ \hfill & =({\displaystyle \frac{\lambda {\prod }_{j=1}^3{\left(p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{{\theta }_j}}{{\prod }_{j=1}^3{\left(1+(\lambda -1)(1-p_1\circ {\xi }_{\sigma \left(j\right)})\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^3{\left(p_1\circ {\xi }_{\sigma \left(j\right)}\right)}^{{\theta }_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{\lambda {\prod }_{j=1}^3{\left(p_3\circ {\xi }_{\sigma \left(j\right)}\right)}^{{\theta }_j}}{{\prod }_{j=1}^3{\left(1+(\lambda -1)(1-p_3\circ {\xi }_{\sigma \left(j\right)})\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^3{\left(p_3\circ {\xi }_{\sigma \left(j\right)}\right)}^{{\theta }_j}}})\hfill \\ \hfill & =({\displaystyle \frac{3\left({\left(0.8237\right)}^{0.3}{\left(0.5472\right)}^{0.4}{\left(0.2014\right)}^{0.3}\right)}{{\left(1+2(1-0.8237)\right)}^{0.3}\times {\left(1+2(1-0.5472)\right)}^{0.4}\times {\left(1+2(1-0.2014)\right)}^{0.3}+2\left({\left(0.8237\right)}^{0.3}{\left(0.5472\right)}^{0.4}{\left(0.2014\right)}^{0.3}\right)}},\hfill \\ \hfill & {\displaystyle \frac{3\left({\left(0.8237\right)}^{0.3}{\left(0.8208\right)}^{0.4}{\left(0.3000\right)}^{0.3}\right)}{{\left(1+2(1-0.8237)\right)}^{0.3}\times {\left(1+2(1-0.8208)\right)}^{0.4}\times {\left(1+2(1-0.3000)\right)}^{0.3}+2\left({\left(0.8237\right)}^{0.3}{\left(0.8208\right)}^{0.4}{\left(0.3000\right)}^{0.3}\right)}},\hfill \\ \hfill & {\displaystyle \frac{3\left({\left(0.8826\right)}^{0.3}{\left(0.6399\right)}^{0.4}{\left(0.5499\right)}^{0.3}\right)}{{\left(1+2(1-0.8826)\right)}^{0.3}\times {\left(1+2(1-0.6399)\right)}^{0.4}\times {\left(1+2(1-0.5499)\right)}^{0.3}+2\left({\left(0.8826\right)}^{0.3}{\left(0.6399\right)}^{0.4}{\left(0.5499\right)}^{0.3}\right)}}),\hfill \\ \hfill & =(0.4905,0.6453,0.6705).\hfill \end{array}$$

We now give two particular cases of mFHHG operator.

• When $\lambda =1$, mFHHG operator converted into mF hybrid geometric (mFHG) operator as below:

  $$\begin{array}{cc}\hfill & {mFHG}_{w,\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨂}}{\left({\tilde{\widehat{\xi }}}_{\sigma \left(j\right)}\right)}^{w_j}\hfill \\ \hfill & =\left(\prod _{j=1}^n{\left(p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j},\prod _{j=1}^n{\left(p_2\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j},\dots ,\prod _{j=1}^n{\left(p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}\right).\hfill \end{array}$$

  (44)
• When $\lambda =2$, mFHHG operator converted into mF Einstein hybrid geometric (mFEHG) operator as below:

  $$\begin{array}{cc}\hfill & mFEH{G}_{w,\theta }(\widehat{{\xi }_1},\widehat{{\xi }_2},\dots ,\widehat{{\xi }_n})=\underset{j=1}{\overset{n}{⨂}}{\left({\tilde{\widehat{\xi }}}_{\sigma \left(j\right)}\right)}^{w_j}\hfill \\ \hfill & =({\displaystyle \frac{2{\prod }_{j=1}^n{\left(p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(2-p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)})\right)}^{w_j}+{\prod }_{j=1}^n{\left(p_1\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{2{\prod }_{j=1}^n{\left(p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}{{\prod }_{j=1}^n{\left(2-p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)})\right)}^{w_j}+{\prod }_{j=1}^n{\left(p_m\circ {\tilde{\xi }}_{\sigma \left(j\right)}\right)}^{w_j}}}).\hfill \end{array}$$

  (45)

3. Mathematical Approach for MADM Using mF Information

We next handle the MADM situations with mF information by applying the mF Hamacher aggregation operators proposed in the preceding sections. The following assumptions or notations are used to represent the MADM problem for the efficient selection of country affected by human decision-making with mF information. Let $A=\{A_1,A_2,\dots ,A_k\}$ be a set of objects (alternatives) and $T=\{T_1,T_2,\dots ,T_n\}$ be the set of attributes. Let $\theta =\{{\theta }_1,{\theta }_2,\dots ,{\theta }_n\}$ be a weight vector for attributes where ${\theta }_j>0,j=1,2,\dots ,n,{\displaystyle \sum _{j=1}^n}{\theta }_j=1.$ Suppose that $\widehat{S}={\left({\widehat{s}}_{ij}\right)}_{k\times n}={\left(p_1\circ {\xi }_{ij},p_2\circ {\xi }_{ij},\dots ,p_m\circ {\xi }_{ij}\right)}_{k\times n}$ is an mF decision matrix, where $p_r\circ A_{ij},r=1,2,\dots ,m$ denote the membership degrees given by the decision-makers that the object $A_i$ satisfies the attribute $t_j$, $p_r\circ A\in [0,1],r=1,2,\dots ,m$.

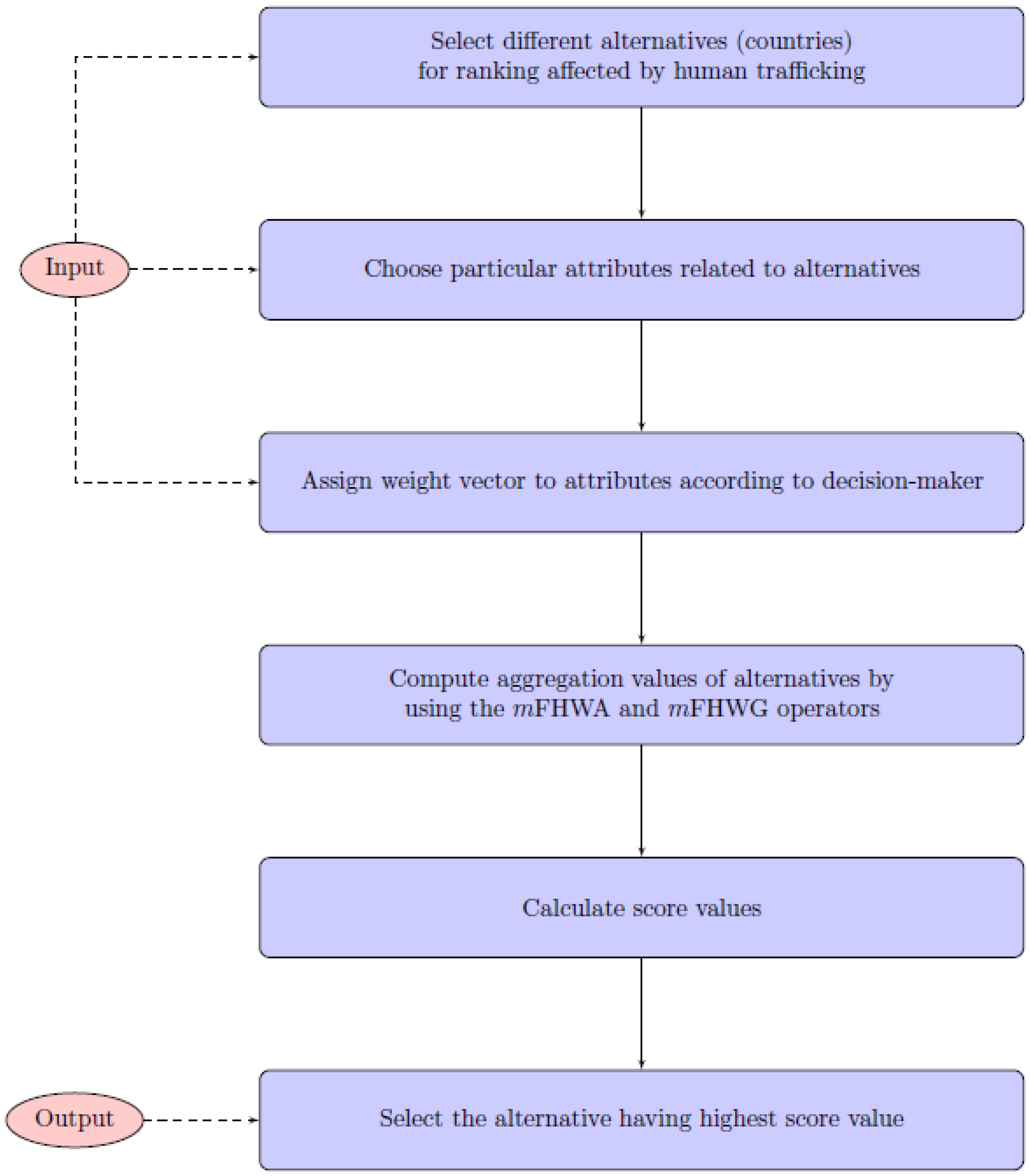
We give the following Algorithm 1 to solve a MADM problem by applying the mFHWA (or mFHWG) operator.

Algorithm 1: Steps to solve MADM problem by applying the mFHWA (or mFHWG) operator

Input: U, the universe with k alternatives. T, the set having n attributes. $\theta =({\theta }_1,{\theta }_2,\dots ,{\theta }_n)$, the weight vector for attributes. Use the mFHWA operator to evaluate the information in mF decision matrix $\widehat{S}$, determine the preference values ${\widehat{s}}_i,i=1,2,\dots ,k$ of the object $A_i$. $$\begin{array}{cc}\hfill & {\widehat{e}}_i=mFHW{A}_{\theta }({\widehat{\xi }}_{i1},{\widehat{\xi }}_{i2},\dots ,{\widehat{\xi }}_{in})=\underset{j=1}{\overset{n}{⨁}}\left({\theta }_j{\widehat{\xi }}_{ij}\right)\hfill \\ \hfill & =({\displaystyle \frac{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_1\circ {\xi }_{ij}\right)}^{{\theta }_j}-{\prod }_{j=1}^n{\left(1-p_1\circ {\xi }_{ij}\right)}^{{\theta }_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_1\circ {\xi }_{ij}\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^n{\left(1-p_1\circ {\xi }_{ij}\right)}^{{\theta }_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_m\circ {\xi }_{ij}\right)}^{{\theta }_j}-{\prod }_{j=1}^n{\left(1-p_m\circ {\xi }_{ij}\right)}^{{\theta }_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)p_m\circ {\xi }_{ij}\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^n{\left(1-p_m\circ {\xi }_{ij}\right)}^{{\theta }_j}}}).\hfill \end{array}$$ Alternatively, if we apply mFHWG operator then $$\begin{array}{cc}\hfill & {\widehat{e}}_i=mFHW{G}_{\theta }({\widehat{\xi }}_{i1},{\widehat{\xi }}_{i2},\dots ,{\widehat{\xi }}_{in})=\underset{j=1}{\overset{n}{⨂}}{\left({\widehat{\xi }}_{ij}\right)}^{{\theta }_j},\hfill \\ \hfill & =({\displaystyle \frac{\lambda {\prod }_{j=1}^n{\left(p_1\circ {\xi }_{ij}\right)}^{{\theta }_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)(1-p_1\circ {\xi }_{ij})\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^n{\left(p_1\circ {\xi }_{ij}\right)}^{{\theta }_j}}},\dots ,\hfill \\ \hfill & {\displaystyle \frac{\lambda {\prod }_{j=1}^n{\left(p_m\circ {\xi }_{ij}\right)}^{{\theta }_j}}{{\prod }_{j=1}^n{\left(1+(\lambda -1)(1-p_m\circ {\xi }_{ij})\right)}^{{\theta }_j}+(\lambda -1){\prod }_{j=1}^n{\left(p_m\circ {\xi }_{ij}\right)}^{{\theta }_j}}}).\hfill \end{array}$$ Compute the scores $S\left({\widehat{e}}_i\right),i=1,2,\dots ,k$. Rank the objects $u_i,i=1,2,\dots ,k$ based on their score values $S\left({\widehat{e}}_i\right),i=1,2,\dots ,k$. If two alternatives have same score, then use the accuracy function to rank the objects. Output: The alternative having the highest score in step 4 will be the decision alternative.

4. Applications

4.1. Assessment of Health Care Waste Treatments Alternatives

A waste management system’s fundamental task is to control, process, store, and dispose waste in accordance with national requirements and international obligations, taking into account the economic and socio-political factors involved. A suitable technology has to be chosen for each step due to the range of procedures, techniques, and equipment available for different steps of a waste management scheme. There is a committee which selects five health care waste treatment alternatives, which are listed as below.

$$\begin{array}{cc}\hfill & A_1:\mathrm{Incineration}\hfill \\ \hfill & A_2:\mathrm{Steam}\mathrm{Sterilization}\hfill \\ \hfill & A_3:\mathrm{Microwaves}\hfill \\ \hfill & A_4:\mathrm{Land}\mathrm{Fill}\mathrm{and}\mathrm{Dumps}\hfill \\ \hfill & A_5:\mathrm{Emulsification}.\hfill \end{array}$$

These waste treatments are assessed on the basis of four factors.

$$\begin{array}{cc}\hfill & T_1:\mathrm{Economic}\mathrm{Factors}\hfill \\ \hfill & T_2:\mathrm{Environmental}\mathrm{Factors}\hfill \\ \hfill & T_3:\mathrm{Technical}\mathrm{Factors}\hfill \\ \hfill & T_4:\mathrm{Social}\mathrm{Factors}.\hfill \end{array}$$

Each factor has been divided into three characteristics to make a 3F number:

• The “Economic Factors” include cost and resources, transport regulations, and physical infrastructure.
• The “Environmental Factors” include geographical conditions, geological conditions, and availability of resources.
• The “Technical Factors” include waste characteristics, complexity and maintainability of facilities, and state of research and development.
• The “Social Factors” include social acceptability, communication, societal responsibilities, and social equity.

1. 

The 3F decision matrix is given in

Table 1. 3F decision matrix.

	${\mathit{T}}_1$	${\mathit{T}}_2$	${\mathit{T}}_3$	${\mathit{T}}_4$
$A_1$	(0.60, 0.40, 0.50)	(0.80, 0.20, 0.60)	(0.20, 0.30, 0.50)	(0.8, 0.7 0.3)
$A_2$	(0.50, 0.70, 0.30)	(0.60, 0.40, 0.60)	(0.40, 0.50, 0.70)	(0.4, 0.6, 0.9)
$A_3$	(0.80, 0.40, 0.60)	(0.40, 0.50, 0.40)	(0.30, 0.60, 0.90)	(0.2, 0.6, 0.7)
$A_4$	(0.50, 0.40, 0.40)	(0.30, 0.50, 0.60)	(0.30, 0.70, 0.40)	(0.7, 0.2, 0.5)
$A_5$	(0.40, 0.60, 0.50)	(0.40, 0.50, 0.50)	(0.50, 0.40, 0.60)	(0.2, 0.5, 0.9)

.

2. 

The weights assigned by the experts are given as

$${\theta }_1=0.40,{\theta }_2=0.20,{\theta }_3=0.30,{\theta }_4=0.10\mathrm{where},\sum _{j=1}^4{\theta }_j=1.$$

We proceed to select the most suitable health care waste treatment alternative by using the mFHWA operator. The steps are as follows:

Step 1 

Assume $\lambda =3$. Use the mFHWA operator to calculate the performance values $e_i$ of the health care waste treatment alternatives.

$$\begin{array}{cc}\hfill & {\widehat{e}}_1=(0.57433,0.36685,0.50257),\hfill \\ \hfill & {\widehat{e}}_2=(0.48273,0.58007,0.57729),\hfill \\ \hfill & {\widehat{e}}_3=(0.5529,0.50409,0.70785),\hfill \\ \hfill & {\widehat{e}}_4=(0.42756,0.50339,0.45310),\hfill \\ \hfill & {\widehat{e}}_5=(0.41163,0.51359,0.59164).\hfill \end{array}$$

Step 2 

Compute the scores $S\left({\widehat{e}}_i\right)$ of all 3F numbers ${\widehat{e}}_i.$

$$\begin{array}{cc}\hfill & S\left({\widehat{e}}_1\right)=0.481284,\hfill \\ \hfill & S\left({\widehat{e}}_2\right)=0.54669,\hfill \\ \hfill & S\left({\widehat{e}}_3\right)=0.58803,\hfill \\ \hfill & S\left({\widehat{e}}_4\right)=0.46135,\hfill \\ \hfill & S\left({\widehat{e}}_5\right)=0.50562.\hfill \end{array}$$

Step 3 

Rank all the health care waste treatment alternatives according to the scores $S\left({\widehat{e}}_i\right),1\le i\le 5$ of all 3F numbers,

$A_3>A_2>A_5>A_1>A_4.$

Step 4 

$A_3$ is the best alternative.

If the mFHWG operator is used for selection, the best alternative can be chosen in a similar manner. Now the steps are as follows:

Step 1 

Suppose $\lambda =3$. Use the mFHWG operator to calculate the performance values ${\widehat{e}}_i$ of the health care waste treatment alternatives.

$$\begin{array}{cc}\hfill & {\widehat{e}}_1=(0.50316,0.34501,0.49608),\hfill \\ \hfill & {\widehat{e}}_2=(0.47699,0.564823,0.51952),\hfill \\ \hfill & {\widehat{e}}_3=(0.45521,0.49591,0.65444),\hfill \\ \hfill & {\widehat{e}}_4=(0.40822,0.47455,0.44650),\hfill \\ \hfill & {\widehat{e}}_5=(0.42129,0.47285,0.56738).\hfill \end{array}$$

Step 2 

Compute the scores $S\left({\widehat{e}}_i\right)$ of all 3F numbers ${\widehat{e}}_i.$

$$\begin{array}{cc}\hfill & S\left({\widehat{e}}_1\right)=0.44808,\hfill \\ \hfill & S\left({\widehat{e}}_2\right)=0.52044,\hfill \\ \hfill & S\left({\widehat{e}}_3\right)=0.535187,\hfill \\ \hfill & S\left({\widehat{e}}_4\right)=0.44309,\hfill \\ \hfill & S\left({\widehat{e}}_5\right)=0.487175.\hfill \end{array}$$

Step 3 

Rank all the health care waste treatment alternatives,

$A_3>A_2>A_5>A_1>A_4.$

Step 4 

$A_3$ is the best alternative.

We apply the mF-ELECTRE-I approach to the same problem.

1. 

Table 2. 3F weighted decision matrix.

	${\mathit{T}}_1$	${\mathit{T}}_2$	${\mathit{T}}_3$	${\mathit{T}}_4$
$C_1$	(0.24, 0.16, 0.20)	(0.16, 0.04, 0.12)	(0.06, 0.09, 0.15)	(0.08, 0.07, 0.03)
$C_2$	(0.20, 0.28, 0.12)	(0.12, 0.08, 0.12)	(0.12, 0.15, 0.21)	(0.04, 0.06, 0.09)
$C_3$	(0.32, 0.16, 0.24)	(0.08, 0.10, 0.08)	(0.09, 0.18, 0.27)	(0.02, 0.06, 0.07)
$C_4$	(0.20, 0.16, 0.16)	(0.06, 0.10, 0.12)	(0.09, 0.21, 0.12)	(0.07, 0.02, 0.05)
$C_5$	(0.16, 0.24, 0.20)	(0.08, 0.10, 0.10)	(0.15, 0.12, 0.18)	(0.02, 0.05, 0.09)

represents the 3F decision matrix.

2. 

Table 3. 3F concordance set.

j	1	2	3	4	5
$F_{1j}$	-	{1, 2}	{2, 4}	{1, 2, 4}	{1, 2, 4}
$F_{2j}$	{1, 2, 3, 4}	-	{2, 4}	{1, 2, 3, 4}	{1, 2, 3, 4}
$F_{3j}$	{1, 3}	{1, 3}	-	{1, 3, 4}	{1, 3}
$F_{4j}$	{3}	{}	{2}	-	{2}
$F_{5j}$	{1, 3}	{1}	{2, 4}	{1, 2, 3, 4}	-

and

Table 4. 3F discordance set.

j	1	2	3	4	5
$G_{1j}$	-	{1, 2, 3, 4}	{1, 3}	{3}	{1, 3}
$G_{2j}$	{1, 2}	-	{1, 3}	{}	{1, 3}
$G_{3j}$	{2, 4}	{2, 4}	-	{2}	{2, 4}
$G_{4j}$	{1, 2, 4}	{1, 2, 3, 4}	{1, 3, 4}	-	{1, 2, 3, 4}
$G_{5j}$	{1, 2, 4}	{1, 2, 3, 4}	{1, 3}	{2}	-

represent the 3F concordance and 3F discordance sets, respectively.

3. 

The 3F concordance matrix is constructed as:

$$F=\left(\begin{array}{ccccc}-& 0.6& 0.3& 0.7& 0.7\\ 1& -& 0.3& 1& 1\\ 0.7& 0.7& -& 0.8& 0.7\\ 0.3& 0& 0.2& -& 0.2\\ 0.7& 0.4& 0.3& 1& -\end{array}\right).$$

4. 

The 3F concordance level $\overline{f}=0.7805.$

5. 

The 3F discordance matrix is constructed as:

$$G=\left(\begin{array}{ccccc}-& 1& 1& 1& 1\\ 1& -& 1& 0& 1\\ 0.7041& 0.28867& -& 0.29233& 0.18077\\ 0.91630& 1& 1& -& 1\\ 1& 1& 1& 0.22867& -\end{array}\right).$$

6. 

The 3F discordance level $\overline{g}=0.58.$

7. 

The 3F concordance dominance and 3F discordance dominance matrix are constructed as:

$$H=\left(\begin{array}{ccccc}-& 1& 0& 1& 1\\ 1& -& 0& 1& 1\\ 1& 1& -& 1& 1\\ 0& 0& 0& -& 0\\ 1& 0& 0& 1& -\end{array}\right),$$

$$L=\left(\begin{array}{ccccc}-& 0& 0& 0& 0\\ 0& -& 0& 1& 0\\ 1& 1& -& 1& 1\\ 0& 0& 0& -& 0\\ 0& 0& 0& 1& -\end{array}\right)$$

.

8. 

The 3F aggregate dominance matrix is constructed as:

$$M=\left(\begin{array}{ccccc}-& 0& 0& 0& 0\\ 0& -& 0& 1& 0\\ 1& 1& -& 1& 1\\ 0& 0& 0& -& 0\\ 0& 0& 0& 1& -\end{array}\right).$$

9. 

The following graph shows the preference relation of the health care treatments (see Figure 1).

Therefore, $A_3$ is the best choice.

4.2. Selection of the Best Company for Investment

Each investment and investment decision entails certain degree of risk. The most obvious factor to consider is the financial performance of the company. The acronym “ESG” collectively refers to economic, social, and governance factors. ESG integration is the method of consideration of economic, social, and governance factors in the investment cycle. Company information is another important factor in assessing a potential business investment. Suppose that an investor wants to invest in a company. Let $\{{\mathcal{C}}_1,{\mathcal{C}}_2,{\mathcal{C}}_3,{\mathcal{C}}_4,{\mathcal{C}}_5\}$ be the set of five companies. The investor chooses three characteristics to assess companies which are given as:

$$\begin{array}{cc}\hfill & T_1:\mathrm{Financial}\mathrm{Performance}\hfill \\ \hfill & T_2:\mathrm{Company}\mathrm{Information}\hfill \\ \hfill & T_3:\mathrm{ESG}\mathrm{Integration}.\hfill \end{array}$$

Each attribute has been divided into four characteristics to make a 4F number.

• The attribute “Financial Performance” includes tax returns, balance sheets, cash flow projections, and current accounts receivables.
• The attribute “Company Information” includes company’s history, accomplishments, product or service offerings, and business plans.
• The attribute “ESG Integration” includes pollution prevention, energy efficiency, regulatory standards, and adherence to environmental safety.

1. 

The 4F decision matrix is given in

Table 5. 4F decision matrix.

	${\mathit{T}}_1$	${\mathit{T}}_2$	${\mathit{T}}_3$
${\mathcal{C}}_1$	(0.36, 0.45, 0.50, 0.41)	(0.25, 0.40, 0.61, 0.50)	(0.50, 0.42, 0.53, 0.63)
${\mathcal{C}}_2$	(0.52, 0.70, 0.46, 0.56)	(0.36, 0.57, 0.48, 0.73)	(0.64, 0.54, 0.72, 0.60)
${\mathcal{C}}_3$	(0.25, 0.35, 0.40, 0.35)	(0.24, 0.37, 0.56, 0.50)	(0.49, 0.38, 0.42, 0.57)
${\mathcal{C}}_4$	(0.73, 0.81, 0.72, 0.69)	(0.65, 0.73, 0.66, 0.82)	(0.75, 0.81, 0.80, 0.72)
${\mathcal{C}}_5$	(0.64, 0.71, 0.60, 0.50)	(0.50, 0.60, 0.50, 0.70)	(0.70, 0.70, 0.60, 0.50)

.

2. 

Weights assigned by the investor are given as,

$${\theta }_1=0.45,{\theta }_2=0.25,{\theta }_3=0.30\mathrm{where},\sum _{j=1}^3{\theta }_j=1.$$

We select the best company for investment by using the mFHWA operator.

Step 1 

Assume $\lambda =3$. Use the mFHWA operator to calculate the performance values ${\widehat{e}}_i$ of the companies.

$$\begin{array}{cc}\hfill & {\widehat{e}}_1=(0.3766,0.42864,0.5378,0.5034),\hfill \\ \hfill & {\widehat{e}}_2=(0.5217,0.6244,0.5536,0.61924),\hfill \\ \hfill & {\widehat{e}}_3=(0.3219,0.3539,0.4479,0.4573),\hfill \\ \hfill & {\widehat{e}}_4=(0.7179,0.7921,0.7332,0.7363),\hfill \\ \hfill & {\widehat{e}}_5=(0.6275,0.6817,0.5762,0.5560).\hfill \end{array}$$

Step 2 

Compute the scores $S\left({\widehat{e}}_i\right)$ of all 4F numbers ${\widehat{e}}_i.$

$$\begin{array}{cc}\hfill & S\left({\widehat{e}}_1\right)=0.46161,\hfill \\ \hfill & S\left({\widehat{e}}_2\right)=0.57974,\hfill \\ \hfill & S\left({\widehat{e}}_3\right)=0.39525,\hfill \\ \hfill & S\left({\widehat{e}}_4\right)=0.74486,\hfill \\ \hfill & S\left({\widehat{e}}_5\right)=0.61035.\hfill \end{array}$$

Step 3 

Rank all alternatives for investment according to the scores $S\left({\widehat{e}}_i\right),1\le i\le 5$ of all 4F numbers,

${\mathcal{C}}_4>{\mathcal{C}}_5>{\mathcal{C}}_2>{\mathcal{C}}_1>{\mathcal{C}}_3.$

Step 4 

Therefore, $C_4$ is the most suitable company for investment.

If the mFHWG operator is used for selection, the best alternative can be chosen in a similar manner.

Step 1 

Assume $\lambda =3$. Use the mFHWG operator to calculate the performance values ${\widehat{e}}_i$ of the alternatives.

$$\begin{array}{cc}\hfill & {\widehat{e}}_1=(0.36652,0.42819,0.53575,0.49436),\hfill \\ \hfill & {\widehat{e}}_2=(0.51044,0.61822,0.53856,0.61352),\hfill \\ \hfill & {\widehat{e}}_3=(0.3074,0.36384,0.4435,0.4474),\hfill \\ \hfill & {\widehat{e}}_4=(0.7159,0.7901,0.7289,0.7315),\hfill \\ \hfill & {\widehat{e}}_5=(0.62142,0.6792,0.5743,0.5477).\hfill \end{array}$$

Step 2 

Compute the scores $S\left({\widehat{e}}_i\right)$ of all 4F numbers ${\widehat{e}}_i.$

$$\begin{array}{cc}\hfill & S\left({\widehat{e}}_1\right)=0.456205,\hfill \\ \hfill & S\left({\widehat{e}}_2\right)=0.570185,\hfill \\ \hfill & S\left({\widehat{e}}_3\right)=0.390535,\hfill \\ \hfill & S\left({\widehat{e}}_4\right)=0.7416,\hfill \\ \hfill & S\left({\widehat{e}}_5\right)=0.60566.\hfill \end{array}$$

Step 3 

Rank all companies for investment based on the scores $S\left({\widehat{e}}_i\right),1\le i\le 5$ of all 4F numbers,

$${\mathcal{C}}_4>{\mathcal{C}}_5>{\mathcal{C}}_2>{\mathcal{C}}_1>{\mathcal{C}}_3.$$

Step 4 

Therefore, $C_4$ is the best alternative.

We apply the mF-ELECTRE-I method to the same problem.

3. 

Table 6. 4F weighted decision matrix.

	${\mathit{T}}_1$	${\mathit{T}}_2$	${\mathit{T}}_3$
${\mathcal{C}}_1$	(0.162, 0.2025, 0.225, 0.1845)	(0.0625, 0.18, 0.2745, 0.125)	(0.15, 0.126, 0.159, 0.189)
${\mathcal{C}}_2$	(0.234, 0.315, 0.207, 0.252)	(0.09, 0.1425, 0.12, 0.1825)	(0.192, 0.162, 0.216, 0.18)
${\mathcal{C}}_3$	(0.1125, 0.1575, 0.18, 0.1575)	(0.06, 0.0925, 0.14, 0.125)	(0.147, 0.114, 0.126, 0.171)
${\mathcal{C}}_4$	(0.3285, 0.3645, 0.324, 0.3105)	(0.1625, 0.1825, 0.165, 0.205)	(0.225, 0.243, 0.24, 0.216)
${\mathcal{C}}_5$	(0.288, 0.3195, 0.27, 0.225)	(0.125, 0.15, 0.125, 0.175)	(0.21, 0.21, 0.18, 0.15)

represents the 4F weighted decision matrix.

4. 

Table 7. 4F concordance set.

j	1	2	3	4	5
$F_{1j}$	-	{2}	{1, 2, 3}	{}	{2}
$F_{2j}$	{1, 3}	-	{1, 2, 3}	{}	{3}
$F_{3j}$	{}	{}	-	{}	{}
$F_{4j}$	{1, 2, 3}	{1, 2, 3}	{1, 2, 3}	-	{1, 2, 3}
$F_{5j}$	{1, 3}	{1, 2, 3}	{1, 2, 3}	{}	-

and

Table 8. 4F discordance set.

j	1	2	3	4	5
$G_{1j}$	-	{1, 3}	{}	{1, 2, 3}	{1, 3}
$G_{2j}$	{2}	-	{}	{1, 2, 3}	{1, 2, 3}
$G_{3j}$	{1, 2, 3}	{1, 2, 3}	-	{1, 2, 3}	{1, 2, 3}
$G_{4j}$	{}	{}	{}	-	{}
$G_{5j}$	{2}	{3}	{}	{1, 2, 3}	-

represent the 4F concordance and 4F discordance sets, respectively.

5. 

The 4F concordance matrix is constructed as:

$$F=\left(\begin{array}{ccccc}-& 0.25& 1& 0& 0.25\\ 0.75& -& 1& 0& 0.3\\ 0& 0& -& 0& 0\\ 1& 1& 1& -& 1\\ 0.75& 1& 1& 0& -\end{array}\right).$$

6. 

The 4F concordance level $\overline{f}=0.515.$

7. 

The 4F discordance matrix is constructed as:

$$G=\left(\begin{array}{ccccc}-& 0.8800& 0& 1& 1\\ 1& -& 0& 1& 1\\ 1& 1& -& 1& 1\\ 0& 0& 0& -& 0\\ 0.9445& 0.7953& 0& 1& -\end{array}\right).$$

8. 

The 4F discordance level $\overline{g}=0.6309.$

9. 

The 4F concordance dominance and 4F discordance dominance matrix are constructed as:

$$H=\left(\begin{array}{ccccc}-& 0& 1& 0& 0\\ 1& -& 1& 0& 0\\ 0& 0& -& 0& 0\\ 1& 1& 1& -& 1\\ 1& 1& 1& 0& -\end{array}\right),$$

$$L=\left(\begin{array}{ccccc}-& 0& 1& 0& 0\\ 0& -& 1& 0& 0\\ 0& 0& -& 0& 0\\ 1& 1& 1& -& 1\\ 0& 0& 1& 0& -\end{array}\right)$$

.

10. 

The 4F aggregate dominance matrix is evaluated as:

$$M=\left(\begin{array}{ccccc}-& 0& 1& 0& 0\\ 0& -& 1& 0& 0\\ 0& 0& -& 0& 0\\ 1& 1& 1& -& 1\\ 0& 0& 1& 0& -\end{array}\right).$$

11. 

The following graph shows the preference relation of the companies (see Figure 2).

Therefore, ${\mathcal{C}}_4$ is the best company for investment.

4.3. Selection of Most Affected Country by Human Trafficking

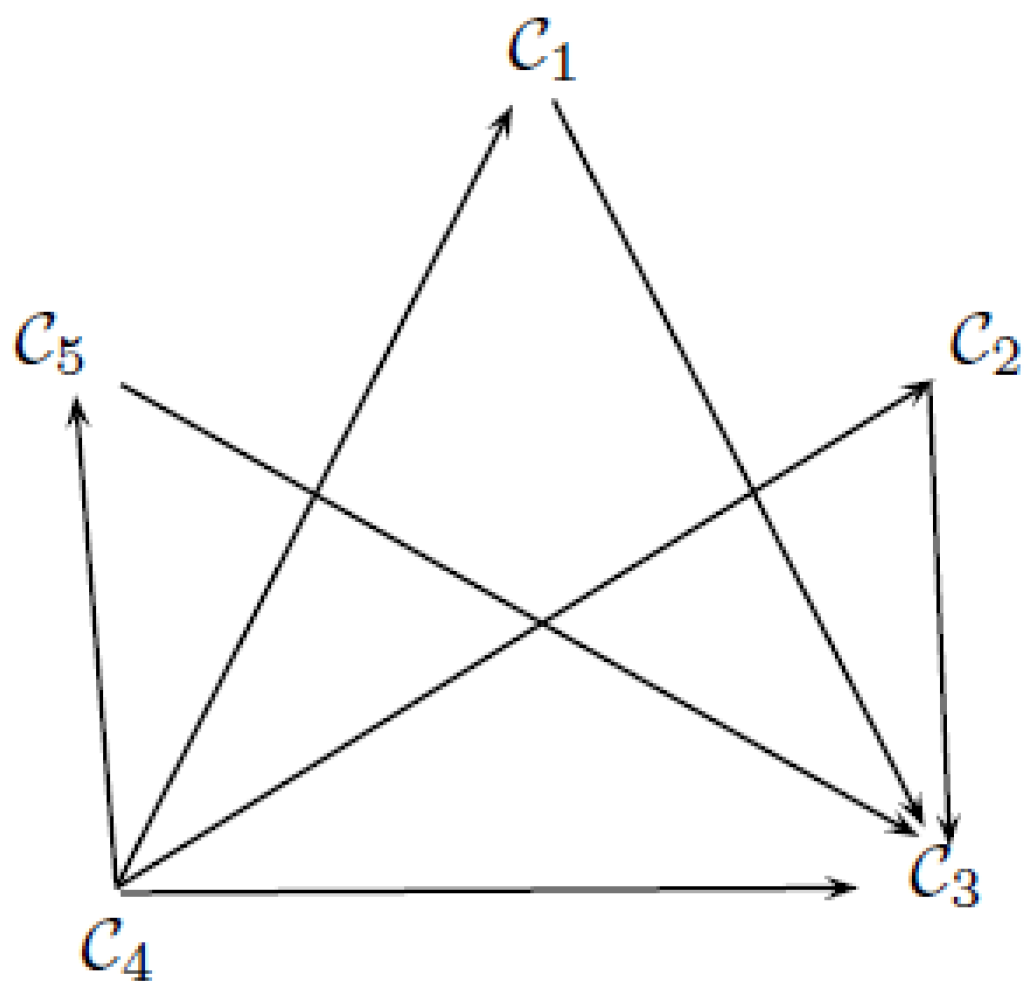
In human trafficking, traffickers use force, coercion, or fraud to lure their victims into commercial sexual exploitation or labor. These people are vulnerable due to different reasons like emotional or psychological susceptibleness, lack of a social welfare system, economic hardships, political instability, or natural disaster. Based on the latest surveys, it can be easily observed that millions of children, women, and men become part of human trafficking all over the world, including Saudi Arabia, China, Russia, Kuwait, and Iran. It is also observed that victims of traffickers can be of any gender, age, or nationality. Traffickers use manipulation, or fake promises of high-paying jobs or romantic connection to attract victims into trafficking. The trauma triggered by the traffickers can be so extreme that people may not even recognize themselves as victims. The main attributes or causes of human trafficking are political instability, poverty, debt, natural disasters, demand, and addiction.

Let $C=\{C_1=\mathrm{Saudi}\mathrm{Arabia},C_2=\mathrm{China},C_3=\mathrm{Russsia},C_4=\mathrm{Kuwait},C_5=\mathrm{Iran}\}$ be a set of five countries and let $T=\{T_1,T_2,T_3,T_4\}$ be the set of four attributes, where

$T_1$ denotes “Poverty”,

$T_2$ denotes “Debt”,

$T_3$ denotes “Demand”,

$T_4$ denotes “Natural Disaster”.

Further characterizations of above attributes are force, fraud, or lure. The purpose of this application is to evaluate the above countries $C_i$’s, $i=1,2,\dots ,5$ concerning the worst in human trafficking with the help of 3F numbers given by the decision-makers under the attributes $T_j$’s, $j=1,2,3,4$. Let $\theta =(0.4,0.3,0.3)$ be the weight vector for the preceding characteristics. The 3F decision matrix is given as below(See

Table 9. 3F decision matrix.

	${\mathit{T}}_1$	${\mathit{T}}_2$	${\mathit{T}}_3$	${\mathit{T}}_4$
$C_1$	(0.3,0.6,0.2)	(0.2,0.5,0.6)	(0.7,0.6,0.1)	(0.5,0.8,0.3)
$C_2$	(0.6,0.9,0.3)	(0.4,0.8,0.1)	(0.5,0.2,0.5)	(0.7,0.4,0.2)
$C_3$	(0.7,0.7,0.6)	(0.4,0.3,0.4)	(0.1,0.3,0.4)	(0.4,0.2,0.5)
$C_4$	(0.5,0.7,0.3)	(0.7,0.8,0.1)	(0.4,0.5,0.6)	(0.7,0.8,0.2)
$C_5$	(0.8,0.6,0.4)	(0.1,0.2,0.5)	(0.3,0.7,0.4)	(0.2,0.8,0.3)

):

For illustration, the 3F number $(0.3,0.6,0.2)$ in the top left entry of the 3F decision matrix means that in the country Saudi Arabia $C_1$ with respect to people in poverty who become a part of human trafficking are sub-classified as follows: 30% due to force, 60% due to fraud, 20% due to lure.

To compute the worst country regarding human trafficking, we apply the two operators, namely, mFHWA and mFHWG, to construct methods to MADM problems with mF information, which are given as follows:

• Take $\lambda =3$. We apply the mFHWA operator to find the preference values ${\widehat{e}}_i$ of the countries $C_i$ regarding human trafficking.

  $$\begin{array}{cc}\hfill {\widehat{e}}_1& =(0.3582,0.6220,0.3382),{\widehat{e}}_2=(0.5580,0.7653,0.2404),\hfill \\ \hfill {\widehat{e}}_3& =(0.5078,0.4620,0.5041),{\widehat{e}}_4=(0.5998,0.7395,0.2523),\hfill \\ \hfill {\widehat{e}}_5& =(0.4732,0.5595,0.4115).\hfill \end{array}$$
• Determine the scores $S\left({\widehat{e}}_i\right)$ of overall 3F numbers ${\widehat{e}}_i$ of the countries $C_i$ involved in human trafficking:

  $$S\left({\widehat{e}}_1\right)=0.4395,S\left({\widehat{e}}_2\right)=0.5212,S\left({\widehat{e}}_3\right)=0.4913,S\left({\widehat{e}}_4\right)=0.5305,S\left({\widehat{e}}_5\right)=0.4814.$$
• Now rank all the countries based on score values $S\left({\widehat{e}}_i\right),(i=1,2,\dots ,5)$ based on overall 3F numbers: $C_4>C_2>C_3>C_5>C_1$.
• $C_4$ has high rate human trafficking.

Similarly, we use the mFHWG operator to select the affected country.

• Take $\lambda =3$. Use the mFHWG operator to find the preference values ${\widehat{e}}_i$ of the countries $C_i$ regarding human trafficking.

  $$\begin{array}{cc}\hfill {\widehat{e}}_1& =(0.3295,0.6078,0.2940),{\widehat{e}}_2=(0.5447,0.6800,0.2146),\hfill \\ \hfill {\widehat{e}}_3& =(0.4577,0.4087,0.4959),{\widehat{e}}_4=(0.5858,0.7290,0.2200),\hfill \\ \hfill {\widehat{e}}_5& =(0.3337,0.4943,0.4061).\hfill \end{array}$$
• Determine the scores $S\left({\widehat{e}}_i\right)$ of overall 3F numbers ${\widehat{e}}_i,(i=1,2,\dots ,5)$ of the countries $C_i$ involved in human trafficking:

  $$S\left({\widehat{e}}_1\right)=0.4104,S\left({\widehat{e}}_2\right)=0.4798,S\left({\widehat{e}}_3\right)=0.4541,S\left({\widehat{e}}_4\right)=0.5116,S\left({\widehat{e}}_5\right)=0.4114.$$
• Now rank all the countries based on score values $S\left(e_i\right),(i=1,2,\dots ,5)$ based on overall 3F numbers: $C_4>C_2>C_3>C_5>C_1$.
• $C_4$ has a high rate of human trafficking.

The method used in the application to select the worst country affected by human trafficking is explained in Figure 3.

5. Comparison Analysis and Discussion

In this section, a comparative study is conducted with the mF-ELECTRE-I method to validate the practicality of the proposed approach based on Hamacher aggregation operators.

• It can be seen from the results of the second application that if the operators mFHWA or mFHWG are used, respectively, then the final ranking is $C_4>C_5>C_2>C_1>C_3.$ However, the final scores are slightly different. From these results, it is clear that $C_4$ is the best choice for investment and $C_3$ is the worst choice for investment. If the mF-ELECTRE-I approach is used, then the optimal alternative is $C_4.$ The final results are the same when using both approaches.
• The mF-ELECTRE-I approach is known as a flexible approach relative to other ELECTRE-I extensions. This approach does not result in a single alternative, but rather in a small subset of favorable alternatives. It is very difficult for the decision-makers to rank all alternatives.
• If more mF numbers are involved using mFHWA (or mFHWG) operators, the number of operations and calculations will increase exponentially. However, the proposed method can more flexibly explain the assessment details and maintain the integrity of original decision-making data, which makes the final results more closely match realistic decision-making issues. The proposed method ranks all the alternatives as compared to the mF-ELECTRE-I method.

6. Conclusions

Most problems in real life have a structure that fits into the framework of multi-polar data that coexist with multiple attributes. As theoretical models develop in order to encompass wider settings, the MADM techniques with better performance need to be adapted to tackle more complex decision-making issues.

In this article we have contributed to the development of MADM with the analysis of problems in an m-polar fuzzy environment. As a preparation to their utilization in decision-making, the theoretical basis of aggregation operators need to be carefully considered. The shortcomings of existing methods plus the beneficial characteristics of Hamacher aggregation operators led us to consider their ability to produce suitable combinations of mF numbers.

Consequently we have introduced arithmetic and geometric operations to construct m-polar fuzzy aggregation operators that closely follow the motivation of Hamacher operations. They include the mF Hamacher weighted average operator (mFHWA), mF Hamacher ordered weighted average operator (mFHOWA), mF Hamacher hybrid weighted average operator (mFHHWA), mF Hamacher weighted geometric operator (mFHWG), mF Hamacher ordered weighted geometric operator (mFHOWG), and mF Hamacher hybrid weighted geometric operator (mFHHWG). The fundamental characteristics of these operators are discussed so that the practitioners can select the version that better fits their needs.

We have utilized these operators to expand a number of strategies to address MADM problems. A comparative analysis of our proposed procedure with the mF-ELECTRE-I approach is performed. Finally, practical examples for the selection of health care waste treatment methods, selection of best company for investment, and the selection of most affected country by human trafficking are given. Altogether they build up a procedure and make a case for the pertinence and adequacy of the proposed approach.

In a nutshell, the main contribution of this article is that it consolidates both the role of Hamacher aggregation operators and the advantageous features of m-polar fuzzy numbers. Once again this model of uncertain knowledge proves its versatility for portraying inexact, imprecise data in complex conditions. The operators also demonstrate that they are highly adaptable, hence becoming a powerful tool that might be applied for further uses. In future research, we will extend the driving ideas of our models to an m-polar fuzzy soft set environment. Their study will prepare us to consider intertemporal settings like in Alcantud et al. [45].