1. Introduction
Multi-attribute decision-making (MADM) plays an efficient role in different domains, ranging from engineering to social sciences. MADM approaches identify how attribute information is to be processed to compute a suitable alternative or to rank the alternatives for supporting decision-making. It has been broadly applied in different domains, including engineering technology [
1], operation research [
2], and management science [
3]. To solve decision-making problems having uncertainty, Atanassov [
4] introduced the idea of intuitionistic fuzzy sets (IFSs) which involve both membership and non-membership functions, an efficient generalization of fuzzy sets [
5] which characterize only membership function.
Aggregation operators (AOs) play a key role in combining information into a single datum and solving MADM issues. For instance, Yager [
6] proposed weighted AOs. Xu [
7] introduced some novel AOs based on intuitionistic fuzzy sets. Xu and Yager [
8] gave some novel geometric AOs with some practical applications in MADM. From the information analysis of an alternative, it is easy to see that there is another property that is its counterpart for each property of the alternative. With this viewpoint, Zhang [
9,
10] initiated the concept of bipolar fuzzy (BF) sets. The membership degree of BF sets enlarged from
to
. In a BF set, there are two membership parts, positive and negative memberships which belong to the intervals
and
, respectively. BF sets have a wide range of applications in many research domains, including medicine science [
11] and decision analysis [
12]. Wei et al. [
13] presented some hesitant BF weighted arithmetic and geometric AOs. Xu and Wei [
14] developed dual hesitant BF arithmetic and geometric AOs. Garg [
15] utilized linguistic prioritized AOs to develop a MADM method under a single-valued neutrosophic environment. Beg and Rashi [
16] proposed a intuitionistic hesitant fuzzy set model for group decision-making. Grzegorzewski [
17] discussed the separability of fuzzy relations. Alcantud et al. [
18] take advantage of the theoretical foundations of aggregation operators to produce the first procedure for the aggregation of infinitely many intuitionistic fuzzy sets, which they use to make decisions in an intertemporal framework (i.e., with decisions that spread over an indefinitely long number of periods).
AOs are an important topic today and are attracting a great deal of attention. Hamacher
t-conorm and
t-norm [
19] are the algebraic and Einstein
t-conorm and
t-norm [
20] expanded variants, respectively. Based on Hamacher operations, AOs play an efficient role in solving different MADM problems. Liu [
21] used Hamacher operations to develop AOs for interval-valued intuitionistic fuzzy sets environment. Many MADM models have been developed using bipolar fuzzy numbers,
t-norms, and
t-conorms, for instance, Wei et al. [
22] proposed some BF Hamacher arithmetic and geometric operators and investigated their basic properties. Gao et al. [
23] introduced dual hesitant BF Hamacher prioritized weighted average and geometric operators. Due to the existence of multi-polar information in many real situations, the concept of
m-polar fuzzy (
mF) sets was introduced by Chen et al. [
24] as an extension of BF sets. Khameneh and Kilucman developed certain
mF soft weighted AOs. We observe that almost all AOs used BF numbers, intuitionistic fuzzy numbers, Pythagorean fuzzy numbers, or
mF numbers without using Hamacher operations. Akram et al. [
25,
26,
27,
28,
29,
30,
31] introduced several decision-making techniques. In this research article, our main focus is how to apply Hamacher operators to aggregate the
mF information. For further terminologies which are not discussed in the paper, the readers are referred to [
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43,
44].
The motivation of this article is described as follows:
The assessment of the best alternative in an mF environment is a very difficult MADM problem and has several imprecise factors. In the present MADM techniques, assessment data is simply portrayed by fuzzy and BF numbers which may prompt data mutilation.
As a prevalent set, mF numbers demonstrates extraordinary execution in providing multi-polar vague, reliable, and inexact assessment information. Therefore, mF numbers might be the best way for the evaluation of alternatives using information having multi-polarity.
Taking into account that Hamacher AOs are a straight forward, however ground-breaking, approach for solving decision-making issues, this article, in general, aims to define Hamacher AOs in the mF context to tackle difficult problems of choice.
Hamacher AOs make the decision results more precise and exact when applied to real-life MADM based on the mF environment.
The proposed operators overcome the limitations of previously existing operators.
Thus, an mF decision-making approach based on Hamacher AOs is proposed to choose the ideal alternative. The proposed method has three main benefits compared to other strategies. First, the method presented uses mF numbers, which can more accurately explain the problems having multiple attributes. Secondly, the proposed method is more efficient and versatile by using only one parameter. Thirdly, it is very important and significant to use Hamacher AOs for mF numbers and to solve practical problems by applying them. The proposed technique is more suitable in tackling complex realistic issues like the selection of the best health care waste treatment methods.
The main contributions of this article are:
The concept of Hamacher AOs is extended to mF environment. Some fundamental properties are discussed. These operators are more flexible and can be taken as the generalization of algebraic and Einstein operators.
An algorithm is developed to handle complex realistic problems with multi-polar data.
Lastly, the strengths and characteristics of these operators are illustrated by comparison analysis.
The remainder of this paper is organized as follows: In
Section 2, we recall some basic notions and then introduce certain Hamacher weighted averaging operators, namely
mF Hamacher weighted average (
mFHWA),
mF Hamacher ordered weighted average (
mFHOWA), and
mF Hamacher hybrid average (
mFHHA) operators. In this section, we also developed some Hamacher weighted geometric operators, namely
mF Hamacher weighted geometric (
mFHWG),
mFHOWG, and
mF Hamacher hybrid geometric (
mFHHG) operators. In
Section 3, we provide mathematical modeling of proposed operators to solve real-life MADM problems. In
Section 4, we solve three practical MADM problems by using the proposed operators and ELECTRE-I method. In
Section 5, we give a comparison analysis. In
Section 6, we give conclusion and future directions.
2. mF Hamacher Aggregation Operators
Definition 1 ([
24])
. An mF set over a universe is a function . The membership of each object is represented by where is the r-th projection mapping. Let be an mF number, where for each .
Definition 2. The score function S of an mF number is formulated as Definition 3. The accuracy function H of an mF number is given by Clearly, for an arbitrary mF number ,
Definition 4. Let , and be two mF numbers. Then
- 1.
, if .
- 2.
, if .
- 3.
, If and .
- 4.
, if , but .
- 5.
, if , but .
Now we describe some fundamental operations on mF numbers as follows:
,
,
,
if and only if
Theorem 1. Let and be two mF numbers, then
- 1.
,
- 2.
,
- 3.
,
- 4.
,
- 5.
,
- 6.
- 7.
Proof. Straightforward. □
2.1. Hamacher Operations of mF Numbers
Hamacher [
19] introduced an extension of t-norm and t-conorm. Hamacher product ⊗ and Hamacher sum ⊕ are respectively t-norm and t-conorm, which are given as follows, for all
.
In particular, when
in Equations (
1) and (2), we get algebraic t-norm and t-conorm, respectively.
and when
in Equations (
1) and (2), we obtain Einstein t-norm and t-conorm, respectively, as follows:
With the help of Hamacher operations defined in [
22,
38] for bipolar fuzzy numbers, we now present the Hamacher operations for
mF numbers. Let
and
be
mF numbers. We define the following basic Hamacher operations for
mF numbers with
.
2.2. mF Hamacher Arithmetic Aggregation Operators
We propose mF Hamacher arithmetic aggregation operators as follows:
Definition 5. Let be a family of mF numbers where ‘j’ varies from 1 to n. Then, an mF Hamacher weighted average (mFHWA) operator is a mapping from to , which is defined aswhere represents the weight vector of for each ‘j’ varies from 1 to n, with and . Theorem 2. Let
be a family of
mF numbers where ‘
j’ varies from 1 to
n. The accumulated value of these
mF numbers using the
mFHWA operator is also an
mF numbers, which is given as
Proof. We use the mathematical induction technique to prove it.
Case 1. When
from Equation (
8), we get
Thus, for
Equation (
8) holds.
Case 2. We now suppose that Equation (
8) holds for
, where
(set of natural numbers), then we get
Therefore, Equation (
8) holds for
. Thus, we conclude that Equation (
8) holds for any
. □
Example 1. Let and be 4F numbers with a weight vector for these 4F numbers. Then, for , We now give two particular cases of the mFHWA operator.
When
,
mFHWA operator reduces into
mF weighted averaging (
mFWA) operator as below:
When
,
mFHWA operator reduces into
mF Einstein weighted averaging (
mFEWA) operator as below:
Theorem 3 (Idempotency Property)
. Let be a family of ‘n’ mF numbers. If all these mF numbers are same, in other words, , then Proof. Since
where ‘j’ varies from 1 to
. Then, from Equation (
8), we get
Hence, holds if . □
The following properties, namely, boundedness and monotonicity, can be easily followed by Definition 5. So, we omit their proofs.
Theorem 4 (Boundedness Property)
. Let be a family of ‘n’ mF numbers, and , then Theorem 5 (Monotonicity Property)
. Let and be two families of mF numbers. If , then We now propose mF Hamacher ordered weighted average operator.
Definition 6. Let be a family of mF numbers where ‘j’ varies from 1 to n. An mF Hamacher ordered weighted average (mFHOWA) operator is a mapping mFHOWA: with weight vector where and . Thus,where is the permutation of the indices , for which , ∀ . Theorem 6. Let be a family of ‘n’ mF numbers. The accumulated value of these mF numbers using the mFHOWA operator is also an mF numbers, which is given by Proof. Its proof follows directly by similar arguments as used in Theorem 2. □
Example 2. Let , and be 4F numbers with a weight vector for these 4F numbers. Then, scores and aggregated values of mF numbers for can be computed as below: Since, , thus In the following, we give two particular cases of mFHOWA operator.
When
,
mFHOWA operator converted into
mF ordered weighted averaging (
mFOWA) operator as below:
When
,
mFHOWA operator reduces into
mF Einstein ordered weighted averaging (
mFEOWA) operator as below:
Theorem 7 (Idempotency Property)
. Let be a family of ‘n’ mF numbers. If all these mF numbers are same, i.e., , then Proof. Since
where ‘j’ varies from 1 to n. Then, from Equation (
16), we obtain
Hence, holds if ∀. □
Theorem 8 (Boundedness Property)
. Let be a family of ‘n’ mF numbers, and , then Theorem 9 (Monotonicity Property)
. Let and be two families of mF numbers where ‘j’ varies from 1 to n. If , then Theorem 10 (Commutativity Property)
. Let and be two families of mF numbers, then where is an arbitrary permutation of . In Definitions 5 and 6, we observe that mFHWA operator and mFHOWA operator weight mF numbers and ordered arrangement of mF numbers, respectively. We now propose another operator, namely, mF Hamacher hybrid averaging operator, which combines the qualities of mFHWA operator and mFHOWA operator.
Definition 7. Let be a family of mF numbers where ‘j’ varies from 1 to n. An mF Hamacher hybrid averaging (mFHHA) operator is given as below:where is the associated-weight vector of the mF numbers , where ‘j’ varies from 1 to n, , is the jth biggest mF numbers, , is the weight vector, with and n serves as the balancing coefficient. Note that if , then mFHHA operator degenerates into mFHWA operator. When , then mFHHA operator degenerates into mFHOWA operator. Therefore, mFHHA operator is an extension of the operators, mFHWA and mFHOWA, which explains the degrees and ordered arrangements of the given mF values.
Theorem 11. Let be a family of ‘n’ mF numbers. The accumulated value of these mF numbers using the mFHHA operator is also an mF numbers, which is given by Proof. Its proof follows immediately by similar arguments used in Theorem 2. □
We give two particular cases of mFHHA operator as below:
When
,
mFHHA operator converted into
mF hybrid averaging (
mFHA) operator as below:
When
,
mFHHA operator converted into
mF Einstein hybrid averaging (
mFEHA) operator as below:
Example 3. Let and be 3F numbers with an associated-weight vector for these 3F numbers and a weight vector . Then, from Definition 7, for Then, scores and aggregated values of mF numbers for can be computed as below: Since, , thus 2.3. mF Hamacher Geometric Aggregation Operators
We now proposes different types of Hamacher geometric aggregation operators with mF numbers, namely, mFHWG operator, mFHOWG operator, and mFHHG operator.
Definition 8. Let be a family of mF numbers where ‘j’ varies from 1 to n. An mFHWG operator of is a function mFHWG: , which is defined as follows:where denotes the weight vector, with . Theorem 12. Let be a family of ‘n’ mF numbers. The accumulated value of these mF numbers using the mFHWG operator is also an mF numbers, which is given as Proof. It can be easily followed using mathematical induction. □
Example 4. Let and be 3F numbers with a weight vector for these 3F numbers. Then, for , Theorem 13 (Idempotency Property)
. Let be a family of ‘n’ mF numbers. If all these mF numbers are same, i.e., , then Theorem 14 (Boundedness Property)
. Let be a family of ‘n’ mF numbers, and , then Theorem 15 (Monotonicity Property)
. Let and be two families of mF numbers. If , then We give two particular cases of mFHWG operator.
When
,
mFHWG operator converted into
mF weighted geometric (
mFWG) operator as below:
When
,
mFHWG operator reduces into
mF Einstein weighted geometric (
mFEWG) operator as below:
We now propose mFHOWG operator.
Definition 9. Let be a family of mF numbers. An mFHOWG operator is a mapping mFHOWG: with weight vector , for which and . Thus,where is the permutation of the indices ‘j’ varies from 1 to n, for which , ∀. Theorem 16. Let be a family of ‘n’ mF numbers. The accumulated value of these mF numbers using the mFHOWG operator is also an mF numbers, which is given by Example 5. Let and be 3F numbers with a weight vector for these 3F numbers. Then, scores and aggregated values of mF numbers for can be computed as below: Since, , thus We give two particular cases of mFHOWG operator.
When
,
mFHOWG operator reduces into
mF ordered weighted geometric (
mFOWG) operator as
When
,
mFHOWG operator reduces into
mF Einstein ordered weighted geometric (
mFEOWG) operator as below:
For the mFHOWG operator, the following properties can be easily shown.
Theorem 17 (Idempotency Property)
. Let be a family of ‘n’ mF numbers. If all these mF numbers are same, in other words, , then Theorem 18 (Boundedness Property)
. Let be a family of mF ‘n’ numbers, and , then Theorem 19 (Monotonicity Property)
. Let and be two families of mF numbers. If , then Theorem 20 (Commutativity Property)
. Let and be two families of mF numbers. If , then where is any permutation of . In Definitions 5 and 6, we observe that mFHWG operator and mFHOWG operator weight mF numbers and their ordered arrangement, respectively. We now propose another operator, namely, mF Hamacher hybrid averaging operator, which combine the features of these operators.
Definition 10. Let be a family of mF numbers where ‘j’ varies from 1 to n. An mF Hamacher hybrid geometric (mFHHG) operator is given as below:where is the permutation of , for which , ∀ and is the associated-weight vector of the mF numbers , . is the jth biggest mF numbers, , represents the weight vector, with and n serves as the balancing coefficient. Theorem 21. Let be a family of mF numbers. The accumulated value of these mF numbers using the mFHHG operator is also an mF numbers, which is given by Proof. It can be easily proved by mathematical induction technique. □
Example 6. Let and be 3F numbers with an associated-weight vector for these 3F numbers and a weight vector . Then, from Definition 7, for Then, scores and aggregated values of mF numbers for can be computed as below: Since, , thus We now give two particular cases of mFHHG operator.
When
,
mFHHG operator converted into
mF hybrid geometric (
mFHG) operator as below:
When
,
mFHHG operator converted into
mF Einstein hybrid geometric (
mFEHG) operator as below:
3. Mathematical Approach for MADM Using mF Information
We next handle the MADM situations with mF information by applying the mF Hamacher aggregation operators proposed in the preceding sections. The following assumptions or notations are used to represent the MADM problem for the efficient selection of country affected by human decision-making with mF information. Let be a set of objects (alternatives) and be the set of attributes. Let be a weight vector for attributes where Suppose that is an mF decision matrix, where denote the membership degrees given by the decision-makers that the object satisfies the attribute , .
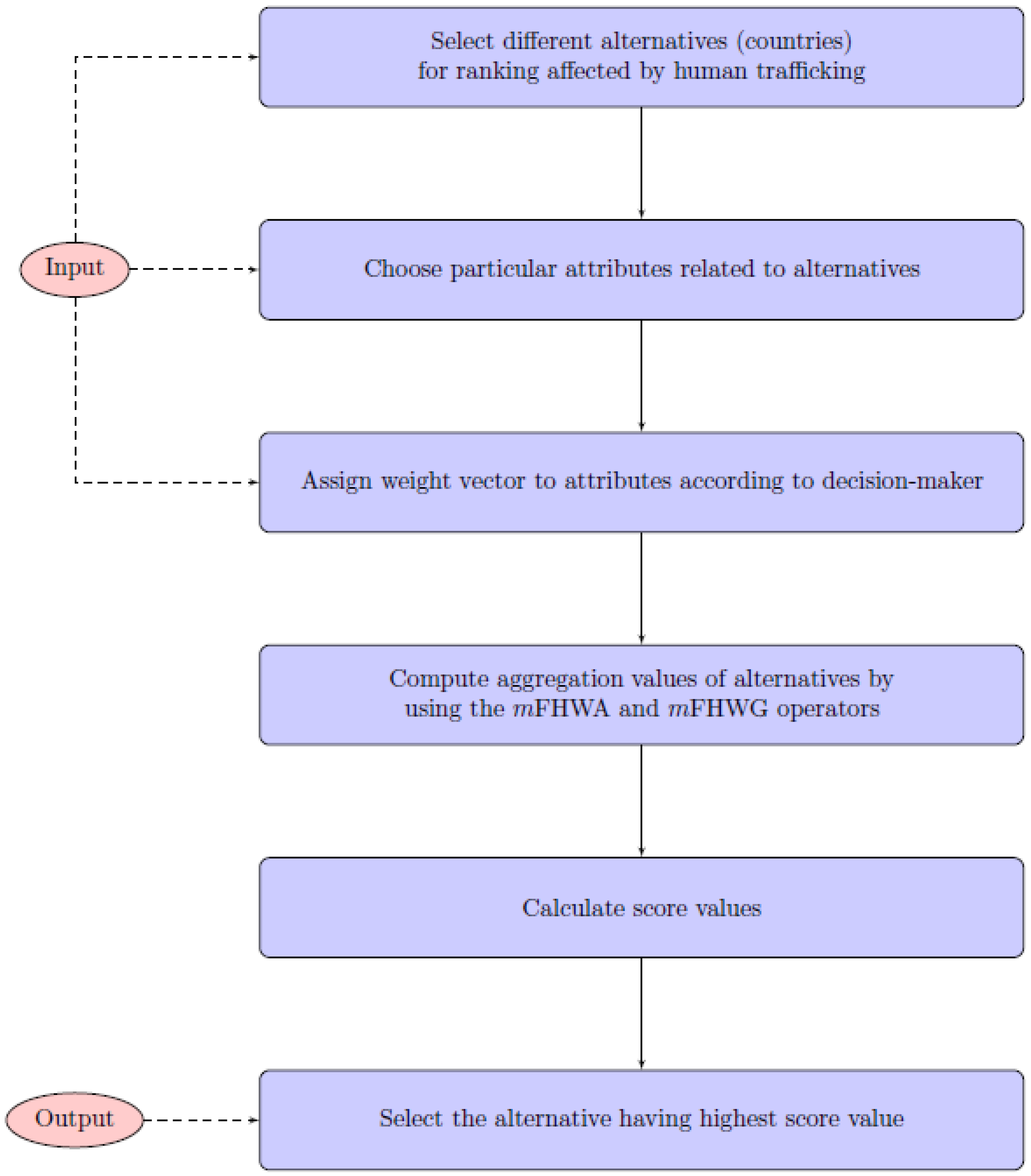
We give the following Algorithm 1 to solve a MADM problem by applying the mFHWA (or mFHWG) operator.
| Algorithm 1: Steps to solve MADM problem by applying the mFHWA (or mFHWG) operator |
Input: U, the universe with k alternatives. T, the set having n attributes. , the weight vector for attributes. Use the mFHWA operator to evaluate the information in mF decision matrix , determine the preference values of the object .
Alternatively, if we apply mFHWG operator then
Compute the scores . Rank the objects based on their score values . If two alternatives have same score, then use the accuracy function to rank the objects.
Output: The alternative having the highest score in step 4 will be the decision alternative. |
4. Applications
4.1. Assessment of Health Care Waste Treatments Alternatives
A waste management system’s fundamental task is to control, process, store, and dispose waste in accordance with national requirements and international obligations, taking into account the economic and socio-political factors involved. A suitable technology has to be chosen for each step due to the range of procedures, techniques, and equipment available for different steps of a waste management scheme. There is a committee which selects five health care waste treatment alternatives, which are listed as below.
These waste treatments are assessed on the basis of four factors.
Each factor has been divided into three characteristics to make a 3F number:
The “Economic Factors” include cost and resources, transport regulations, and physical infrastructure.
The “Environmental Factors” include geographical conditions, geological conditions, and availability of resources.
The “Technical Factors” include waste characteristics, complexity and maintainability of facilities, and state of research and development.
The “Social Factors” include social acceptability, communication, societal responsibilities, and social equity.
- 1.
The 3F decision matrix is given in
Table 1.
- 2.
The weights assigned by the experts are given as
We proceed to select the most suitable health care waste treatment alternative by using the mFHWA operator. The steps are as follows:
- Step 1
Assume
. Use the
mFHWA operator to calculate the performance values
of the health care waste treatment alternatives.
- Step 2
Compute the scores
of all 3F numbers
- Step 3
Rank all the health care waste treatment alternatives according to the scores of all 3F numbers,
- Step 4
is the best alternative.
If the mFHWG operator is used for selection, the best alternative can be chosen in a similar manner. Now the steps are as follows:
- Step 1
Suppose
. Use the
mFHWG operator to calculate the performance values
of the health care waste treatment alternatives.
- Step 2
Compute the scores
of all 3F numbers
- Step 3
Rank all the health care waste treatment alternatives,
- Step 4
is the best alternative.
We apply the mF-ELECTRE-I approach to the same problem.
- 1.
Table 2 represents the 3F decision matrix.
- 2.
Table 3 and
Table 4 represent the 3F concordance and 3F discordance sets, respectively.
- 3.
The 3F concordance matrix is constructed as:
- 4.
The 3F concordance level
- 5.
The 3F discordance matrix is constructed as:
- 6.
The 3F discordance level
- 7.
The 3F concordance dominance and 3F discordance dominance matrix are constructed as:
- 8.
The 3F aggregate dominance matrix is constructed as:
- 9.
The following graph shows the preference relation of the health care treatments (see
Figure 1).
Therefore, is the best choice.
4.2. Selection of the Best Company for Investment
Each investment and investment decision entails certain degree of risk. The most obvious factor to consider is the financial performance of the company. The acronym “ESG” collectively refers to economic, social, and governance factors. ESG integration is the method of consideration of economic, social, and governance factors in the investment cycle. Company information is another important factor in assessing a potential business investment. Suppose that an investor wants to invest in a company. Let
be the set of five companies. The investor chooses three characteristics to assess companies which are given as:
Each attribute has been divided into four characteristics to make a 4F number.
The attribute “Financial Performance” includes tax returns, balance sheets, cash flow projections, and current accounts receivables.
The attribute “Company Information” includes company’s history, accomplishments, product or service offerings, and business plans.
The attribute “ESG Integration” includes pollution prevention, energy efficiency, regulatory standards, and adherence to environmental safety.
- 1.
The 4F decision matrix is given in
Table 5.
- 2.
Weights assigned by the investor are given as,
We select the best company for investment by using the mFHWA operator.
- Step 1
Assume
. Use the
mFHWA operator to calculate the performance values
of the companies.
- Step 2
Compute the scores
of all 4F numbers
- Step 3
Rank all alternatives for investment according to the scores of all 4F numbers,
- Step 4
Therefore, is the most suitable company for investment.
If the mFHWG operator is used for selection, the best alternative can be chosen in a similar manner.
- Step 1
Assume
. Use the
mFHWG operator to calculate the performance values
of the alternatives.
- Step 2
Compute the scores
of all 4F numbers
- Step 3
Rank all companies for investment based on the scores of all 4F numbers,
- Step 4
Therefore, is the best alternative.
We apply the mF-ELECTRE-I method to the same problem.
- 3.
Table 6 represents the 4F weighted decision matrix.
- 4.
Table 7 and
Table 8 represent the 4F concordance and 4F discordance sets, respectively.
- 5.
The 4F concordance matrix is constructed as:
- 6.
The 4F concordance level
- 7.
The 4F discordance matrix is constructed as:
- 8.
The 4F discordance level
- 9.
The 4F concordance dominance and 4F discordance dominance matrix are constructed as:
- 10.
The 4F aggregate dominance matrix is evaluated as:
- 11.
The following graph shows the preference relation of the companies (see
Figure 2).
Therefore, is the best company for investment.
4.3. Selection of Most Affected Country by Human Trafficking
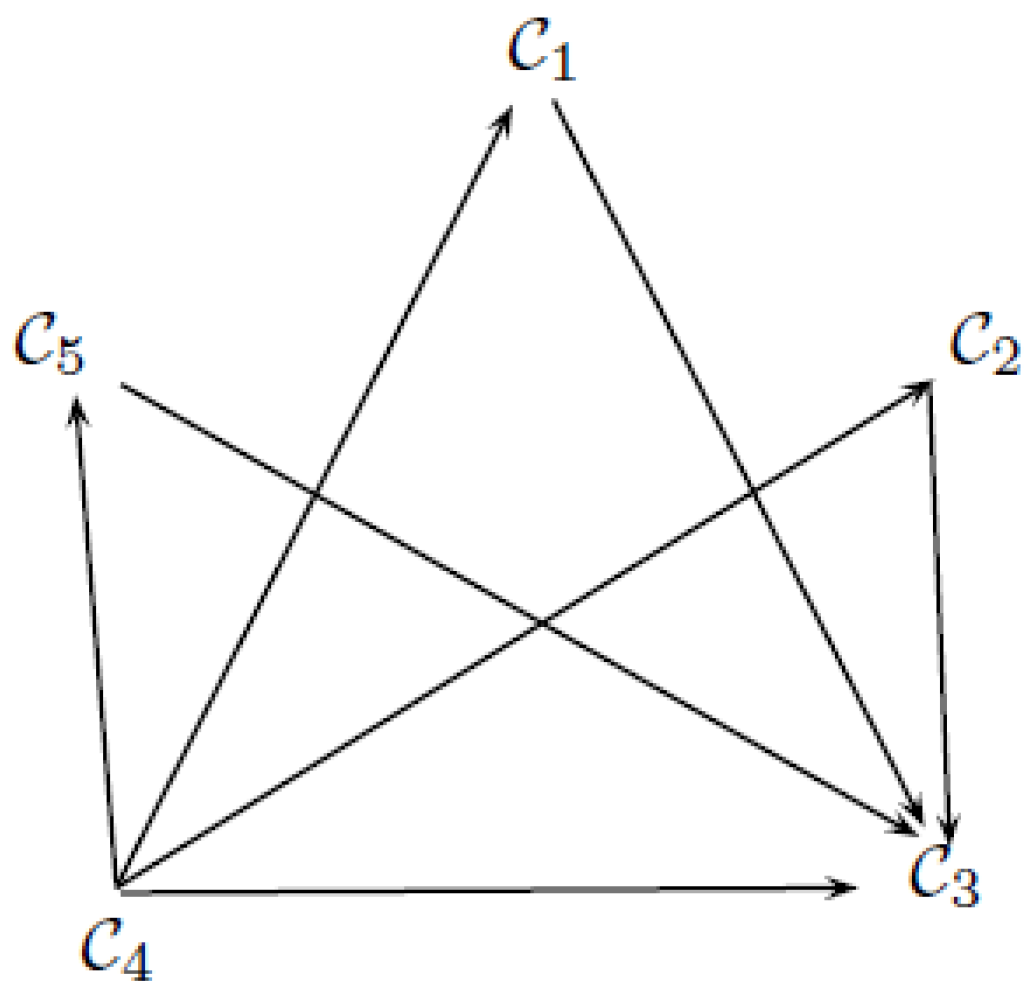
In human trafficking, traffickers use force, coercion, or fraud to lure their victims into commercial sexual exploitation or labor. These people are vulnerable due to different reasons like emotional or psychological susceptibleness, lack of a social welfare system, economic hardships, political instability, or natural disaster. Based on the latest surveys, it can be easily observed that millions of children, women, and men become part of human trafficking all over the world, including Saudi Arabia, China, Russia, Kuwait, and Iran. It is also observed that victims of traffickers can be of any gender, age, or nationality. Traffickers use manipulation, or fake promises of high-paying jobs or romantic connection to attract victims into trafficking. The trauma triggered by the traffickers can be so extreme that people may not even recognize themselves as victims. The main attributes or causes of human trafficking are political instability, poverty, debt, natural disasters, demand, and addiction.
Let be a set of five countries and let be the set of four attributes, where
denotes “Poverty”,
denotes “Debt”,
denotes “Demand”,
denotes “Natural Disaster”.
Further characterizations of above attributes are force, fraud, or lure. The purpose of this application is to evaluate the above countries
’s,
concerning the worst in human trafficking with the help of 3F numbers given by the decision-makers under the attributes
’s,
. Let
be the weight vector for the preceding characteristics. The 3F decision matrix is given as below(See
Table 9):
For illustration, the 3F number in the top left entry of the 3F decision matrix means that in the country Saudi Arabia with respect to people in poverty who become a part of human trafficking are sub-classified as follows: 30% due to force, 60% due to fraud, 20% due to lure.
To compute the worst country regarding human trafficking, we apply the two operators, namely, mFHWA and mFHWG, to construct methods to MADM problems with mF information, which are given as follows:
Take
. We apply the
mFHWA operator to find the preference values
of the countries
regarding human trafficking.
Determine the scores
of overall 3F numbers
of the countries
involved in human trafficking:
Now rank all the countries based on score values based on overall 3F numbers: .
has high rate human trafficking.
Similarly, we use the mFHWG operator to select the affected country.
Take
. Use the
mFHWG operator to find the preference values
of the countries
regarding human trafficking.
Determine the scores
of overall 3F numbers
of the countries
involved in human trafficking:
Now rank all the countries based on score values based on overall 3F numbers: .
has a high rate of human trafficking.
The method used in the application to select the worst country affected by human trafficking is explained in
Figure 3.
6. Conclusions
Most problems in real life have a structure that fits into the framework of multi-polar data that coexist with multiple attributes. As theoretical models develop in order to encompass wider settings, the MADM techniques with better performance need to be adapted to tackle more complex decision-making issues.
In this article we have contributed to the development of MADM with the analysis of problems in an m-polar fuzzy environment. As a preparation to their utilization in decision-making, the theoretical basis of aggregation operators need to be carefully considered. The shortcomings of existing methods plus the beneficial characteristics of Hamacher aggregation operators led us to consider their ability to produce suitable combinations of mF numbers.
Consequently we have introduced arithmetic and geometric operations to construct m-polar fuzzy aggregation operators that closely follow the motivation of Hamacher operations. They include the mF Hamacher weighted average operator (mFHWA), mF Hamacher ordered weighted average operator (mFHOWA), mF Hamacher hybrid weighted average operator (mFHHWA), mF Hamacher weighted geometric operator (mFHWG), mF Hamacher ordered weighted geometric operator (mFHOWG), and mF Hamacher hybrid weighted geometric operator (mFHHWG). The fundamental characteristics of these operators are discussed so that the practitioners can select the version that better fits their needs.
We have utilized these operators to expand a number of strategies to address MADM problems. A comparative analysis of our proposed procedure with the mF-ELECTRE-I approach is performed. Finally, practical examples for the selection of health care waste treatment methods, selection of best company for investment, and the selection of most affected country by human trafficking are given. Altogether they build up a procedure and make a case for the pertinence and adequacy of the proposed approach.
In a nutshell, the main contribution of this article is that it consolidates both the role of Hamacher aggregation operators and the advantageous features of
m-polar fuzzy numbers. Once again this model of uncertain knowledge proves its versatility for portraying inexact, imprecise data in complex conditions. The operators also demonstrate that they are highly adaptable, hence becoming a powerful tool that might be applied for further uses. In future research, we will extend the driving ideas of our models to an
m-polar fuzzy soft set environment. Their study will prepare us to consider intertemporal settings like in Alcantud et al. [
45].