Human Visual Perception-Based Multi-Exposure Fusion Image Quality Assessment
Abstract
1. Introduction
- (1)
- The difference of chrominance components between fused images and the defined pseudo images with the most severe color attenuation is calculated to measure the global color degradation, and the color saturation similarity is added to eliminate the influence of over-saturated color.
- (2)
- A set of distorted source images with strong edge information of fused image is constructed by the structural transfer characteristic of guided filter; thus, structure similarity and structure saturation are computed to measure the local detail loss and enhancement, respectively.
- (3)
- The Gauss function is designed to accurately detect the over-exposed or under-exposed areas of images; then, the local luminance of each source images and the global luminance of fused image are used to measure the luminance consistency between them.
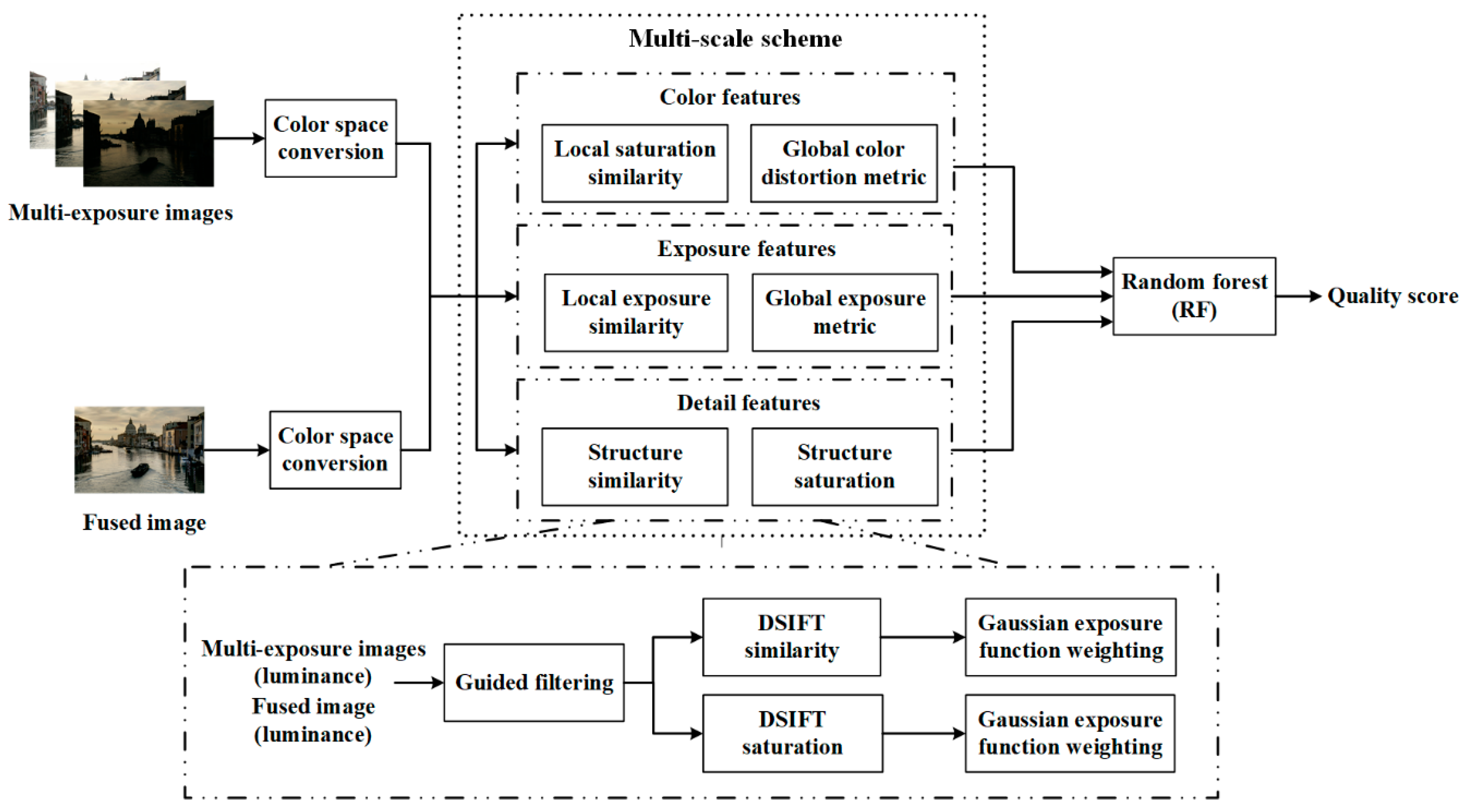
2. Proposed Human Visual Perception-Based MEF-IQA Method
2.1. Local and Global Color Metrics
2.1.1. Global Color Distortion Metric
2.1.2. Local Saturation Similarity
2.2. Structure Similarity and Saturation Metric
2.2.1. DSIFT Similarity
2.2.2. DSIFT Saturation
2.3. Local and Global Exposure Metrics
2.3.1. Local Exposure Similarity
2.3.2. Global Exposure Metric
2.4. Quality Prediction
3. Experimental Results
3.1. Experimental Settings
3.1.1. Database
3.1.2. Evaluation Criteria
3.1.3. Experimental Parameters
3.2. Performance Comparison
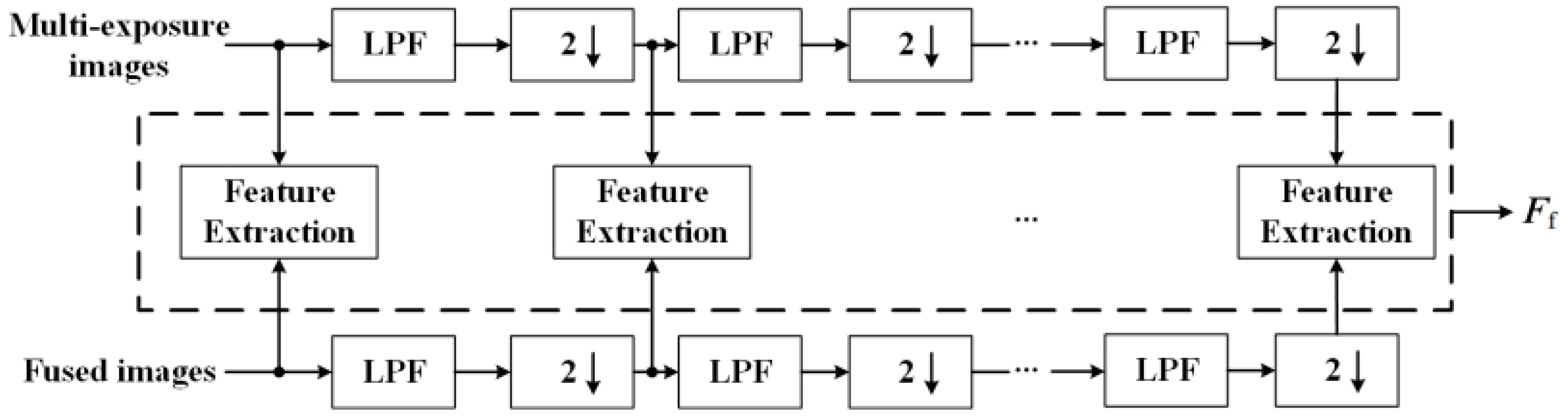
3.3. Impacts of Multi-Scale Scheme and Different Feature
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, K.F.; Li, H.; Kuang, H.L.; Li, C.Y.; Li, Y.J. An adaptive method for image dynamic range adjustment. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 640–652. [Google Scholar] [CrossRef]
- Yue, G.H.; Hou, C.P.; Zhou, T.W. Blind quality assessment of tone-mapped images considering colorfulness, naturalness, and structure. IEEE Trans. Ind. Electron. 2019, 66, 3784–3793. [Google Scholar] [CrossRef]
- Wang, J.G.; Zhou, L.B. Traffic light recognition with high dynamic range imaging and deep learning. IEEE Trans. Intell. Transp. Syst. 2019, 20, 1341–1352. [Google Scholar] [CrossRef]
- Mertens, T.; Kautz, J.; Reeth, F.V. Exposure fusion: A simple and practical alternative to high dynamic range photography. Comput. Graph. Forum 2009, 28, 161–171. [Google Scholar] [CrossRef]
- Li, Z.G.; Zheng, J.H.; Rahardja, S. Detail-enhanced exposure fusion. IEEE Trans. Image Process. 2012, 21, 4672–4676. [Google Scholar] [PubMed]
- Gu, B.; Li, W.J.; Wong, J.T.; Zhu, M.Y.; Wang, M.H. Gradient field multi-exposure images fusion for high dynamic range image visualization. J. Vis. Commun. Image Represent. 2012, 23, 604–610. [Google Scholar] [CrossRef]
- Raman, S.; Chaudhuri, S. Bilateral filter based compositing for variable exposure photography. In Proceedings of the Eurographics (Short Papers), Munich, Germany, 1–3 April 2009. [Google Scholar]
- Li, S.T.; Kang, X.D. Fast multi-exposure image fusion with median filter and recursive filter. IEEE Trans. Consum. Electron. 2012, 58, 626–632. [Google Scholar] [CrossRef]
- Li, S.T.; Kang, X.D.; Hu, J.W. Image fusion with guided filtering. IEEE Trans. Image Process. 2013, 22, 2864–2875. [Google Scholar] [PubMed]
- Zhang, C.; Cheng, W.; Hirakawa, K. Corrupted reference image quality assessment of denoised images. IEEE Trans. Image Process. 2019, 28, 1731–1747. [Google Scholar] [CrossRef] [PubMed]
- Hossny, M.; Nahavandi, S.; Creighton, D. Comments on information measure for performance of image fusion. Electron. Lett. 2008, 44, 1066–1067. [Google Scholar] [CrossRef]
- Cvejic, N.; Canagarajah, C.N.; Bull, D.R. Image fusion metric based on mutual information and Tsallis entropy. Electron. Lett. 2006, 42, 626–627. [Google Scholar] [CrossRef]
- Xydeas, C.S.; Petrovic, V.S. Objective pixel-level image fusion performance measure. In Sensor Fusion: Architectures, Algorithms, and Applications IV; International Society for Optics and Photonics: Orlando, FL, USA, 2000. [Google Scholar]
- Wang, P.W.; Liu, B. A novel image fusion metric based on multi-scale analysis. In Proceedings of the 2008 9th International Conference on Signal Processing, Beijing, China, 26–29 October 2008. [Google Scholar]
- Zheng, Y.; Essock, E.A.; Hansen, B.C.; Haun, A.M. A new metric based on extended spatial frequency and its application to DWT based fusion algorithms. Inf. Fusion 2007, 8, 177–192. [Google Scholar] [CrossRef]
- Piella, G.; Heijmans, H. A new quality metric for image fusion. In Proceedings of the 2003 International Conference on Image Processing, Barcelona, Spain, 14–17 September 2003. [Google Scholar]
- Ma, K.D.; Zeng, K.; Wang, Z. Perceptual quality assessment for multi-exposure image fusion. IEEE Trans. Image Process. 2015, 24, 3345–3356. [Google Scholar] [CrossRef]
- Xing, L.; Cai, L.; Zeng, H.G.; Chen, J.; Zhu, J.Q.; Hou, J.H. A multi-scale contrast-based image quality assessment model for multi-exposure image fusion. Signal Process. 2018, 145, 233–240. [Google Scholar] [CrossRef]
- Deng, C.W.; Li, Z.; Wang, S.G.; Liu, X.; Dai, J.H. Saturation-based quality assessment for colorful multi-exposure image fusion. Int. J. Adv. Robot. Syst. 2017, 14, 1–15. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–100. [Google Scholar] [CrossRef]
- Multi-exposure Fusion Image Database. Available online: http://ivc.uwaterloo.ca/database/MEF/MEF-Database.php (accessed on 11 July 2015).
- Antkowiak, J.; Baina, T.J. Final Report from the Video Quality Experts Group on the Validation of Objective Models of Video Quality Assessment; ITU-T Standards Contributions COM: Geneva, Switzerland, March 2000. [Google Scholar]





| No. | Source Sequences | Size | Image Source |
|---|---|---|---|
| 1 | Balloons | 339 × 512 × 9 | Erik Reinhard |
| 2 | Belgium house | 512 × 384 × 9 | Dani Lischinski |
| 3 | Lamp1 | 512 × 384 × 15 | Martin Cadik |
| 4 | Candle | 512 × 364 × 10 | HDR Projects |
| 5 | Cave | 512 × 384 × 4 | Bartlomiej Okonek |
| 6 | Chinese garden | 512 × 340 × 3 | Bartlomiej Okonek |
| 7 | Farmhouse | 512 × 341 × 3 | HDR Projects |
| 8 | House | 512 × 340 × 4 | Tom Mertens |
| 9 | Kluki | 512 × 341 × 3 | Bartlomiej Okonek |
| 10 | Lamp2 | 512 × 342 × 6 | HDR Projects |
| 11 | Landscape | 512 × 341 × 3 | HDRsoft |
| 12 | Lighthouse | 512 × 340 × 3 | HDRsoft |
| 13 | Madison capitol | 512 × 384 × 30 | Chaman Singh Verma |
| 14 | Memorial | 341 × 512 × 16 | Paul Debevec |
| 15 | Office | 512 × 340 × 6 | Matlab |
| 16 | Tower | 341 × 512 × 3 | Jacques Joffre |
| 17 | Venice | 512 × 341 × 3 | HDRsoft |
| No. | GF-IQA | MEF-IQA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [11] | [12] | [13] | [14] | [15] | [16] | [17] | [18] | [19] | Proposed | |
| 1 | −0.542 | 0.761 | 0.705 | 0.439 | 0.665 | 0.504 | 0.930 | 0.936 | 0.924 | 0.954 |
| 2 | −0.385 | 0.174 | 0.802 | 0.626 | 0.561 | 0.502 | 0.931 | 0.965 | 0.990 | 0.989 |
| 3 | −0.121 | −0.479 | 0.729 | 0.728 | 0.402 | 0.432 | 0.891 | 0.984 | 0.970 | 0.976 |
| 4 | 0.265 | −0.729 | 0.939 | 0.892 | 0.106 | 0.179 | 0.951 | 0.946 | 0.954 | 0.977 |
| 5 | −0.214 | 0.053 | 0.695 | 0.814 | 0.621 | 0.630 | 0.772 | 0.643 | 0.874 | 0.912 |
| 6 | −0.224 | −0.294 | 0.768 | 0.836 | 0.481 | 0.409 | 0.956 | 0.842 | 0.960 | 0.910 |
| 7 | −0.641 | 0.504 | 0.641 | 0.600 | 0.693 | 0.216 | 0.863 | 0.919 | 0.875 | 0.951 |
| 8 | −0.289 | −0.524 | 0.621 | 0.596 | 0.476 | 0.481 | 0.841 | 0.956 | 0.961 | 0.990 |
| 9 | −0.091 | 0.021 | 0.391 | 0.359 | −0.112 | −0.049 | 0.824 | 0.910 | 0.863 | 0.933 |
| 10 | −0.387 | 0.621 | 0.845 | 0.752 | 0.649 | 0.600 | 0.829 | 0.906 | 0.873 | 0.887 |
| 11 | −0.211 | 0.539 | 0.320 | 0.448 | 0.081 | 0.031 | 0.746 | 0.612 | 0.879 | 0.954 |
| 12 | −0.296 | −0.261 | 0.838 | 0.655 | 0.246 | −0.023 | 0.942 | 0.886 | 0.857 | 0.970 |
| 13 | −0.406 | 0.031 | 0.628 | 0.423 | 0.541 | 0.618 | 0.914 | 0.915 | 0.971 | 0.907 |
| 14 | −0.418 | 0.445 | 0.828 | 0.678 | 0.588 | 0.733 | 0.898 | 0.981 | 0.969 | 0.980 |
| 15 | −0.203 | 0.302 | 0.498 | 0.473 | 0.316 | 0.324 | 0.963 | 0.956 | 0.981 | 0.992 |
| 16 | −0.478 | −0.116 | 0.772 | 0.835 | 0.572 | 0.594 | 0.956 | 0.947 | 0.957 | 0.913 |
| 17 | −0.358 | −0.022 | 0.795 | 0.654 | 0.479 | 0.280 | 0.970 | 0.971 | 0.950 | 0.989 |
| Average | −0.294 | 0.060 | 0.695 | 0.636 | 0.433 | 0.400 | 0.893 | 0.899 | 0.930 | 0.952 |
| Hit count | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 8 | 10 | 15 |
| No. | GF-IQA | MEF-IQA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [11] | [12] | [13] | [14] | [15] | [16] | [17] | [18] | [19] | Proposed | |
| 1 | −0.429 | 0.714 | 0.667 | 0.500 | 0.595 | 0.452 | 0.833 | 0.952 | 0.935 | 0.929 |
| 2 | −0.299 | 0.000 | 0.779 | 0.755 | 0.539 | 0.467 | 0.970 | 0.958 | 0.934 | 0.934 |
| 3 | −0.071 | −0.381 | 0.786 | 0.619 | 0.476 | 0.405 | 0.976 | 1.000 | 0.954 | 0.976 |
| 4 | 0.357 | −0.667 | 0.976 | 0.786 | 0.167 | 0.548 | 0.927 | 0.952 | 0.927 | 0.905 |
| 5 | −0.119 | 0.024 | 0.714 | 0.810 | 0.643 | 0.571 | 0.833 | 0.619 | 0.851 | 0.762 |
| 6 | −0.214 | −0.286 | 0.691 | 0.786 | 0.548 | 0.524 | 0.929 | 0.762 | 0.946 | 0.881 |
| 7 | −0.452 | 0.500 | 0.738 | 0.810 | 0.500 | 0.286 | 0.929 | 0.810 | 0.883 | 0.952 |
| 8 | −0.048 | −0.691 | 0.595 | 0.452 | 0.524 | 0.405 | 0.857 | 0.905 | 0.909 | 0.976 |
| 9 | −0.238 | 0.167 | 0.262 | 0.286 | 0.048 | 0.119 | 0.786 | 0.905 | 0.867 | 0.929 |
| 10 | −0.429 | 0.833 | 0.762 | 0.619 | 0.691 | 0.548 | 0.714 | 0.905 | 0.844 | 0.714 |
| 11 | −0.738 | 0.548 | 0.024 | 0.405 | 0.143 | 0.143 | 0.524 | 0.881 | 0.760 | 0.810 |
| 12 | −0.833 | −0.429 | 0.500 | 0.429 | 0.381 | 0.071 | 0.881 | 0.691 | 0.815 | 0.881 |
| 13 | −0.214 | 0.310 | 0.524 | 0.357 | 0.524 | 0.476 | 0.881 | 0.881 | 0.955 | 0.881 |
| 14 | 0.000 | 0.810 | 0.762 | 0.548 | 0.524 | 0.667 | 0.857 | 0.857 | 0.907 | 0.857 |
| 15 | −0.193 | 0.084 | 0.277 | 0.398 | 0.386 | 0.458 | 0.783 | 0.988 | 0.907 | 0.988 |
| 16 | −0.476 | −0.214 | 0.571 | 0.524 | 0.595 | 0.571 | 0.952 | 0.929 | 0.941 | 0.857 |
| 17 | −0.335 | 0.299 | 0.910 | 0.731 | 0.563 | 0.311 | 0.934 | 0.934 | 0.893 | 0.934 |
| Average | −0.278 | 0.059 | 0.620 | 0.577 | 0.461 | 0.413 | 0.857 | 0.878 | 0.896 | 0.897 |
| Hit count | 0 | 0 | 1 | 0 | 0 | 0 | 7 | 8 | 9 | 11 |
| Feature Category | PLCC | SROCC | RMSE |
|---|---|---|---|
| F1 | 0.711 | 0.591 | 1.029 |
| F2 | 0.890 | 0.793 | 0.608 |
| F3 | 0.663 | 0.566 | 1.096 |
| Scale (l) | PLCC | SROCC | RMSE |
|---|---|---|---|
| 1 | 0.933 | 0.868 | 0.495 |
| 2 | 0.945 | 0.880 | 0.465 |
| 3 | 0.952 | 0.897 | 0.442 |
| 4 | 0.947 | 0.889 | 0.453 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Chen, A.; Yang, B.; Zhang, S.; Wang, Y. Human Visual Perception-Based Multi-Exposure Fusion Image Quality Assessment. Symmetry 2019, 11, 1494. https://doi.org/10.3390/sym11121494
Cui Y, Chen A, Yang B, Zhang S, Wang Y. Human Visual Perception-Based Multi-Exposure Fusion Image Quality Assessment. Symmetry. 2019; 11(12):1494. https://doi.org/10.3390/sym11121494
Chicago/Turabian StyleCui, Yueli, Aihua Chen, Benquan Yang, Shiqing Zhang, and Yang Wang. 2019. "Human Visual Perception-Based Multi-Exposure Fusion Image Quality Assessment" Symmetry 11, no. 12: 1494. https://doi.org/10.3390/sym11121494
APA StyleCui, Y., Chen, A., Yang, B., Zhang, S., & Wang, Y. (2019). Human Visual Perception-Based Multi-Exposure Fusion Image Quality Assessment. Symmetry, 11(12), 1494. https://doi.org/10.3390/sym11121494




