1. Introduction
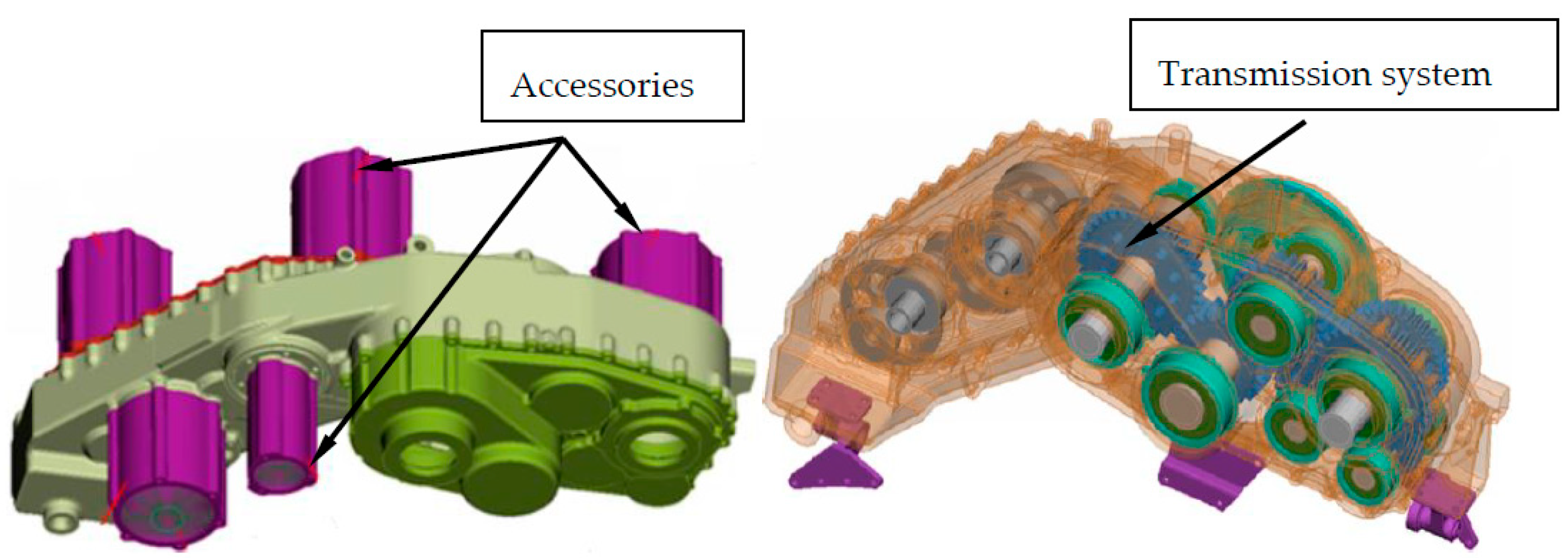
In an aircraft’s gas turbine engine, the transmission system transmits power to accessories, such as the oil pump (as shown in
Figure 1). In order to reduce the weight of the engine, the transmission gears often have a thin-walled structure. However, these gears also easily cause resonance in the operating speed range, stressing on the need to reduce vibration and avoid resonance failure. Common strategies to prevent this include active and passive damping. Active damping involves redesigning of the gear structure to limit resonance points in the operating range; this is difficult to realize in an aircraft gas turbine engine, where multiple resonance points exist. The passive method utilizes damping devices to increase system damping and subsequently suppress vibration [
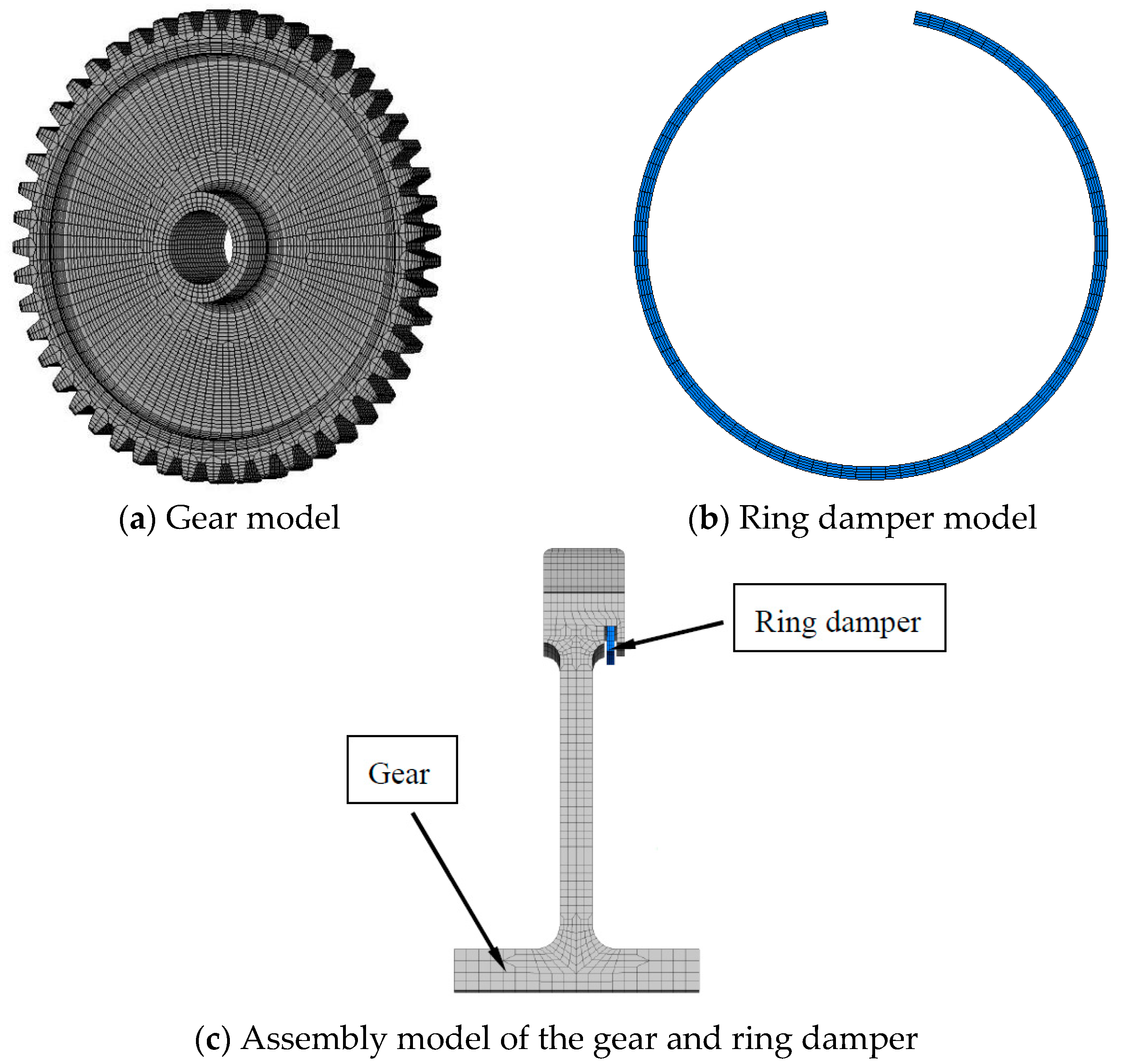
1]. The ring damper is one such device; its structure is shown in
Figure 2.
A ring damper is a device used to improve the damping of gears. Via relative motion on the contact interface between the ring damper and the gear, vibration energy is dissipated and vibration amplitude/stress is reduced [
2].
Most research is currently focused on analyzing the forced response of the structure with an additional ring damper. Laxalde et al. [
3,
4] used a dynamic time-frequency conversion method to analyze the forced response of a bladed disk structure with a ring damper; they found that the effect of the ring damper depends on friction energy dissipation on the contact surface between the ring damper and the structure. Zucca et al. [
5,
6] characterized the frictional force of the contact surface as a function of the tangent and normal stiffness as depending on the amplitude, and calculated the periodic response of the system in the frequency domain via the harmonic balance method. Epureanu et al. [
7] expressed nonlinear frictional force as a function of equivalent damping and stiffness to improve the speed of steady-state response iteratively. Tang et al. [
8,
9] proposed a reduced order model. First, the dynamic substructure method was used to reduce the size of the finite element model. Second, the time-frequency conversion method was employed to solve the equations of motion in the frequency domain to further reduce the calculation amount of the model [
10]. Lopez et al. [
11,
12] obtained the magnitude of friction energy dissipation under different vibration conditions by deducing the relative motion between the ring damper and the main structure, and concluded that the larger the damping ring mass, the better the vibration reduction, under the condition of small mass rate (mass of the damping ring/mass of the main structure). However, real excitation of the gear is an aircraft engine is complex, and the limitations of these response methods become obvious when the excitation cannot be predicted accurately.
Gear vibration can be divided into two categories: axial and radial. Some vibration modes are mainly in the axial direction, while the others are in a radial direction. In addition, the vibration reduction mechanisms of these two types are different. For radial vibration, since deformation of the ring damper and gear at the same position are different when resonance occurs (yielding a relative motion and friction), vibration energy is dissipated [
13]. For axial vibration, inertia induces a relative motion between the ring damper and the gear, in an effort to reduce the vibration [
14,
15,
16].
The main purpose of this paper is to establish a numerical model to predict the equivalent damping of ring dampers under axial vibration. In this model, friction-induced nonlinear damping (at the interface of the gear and the ring damper) is expressed as equivalent structural damping associated with vibration loads. The macro sliding model is used to calculate the energy dissipation capacity of the ring damper. The influence of ring damper mass and friction coefficient on damping effect is investigated.
2. Vibration Equation of the GEAR-Ring Damper System
The vibration equation of a gear with a ring damper can be expressed as:
where
u is the vibration displacement; (·) is the differentiation of time;
M,
C, and
K are the mass matrix, damping matrix, and stiffness matrix of the gear system, respectively;
is the external exciting force with time;
is the nonlinear friction force on the surface of the groove, which can be expressed as the equivalent damping and equivalent stiffness form:
Therefore, from the orthogonality of the mode vector, Equation (1) can be expressed as a linear superposition of the orthogonal mode of the undamped gear system.
where
Φ is the gear system modal matrix;
q is the modal displacement vector.
Taking Equations (2) and (3) into Equation (1) and multiplying
ΦT:
where
I is the unit matrix, and
Z,
Λ,
Zeq,
Λeq are diagonal matrices. When the system vibrates at the
jth natural frequency, the
jth mode is dominant, and the contribution of other modes is negligible. Therefore, Equation (1) can be expressed as:
where
and
are the intrinsic modal damping ratio of the
jth mode of the gear and the equivalent modal damping ratio provided by the ring damper under the
jth mode of the gear, respectively.
and
, respectively, represent the
jth modal stiffness of the gear and the equivalent stiffness of the ring damper under the
jth mode of the gear, and
.
represents the
jth natural frequency (rad/s) of the undamped gear. Both
and
depend on the gear amplitude, and when the amplitude is 0,
,
.
Generally, ring damper mass is much smaller than gear mass, which is a requirement of the dry friction damper. Define damping ring mass rate as:
where
md represents the mass of the ring damper and
mg represents the mass of the gear.
In this paper, ring damper mass rate
β is less than 5%. It should be noted that the mass of the gear and the amplitude of the stiffness matrix are much larger than the magnitude of the nonlinear friction. Therefore,
is much smaller than
This means that the ring damper hardly affects the stiffness and mode shape of the structure, and only touches the amplitude. Therefore, the effect of the ring damper on resonant frequency of the gear is negligible. Other scholars [
4,
5,
7] have also shown that the effect of the ring damper on resonant frequency of the structure is less than 1%. The ring damper mainly reduces the amplitude and vibration loads of the structure by friction energy dissipation.
It can be seen from Equation (5) that the deformation of the gear under static load is
. For a gear system without a ring damper, the response amplitude at the
jth order resonance frequency
qre is:
For a gear with given excitation and damping, the response amplitude
qre in Equation (7) can be obtained by forced response analysis. For a gear system with a damper ring, the response amplitude at the
jth order resonant frequency
qre is:
where the equivalent modal damping ratio
provided by the ring damper is a function of the response amplitude
.
Equation (8) shows that for a particular structure, the resonance peak is proportional to the magnitude of the excitation force and inversely proportional to the modal damping ratio. Under small vibration amplitude (within the linear elastic range), vibration loads are related to the differential of the vibration displacement. For a given mode shape, the amplitude
qre is linear with the vibration loads
σre. Therefore, the relationship among the vibration loads
σ, the excitation amplitude of the
jth order mode of the gear, and the damping ratio can be written as:
where
αj represents the proportional coefficient under the
jth mode, and the proportional coefficient is hardly affected by the damper.
The finite element method is used to analyze the natural vibration characteristics of the gear system. The modal vibration mode and modal stress of the gear are used as reference. The relationship between allowable vibration loads
σa, allowable vibration amplitude
qa, reference modal stress
σref, and reference modal displacement
qref can be obtained:
Through Equation (10), the amplitude-dependent friction damping can be transformed into a relationship with the vibration loads, which facilitates the analysis of the ring damper design.
4. Ring Damper Friction Energy Dissipation Model
The axial displacement equation of the gear damper groove position is:
where
A is the maximum axial amplitude of the damper groove,
θ is the circumferential position,
represents the amplitude as a cosine distribution in the circumferential direction, and
ω0 represents the vibration circle frequency (rad/s).
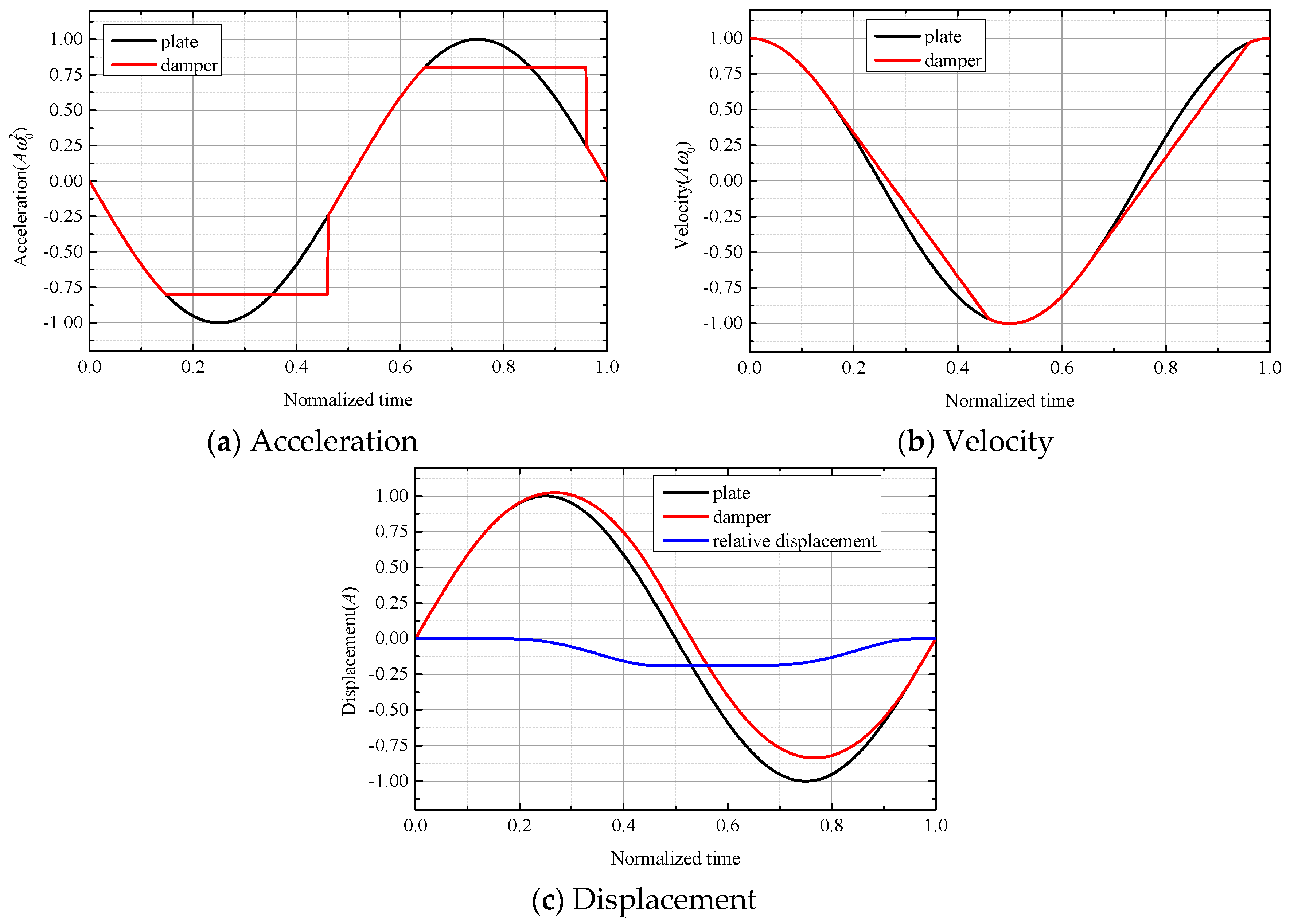
The axial displacement equation of the ring damper is
, and the motion state of the ring damper is determined by the frictional force. The velocity and acceleration of the ring damper in the viscous state are the same as the velocity and acceleration of the gear damper groove position, which can be obtained by the axial displacement equation of the gear groove:
When the acceleration of the damper ring reaches the maximum acceleration provided by the friction force, the motion state becomes a slip:
where
is the angular velocity of gear,
r is the radius of ring damper. Only when
, Equation (35) has a solution.
indicates that the maximum frictional force provided by the contact surface is greater than the frictional force required to maintain the synchronous movement of the ring damper and the gear. The ring damper is subjected to static friction and in a viscous state.
t1 is a function of the circumferential position angle
θ. Since the normalized frictional force of different circumferential positions of the ring damper is variable, the minimum normalized frictional force occurs at the maximum amplitude, defined as:
When the damping ring begins to slip,
k0 = 1, thereby obtaining the critical amplitude under given conditions.
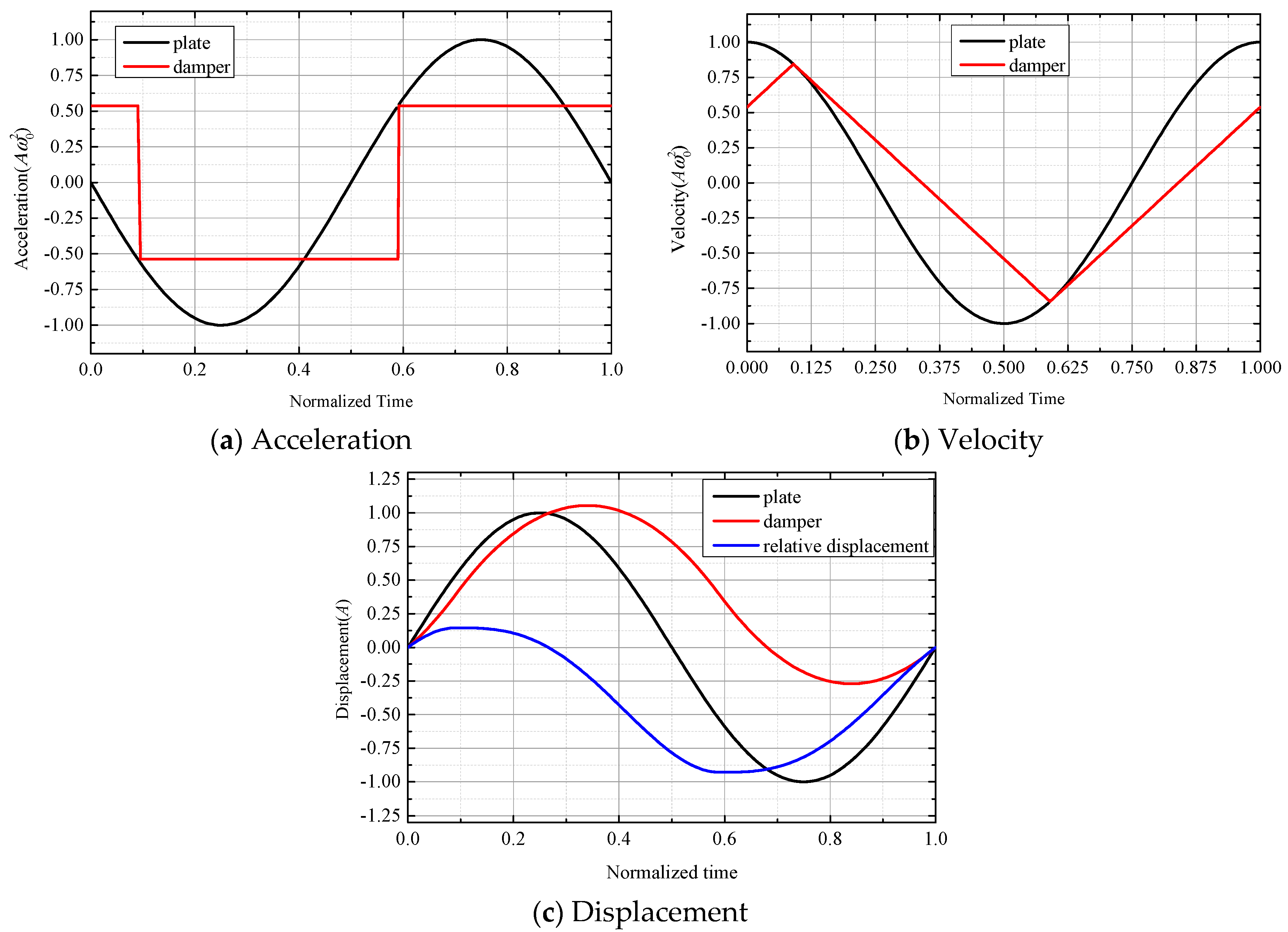
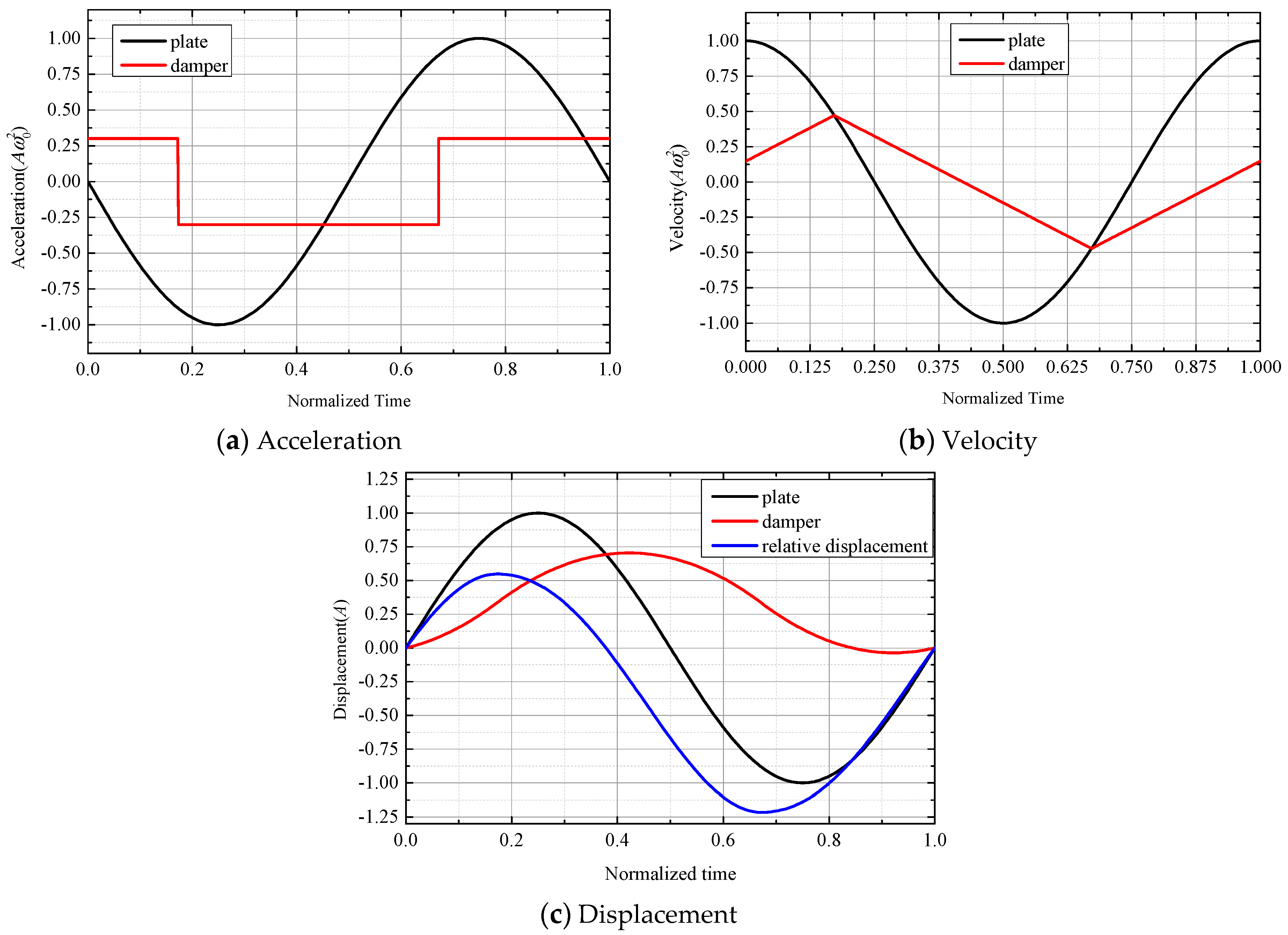
When a slip occurs, the ring damper is subjected to a sliding frictional force, the acceleration is constant, and the velocity and acceleration equations are:
When the velocity of the ring damper is equal to the speed of the gear, the motion state will become viscous again, and .
According to the above equation, the relationship between
and
can be obtained:
When the sliding frictional force is small, there is no viscous state in one vibration cycle, which is called a full sliding state. In this case,
, and:
As the sliding frictional force increases, i.e.,
gradually increases, there is an alternating slip and viscous in a vibration cycle, which is called a viscous-sliding state. In this case, the critical moment of the first slip zone and the viscous zone is obtained by Equation (35):
can be obtained by Equations (39) and (42):
It should be noted that is a transcendental equation and requires numerical solution.
At the critical value of full sliding and viscous-sliding, the
obtained by Equations (41) and (42) are equal, and further obtain:
The relative displacement of the ring damper to the gear at circumferential position
θ can be obtained by integration:
The energy dissipated by the ring damper in one vibration cycle can be calculated by integrating the relative displacement of the circumferential points with the friction product:
is defined as the normalized friction energy dissipation, and
mr is the ring damper mass. The physical meaning of the normalized friction energy dissipation is the ratio of the friction energy dissipation to the maximum kinetic energy of the ring damper. Damping ratio can be expressed as:
where
Meq is the equivalent mass of the gear in a given mode, relating to the vibration form and gear.
where
M represents the physical mass matrix of the gear and
Φ represents the mode matrix.
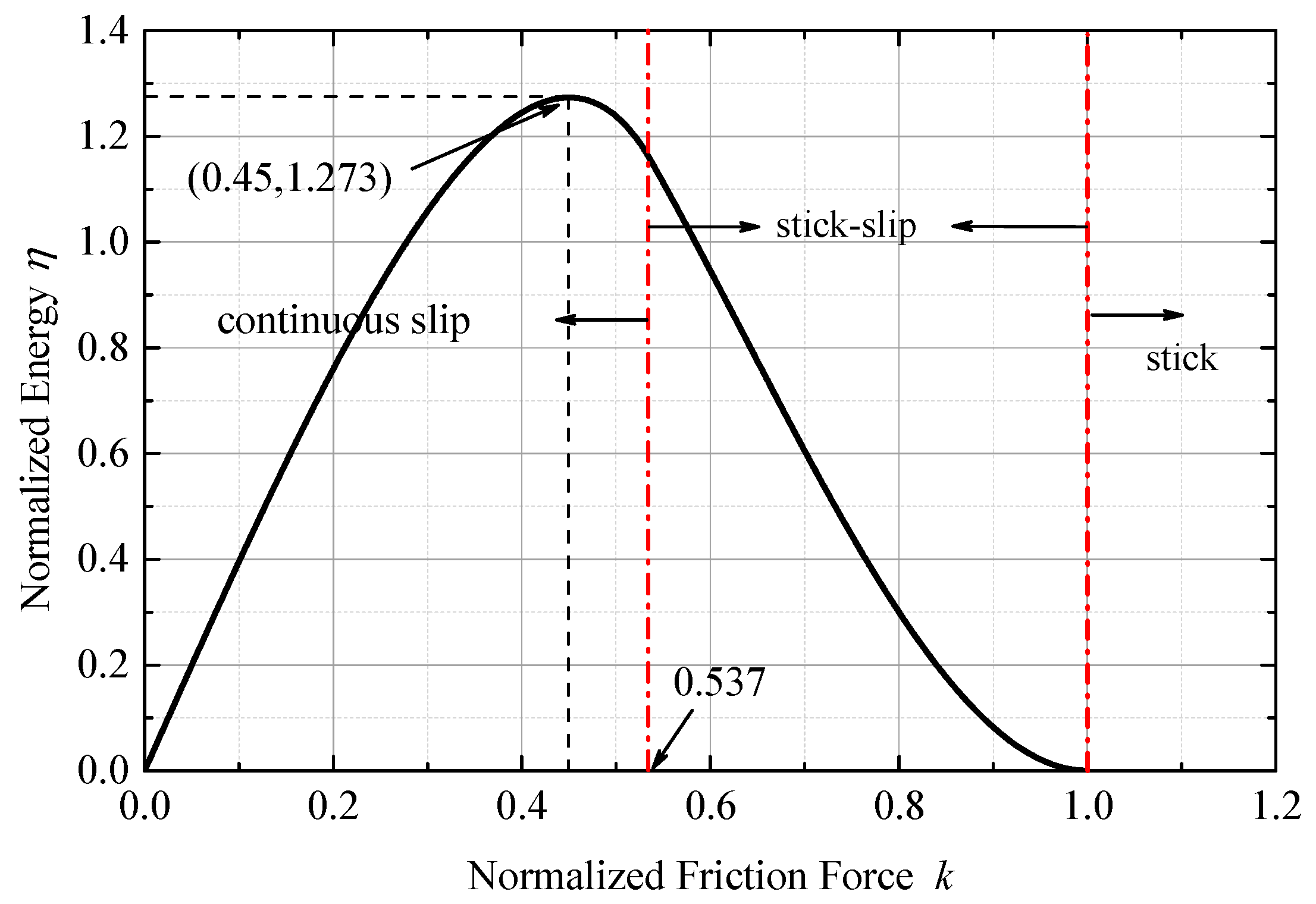
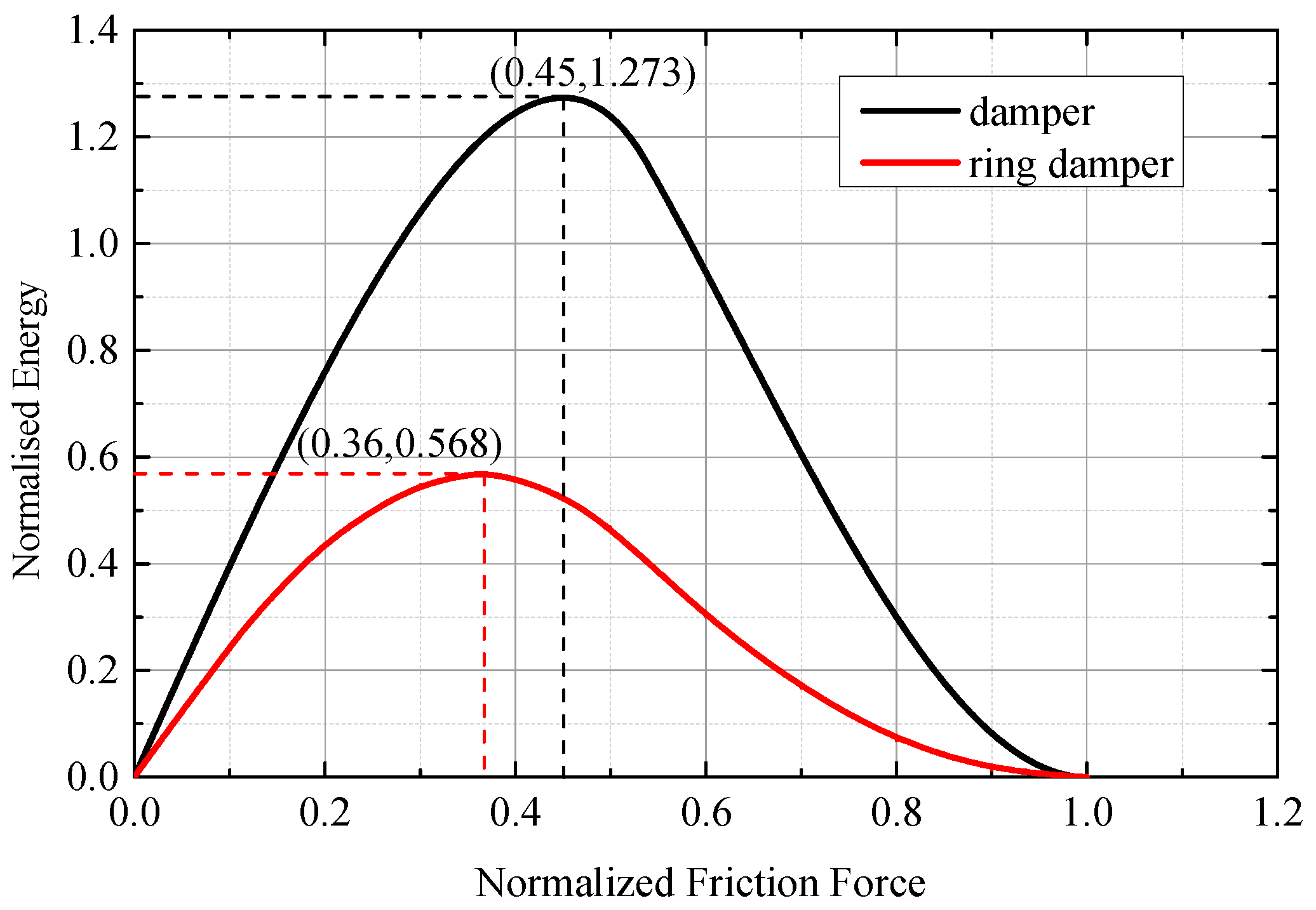
Figure 9 shows the relationship between the frictional force and the energy dissipation of the axial-vibration in the flat plate-slider model and ring damper-gear model. The energy dissipation of the flat plate-slider model was found to be greater. This is because the ring damper has a small amplitude near the nodal line under nodal diameter vibration, and its corresponding normalized frictional force is close to 1 or even greater than 1; thus, friction energy dissipation is little. The ring damper-gear model under axial vibration is similar to the flat plate-slider model, and there is a constant optimal normalized frictional force of approximately 0.365, which is smaller than the flat plate-slider model.
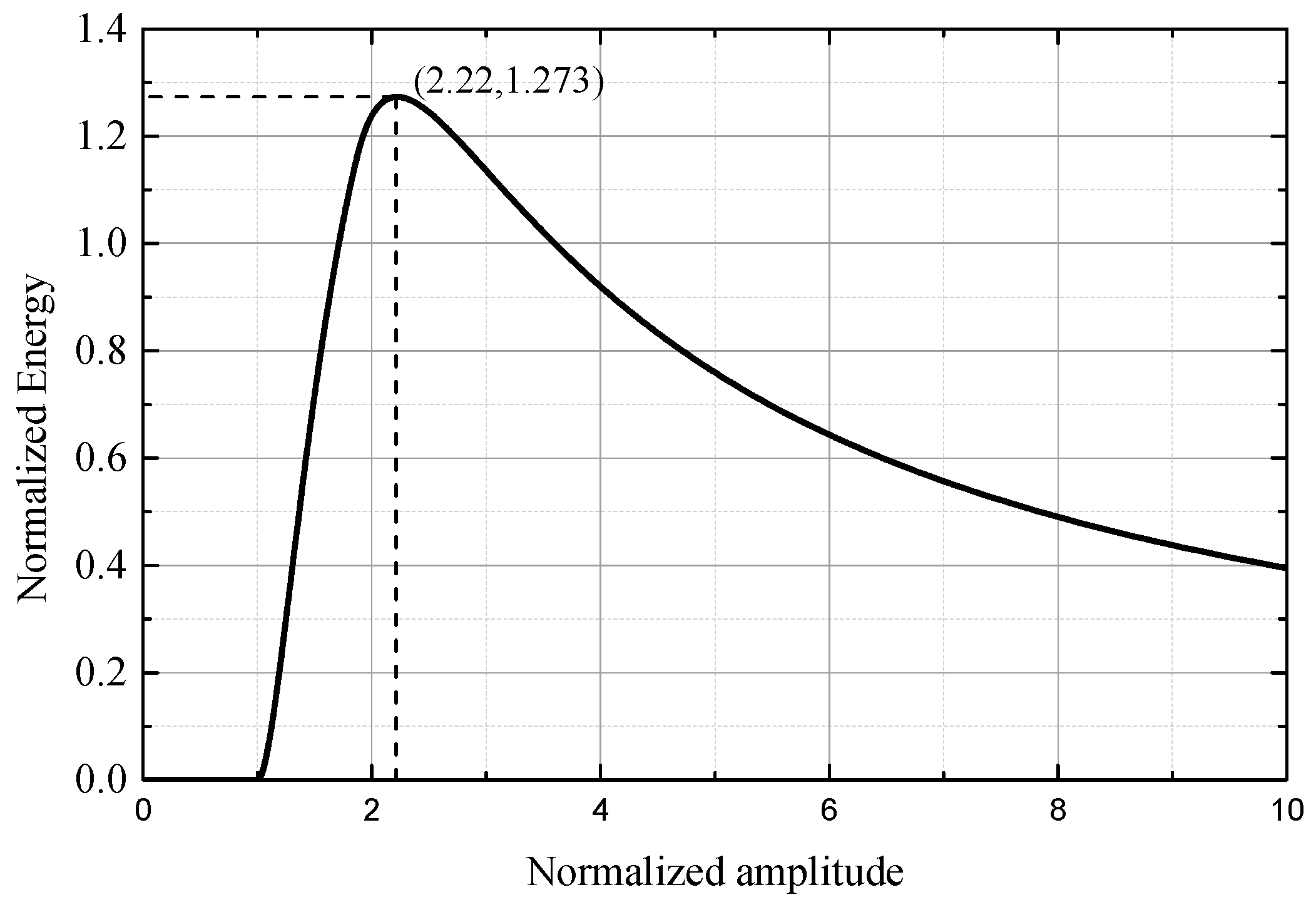
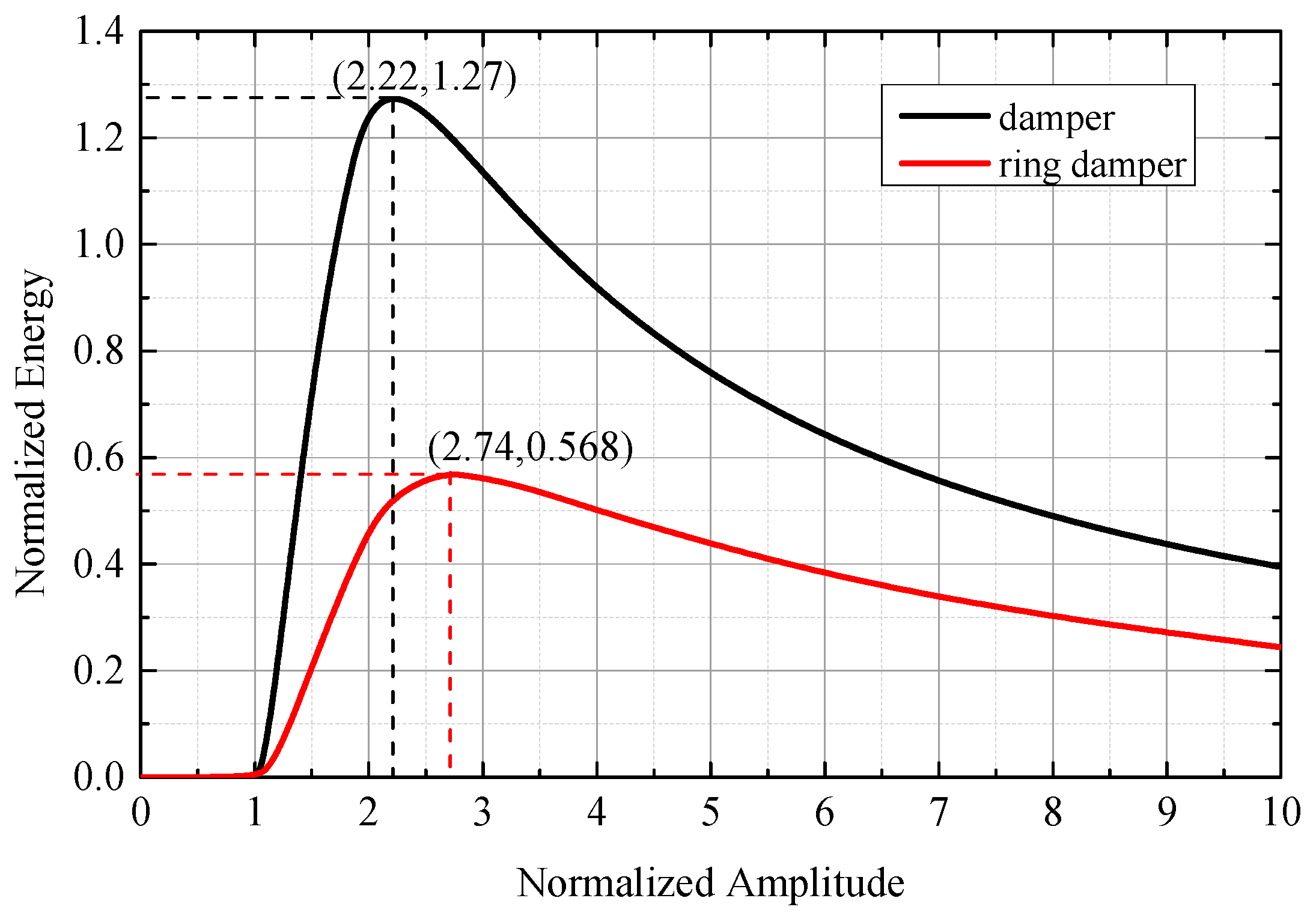
Figure 10 shows the relationship between the amplitude and energy dissipation of the axial vibration in the flat plate-slider model and the ring damper-gear model. The definition of normalized amplitude is the same as above. When the amplitude is small, the acceleration provided by the friction can maintain the non-slip motion between the damper and the main structure, so there is no friction energy dissipation. As the amplitude increases, there is a slip in the damper and the main structure. The friction energy dissipation increases rapidly with the increase of the amplitude. After peak energy dissipation, the increase of friction energy dissipation is smaller than the kinetic energy increase of the damper as the amplitude increases, and the normalized energy dissipation begins to decrease. The optimum amplitude of the flat plate-slider model appears at a critical amplitude of 2.22 times. The optimal amplitude of the ring damper under the nodal diameter axial vibration is about 2.74 times the critical amplitude.
5. Effect of Ring Damper Parameters
In order to discuss the effect of mass and friction coefficient on equivalent damping, a gear model with the following parameters was used: steel, with a density of 7830 kg/m
3, Poisson’s ratio of 0.3 and an elastic modulus of 210 Gpa (room temperature), as shown in
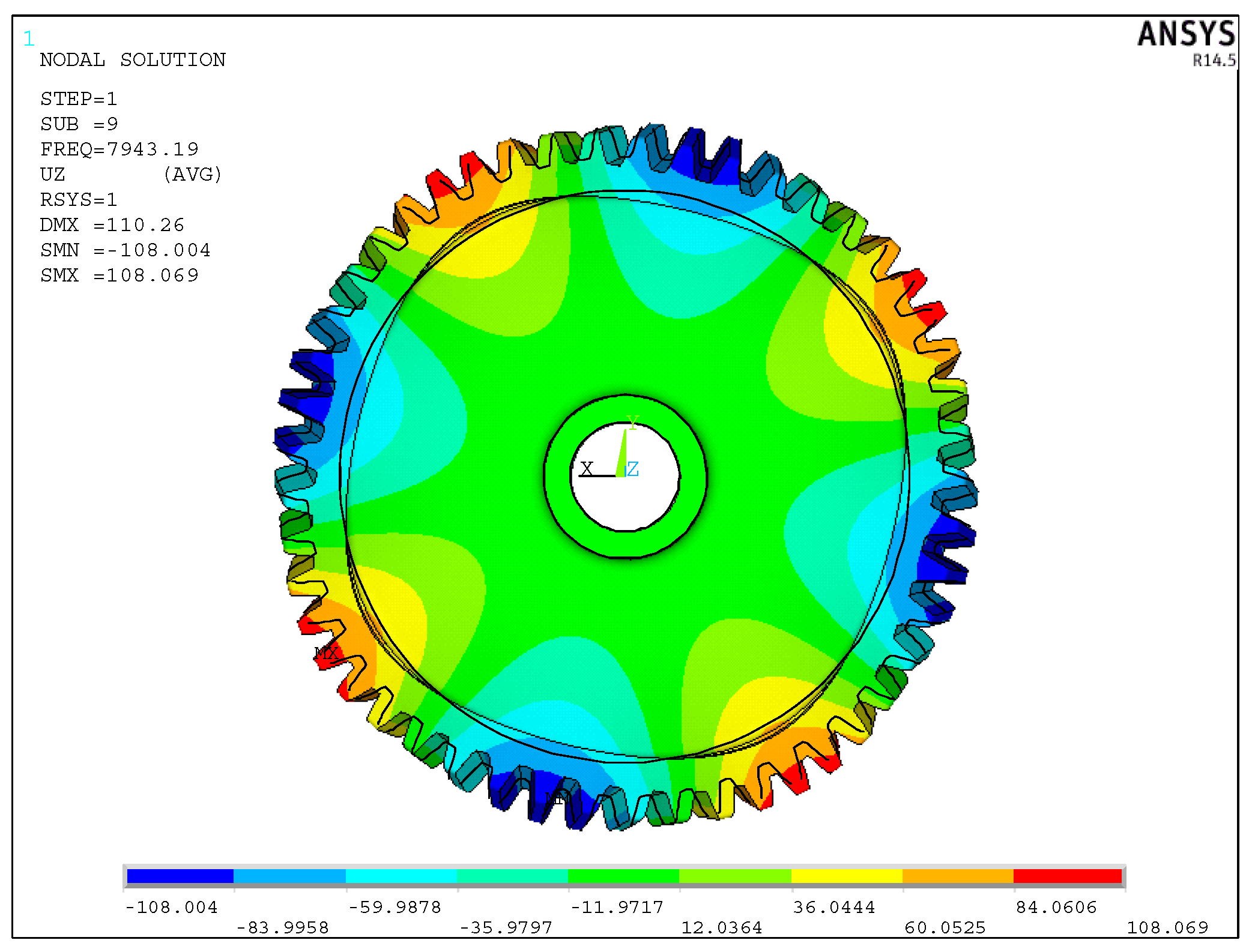
Figure 2a. According to the modal calculation, the gear has a 4 nodal diameter resonance at a working speed of 10,590 r/min; a vibration mode diagram is presented in
Figure 11. Taking the 4 nodal diameter vibration of the gear as an example, the effect of mass on equivalent damping is shown in
Figure 12, and the effect of friction coefficient on equivalent damping is shown in
Figure 13.
Figure 12 shows the effect of the ring damper mass on the equivalent damping. Equation (46) shows that the equivalent damping ratio is positively correlated with its mass. When the ring damper mass is much smaller than the gear mass, the equivalent damping ratio of the ring damper under axial vibration is approximately linear. It can be seen from Equation (37) that the critical amplitude is independent of the mass of the ring damper because the frictional force and inertial force of the ring damper are both proportional to its mass, and the critical amplitude is related to the ratio of the frictional force and the inertial force. Therefore, in the computational model of this paper, the ring damper mass is linear with critical amplitude. Increasing the ring damper mass will be beneficial in increasing its equivalent damping.
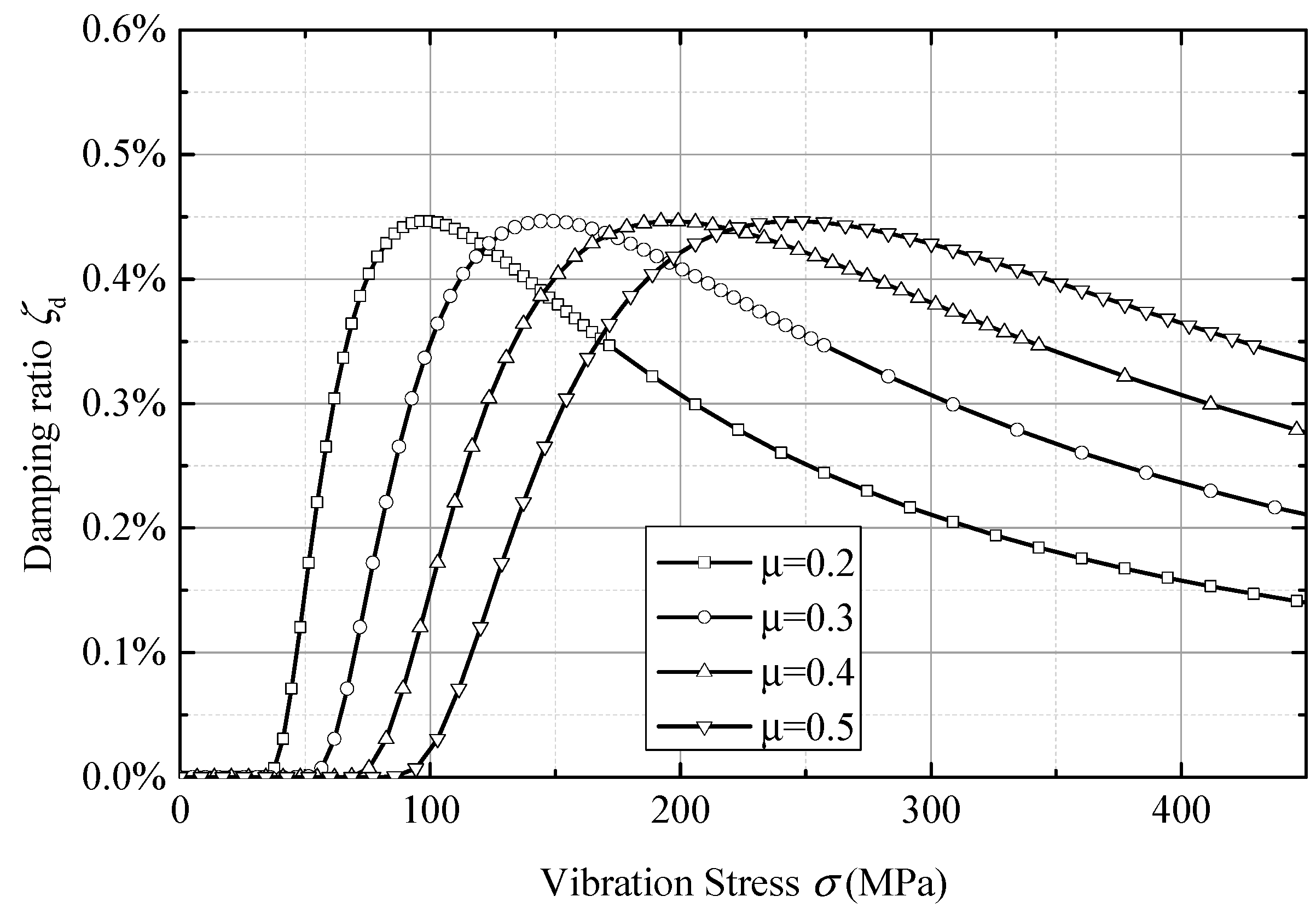
Figure 13 shows the effect of friction coefficient on equivalent damping. The friction coefficient is linear with the critical vibration loads, and does not affect the damping ratio peak. In the ring damper design, the critical vibration load must be less than the allowable vibration load, otherwise the ring damper will lose its damping effect; however, when the critical vibration load is too small, it may cause the ring damper to work on the right side of the damping peak. As can be seen from
Figure 13, on the right side of the damping peak, the damping ratio decreases as the vibration loads increases. Thus, for a vibration state, there is an optimal friction coefficient provided by the ring damper.