1. Introduction
The detailed explanation of a lifetime phenomenon often follows from a deep data analysis based on a well-chosen statistical model. Since the “universal best model” remains an Utopian idea, a lot of effort has been put into the construction of models with different features, involving the development of new probability distributions. The mathematical techniques for creating new probability distributions are numerous. A common technique is to introduce one or several additional tuning parameters to a standard probability distribution, with the aim to improve it, in the theoretical and practical sense. We refer the reader to the following families of distributions: the exponentiated-G (or exp-G) family [
1], the beta-G family [
2], the Marshall-Olkin-G family [
3], the gamma-G family [
4], the Kumaraswamy-G family [
5], the type I half-logistic-G family [
6], the transmuted-G family [
7], the odd power Cauchy family [
8], the exponentiated generalised Topp–Leone-G family [
9], the type II Topp–Leone-G family [
10] and the type II general inverse exponential-G family [
11].
Let us now show some basics of the type II Topp–Leone-G family of distributions introduced by [
10]. The corresponding cumulative distribution function (cdf) and probability density function (pdf) are, respectively, given by
and
where
,
denotes a baseline cdf of a continuous distribution which may depend on a parameter vector
and
denotes the corresponding pdf. In addition to the special cases presented in [
10], recent studies have highlighted the qualities of this family, and its ability to fit data sets by considering new baseline cdf
. See, for instance, [
12,
13] with the consideration of the generalised Rayleigh and Rayleigh distributions as baselines, respectively. There was, however, an area that needed to be explored by considering other kinds of
, which constituted the first piece of the idea of this study.
On the other side of things, with the aim to analyze lifetime data sets at their best, a new two-parameter distribution was introduced by [
14]. It is called the inverted Kumaraswamy distribution. The corresponding cdf and pdf are, respectively, given by
and
where
. This distribution, literally constructed from the inverse of a random variable following the so-called Kumaraswamy distribution minus one (see [
15]), has been proven to be very rich. In particular, deep connexions exist with the so-called Lomax, inverted beta, log-logistic, inverted Weibull and generalised exponential distributions. However, a slight lack of flexibility can be seen in [
14] (Figure 2): the hazard rate function seems to be limited in terms of curvatures (no J shape, no upside-down bathtub shape…). An immediate, elegant way to solve this problem is to extend it by using the simple transmuted technique proposed by [
7]. Hence, the corresponding cdf and pdf are, respectively, given by
and
with
. To the best of our knowledge, this remains a new three-parameter lifetime distribution in the literature. This constitutes the last piece of idea of the study.
That is, we introduce the type II Topp–Leone (transmuted) inverted Kumaraswamy (TIITLIK) distribution defined by combining the type II Topp–Leone-G family and the transmuted inverted Kumaraswamy distribution. We aim to offer a new ultra flexible four-parameter lifetime distribution, combining the qualities of these parents distributions, with a high potential of applicability. New statistical models for sophisticated data sets are the perspectives.
The plan of the paper is the following. In
Section 2, we introduce the TIITLIK distribution, its main functions and some graphics illustrating the behaviour of the corresponding probability density and hazard rate functions. In
Section 3, by the means of two practical data sets and the consideration of the maximum likelihood method, we show that the TIITLIK distribution fits better than well-established and modern adversary models. The details on the maximum likelihood method in the context of the TIITLIK distribution are given in
Section 4, including a simulation study to show the nice numerical performances of the estimates.
Section 5 presents the mathematical properties of the TIITLIK distribution, including asymptotes and critical points of the corresponding pdf and hrf, the quantile function, mixture representations, ordinary and central moments, incomplete moments, weighted probability moments, stress-strength reliability parameter and order statistics. Finally, some concluding remarks are given in
Section 6.
2. TIITLIK Distribution
By adopting the notations above, the cdf of the TIITLIK distribution is given by
with
and
. To illustrate the richness of this cdf, some special cases are described below. When
, we get the cdf of the two exponentiated, transmuted, inverted Kumaraswamy distributions with parameters
a,
b and
. When
, we get the cdf of the Kumaraswamy inverted Kumaraswamy distribution with parameters
,
a and
. When
and
, we get the cdf of the inverted Kumaraswamy distribution with parameters
a and
. All these special cases contain several notable special cases themselves.
The survival function (sf) of the TIITLIK distribution is given by
Upon differentiation of
, the corresponding pdf is given by
The corresponding hazard rate function (hrf) and cumulative hazard rate function (chrf) are, respectively, given by
and
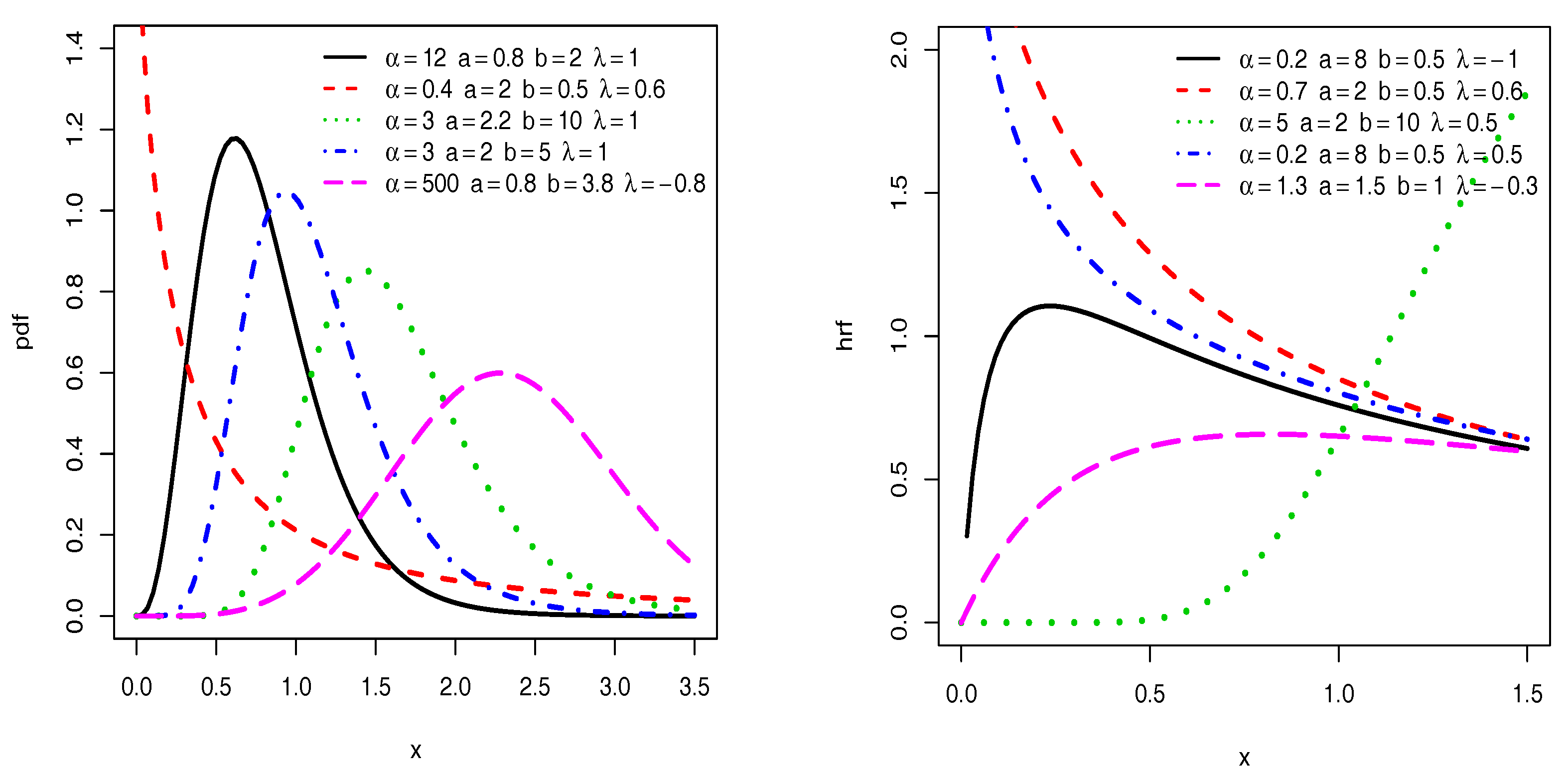
Figure 1 presents plots of the pdf and hrf of the TIITLIK distribution for fixed values of
,
a,
b and
, showing a great diversity in terms of curvature. In particular, the plots of the pdf is left, right skewed, near symmetrical and reverse J shaped, with a notable difference on the right tailed-ness. The plots of the hrf are increasing, decreasing and upside-down bathtub (contrary to the former inverted Kumaraswamy distribution; see [
14] (
Figure 2)). These facts ensure a great ability of the related TIITLIK model to fit a wide variety of practical data sets. This aspect will be developed in detail in
Section 3.
3. Applications
We claim that the TIITLIK distribution has a high potential of applicability. In order to illustrate this claim, we analysed two practical data sets, with fair comparison to useful models in the literature, and discussions. Thus, we compared the TIHLIK distribution with the inverted Kumaraswamy (IK) distribution [
14], generalised inverted Kumaraswamy (GIK) distribution by [
16], Marshall–Olkin extended inverted Kumaraswamy (MOEIK) distribution [
17] and Topp–Leone generalised inverted Kumaraswamy (TLGIK) distribution [
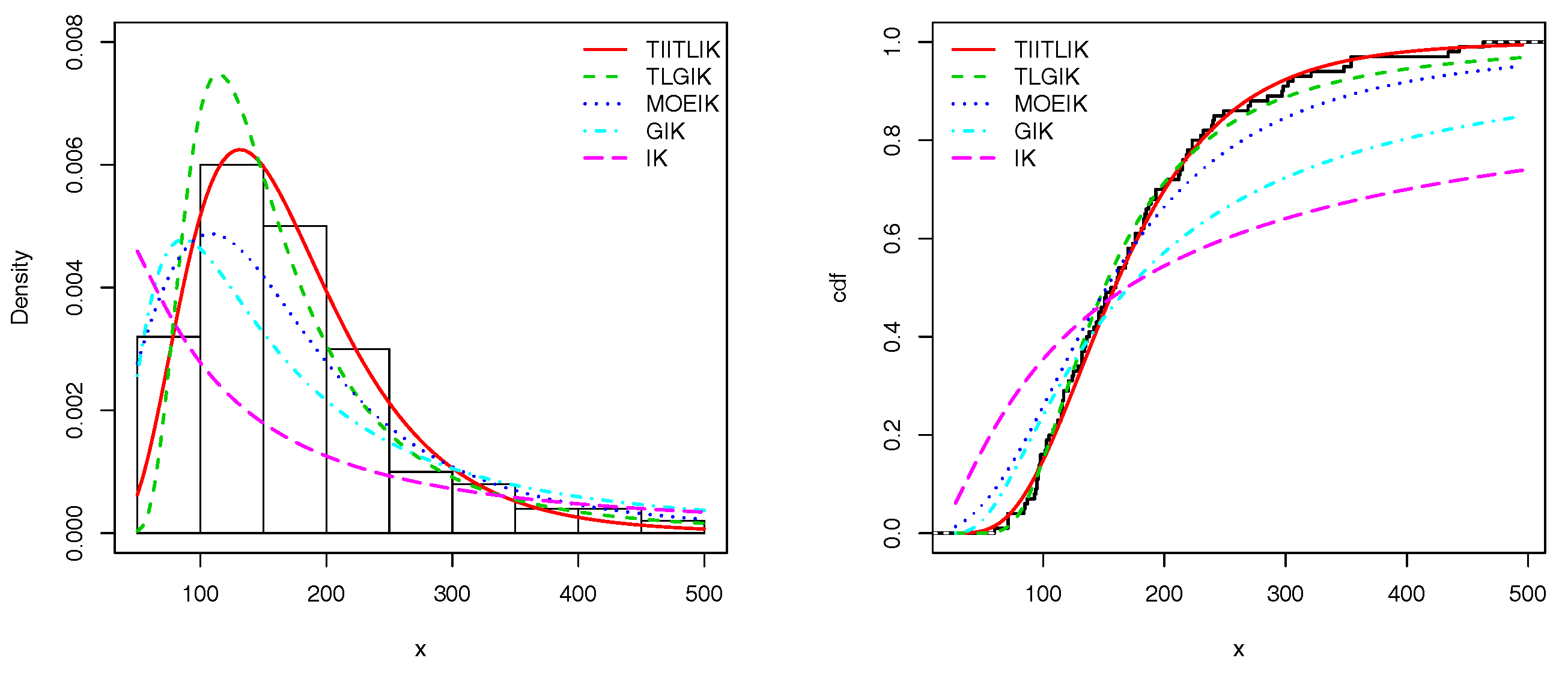
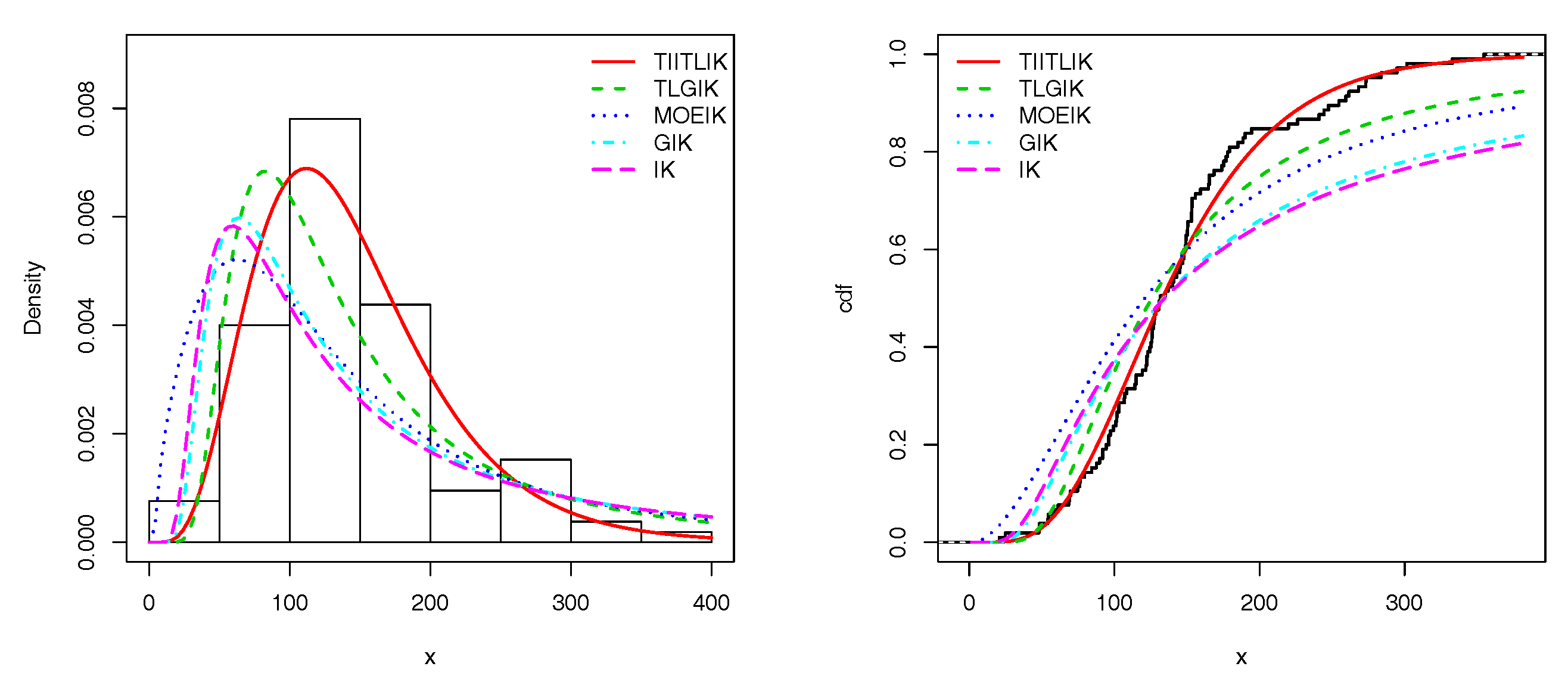
18]. We refer to these papers for the exact definitions of the corresponding pdfs.
We estimated the parameters of the corresponding models by the maximum likelihood method. The estimates, called maximum likelihood estimates (MLEs), were computed using R software with the library
AdequacyModel, in which the function
goodness.fit was used. We refer to
Section 4 for the definitions and theoretical background of the MLEs in the context of the TIITLIK model.
The following statistical measures were calculated: log-likelihood , Akaike information criterion (AIC), Bayesian information criterion (BIC), Anderson–Darling statistic (A*) and Cramer–von Mises statistic (W*). The lower the values of these criteria, the better the fit. We also provide the value for the Kolmogorov–Smirnov (KS) statistic and its p-value.
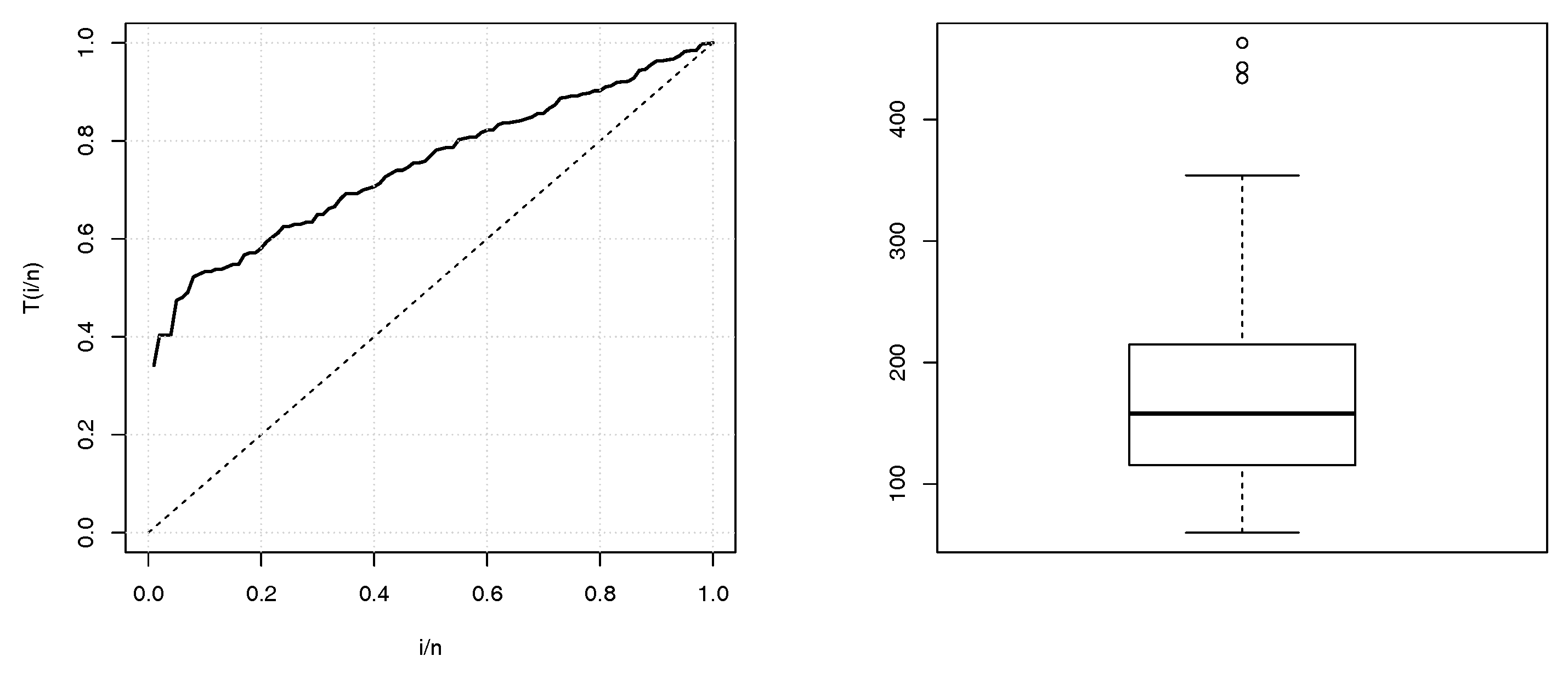
The first data set (data set 1): The first data set, given in [
19], represents the annual maximum precipitation (in inches) for one rain gauge in Fort Collins (Colorado, USA) from 1900 through 1999. The heading of the data is as follows: 239, 232, 434, 85, 302, 174…
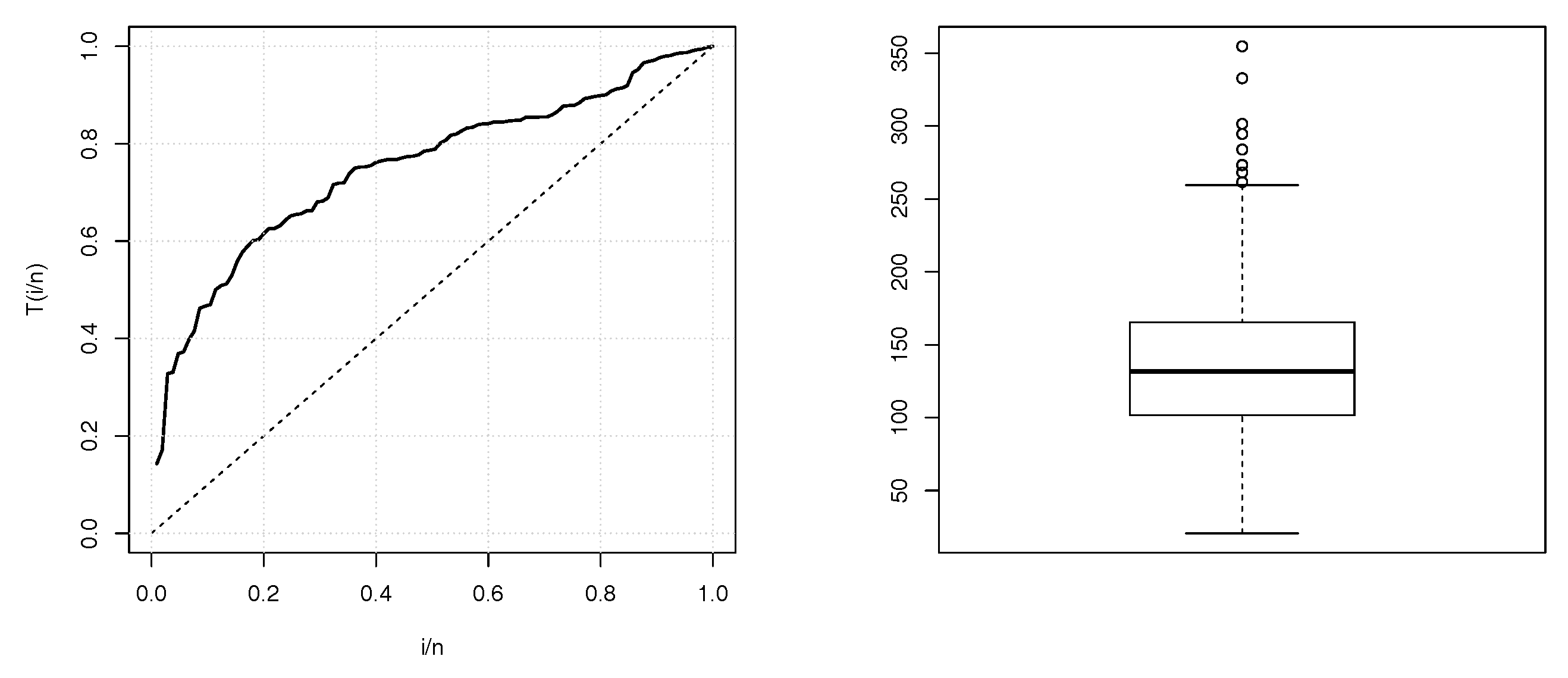
The second data set (data set 2): The second data set consists of annual maximum daily precipitation (in unit: mm) at Busan(Korea) from 1904 through 2011 period. The data set has recently been used by [
20]. The heading of the data is as follows: 24.8, 140.9, 54.1, 153.5, 47.9, 165.5…
Some descriptives statistics of these two data sets are given in
Table 1. The TTT plots and boxplots for data sets 1 and 2 are shown in
Figure 2 and
Figure 3, respectively. From the both TTT plots, we see a concave curve, indicating that the hrf behind the data is possibly increasing. This specificity also belongs to the hrf for the TIITLIK distribution for some values, justifying its consideration for these data sets. Further detail on the TTT plots can be found in [
21]. MLEs and their standard errors (in parentheses) are presented in
Table 2 and
Table 3 for data sets 1 and 2, respectively. The
, AIC, BIC, W*, A*, KS and
p-value values are provided in
Table 4 and
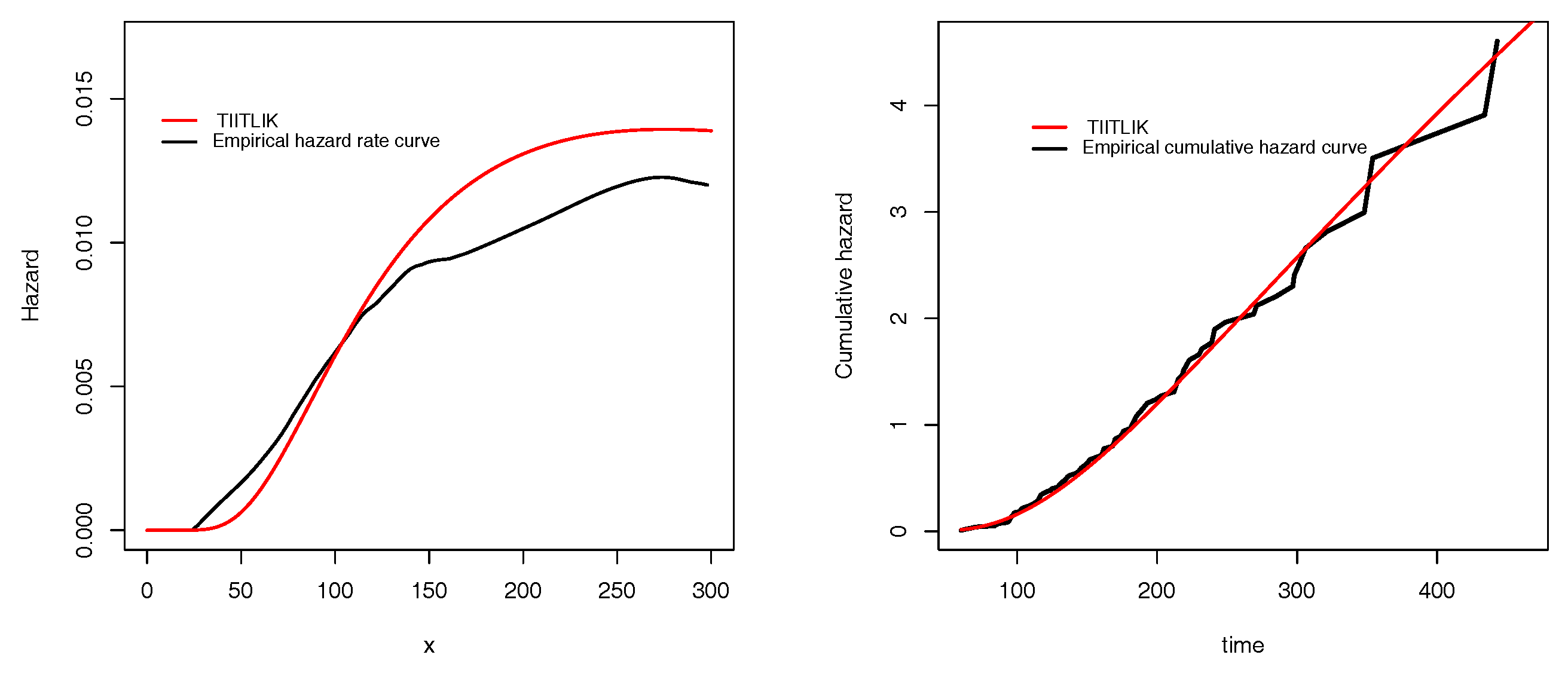
Table 5 for data sets 1 and 2, respectively. In all cases, we see that the TIITLIK is the best. To illustrate this numerical fact with graphics,
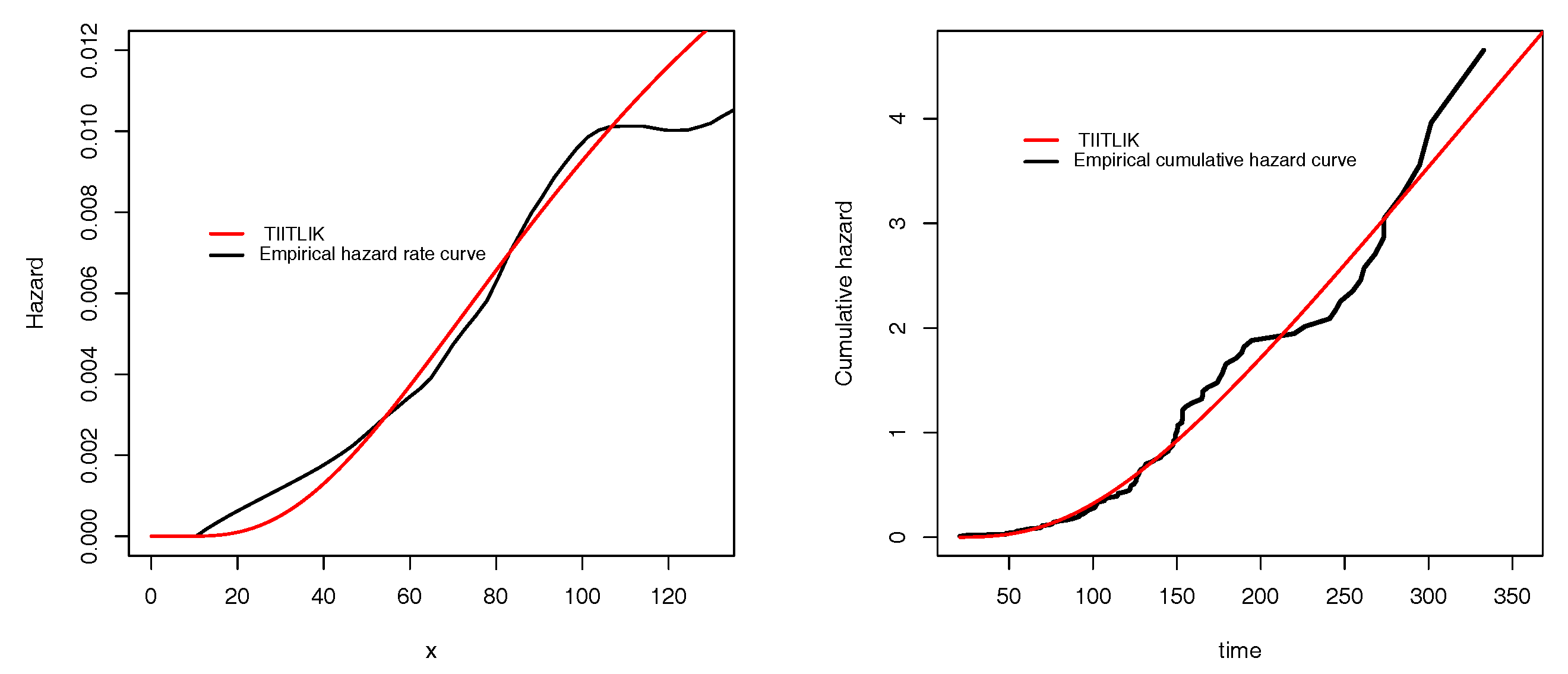
Figure 4 and
Figure 5 present the empirical and estimated TIITLIK, hrfs and chrfs for data sets 1 and 2, respectively. Also,
Figure 6 and
Figure 7 show the estimated pdfs for data sets 1 and 2, respectively. For these four last figures, nice fits are observed for the TIITLIK distribution, attesting its applicability for these data sets.
5. Mathematical Properties
After the practical aspect, this section is devoted to the main mathematical properties of the TIITLIK distribution. Hereafter, we consider a random variable
X following the TIITLIK distribution; i.e., having the cdf given by (
1) and the pdf given by (
2).
5.1. Asymptotic Results and Critical Points
Some asymptotic results and critical points of the main functions of the TIITLIK distribution are presented below. When
, by using standard equivalence formulas, we get
and
Hence, the limits of these functions mainly depend on
b. When
, we get
; when
, we obtain
; and when
, we get
. Similarly, when
, we get
; when
, we obtain
; and when
, we get
.
Now, when
, we get
and
Hence, in all cases, we have and . We would like to mention that plays no role for these asymptotes.
Let us now study the critical points of
and
. The critical point(s) of
is(are) given by the solution(s) of the following equation:
(the derivative is according to
x), where
Then, a critical point
of
satisfies the following equation:
The nature of can be determined by investigating the sign of . Due to the complexity of these equations, for given values of , a, b and , one can make use of mathematical software to determine : R, Mathematica, Matlab, etc.
Similarly, the critical point(s) of
is(are) given by the solution(s) of the following equation:
. If such a critical point is denoted by
, it satisfies the following equation:
Again, the nature of can be determined by investigating the sign of .
5.2. Quantile Function
The quantile function (qf) of
X, say
, is characterised by the following equation:
,
. After some algebra, we obtain
Several quantities can be defined via the quantile function. For instance, the second quartile (median) is given by and the inter-quantile range can be expressed as .
Also, one can generate values from
X by using the following result. Let
, where
U denotes a random variable following the uniform distribution
. Then,
follows the TIITLIK distribution. This result was used in
Section 4.2.
5.3. Bowley Skewness and Moors Kurtosis
The Bowley skewness and Moors kurtosis of
X are defined by, respectively,
and
Here,
S is a measure of the asymmetry of the TIITLIK distribution and
K is a measure of whether the TIITLIK distributions are heavy-tailed or light-tailed (relatively to a normal distribution). These measures have the advantage of always being well-defined from the mathematical point of view, contrary to other skewness and kurtosis measures (based on moments, for instance). More detail can be found in [
22] for the Bowley skewness and [
23] for the Moors kurtosis.
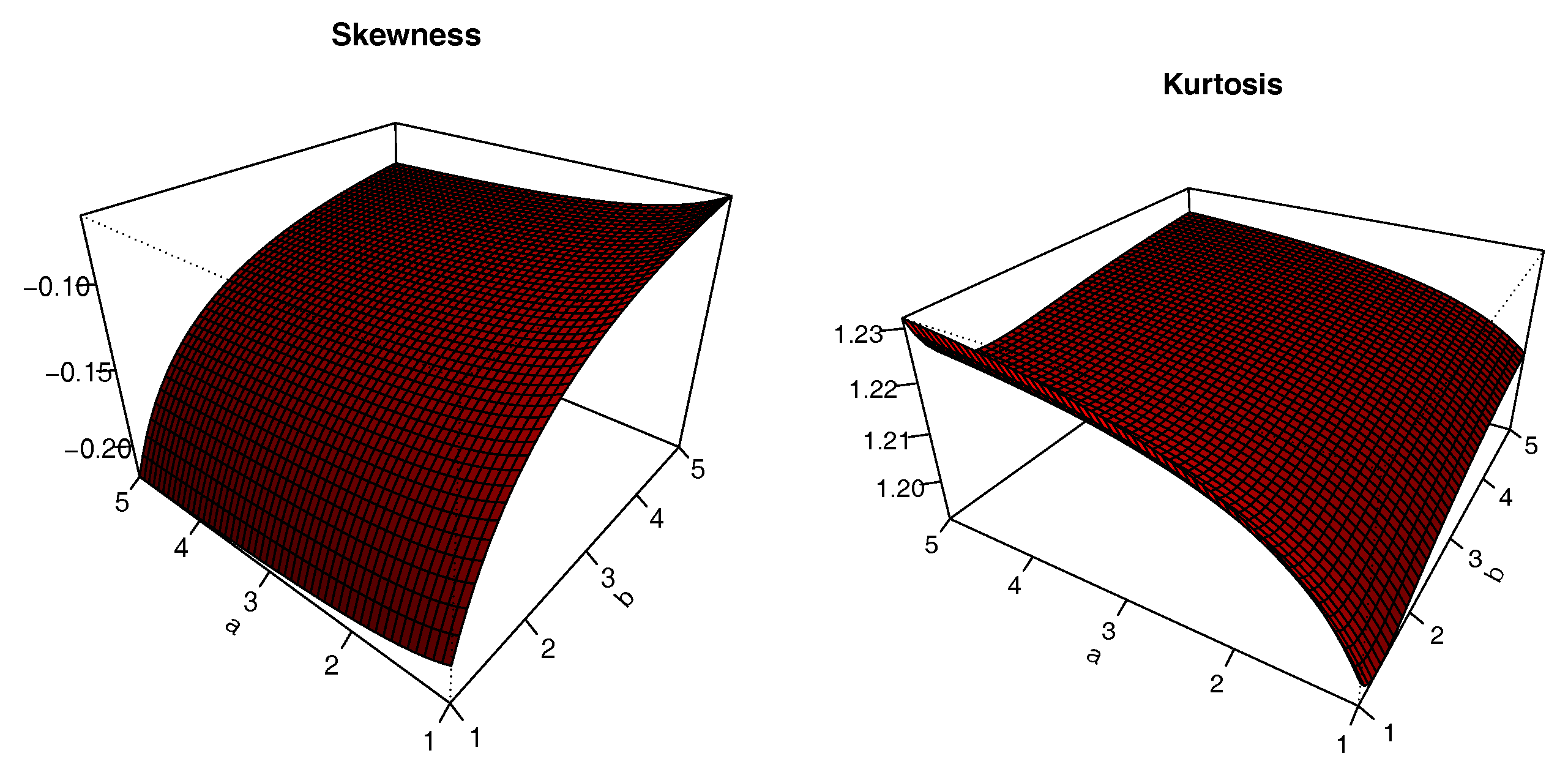
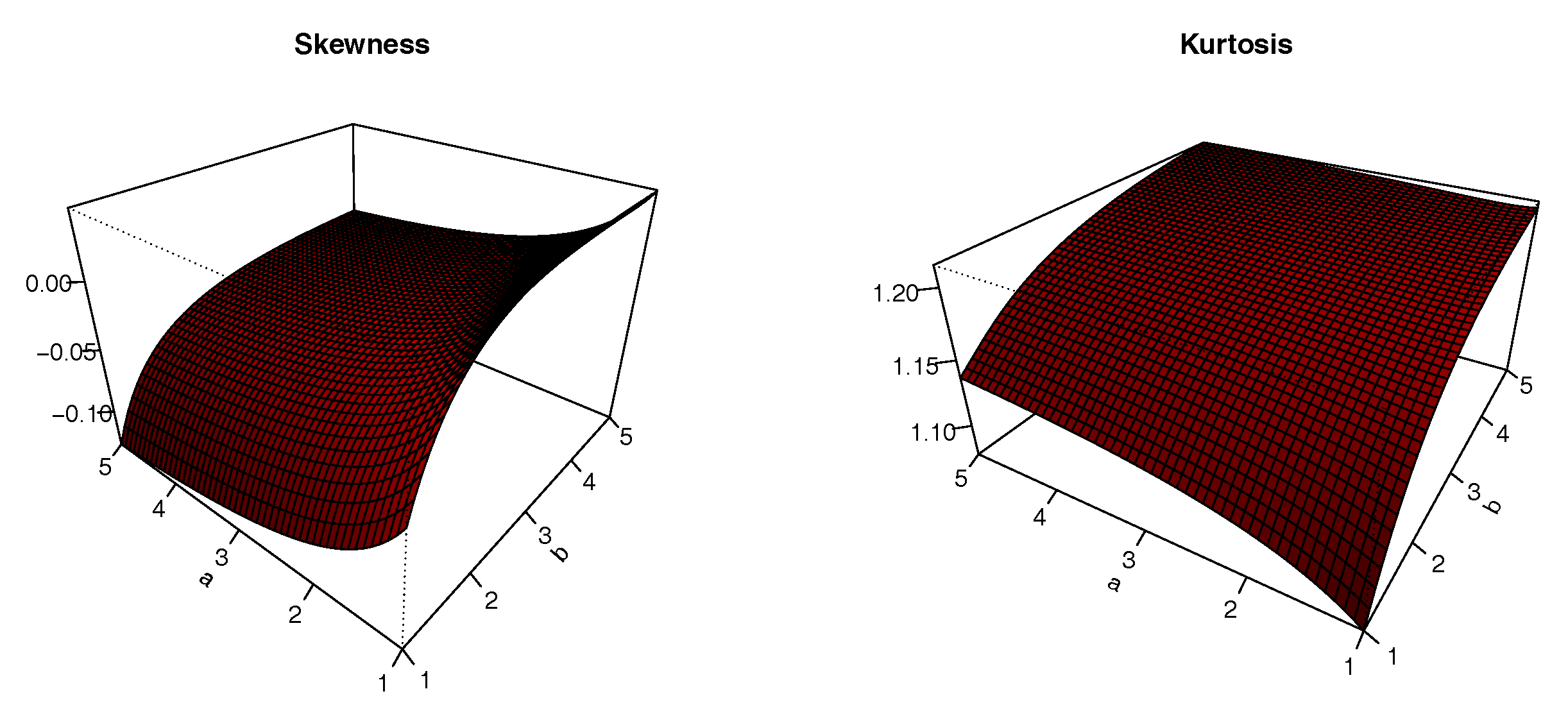
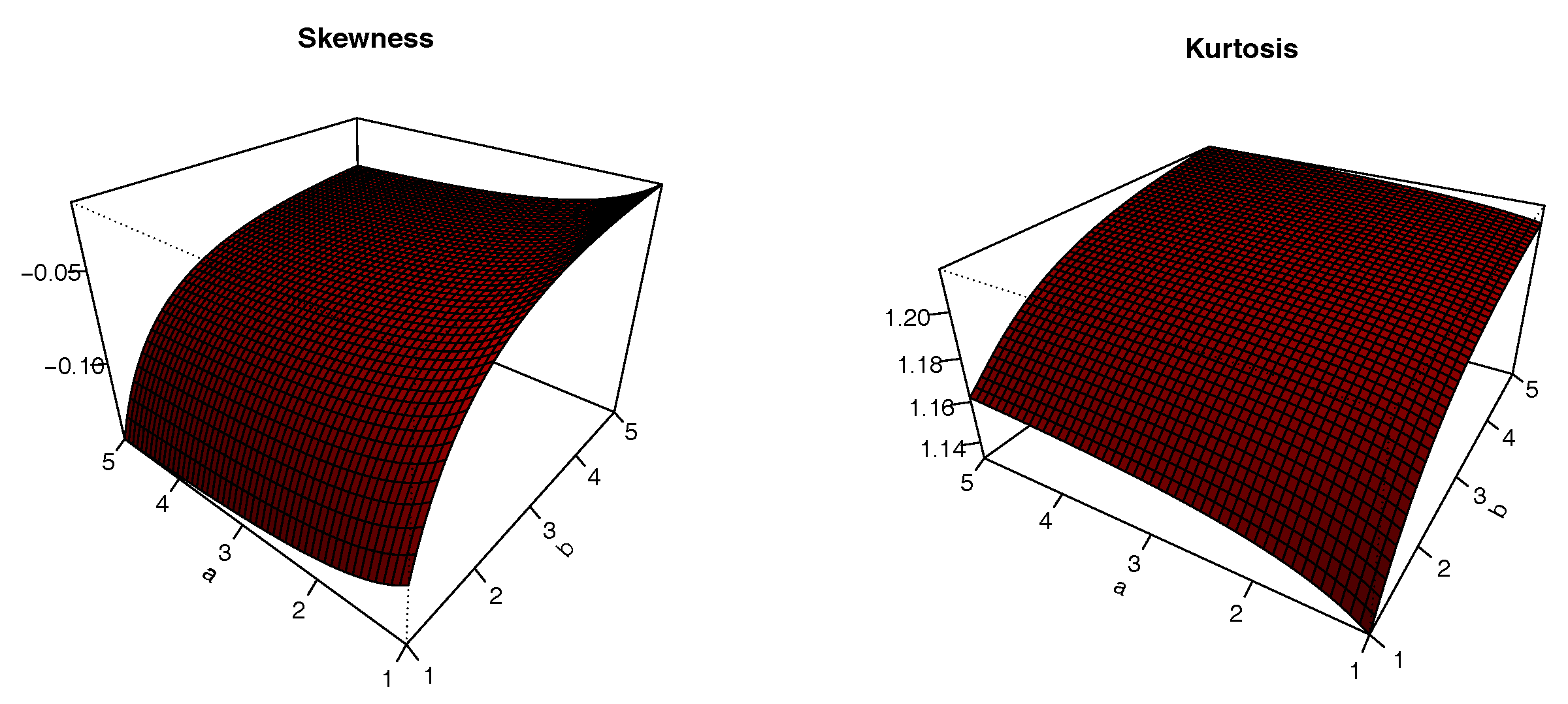
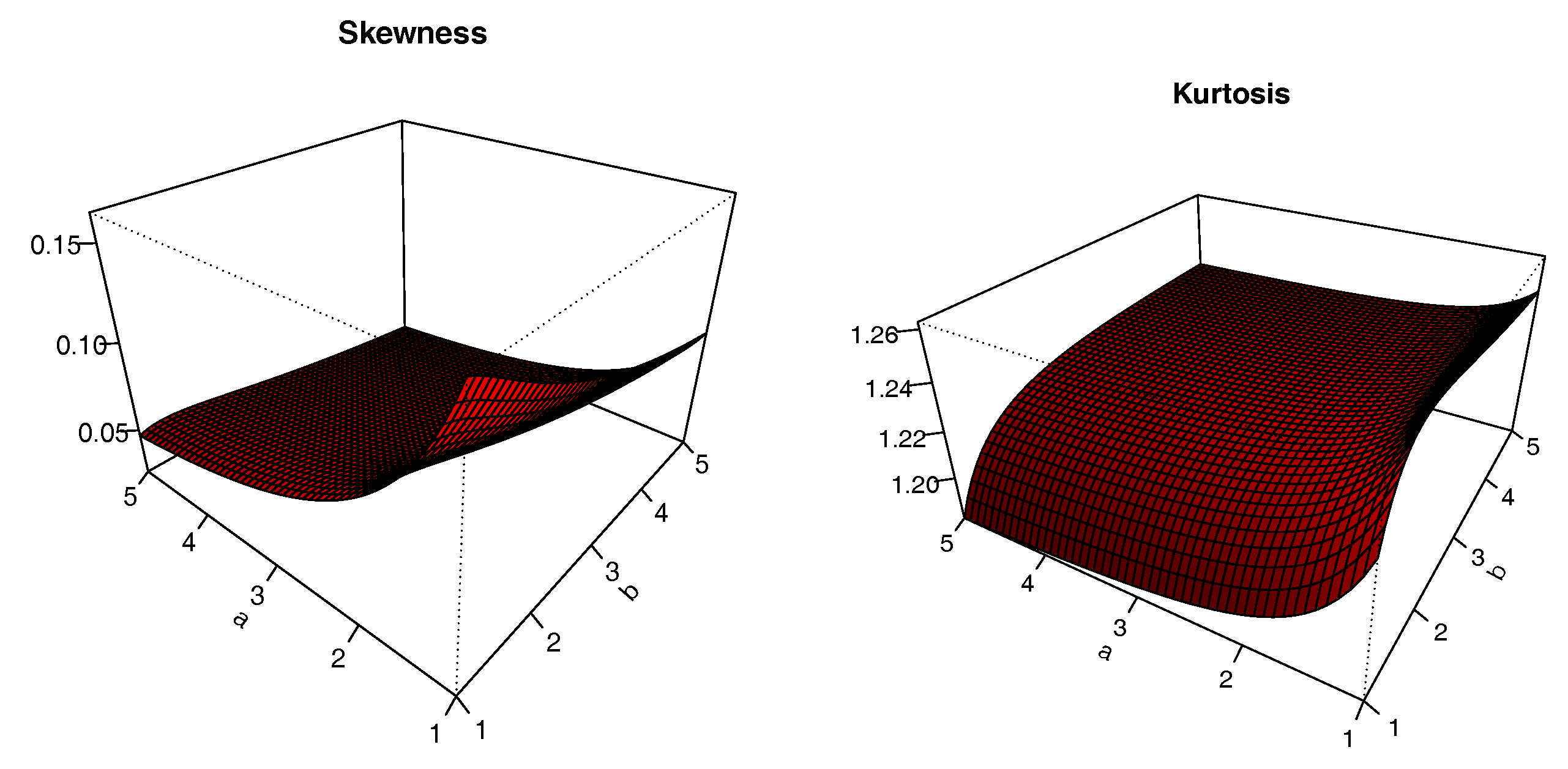
The plots of
S and
K are presented in
Figure 8,
Figure 9,
Figure 10 and
Figure 11 for
,
and varying values for
; i.e.,
. The impacts of the values of the parameters on
S and
K are significant; we can see that
S can be both positive and negative, with complex variations. Similarly,
K either increases or decreases, depending on the values of the parameters.
5.4. Mixture Representations
The three following results present a mixture of representations of some functions of the TIITLIK distribution in terms of Lomax distribution functions. In the proofs, for the sake of simplicity, we adopted the notation introduced in
Section 1.
Proposition 1. The following is a mixture representation for :where , (with ) and denote the sf of the Lomax distribution with parameters and 1; i.e., . Proof. Since
(excluding the limit points), the generalised binomial formula gives
Furthermore, it follows from the standard binomial formula that
Since
, by applying again the generalised binomial formula, we have
We end the proof by combining the above equalities together. □
Proposition 2. We have the following mixture representation for :where is defined as in Proposition 1 and denotes the pdf of the Lomax distribution with parameters and 1, i.e., . Proof. The result follows from differentiation of the mixture expansion of established in Proposition 1. □
Owing to Proposition 2, we can exploit the properties of the Lomax distribution to derive new properties for the TIITLIK distribution. This methodology will be used in the next subsections.
Proposition 3. Let ξ be a positive integer. Then, we have the following mixture representation:where and denotes the pdf of the Lomax distribution with parameters and 1. Proof. We will investigate a mixture representation for
first, then consider the relation:
. Thus, it follows from the standard binomial formula that
Since
, the generalised binomial formula gives
Then, we should proceed as in the proof of Proposition 1. The standard binomial formula gives
and, by the generalised binomial formula using
, we get
By putting the above equalities together, we get
where
. Upon differentiation of this series expansion, we get
where
, which is the desired result. □
5.5. The Ordinary and Central Moments
Let
r be a positive integer. Then, the
r-th moment of
X, i.e.,
, exists if, and only if,
. Under this assumption, we have
For given values of
,
a,
b and
, this integral can be evaluated by any mathematical software. Additionally, one can use Proposition 2 for a series expression, which is performed below. Let us introduce the gamma function defined by
,
. Then, by assuming that
and noticing that
we obtain
For practical purposes, one can consider a large integer
K, says
, and the approximation:
therefore, assuming that
, the mean and the variance of
X are given by, respectively,
and
.
Always under the assumption
, the
r-th central moment of
X, i.e.,
, exists. It is given by
The standard binomial formula gives
One can notice that
. Additionally, important quantities can be derived, such as the
r-th cumulant of
X defined by
with
, and the Pearson measures of skewness and kurtosis of
X defined by
and
, respectively.
5.6. Incomplete Moments
Let
and
r be positive integers. Then, the
r-th incomplete moment of
X, i.e.,
exists and is given by
For given values for
t,
,
a,
b and
, a numerical evaluation of the integral term is possible. Incomplete moments appear naturally in several useful quantities. For instance, the mean deviations of
X about the mean and the median use
; i.e.,
One can also construct Lorenz and Bonferroni curves, which find applications in economics, insurance and medicine, among others.
5.7. Weighted Probability Moments
Let
r and
s be two positive integers. Then, the
-th weighted probability moment for
X, i.e.,
exists if, and only if,
. It is defined by
It follows from Proposition 3 applied with
that
The probability weighted moments naturally appear when we deal with some natural statistics, as order statistics. Further details will be presented in
Section 5.9.
5.8. Stress–Strength Reliability Parameter
Let X and Y be independent random variables having the TIITLIK distribution with the sets of parameters and , respectively. Then, the corresponding stress-strength reliability parameter is defined by . We should then determine it with several sets of assumptions on the parameter. We begin with a tractable result in that regard.
Proposition 4. Under the above setting, assume that , and . Then, we have Proof. By using the definitions of
and
, we get
The proof of Proposition 4 is ended. □
The result below proposes a more general alternative result.
Proposition 5. Without special assumptions on the parameters, we havewhere, for , . Proof. Owing to Propositions 1 and 2, we have
Then, by introducing the pdf
of the Lomax distribution with parameters
and 1, we get
This ends the proof of Proposition 5. □
5.9. Order Statistics
Since the former study of [
24], order statistics found a place as the model of choice for various phenomena dealing with the infima or suprema of random variables. Here, we present some basics on the order statistics in the context of the TIITLIK distribution. Let
be
n independent random having the TIITLIK distribution as the common distribution and
be the
i-th order statistic defined by the
i-th random variable; i.e.,
after rearranging
in an increasing order. Then, the pdf of
is given by
Owing to Proposition 3 applied with
, we obtain the following mixture representation:
where
and
denotes the pdf of the Lomax distribution with parameters
and 1.
Let
r be a positive integer. Then, the
r-th moment of
is given by
Among others, these moments can be used to define the L moments of
X. Thus, for any
, the
s-th L moment of
X is given by
We refer the reader to [
25,
26] for further details on
L moments.
6. Conclusions
In this paper, we introduced a new, four-parameter lifetime distribution called the type II Topp–Leone (transmuted) inverted Kumaraswamy (TIITLIK) distribution. Two applications on practical data sets showed that the TIITLIK distribution provides better fits than several serious competitors, validating its potential in terms of applicability. In order to complete the practical aspect, we provided the main mathematical properties of the new distribution, including asymptotic results, quantile function, Bowley skewness and Moors kurtosis, mixture representations for the probability density and cumulative density functions, ordinary moments, incomplete moments, probability weighted moments, stress-strength reliability and order statistics.