Study of Indoor Ventilation Based on Large-Scale DNS by a Domain Decomposition Method
Abstract
:1. Introduction
2. Methods
2.1. Governing Equations
2.2. Characteristic Finite Element Scheme
2.3. Domain Decomposition Method
3. Numerical Simulation
3.1. DDM for large scale computation
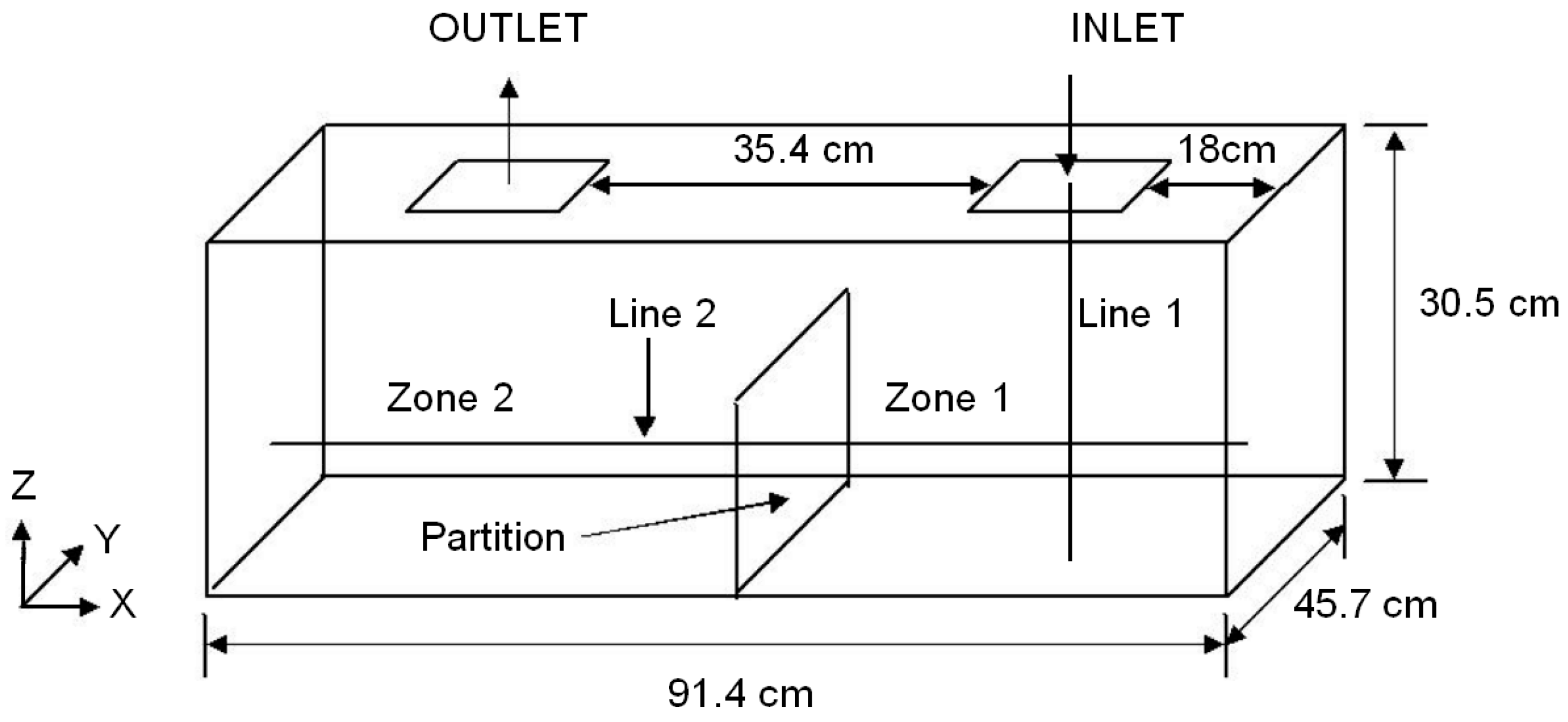
3.2. An Indoor Ventilation Model
3.3. Parameters and Conditions
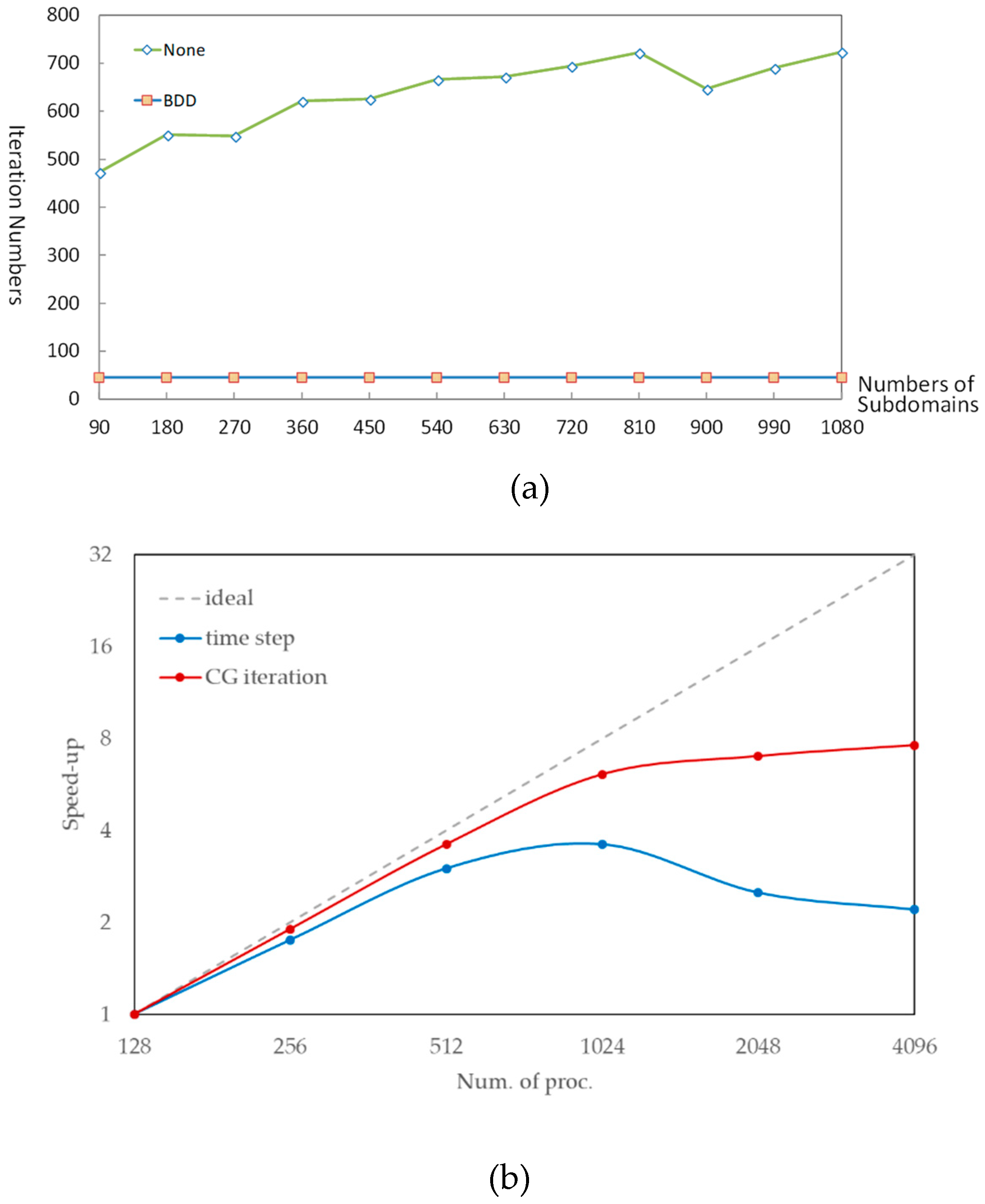
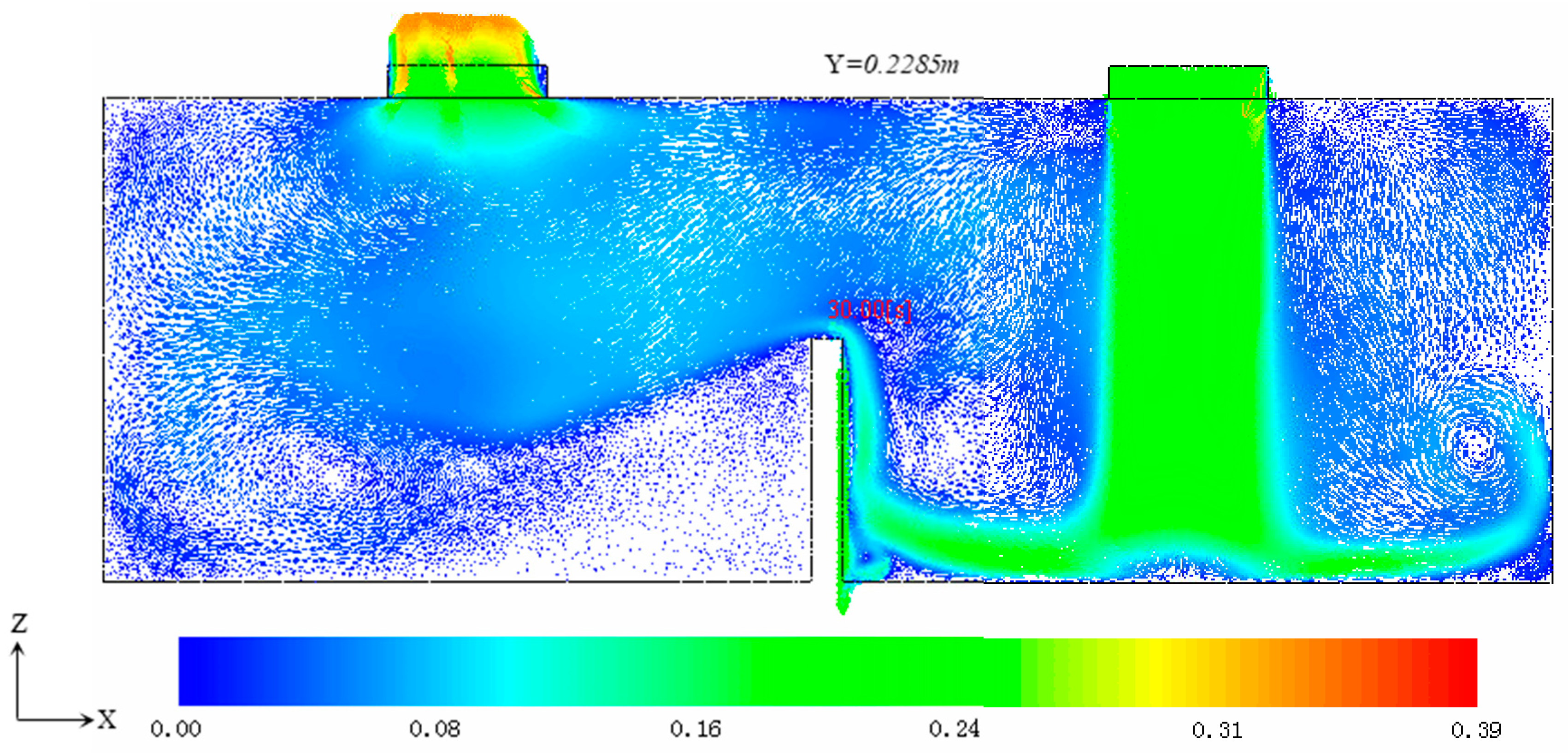
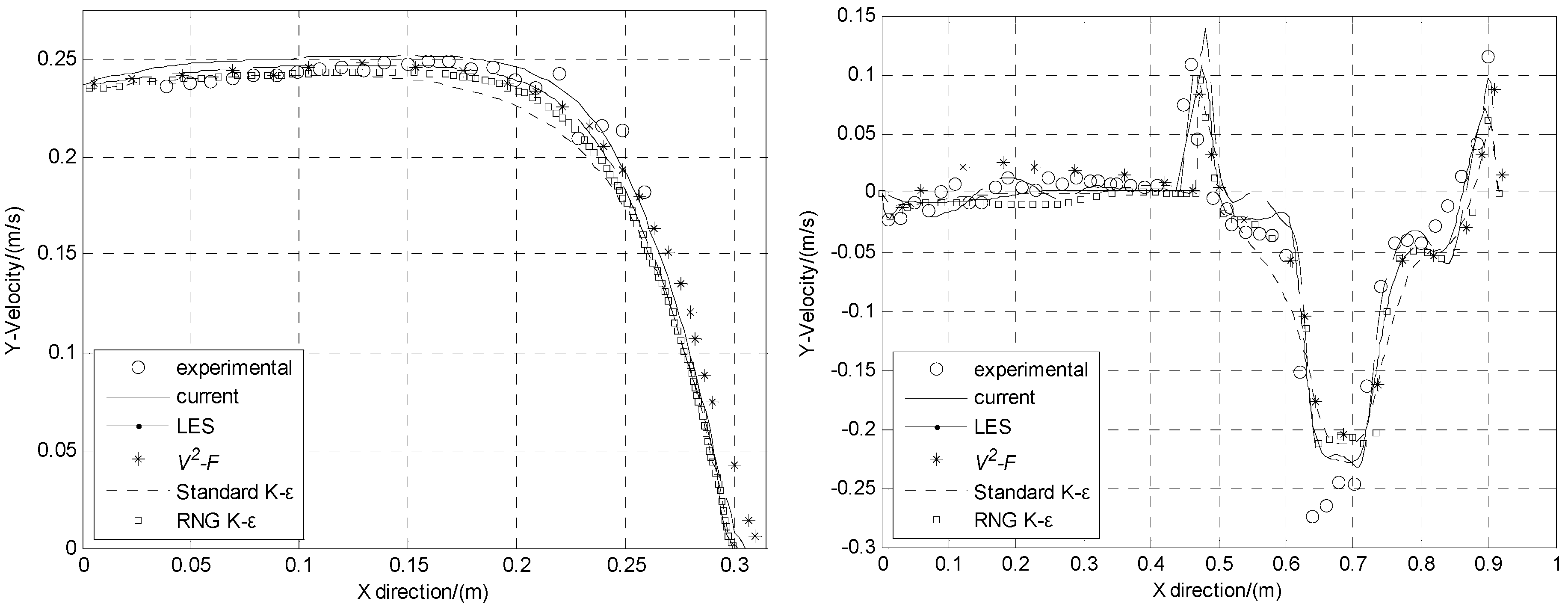
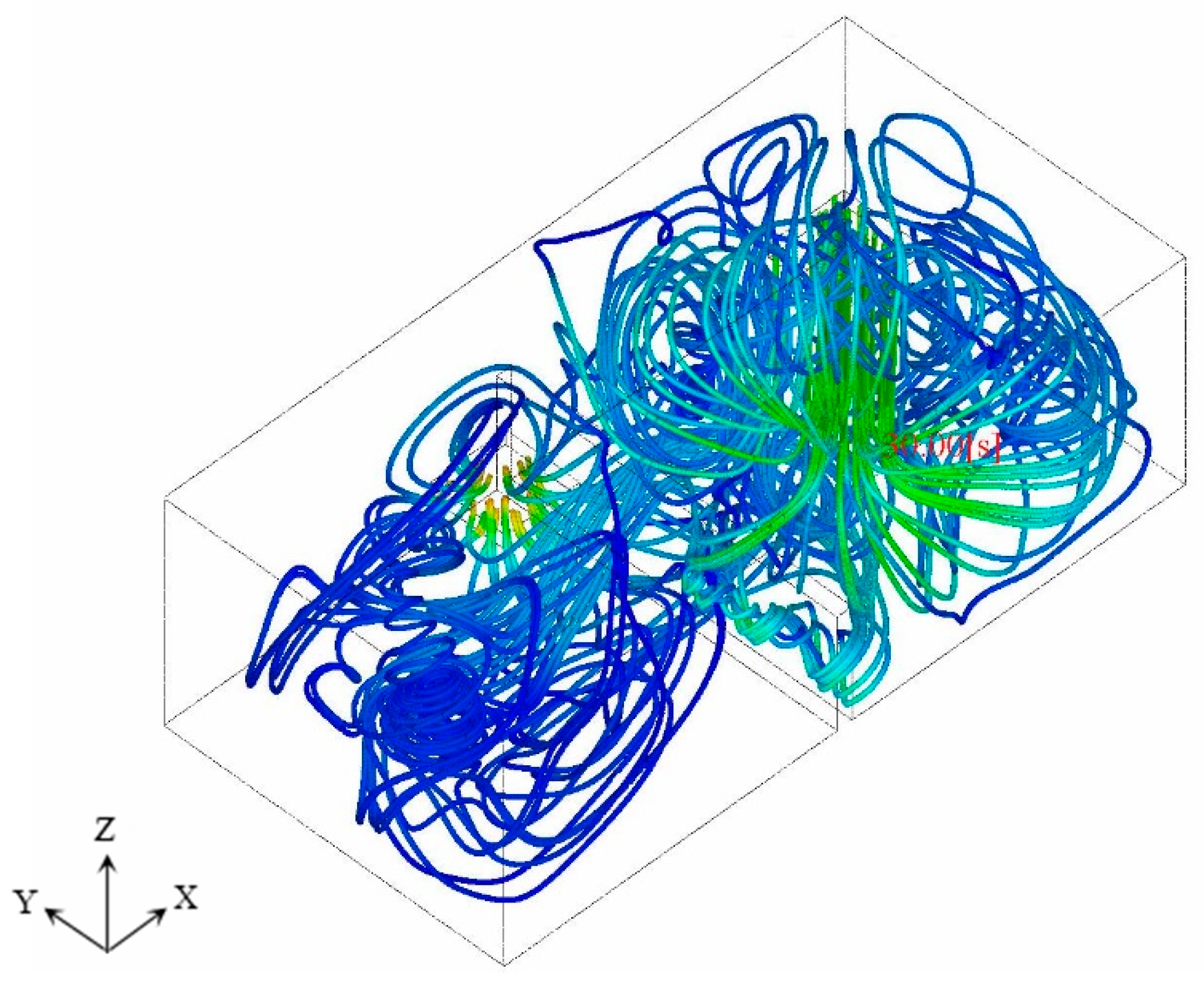
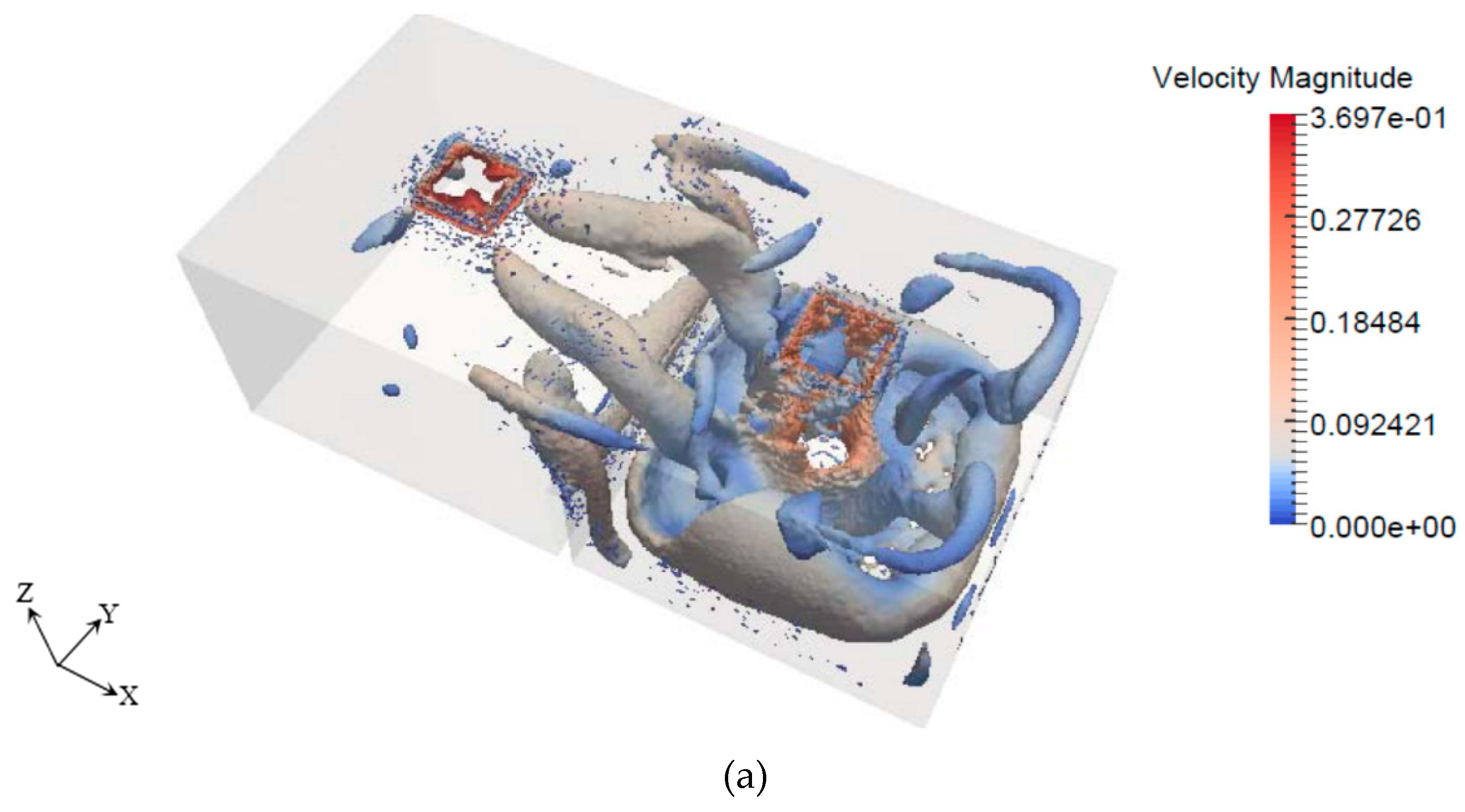
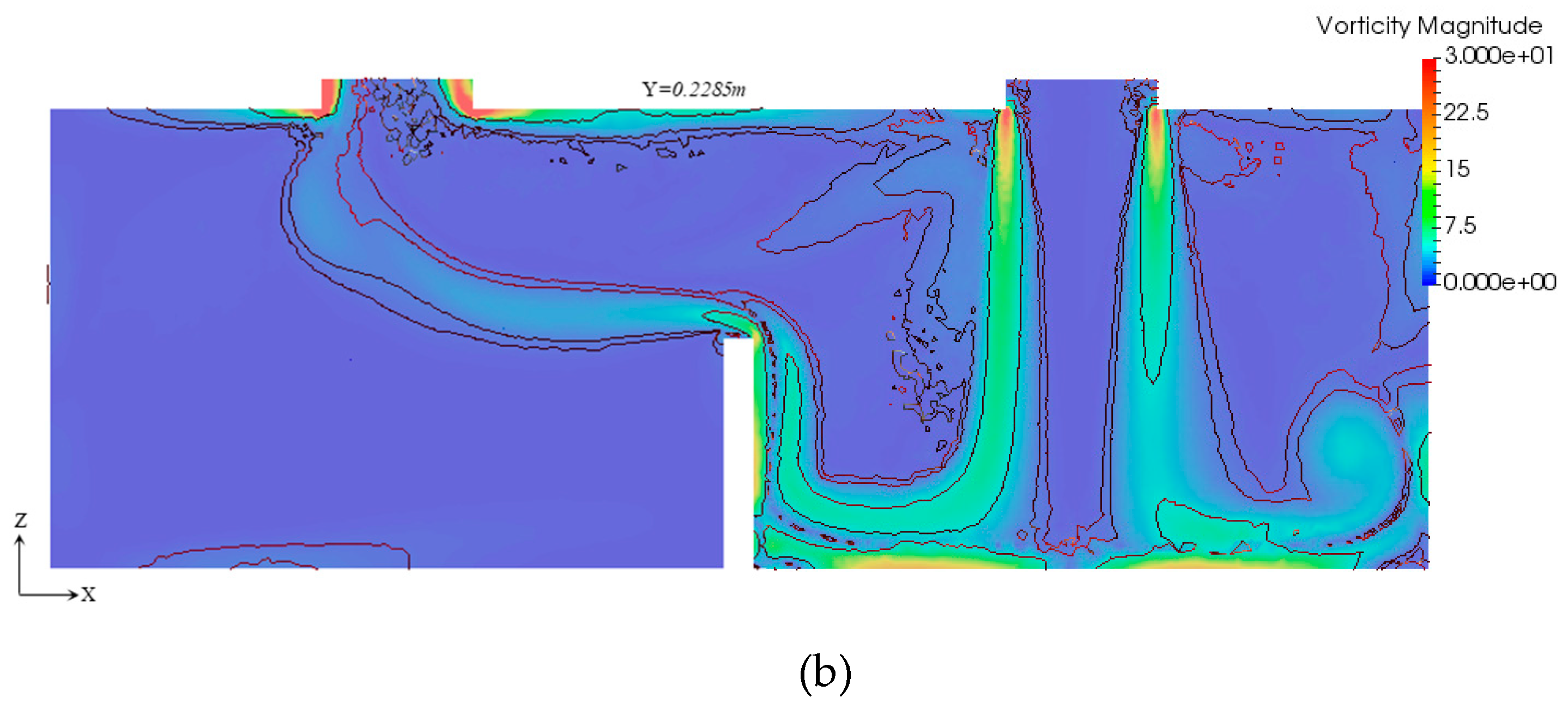
4. Results and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Asikainen, A.; Carrer, P.; Kephalopoulos, S.; Fernandes, E.D.; Wargocki, P.; Hänninen, O. Reducing burden of disease from residential indoor air exposures in Europe (HEALTHVENT project). Environ. Health A Glob. Access Sci. Source 2016, 15, 61–72. [Google Scholar] [CrossRef]
- Kim, E.H.; Kim, S.; Lee, J.H.; Kim, J.; Han, Y.; Kim, Y.M.; Ahn, K. Indoor Air Pollution Aggravates Symptoms of Atopic Dermatitis in Children. PLoS ONE 2015, 10, e0119501. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Wu, H. Indoor Air Pollution by Methylsiloxane in Household and Automobile Settings. PLoS ONE 2015, 10, e0135509. [Google Scholar] [CrossRef] [PubMed]
- Ye, X.; Peng, L.; Kan, H.; Wang, W.; Geng, F.; Mu, Z.; Yang, D. Acute Effects of Particulate Air Pollution on the Incidence of Coronary Heart Disease in Shanghai, China. PLoS ONE 2016, 11, e0151119. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Li, X.; Wang, S.; Wang, C.; Huang, F.; Gao, Q.; Guo, X. Fine Particulate Air Pollution and Hospital Emergency Room Visits for Respiratory Disease in Urban Areas in Beijing, China, in 2013. PLoS ONE 2016, 11, e0153099. [Google Scholar] [CrossRef] [PubMed]
- Posner, J.D.; Buchanan, C.R.; Dunn-Rankin, D. Measurement and prediction of indoor air flow in a model room. Energy Build. 2003, 35, 515–526. [Google Scholar] [CrossRef]
- Friedlander, S.K.; Marlow, W.H. Smoke, Dust and Haze: Fundamentals of Aerosol Behavior. Phys. Today 2000, 30, 58–59. [Google Scholar] [CrossRef]
- Tong, Z.; Chen, Y.; Malkawi, A.; Adamkiewicz, G.; Spengler, J.D. Quantifying the impact of traffic-related air pollution on the indoor air quality of a naturally ventilated building. Environ. Int. 2016, 89–90, 138–146. [Google Scholar] [CrossRef]
- Cheong, K.W.D.; Djunaedy, E.; Poh, T.K.; Tham, K.W.; Sekhar, S.C.; Wong, N.H.; Ullah, M.B. Measurements and computations of contaminant’s distribution in an office environment. Build. Environ. 2003, 38, 135–145. [Google Scholar] [CrossRef]
- Chung, K.C. Three-dimensional analysis of airflow and contaminant particle transport in a partitioned enclosure. Build. Environ. 1998, 34, 7–17. [Google Scholar] [CrossRef]
- Lu, W.; Howarth, A.T. Numerical analysis of indoor aerosol particle deposition and distribution in two-zone ventilation system. Build. Environ. 1996, 31, 41–50. [Google Scholar] [CrossRef]
- Cehlin, M.; Karimipanah, T.; Larsson, U. "Unsteady CFD simulations for prediction of airflow close to a supply device for displacement ventilation. In Proceedings of the 13th International Conference on Indoor Air Quality and Climate, Indoor Air 2014, Hong Kong, China, 7–12 July 2014; p. 47. [Google Scholar]
- Chen, Q. Using computational tools to factor wind into architectural environment design. Energy Build. 2004, 36, 1197–1209. [Google Scholar] [CrossRef]
- Bogodage, S.G.; Leung, A.Y.T. CFD simulation of cyclone separators to reduce air pollution. Powder Technol. 2015, 286, 488–506. [Google Scholar] [CrossRef]
- Ioannis, K.P.; Athanasios, N.K.; Pavlos, K.; Kostantinos, A. A CFD Simulation Study of VOC and Formaldehyde Indoor Air Pollution Dispersion in an Apartment as Part of an Indoor Pollution Management Plan. Aerosol Air Qual. Res. 2011, 11, 758. [Google Scholar]
- Jiang, Y.; Alexander, D.; Jenkins, H.; Arthur, R.; Chen, Q. Natural ventilation in buildings: Measurement in a wind tunnel and numerical simulation with large-eddy simulation. J. Wind Eng. Ind. Aerodyn. 2003, 91, 331–353. [Google Scholar] [CrossRef]
- Kobayashi, T.; Sugita, K.; Umemiya, N.; Kishimoto, T.; Sandberg, M. Numerical investigation and accuracy verification of indoor environment for an impinging jet ventilated room using computational fluid dynamics. Build. Environ. 2017, 115, 251–268. [Google Scholar] [CrossRef]
- Pulat, E.; Ersan, H.A. Numerical simulation of turbulent airflow in a ventilated room: Inlet turbulence parameters and solution multiplicity. Energy Build. 2015, 93, 227–235. [Google Scholar] [CrossRef]
- Pavarino, L.; Widlund, O. Balancing Neumann-Neumann Methods for Incompressible Stokes Equations. Commun. Pure Appl. Math. 2002, 55, 302–335. [Google Scholar] [CrossRef]
- Yudison, A.P.; Driejana, R. Development of Indoor Air Pollution Concentration Prediction by Geospatial Analysis. J. Eng. Technol. Sci. 2015, 47, 306–319. [Google Scholar]
- Kao, H.-M.; Chang, T.-J.; Hsieh, Y.-F.; Wang, C.-H.; Hsieh, C.-I. Comparison of airflow and particulate matter transport in multi-room buildings for different natural ventilation patterns. Energy Build. 2009, 41, 966–974. [Google Scholar] [CrossRef]
- Guerra, D.R.S.; Su, J.; Freire, A.P.S. The near wall behavior of an impinging jet. Int. J. Heat Mass Transf. 2005, 48, 2829–2840. [Google Scholar] [CrossRef]
- Piomelli, U. Large-eddy simulation: Achievements and challenges. Prog. Aerosp. Sci. 1999, 35, 335–362. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, Q. Large eddy simulation of indoor airflow with a filtered dynamic subgrid scale model. Int. J. Heat Mass Transf. 2000, 43, 3219–3231. [Google Scholar] [CrossRef]
- Tian, Z.F.; Tu, J.Y.; Yeoh, G.H.; Yuen, R.K.K. Numerical studies of indoor airflow and particle dispersion by large Eddy simulation. Build. Environ. 2007, 42, 3483–3492. [Google Scholar] [CrossRef]
- Lu, W.; Howarth, A.T.; Adam, N.; Riffat, S.B. Modelling and measurement of airflow and aerosol particle distribution in a ventilated two-zone chamber. Build. Environ. 1996, 31, 417–423. [Google Scholar] [CrossRef]
- Chang, T.-J.; Hsieh, Y.F.; Kao, H.M. Numerical investigation of airflow pattern and particulate matter transport in naturally ventilated multi-room buildings. Indoor Air 2006, 16, 136–152. [Google Scholar] [CrossRef]
- Durbin, P.A. Separated flow computations with the k-epsilon-v-squared model. AIAA J. 1995, 33, 659–664. [Google Scholar] [CrossRef]
- Li, K.; Gong, G. Numerical simulation of indoor suspension particles based on v2-f model. Appl. Math. Model. 2012, 36, 2510–2520. [Google Scholar] [CrossRef]
- Choi, J.; Hur, N.; Kang, S.; Lee, E.D.; Lee, K.-B. A CFD simulation of hydrogen dispersion for the hydrogen leakage from a fuel cell vehicle in an underground parking garage. Int. J. Hydrog. Energy 2013, 38, 8084–8091. [Google Scholar] [CrossRef]
- Yao, Q.; Zhu, Q. A Pressure-Stabilized Lagrange-Galerkin Method in a Parallel Domain Decomposition System. Abstr. Appl. Anal. 2013, 2013, 161873. [Google Scholar] [CrossRef]
- Brezzi, F.; Fortin, M. Mixed and Hybrid Finite Element Methods; Springer: New York, NY, USA, 1991; p. 350. [Google Scholar]
- Qinghe, Y.; Kanayama, H. A Coupling Analysis of Thermal Convection Problems Based on a Characteristic Curve Method. Theor. Appl. Mech. Jpn. 2011, 59, 257–264. [Google Scholar]
- Farhat, C.; Roux, F.X.; Mechanics, I.A.F.C.; Oden, J.T. Implicit Parallel Processing in Structural Mechanics; North-Holland: North Holland, Holland, 1994. [Google Scholar]
- Mandel, J. Balancing domain decomposition. Commun. Numer. Methods Eng. 1993, 9, 233–241. [Google Scholar] [CrossRef]
- Shioya, R.; Ogino, M.; Kanayama, H.; Tagami, D. Large scale finite element analysis with a Balancing Domain Decomposition method. In Progress in Experimental and Computational Mechanics in Engineering; Geni, M.K.M., Ed.; Key Engineering Materials; Trans Tech Publications: Zurich, Switzerland, 2003; Volume 243, pp. 21–26. [Google Scholar]
- Mukaddes, A.M.M.; Ogino, M.; Kanayama, H.; Shioya, R. A Scalable Balancing Domain Decomposition Based Preconditioner for Large Scale Heat Transfer Problems. JSME Int. J. Ser. BFluids Therm. Eng. 2006, 49, 533–540. [Google Scholar] [CrossRef]
- Yao, Q.; Kanayama, H.; Ognio, M.; Notsu, H. Incomplete Balancing Domain Decomposition for Large scale 3-D non-stationary incompressible flow problems. IOP Conf. Ser. Mater. Sci. Eng. 2010, 10, 012029. [Google Scholar] [CrossRef]
- Yao, Q.; Zhu, Q. Investigation of the Contamination Control in a Cleaning Room with a Moving AGV by 3D Large-Scale Simulation. J. Appl. Math. 2013, 2013, 570237. [Google Scholar] [CrossRef] [Green Version]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Jiang, Z.; Kwan, T.H.; Liu, C.-H.; Yao, Q. Study of Indoor Ventilation Based on Large-Scale DNS by a Domain Decomposition Method. Symmetry 2019, 11, 1416. https://doi.org/10.3390/sym11111416
Jiang J, Jiang Z, Kwan TH, Liu C-H, Yao Q. Study of Indoor Ventilation Based on Large-Scale DNS by a Domain Decomposition Method. Symmetry. 2019; 11(11):1416. https://doi.org/10.3390/sym11111416
Chicago/Turabian StyleJiang, Junyang, Zichao Jiang, Trevor Hocksun Kwan, Chun-Ho Liu, and Qinghe Yao. 2019. "Study of Indoor Ventilation Based on Large-Scale DNS by a Domain Decomposition Method" Symmetry 11, no. 11: 1416. https://doi.org/10.3390/sym11111416
APA StyleJiang, J., Jiang, Z., Kwan, T. H., Liu, C.-H., & Yao, Q. (2019). Study of Indoor Ventilation Based on Large-Scale DNS by a Domain Decomposition Method. Symmetry, 11(11), 1416. https://doi.org/10.3390/sym11111416




