Modified Power-Symmetric Distribution
Abstract
1. Introduction
2. Genesis and Properties of Modified Power-Normal Distribution
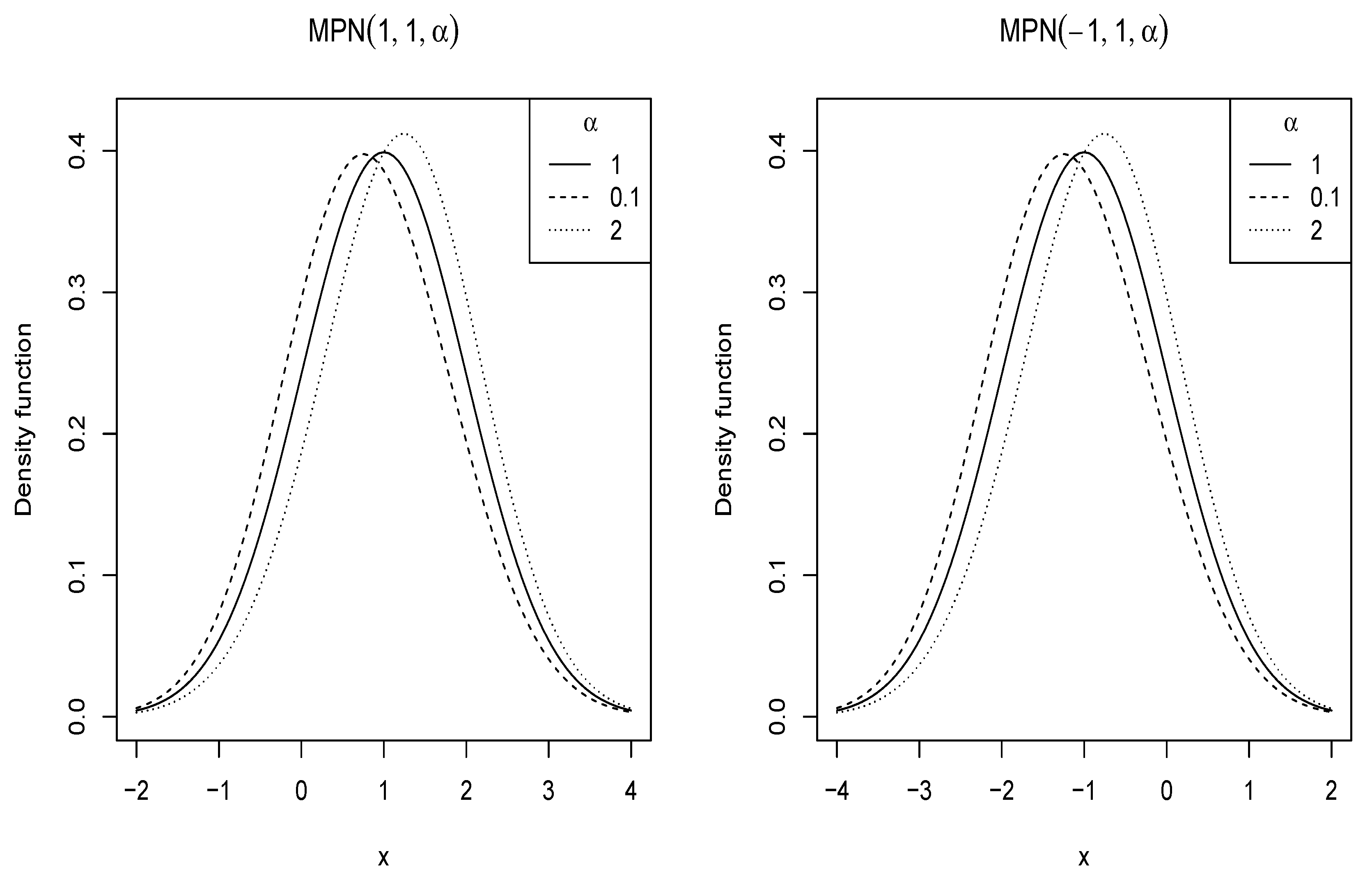
2.1. Probability Density Function
2.2. Statistical Properties
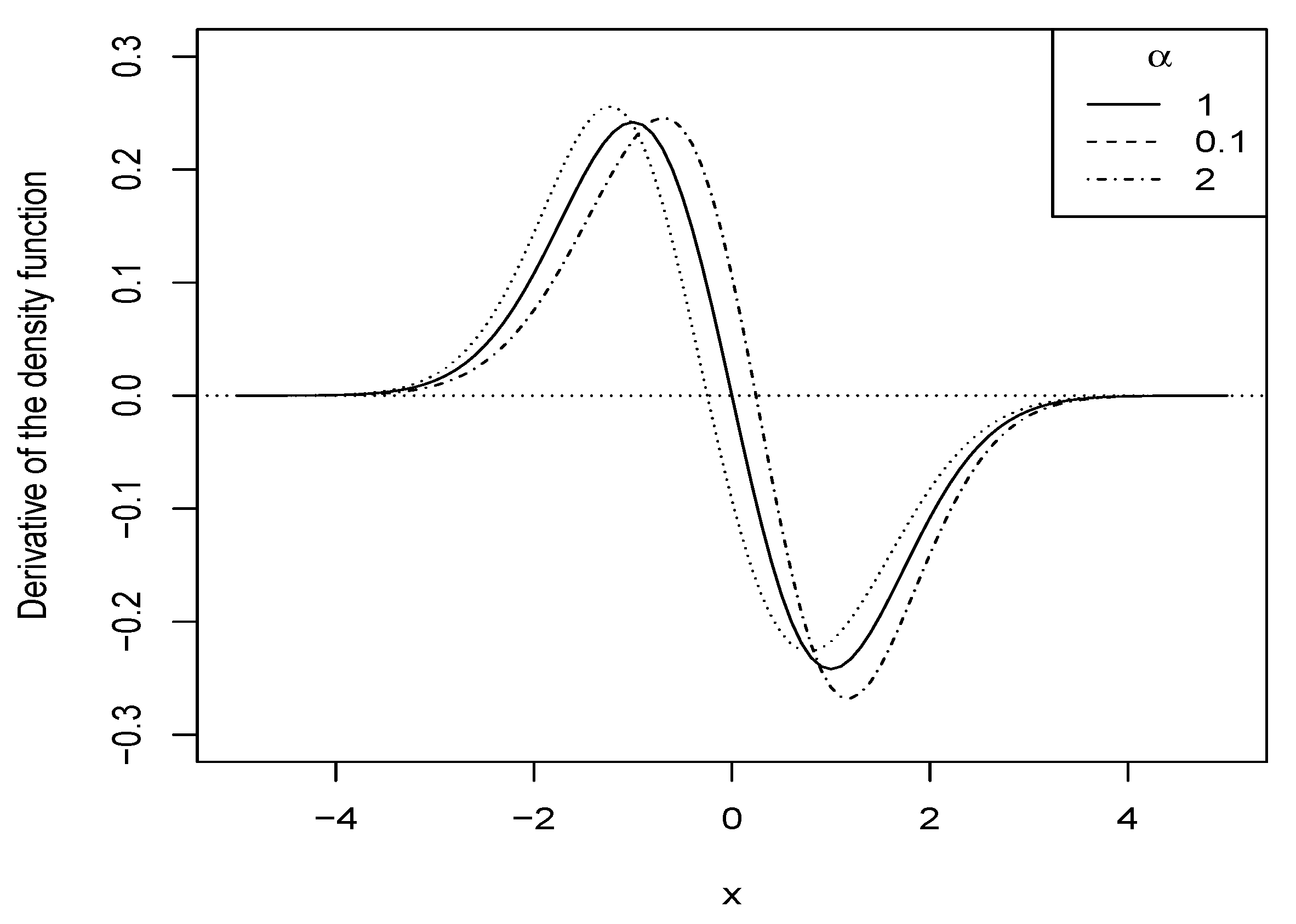
2.2.1. Shape of the Density
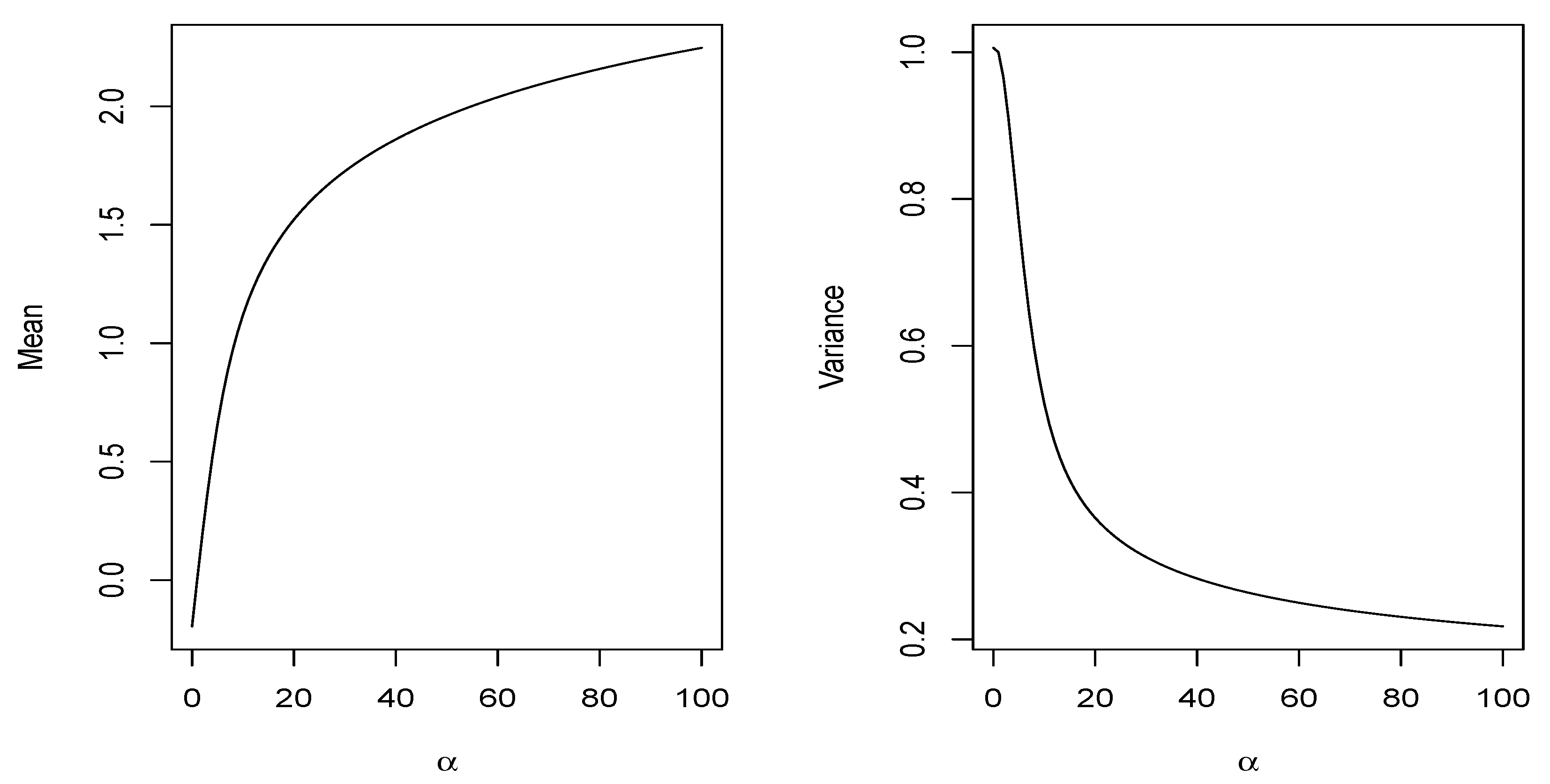
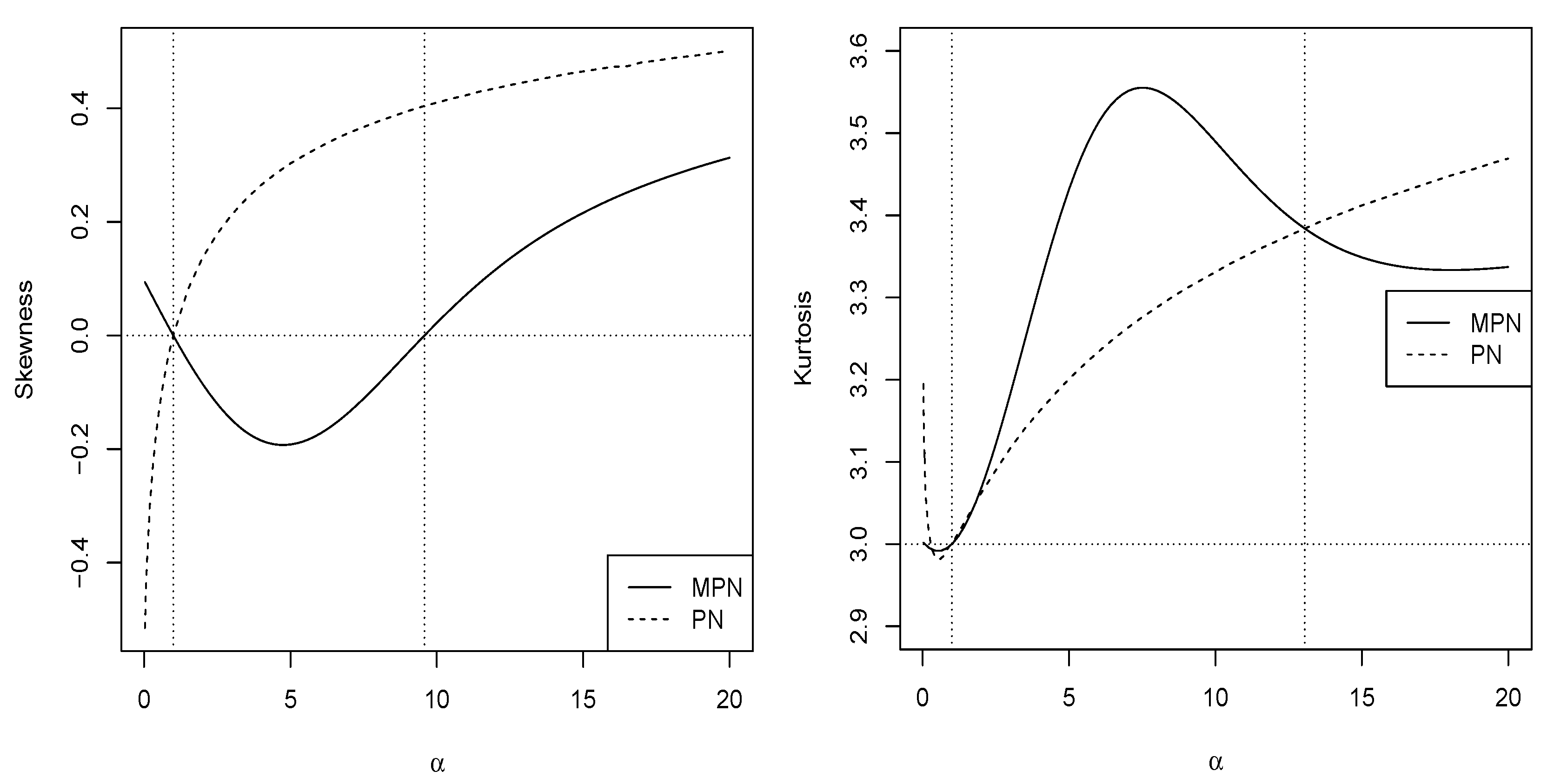
2.2.2. Moments
2.2.3. Stochastic Ordering
3. Inference
3.1. Method of Moments
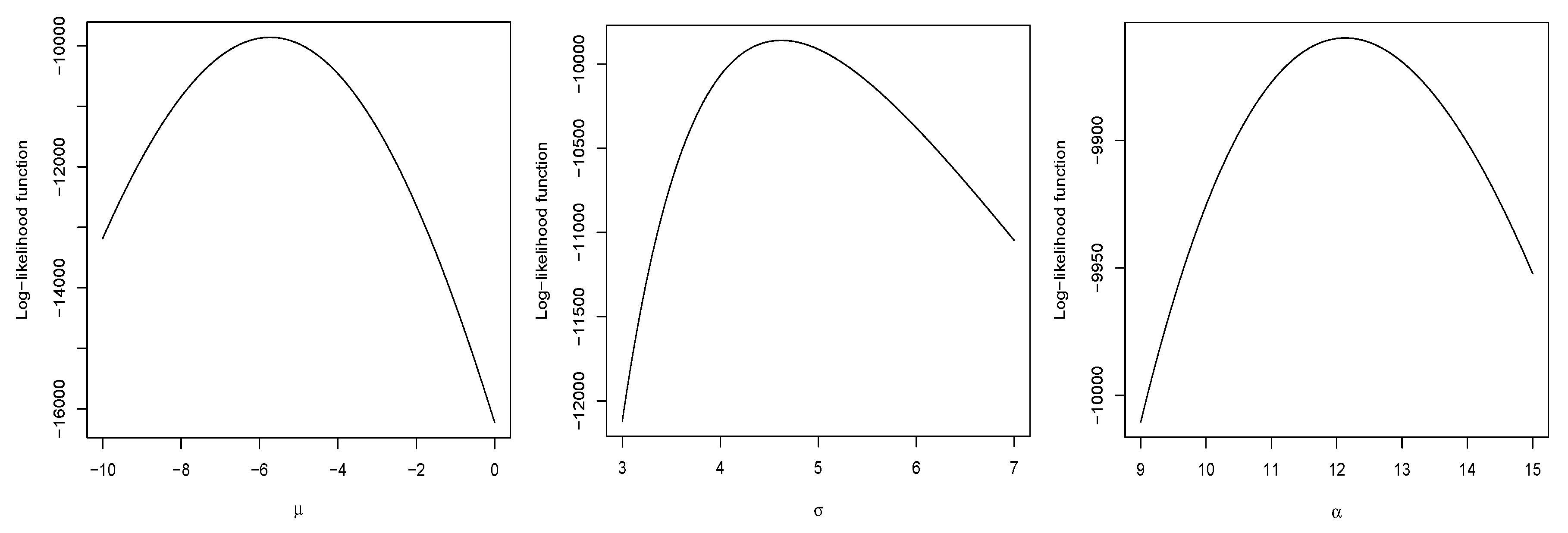
3.2. Maximum Likelihood Estimation
3.3. Simulation Study
- Step 1: Generate
- Step 2: Compute
Fisher’s Information Matrix
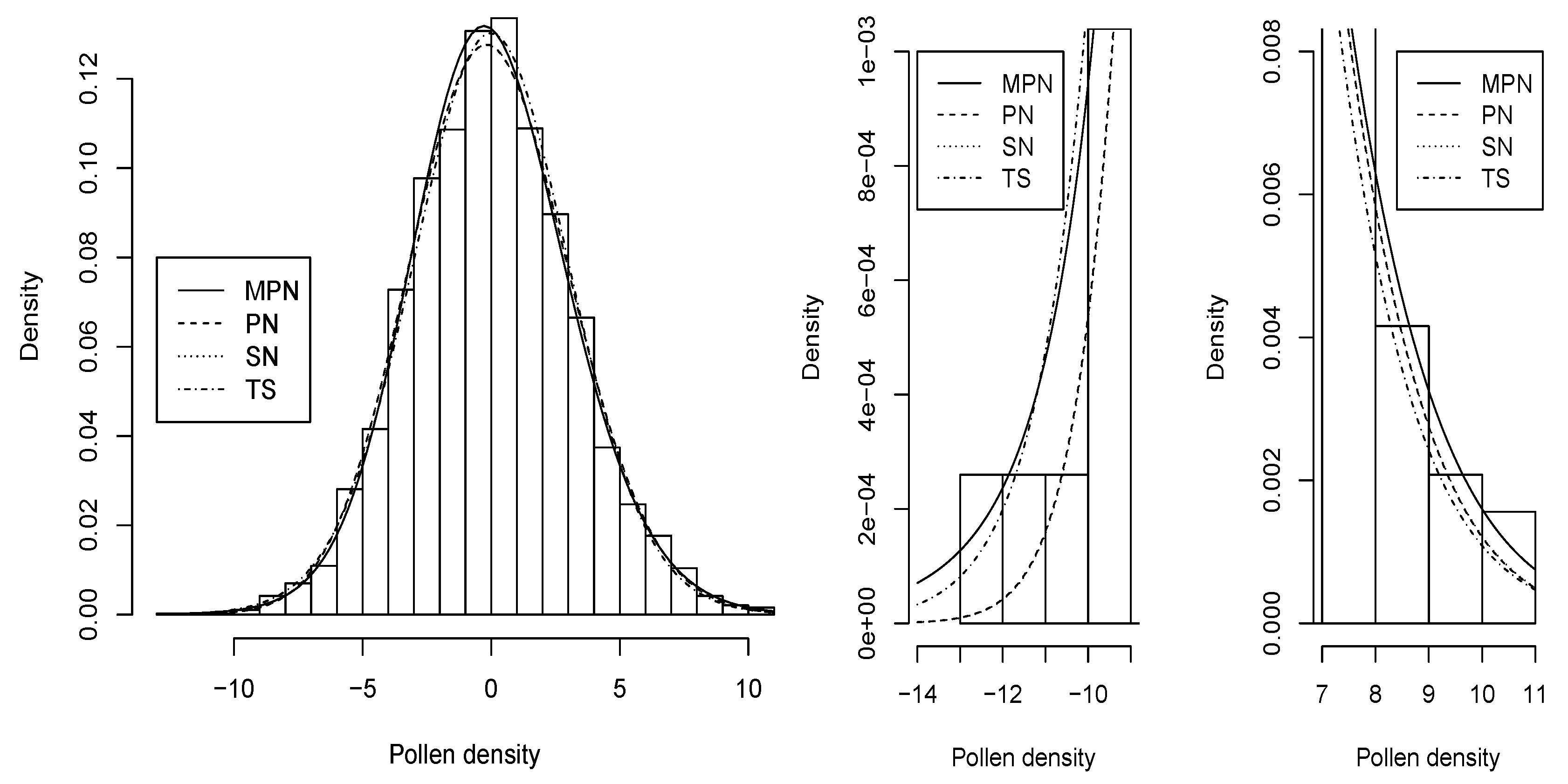
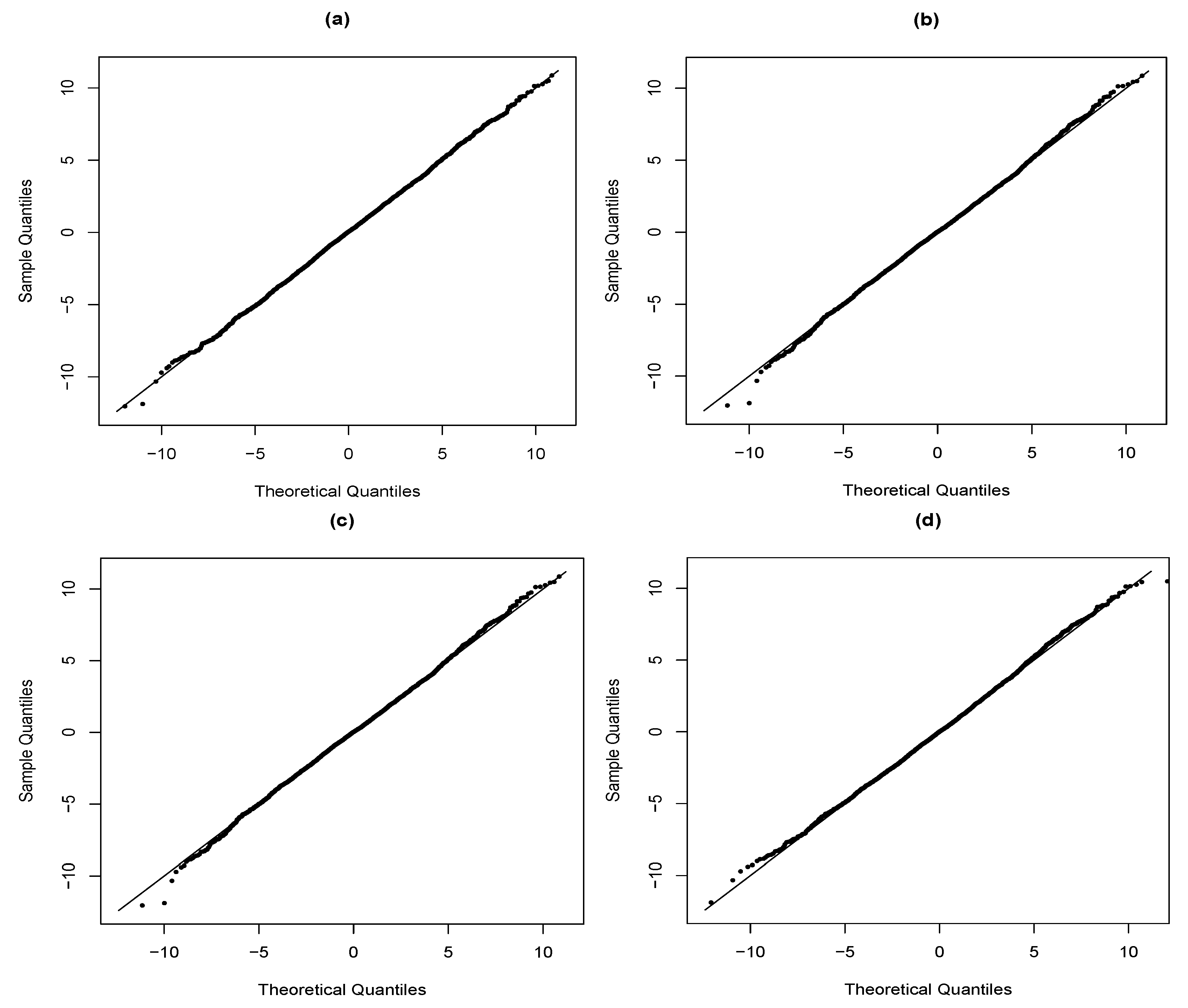
4. Application
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Azzalini, A. A class of distributions which includes the normal ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Arellano-Valle, R.B.; Gómez, H.W.; Quintana, F.A. A New Class of Skew-Normal Distributions. Commun. Stat. Theory Methods 2004, 33, 1465–1480. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Gómez, H.W.; Salinas, H.S. A note on the Fisher information matrix for the skew-generalized-normal model. Stat. Oper. Res. Trans. 2013, 37, 19–28. [Google Scholar]
- Azzalini, A. The Skew-Normal and Related Families; IMS monographs; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Martínez-Flórez, G.; Barranco-Chamorro, I.; Bolfarine, H.; Gómez, H.W. Flexible Birnbaum–Saunders Distribution. Symmetry 2019, 11, 1305. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E.; Arellano-Valle, R.B. Kullback–Leibler Divergence Measure for Multivariate Skew-Normal Distributions. Entropy 2012, 14, 1606–1626. [Google Scholar] [CrossRef]
- Chiogna, M. A note on the asymptotic distribution of the maximum likelihood estimator for the scalar skew-normal distribution. Stat. Methods Appl. 2005, 14, 331–341. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Azzalini, A. The centred parametrization for the multivariate skew-normal distribution. J. Multivar. Anal. 2008, 99, 1362–1382. [Google Scholar] [CrossRef]
- Pewsey, A.; Gómez, H.W.; Bolfarine, H. Likelihood-based inference for power distributions. Test 2012, 21, 775–789. [Google Scholar] [CrossRef]
- Lehmann, E.L. The power of rank tests. Ann. Math. Statist. 1953, 24, 23–43. [Google Scholar] [CrossRef]
- Durrans, S.R. Distributions of fractional order statistics in hydrology. Water Resour. Res. 1992, 28, 1649–1655. [Google Scholar] [CrossRef]
- Gupta, D.; Gupta, R.C. Analyzing skewed data by power normal model. Test 2008, 17, 197–210. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Arnold, B.C.; Bolfarine, H.; Gómez, H.W. The Multivariate Alpha-power Model. J. Stat. Plan. Inference 2013, 143, 1236–1247. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, H.W. Asymmetric regression models with limited responses with an application to antibody response to vaccine. Biom. J. 2013, 55, 156–172. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, H.W. The log alpha-power asymmetric distribution with application to air pollution. Environmetrics 2014, 25, 44–56. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, H.W. Doubly censored power-normal regression models with inflation. Test 2015, 24, 265–286. [Google Scholar] [CrossRef]
- Castillo, N.O.; Gallardo, D.I.; Bolfarine, H.; Gómez, H.W. Truncated Power-Normal Distribution with Application to Non-Negative Measurements. Entropy 2018, 20, 433. [Google Scholar] [CrossRef]
- Maciak, M.; Peštová, B.; Pešta, M. Structural breaks in dependent, heteroscedastic, and extremal panel data. Kybernetika 2018, 54, 1106–1121. [Google Scholar] [CrossRef]
- Pesˇta, M. Total least squares and bootstrapping with application in calibration. Statistics 2013, 47, 966–991. [Google Scholar] [CrossRef]
- Shaked, M.; Shanthikumar, J.G. Stochastic Orders; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- R Development Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Statist. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Ja¨ntschi, L.; Bolboacă, S.D. Computation of Probability Associated with Anderson–Darling Statistic. Mathematics 2018, 6, 88. [Google Scholar] [CrossRef]
- Ja¨ntschi, L. A Test Detecting the Outliers for Continuous Distributions Based on the Cumulative Distribution Function of the Data Being Tested. Symmetry 2019, 11, 835. [Google Scholar] [CrossRef]
| 0.5 | −0.136 | −1.135 | 0.886 | 0.397 | 0.239 | 0.241 |
| 1.0 | 0.000 | −1.000 | 1.000 | 0.399 | 0.242 | 0.242 |
| 2.0 | 0.243 | −0.691 | 1.173 | 0.412 | 0.261 | 0.251 |
| 3.0 | 0.435 | −0.414 | 1.299 | 0.433 | 0.282 | 0.266 |
| 4.0 | 0.586 | −0.203 | 1.396 | 0.457 | 0.298 | 0.284 |
| 5.0 | 0.706 | −0.041 | 1.475 | 0.481 | 0.316 | 0.301 |
| 0.5 | −0.097 | 1.006 |
| 1.0 | 0.000 | 1.000 |
| 5.0 | 0.659 | 0.770 |
| 10.0 | 1.119 | 0.521 |
| 100.0 | 2.247 | 0.218 |
| (SD) | (SD) | (SD) | |||
| 0 | 1 | 0.1 | −0.352478 (0.149214) | 0.994441 (0.091321) | 0.190243 (0.175202) |
| 0.5 | −0.19534 (0.14501) | 0.990622 (0.094550) | 0.613052 (0.272096) | ||
| 0.8 | −0.083183 (0.144587) | 0.990286 (0.098669) | 0.854338 (0.164924) | ||
| 1 | −0.009586 (0.141691) | 0.995312 (0.0997256) | 1.007328 (0.122688) | ||
| 5 | 0.004225 (0.100001) | 0.997408 (0.088254) | 5.030272 (0.229064) | ||
| 10 | 0.001108 (0.066610) | 0.999124 (0.068611) | 10.060478 (0.475019) | ||
| 100 | 0.002171 (0.017362) | 1.001152 (0.029604) | 100.437990 (2.668190) | ||
| 0 | 1 | 0.1 | −0.351446 (0.104552) | 0.998513 (0.070831) | 0.180054 (0.111930) |
| 0.5 | −0.19268 (0.101786) | 0.997622 (0.068806) | 0.576957 (0.223378) | ||
| 0.8 | −0.08140 (0.099360) | 0.997674 (0.069451) | 0.830318 (0.152995) | ||
| 1 | 0.002786 (0.097411) | 0.996444 (0.069648) | 1.002200 (0.088749) | ||
| 5 | 0.002014 (0.099305) | 0.996788 (0.085987) | 5.023032 (0.221756) | ||
| 10 | 0.002897 (0.046109) | 1.000515 (0.050192) | 10.032857 (0.339106) | ||
| 100 | 0.000623 (0.012137) | 1.000185 (0.019759) | 100.168752 (1.866302) | ||
| 0 | 1 | 0.1 | −0.348177 (0.072732) | 0.999433 (0.047548) | 0.170978 (0.076165) |
| 0.5 | −0.196617 (0.072015) | 0.999142 (0.047896) | 0.562935 (0.218890) | ||
| 0.8 | −0.076657 (0.069510) | 0.997719 (0.050718) | 0.824700 (0.127661) | ||
| 1 | 0.001158 (0.06877) | 0.998408 (0.050586) | 1.003651 (0.058344) | ||
| 5 | −0.000165 (0.053006) | 1.000623 (0.044182) | 5.005130 (0.115719) | ||
| 10 | −0.000239 (0.033615) | 1.000017 (0.035902) | 10.014958 (0.246652) | ||
| 100 | 0.000514 (0.008452) | 1.000491 (0.014599) | 100.104380 (1.295144) | ||
| Mean | Median | Variance | Skewness | Kurtosis |
|---|---|---|---|---|
| 0.000 | −0.030 | 9.887 | 0.109 | 3.193 |
| Parameters | ||||
|---|---|---|---|---|
| −0.010 (0.05) | −2.04 (0.24) | −1.74 (0.68) | −5.73 (0.43) | |
| 3.037 (0.05) | 3.75 (0.14) | 3.69 (0.21) | 4.62 (0.14) | |
| 29.995 (13.01) | 0.93 (0.14) | 1.77 (0.37) | 12.13 (1.21) | |
| −9864.99 | −9863.42 | −9863.37 | −9861.98 |
| Criteria | ||||
|---|---|---|---|---|
| AIC | 19,735.98 | 19,732.84 | 19,732.74 | 19,729.96 |
| BIC | 19,754.74 | 19,751.61 | 19,751.50 | 19,748.72 |
| KSS (p-value) | 0.014 (0.516) | 0.013 (0.559) | 0.012 (0.627) | 0.010 (0.820) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez-Déniz, E.; Iriarte, Y.A.; Calderín-Ojeda, E.; Gómez, H.W. Modified Power-Symmetric Distribution. Symmetry 2019, 11, 1410. https://doi.org/10.3390/sym11111410
Gómez-Déniz E, Iriarte YA, Calderín-Ojeda E, Gómez HW. Modified Power-Symmetric Distribution. Symmetry. 2019; 11(11):1410. https://doi.org/10.3390/sym11111410
Chicago/Turabian StyleGómez-Déniz, Emilio, Yuri A. Iriarte, Enrique Calderín-Ojeda, and Héctor W. Gómez. 2019. "Modified Power-Symmetric Distribution" Symmetry 11, no. 11: 1410. https://doi.org/10.3390/sym11111410
APA StyleGómez-Déniz, E., Iriarte, Y. A., Calderín-Ojeda, E., & Gómez, H. W. (2019). Modified Power-Symmetric Distribution. Symmetry, 11(11), 1410. https://doi.org/10.3390/sym11111410






