Normal-G Class of Probability Distributions: Properties and Applications
Abstract
:1. Introduction
- ;
- is differentiable and monotonically non-decreasing;
- as and as ;
2. The Normal-G Class and Some Mathematical Properties
- (c1)
- H is a cdf and and are non-negative;
- (c2)
- , and are non-decreasing and , , are non-increasing ;
- (c3)
- If , then or , and or ;
- (c4)
- If , then and ;
- (c5)
- and if , then ;
- (c6)
- and ;
- (c7)
- ;
- (c8)
- or and ;
- (c9)
- and ;
- (c10)
- H is a cdf without points of discontinuity or all functions and are constant at the right of the vicinity of points whose image are points of discontinuity of H, being also continuous in that points. Moreover, H does not have any point of discontinuity in the set for some ;
2.1. Special Normal-G Sub-Models
2.1.1. The Normal-Weibull Distribution
2.1.2. The Normal-Log-Logistic Distribution
2.2. Series Representation
2.3. Quantile Function
2.4. Raw Moments, Incomplete Moments and Moment Generating Function
2.5. Estimation and Inference
3. Numerical Analysis
3.1. Simulation Study
3.2. Applications
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Mudholkar, G.S.; Srivastava, D.K.; Freimer, M. The exponentiated Weibull family: A reanalysis of the bus motor failure data. Technometrics 1995, 37, 436–445. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Generalized Exponential Distributions. Aust. N. Z. J. Stat. 1999, 41, 173–188. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A new method for adding a parameter to a family of distributions with application to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Nadarajah, S. A Generalized Normal Distribution. J. Appl. Stat. 2005, 32, 685–694. [Google Scholar] [CrossRef]
- Azzalini, A. A Class of Distributions which includes the Normal ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Robertson, H.T.; Allison, D.B. A Novel Generalized Normal Distribution for Human Longevity and other Negatively Skewed Data. PLoS ONE 2012, 7, e37025. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Hashimoto, E.M.; Ortega, E.M.M. The McDonald Weibull Model. Statistics 2014, 48, 256–278. [Google Scholar] [CrossRef]
- Famoye, F.; Lee, C.; Olumolade, O. The Beta-Weibull distribution. J. Stat. Theory Appl. 2005, 4, 121–136. [Google Scholar]
- Cordeiro, G.M.; Castro, M. A new family of generalized distributions. J. Stat. Comput. Simul. 2010, 81, 883–898. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Lee, C.; Famoye, F. A new method for generating families of continuous distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef]
- Alizadeh, M.; Cordeiro, G.M.; Pinho, L.G.B.; Ghosh, I. The Gompertz-G family of distributions. J. Stat. Theory Pract. 2017, 11, 179–207. [Google Scholar] [CrossRef]
- Brito, C.R.; Rêgo, L.C.; Oliveira, W.R.; Gomes-Silva, F. Method for Generating Distributions and Classes of Probability Distributions: The Univariate Case. Hacet. J. Math. Stat. 2019, 48, 897–930. [Google Scholar]
- Xie, M.; Tang, Y.; Goh, T.N. A modified Weibull extension with bathtub-shaped failure rate function. Reliab. Eng. Syst. Safe. 2002, 76, 279–285. [Google Scholar] [CrossRef]
- Bebbington, M.; Lai, C.D.; Zitikis, R. A flexible Weibull extension. Reliab. Eng. Syst. Safe. 2007, 92, 719–726. [Google Scholar] [CrossRef]
- Tahir, M.H.; Nadarajah, S. Parameter induction in continuous univariate distributions: Well-established G families. An. Acad. Bras. Ciênc. 2015, 87, 539–568. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.M.; Cunha, D.C.C. The Exponentiated Generalized Class of Distributions. J. Data Sci. 2013, 11, 1–27. [Google Scholar]
- Silva, R.; Gomes-Silva, F.; Ramos, M.; Cordeiro, G.; Marinho, P.; Andrade, T.A.N. The Exponentiated Kumaraswamy-G Class: General Properties and Application. Rev. Colomb. Estad. 2019, 42, 1–33. [Google Scholar] [CrossRef]
- Cakmakyapan, S.; Ozel, G. The Lindley Family of Distributions: Properties and Applications. Hacet. J. Math. Stat. 2017, 46, 1113–1137. [Google Scholar] [CrossRef]
- Barreto-Souza, W.; Cordeiro, G.M.; Simas, A.B. Some Results for Beta Fréchet Distribution. Commun. Stat. Theory Methods 2011, 40, 798–811. [Google Scholar] [CrossRef]
- Huang, S.; Oluyede, B.O. Exponentiated Kumaraswamy-Dagum distribution with applications to income and lifetime data. J. Stat. Dist. Appl. 2014, 1, 1–20. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Bager, R.S.B. Moments for Some Kumaraswamy Generalized Distributions. Comm. Statist. Theory Methods 2015, 44, 2720–2737. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Von Neumann, J. Various techniques used in connection with random digits. In Applied Mathematics Series 12; National Bureau of Standards: Washington, DC, USA, 1951; pp. 36–38. [Google Scholar]
- Fonseca, M.B. A influência da fertilidade do solo e caracterização da fixação biológica de N2 para o crescimento de Dimorphandra wilsonii Rizz. Master’s Thesis, Federal University of Minas Gerais, Belo Horizonte, Brazil, 2007. [Google Scholar]
- Silva, R.B.; Bourguignon, M.; Dias, C.R.B.; Cordeiro, G.M. The compound class of extended Weibull power series distributions. Comput. Stat. Data Anal. 2013, 58, 352–367. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Lemonte, A.J. On the Marshall–Olkin extended Weibull distribution. Stat. Pap. 2013, 54, 333–353. [Google Scholar] [CrossRef]
- Chen, G.; Balakrishnan, N. A general purpose approximate goodness-of-fit test. J. Qual. Technol. 1995, 27, 154–161. [Google Scholar] [CrossRef]
- StatSci.org. Available online: http://www.statsci.org/data/oz/kiama.html (accessed on 21 October 2019).
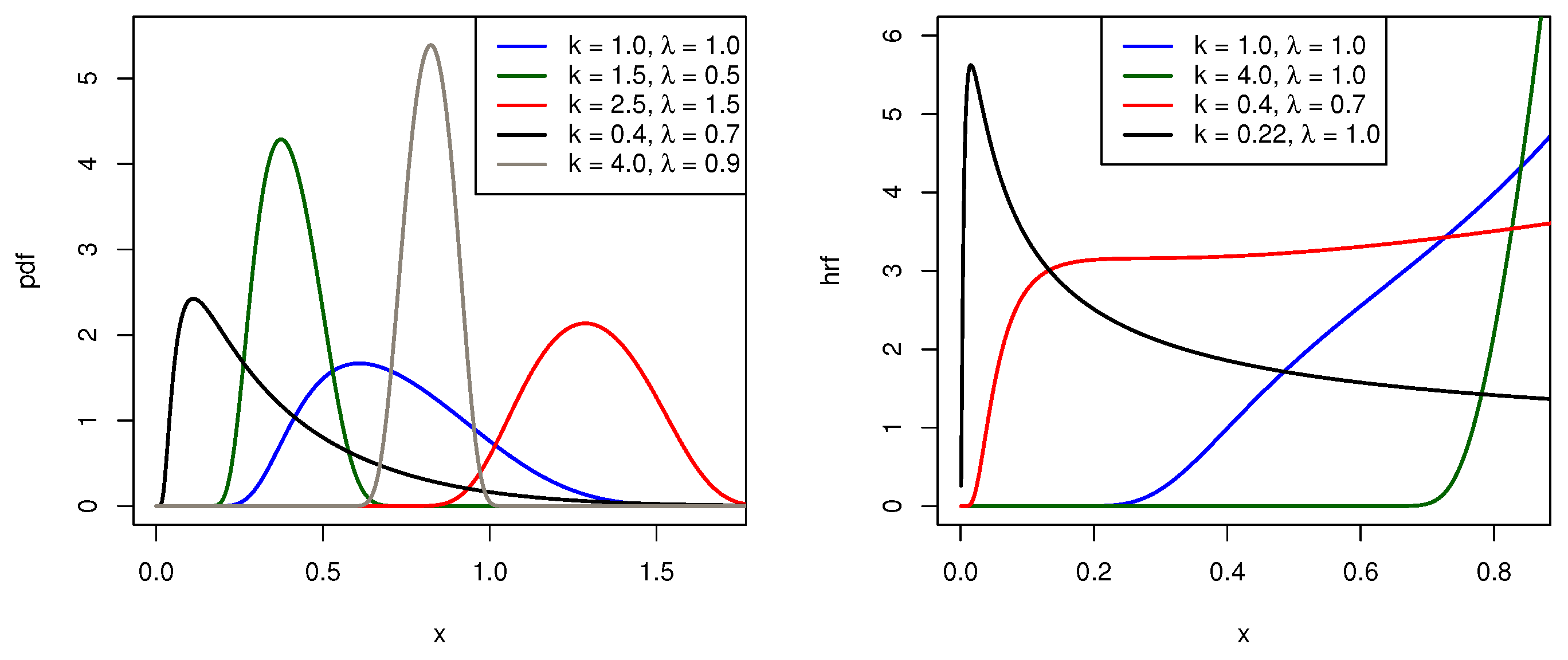
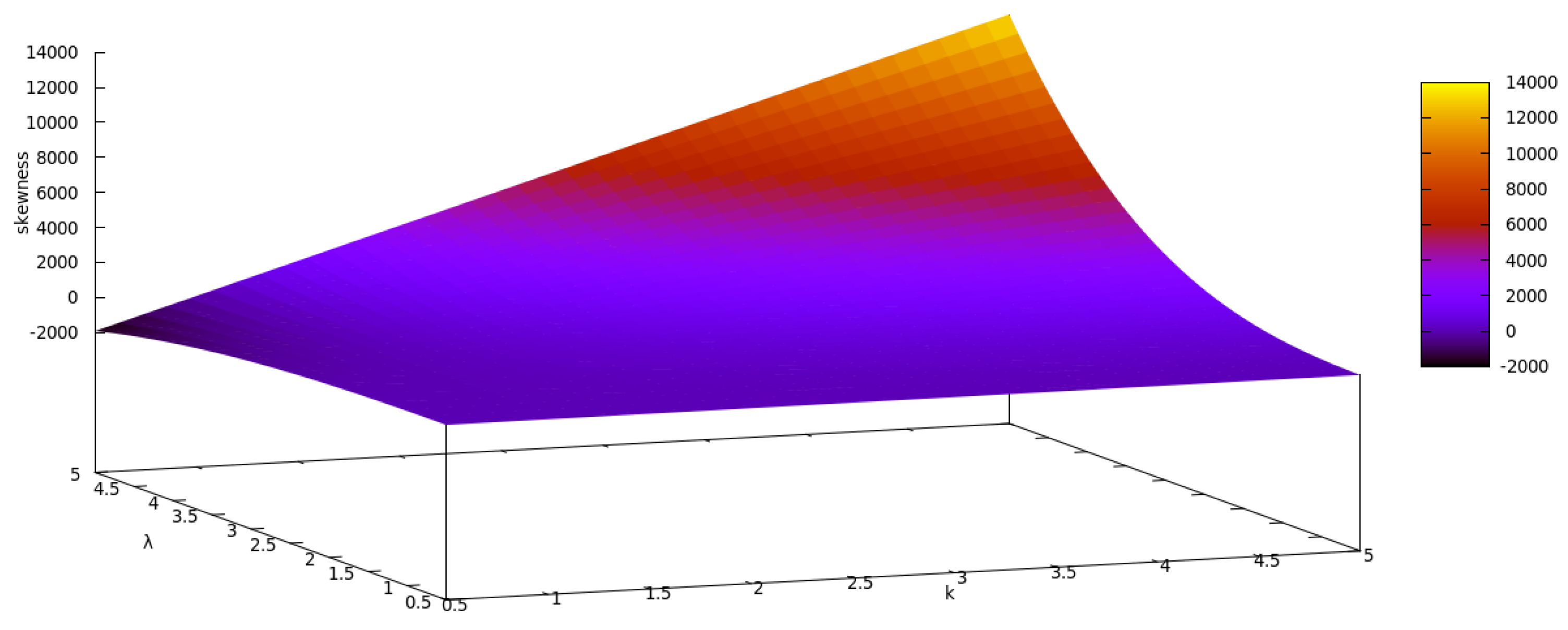
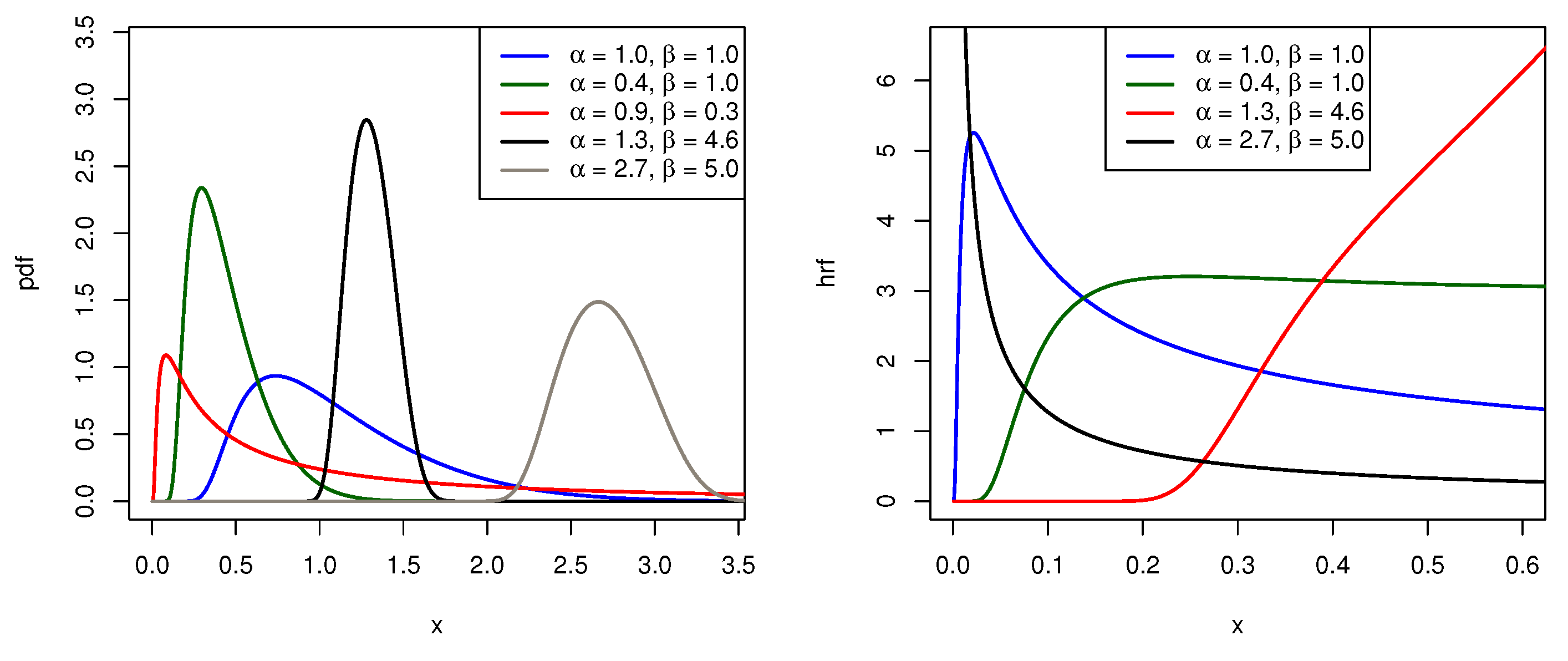
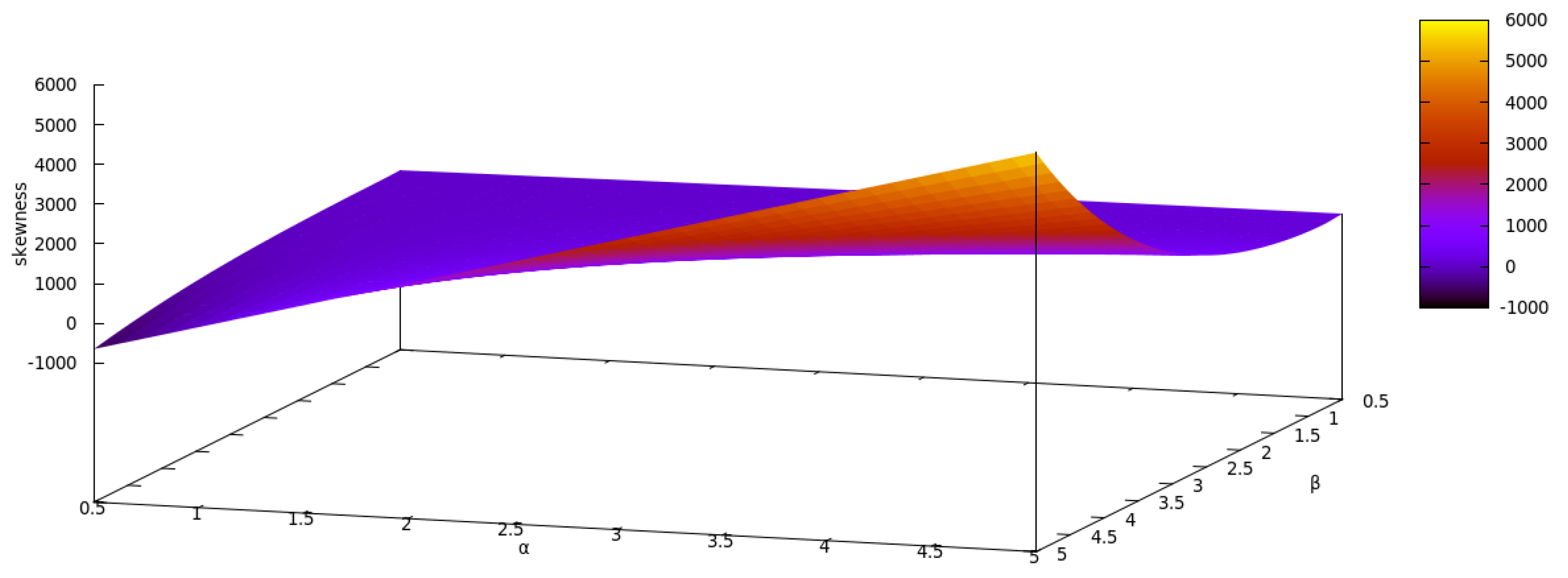
| Actual Value | Bias | MSE | ||||
|---|---|---|---|---|---|---|
| 50 | 1.0 | 1.7 | 0.02707850 | −0.00948110 | 0.00822299 | 0.00659991 |
| 0.5 | 2.0 | 0.01446186 | −0.02037125 | 0.00209051 | 0.03647395 | |
| 3.0 | 0.5 | 0.07878343 | −0.00096778 | 0.07352625 | 0.00006357 | |
| 0.9 | 4.0 | 0.02586182 | −0.02752101 | 0.00675452 | 0.04497248 | |
| 7.1 | 5.8 | 0.19086399 | −0.00540407 | 0.41402178 | 0.00153179 | |
| 100 | 1.0 | 1.7 | 0.01306919 | −0.00453981 | 0.00377883 | 0.00332042 |
| 0.5 | 2.0 | 0.00726917 | −0.01412373 | 0.00095786 | 0.01838681 | |
| 3.0 | 0.5 | 0.03914672 | −0.00057766 | 0.03400929 | 0.00003204 | |
| 0.9 | 4.0 | 0.01167774 | −0.01403219 | 0.00305903 | 0.02273089 | |
| 7.1 | 5.8 | 0.08363335 | −0.00279451 | 0.18835856 | 0.00077190 | |
| 200 | 1.0 | 1.7 | 0.00651588 | −0.00253820 | 0.00181409 | 0.00166703 |
| 0.5 | 2.0 | 0.00358578 | −0.00678178 | 0.00045681 | 0.00923355 | |
| 3.0 | 0.5 | 0.01901041 | −0.00029362 | 0.01628677 | 0.00001604 | |
| 0.9 | 4.0 | 0.00658567 | −0.00745541 | 0.00148059 | 0.01138373 | |
| 7.1 | 5.8 | 0.03656102 | −0.00066316 | 0.09041610 | 0.00038519 | |
| 500 | 1.0 | 1.7 | 0.00317837 | −0.00127234 | 0.00071164 | 0.00066754 |
| 0.5 | 2.0 | 0.00195165 | −0.00609800 | 0.00017967 | 0.00370983 | |
| 3.0 | 0.5 | 0.00748033 | −0.00008804 | 0.00636008 | 0.00000641 | |
| 0.9 | 4.0 | 0.00297109 | −0.00200533 | 0.00057744 | 0.00455810 | |
| 7.1 | 5.8 | 0.01427116 | −0.00045889 | 0.03550063 | 0.00015444 | |
| Actual Value | Bias | MSE | ||||
|---|---|---|---|---|---|---|
| 50 | 2.7 | 5.0 | 0.00054404 | 0.13424700 | 0.00109551 | 0.20695579 |
| 0.4 | 1.2 | 0.00024567 | 0.03275857 | 0.00041864 | 0.01195999 | |
| 6.0 | 2.5 | −0.00002168 | 0.06835325 | 0.02161847 | 0.05192641 | |
| 4.0 | 3.4 | 0.00185659 | 0.08997153 | 0.00521251 | 0.09539035 | |
| 1.0 | 8.0 | 0.00010181 | 0.21835854 | 0.00005868 | 0.53164800 | |
| 100 | 2.7 | 5.0 | 0.00012046 | 0.06377031 | 0.00055694 | 0.09509012 |
| 0.4 | 1.2 | 0.00005101 | 0.01519026 | 0.00021246 | 0.00547655 | |
| 6.0 | 2.5 | 0.00191769 | 0.03297888 | 0.01099844 | 0.02386620 | |
| 4.0 | 3.4 | −0.00004923 | 0.04701171 | 0.00263820 | 0.04439236 | |
| 1.0 | 8.0 | 0.00009827 | 0.11057419 | 0.00002980 | 0.24582360 | |
| 200 | 2.7 | 5.0 | 0.00015504 | 0.03299212 | 0.00028047 | 0.04585339 |
| 0.4 | 1.2 | 0.00006551 | 0.00866507 | 0.00010677 | 0.00265802 | |
| 6.0 | 2.5 | −0.00106277 | 0.01625314 | 0.00553891 | 0.01145699 | |
| 4.0 | 3.4 | −0.00002407 | 0.02295567 | 0.00133064 | 0.02123514 | |
| 1.0 | 8.0 | 0.00000852 | 0.05090923 | 0.00001503 | 0.11715066 | |
| 500 | 2.7 | 5.0 | 0.00021558 | 0.01327469 | 0.00011277 | 0.01789692 |
| 0.4 | 1.2 | −0.00008941 | 0.00435633 | 0.00004284 | 0.00104215 | |
| 6.0 | 2.5 | −0.00042358 | 0.00648252 | 0.00222639 | 0.00447192 | |
| 4.0 | 3.4 | −0.00007789 | 0.00855609 | 0.00053513 | 0.00826466 | |
| 1.0 | 8.0 | 0.00003954 | 0.01663711 | 0.00000604 | 0.04559331 | |
| n | mean | median | min | max | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
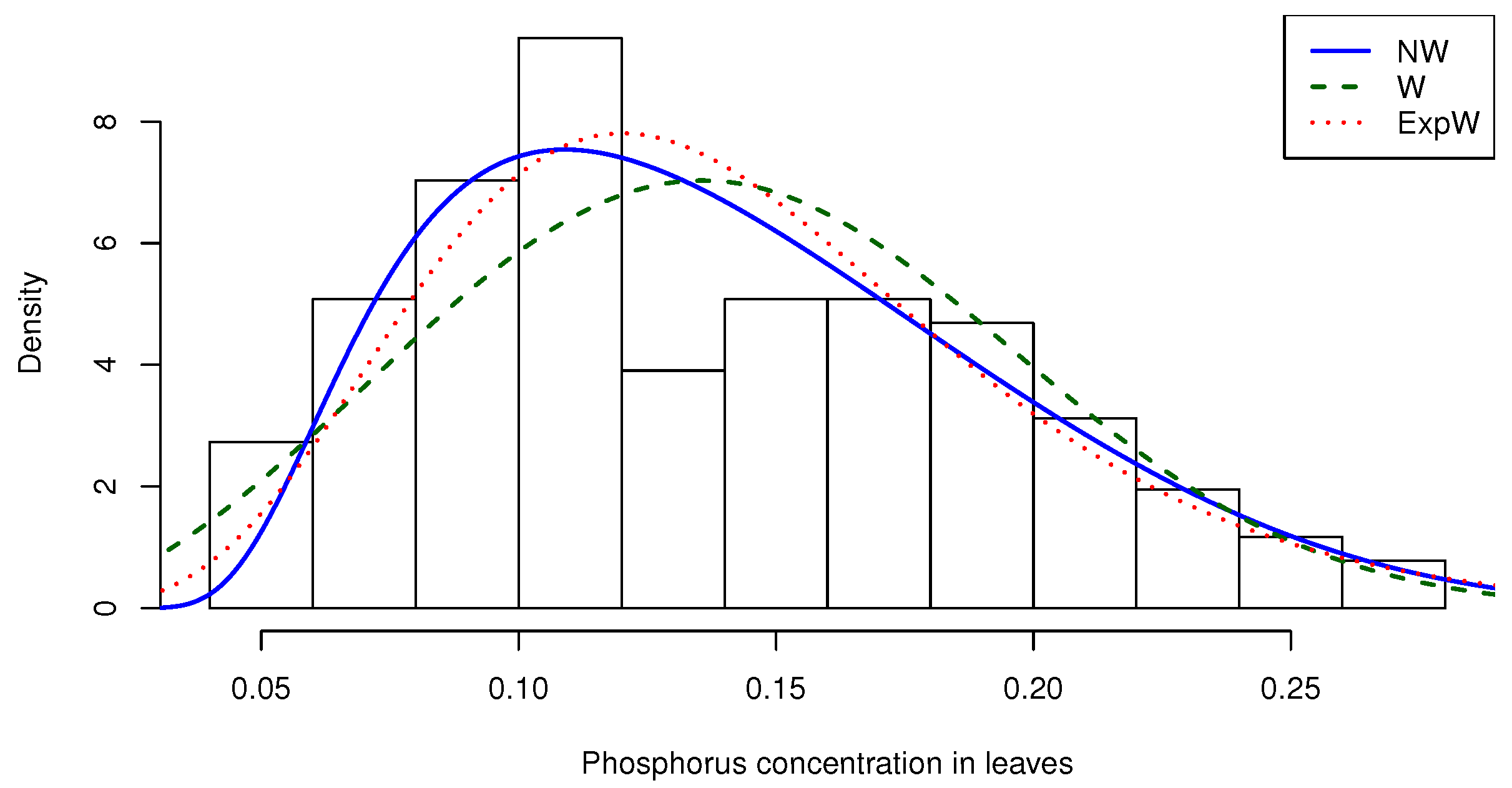
| 128 | 0.14078 | 0.13 | 0.05 | 0.28 | 0.00296 | 0.45438 | −0.64478 |
| Distribution | Parameters | Estimates (SE) | AIC | CAIC | BIC | HQIC |
|---|---|---|---|---|---|---|
| NW | k | 0.8398477 (0.0445182) | ||||
| 0.2049909 (0.0074017) | ||||||
| W | k | 2.8185566 (0.1919639) | ||||
| 0.1584836 (0.0052564) | ||||||
| ExpW | k | 1.5321145 (0.5023377) | ||||
| 0.0939938 (0.0374090) | ||||||
| a | 3.5076974 (2.6763009) | |||||
| MOEW | k | 3.9300962 (0.2426080) | ||||
| 8.9163819 (4.5940983) | ||||||
| a | 0.0031628 (0.0007240) | |||||
| KwW | k | 1.1503912 (0.3443931) | ||||
| 0.1953371 (0.1291154) | ||||||
| a | 3.3444607 (1.5352029) | |||||
| b | 7.5480698 (10.206142) | |||||
| BW | k | 0.8477957 (0.2166409) | ||||
| 0.3304922 (0.4395169) | ||||||
| a | 9.0436364 (4.5271059) | |||||
| b | 15.211970 (22.481984) | |||||
| McW | k | 5.6665646 (8.3928707) | ||||
| 0.5912941 (0.5124852) | ||||||
| a | 13.441193 (23.051917) | |||||
| b | 14.363802 (18.264058) | |||||
| c | 0.0870787 (0.1234075) |
| Distribution | ||
|---|---|---|
| NW | 0.454008 | 0.079841 |
| W | 1.156994 | 0.207118 |
| ExpW | 0.784451 | 0.138403 |
| MOEW | 1.123759 | 0.183128 |
| KwW | 0.907239 | 0.163617 |
| BW | 0.750593 | 0.130501 |
| McW | 0.758296 | 0.137509 |
| n | Mean | Median | min | max | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
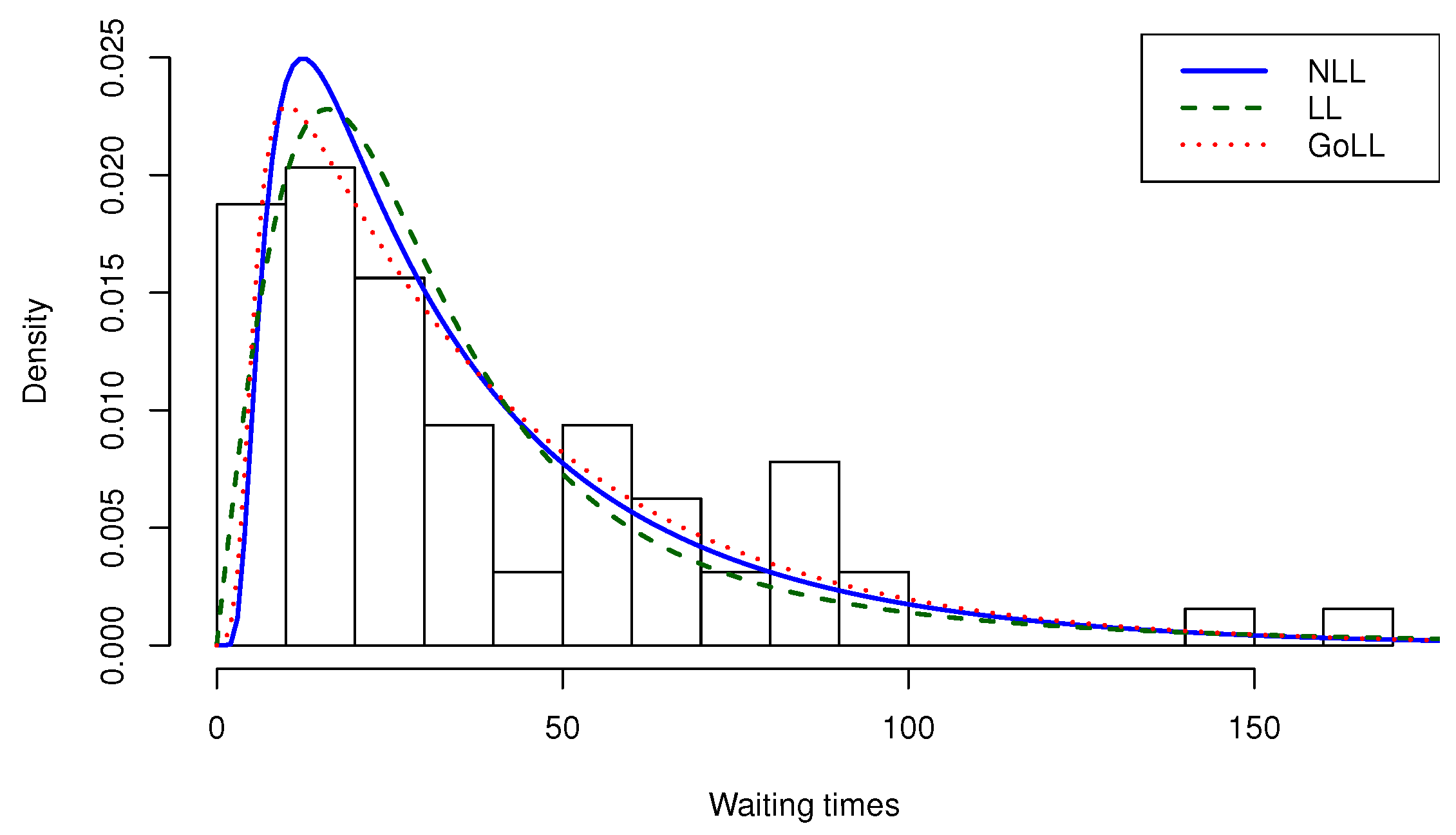
| 64 | 39.82812 | 28 | 7 | 169 | 1139.097 | 1.54641 | 2.77108 |
| Distribution | Parameters | Estimates (SE) | AIC | CAIC | BIC | HQIC |
|---|---|---|---|---|---|---|
| NLL | 28.71747 (2.751091) | 587.5681 | 587.7649 | 591.8859 | 589.2691 | |
| 0.568200 (0.042998) | ||||||
| LL | 28.27831 (3.203986) | 597.1497 | 597.3464 | 601.4674 | 598.8506 | |
| 1.969345 (0.198878) | ||||||
| ExpLL | 7.394859 (6.479904) | 597.3629 | 597.7629 | 603.8396 | 599.9144 | |
| 1.461528 (0.197256) | ||||||
| a | 4.572569 (4.470086) | |||||
| BLL | 7.445103 (10.72863) | 596.186 | 596.864 | 604.8215 | 599.588 | |
| 0.484528 (0.223626) | ||||||
| a | 17.28664 (13.82502) | |||||
| b | 9.285354 (9.566756) | |||||
| KwLL | 2.107772 (5.325557) | 596.68 | 597.358 | 605.3156 | 600.082 | |
| 0.511324 (0.130629) | ||||||
| a | 12.14489 (12.25210) | |||||
| b | 11.42477 (8.749787) | |||||
| GoLL | 5.667167 (1.680598) | 591.7172 | 592.3952 | 600.3528 | 595.1192 | |
| 4.348435 (1.450980) | ||||||
| a | 0.035617 (0.017111) | |||||
| b | 0.234894 (0.100666) |
| Distribution | ||
|---|---|---|
| NLL | 0.612291 | 0.0803799 |
| LL | 1.019129 | 0.1413872 |
| ExpLL | 1.138218 | 0.1617136 |
| BLL | 0.837211 | 0.1141264 |
| KwLL | 0.818072 | 0.1118931 |
| GoLL | 0.605822 | 0.0805111 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silveira, F.V.J.; Gomes-Silva, F.; Brito, C.C.R.; Cunha-Filho, M.; Gusmão, F.R.S.; Xavier-Júnior, S.F.A. Normal-G Class of Probability Distributions: Properties and Applications. Symmetry 2019, 11, 1407. https://doi.org/10.3390/sym11111407
Silveira FVJ, Gomes-Silva F, Brito CCR, Cunha-Filho M, Gusmão FRS, Xavier-Júnior SFA. Normal-G Class of Probability Distributions: Properties and Applications. Symmetry. 2019; 11(11):1407. https://doi.org/10.3390/sym11111407
Chicago/Turabian StyleSilveira, Fábio V. J., Frank Gomes-Silva, Cícero C. R. Brito, Moacyr Cunha-Filho, Felipe R. S. Gusmão, and Sílvio F. A. Xavier-Júnior. 2019. "Normal-G Class of Probability Distributions: Properties and Applications" Symmetry 11, no. 11: 1407. https://doi.org/10.3390/sym11111407
APA StyleSilveira, F. V. J., Gomes-Silva, F., Brito, C. C. R., Cunha-Filho, M., Gusmão, F. R. S., & Xavier-Júnior, S. F. A. (2019). Normal-G Class of Probability Distributions: Properties and Applications. Symmetry, 11(11), 1407. https://doi.org/10.3390/sym11111407





