A Haptic Model of Entanglement, Gauge Symmetries and Minimal Interaction Based on Knot Theory

Abstract

The Heegaard splitting of $SU(2)$ is a particularly useful representation for quantum phases of spin j-representation arising in the mapping $S_1\to S_3$, which can be related to $(2j,2)$ torus knots in Hilbert space. We show that transitions to homotopically equivalent knots can be associated with gauge invariance, and that the same mechanism is at the heart of quantum entanglement. In other words, (minimal) interaction causes entanglement. Particle creation is related to cuts in the knot structure. We show that inner twists can be associated with operations with the quaternions $(I,J,K)$, which are crucial to understand the Hopf mapping $S_3\to S_2$. We discuss the relationship between observables on the Bloch sphere $S_2$, and knots with inner twists in Hilbert space. As applications, we discuss selection rules in atomic physics, and the status of virtual particles arising in Feynman diagrams. Using a simple paper strip model revealing the knot structure of quantum phases in Hilbert space including inner twists, a $haptic$ model of entanglement and gauge symmetries is proposed, which may also be valid for physics education.

1. Introduction

The importance of topology for various applications in physics is constantly increasing, in particular, in quantum information theory [1,2]. Recently, a haptic ‘paper strip’ model for quantum phases of spin j-states was introduced, which generalizes the Dirac belt describing a spin $1/2$ particle, to general spin j in Hilbert space [3,4].

In this paper, we show that quantum entanglement and gauge symmetries can also be modeled using that paper strip representation of the emerging knots. In all cases, unitary time development is at the heart of the physical problems, thus, the geometry of $SU(N)$ is the common feature that must be understood. In Section 2 and Section 3, we study the situation for $SU(2)$ in detail, based on the Heegaard splitting and the paper strip model of quantum phases for spin j-representations [3], and the Hopf mapping $S_3\to S_2$ to the Bloch sphere. In particular, we argue that albeit the usual Bloch sphere representation is sufficient for the description of observables, crucial features in Hilbert space which will be relevant for our haptic model of entanglement and gauge symmetry are invisible, since knots can only arise in Hilbert space. In Section 4, we apply the paper strip model to the $SU(2)$-Chern–Simons gauge field and discuss the importance of inner twists in addition to the knot structure.

In Section 5, the simplest example for quantum entanglement is described, arising due to the $SU(4)$-interaction between two qubits. We propose a haptic model of Bell states based on transitions to homotopically equivalent knots in Hilbert space. In Section 6, gauge symmetries are introduced in close analogy to entanglement arising due to (minimal) interaction. As applications, we consider selection rules in atomic physics, and the role of Feynman diagrams in QED. In both cases, transitions to homotopically equivalent knots describing the quantum phase are the key ingredient of our model, revealing the close relation between minimal interaction and entanglement.

The main purpose of the present paper is the introduction of haptic models giving some topological insights into some key ideas of modern physics. If we compare mathematics to a musical score, then in case of music the direct and more intuitive representation of music as soundwave is obvious. In some sense, we try to reveal this direct and more intuitive representation that is hidden within the mathematical formalism of modern quantum physics using haptic models and visualizations.

2. The Hopf Mapping $S_3\to S_2$ for a Single Qubit

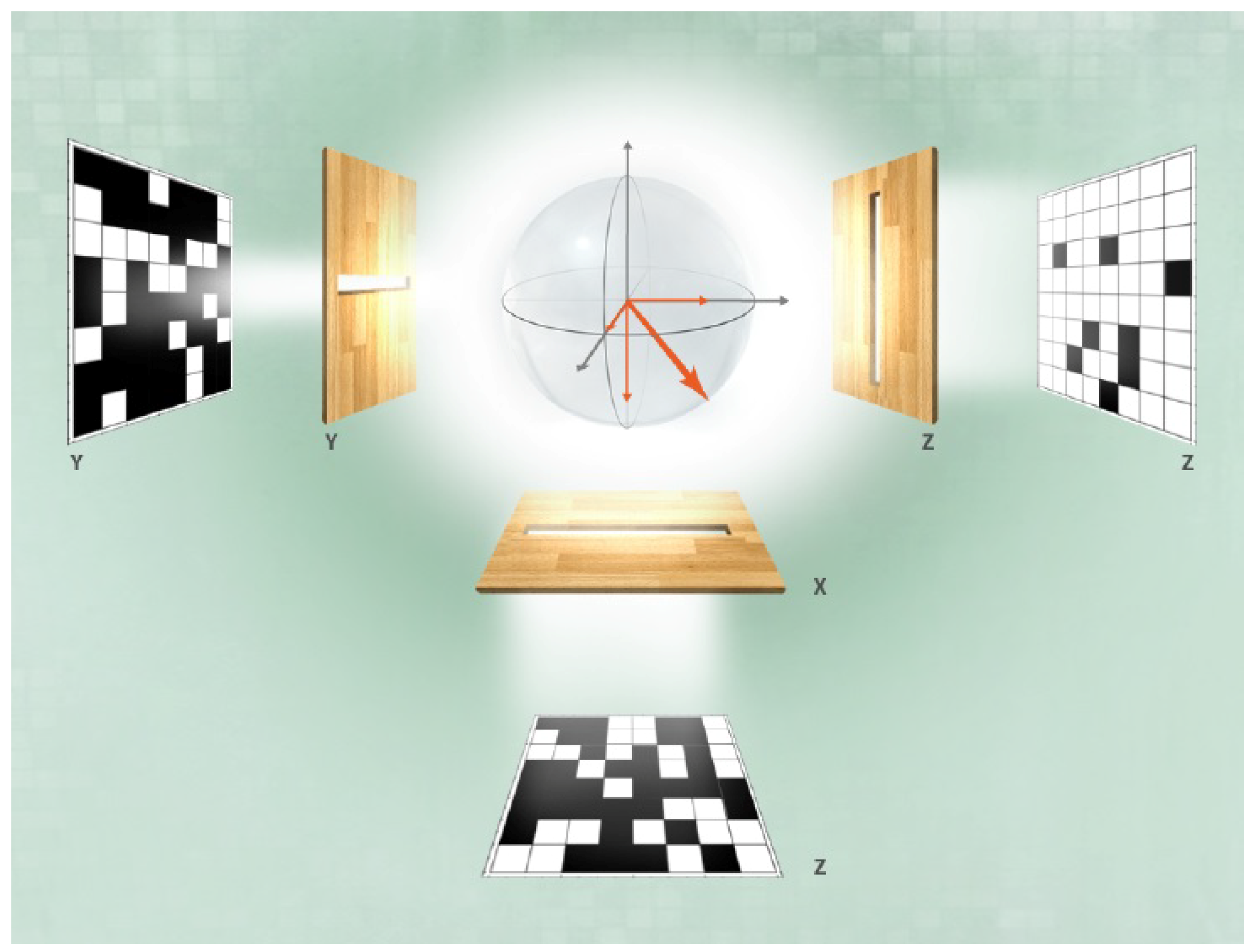
We introduce the standard basis $|0\rangle ,|1\rangle$ for an arbitrary qubit. The general (pure) orthonormal superposition states of a qubit are given by $|0_n\rangle =u|0\rangle +v|1\rangle$ and $|1_n\rangle =-\overline{v}|0\rangle +\overline{u}|1\rangle$, with complex amplitudes $(u,v)\in C^2$ fulfilling ${|u|}^2+{|v|}^2=1$. Geometrically, all these spin states form the hypersphere $S_3$ in four dimensions. In many applications, the geometry of $S_3$ is not considered in detail, as observables such as e.g., $n_k= \langle 0_n|{\sigma }_k|0_n\rangle$ are obtained after Hopf mapping $S_3\to S_2$, where ${\sigma }_k$ denote the Pauli matrices. As shown in Figure 1, the difference $n_k=p_k^{+}-p_k^{-}$ between the probabilities for the eigenvalues $\pm 1$ define the coordinates of the vector $\overrightarrow{n}=(n_x,n_y,n_z)$ on the Bloch sphere, which just defines the Hopf mapping $S_3\to S_2$ in case of spin $\frac{1}{2}$ [5,6]. Please note that the state $|1_n\rangle$ orthogonal to $|0_n\rangle$ is mapped to the vector $-\overrightarrow{n}$ on the Bloch sphere.

In this paper, we want to show that a more detailed understanding of the geometry of the qubit (and its generalization to higher spin states) in $S_3$ is important not only in order to reveal the knot structure of bosonic and fermionic quantum states, but also to find some appropriate models for gauge interaction and entanglement.

First, we introduce some coordinates on $S_3$. Similar to [4], we introduce the homogeneous coordinates $(Z_0,Z_1)\equiv (u,v)$, and define the mapping $C^2\to C{P}^1$ as $z=u/v$. The single complex coordinate z on $C{P}^1$ is equivalent to the Bloch sphere $S_2$ via stereographic projection, $S_2\simeq C{P}^1$. All observables can be described on the Bloch sphere (or $C{P}^1$), which is $2\pi$-periodic. For this reason, we denote $S_2$ as ‘$(2\pi )$-realm’. The points $(\pm u,\pm v)$ are different on $S_3$, which means that in $S_3$, periodicity is doubled to $(4\pi )$. Indeed, introducing the quaterions $I,J,K$ as

$$\begin{array}{c}\hfill I\equiv -i{\sigma }_x,J\equiv -i{\sigma }_y,K\equiv -i{\sigma }_z\end{array}$$

(1)

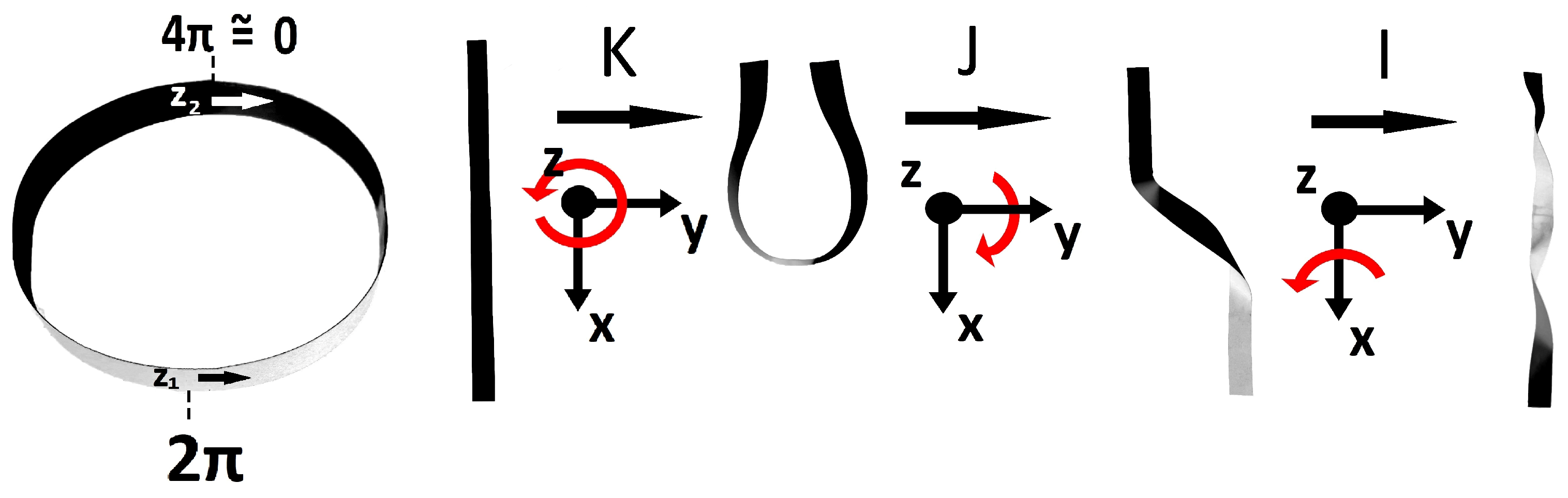
we may view the sign change $(\pm u,\pm v)$ as a rotation around $2\pi$ in $S_3$, since $K^2(u,v)=(e^{-i(2\pi )/2}u,e^{+(2\pi )/2}v)=-(u,v)$. Only after a $(4\pi )$-rotation, the original point is reached, $K^4=1$. For this reason, we call $S_3$ the ‘$(4\pi )$-realm’. The operations with quaternions induce $inner$ $twists$ on the (generalized) Dirac belt as shown in Figure 2.

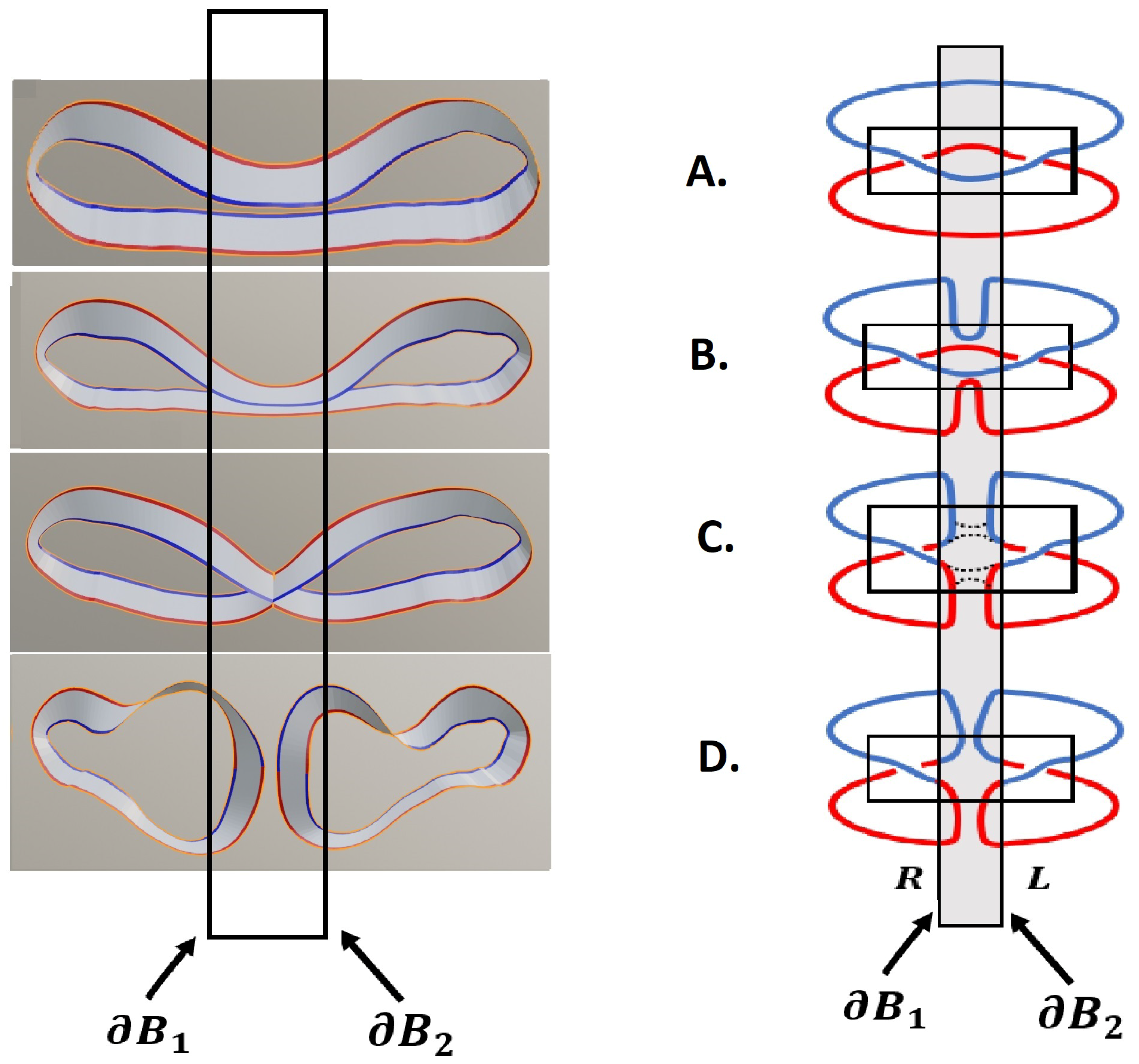
We want to introduce the so-called Heegaard splitting of $S_3$ [7], which is convenient to describe the relation between the $(4\pi )$-realm and the $(2\pi )$-realm. The geometry of $S_3$ can be seen as two unit balls $B_1$ and $B_2$ in three dimensions, where the two-dimensional boundaries $\partial B_1$ and $\partial B_2$ are identified via a homeomorphism $\mathcal{F}$ (The Heegaard splitting of $S_3$ can also be done using the boundary of torus $T_1$ and $T_2$ identified via a homeomorphism). Using this decomposition, the Hopf mapping $S_3\to S_2$ can be understood as follows: In $S_3$, $(p,2)$ (torus) knots emerge for the spin j representation with $p=2j$ [3]. The knot structure in the full Hilbert space—the $(4\pi )$-realm - is projected to the boundary, where observables are defined—the $(2\pi )$-realm. This mapping is 2:1, since the knots in the two unit balls $B_1$ and $B_2$ are projected to the boundaries $\partial B_1$ and $\partial B_2$, which are then identified by $\mathcal{F}$ to become $C{P}^1$. After stereographic projection, the $knot$ structure in the three-dimensional bulk $S_3$ is mapped to a $node$ structure on the boundary, which is nothing but the Bloch sphere $S_2$ as shown in Figure 3 and Figure 4 for the case $j=1/2$. Here, the so-called Dirac belt describing the quantum phase of spin $j=1/2$ states emerges in $S_3$. 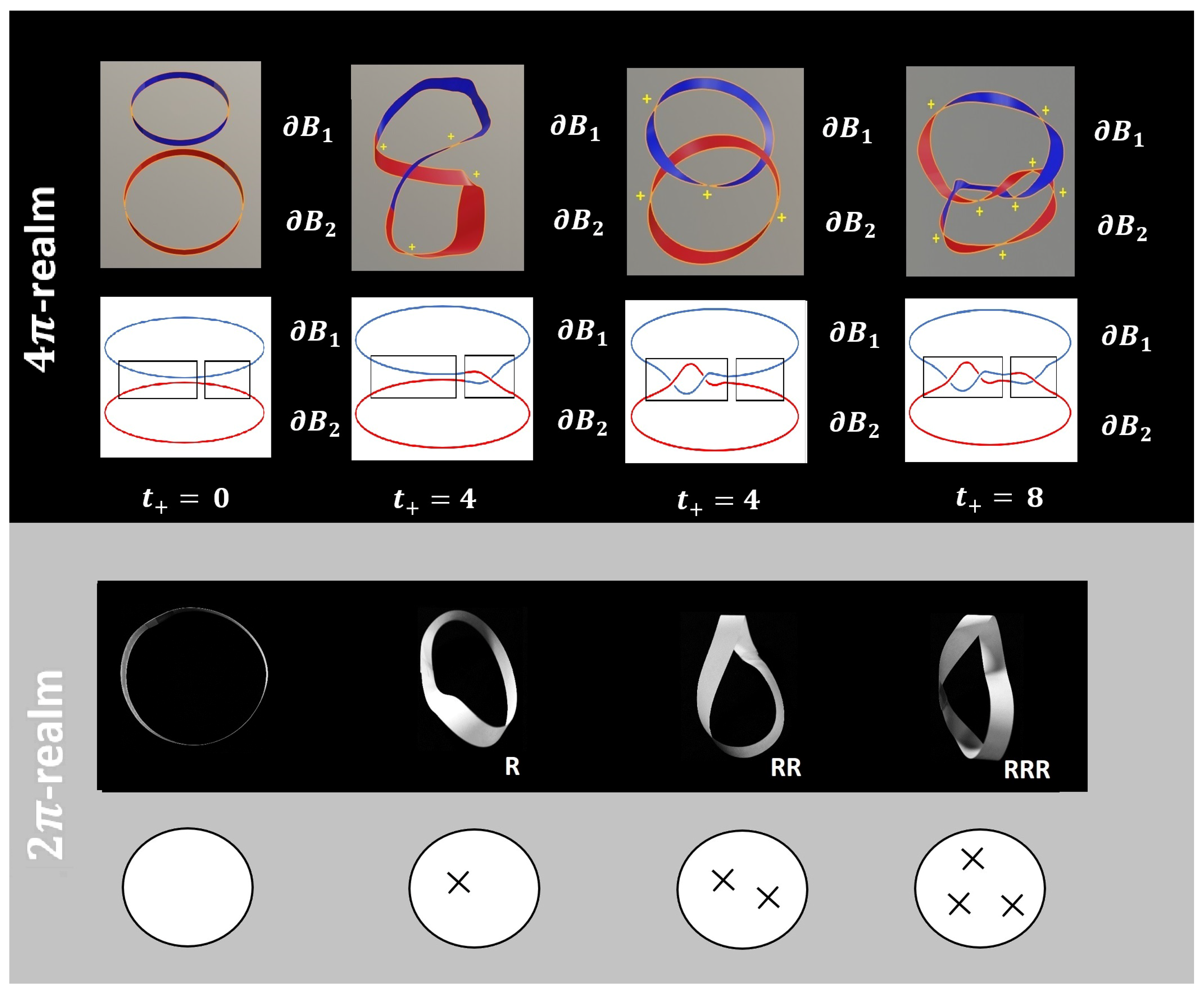The Heegaard splitting helps to visualize the homotopy mappings $S_1\to S_2$ and $S_1\to S_3$. Indeed, two traversals of a great circle on $S_2$ are necessary to complete the homotopy in $S_3$, see Figure 3. Using the paper strip model, the relation between inner twists and the Möbius strip can easily be derived by considering the double traversal $(0,4\pi )$. Due to the four inner twists, the Dirac belt it is equivalent to a Möbius strip, which is mapped after identification of the boundaries $\partial B_1$ and $\partial B_2$ to the stellar representation ${\varphi }_{j=1/2}=(z-z_0)$. The node $z=z_0$ corresponds to the point $-\overrightarrow{n}$ of the Bloch sphere, since the amplitude of the state $|0_n\rangle$ vanishes at $|1_n\rangle$.

We want to model the relation between knots and nodes using the paper strip model using the explicit coordinates

$$\begin{array}{c}\hfill Z_0\equiv u=e^{i\frac{\tau }{2}-i\frac{\varphi }{2}}cos[\frac{\theta }{2}]\\ \hfill Z_1\equiv v=e^{i\frac{\tau }{2}+i\frac{\varphi }{2}}sin[\frac{\theta }{2}].\end{array}$$

(2)

We choose the qubits $|0\rangle ,|1\rangle$ in the standard basis, described by the vectors ${\overrightarrow{n}}_0=(1,0,0)$ and ${\overrightarrow{n}}_1=(-1,0,0)$ and corresponding nodes at the antipodes, as shown in Figure 5 (in the stellar representation, these nodes would be mapped to $z(n_0)=0$ and $z(n_1)\to \infty$). The probability to detect the eigenvalue $+1$ at position $\overrightarrow{n}$ is given by $p_n^{+}=|\langle 0|0_n\rangle {|}^2={|u|}^2$ and $p_n^{+}=|\langle 1|0_n\rangle {|}^2={|v|}^2$. We wish to model the homotopy on the equatorial line with $\theta =\pi /2$. Here, the corresponding amplitudes (for $\tau =0$) are $u=e^{i\varphi /2}/\sqrt{2}$ and $v=e^{-i\varphi /2}/\sqrt{2}$. In the paper strip model, these amplitudes can be modeled as Möbius strips with one right-moving (R) and with one left-moving (L) twist, respectively. The Heegard splitting also helps to visualize the homotopy mappings $S_1\to S_2$ and $S_1\to S_3$. Indeed, a double winding on $S_2$ is necessary to complete the homotopy in $S_3$, see Figure 3.

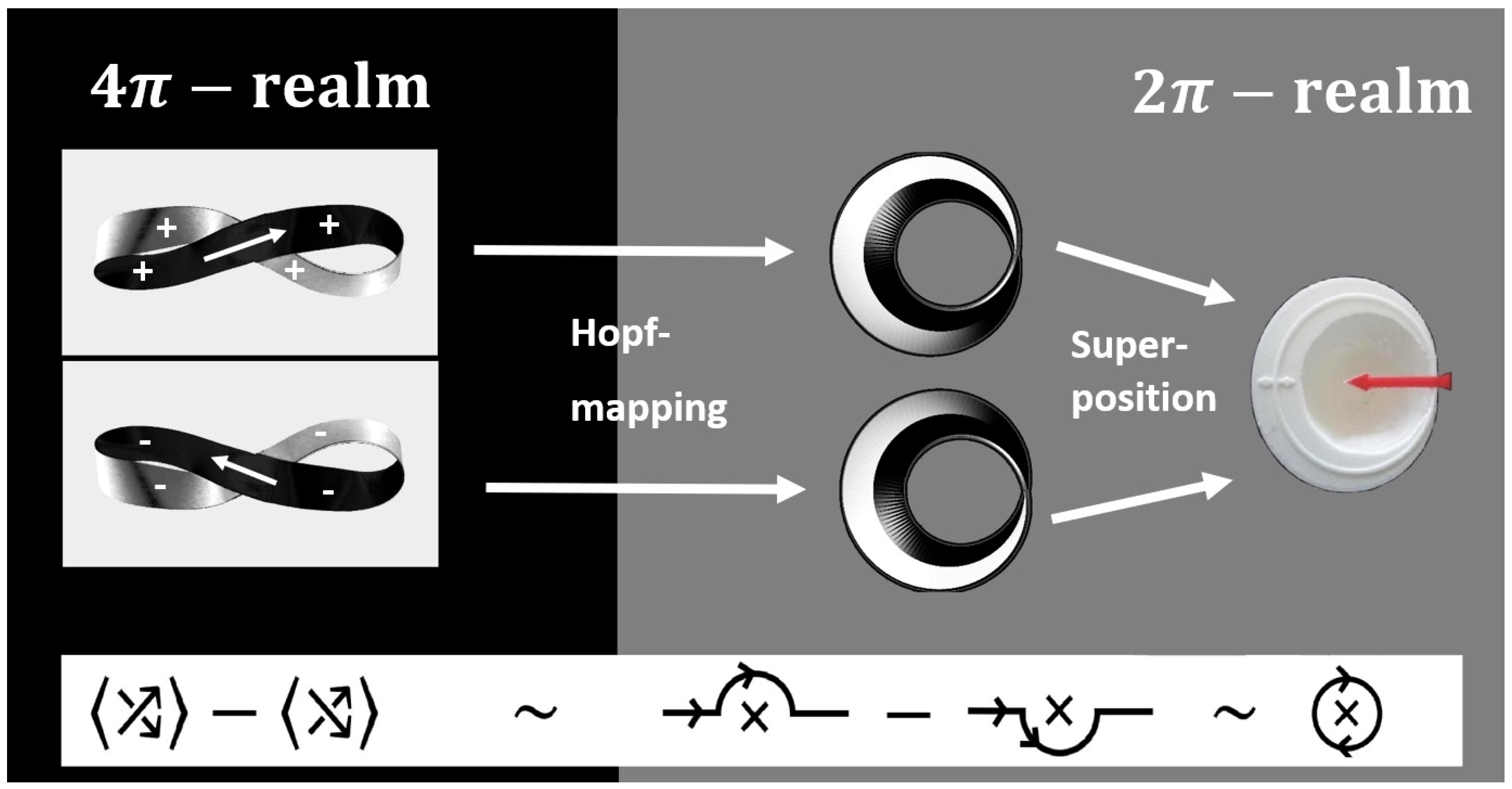
For the superposition state $|-\rangle =\frac{1}{\sqrt{2}}(|0\rangle -|1\rangle )$, the corresponding amplitude at $\theta =\pi /2$ is given by $\frac{1}{\sqrt{2}}(e^{i\varphi /2}-e^{-i\varphi /2})$ which indeed has a node at $\theta =\pi /2,\varphi =0$, i.e., at $\overrightarrow{n}=(0,+1,0)$.

However, this is not the most general situation in $S_3$. We have chosen a particularly suitable homotopy, where the Dirac belt has already been glued together when we traverse twice the equatorial line in $S_2$. In general, the homotopy $S_1\to S_3$ can be anywhere in the unit balls $B_1$ and $B_2$, and describe a Dirac belt with four inner twists, as depicted in Figure 4. The superposition translates into a knot theoretic relation, which—in a somewhat sloppy notation—is shown in Figure 4. Here, it is sufficient to note that the nodes on the Bloch sphere indeed translate to knots in $S_3$. The exact relations valid for Homfley-polynomials are discussed in [8]. Please note that the Dirac belt would be equivalent to the trivial knot, if inner twists were ignored.

3. Knots and Inner Twists for Spin j States

Similar to [3], spin j states with homogeneous coordinates $(Z_0,Z_1,\dots Z_{2j})$ are defined as

$$\begin{array}{c}\hfill Z_k={\left(\genfrac{}{}{0pt}{}{2j}{k}\right)}^{1/2}{u}^k{v}^{2j-k}.\end{array}$$

(3)

Here, ${|Z|}^2={\sum }_k{Z}_k^{*}{Z}_k={(|u|}^2+{|v|}^2{)}^{2j}=1^{2j}=1$ defines a $(2j)$-to-one mapping $S_3\to S_3$ [9].

Using the paper strip model, it is possible to map the quantum phase related to the homotopy for a spin j representation from the $4\pi$-realm to the $2\pi$-realm. As shown in Figure 6, we may choose the knot structure to be close to the boundaries $\partial B_1$ and $\partial B_2$. The $knots$ are mapped to $nodes$ as shown in Figure 6 due to the Hopf mapping. We can distinguish five different representations:

• The knot in the $(4\pi )$-realm $S_3$ including $t^{\prime }$ inner twists ($t^{\prime }=4l$ for bosons, $t^{\prime }=4l\pm 2$ for fermions), modeled with the paper strip in the $(4\pi )$-realm.
• The corresponding Jones polynomial $J_j(t)$, describing the knot structure of the spin j state on a homotopic loop in the $(4\pi )$-realm ignoring inner twists.
• The quantum phase of the observable in the $(2\pi )$-realm with $T=2j$ twists, obtained by ‘gluing together’ the two parts of the knot on the surface $\partial B_1\simeq \partial B_2$ upon identification of the two pieces $(0,2\pi )$ and $(2\pi ,4\pi )$.
• The corresponding stellar representation on $C{P}^1$ given by ${\varphi }_j(z)={\prod }_{k=0}^{2j}(z-z_k)$ with $2j$ nodes and $z=u/v$.
• Stereographic projection of the stellar representation on the Bloch sphere $S_2$. For bosons with $j=l$ the result is equivalent to spherical harmonics $Y_{lm}$.

4. A Haptic Model of Topological Gauge Fields

The main purpose of our paper is a topological understanding of gauge fields and entanglement. We $translate$ the operations of quaternions on the state $(u,v)$ to motions in $S_3$ (and the corresponding $(2j+1)$-representation of $I,J,K$)

For quaternions, the well-known identities

$$\begin{array}{c}\hfill IJK=JKI=KIJ=-1\end{array}$$

(4)

hold true and can be reproduced using the paper strip model shown in Figure 2 in the $(4\pi )$-realm [8]. Note that the operator $IJK=K^2=K^{-2}=-1$ corresponds to a rotation around $2\pi$ and induces two inner twists $t^{\prime }=\pm 2$.

As an application, we consider the well-known $SU(2)$ Chern–Simons action. We will not contribute anything new to the mathematical formalism; however, we want to model the interplay between the emerging knot structure in the $(4\pi )$-realm $S_3$, and observables in the $(2\pi )$-realm in the paper strip model. These insights will be helpful for the main purpose of our paper, i.e., a haptic model of gauge symmetries and entanglement. We use the notations introduced in [10].

In imaginary time formalism, we define the 1-form $A\equiv A_{\mu }d{x}_{\mu }$ with $\mu \in \{0,1,2,3\}$ (the gauge field), and the two-form $F=dA+A^2$ (the field strength). Then, the well-known relation

$$\begin{array}{c}\hfill \mathrm{Tr}(F\wedge F)=d\mathrm{Tr}(A\wedge dA+\frac{2}{3}A\wedge A\wedge A)\end{array}$$

(5)

holds. The Chern–Simons action $S_{C.S.}$ is then defined by

$$\begin{array}{ccc}\hfill S_{C.S.}& =& \frac{k}{4\pi }{\int }_M\mathrm{Tr}(F\wedge F)\hfill \\ \hfill & =& \frac{k}{4\pi }{\int }_{\partial M}\mathrm{Tr}(A\wedge dA+\frac{2}{3}A\wedge A\wedge A).\hfill \end{array}$$

(6)

Interestingly, the relation between bulk (4D manifold M) and boundary (3D-manifold $\partial M\simeq S_3$) emerges again. Note, however, that the boundary $S_3$ is three-dimensional, allowing for a knot structure. From the $g\in SU(2)$ gauge transformation

$$\begin{array}{c}\hfill A\to A_g=gU{g}^{-1}+gd{g}^{-1}\end{array}$$

(7)

only the term $gd{g}^{-1}$ makes a relevant contribution to the boundary integral $\mathcal{M}\simeq S_3$, leading to

$$\begin{array}{c}\hfill S_{C.S.}(A_g)=S_{C.S.}(A)-8{\pi }^{2}k\nu .\end{array}$$

(8)

Here, the so-called winding number $\nu$ is given by [10]

$$\begin{array}{c}\hfill \nu =-\frac{1}{24{\pi }^2}{\int }_{S^3}d\mu {ϵ}^{ijk}\mathrm{tr}[(g{\partial }_i{g}^{-1})(g{\partial }_j{g}^{-1})(g{\partial }_k{g}^{-1})]\end{array}$$

(9)

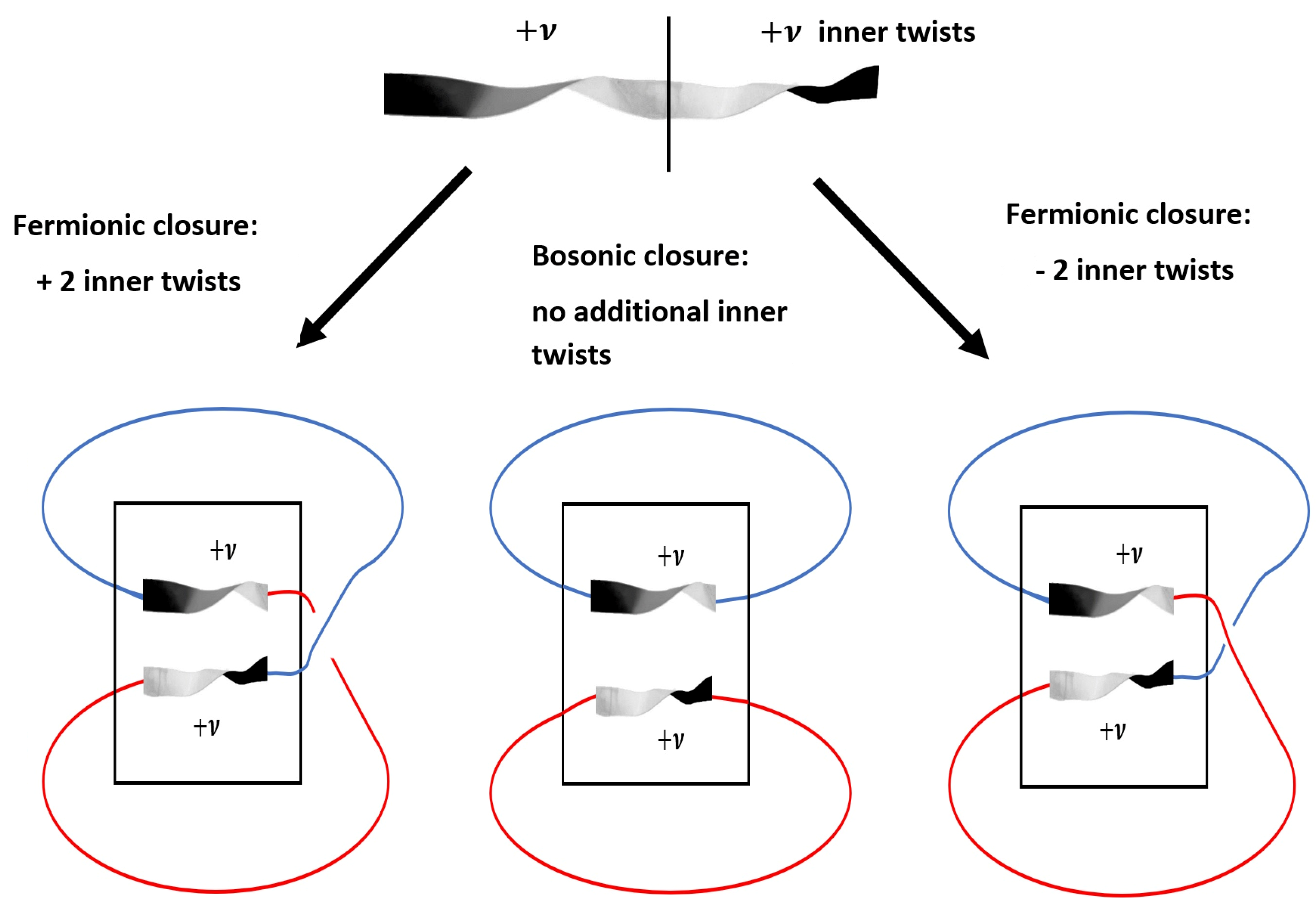
where g is a general SU(2) gauge field with $g^{†}g=\mathrm{id}$, and $d\mu$ is the Haar measure of $S_3.$ For the abelian case with $h_{\nu }=e^{i\nu \varphi }$ and $h\in U(1)$, this integral corresponds to $\nu =-\frac{1}{2\pi }\int hd{h}^{-1}$. The Chern–Simons action and its knot theoretic implications have been extensively studied [11]. For our purpose, we want to focus on the importance of the interplay between knots including their inner twists, and the mapping to observables onto the (generalized) Bloch sphere. For this purpose, we want to show that the number of inner twists $t^{\prime }$ of configurations contained in g is related to the winding number (9) as $t_{+}^{\prime }\le 2|\nu |$.

For the standard mapping, choose $(X,Y,Z,U)$ with $R^2=X^2+Y^2+Z^2+U^2$

$$\begin{array}{ccc}\hfill g_1& =& \frac{1}{R}(U+iX{\sigma }_x+iY{\sigma }_Y+Z{\sigma }_Z)\hfill \\ \hfill & =& \frac{1}{R}\left[\begin{array}{cc}U+iZ& iX+Y\\ iX-Y& U-iZ\end{array}\right].\hfill \end{array}$$

(10)

We obtain for the standard mapping $g_1$

$$\begin{array}{c}\hfill g_1{\partial }_X{g}_1^{-1}=-i{\sigma }_X\end{array}$$

(11)

and cyclic, i.e., for the standard mapping, (9) boils down to

$$\begin{array}{cc}\hfill -{\int }_{S^3}d\mu \frac{{ϵ}^{ijk}}{24{\pi }^2}\mathrm{tr}[(g_1{\partial }_i{g}_1^{-1})(g_1{\partial }_j{g}_1^{-1})(g_1{\partial }_k{g}_1^{-1})]& =\\ \hfill -(\frac{1}{2{\pi }^2}{\int }_{S^3}d\mu )\frac{1}{12}\mathrm{tr}(IJK+JKI+KIJ-IKJ-KJI-JIK)& =& 1\hfill \end{array}$$

The integral ${\int }_{S^3}d\mu =2{\pi }^2$ just gives the volume of $S_3$. We wrote the explicit contributions to compare with Figure 2 to find the relation of this integral to our haptic model. Indeed, the number of inner twists of each configuration is $t_{\nu =1}^{\prime }\le 2$.

As shown in [10], if the winding number of the gauge configuration $g_a$ and $g_b$ are given by ${\nu }_a$ and ${\nu }_b$, then the winding number of $g_a{g}_b$ is given by ${\nu }_a+{\nu }_b$. Because the Chern–Simons action (9) is a homotopy invariant, it suffices to consider the following class of mappings

$$g^{(\nu )}\equiv {(g\_1)}^{\nu }$$

(12)

Since $t_{\nu =1}^{\prime }\le 2$, due to the additivity of the winding number, it follows that $t_{\nu }^{\prime }\le 2\nu$ for $\nu \ge 0$.

Next, suppose the Chern–Simons gauge field interacts with fermions. If we define $u=U+iZ,v=Y+iX$, we find $\det (g^{(\nu )})={(|u|}^2+{|v|}^2{)}^{\nu }$. On the level of the elements of the group, compared to (3), we conclude that the class $g^{(\nu )}$ with winding number $\nu$ contains knot structures up to spin $\nu =2j$. For observables, the number of inner twists is crucial. As shown in [4], the inner twists must be (additional to the knot structures as defined by Jones polynomial) equal to $t^{\prime }=4j+2$ for fermions, and $t^{\prime }=4j$ for bosons. Indeed, the mapping $g^{(\nu )}$ allows for $t\prime \le 2\nu =4j$ inner twists. As shown in Figure 7, for a fermionic closure of the quantum phase, the number of inner twists is changed by $\pm 2$. For bosons, the number remains the same. Indeed, for bosons, we obtain $t^{\prime }=4j$ (corresponding to $2l\times 2l$ inner twists, related to $2l$ nodes in the stellar representation and l nodal lines e.g., for spherical harmonics). For fermions, we obtain $t^{\prime }=4j\pm 2$ inner twists, corresponding to spin states $j=l\pm 1/2$ with the odd number of $2j$ nodes in the stellar representation.

Using the paper strip model of gauge interaction shown in Figure 12, sum rules can be derived for the interaction of gauge fields with quarks [10], leading to a topological interpretation of Ward-Takahashi identities. As this application of the paper strip model is not the main purpose of the present paper, details will be shown elsewhere.

It is instructive to relate the topological meaning of the Chern–Simons action $S_{C.S.}$ with the Heegaard splitting. As shown in [8], the following relation holds

$$\begin{array}{c}\hfill \langle exp[S_{C.S.}]\rangle \rangle = B_1|\mathcal{G}|B_2\rangle \end{array}$$

(13)

with the vacuum given by $\langle B_1|B_2\rangle$, compare Figure 3. Here, $\mathcal{G}$ is a diffeomorphism connecting the two boundaries of the unit balls $B_1$ and $B_2$ with each other as

$$\begin{array}{c}\hfill \mathcal{G}:\partial B_1\to \partial B_2.\end{array}$$

(14)

Indeed, this diffeomorphism $\mathcal{G}$ just defines the knot structure contained in $S_{C.S.}$ and can be described using the paper strip model.

5. A Haptic Model of Quantum Entanglement

To model entanglement using the paper strip model, we start with the simplest possible case, i.e., the interaction of two qubits. The most general pure two-qubit state is obtained as the orbit $|\psi \rangle =h|00\rangle$ of the state $|00\rangle$, where $h\in SU(4)$ is a unitary rotation,

$$\begin{array}{ccc}\hfill |\psi \rangle & =& w_{00}|00\rangle +w_{01}|01\rangle +w_{10}|10\rangle +w_{11}|11\rangle \hfill \end{array}$$

(15)

with $w_{ij}\in \mathcal{C}$ and ${\sum }_{ij}{|w_{ij}|}^2=1$. Geometrically, this is the hypersphere $S^7$. For two qubits, we face the generalized Hopf mapping $S^7\to S^2\times S^2$. Much, if not all of the fascinating properties of quantum physics originate from the fact that all observables must be in the $(2\pi )$-realm, in contrast to the quantum states spreading around in the high-dimensional, complex Hilbert space. In what follows, we want to discuss some properties of this mapping in view of the knot theoretic structures discussed in the last section.

The degree of entanglement of the pure two-qubit state can be expressed by the so-called concurrence (for a review of concurrence, see e.g., [12])

$$\begin{array}{c}\hfill c=2|w_{00}{w}_{11}-w_{01}{w}_{10}|.\end{array}$$

(16)

For $c=0$, the qubits are independent and $|\psi \rangle$ is just given by a product state. Symmetric maximally entangled ($c=1$) Bell states can be expressed as (up to an irrelevant global phase factor)

$$\begin{array}{ccc}\hfill |{\mathsf{\Psi }}^{+}\rangle & =& \frac{1}{\sqrt{2}}(|0_a{1}_a\rangle + |1_a{0}_a\rangle ).\hfill \end{array}$$

(17)

All symmetric Bell states can be brought into this form by choosing an appropriate basis [13]. The antisymmetric Bell state is basis-independent:

$$\begin{array}{ccc}\hfill |{\mathsf{\Psi }}^{-}\rangle & =& \frac{1}{\sqrt{2}}(|0_a{1}_a\rangle -|1_a{0}_a\rangle )\hfill \\ \hfill & =& \frac{1}{\sqrt{2}}(|01\rangle -|10\rangle )\hfill \end{array}$$

(18)

In this model, any kind of interaction leads to entanglement. As an example for the interaction, we choose the Hamiltonian $\mathbf{H}=\hslash \omega ({\sigma }_z\times {\sigma }_z)$, leading to the unitary time development

$$\begin{array}{ccc}\hfill \mathbf{U}(t)& =& exp[i\omega t({\sigma }_z\otimes {\sigma }_z)]\hfill \\ & =& \mathrm{diag}(e^{i\omega t},e^{-i\omega t},e^{-i\omega t},e^{i\omega t})\hfill \end{array}$$

(19)

resulting in

$$\begin{array}{ccc}\hfill \mathbf{U}(t)|+\rangle |+\rangle & =& \frac{1}{2}{e}^{it\omega }(|0\rangle |0\rangle +|1\rangle |1\rangle )\hfill \\ & +& \frac{1}{2}{e}^{-it\omega }(|0\rangle |1\rangle +|1\rangle |0\rangle ).\hfill \end{array}$$

Due to the interaction, the state oscillates between a product state (at $t=0)$ and a maximally entangled state ($\omega t=\pi /4)$. Thus, the concurrence oscillates as $c=|sin(2\omega t)|$. Indeed, the maximally entangled state can be written (up to an irrelevant global phase) in the form (17), since

$$\begin{array}{cc}\hfill \frac{1}{\sqrt{2}}(|0_a{1}_a\rangle +|1_a{0}_a\rangle & =\\ \hfill e^{+i\pi /4}[e^{-i\pi /4}\frac{1}{2}|0\rangle |1\rangle +|1\rangle |0\rangle )& +& e^{i\pi /4}(|0\rangle |0\rangle +|1\rangle |1\rangle )]\hfill \end{array}$$

(20)

with the specific choice for $(u,v)$ given by

$$\begin{array}{ccc}\hfill |0_a\rangle & =& +u|0\rangle +v|1\rangle \equiv +cos(\pi /8)e^{-i\pi /4}|0\rangle +sin(\pi /8)e^{+i\pi /4}|1\rangle \hfill \\ \hfill |1_a\rangle & =& -\overline{v}|0\rangle +\overline{u}|1\rangle \equiv -sin(\pi /8)e^{-i\pi /4}|0\rangle +cos(\pi /8)e^{+i\pi /4}|1\rangle .\hfill \end{array}$$

For any other interaction Hamiltonian of the form $\mathbf{H}\propto ({\sigma }_k\times {\sigma }_l)$, a similar result holds with different choice for the basis $|0_a\rangle ,|1_a\rangle$.

Suppose we have created a maximally entangled Bell state. Independent of the way it is created, and independent of the explicit form of the basis $|0_a\rangle ,|1_a\rangle$, we can find visualizations and haptic models which reveal the unique features of quantum entanglement.

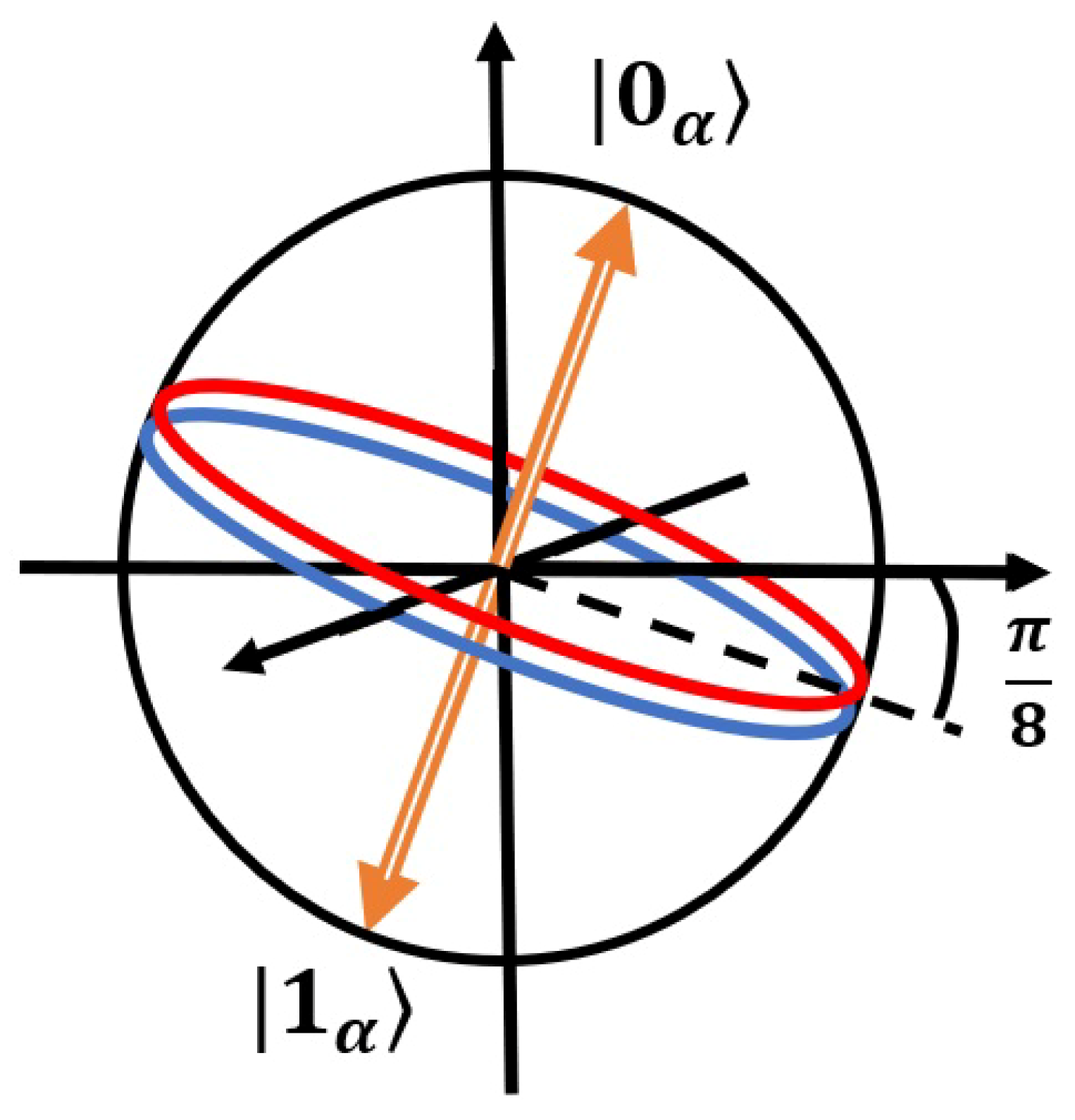
As proposed in [13], the state $|{\mathsf{\Psi }}^{+}\rangle$ can be visualized as shown in Figure 8 on the Bloch sphere. Geometrically, this corresponds to $R{P}^3$, i.e., a sphere $S^2$ with antipodes identified with each other.

Next, using the different representations for the quantum phase introduced in Section 3, we introduce a haptic model of maximally entangled Bell states using knot theory. Similar to Section 2, we consider a homotopy on $S_2$ which is perpendicular to the direction of the state vector on the Bloch sphere as shown in Figure 8 in the $(2\pi )$-realm, compare Figure 3 for the Heegard splitting in the $(4\pi )$-realm. For $|{\mathsf{\Psi }}^{+}\rangle$, the phase is constant, for $|{\mathsf{\Psi }}^{-}\rangle$ the phase vanishes in the $(2\pi )$-realm due to antisymmetry. We start with the knot structure ignoring inner twists. Obviously, for a constant phase, the knot structure is trivial, as shown in Figure 9 (middle part). However, using Type-2 Reidemeister moves, it becomes evident that a constant phase can also be viewed e.g., as the phase of the combination of two orthogonal qubits.

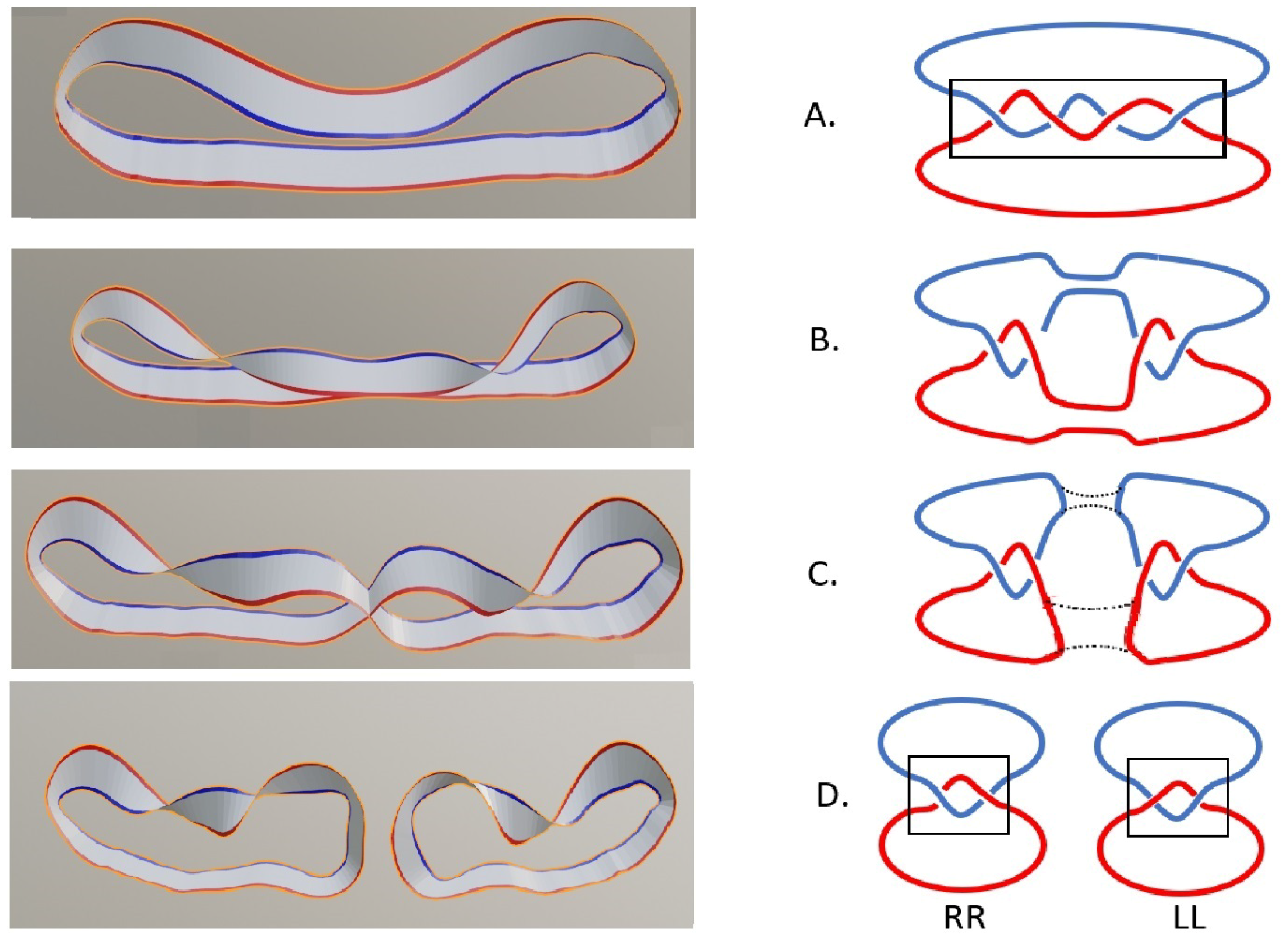
Now, we discuss the transition of the entangled state with constant phase to a pair of qubits in the paper strip model including twists, see Figure 10. Here, we restrict to the case near the boundaries $\partial B_1$ and $\partial B_2$, where we suppose that the quantum phases ranging from $(0,2\pi )$ and those ranging from $(2\pi ,4\pi )$ are glued together. The general case within the bulk of $B_1$ and $B_2$ will be discussed in Section 6. The Reidemeister move shown in Figure 9 correspond to the insertion of one R and one L twist by a single $rotation$ of one part of the paper strip, see Figure 10A. In Figure 10B, the rotated part meets the paper strip at an arbitrary, different position. Particle creation can be visualized as a transition which we call a $torus$ $splitting$: Angular momentum conservation implies that the total number of twists in the initial state $T_I$ in the $(2\pi )$-realm is the same as the total number of twists $T_F$ in the final state, $\Delta T=T_I-T_F=0$. This requirement uniquely defines the torus splitting, where two cuts arise as shown in Figure 10C and the phase is rejoined as shown in Figure 10D.

In the example shown in Figure 10, $T_I=0$, and $T_F=+1-1=0$. Before the splitting, a distinction between both particles is impossible, as shown in Figure 10A–C. In this sense, the entangled state is $one$ single quantum state.

Taking the partial trace, the entangled state is reduced to a mixed state

$$\begin{array}{c}\hfill {\mathrm{tr}}_B|{\mathsf{\Psi }}^{+}\rangle \langle {\mathsf{\Psi }}^{+}| = \frac{1}{2}|0_a\rangle \langle 0_a| + \frac{1}{2}|1_a\rangle \langle 1_a| = \frac{1}{2}\mathbf{id}.\end{array}$$

(21)

Please note that this result is independent of the choice of basis. Topologically, this corresponds to the splitting of both qubits; however, the association of both parts to the particles observed from Alice (A) of Bob (B) can emerge in two different permutations, compare to Figure 10D. This leads to observation of $|0_a\rangle \langle 0_a|$ with probability $p=1/2$, and $|1_a\rangle \langle 1_a|$ with probability $p=1/2$ by Alice and Bob.

Next, we discuss the case $|{\mathsf{\Psi }}^{-}\rangle$. As shown in Figure 11, the constant phase at boundary $\partial B_1$ and $\partial B_2$ in the $(4\pi )$-realm does not vanish, but is constant. In the $(2\pi )$-realm, both parts can be combined either in constructive or in destructive interference. In the latter case, the amplitude is zero in the $(2\pi )$-realm. The knot structure and the creation mechanism of the qubits remains the same as for the case of $|{\mathsf{\Psi }}^{+}\rangle$ discussed above, and shown in Figure 10.

In this example, the number of inner twists also remains constant, as two fermions are created with $\pm 4$ inner twists. Note however that the total number of inner twists may change, since bosons and fermions differ by $\pm 2$ twist due to the mechanism shown in Figure 7.

6. A Haptic Model of Gauge Symmetries

6.1. Minimal Interaction

In what follows, we will restrict to $U(1)$-gauge symmetry. In Figure 2, we may think that due to symmetry breaking, two degrees of freedom are frozen out and become immobile (This idea was first proposed by Christian Klein-Bösing.). We consider the phase of an arbitrary quantum state with J twists on a given homotopic loop. Gauge invariance just amounts to the fact that an arbitrary number of topologically equivalent quantum phases exist which all map to the same observable state in the $(2\pi )$-realm, compare Figure 3. In particular, we may include additional twists as $J=J+T-T$, see Figure 12. Let $h=e^{i\eta }$ be an additional $h\in U(1)$-phase factor in the ($2\pi$)-realm with T additional twists.

The insertion of this additional phase leads for the momentum operator $\overrightarrow{\mathbf{p}}=(\hslash /i)\overrightarrow{\nabla }$ to

$$\begin{array}{c}\hfill e^{i\eta }\overrightarrow{\mathbf{p}}{e}^{-i\eta }=\overrightarrow{\mathbf{p}}-\hslash \overrightarrow{\nabla }\eta .\end{array}$$

(22)

Obviously, gauge invariance in $not$ valid. It is well known that the requirement of gauge invariance leads to so-called minimal interaction, which is the cornerstone of the standard model of particle physics. We here discuss the key ideas in the non-relativistic case; the generalization to the relativistic case is straightforward and can be found in textbooks [10]. We introduce a generalized momentum operator $\overrightarrow{\mathsf{\Pi }}$ which is required to obey gauge invariance as follows:

$$\begin{array}{c}\hfill e^{i\eta }{\overrightarrow{\mathsf{\Pi }}}_{\eta }{e}^{-i\eta }=\overrightarrow{\mathsf{\Pi }}.\end{array}$$

(23)

This change of the momentum operator can be realized by the introduction of the gauge field $\overrightarrow{\mathbf{A}}$. With

$$\begin{array}{c}\hfill \overrightarrow{\mathsf{\Pi }}\equiv \overrightarrow{\mathbf{p}}-e\overrightarrow{\mathbf{A}}\end{array}$$

(24)

gauge invariance is maintained if the gauge field compensates for the transformation of the phase $e^{i\eta }$ of the wave function as

$$\begin{array}{ccc}\hfill {\psi }_{\eta }& =& e^{i\eta }\psi \hfill \\ \hfill {\overrightarrow{\mathbf{A}}}_{\eta }& =& \overrightarrow{\mathbf{A}}-\frac{\hslash }{e}\overrightarrow{\nabla }\eta .\hfill \end{array}$$

(25)

This is the $U(1)$-version (with explicit prefactor) of the $SU(2)$-gauge transformation defined in (7). As shown in Figure 12, the $combined$ change of the phase of the wave function and of the gauge field

$$\begin{array}{c}\hfill \psi =[\psi e^{i\eta }]e^{-i\eta }=[\psi e^{-i\frac{e}{\hslash }\int \overrightarrow{\mathbf{A}}d\overrightarrow{s}}][e^{+i\frac{e}{\hslash }\int \overrightarrow{\mathbf{A}}d\overrightarrow{s}}]\end{array}$$

(26)

just corresponds to T rotations of the paper strip, leading to a homotopically equivalent quantum phase with $J+T-T$ twists. Particle $creation$ corresponds topologically to torus splitting, where two cuts separate the quantum phases with the twists $J+T$ and $-T$. Then, $\psi e^{-i\frac{e}{\hslash }\int \overrightarrow{\mathbf{A}}d\overrightarrow{s}}$ is the phase of the wave function with $J+T$ twists, and $e^{+i\frac{e}{\hslash }\int \overrightarrow{\mathbf{A}}d\overrightarrow{s}}$ corresponds to the compensating phase of the gauge field with $-T$ twists. Please note that the situation for $J=0$ and $T=1$ exactly corresponds to the quantum phase of two entangled Bell states, compare Figure 10.

6.2. Selection Rules

As an application, we discuss transition amplitudes for bound electrons in the hydrogen atom. We want to demonstrate the power of the paper strip model for a topological understanding of gauge interaction. Using Figure 12, we can make predictions on allowed and forbidden transitions, i.e., on selection rules in the atom. Consider an electron in the quantum state $2s$ with $J=0$. As the photon has $l=1$, we have to deform the quantum phase by rotating ($T=2$) the closed paper strip twice, see Figure 13 and Figure 14A,B. Note that, when orbital angular momentum is included, $l\ge 1$ is also possible. After particle creation (corresponding in the paper strip model to the torus splitting, Figure 14C,D), the remaining phase of the electron must contain $\pm 2$ twists, which cannot be achieved in the $1s$ state with $l=0$. For this reason, the fact that the state $2s$ is metastable can be modeled using the paper strip model. On the other hand, the state $3s$ can decay to a $2p$ state with $m=\pm 1$. Due to the minimal interaction, the entangled state

$$\begin{array}{ccc}\hfill |3s\rangle & \to & \\ \hfill |{\psi }^{+}\rangle =\frac{1}{\sqrt{2}}(|2p,+1\rangle |L\rangle & +& |2p,-1\rangle |R\rangle )\hfill \end{array}$$

(27)

will emerge, which due to decoherence will decay to a mixture of left-circular polarized light with an electron in the state $m=+1$, or right-circular polarized light with an electron in the state $m=-1$, see Figure 13. Please note that we come to this prediction without explicit calculation, just by considering the topology of the quantum phase.

It is fascinating to see that the quantum phase does not change due to the interaction - the constant phase of the $|3s\rangle$ state is homotopically equivalent to the quantum phase of the entangled state $\frac{1}{\sqrt{2}}(|2p,+1\rangle |L\rangle +|2p,-1\rangle |R\rangle )$ and remains constant, showing that it is truly a $minimal$ interaction. Only after reduction to a mixed state, similar to the simple two-qubit model described in Section 5, by ignoring one of the possible realizations $|2p,+1\rangle |L\rangle$ or $|2p,-1\rangle |R\rangle$, the phase is changed. Formally, this is described by taking the partial trace over both possible polarizations of the photon

$$\begin{array}{ccc}\hfill {\mathrm{tr}}_{R,L}|{\psi }^{+}\rangle \langle {\psi }^{+}|& =& \\ \hfill \frac{1}{2}(|2p,+1\rangle \langle 2p,+1|& +& |2p,-1\rangle \langle 2p,-1|).\hfill \end{array}$$

(28)

In some sense, interaction can be viewed as ignorance of the remaining part of the entangled state. Physically, this may be achieved by decoherence due to interaction of the photon with the environment, which may be modeled as a heat bath.

It is instructive to compare the mathematical formalism necessary for the derivation of transition rules to the ansatz based on the paper strip model. The minimal interaction scheme leads in non-relativistic quantum physics to the Hamiltonian

$$\begin{array}{c}\hfill \mathbf{H}=\frac{1}{2m}(\overrightarrow{\mathbf{p}}-e{\overrightarrow{\mathbf{A}})}^2+V(r)={\mathbf{H}}_0+{\mathbf{H}}_{\mathrm{int}}.\end{array}$$

(29)

Gauge invariance can be proven using (23) and

$$\begin{array}{c}\hfill e^{i\eta }{{\overrightarrow{\mathsf{\Pi }}}_{\eta }}^2{e}^{-i\eta }={\overrightarrow{\mathsf{\Pi }}}^2.\end{array}$$

(30)

The free Hamiltonian ${\mathbf{H}}_0={\mathbf{p}}^2/(2m)$ describes the bound electron in the hydrogen atom; and ${\mathbf{H}}_{\mathrm{int}}$ describes the interaction with the gauge field as

$$\begin{array}{c}\hfill {\mathbf{H}}_{\mathrm{int}}=-\frac{e}{2m}[\overrightarrow{\mathbf{p}}\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{A}}\overrightarrow{\mathbf{p}}]+\frac{e^2}{2m}{\overrightarrow{\mathbf{A}}}^2.\end{array}$$

(31)

For the evaluation of transition amplitudes, we must consider the matrix elements $M_{if}$ between some initial and final state, defined by

$$\begin{array}{c}\hfill M_{if}=\langle f|{\mathbf{H}}_{\mathrm{int}}|i\rangle .\end{array}$$

(32)

For electromagnetic transitions, the relevant interaction is given by

$$\begin{array}{c}\hfill {\mathbf{H}}_{\mathrm{EM}}=-\frac{e}{m}\overrightarrow{\mathbf{p}}\overrightarrow{\mathbf{A}}\end{array}$$

(33)

with

$$\begin{array}{c}\hfill \overrightarrow{\mathbf{A}}=\sqrt{\frac{\hslash }{2{ϵ}_{0}V}}\sum _{\overrightarrow{k},\lambda }\frac{1}{\sqrt{{\omega }_k}}{\overrightarrow{e}}_{\lambda }[{\mathbf{a}}_{\lambda }{e}^{i\overrightarrow{k}\overrightarrow{r}}+{\mathbf{a}}_{\lambda }^{†}{e}^{-i\overrightarrow{k}\overrightarrow{r}}].\end{array}$$

(34)

The creation and annihilation operator fulfil the commutation relation

$$\begin{array}{c}\hfill [{\mathbf{a}}_{\lambda },{\mathbf{a}}_{{\lambda }^{\prime }}^{†}]={\delta }_{\lambda {\lambda }^{\prime }}.\end{array}$$

(35)

Here, $\lambda$ described the polarization of the photon created. In the $(2\pi )$-realm, all polarization states can be described on the Bloch sphere. Here, a subtle remark is in order. Since the photon is massless, no longitudinal modes emerge. For this reason, the degree of freedom of polarization is effectively two-dimensional. In contrast to spin, however, no sign change after a $2\pi$-rotation emerges.

In view of Fermi’s golden rule, only those modes of the gauge field with $E_{fi}=\hslash {\omega }_{fi}=\hslash c|{\overrightarrow{k}}_{fi}|$ are relevant for the transition. Thus, we may write to the interaction operator relevant for the creation and emission of a photon as

$$\begin{array}{c}\hfill {\mathbf{H}}_{\mathrm{cr}}=-\frac{e}{m}{A}_0({\overrightarrow{e}}_{\lambda }\overrightarrow{\mathbf{p}})e^{-i\overrightarrow{k}\overrightarrow{r}}{\mathbf{a}}_{\lambda }^{†}.\end{array}$$

(36)

The multipole expansion of $e^{i\overrightarrow{k}\overrightarrow{r}}=1+i\overrightarrow{k}\overrightarrow{r}+\dots$ leads all possible electric and magnetic transitions with creation of a single photon with $l\ge 1$. For leading order, the matrix element $M_{if}$ is given by

$$\begin{array}{c}\hfill M_{if}=i\sqrt{\frac{\hslash {\omega }_{fi}}{2{ϵ}_{0}V}}\langle f|{\overrightarrow{e}}_{\lambda }(e\overrightarrow{x})|i\rangle .\end{array}$$

(37)

Here, we used $[x_k,{\mathbf{H}}_0]=[x,\frac{{\overrightarrow{\mathbf{p}}}^2}{2m}]=i\hslash {\mathbf{p}}_k/m$. From this expression, the selection rule $\Delta l=1$ and $\Delta m=\pm 1$ can be derived [14], as anticipated using the paper strip model. Using similar arguments, the higher multipole transitions can also be modeled with the paper strip model.

Finally, we want to comment on the role of the creation and annihilation operators within the paper strip model. As obvious from Figure 12, torus splitting and torus merging correspond to the creation and annihilation of particles. Therefore, the expansion of the unitary time development operator $exp[-(i{\mathbf{H}}_{\mathrm{EM}}t)/\hslash ]$ describes multi-photon processes, where those terms containing ${\mathbf{H}}_{\mathrm{EM}}^k$ involve k torus splittings. Much the same as higher order terms in the multipole expansion for $k=1$, see Equation (36), terms with $k>1$ are suppressed by higher powers in the fine structure constant $\alpha =\frac{e^2}{4\pi {ϵ}_0\hslash c}\simeq 1/137$.

6.3. Feynman Diagrams and Entanglement

As a final example, we discuss the relation between Feynman diagrams and the paper strip model. We consider the interaction between two ingoing particles $I_1,I_2$, which after the interaction asymptotically lead to the final particles $F_1,F_2$. To be specific, we consider two examples: electron-electron and electron-positron interaction ( For simplicity, we do not discuss the creation of new particles, although this would be possible as straightforward generalization of the arguments given in the last section, including one additional torus splitting for each particle). In both cases, we denote by $p_1^{\mu },p_2^{\mu }$ the four-momentum of the ingoing particles, and by $q_1^{\mu },q_2^{\mu }$ those of the outgoing particles. The conservation of energy and momentum reads

$$\begin{array}{c}\hfill p_1^{\mu }+p_2^{\mu }=q_1^{\mu }+q_2^{\mu }\end{array}$$

(38)

with $\mu \in \{0,1,2,3\}$. The interaction can be described by generalizing the $U(1)$-gauge invariance from non-relativistic quantum physics to quantum field theory. The resulting theory is called QED. We want to emphasize that interaction and entanglement are closely related, as we will show in what follows. Let us denote the transition amplitude to the final state $(F_1,q_1^{\mu };F_2,q_2^{\mu })$ as $M(F_1,q_1^{\mu }|F_2,q_2^{\mu })$. If we exchange the four-momentum of the final particles, the matrix element is given by $M(F_1,q_2^{\mu }|F_2,q_1^{\mu })$.

In case of the scattering of two electrons, both contributions lead to an indistinguishable result. Thus, the total amplitude is given as a superposition

$$\begin{array}{ccc}\hfill M(e^{-}{e}^{-}\to e^{-}{e}^{-})& =& \\ \hfill M(F_1,q_1^{\mu }|F_2,q_2^{\mu })& -& M(F_1,q_2^{\mu }|F_2,q_1^{\mu })+\mathrm{o}({\alpha }^2).\hfill \end{array}$$

(39)

Finkelstein and Rubinstein have shown that the exchange of two particles is homotopically equivalent to a $2\pi$ rotation of one of the particles in the $(4\pi )$-realm [15]. As $K^2=-1$ corresponds to this $2\pi$-rotation, the exchange of two fermions leads to a minus sign. Indeed, the result is an entangled state, since the difference of both permutations lead to superposition of product states.

In case of electron-positron scattering, exchange of the electron and positron lead to a different final state, thus no superposition emerges. Instead, there exist different types of amplitudes, which we call scattering $M_s(F_1,q_1^{\mu }|F_2,q_2^{\mu })$ and annihilation $M_a(F_1,q_1^{\mu }|F_2,q_2^{\mu })$ processes, see Figure 15. The result is again an entangled state,

$$\begin{array}{ccc}\hfill M(e^{-}{e}^{+}\to e^{-}{e}^{+})& =& \\ \hfill M_s(F_1,q_1^{\mu }|F_2,q_2^{\mu })& +& M_a(F_1,q_1^{\mu }|F_2,q_2^{\mu })+\mathrm{o}({\alpha }^2).\hfill \end{array}$$

(40)

Since the interaction of two particles of spin $1/2$ is discussed, we conclude that the entangled state can be described as shown in Figure 10. Indeed, after the Reidemeister move, we may view the knot either as a composition of two spin $1/2$ particles, or as a gauge field with two twists. Since all these configurations are topologically equivalent, the question whether virtual particles ‘exist’ or not boils down to the question whether the infinite number of possible Reidemeister moves ‘exist’ or not: Of course they do, but the knot structure is only changed when a torus splitting divides the knot structure, which corresponds to particle creation. Thus, the quantum phase of the scattering and the annihilation processes cannot be separated from each other, since in the entangled state, all these configurations coexist as homotopically equivalent realizations.

It is instructive to consider the phase of the entangled state also in the $(4\pi )$-realm. The corresponding operations with Jones polynomials are derived in Appendix A. In Figure 16A), we show the constant phase of the entangled state of two spin $1/2$-particles (e.g., two electrons, or one electron and one positron) with total for momentum $q_1^{\mu }+q_2^{\mu }$. Homotopically equivalent is b.), which can also be viewed as gauge interaction, see Figure 12 with $J=0,T=1$. In contrast to the Feynman diagrams, which separate the different amplitudes, in the paper strip model, all possible contributions are contained as homotopically equivalent configurations in a single quantum phase of the entangled state.

In the $(4\pi )$-realm, the torus splitting can be described in two separate steps. The configuration c.) after one split is not an observable, as it does not meet the requirement on inner twists for Hopf mapping $S_3\to S_2$ discussed in Section 3. Instead, only after a second split as shown in d.), two Dirac belts emerge, with opposite inner twisting (e.). The four-momentum is distributed among them such that the sum is $q_1^{\mu }+q_2^{\mu }$.

Of course, for explicit calculations, Feynman diagrams are the (mathematical) tool to be addressed. However, a literal reading of single Feynman diagrams as certain physical processes occurring in space time can lead to misconceptions [16]. The advantage of the paper strip model is thus conceptual: The fascinating properties of entanglement can be grasped better, since the intermediate state $cannot$ be divided into separate processes. Rather, the close relation between interaction and entanglement becomes evident.

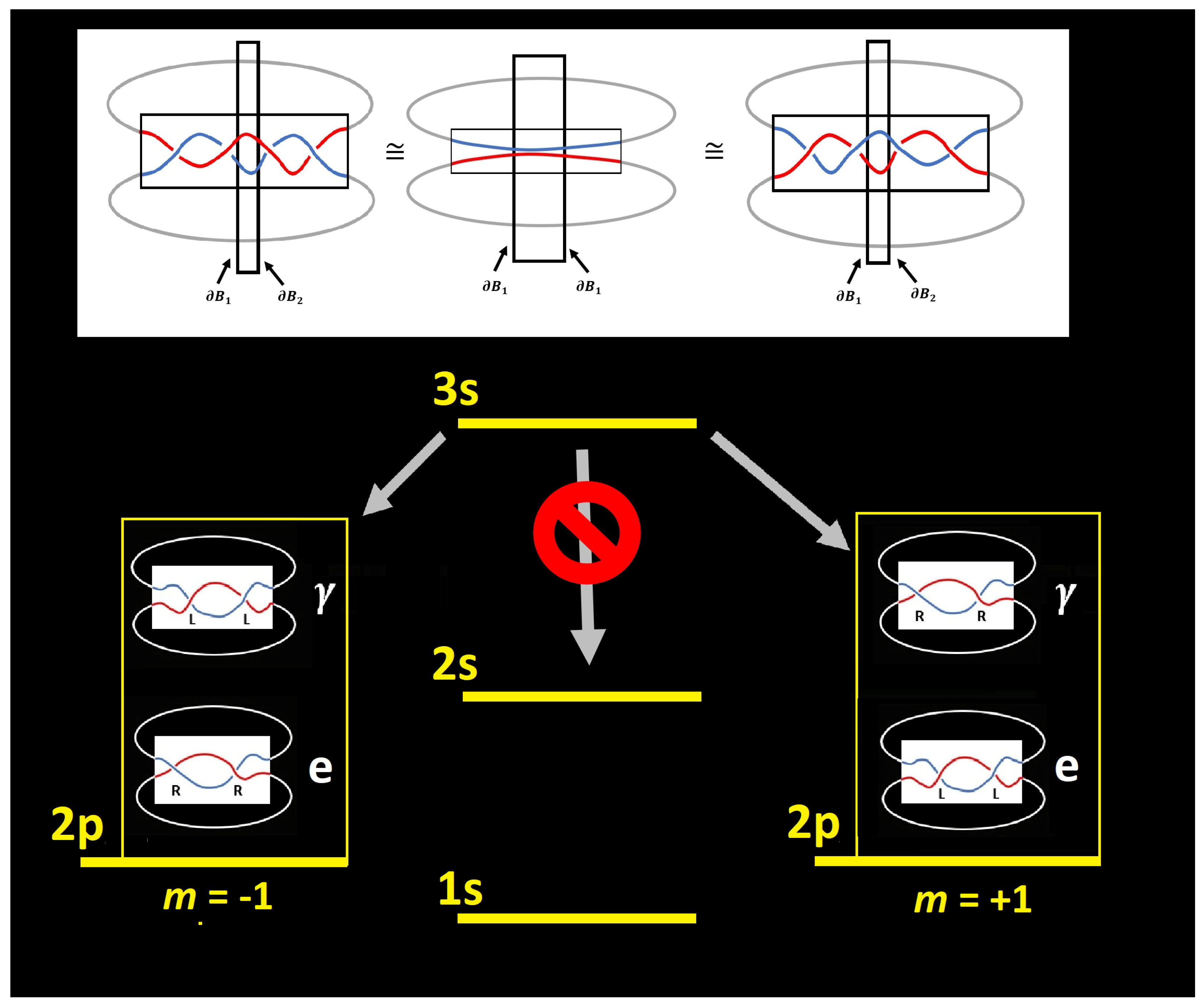
7. Discussion

Our key idea can be explained just by considering the paper strip model of a constant phase shown in Figure 11. By rotating one piece of the paper strip, the total number of twists does not change. Indeed, T rotations lead to $0=+T-T$ twists in the closed paper strip. For $T=1$, we obtain a model of Bell states as shown in Figure 10, Section 5, and a model of scattering amplitudes as shown in Figure 14, Section 6.

For $T=2$, we obtain a model of emission and absorption of a spin 1 gauge boson (a photon), as shown in Figure 14, Section 6. The twists in the $(2\pi )$-realm are related to inner twists and knots in the $(4\pi )$-realm as shown in Figure 6. For example, for the $T=1$ rotation, four inner twists are created as shown in Figure 16 in the $(4\pi )$-realm. Please note that $t^{\prime }=(+,+,+,+,-,-,-,-)$ inner twists can be undone by the Dirac belt trick (This version of the Dirac belt trick is shown in https://vimeo.com/62228139).

For the $SU(2)$-gauge field emerging in the Chern–Simons action given by Equation (5), Section 4, the number of inner twists $t^{\prime }$ is related to the winding number as $t^{\prime }\le 2\nu$. Just by adapting the argument leading to the haptic model of gauge symmetry in the $(2\pi )$-realm shown in Figure 12 to the situation in the $(4\pi )$-realm, we can derive sum rules. Let us start with a paper strip with zero inner twists. By rotating $0=t^{\prime }-t^{\prime }$ times, $t^{\prime }=2\nu$ inner twists emerge in the gauge field. Therefore, $-t^{\prime }$ inner twists emerge in the wave function (e.g., of the quark field) interacting with the gauge field. As shown in Figure 7, the standard mapping $g_1$ (11) related to $t^{\prime }=2$ inner twists in the gauge field necessarily leads to one spin $1/2$ zero mode field with $t^{\prime }=4$ inner twists. More details on sum rules will be discussed elsewhere.

Using the paper strip model in the $(4\pi )$-realm and the corresponding paper strip where the parts $(0,2\pi )$ and $(2\pi ,4\pi )$ are glued together in the $(2\pi )$-realm, the close relation between the different applications ranging from entanglement to minimal interaction becomes obvious. However, the mathematical formalism looks quite different and the intimate relations are not directly visible in the equations. For this reason, we think that the paper strip model may have particular merits for science education.