1. Introduction
People all around the world are increasingly using the Internet and a tremendous amount of information is transferred every day. When sensitive data is transmitted over the Internet, malicious actors may use various techniques to intercept messages and steal information. Therefore, information security has become a critical issue and many methods have been proposed to protect it. In recent years, multimedia files become prevalent in network transmissions, and some efficient data hiding techniques have been proposed for such applications. Data hiding techniques embed secret data into various multimedia files, such as image, audio, video, and in other forms for transmission over the network, so that others are unaware of the existing embedded data [
1]. Because of the practicability and convenience of images, adopting a data hiding method to embed secret data in a digital image is of keen research interest [
2].
Current data hiding methods are mainly divided into four types: data hiding in the spatial domain, the transform domain, the encryption domain and the compressed domain. In the spatial domain, the difference expansion technique and the histogram shifting technique are two of the most famous methods. The difference expansion technique uses differences between neighboring pixel values to explore redundancy and to find the embedding area [
3]. The histogram shifting technique treats pixels as a histogram and vacates room for data embedding by shifting the points between the peak and zero points toward the zero point of the histogram [
4]. Due to higher operability, data hiding in the spatial domain has attracted wide attention, and a series of related methods have been proposed to improve the performance of hiding capacity and image quality [
5,
6,
7,
8]. In the transform domain, images are first converted into frequency coefficients using different techniques such as discrete wavelet transform (DWT) [
9], discrete Fourier transform (DFT) [
10], or discrete cosine transform (DCT) [
11]. Subsequently, redundant coefficients can be used for data hiding. In the encryption domain, images are encrypted before transmission over the Internet and no useful content is accessible to others [
12]. Then, the data hider will embed data into the encrypted image.
With the rapid development of smartphones, cloud storage, and wireless communications, compressed images are widely used for such applications because of fast transmission and reduced storage requirements. Therefore, data hiding methods in the compressed domain have received more attention. Various data hiding methods in different compression techniques have been proposed, such as vector quantization (VQ) [
13], side match vector quantization (SMVQ) [
14], joint photographic experts group (JPEG) [
15], block truncation coding (BTC), and absolute moment block truncation coding (AMBTC). The BTC compression method divides an image into non-overlapping blocks and stores two quantization values and a bitmap of each block as one compressed block code [
16]. AMBTC is an improved version of BTC [
17], and has advantages both in computing speed and image quality. A detailed description is provided in
Section 2.1. Because the AMBTC compression technique is easy to implement, many data hiding methods have been proposed based on AMBTC compressed images.
To date, data hiding methods in AMBTC compressed images are mainly divided into two categories: embedding data into AMBTC compressed images while changing the final file size, and embedding data into AMBTC compressed images while preserving the final file size. For the first category, Lin et al. [
18] proposed a novel data hiding method by adjusting the two quantization values of each block according to the combination of the secret bit and the bitmap. After embedding, one 4 × 4 block contains four quantization values and one double sized bitmap. Kim et al. [
19] applied histogram modification to use ’1s’ of the bitmap to embed almost 8 bits of secret data and to add one new quantization value for one block to reduce the compression ratio while increasing image quality compared with [
18]. Later, Chen et al. [
20] adopted four disjointed embedding strategies according to the four corner values of the bitmap. This method can achieve the same hiding capacity and compression ratio as [
18] and offer almost the same image quality as [
19]. Malik et al. [
21] converted secret data into a ternary system which can embed, at most, 23 bits into one block by adding or subtracting the ternary secret data; as a result, four new quantization values are added and the size of the bitmap changes to 32 bits. Huynh et al. [
22] provided a minima–maxima preserving algorithm to replace 1 LSB or 2 LSBs of the reconstructed image block to achieve an almost 2 bpp hiding capacity, but the final stego-code has the same size as the original image. All the above methods will increase the final size of the compressed image code. Sun et al. [
23] proposed a JNC predictor-based RDH method to embed four bits into one modified compressed block code and reduced the size of the final compressed image codes at the same time. Later, Hong et al. proposed two methods [
24,
25] to improve the performance of Sun et al.’s method by achieving a higher hiding capacity and lower bitrate, i.e., a smaller file size. A MED predictor was used in these two methods and a series of improvements were proposed to achieve better performance.
All of the above methods will increase or decrease the size of the final stego-compressed image code, and these significant changes in file size will no doubt become a clue for malicious actors. For the second category, Chuang and Chang [
26] first proposed a bitmap replacement method that can embed 16 bits of data into a block when the block is smooth while preserving edge blocks. Hong et al. [
27] proposed a method where a compressed block code (
L,
H,
BM) is stored when the embedded secret bit is ‘0’ and changes to (
H,
L,
) when the embedded secret bit is ‘1’, and cannot embed data when
L is equal to
H. Combining advantages of these two methods, Ou and Sun [
28] divided blocks into smooth blocks and complex blocks, then replaced the bitmap with secret data and recalculated two quantization values in a smooth block, and used Hong et al.’s method to embed one bit into a complex block. Later, Chen and Chi [
29] sub-divided complex blocks into less complex blocks and highly complex blocks, then used the method of [
28] to process the smooth blocks and less complex blocks while embedding 2 bits into a highly complex block by changing the number of ‘1’s in the bitmap to even or odd. Kumar et al. [
30] further improved the above methods by using the Hamming distance and pixel value differencing to embed 8 bits into a less complex block and 5 bits into a highly complex block, respectively. In the AMBTC compressed image, each block is strictly represented by a code (
L,
H,
BM). However, except for [
26], all of the other methods will exchange the order of two quantization values in some blocks of the final stego-compressed code, and thus, the reversed two quantization values will undoubtedly draw attacker attention. In this paper, we treat these blocks as the error blocks and try to avoid them.
After reviewing the previous AMBTC-based data hiding methods, some methods will change the size of the final compressed image code, while other methods will exchange the order of two quantization values. These two obvious changes are no doubt violating the file format. Thus, in this paper, we propose a data hiding method for strict AMBTC format images. Three different strategies are adopted in three block types: smooth blocks, less complex blocks and highly complex blocks. The first two strategies preserve the difference and the third strategy will not reduce the difference of each block, so we can define the hiding order of the difference from low to high when the block belongs to the smooth or less complex blocks, and from left to right and top to bottom of the image when the block belongs to the highly complex blocks. Therefore, our proposed method provides high-fidelity when the hiding amount is lower.
The rest of this paper is organized as follows.
Section 2 introduces the AMBTC compression technique and matrix coding technique.
Section 3 explains block classification and the three different strategies of our proposed method and offers some simple examples to illustrate the embedding and extraction phases.
Section 4 provides the experimental results and discussions, including visual comparisons, PSNR under different amounts of the hiding data, and performance under the various thresholds. Finally,
Section 5 gives some conclusions.
3. The Proposed Method
In this section, we propose a data hiding method for AMBTC compressed images using a hybrid strategy to process different types of AMBTC compressed blocks that can maintain the strict AMBTC format. The proposed method also uses two thresholds to define three block types as done in [
30]: smooth blocks, less complex blocks and highly complex blocks. Three strategies named bitmap replacement, matrix encoding, and symmetric quantization value embedding are then applied to embed data into the blocks of different types and no error blocks are generated after embedding. We also designed an efficient data hiding order to achieve higher-fidelity. In
Section 3.1, we first define our block classification rule and their corresponding strategies. Detailed processes regarding the data embedding and extraction phases are described in
Section 3.2 and
Section 3.3, respectively. Subsequently in
Section 3.4, some examples are provided to illustrate the proposed method.
3.1. Block Classification and Hybrid Strategy
After AMBTC compression, the original
M ×
N sized image is divided into
i (
i = 1, 2, …,
) non-overlapping
k ×
k sized blocks, and the block size is set to 4 × 4, i.e.,
k = 4 for the experiments. Each block has only two quantization values
,
, and one bitmap
, the carriers for data embedding are chosen from them. Equation (6) is first used to calculate the difference
. Then, according to
, we set two thresholds
thr1 and
thr2 to classify each block into three block types: smooth blocks, less complex blocks and highly complex blocks.
Figure 1 shows an example of block classification under different thresholds. The complex blocks are the edges of the image and more data are embedded into edges will lead to a significant decline in image quality. To maintain a balance between embedding capacity and image quality, a hybrid strategy contains three different hiding methods is used to process different block types for different sized data embedding.
The changes in the smoother blocks will reduce the image quality less. Therefore, data are embedded following the order of ascending difference value in smooth blocks and less complex blocks, while from left to right and top to bottom of the image in highly complex blocks in our method. On this account, in our hybrid hiding strategy, first two strategies will preserve blocks’ difference, and guarantee blocks’ difference will not decrease in the rest blocks.
3.1.1. Strategy 1 for Smooth Blocks: Bitmap Replacement
For smooth blocks, the two quantization values are very close, and thus, changes of the bitmap have a slight effect on image quality. Therefore, the bitmap can be totally replaced by 16 bits of secret data. Then, refer to the original image blocks and original pixels
, Equations (7) to (10) are used to calculate two new quantization values
and
to obtain the best image quality that is closer to the original image, i.e., minimizing the square error of the final stego-compressed block while preserving the same difference
. A detailed proof for the optimization is provided in the
Appendix A.
where
q′ represents the number of ‘1’ in the new bitmap,
and
denote two original pixel sets which the corresponding bits are ‘0’ and ‘1’, respectively, in a new bitmap.
3.1.2. Strategy 2 for Less Complex Blocks: Matrix Encoding
For less complex blocks, the difference between
and
is large, and the image quality is going to decline dramatically if we change all the values of the bitmap like the smooth blocks. Therefore, the matrix coding that can embed three bits by at most changing one of seven bits is used in less complex blocks. First, the bitmap is divided into two non-overlapping sub-blocks, i.e., the upper sub-block and the lower sub-block. The first seven bits of each sub-block are treated as code-words for data embedding. For details of the method, please refer to
Section 2.2. This strategy embeds data by modifying the bitmap and thus, does not change
.
3.1.3. Strategy 3 for Highly Complex Blocks: Symmetric Quantization Value Embedding
For highly complex blocks,
is too large, such that even a one bit change of the bitmap is intolerable. Therefore, in consideration of the image quality, we turn to hiding data by modifying two quantization values to embed 2 bits into one of them, i.e., 4 bits can be embedded into one block. To guarantee that
will not reduce, instead of the LSB replacement method, the symmetric quantization value embedding method is used to obtain two new nearest expanding quantization values which is given by Equations (11) to (14). After embedding,
will decrease and
will increase, i.e., the difference
will not reduce, thus, misjudgments will not happen in the data extraction phase.
where
and
denote two quaternary system secret data where each one is converted by 2 bit binary system secret data. When extracting data, we only apply modulo-4 operation on two quantization values and convert two results into the binary to get the embedded secret data.
By utilizing the proposed hybrid strategy, we can embed 16 bits, 6 bits, and 4 bits into one smooth block, one less complex block and one highly complex block, respectively. Additionally, in smooth blocks and less complex blocks, our method can preserve the same value of , and can guarantee will not reduce in highly complex blocks. Therefore, the hiding order can be used to embed data into blocks in order of from low to high when , and embed secret data into blocks from left to right and top to bottom of the image when , and the extraction process will not violate the order of embedding.
3.2. Data Embedding Phase
According to the block classification, in the data embedding phase, the blocks are first classified into smooth blocks, less complex blocks, and highly complex blocks based on two thresholds, thr1 and thr2. Three corresponding data embedding strategies are used to embed secret data into the three block types. As mentioned before, the order of data embedding is followed in from low to high when , and from left to right and top to bottom of the image when . Based on the above discussions, the detailed data embedding algorithm is given below:
Input: Original M × N sized image O, secret data bit stream S, and two thresholds thr1, thr2.
Output: Stego-AMBTC compressed code C’.
Step 1. Divide the original image into non-overlapping 4 × 4 sized blocks. Next, apply the AMBTC compression method to compress each block and obtain the compressed block code with two quantization values and one bitmap (, , ).
Step 2. Calculate by Equation (6), sort the compressed blocks according to the ascending order of when and the raster scan order of image for the rest of the blocks.
Step 3. Extract the compressed block code of the i-th block according to the ascending sort order. If , the block belongs to the smooth blocks and go to Step 4; or else if , the block belongs to the less complex blocks and go to Step 5; or else the block belongs to the highly complex blocks and go to Step 6.
Step 4. Extract the 16 bits from S, and totally replace the bitmap with to get the new bitmap . Then, use Equations (7) to (10) to calculate two new quantization values and . Therefore, the final stego-compressed block code can be obtained by concatenating , , and , i.e., (, , ).
Step 5. Extract the 6 bits from S, and divide into and both with 3 bits of secret data. Then, divide into non-overlapping upper sub-block and lower sub-block , and extract the first seven bits of and to form two code-words and . Use Equation (4) to calculate which bits of and need to be flipped, respectively. Flip two corresponding bits of to obtain the new bitmap , and the final stego-compressed block code can be obtained by concatenating , , and , i.e., (, , ).
Step 6. Extract 4 bits of from S, then divide into and , both with 2 bits of secret data. Then, convert and into a quaternary system and use Equations (11) to (14) to calculate two new quantization values, and . Finally, concatenate , , and to obtain the final stego-compressed block code : (, , ).
Step 7. Finish the algorithm when all of the final stego-compressed block codes are obtained, and concatenate each according its location in the original image to form the final stego-AMBTC compressed code C’. The stego-image
with secret data can also be obtained by AMBTC decoding.
3.3. Data Extraction Phase
In the data extraction phase, the secret data can be extracted follow the order of from low to high when , and from left to right and top to bottom of the image when without any loss. Details on the extraction algorithm are given below:
Input: Stego-AMBTC compressed code C’, and two thresholds thr1, thr2.
Output: Secret data bit stream S.
Step 1. Collect all stego-compressed block code .
Step 2. Calculate by Equation (6), sort each stego-compressed block code according to the order for from low to high when and the raster scan order of image for the rest of the blocks.
Step 3. Extract the stego-compressed block code of the i-th block according to the ascending sort order. If , the block belongs to the smooth blocks and go to Step 4; or else if , the block belongs to the less complex blocks and go to Step 5; or else, go to Step 6.
Step 4. Extract the 16 bits of bitmap from the stego-compressed block code , and add these 16 bits directly into S.
Step 5. Divide into non-overlapping upper sub-block and lower sub-block , and extract the first seven bits of and to form two code-words and , respectively. Use Equation (5) to calculate two parts of secret data and both with 3 bits. Then, add these 6 bits into S.
Step 6. Apply modulo-4 operation on its two quantization values and convert the results into the binary system, respectively. By doing so, 4 bits secret data can be obtained, then, add these 4 bits into S.
Step 7. Finish the algorithm when all of the stego-compressed block codes are processed, and the final secret data bit stream S can be obtained.
3.4. Example of Our Proposed Method
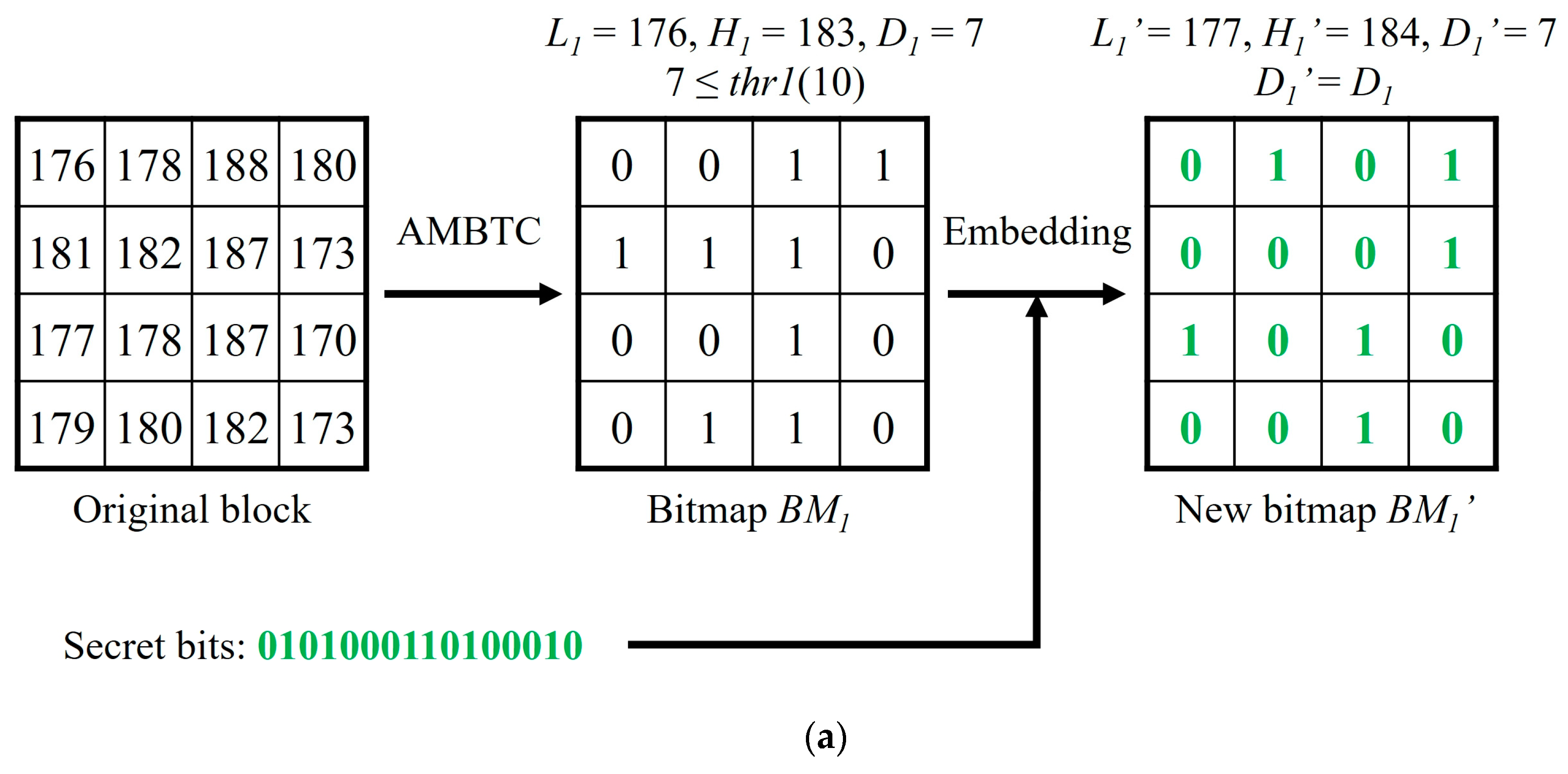
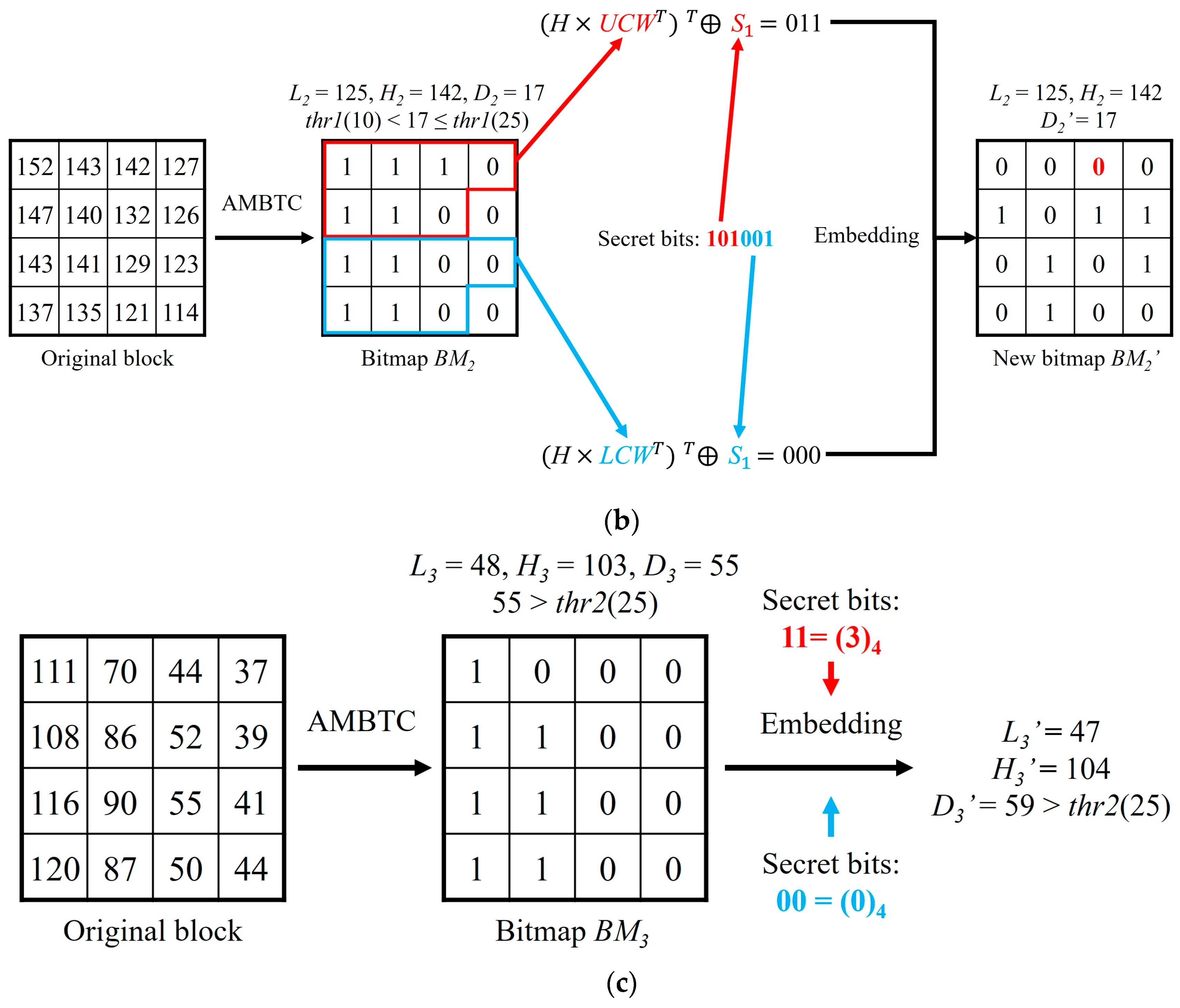
In this section, we will use three simple examples to illustrate the data embedding and data extraction phases of our proposed method. Three 4 × 4 sized blocks of the original image are assumed in the
Figure 2a–c, i.e., (176, 178, 188, 180; 181, 182, 187, 173; 177, 178, 187, 170; 179, 180, 182, 173), (152, 143, 142, 127; 147, 140, 132, 126; 143, 141, 129, 123; 137, 135, 121, 114), and (111, 70, 44, 37; 108, 86, 52, 39; 116, 90, 55, 41; 120, 87, 50, 44). After being compressed by AMBTC, three compressed codes (176, 183,
), (125, 142,
), and (48, 103,
) are obtained. We set
thr1 = 10 and
thr2 = 25.
For the first compressed code (176, 183,
), the difference
= 7 <
thr1, so the block belongs to the smooth blocks, and
can be totally replaced by 16 bits of secret data, as shown in
Figure 2a. Then, use Equations (7) to (10) to calculate two new quantization values
and
. Even when the two quantization values are changed, the value of the difference between them is maintained.
For the second compressed code (125, 142,
), difference
= 17, which is between
thr1 and
thr2, so the block belongs to the less complex blocks. The matrix coding method is used to embed 6 bits of secret data in
. First, the secret bits are divided into
and
. Then, use Equation (4) to separately calculate which bit needs to be flipped in the upper code-word and the lower code-word. As shown in
Figure 2b, the third bit needs to be flipped in the upper code-word and the lower code-word is unchanged. Therefore, the secret bits ‘101001’ can be embedded by just changing the third bit of
from ‘1’ to ‘0’, and the two quantization values are preserved.
For the third compressed code (48, 103, ), difference = 55 > thr2, so the block belongs to the highly complex blocks. First, two secret data sequences ‘11’ and ‘00’ are converted into the quaternary system ‘3’ and ‘0’, respectively. Then, use Equations (11) to (14) to calculate two new quantization values and . By doing so, 4 bits secret data can be embedded into this block. The difference between 47 and 104 is 59, which is higher than thr2, as expected. Therefore, misjudgments will not happen in the data extraction phase.
When extracting data, we also need to follow the order as mentioned above. For the first stego-compressed code (177, 184, ), , we just extract the 16 bits of bitmap ‘0101000110100010’ to obtain the secret data. For the second stego-compressed code (125, 142, ), = 17, which is between thr1 and thr2. The upper code-word and the lower code-word are used to calculate the secret data by Equation (5). After calculation, two parts of the secret data ‘101’ and ‘001’ can be obtained. For the third stego-compressed code (47, 104, ), = 59 > thr2, we just apply modulo-4 operation on two quantization values and convert the results into a binary system to obtain two parts of secret data ‘11’ and ‘00’.
4. Experimental Results and Discussion
This section presents the experimental data and compares the results of our proposed method with three relevant methods. Eight common 512 × 512 sized grayscale images, “Airplane”, “Baboon”, “Boat”, “Couple”, “House”, “Lena”, “Peppers”, and “Sailboat” are used as test images as shown in
Figure 3. In our experiments, the block size used for AMBTC compression of each method is set to 4 × 4. All the experiments were implemented by MATLAB R2017a, and run on a platform with an Intel (R) Core i5-8500 3.00 GHz processor, 8 GB RAM and Windows 10 operating system. The embedded secret data used in our experiments were generated by a pseudo-random number generator.
Hiding capacity and PSNR are used to quantitatively compare and evaluate our proposed method with other methods. Hiding capacity refers to the number of secret bits that can be embedded into the test images. Peak signal-to-noise ratio (PSNR) is used to estimate the visual quality of the stego-images compared to the original images. The definitions of mean square error (MSE) and PSNR are shown in Equations (15) and (16), respectively.
where (
m,
n) denotes the coordinate of each pixel.
Three relevant data hiding methods which embed data into AMBTC compressed images while preserving the final file size that were proposed by Ou and Sun [
28], Chen and Chi [
29], and Kumar et al. [
30] are used to compare with our proposed method. For a fair comparison, two thresholds are set to the same values in the four methods. The visual comparison is shown in
Figure 4. We can see that in (c), noticeable distortions appear on some edge regions such as the bridge of the nose and the eyebrows. In (d), there are some black points in the white blocks or some white points in the black blocks on the edge. The stego-images of our proposed method and Ou and Sun’s method are closer to the original AMBTC compressed image.
Then, we use PSNR to evaluate each method accurately.
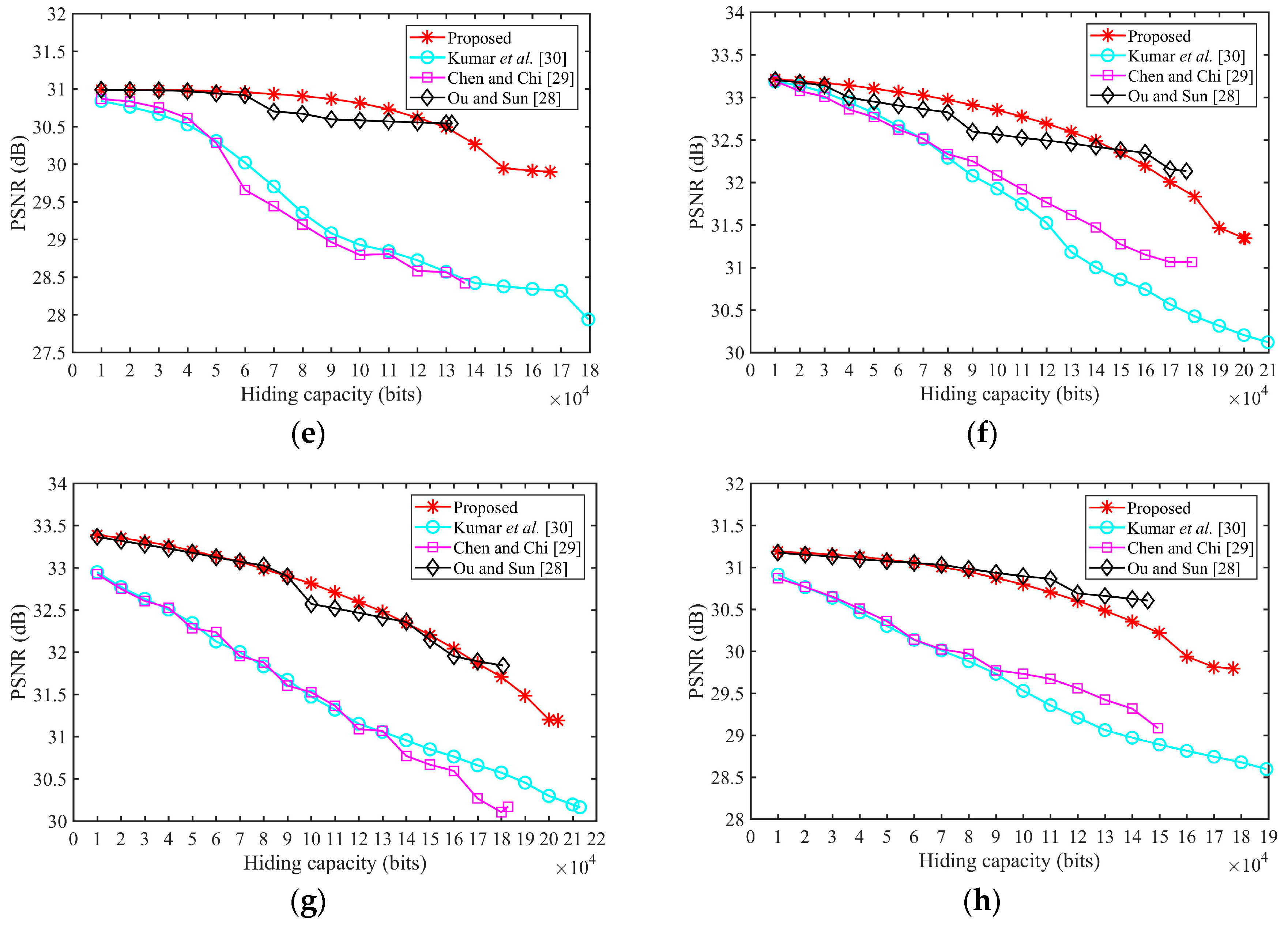
Figure 5 shows the PSNR for different amounts of the hiding data (from 1000 bits to the highest hiding capacity) of eight test images when
thr1 = 10 and
thr2 = 25.
Kumar et al.’s method achieves the highest hiding capacity; however, the image quality is the worst. In the Ou and Sun method, the PSNR will not change when embedding bits into complex blocks. Therefore, the image quality of [
28] is the best, but the hiding capacity is the lowest in most images. Our proposed method can achieve the second highest hiding capacity, i.e., only lower than [
30]. In addition, our proposed method can achieve a relatively higher image quality. This is especially the case in smooth images such as Airplane, where the PSNR of our proposed method is the highest, and in Lena, when hiding capacity is lower, the PSNR of our proposed is also the highest. In
Figure 5a, the PSNR of the other methods are rapidly declining when hiding capacity is higher than 8000 because the image becomes complex in the rear areas. Due to the hiding order of our proposed method, the PSNR of our proposed method will decline slowly with the increasing amount of hiding data. Therefore, our proposed method can achieve an excellent balance between image quality and hiding capacity, and can obtain high-fidelity images when the hiding amount is lower.
Table 2 shows the performance under different thresholds in eight test images. HC and ER denote hiding capacity and error ratio, respectively. The error ratio is the ratio of the error blocks to all blocks, and the error blocks are blocks where two quantization values are exchanged. Our proposed method can embed 6 bits and 4 bits into one less complex block and one highly complex block, with 2 bits and 1 bit less than [
30], respectively. Thus, the gap in hiding capacity between our proposed method and [
30] decreases when thresholds are enlarged, and the hiding capacity of our proposed method is always higher than the remaining two methods. The most important benefit of our proposed method is that there are no error blocks. The ER of the other three methods are all greater than 30%, and the ER increases with the decrease of thresholds, because the hiding strategy for smooth blocks in these three methods exchange the order of two quantization values. Method [
28] has the highest ER in the most cases because of the embedding strategy in the complex block, thus, its security is the worst. Our proposed method can achieve a strict AMBTC format while the other methods cannot, and as such, security can be perfectly guaranteed in data transmission.