Scaling Relationships between Leaf Shape and Area of 12 Rosaceae Species
Abstract
1. Introduction
2. Materials and Methods
2.1. Plants, Sampling, and Image Processing
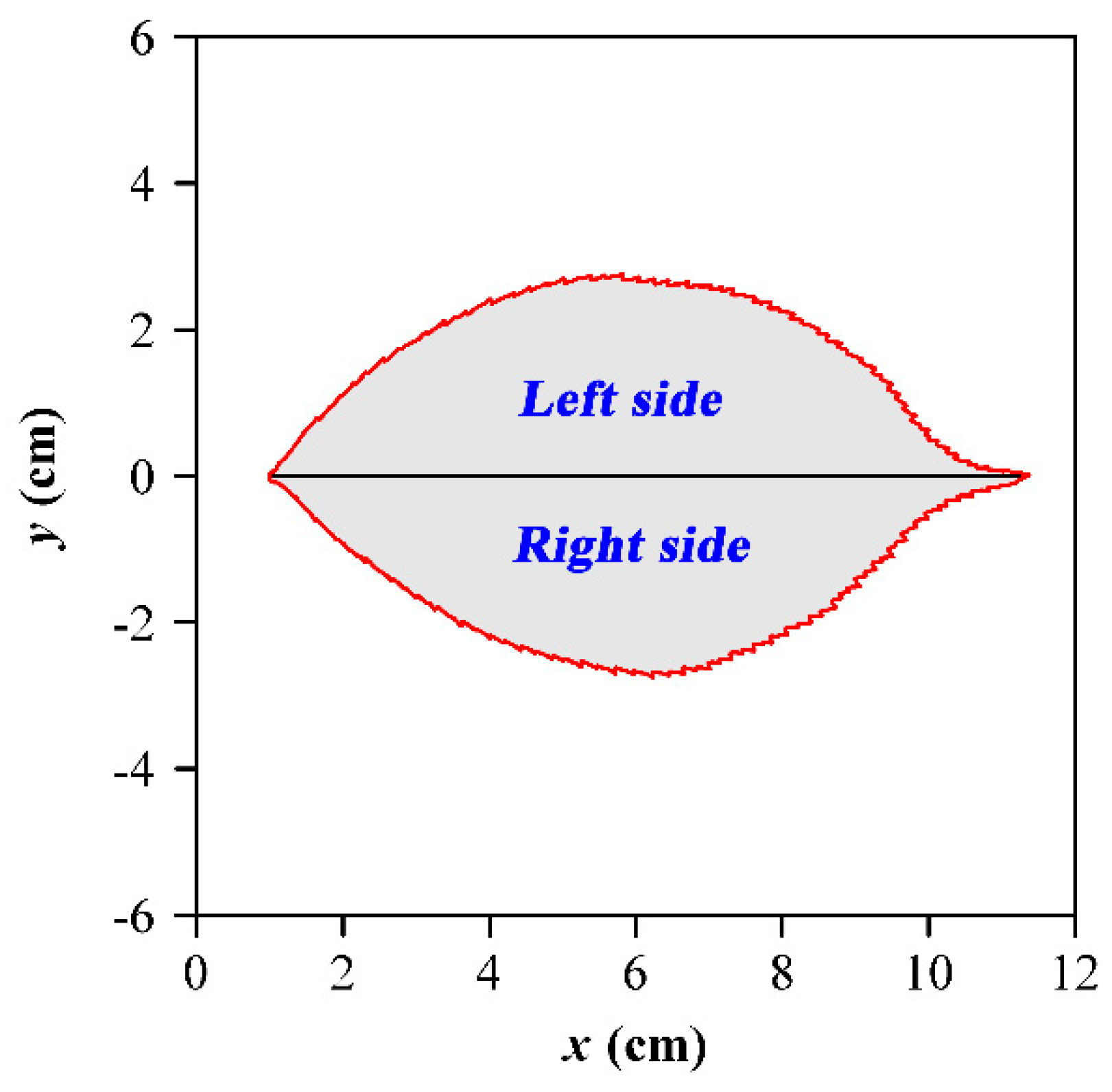
2.2. Leaf Data Acquisition
2.3. Models and Data Analysis
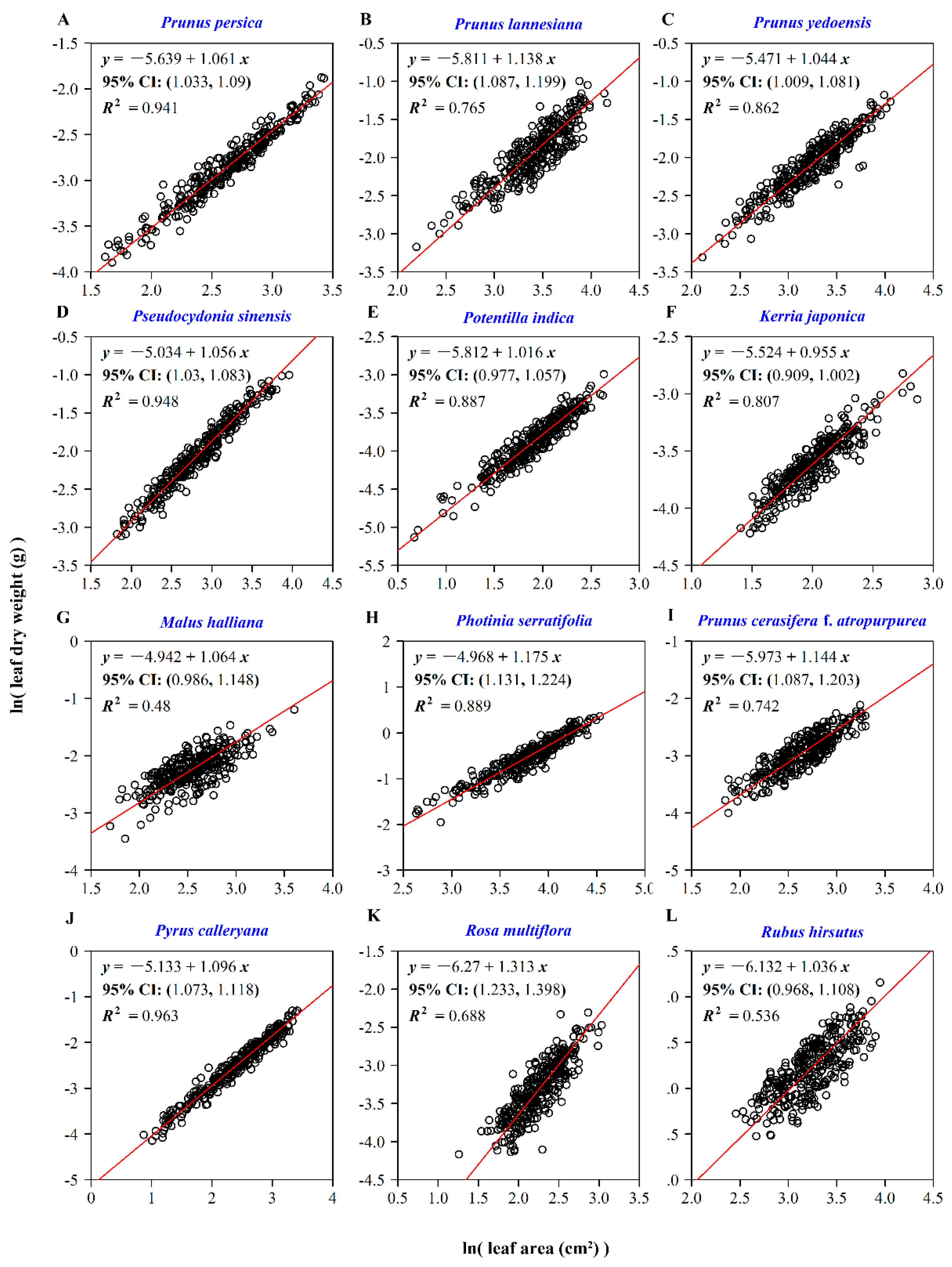
2.3.1. The Relationship between Leaf Dry Weight and Leaf Surface Area
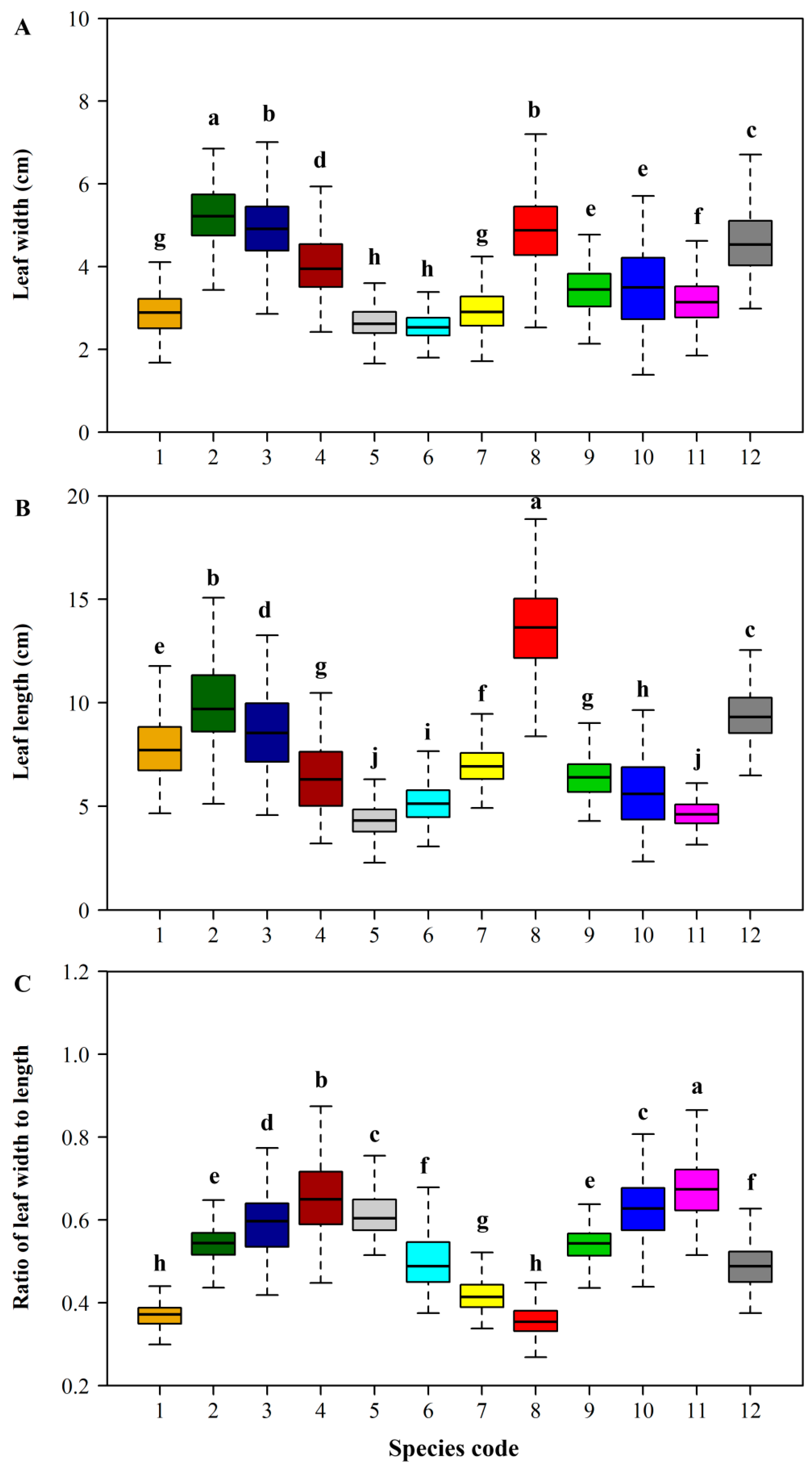
2.3.2. The Relationships among Lamina Area, Length, and Width
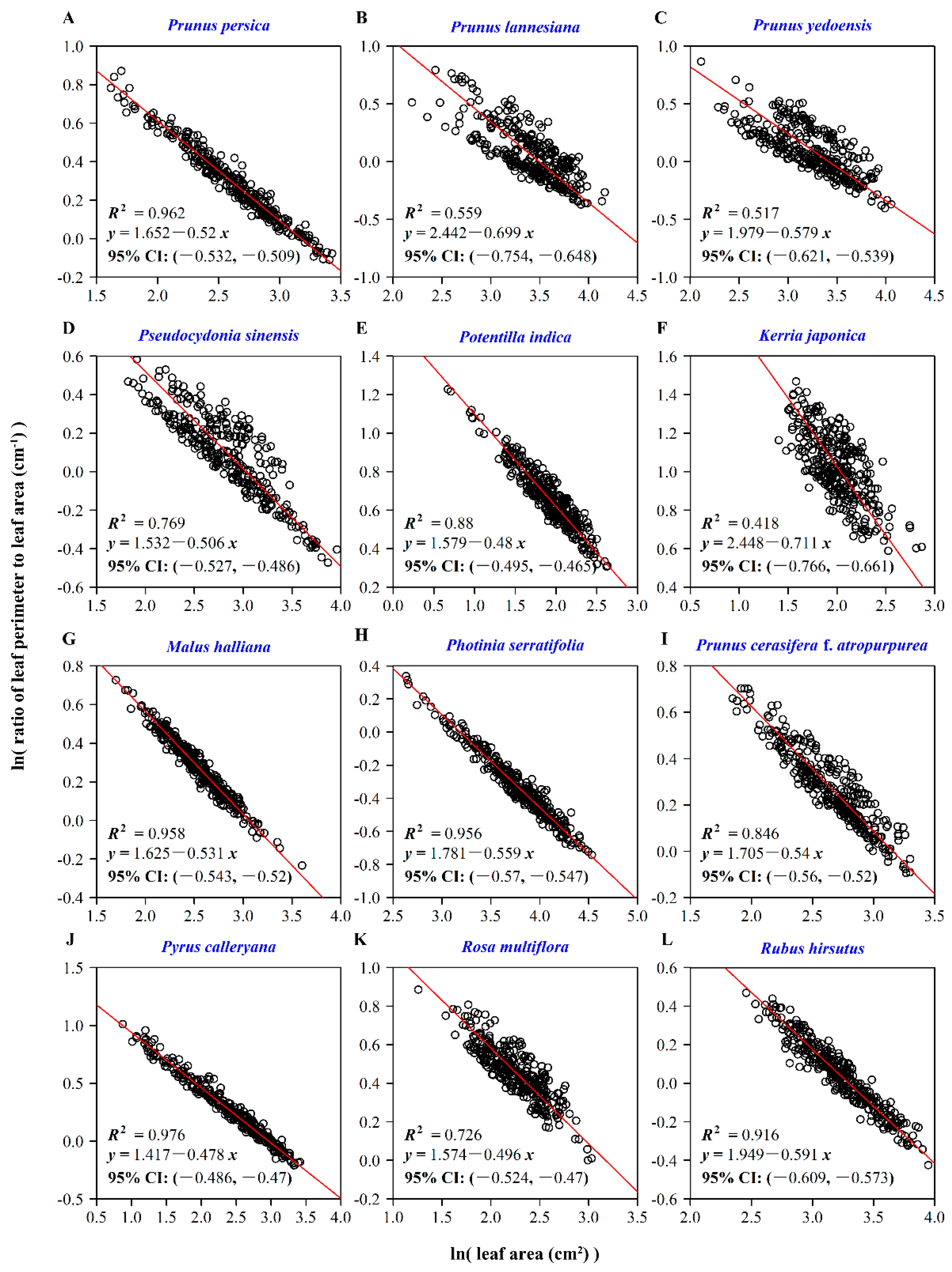
2.3.3. Leaf-Shape Indices and the Scaling Relationships with Leaf Area
2.3.4. Statistical Analysis
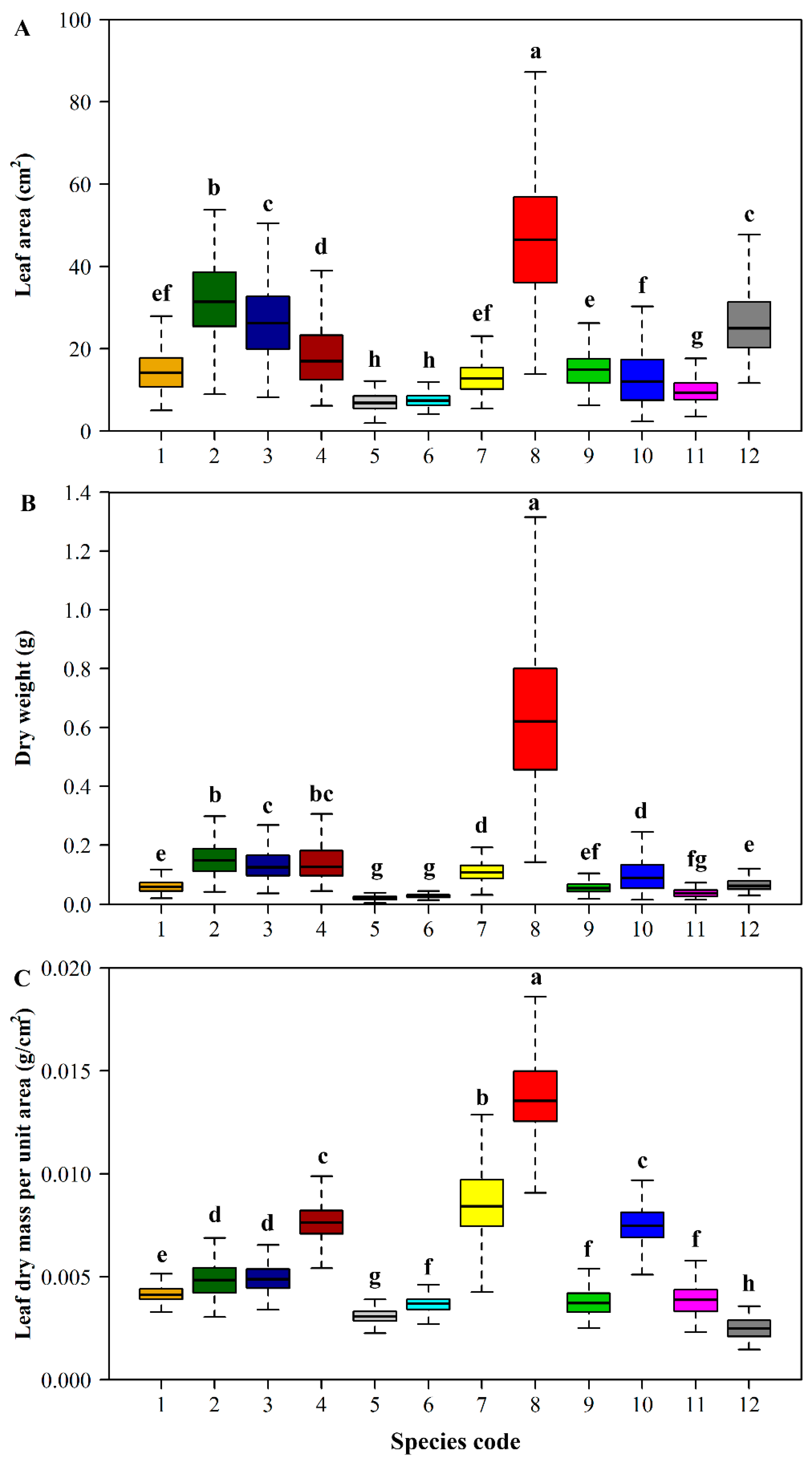
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Musarella, C.M.; Cano-Ortiz, A.; Pinar Fuentes, J.C.; Navas-Urena, J.; Pinto Gomes, C.J.; Quinto-Canas, R.; Cano, E.; Spampinato, G. Similarity analysis between species of the genus Quercus L. (Fagaceae) in southern Italy based on the fractal dimension. PhytoKeys 2018, 113, 79–95. [Google Scholar] [CrossRef] [PubMed]
- De Araujo Mariath, J.E.; Pires Dos Santos, R.; Pires Dos Santos, R. Fractal dimension of the leaf vascular system of three Relbunium species (Rubiaceae). Braz. J. Biol. Sci. 2010, 8, 30–33. [Google Scholar]
- Dengler, N.G.; Kang, J. Vascular patterning and leaf shape. Curr. Opin. Plant Biol. 2001, 4, 50–56. [Google Scholar] [CrossRef]
- Runions, A.; Fuhrer, M.; Lane, B.; Federl, P.; Rolland-Lagan, A.-G.; Prusinkiewicz, P. Modeling and visualization of leaf venation patterns. ACM Trans. Graphics 2005, 24, 702–711. [Google Scholar] [CrossRef]
- Roderick, M.L.; Berry, S.L.; Noble, I.R.; Farquhar, G.D. A theoretical approach to linking the composition and morphology with the function of leaves. Funct. Ecol. 1999, 13, 683–695. [Google Scholar] [CrossRef]
- Brodribb, T.J.; Field, T.S.; Jordan, G.J. Leaf maximum photosynthetic rate and venation are linked by hydraulics. Plant Physiol. 2007, 144, 1890–1898. [Google Scholar] [CrossRef]
- Nicotra, A.B.; Leigh, A.; Boyce, C.K.; Jones, C.S.; Niklas, K.J.; Royer, D.L.; Tsukaya, H. The evolution and functional significance of leaf shape in the angiosperms. Funct. Plant Biol. 2011, 38, 535–552. [Google Scholar] [CrossRef]
- Niinemets, Ü.; Kull, K. Leaf weight per area and leaf size of 85 Estonian woody species in relation to shade tolerance and light availability. For. Ecol. Manag. 1994, 70, 1–10. [Google Scholar] [CrossRef]
- Smith, W.K.; Vogelmann, T.C.; DeLucia, E.H.; Bell, D.T.; Shepherd, K.A. Leaf form and photosynthesis: Do leaf structure and orientation interact to regulate internal light and carbon dioxide? BioScience 1997, 47, 785–793. [Google Scholar] [CrossRef]
- Niinemets, Ü. Research review: Components of leaf dry mass per area-thickness and density-alter leaf photosynthetic capacity in reverse directions in woody plants. New Phytol. 1999, 144, 35–47. [Google Scholar] [CrossRef]
- Niinemets, Ü. Global-scale climatic controls of leaf dry mass per area, density, and thinness in trees and shrubs. Ecology 2001, 82, 453–469. [Google Scholar] [CrossRef]
- Funk, J.L.; Cornwell, W.K. Leaf traits within communities: Context may affect the mapping of traits to function. Ecology 2013, 94, 1893–1897. [Google Scholar] [CrossRef] [PubMed]
- Onoda, Y.; Saluñga, J.B.; Akutsu, K.; Aiba, S.; Yahara, T.; Anten, N.P.R. Trade-off between light interception efficiency and light use efficiency: Implications for species coexistence in one-sided light competition. J. Ecol. 2014, 102, 167–175. [Google Scholar] [CrossRef]
- Puglielli, G.; Crescente, M.F.; Frattaroli, A.R.; Gratani, L. Leaf mass per area (LMA) as a possible predictor of adaptive strategies in two species of Sesleria (Poaceae): Analysis of morphological, anatomical and physiological leaf traits. Ann. Bot. Fenn. 2015, 52, 135–143. [Google Scholar] [CrossRef]
- Yu, X.J.; Shi, P.J.; Hui, C.; Miao, L.F.; Liu, C.L.; Zhang, Q.Y.; Feng, C.N. Effects of salt stress on the seaf shape and scaling of Pyrus betulifolia Bunge. Symmetry 2019, 11, 991. [Google Scholar] [CrossRef]
- Jurik, T.W. Temporal and spatial patterns of specific leaf weight in successional northern hardwood tree species. Am. J. Bot. 1986, 73, 1083–1092. [Google Scholar] [CrossRef]
- Niklas, K.J.; Cobb, E.D.; Niinemets, Ü.; Reich, P.B.; Sellin, A.; Shipley, B.; Wright, I.J. “Diminishing returns” in the scaling of functional leaf traits across and within species groups. Proc. Natl. Acad. Sci. USA 2007, 104, 8891–8896. [Google Scholar] [CrossRef] [PubMed]
- Howland, H.C. Structural, Hydraulic, and ‘Economic’ Aspects of Leaf Venation and Shape. In Biological Prototypes and Synthetic Systems; Bernard, E.E., Kare, M.R., Eds.; Plenum Press: New York, NY, USA, 1962. [Google Scholar]
- Grubb, P.J. A reassessment of the strategies of plants which cope with shortages of resources. Perspect. Plant Ecol. 1998, 1, 3–31. [Google Scholar] [CrossRef]
- Wright, I.J.; Reich, P.B.; Westoby, M.; Ackerly, D.D.; Baruch, Z.; Bongers, F.; Cavender-Bares, J.; Chapin, T.; Cornelissen, J.H.C.; Diemer, M.; et al. The worldwide leaf economics spectrum. Nature 2004, 428, 821–827. [Google Scholar] [CrossRef]
- Pan, S.; Liu, C.; Zhang, W.P.; Xu, S.S.; Wang, N.; Lin, Y.; Gao, J.; Wang, Y. The scaling relationships between leaf mass and leaf area of vascular plant species change with altitude. PLoS ONE 2013, 8, e76872. [Google Scholar] [CrossRef]
- Huang, W.W.; Su, X.F.; Ratkowsky, D.A.; Niklas, K.J.; Gielis, J.; Shi, P.J. The scaling relationships of leaf biomass vs. leaf surface area of 12 bamboo species. Glob. Ecol. Conserv. 2019, 20, e00793. [Google Scholar] [CrossRef]
- Klingenberg, C.P.; Barluenga, M.; Meyer, A. Shape analysis of symmetric structures: Quantifying variation among individuals and asymmetry. Evolution 2002, 56, 1909–1920. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Ratkowsky, D.A.; Xiao, X.; Yu, X.J.; Su, J.L.; Zhang, L.F.; Shi, P.J. Taylor’s power law for leaf bilateral symmetry. Forests 2018, 9, 500. [Google Scholar] [CrossRef]
- Leigh, A.; Zwieniecki, M.A.; Rockwell, F.E.; Boyce, C.K.; Nicotra, A.B.; Holbrook, N.M. Structural and hydraulic correlates of heterophylly in Ginkgo biloba. New Phytol. 2011, 189, 459–470. [Google Scholar] [CrossRef] [PubMed]
- Editorial Board of Flora of China, Chinese Academy of Sciences. Flora of China; Science Press: Beijing, China, 1993. [Google Scholar]
- Niklas, K.J.; Christianson, M.L. Differences in the scaling of area and mass of Ginkgo biloba (Ginkgoaceae) leaves and their relevance to the study of specific leaf area. Am. J. Bot. 2011, 98, 1381–1386. [Google Scholar] [CrossRef]
- Poorter, H.; Niinemets, Ü.; Poorter, L.; Wright, I.J.; Villar, R. Causes and consequences of variation in leaf mass per area (LMA): A meta-analysis. New Phytol. 2009, 182, 565–588. [Google Scholar] [CrossRef] [PubMed]
- Shi, P.J.; Huang, J.G.; Hui, C.; Grissino-Mayer, H.D.; Tardif, J.C.; Zhai, L.H.; Wang, F.S.; Li, B.L. Capturing spiral radial growth of conifers using the superellipse to model tree-ring geometric shape. Front. Plant Sci. 2015, 6, 856. [Google Scholar] [CrossRef]
- Shi, P.J.; Ratkowsky, D.A.; Li, Y.; Zhang, L.F.; Lin, S.Y.; Gielis, J. A general leaf area geometric formula exists for plants-evidence from the simplified Gielis equation. Forests 2018, 9, 714. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2015; Available online: http://www.R-project.org (accessed on 17 April 2018).
- Su, J.L.; Niklas, K.J.; Huang, W.W.; Yu, X.J.; Yang, Y.Y.; Shi, P.J. Lamina shape does not correlate with lamina surface area: An analysis based on the simplified Gielis equation. Glob. Ecol. Conserv. 2019, 19, e00666. [Google Scholar] [CrossRef]
- Milla, R.; Reich, P.B. The scaling of leaf area and mass: The cost of light interception increases with leaf size. Proc. R. Soc. B Biol. Sci. 2007, 274, 2109–2114. [Google Scholar] [CrossRef]
- Montgomery, E.G. Correlation Studies in Corn; Annual Report No. 24.; Agricultural Experimental Station: Lincoln, NB, USA, 1911. [Google Scholar]
- Shi, P.J.; Liu, M.D.; Yu, X.J.; Gielis, J.; Ratkowsky, D.A. Proportional relationship between leaf area and the product of leaf length and width of four types of special leaf shapes. Forests 2019, 10, 178. [Google Scholar] [CrossRef]
- Smith, R.J. Used and misuse of the reduced major axis for line-fitting. Am. J. Phys. Anthropol. 2009, 140, 476–786. [Google Scholar] [CrossRef] [PubMed]
- Hsu, J.C. Multiple Comparisons: Theory and Methods; Chapman and Hall/CRC: New York, NY, USA, 1996. [Google Scholar]
- Lin, S.Y.; Shao, L.J.; Hui, C.; Song, Y.; Reddy, G.V.P.; Gielis, J.; Li, F.; Ding, Y.L.; Wei, Q.; Shi, P.J. Why does not the leaf weight-area allometry of bamboos follow the 3/2-power law? Front. Plant Sci. 2018, 9, 583. [Google Scholar] [CrossRef] [PubMed]
- Shi, P.J.; Liu, M.D.; Ratkowsky, D.A.; Gielis, J.; Su, J.L.; Yu, X.J.; Wang, P.; Zhang, L.F.; Lin, Z.Y.; Schrader, J. Leaf area-length allometry and its implications in leaf-shape evolution. Trees 2019, 33, 1073–1085. [Google Scholar] [CrossRef]
- Hughes, A.P.; Cockshull, K.E.; Heath, O.V.S. Leaf area and absolute water content. Ann. Bot. 1970, 34, 259–266. [Google Scholar] [CrossRef]
- Witkowski, E.T.F.; Lamont, B.B. Leaf specific mass confounds leaf density and thickness. Oecologia 1991, 88, 486–493. [Google Scholar] [CrossRef] [PubMed]
- Boardman, N.K. Comparative photosynthesis of sun and shade plants. Annu. Rev. Plant Physiol. 1977, 28, 355–377. [Google Scholar] [CrossRef]
- Ostman, N.L.; Weaver, G.T. Autumnal nutrient transfers by retranslocation, leaching, and litter fall in a chestnut oak forest in southern Illinois. Can. J. For. Res. 1982, 12, 40–51. [Google Scholar] [CrossRef]
- Küppers, M. Ecological significance of above-ground architectural patterns in woody plants: A question of cost-benefit relationships. Trends Ecol. Evol. 1989, 4, 375–379. [Google Scholar] [CrossRef]
- Sumida, A.; Komiyama, A. Crown spread patterns for five deciduous broad-leaved woody species ecological significance of the retention patterns of larger branches. Ann. Bot. 1997, 80, 759–766. [Google Scholar] [CrossRef]
- Sumida, A.; Terazawa, I.; Togashi, A.; Komiyama, A. Spatial arrangement of branches in relation to slope and neighbourhood competition. Ann. Bot. 2002, 89, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Wierman, C.A.; Oliver, C.D. Crown stratification by species in even-aged mixed stands of Douglas-fir-western hemlock. Can. J. For. Res. 1979, 9, 1–9. [Google Scholar] [CrossRef]
- Kuuluvainen, T. Tree architectures adapted to efficient light utilization: Is there a basis for latitudinal gradients? Oikos 1992, 65, 275–284. [Google Scholar] [CrossRef]
- Clatterbuck, W.K.; Hodges, J.D. Development of cherrybark oak and sweet gum in mixed, even-aged bottomland stands in central Mississippi, U.S.A. Can. J. For. Res. 1988, 18, 12–18. [Google Scholar] [CrossRef]
- Itô, H.; Sumida, A.; Isagi, Y.; Kamo, K. The crown shape of an evergreen oak, Quercus glauca, in a hardwood community. J. For. Res. 1997, 2, 85–88. [Google Scholar] [CrossRef]
- Wu, J. Landscape Ecology: Pattern, Process, Scale and Hierarchy, 2nd ed.; Higher Education Press: Beijing, China, 2007. [Google Scholar]


| Species Code | Latin Name | Sampling Time | Sampling Location | Sample Size |
|---|---|---|---|---|
| 1 | Prunus persica Stokes | 22 April, 2018 | (32°04′44″N, 118°48′25″ E) | 308 |
| 2 | Prunus lannesiana E.H. Wilson | 30 April, 2018 | (32°04′50″ N, 118°48′39″ E) | 326 |
| 3 | Prunus yedoensis Matsum. | 26 April, 2018 | (32°04′49″ N, 118°48′29″ E) | 320 |
| 4 | Pseudocydonia sinensis C.K. Schneid. | 11 May, 2018 | (32°04′46″ N, 118°48′25″ E) | 316 |
| 5 | Potentilla indica (Andrews) T. Wolf | 9 May, 2018 | (32°05′03″ N, 118°48′45″ E) | 324 |
| 6 | Kerria japonica (L.) DC. | 29 April, 2018 | (32°04′46″ N, 118°48′33″ E) | 323 |
| 7 | Malus halliana Koehne | 26 April, 2018 | (32°05′03″ N, 118°48′47″ E) | 326 |
| 8 | Photinia serratifolia (Desf.) Kalkman | 2 May, 2018 | (32°04′49″ N, 118°48′40″ E) | 320 |
| 9 | Prunus cerasifera Ehrhar f. atropurpurea (Jacq.) Rehd. | 28 April, 2018 | (32°04′44″ N, 118°48′26″ E) | 323 |
| 10 | Pyrus calleryana Decne. | 3 July, 2018 | (32°04′44″ N, 118°48′26″ E) | 320 |
| 11 | Rosa multiflora Thunb. | 27 April, 2018 | (32°04′50″ N, 118°48′50″ E) | 327 |
| 12 | Rubus hirsutus Thunb. | 4 May, 2018 | (32°05′03″ N, 118°48′45″ E) | 324 |
| Data Set | Estimate | SD | R2 |
|---|---|---|---|
| 1 | 0.4012 | 0.0022 | 0.9907 |
| 2 | 0.5548 | 0.0033 | 0.9884 |
| 3 | 0.5995 | 0.0043 | 0.9836 |
| 4 | 0.6505 | 0.0053 | 0.9796 |
| 5 | 0.6332 | 0.0032 | 0.9920 |
| 6 | 0.5261 | 0.0039 | 0.9825 |
| 7 | 0.4638 | 0.0028 | 0.9885 |
| 8 | 0.3800 | 0.0022 | 0.9897 |
| 9 | 0.5724 | 0.0030 | 0.9912 |
| 10 | 0.6623 | 0.0044 | 0.9861 |
| 11 | 0.6940 | 0.0042 | 0.9884 |
| 12 | 0.5165 | 0.0029 | 0.9898 |
| Data Set | r | P | CV in Leaf Area (%) |
|---|---|---|---|
| 1 | −0.0166 | 0.7718 | 36.13 |
| 2 | −0.0344 | 0.5365 | 30.54 |
| 3 | 0.0765 | 0.1722 | 34.68 |
| 4 | 0.1171 | 0.0376 | 44.93 |
| 5 | 0.0495 | 0.3742 | 30.35 |
| 6 | 0.0786 | 0.1586 | 26.51 |
| 7 | −0.0617 | 0.2662 | 30.69 |
| 8 | 0.0702 | 0.2102 | 32.73 |
| 9 | −0.0133 | 0.8116 | 29.14 |
| 10 | 0.0404 | 0.4718 | 50.51 |
| 11 | 0.0508 | 0.3601 | 28.45 |
| 12 | 0.0254 | 0.6480 | 29.62 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Hui, C.; Sandhu, H.S.; Lin, Z.; Shi, P. Scaling Relationships between Leaf Shape and Area of 12 Rosaceae Species. Symmetry 2019, 11, 1255. https://doi.org/10.3390/sym11101255
Yu X, Hui C, Sandhu HS, Lin Z, Shi P. Scaling Relationships between Leaf Shape and Area of 12 Rosaceae Species. Symmetry. 2019; 11(10):1255. https://doi.org/10.3390/sym11101255
Chicago/Turabian StyleYu, Xiaojing, Cang Hui, Hardev S. Sandhu, Zhiyi Lin, and Peijian Shi. 2019. "Scaling Relationships between Leaf Shape and Area of 12 Rosaceae Species" Symmetry 11, no. 10: 1255. https://doi.org/10.3390/sym11101255
APA StyleYu, X., Hui, C., Sandhu, H. S., Lin, Z., & Shi, P. (2019). Scaling Relationships between Leaf Shape and Area of 12 Rosaceae Species. Symmetry, 11(10), 1255. https://doi.org/10.3390/sym11101255






