Vector-Coupled Flight Controller Design Based on Multivariable Backstepping Sliding Mode
Abstract
1. Introduction
- Cross-coupling that is inherent to flight dynamics. In previous studies [13,14,16,17,18,19,20,21], the models used to design flight control were decoupled into a scalar form, i.e., state equations with velocity, AOA, sideslip angle, roll rate, pitch rate, and yaw rate, and multiple single-channel controllers were designed. During the decoupling process, some coupling components terms are first calculated/estimated and then compensated for, while the other coupling terms may be disregarded owing to their negligible influence. However, this is a conservative method because the coupling terms may include the control input.
- Design of control laws that ensure the stability of the whole control system. In some studies [22,23], the design of the control systems is based on the assumption with “timescale separation”, wherein the slow attitude dynamics are separated from the fast angular-rate dynamics. The outer and inner controllers correspond to the slow and fast subsystems, respectively. They can be designed individually to simplify the complexity of the control system. However, the inherent weakness of this framework is that the overall system’s stability cannot be achieved theoretically.
- Uncertainties regarding various disturbances, including external disturbances, un-modeled dynamics, and parameter uncertainties. Balancing the robustness and the control performance of an aircraft control system during the design process is important. The robustness and control performance of a control system have an inverse relationship, i.e., a more robust controller implies more certain attenuation; however, the robustness is obtained by sacrificing the nominal control performance to a certain extent.
- We model the flight dynamics using a body-fixed frame in the vectorial form and consider both matched and unmatched disturbances. The attitude control of an aircraft, along with the total velocity, can be converted into a space-vector tracking equation. The triplet airspeed (), AOA () and sideslip angle () are controlled simultaneously in a vectorial manner. This also allows us to deal with the cross-term actively and correctly. A key aspect of this study is the active use of the cross-coupling in terms of flight dynamics instead of decoupling and passive suppression and compensation.
- The control-oriented model has a lower-triangular form. Then, the structure of a Lyapunov-based backstepping approach [24,25] is used in this study to ensure the stability of the closed-loop system theoretically. This work establishes a combined multivariable backstepping sliding mode controller, along with nonlinear disturbance observers. The disturbance observers enhance the scheme of construction of the control law by combining the backstepping sliding mode control feedback with disturbance estimation, based on straightforward and feedforward compensation. Unlike similar works [12,16,17,18,19], the developed controller not only avoids solving complex matrix equations and treating inverse matrixes, but also fully realizes vector-coupled control.
- The developed control structure is concise and aesthetically appealing compared with traditional control structures that use a decoupled collection of single variables. The combined control scheme has a symmetry structure and each term is meaningful, and this feature is significant in that the control parameters can be adjusted in each term directively.
2. Modelling
- Body-fixed Frame: , the reference frame with the origin at the gravity center and axes pointing forward, over the right wing, and down (relative to the pilot).
- Inertial Frame: , the reference frame with a specific ground origin and axes pointing the North, East, and down to the Earth center.
- Wind Frame: , the reference frame with the origin at the gravity center and the x-axis pointing to the velocity direction of the flight. The orientation of this frame relative to the body-fixed frame is determined by AOA () and sideslip angle (). The lift, drag, and side forces are defined naturally in this reference frame, respectively.
3. Vector-Coupled Flight Controller Design
3.1. Control Objective
3.2. Control Law Design
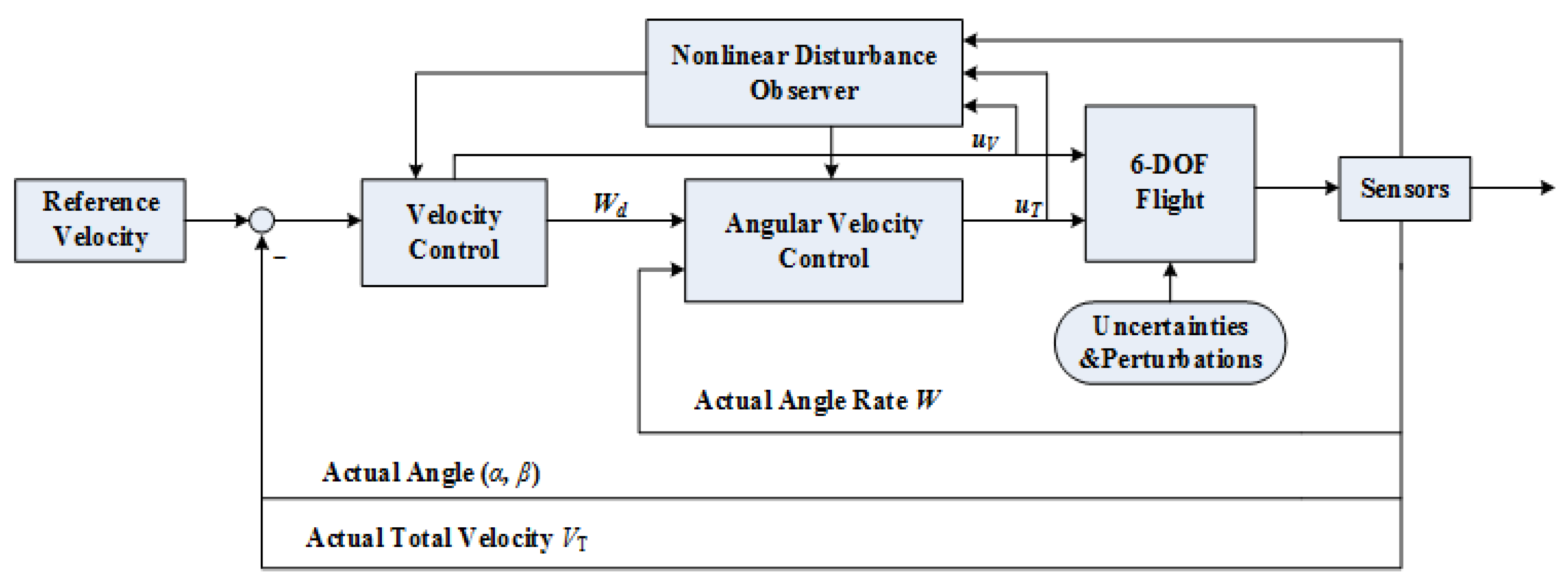
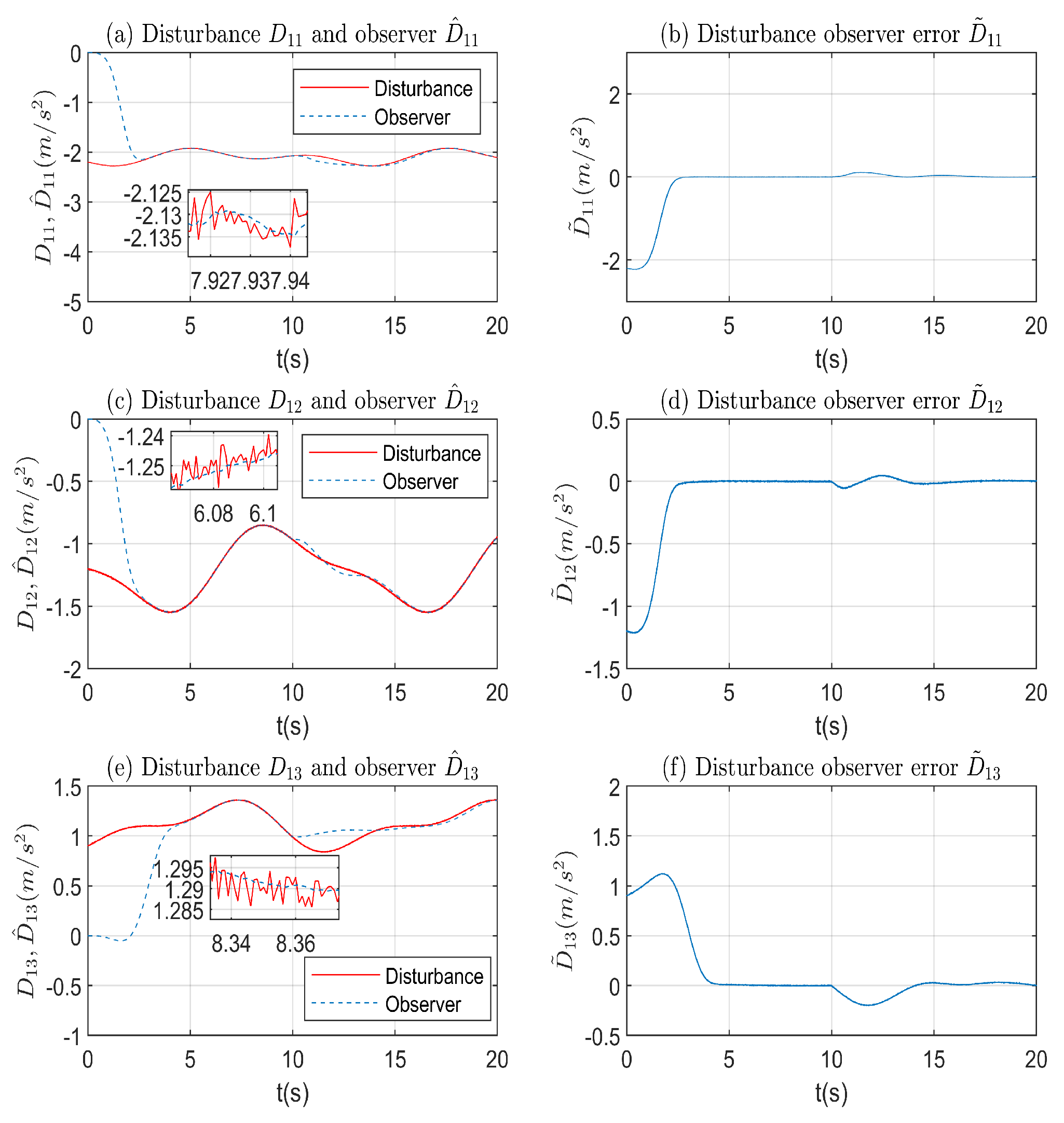
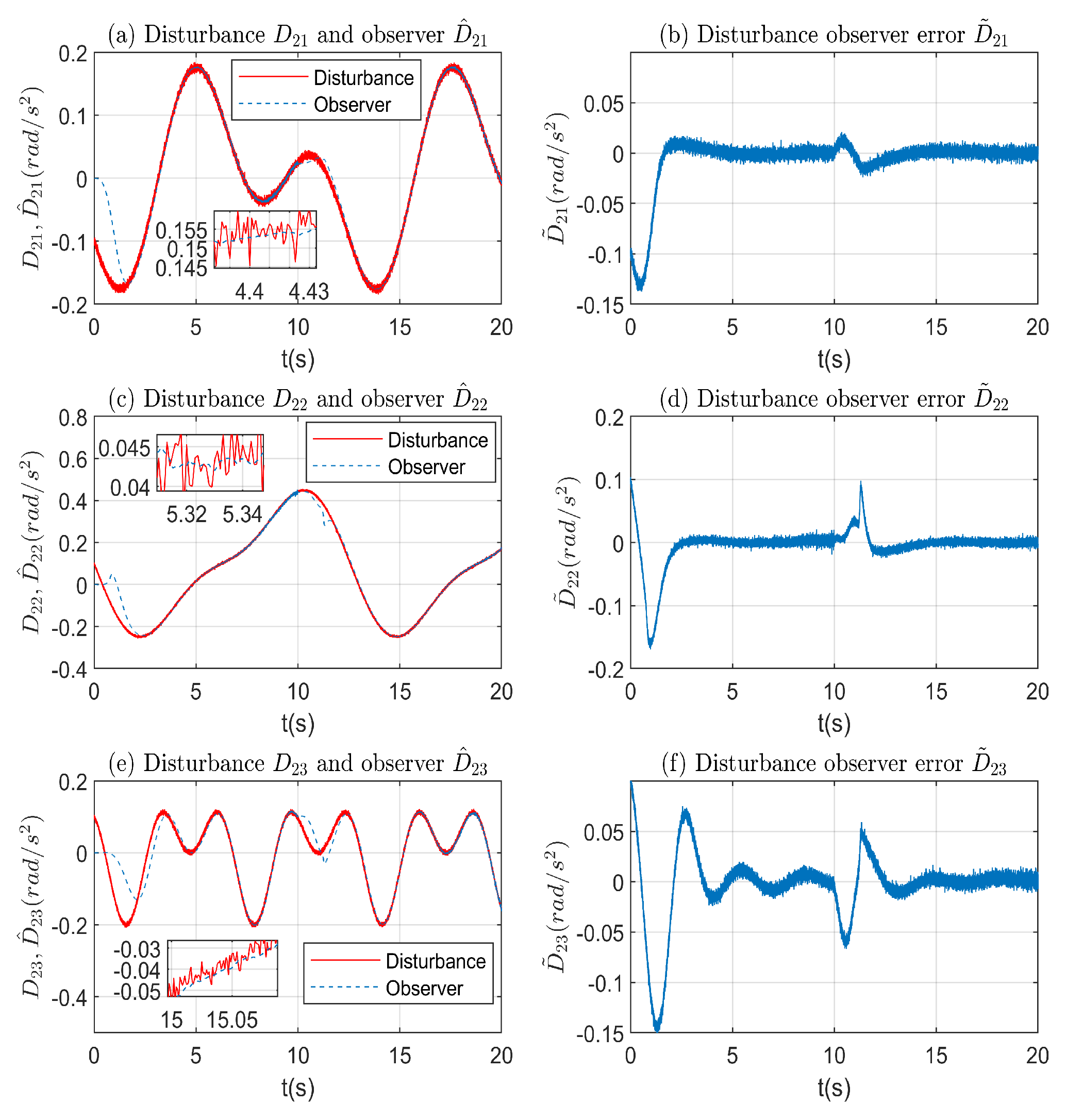
3.2.1. Nonlinear Disturbance Observer
3.2.2. Multivariable Backstepping Sliding Mode Controller
4. Simulations
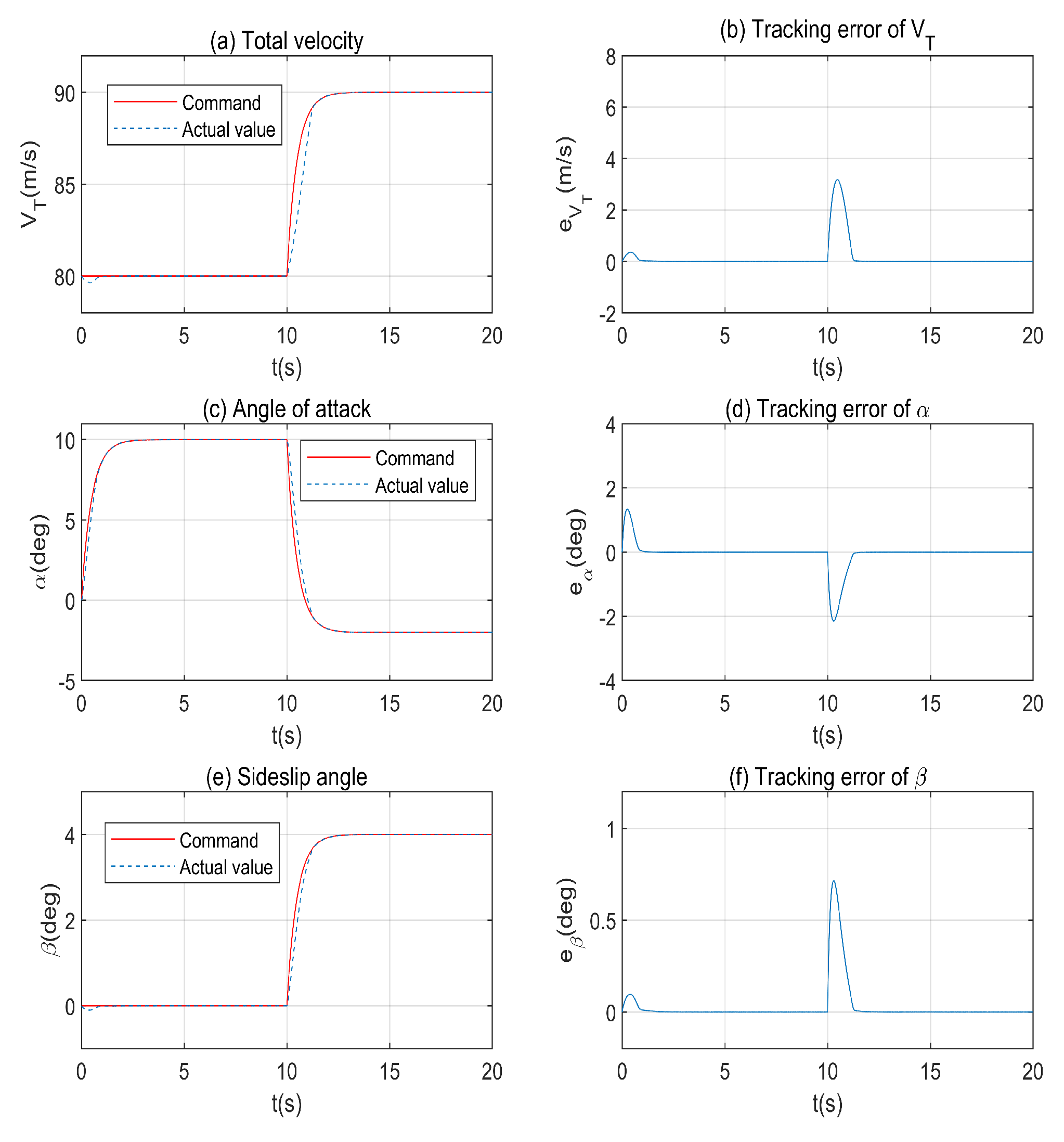
4.1. Effectiveness of the Proposed Controller
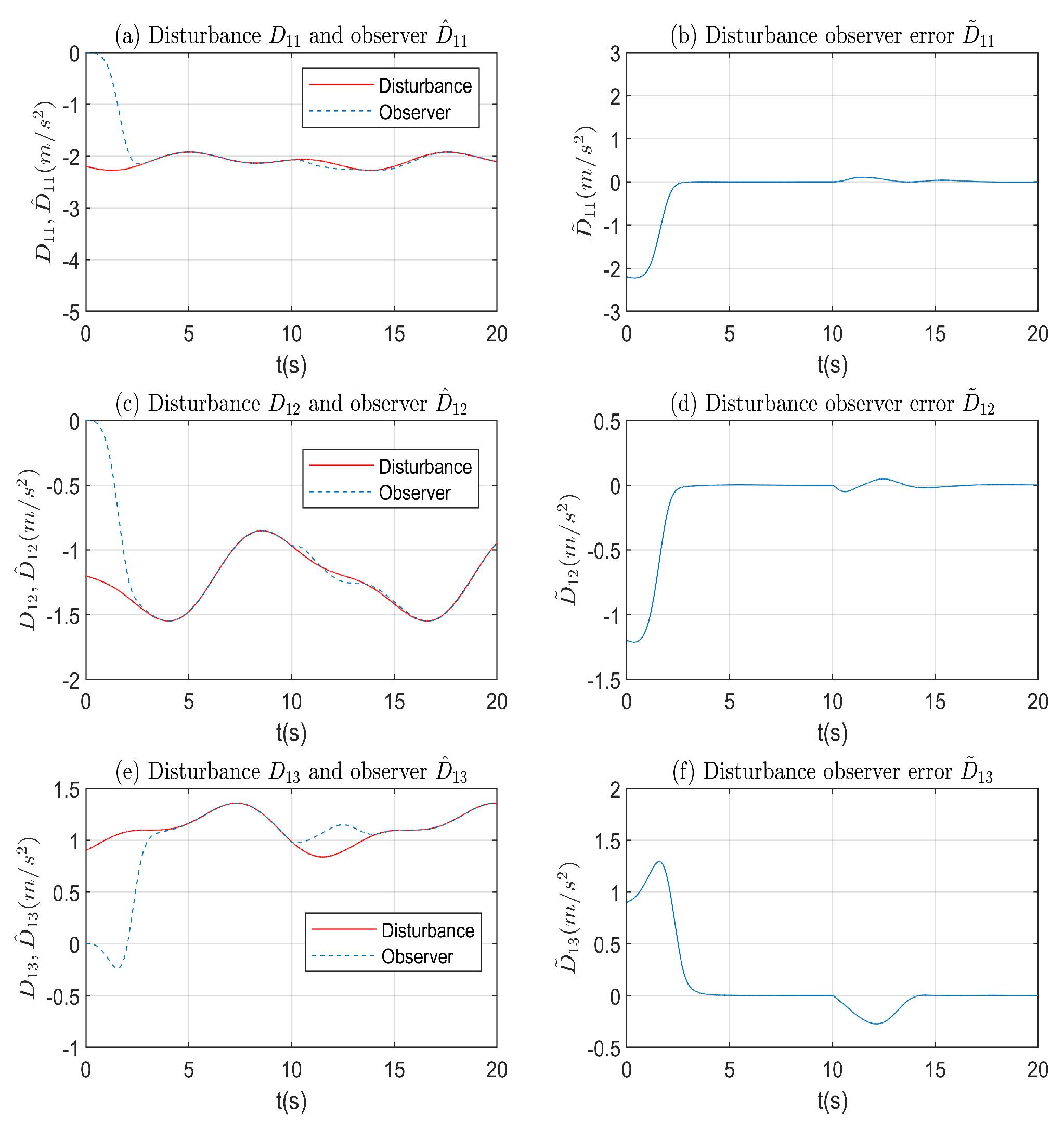
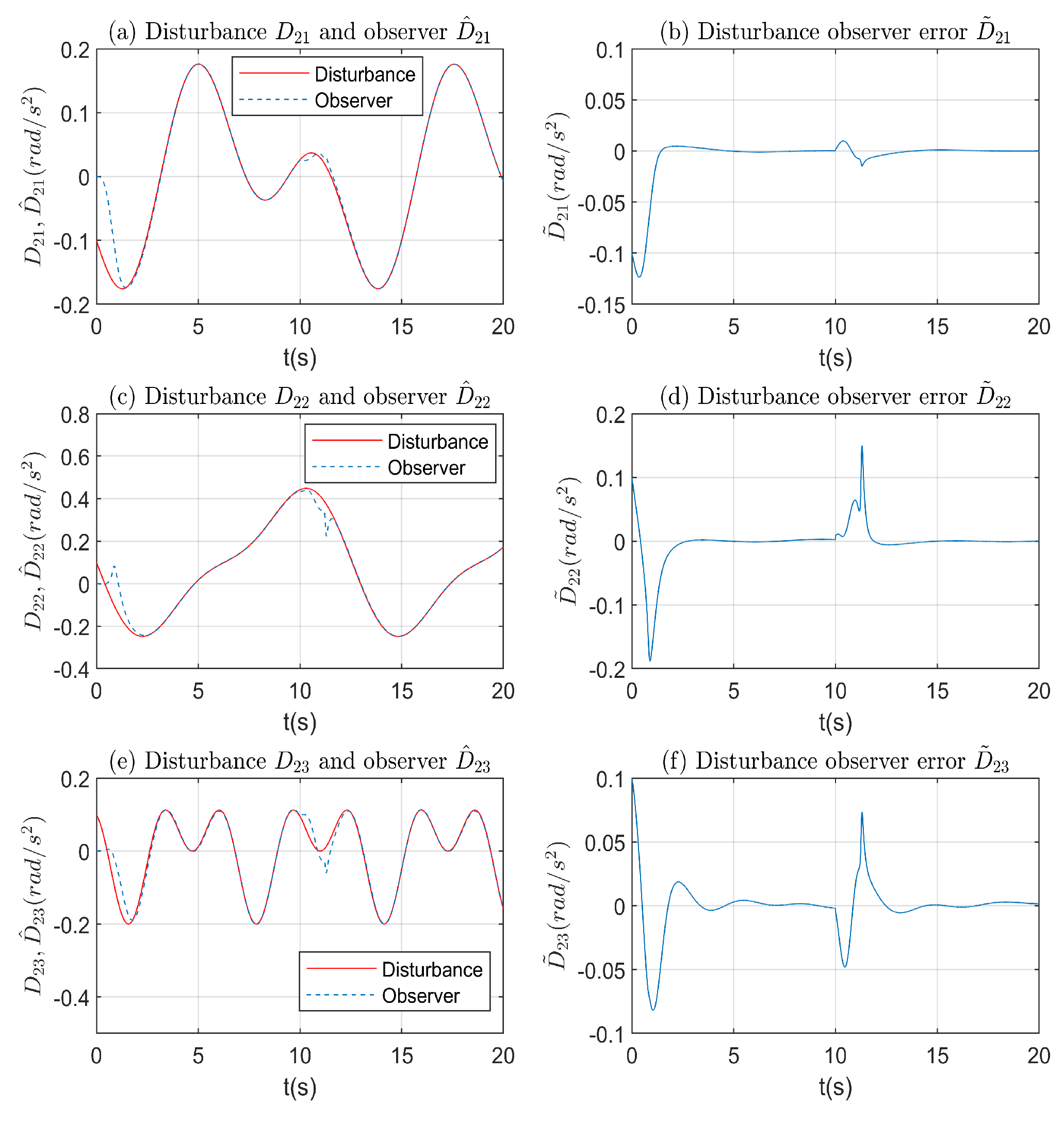
4.2. Robustness of the Proposed Nonlinear Disturbance Observer Enhanced Controller
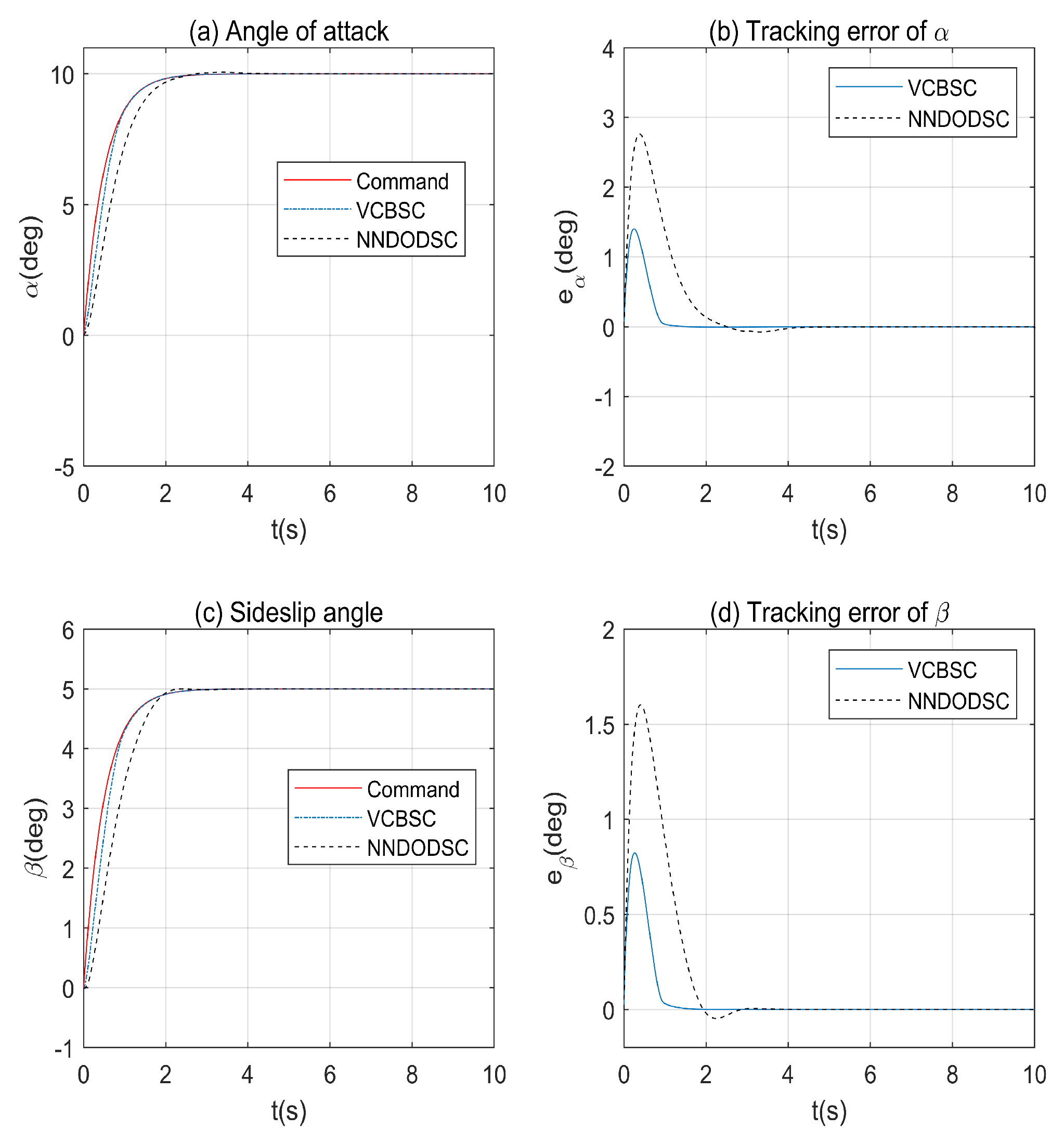
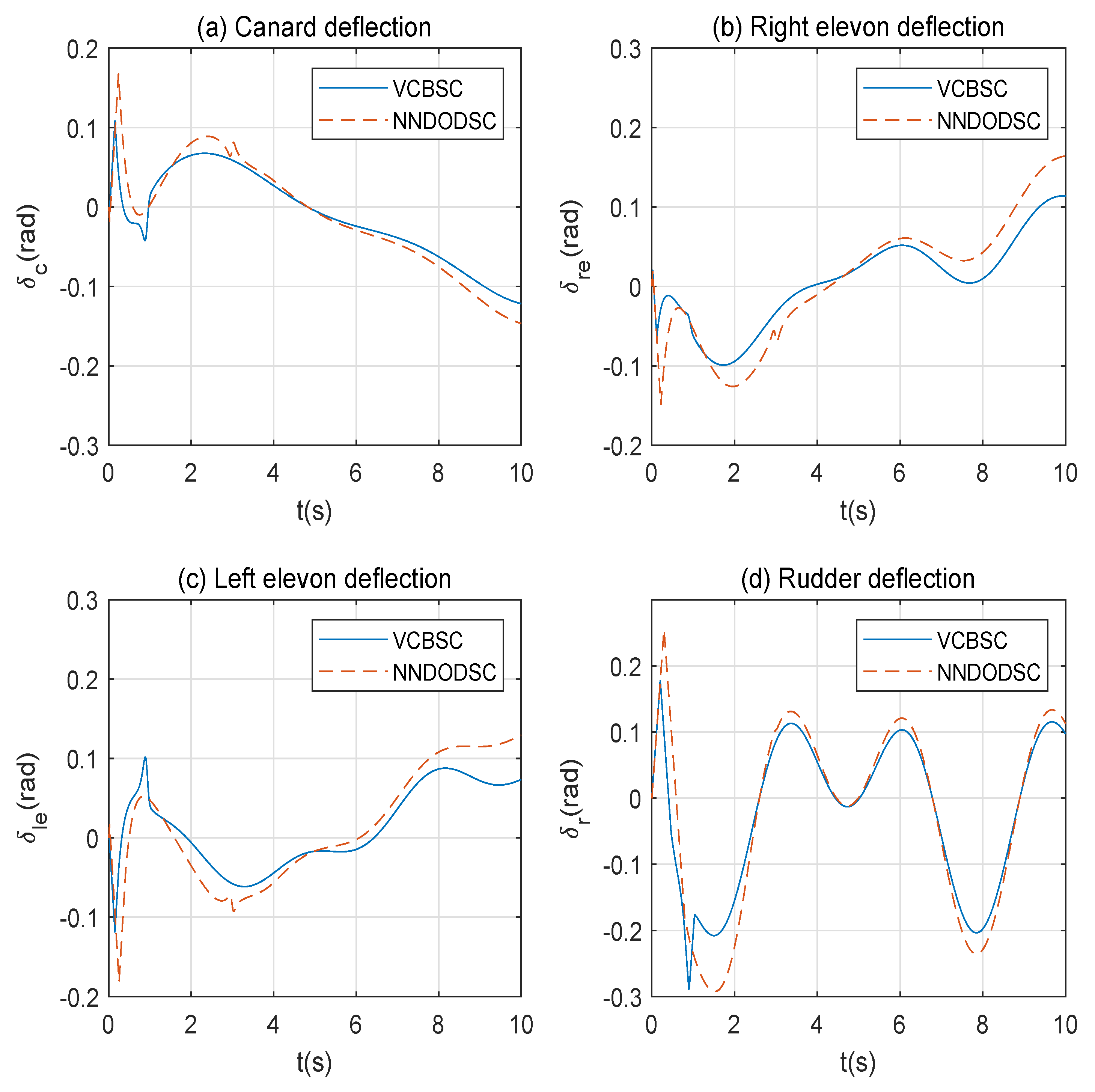
4.3. Comparison with a Decoupled Controller
5. Conclusions
- The developed control scheme allowed the conversion of attitude and airspeed control of an aircraft into a space-vector tracking problem. The results showed that the triplet airspeed (), AOA (), and sideslip angle () could be controlled separately and simultaneously in the form of vectors. A key feature of this study is the active use of cross-coupling in the flight dynamics instead of decoupling and passive suppression and compensation.
- The use of the Lyapunov stability theory enabled the development of a flight control system that is semi-globally uniformly ultimately bounded. The simulation results were comparable to the theoretical results, and it was shown that the developed controller is effective and robust.
- The developed control scheme is concise and aesthetically more appealing compared with traditional control structures, which uses decoupled collections of single variables. The combined control scheme has a symmetry structure and each term is meaningful. The feature that the control parameters can be considered and adjusted in each term directively is significant.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ∼ | Error signal |
| ∧ | Estimation signal |
| Angle of attack (AOA) (rad) | |
| Sideslip angle (rad) | |
| Roll angle (rad) | |
| Yaw angle (rad) | |
| Atmospheric density (kg/) | |
| Pitch angle (rad) | |
| g | Acceleration of gravity () |
| m | Flight mass (kg) |
| Roll, pitch and yaw rates (rad/s) | |
| Dynamic pressure () | |
| Deflection vector (rad) | |
| Distribution matrix | |
| External force vector (N) | |
| Gravity vector (N) | |
| Inertia matrix () | |
| Aerodynamics force vector (N) | |
| Thrust force vector (N) | |
| Thrust control term () | |
| Unit vector of flight velocity | |
| Flight velocity vector (m/s) | |
| Flight angular velocity vector (rad/s) | |
| Virtual angular velocity control term (rad/s) | |
| Control torque vector () | |
| Body-fixed frame coordinates | |
| Inertial frame coordinates | |
| Wind frame coordinates | |
| Magnitude of velocity (m/s) | |
| Flight position in the inertial frame (m) | |
| Lumped acceleration disturbances vector () | |
| Lumped angular acceleration disturbances vector () |
Appendix A
References
- Zhu, J.H. A Survey of Advanced Flight Control Theory and Application. In Proceedings of the Conference on Computational Engineering in Systems Applications, Beijing, China, 4–6 October 2007; pp. 655–658. [Google Scholar]
- Shkolnikov, A.; Shtessel, Y. Aircraft Nonminimum Phase Control in Dynamic Sliding Manifolds. J. Guid. Control Dyn. 2001, 24, 566–571. [Google Scholar] [CrossRef]
- Zong, Q.; Wang, F.; Tian, B. Nonlinear adaptive filter backstepping flight control for reentry vehicle with input constraint and external disturbances. J. Aerosp. Eng. 2013, 28, 889–907. [Google Scholar] [CrossRef]
- You, M.; Zong, Q.; Tian, B.; Zhao, X.; Zeng, F. The comprehensive design of uniform robust exact disturbance observer and fixed-time controller for reusable launch vehicles. IET Control Threory Appl. 2018, 12, 638–648. [Google Scholar] [CrossRef]
- Li, P.; Yu, X.; Zhang, Y. Adaptive Multivariable Integral TSMC of a Hypersonic Gliding Vehicle With Actuator Faults and Model Uncertainties. IEEE/ASME Trans. Mechatron. 2017, 22, 2723–2735. [Google Scholar] [CrossRef]
- Zhang, L.; Bi, S.; Yang, H. Fuzzy-PID Control Algorithm of the Helicopter Model Flight Attitude Control. In Proceedings of the 2010 Chinese Control and Decision Conference, Xuzhou, China, 26–28 May 2010; pp. 1438–1443. [Google Scholar]
- Amato, F.; Mattei, M.; Scala, S.; Verde, L. Robust Flight Control Design for the HIRM based on Linear Quadratic Control. Aerosp. Sci. Technol. 2000, 4, 423–438. [Google Scholar] [CrossRef]
- Yoshimasa, O. Design of a Flight Controller for Hypersonic Flight Experiment Vehicle. Asian J. Control 2004, 6, 353–361. [Google Scholar]
- Huang, Y.; Xu, K.; Han, J.; Lam, J. Flight Control Design Using Extended State Observer and Non-smooth Feedback. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; pp. 223–228. [Google Scholar]
- Snell, A.; Enns, D.; Garrard, W. Nonlinear Inversion Flight Control for a Supermaneuverable Aircraft. J. Guid. Control Dyn. 1992, 15, 976–984. [Google Scholar] [CrossRef]
- Da Costa, R.; Chu, Q.; Mulder, J. Reentry Flight Controller Design Using Nonlinear Dynamic Inversion. J. Guid. Control Dyn. 2003, 40, 64–71. [Google Scholar] [CrossRef]
- Sonneveldt, L.; Chu, Q.; Mulder, J. Nonlinear Flight Control Design Using Constrained Adaptive Backstepping. J. Guid. Control Dyn. 2007, 30, 322–336. [Google Scholar] [CrossRef]
- Hao, A.; Fidan, B.; Wu, Q.; Wang, C.; Cao, X. Sliding Mode Differentiator Based Tracking Control of Uncertain Nonlinear Systems with Application to Hypersonic Flight. Asian J. Control 2019, 21, 143–155. [Google Scholar]
- Castañeda, H.; Salas-Peña, O.; Leon-Morales, J. Robust flight control for a fixed-wing unmanned aerial vehicle using adaptive super-twisting approach. J. Aerosp. Eng. 2014, 228, 2310–2322. [Google Scholar]
- Nagesh, I.; Edwards, C. A multivariable super-twisting sliding mode approach. Automatica 2014, 50, 984–988. [Google Scholar] [CrossRef]
- Li, P.; Ma, J.; Zheng, Z. Disturbance-observer-based fixed-time second-order sliding mode control of an air-breathing hypersonic vehicle with actuator faults. J. Aerosp. Eng. 2017, 232, 344–361. [Google Scholar] [CrossRef]
- Chen, M.; Yu, J. Disturbance Observer-Based Adaptive Sliding Mode Control For Near-Space Vehicles. Nonlinear Dyn. 2015, 15, 1671–1682. [Google Scholar] [CrossRef]
- Vansoest, W.R.; Chu, Q.P.; Mulder, J.A. Combined feedback linearization and constrained model predictive control for entry flight. J. Guid. Control Dyn. 2006, 29, 427–434. [Google Scholar] [CrossRef]
- Li, C.Y.; Jing, W.X.; Gao, C.S. Adaptive backstepping-based flight control system using integral filters. Aerosp. Sci. Technol. 2009, 13, 105–113. [Google Scholar] [CrossRef]
- Ma, J.; Li, P.; Zheng, Z. Disturbance observer based dynamic surface flight control for an uncertain aircraft. J. Aerosp. Eng. 2017, 232, 729–744. [Google Scholar] [CrossRef]
- Yu, P.; Shtessel, Y. Continuous Higher Order Sliding Mode Control with Adaption of Air Breathing Hypersonic Missile. Int. J. Adapt. Control Signal Process. 2016, 30, 1099–1117. [Google Scholar] [CrossRef]
- Shtessel, Y. Multiple Time Scale Flight Control Using Re-configurable Sliding Modes. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007; pp. 1–10. [Google Scholar]
- Dong, Q.; Zong, Q.; Tian, B.; Wang, F. Adaptive-gain multivariable super-twisting sliding mode control for reentry RLV with torque perturbation. Int. J. Robust Nonlinear Control 2016, 27, 620–638. [Google Scholar] [CrossRef]
- Härkegård, O.; Glad, T. Vector backstepping design for flight control. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007; pp. 1–10. [Google Scholar]
- Fossena, T.; Berg, S. Nonlinear Vectorial Backstepping Design for Global Exponential Backing of Marine Vessels in the Presence of Actuator Dynamics. In Proceedings of the 36th Conference on Decision and Control, San Diego, CA, USA, 12 December 2003; pp. 4237–4242. [Google Scholar]
- Bates, D.; Hagström, M. Nonlinear Analysis and Synthesis Techniques for Aircraft Control; Springer: Berlin, Geramany, 2007. [Google Scholar]
- Tian, B.; Yin, L.; Wang, H. Finite Time Reentry Attitude Control Based on Adaptive Multivariable Disturbance Compensation. IEEE Trans. Ind. Electron. 2015, 62, 5889–5898. [Google Scholar] [CrossRef]
- Yu, X.; Li, P.; Zhang, Y. The design of fixed-time observer and finite-time fault-tolerant control for hypersonic gliding vehicles. IEEE Trans. Ind. Electron. 2017, 65, 4135–4144. [Google Scholar] [CrossRef]
- Lie, F.; Pradipta, A.; Gebre-Egziabher, D. Synthetic Air Data System. J. Aircr. 2013, 50, 1234–1249. [Google Scholar] [CrossRef]
- Chen, W. Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Swaroop, D. Dynamic Surface Control of Nonlinear Systems. In Proceedings of the American Control Conference Albuquerque, Albuquerque, NM, USA, 6 June 1997; pp. 3028–3034. [Google Scholar]
- Swaroop, D. Dynamic Surface Control for Nonlinear Systems. IEEE Trans. Autom. Control 2000, 45, 1893–1899. [Google Scholar] [CrossRef]
- Forssell, L.; Nilsson, U. ADMIRE the Aero-Data Model in a Research Environment Version 4.0, Model Description; Technical Report, FOI-R-1624-SE; FOI: Stockholm, Sweden, 2005. [Google Scholar]


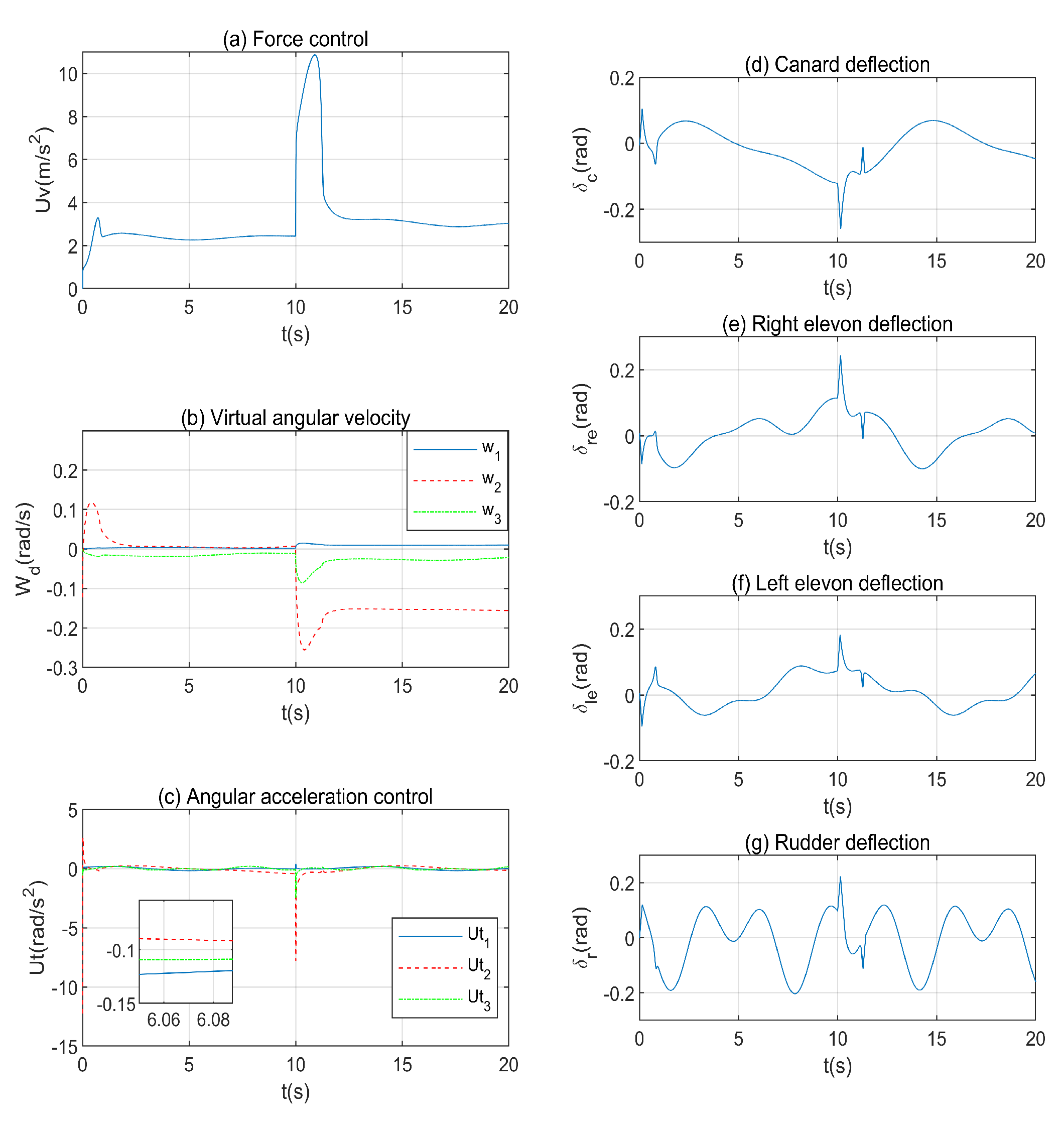
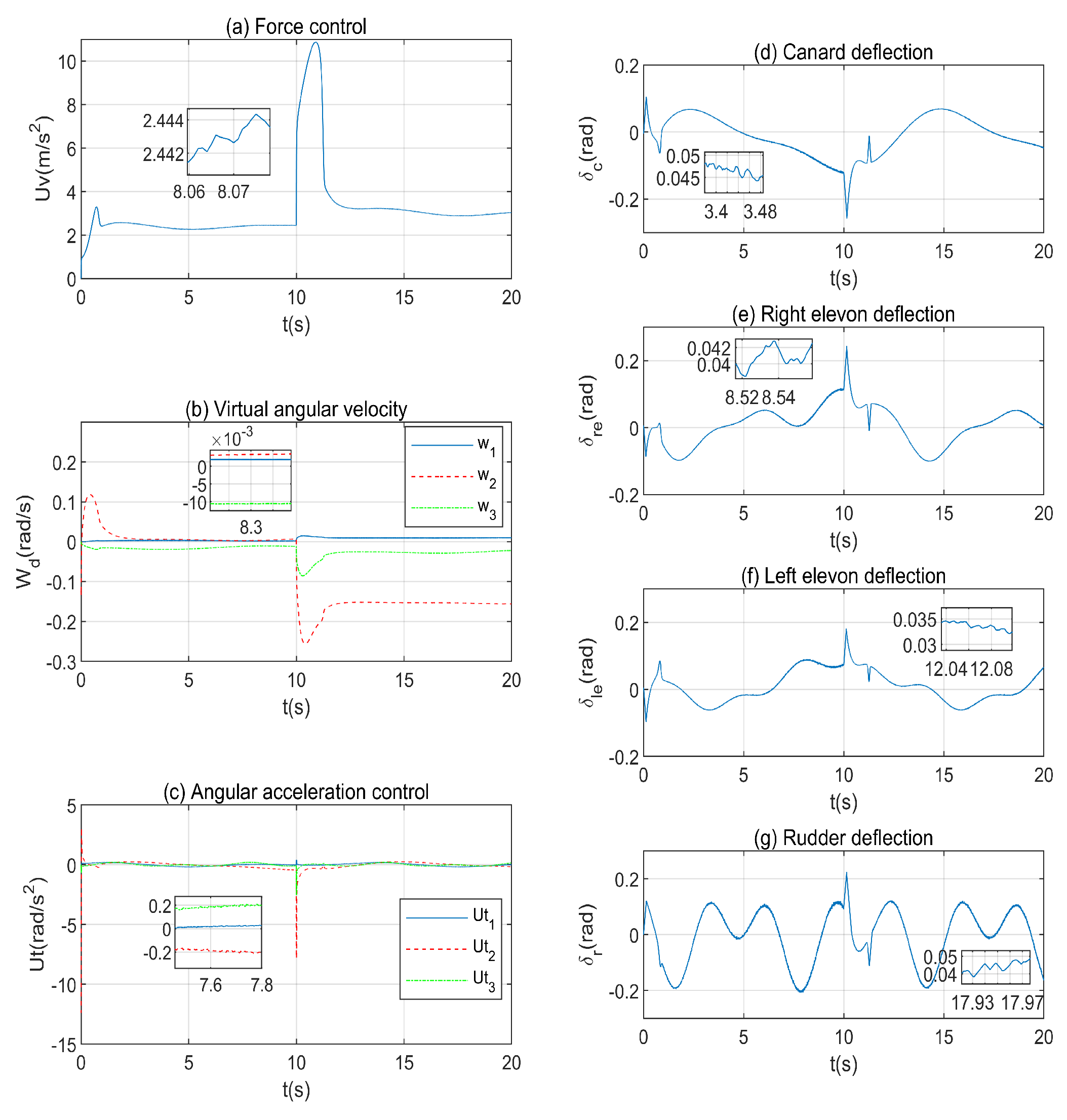
| Control | Unit | Min. | Max. | Rate Limit |
|---|---|---|---|---|
| Canard wings | deg | −55 | 25 | ±50 deg/s |
| Right elevon | deg | −25 | 25 | ±50 deg/s |
| Left elevon | deg | −25 | 25 | ±50 deg/s |
| Rudder | deg | −30 | 30 | ±50 deg/s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Li, P.; Ma, J. Vector-Coupled Flight Controller Design Based on Multivariable Backstepping Sliding Mode. Symmetry 2019, 11, 1225. https://doi.org/10.3390/sym11101225
Han Y, Li P, Ma J. Vector-Coupled Flight Controller Design Based on Multivariable Backstepping Sliding Mode. Symmetry. 2019; 11(10):1225. https://doi.org/10.3390/sym11101225
Chicago/Turabian StyleHan, Yang, Peng Li, and Jianjun Ma. 2019. "Vector-Coupled Flight Controller Design Based on Multivariable Backstepping Sliding Mode" Symmetry 11, no. 10: 1225. https://doi.org/10.3390/sym11101225
APA StyleHan, Y., Li, P., & Ma, J. (2019). Vector-Coupled Flight Controller Design Based on Multivariable Backstepping Sliding Mode. Symmetry, 11(10), 1225. https://doi.org/10.3390/sym11101225





