On the Analysis and Computation of Topological Fuzzy Measure in Distributed Monoid Spaces

Abstract

The computational applications of fuzzy sets are pervasive in systems with inherent uncertainties and multivalued logic-based approximations. The existing fuzzy analytic measures are based on regularity variations and the construction of fuzzy topological spaces. This paper proposes an analysis of the general fuzzy measures in n-dimensional topological spaces with monoid embeddings. The embedded monoids are topologically distributed in the measure space. The analytic properties of compactness and homeomorphic, as well as isomorphic maps between spaces, are presented. The computational evaluations are carried out with n = 1, considering a set of translation functions with different symmetry profiles. The results illustrate the dynamics of finite fuzzy measure in a monoid topological subspace.

1. Introduction

The fuzzy set theory has numerous applications in a diverse array of complex systems. Decision making in information systems in the presence of uncertainties or incompleteness can be performed by employing fuzzy sets [1,2,3]. The inherent uncertainties and imprecision of information can be modeled by employing ordered fuzzy numbers, where the fuzzy ordering is formulated by using trapezoidal structures [4]. In general, the fuzzy decision-making process involves computations on multi-granular rough fuzzy sets [2]. The variations in granularities are reflected in the efficiency of information aggregation and filtering. The convergence theory can be applied in analyzing fuzzy inference techniques with various topological applications. In general, the formation of fuzzy sets and fuzzy topology are constructed based on relational algebra, on a crisp set with an upper limit and lower limit [1].

The hybridizations of fussy sets, lattices, and topology have resulted in the formation of various structures of fuzzy topological spaces with different interpretations. In one approach, the fuzzy set theory is applied to the topology in order to construct fuzzy topological spaces [5]. This formulation has created the structures of L-topology based on lattice models. In a different approach, the topological spaces are constructed based on the L-subset of the power set of any arbitrary set X [6]. Hence, the topology based on the L-subset is called L-fuzzy topology, which is a distinct structure as compared to L-topology [7]. An interrelationship exists between the fuzzy sets and the convexity of the underlying spaces. The L-convex spaces are formulated based on a continuous and complete lattice [8]. The L-convex space supports the embedding of various categories of algebraic structures.

The analysis of compactness of the fuzzy sets and topological spaces is important for formulating corresponding measures [9]. The degree of compactness and countability in L-fuzzy pretopological spaces can be analyzed [10]. The formulation of pretopological spaces is based on the combination of a non-distributive lattice and implication operator algebra. Recently, the graph theoretic view of the topology is applied for analyzing the physical lattice-like structures of the honeycomb networks of physical systems [11]. The invariant parameters in the topologically characterized graph-like structures are the topological indices and related connectivity polynomials.

The definitions of the fuzzy topological spaces are refined by incorporating two functors in order to form a category preserving the fuzzy compactness [12]. The concept of the fuzzy ultrametric is introduced based on the sets of probability measures in a supported space [13]. The measure is constructed in a fuzzy metric space with a compact support. The measures of noncompact fuzzy subsets in standard and fuzzy metric spaces are formulated [14]. The regularity of the null-additivity of fuzzy measures on a metric space can be maintained, preserving the consistency of the respective measures [15]. The fuzzy measure on any arbitrary topological space is constructed based on the general Borel sets [16]. The measure preserves the monotone class of the Borel sets and may not be finite in all cases. From the algebraic point of view, the measure on an Abelian group is constructed, which is named as the Haar measure [17]. It is considered that Haar measurable groups are locally compact in nature. The commutative convolution measure algebra is isomorphic to $L^1(G)$, with finite dimensional involution representation [18]. If a space is not separable, then an uncountable number of pairwise disjoint subsets exist, which are open and measurable on any locally compact Abelian group [19].

This paper proposes the analysis and computational evaluations of topological fuzzy measures in distributed monoid spaces. It is considered that the underlying space is n-dimensional and the distributed embeddings of the monoids are arbitrary in the space. The topological fuzzy measures are finite and can be applied on the subspaces under appropriate translations. The computation of measure is performed in a 1D space under the influence of a set of translation functions with various symmetry profiles. The computational evaluations illustrate that the computed measures exhibit various covering and saturation effects, based on the incorporated beta control of the measure.

The rest of the paper is organized as follows. Section 2 presents the preliminary concepts. Section 3 presents definitions related to the presented model, and Section 4 presents a set of analytical properties. Section 5 presents computational evaluations. Finally, Section 6 concludes the paper.

2. Preliminaries

Let $X$ be any arbitrary set equipped with a binary relation (or operation) $\ast :X^2\to X$. The structure $(X,\ast )$ is called a group if the following axioms are maintained [20]:

$$\begin{array}{l}\forall x,y,z\in X,x\ast (y\ast z)=(x\ast y)\ast z,\\ \exists e\in X:\forall x\in X,e\ast x=x\ast e=x,\\ \forall x\in X,\exists x^{-1}\in X:x\ast x^{-1}=x^{-1}\ast x=e\end{array}$$

(1)

The group $(X,\ast )$ is called Abelian if $\forall x,y\in X,x\ast y=y\ast x$. If $X$ represents an underlying space, then a corresponding topology $\tau \subseteq P(X)$ can be constructed on it. The topology $\tau$ should maintain the following axioms ($I$ represents the index set) [21]:

$$\begin{array}{l}\forall A_i\in \tau ,i\in I,{\displaystyle \underset{i\in I}{\cup }{A}_i\in \tau ,}\\ \forall A_i,A_k\in \tau ,A_i\cap A_k\in \tau ,\\ \{\varphi ,X\}\subset \tau \end{array}$$

(2)

A space is called a sigma measurable if it can be equipped with a function, $\mu :(A_i\subset X)\to [0,+\infty ]$. A measure is finite if $\forall A_i\subset X,\mu (A_i)<+\infty$. A fuzzy set is a set equipped with a nonbinary discrete measure, given as $(X,{\mu }_F)$, such that ${\mu }_F:X\to [0,1]$. A fuzzy set can have a support built into it.

3. Definitions

3.1. Groupoid Space

Let $X$ be any arbitrary point set and $A\subset X$ is equipped with an operation in n-dimensional space as $o_x:A^{2n}\to A^n$, such that $\forall a,b\in A^n,\exists c\in A^n$, where $c=a{o}_{x}b$. The $(X^n,o_x)$ is a groupoid space.

3.2. Distributed Monoid Space

Let $(X^n,o_x)$ be a groupoid space and $M=\{B_i\subset A^n:i\in I\subset Z^{+}\}$, where $B_i\cap B_k=\varphi$ if $i\ne k$ and ${\displaystyle \underset{i\in I}{\cup }{B}_i=A^n}$. The $M$ is a distributed monoid (DM) if $\forall B_i\in M$ the following properties are satisfied [20]:

$$\begin{array}{l}\forall a,b,c\in B_i,(a{o}_{x}b)o_{x}c=a{o}_x(b{o}_{x}c),\\ \forall a\in B_i,\exists e_i\in B_i:a{o}_x{e}_i=e_i{o}_{x}a=a\end{array}$$

(3)

3.3. Topological Distributed Monoid (DM)

Let $(X^n,o_x)$ be a groupoid space with a distributed monoid $M$. The $(X^n,M,\tau )$ is a topological DM space if the following topological properties are satisfied in topology $\tau$ on $X^n$:

$$\begin{array}{l}\tau \subseteq P(X^n),M\subset \tau ,\\ \tau \backslash M\ne \varphi \end{array}$$

(4)

3.4. Topological Translation

Let $(X^n,M,\tau )$ be a topological DM space. The $g:X^n\to R$ is a real valued translation function in $(X^n,M,\tau )$, such that $\forall a\in X^n,g(a)\in (-\infty ,0)\cup (0,+\infty )$.

3.5. Fuzzy Topological Measure

A fuzzy topological measure in $(X^n,M,\tau )$ is defined as ${\mu }_{\tau }:\tau \to [0,1]$, such that

$$\begin{array}{l}{\mu }_{\tau }(\varphi )=0,\exists {\beta }_i\in (1,+\infty ),\\ \forall D_i\in \tau ,{\mu }_{\tau }(D_i)=\frac{1}{{\beta }_i}{\displaystyle \sum _{\forall a\in D_i}|g{(a)}^{-1}|}\end{array}$$

(5)

The scaling factor ${\beta }_i$ is a control parameter for the quantization in a fuzzy range for any arbitrary translation function in the topological DM space.

3.6. Local Isomorphism

If there is a bijection $f:M\to M$ in $(X^n,M,\tau )$, such that $\forall B_i\in M,\exists B_k\in M:B_i=f^{-1}(B_k)$, then $f(.)$ is a local isomorphism.

3.7. Local Homeomorphism

If there is a bijection $h:M_x\to M_y$ in $(X^n,M_x,{\tau }_x)$ and $(Y^n,M_y,{\tau }_y)$, respectively, such that $\forall B_i\in M_x,\exists B_k\in M_y:B_i=h^{-1}(B_k)$, then $h(.)$ is a local homeomorphism.

4. Analytical Properties

Theorem 1.

In $(X^n,M,\tau )$, the topological fuzzy measure in the topological DM subspace is countably additive as ${\mu }_{\tau }({\displaystyle \underset{i\in I}{\cup }{B}_i})={\displaystyle \sum _{i\in I}{\mu }_{\tau }(B_i)}$.

Proof. 

Let $(X^n,M,\tau )$ be a topological DM space. Let $\forall B_i\in M,\exists {\beta }_i\in (1,+\infty )$, such that ${\mu }_{\tau }(B_i)={\beta }_i{}^{-1}{\displaystyle \sum _{\forall a\in B_i}|g{(a)}^{-1}|}$, where $0<{\mu }_{\tau }(B_i)<1$. As $[i\ne k]\Rightarrow [B_i\cap B_k=\varphi ]$, thus ${\mu }_{\tau }(M)={\displaystyle \sum _{i\in I}[{\beta }_i{}^{-1}{\displaystyle \sum _{\forall a\in B_i}|g{(a)}^{-1}|}]}$. However, in the distributed monoid subspace, ${\displaystyle \sum _{i\in I}{\mu }_{\tau }(B_i)}={\displaystyle \sum _{i\in I}[{\beta }_i{}^{-1}{\displaystyle \sum _{\forall a\in B_i}|g{(a)}^{-1}|}]}$. Hence, ${\mu }_{\tau }({\displaystyle \underset{i\in I}{\cup }{B}_i})={\displaystyle \sum _{i\in I}{\mu }_{\tau }(B_i)}$ in the topological DM space $(X^n,M,\tau )$. □

Theorem 2.

In the $(X^n,M,\tau )$ space $\exists D,E\in X^n$, such that ${\mu }_{\tau }(D\cap E)=0$ and ${\mu }_{\tau }(D\cup E)\in (0,1)$.

Proof. 

Let $(X^n,M,\tau )$ be a topological DM space, such that $\exists D,E\subset X^n$, where $\{D,E\}\subset \tau$. Let $\{D,E\}\not\subset \tau \backslash M$ and, by following topological properties, $D\cup E\in \tau$. However, this indicates that ${\mu }_{\tau }(D\cap E=\varphi )=0$ in $(X^n,M,\tau )$. On the other hand, $X^n\backslash \{D\cup E\}\ne \varphi$ and ${\mu }_{\tau }(D)+{\mu }_{\tau }(E)>0$. As $X^n\ne \varphi$ and $0<{\mu }_{\tau }(X^n)\le 1$, thus ${\mu }_{\tau }(D\cup E)<1$, where $g(.)\in R\backslash \{-\infty ,0,+\infty \}$. Hence, ${\mu }_{\tau }(D\cup E)\in (0,1)$ in the topological DM space $(X^n,M,\tau )$. □

Lemma. 

In the$(X^n,M,\tau )$space, the monotonicity of the topological fuzzy measure is preserved as${\mu }_{\tau }(\tau )>{\mu }_{\tau }(M)$.

Proof. 

In the $(X^n,M,\tau )$ space, $\tau \ne \varphi$, and it results in the condition that ${\mu }_{\tau }(\tau \backslash \{\varphi \})\in (0,1]$. However, $\tau \backslash M\ne \varphi$ and ${\mu }_{\tau }(\tau \backslash M)\in (0,1)$ in the underlying topological DM space. Hence, ${\mu }_{\tau }(\tau )>{\mu }_{\tau }(M)$, preserving the monotonicity of the topological fuzzy measure in the $(X^n,M,\tau )$ space. □

Theorem 3.

In the$(X^n,M,\tau )$space, the topological fuzzy measure of a monoid is bounded as${\mu }_{\tau }({\displaystyle \underset{i\in I}{\cup }{B}_i})<{\displaystyle \sum _{i\in I}{\mu }_{\tau }(\overline{B_i})}$.

Proof. 

Let $(X^n,M,\tau )$ be a topological DM space, where $\overline{M}=\{\overline{B_i}:\forall B_i\in M\}$ and $\overline{B_i}=B_i\cup \partial B_i$. As $M\subset \tau$, thus $\forall B_i\in M,\partial B_i\subset B_i^c\subset X^n$ in the topological DM space. Hence, $[\partial B_i\ne \varphi ]\Rightarrow [{\mu }_{\tau }(\overline{B_i}\in \overline{M})>{\mu }_{\tau }(B_i\in M)]$ in the respective space. □

Theorem 4.

If$(X^n,M,\tau )$is a Hausdorff space, then$\exists D,E\in \tau$, such that${\mu }_{\tau }(D)={\mu }_{\tau }(E)>0$.

Proof. 

Let $(X^n,M,\tau )$ be a Hausdorff topological DM space and $\exists D,E\in \tau$, such that $D\cap E=\varphi$. However, if $|D|=|E|=1$, then $\{D,E\}\subset \tau \backslash M$, where $M\subset \tau$. As the topological translation maintains the property that $\forall a\in D\subset X^n:g(a)\in (-\infty ,0)\cup (0,+\infty )$, thus ${\mu }_{\tau }(D\cup E)>0$ if $D\cup E\ne \varphi$. However, if $|D|=|E|=1$ and $a\in D,b\in E$, then ${\mu }_{\tau }((D\cup E)\backslash \{a,b\})=0$. Hence, $\exists {\beta }_D,{\beta }_E:{\beta }_D\ne {\beta }_E$ and ${\beta }_D,{\beta }_E\in (1,+\infty )$, such that ${\mu }_{\tau }(D)={\mu }_{\tau }(E)>0$. □

Theorem 5.

In the two Hausdorff topological DM spaces$(X^n,M_x,{\tau }_x)$and$(Y^n,M_y,{\tau }_y)$, the monoid subspaces are homeomorphic if$t:Y^n\to X^n$and$(h_{o}t)(M_y)={(h_{o}t)}^{-1}(M_y)$.

Proof. 

Let $(X^n,M_x,{\tau }_x)$ and $(Y^n,M_y,{\tau }_y)$ be two Hausdorff topological DM spaces, and $t:Y^n\to X^n$ be any arbitrary function, such that the following property is maintained:

$$\begin{array}{l}S={\displaystyle \underset{i\in I}{\cup }(B_i\in M_x),}\\ T={\displaystyle \underset{k\in I}{\cup }(B_k\in M_y),}\\ \forall a\in T,\exists b\in S:a=t^{-1}(b),\\ [\{b,c\}\subset S\wedge (b\ne c)]\Rightarrow [t^{-1}(b)\ne t^{-1}(c)],\\ t(T)\subseteq S\end{array}$$

(6)

Furthermore, if $\forall B_i\in M_x,\exists B_k\in M_y:t^{-1}(B_i)=B_k$, then $t(M_y)=h^{-1}(M_y)$. Hence, $(h_{o}t)(M_y)={(h_{o}t)}^{-1}(M_y)$ in the $(X^n,M_x,{\tau }_x)$ and $(Y^n,M_y,{\tau }_y)$ Hausdorff topological DM spaces. □

Theorem 6.

In the two Hausdorff topological DM spaces$(X^n,M_x,{\tau }_x)$and$(Y^n,M_y,{\tau }_y)$equipped with$t:Y^n\to X^n$, the monoid homeomorphic subspaces are measure equivalent as${\mu }_{\tau }(t^{-1}(S))=\lambda {\mu }_{\tau }(h(S))$, where$\lambda >0$and,$S={\displaystyle \underset{i\in I}{\cup }(B_i\in M_x)}$.

Proof. 

Let $(X^n,M_x,{\tau }_x)$ and $(Y^n,M_y,{\tau }_y)$ be two Hausdorff topological DM spaces and $t:Y^n\to X^n$, such that $(h_{o}t)(M_y)={(h_{o}t)}^{-1}(M_y)$. As $S={\displaystyle \underset{i\in I}{\cup }(B_i\in M_x)}\ne \varphi$, thus ${\mu }_{\tau }(S)>0$ in the monoid subspace. This indicates that ${\mu }_{\tau }(h(S))>0$ as $h(S)\ne \varphi$. Let $\exists \lambda >0$, such that ${\mu }_{\tau }(S)=\lambda {\mu }_{\tau }(h(S))$. However, as $(h_{o}t)(M_y)={(h_{o}t)}^{-1}(M_y)$ in the spaces, so $t^{-1}(S)=h(S)$. Hence ${\mu }_{\tau }(t^{-1}(S))=\lambda {\mu }_{\tau }(h(S))$. □

Theorem 7.

$(X^n,M,\tau )$is at least a Haar measurable commutative space if the inverses exists.

Proof. 

Let $(X^n,M,\tau )$ be a topological DM space. As $M$ is a monoid subspace, thus $\forall B_i\in M,\exists e_i\in B_i$, such that $e_i{o}_{x}E=E$, where $E\subseteq B_i$. In the monoid subspace, ${\mu }_{\tau }(e_i{o}_x{B}_i)=[{\mu }_{\tau }(B_i)\in (0,1)]$. However, if $e_i{o}_{x}E=E$, then $E{o}_x{e}_i=e_i{o}_{x}E$ in $M\subset P(X^n)$. Hence, $(X^n,M,\tau )$ is at least a Haar measurable commutative space if $\forall B_i\in M,\forall a\in B_i,\exists a^{-1}\in B_i:a{o}_x{a}^{-1}=a^{-1}{o}_{x}a=e_i$. □

Theorem 8.

If$X$is compact, then$\underset{i\to +\infty }{\lim }{\mu }_{\tau }({\displaystyle \underset{i\in I}{\cup }{B}_i)\to 1}$.

Proof. 

Let $X$ be a compact set and $(X^n,M,\tau )$ be a compact topological DM space. If $C$ is a cover of $X^n$, then $X^n\subseteq {\displaystyle \underset{m\in I}{\cup }(D_m\in C)}$. Let $M\subset C$, such that $|X^n\backslash {\displaystyle \underset{i\in I}{\cup }{B}_i}|\in (0,+\infty )$. This indicates that $\underset{i\to +\infty }{\lim }|X^n\backslash {\displaystyle \underset{i\in I}{\cup }{B}_i|\to 0}$ in $(X^n,M,\tau )$. However, $0<{\mu }_{\tau }(X^n\in \tau )\le 1$ in the respective compact space, where $X^n\ne \varphi$. Hence, $\underset{i\to +\infty }{\lim }{\mu }_{\tau }({\displaystyle \underset{i\in I}{\cup }{B}_i)\to 1}$ in the compact $(X^n,M,\tau )$. □

Theorem 9.

In the$(X^n,M,\tau )$space${\mu }_{\tau }(D)>0$, where$D={\left({\displaystyle \underset{i\in I}{\cup }{B}_i}\right)}^c$.

Proof. 

Let $(X^n,M,\tau )$ be a topological DM space. If $D={\displaystyle \underset{i\in I}{\cup }(B_i\in M)}$ in the space, then $X^n\backslash D\ne \varphi$, because $\tau \backslash M\ne \varphi$. This indicates that in $(X^n,M,\tau )$, the closed space $D^c\ne \varphi$, which results in ${\mu }_{\tau }(D^c)>0$. □

Theorem 10.

In the$(X^n,M_x,{\tau }_x)$and$(Y^n,M_y,{\tau }_y)$locally homeomorphic topological DM spaces,${\displaystyle \sum _{i\in I}{\mu }_{\tau }(B_i\in M_x)={\mu }_{\tau }({\displaystyle \underset{k\in I}{\cup }{h}^{-1}(B_k\in M_y))}}$.

Proof. 

Let $(X^n,M_x,{\tau }_x)$ and $(Y^n,M_y,{\tau }_y)$ be two locally homeomorphic topological DM spaces. Thus, $\forall B_k\in M_y,\exists B_i\in M_x:B_i=h^{-1}(B_k)$ and ${\displaystyle \underset{i\in I}{\cup }(B_i\in M_x)}={\displaystyle \underset{k\in I}{\cup }{h}^{-1}(B_k\in M_y)}$. This results in ${\displaystyle \sum _{i\in I}{\mu }_{\tau }(B_i\in M_x)={\mu }_{\tau }({\displaystyle \underset{k\in I}{\cup }{h}^{-1}(B_k\in M_y))}}$. □

Theorem 11.

In the$(X^n,M_x,{\tau }_x)$and$(Y^n,M_y,{\tau }_y)$locally isomorphic as well as homeomorphic topological DM spaces,${\mu }_{\tau }({\displaystyle \underset{i\in I}{\cup }(B_i\in M_x)})={\mu }_{\tau }({\displaystyle \underset{k\in I}{\cup }{(h_{o}f)}^{-1}}(B_k\in M_y))$.

Proof. 

Let $(X^n,M_x,{\tau }_x)$ and $(Y^n,M_y,{\tau }_y)$ be two locally isomorphic as well as homeomorphic topological DM spaces. This indicates that $\forall B_i\in M_x,\exists B_u\in M_x:B_i=f^{-1}(B_u)$ and $\exists B_k\in M_y:B_i={(h_{o}f)}^{-1}(B_k)$. Thus, in the two topological DM spaces ${\displaystyle \underset{i\in I}{\cup }(B_i\in M_x)}={\displaystyle \underset{k\in I}{\cup }{(h_{o}f)}^{-1}}(B_k\in M_y)$, which results in ${\mu }_{\tau }({\displaystyle \underset{i\in I}{\cup }(B_i\in M_x)})={\mu }_{\tau }({\displaystyle \underset{k\in I}{\cup }{(h_{o}f)}^{-1}}(B_k\in M_y))$. □

Theorem 12.

The topological fuzzy measure is consistent under compression if$\forall D_i\in \tau \backslash \left\{\varphi \right\},$${\beta }_s>\sup (\{{\beta }_i:D_i\in \tau \backslash \left\{\varphi \right\}\})$and,${\mu }_{\tau }(D_i)=\frac{1}{{\beta }_s}{\displaystyle \sum _{\forall a\in D_i}|g{(a)}^{-1}|}$.

Proof. 

Let $(X^n,M,\tau )$ be a topological DM space equipped with fuzzy measure ${\mu }_{\tau }(.)$. The translation function maintains $\forall a\in X^n,|g{(a)}^{-1}|\in (0,+\infty )$. Let the topological DM space be $\forall D_i\in \tau ,$ ${\beta }_s=\sup (\{{\beta }_i:D_i\in \tau \backslash \left\{\varphi \right\}\})+(\epsilon >0)$, where ${\mu }_{\tau }(D_i)\in [0,1]$. As a result, the following condition will be maintained by compressed measure:

$$\begin{array}{l}\forall D_i\in \tau \backslash \left\{\varphi \right\},\\ \frac{1}{{\beta }_s}{\displaystyle \sum _{\forall a\in D_i}|g{(a)}^{-1}|}<\frac{1}{{\beta }_i}{\displaystyle \sum _{\forall a\in D_i}|g{(a)}^{-1}|}\end{array}$$

(7)

However, $\forall D_i\in \tau \backslash \left\{\varphi \right\},{\mu }_{\tau }(D_i)\in (0,1]$ in $(X^n,M,\tau )$.

Hence, $0<\frac{1}{{\beta }_s}{\displaystyle \sum _{\forall a\in D_i}|g{(a)}^{-1}|}<1$, maintaining consistency under compression. □

5. Computational Evaluations

The computational evaluations are carried out in a 1D topological DM space with distributed monoid embedding, such that $\forall a\in X\subset R,a\in (-\infty ,+\infty )$. The computational model of measure in the distributed monoid considers, $M=\{(A\subset X,o_x)\}$, where $A=\{a:\forall a\in [-1,1]\backslash \{0\left\}\right\}$, such that $\forall a,b\in A:a{o}_{x}b\Rightarrow [a.b\in A]$. The measures are numerically computed by employing translation functions having various profiles, such as (a) inverse translation $(g{(a)}^{-1}=a^{-1})$, (b) fixed coefficient translation $(g{(a)}^{-1}=ka,k\in R^{+})$, and (c) nonlinear periodic translation $(g{(a)}^{-1}={\cos }^{-1}(ka)\ne 0)$ in a topological DM space. The numerical datasets are generated by software written in C language with installed Math-libraries. The samples are collected in datasets covering entirely positive and negative domains. The resulting profiles of the translation functions of different categories with various symmetries are presented in Figure 1, Figure 2 and Figure 3.

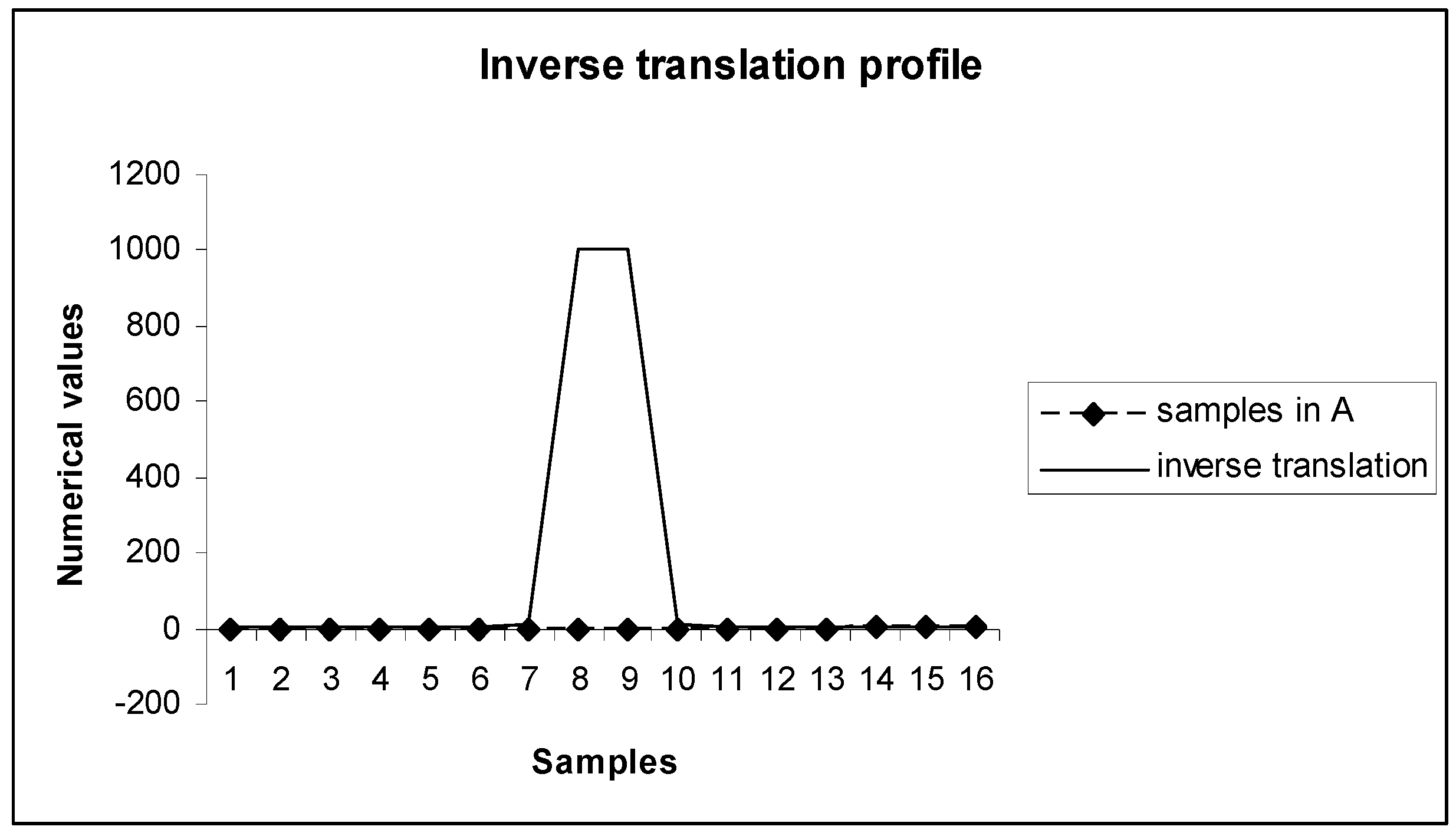
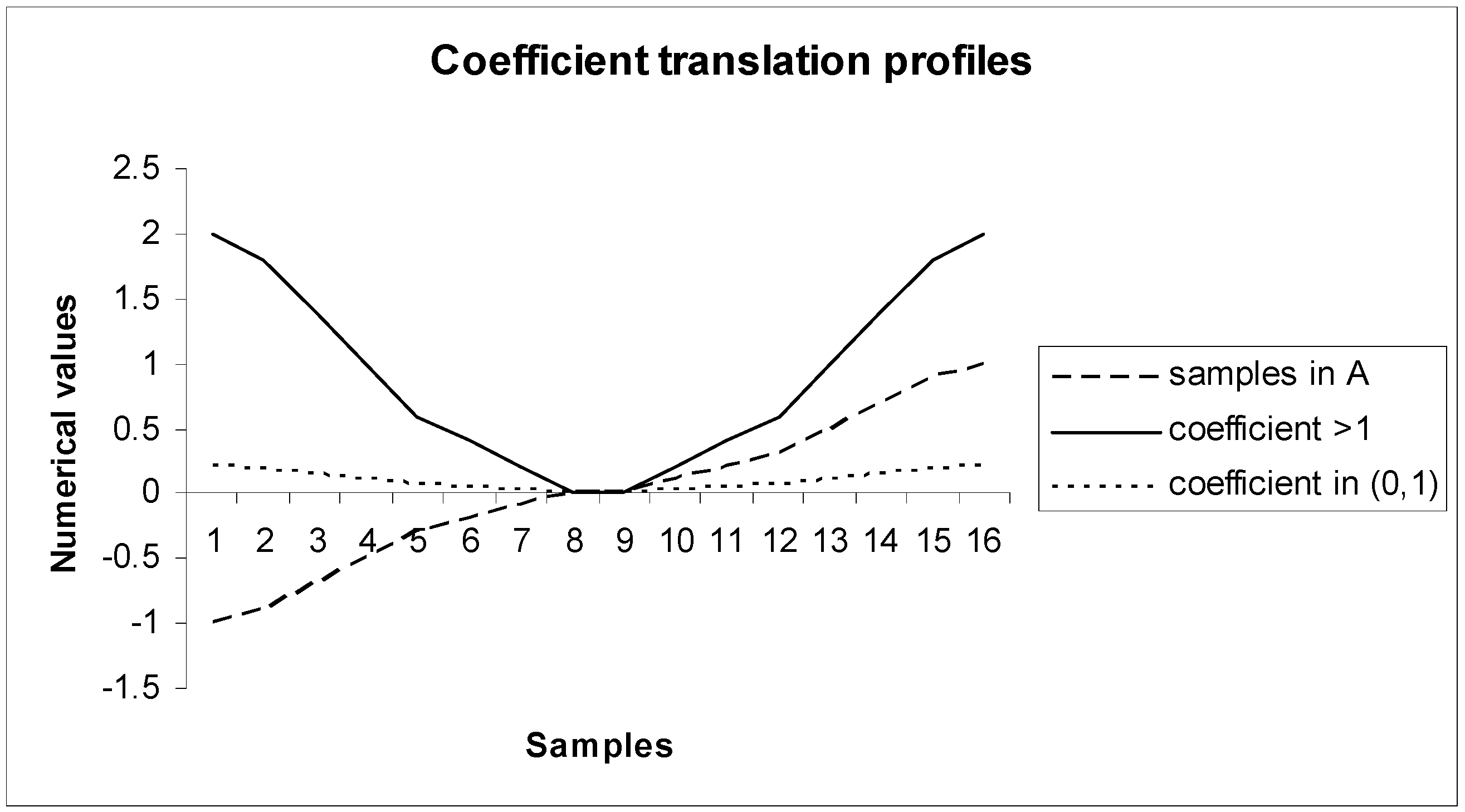
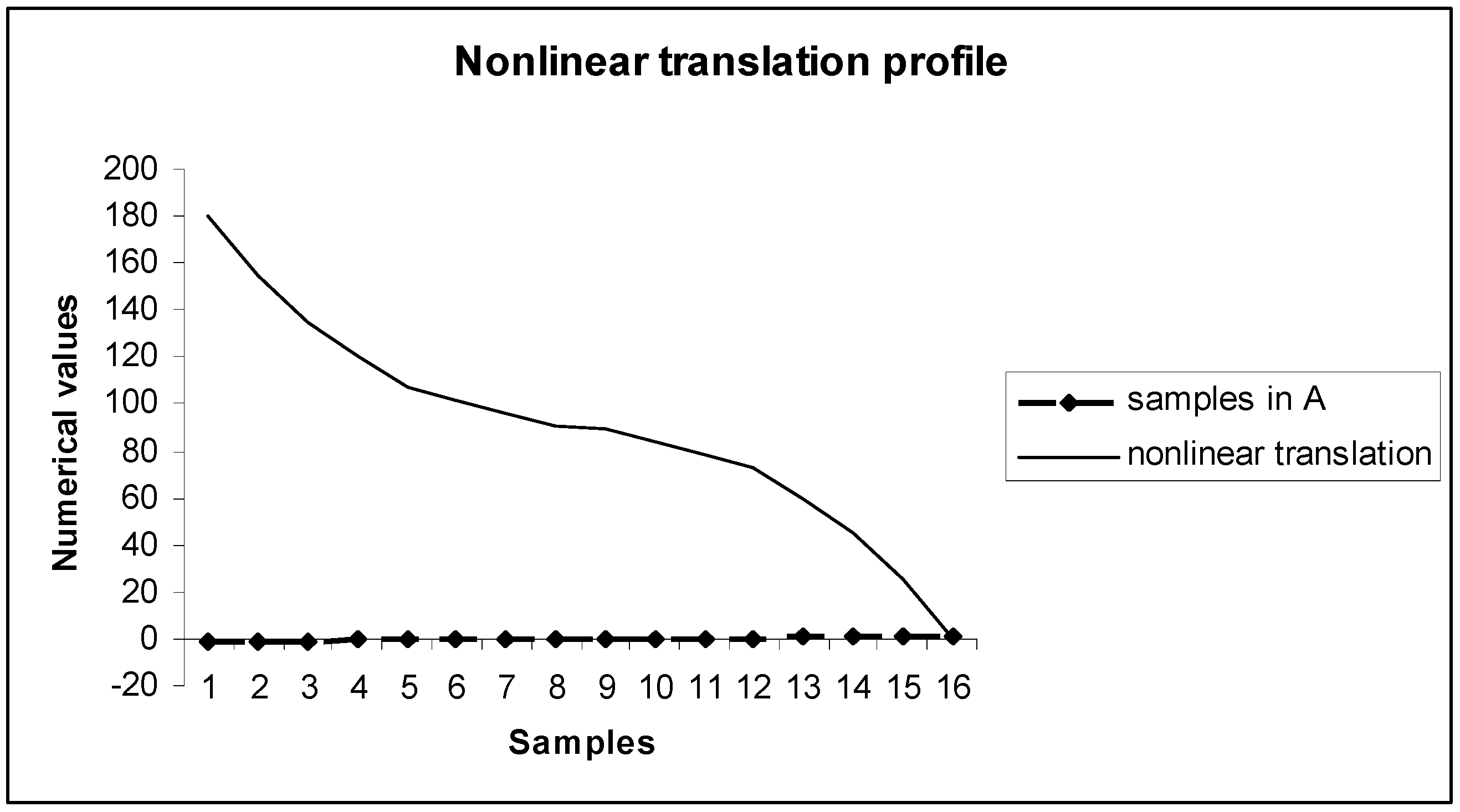
The profile of inverse translation, presented in Figure 1, illustrates that the translation has a higher concentration zone around the origin, and appears to have symmetric distribution. The fixed coefficient translation profiles presented in Figure 2 consider two coefficient values, and the resulting profiles illustrate that the variations in translations have approximately symmetric distributions in the domain. The inverse and fixed coefficient translations do not cover a null (zero) translation point (i.e., translations are always in the non-zero positive range). 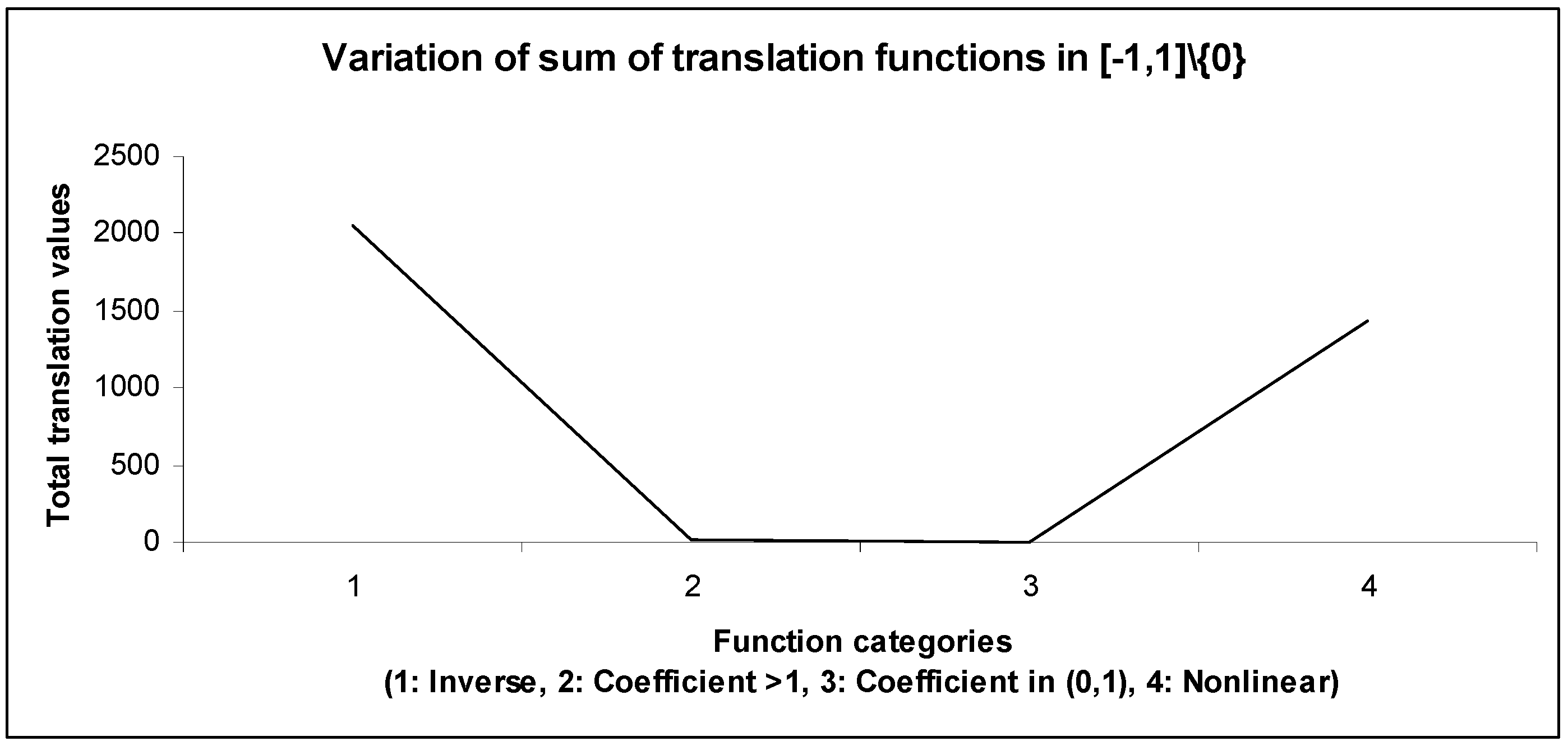The profile of the nonlinear periodic translation is presented in Figure 3, which is asymmetric in nature, with a monotonic reduction of translation in the domain. Moreover, the nonlinear periodic translation covers a null (zero) translation point (i.e., preserving translation invariant fixed point). The variations of the aggregate (sum) of translations covering $M=\{(A,o_x)\}$ in different cases are presented in Figure 4.

The aggregated translation is much smaller in case of the fixed coefficient translations as compared to the other categories of translations. The inverse translation has the highest aggregated value because of the existence of a singularity at the origin. However, the nonlinear periodic translation exhibits a moderately higher aggregated translation value.

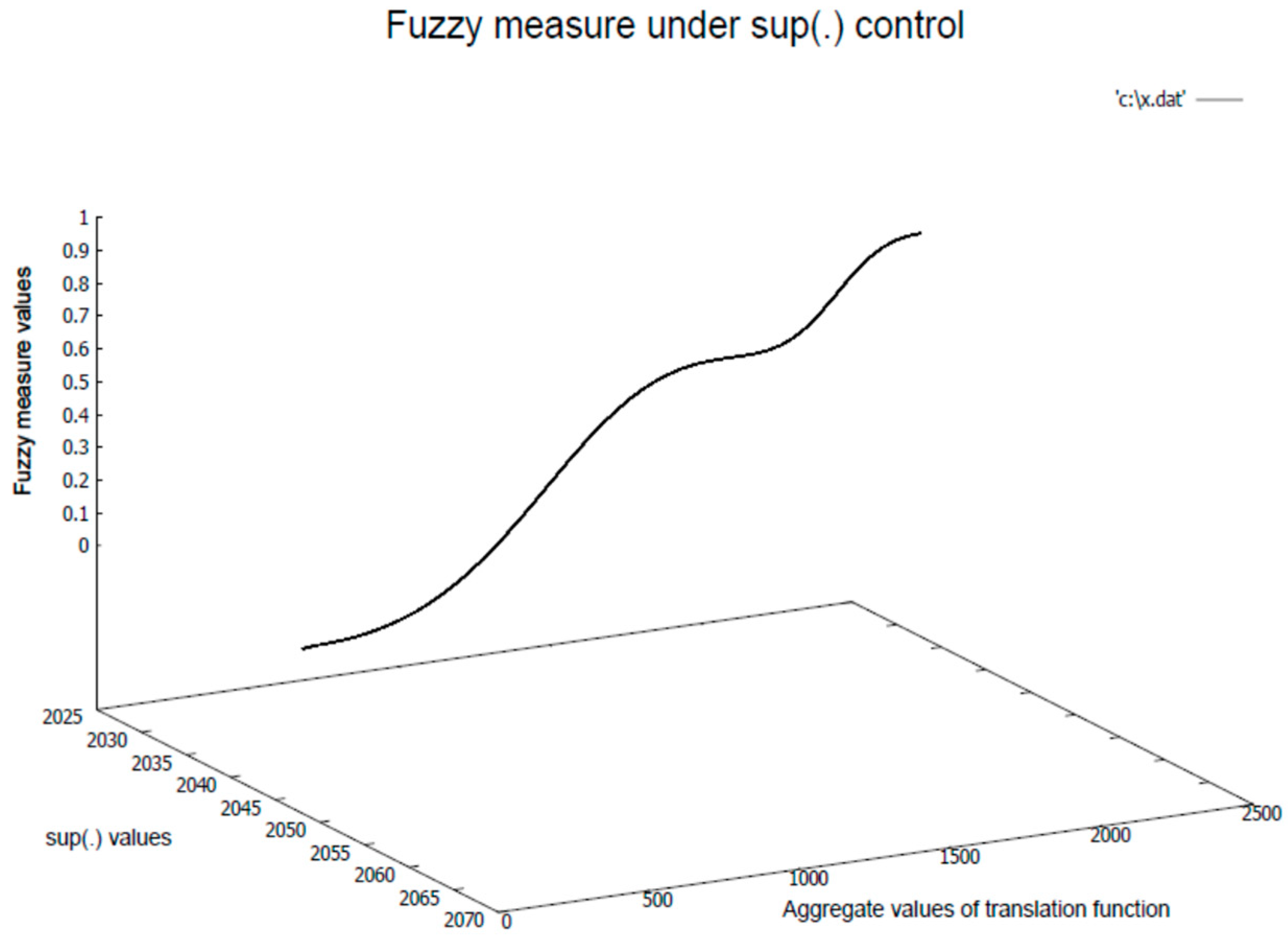
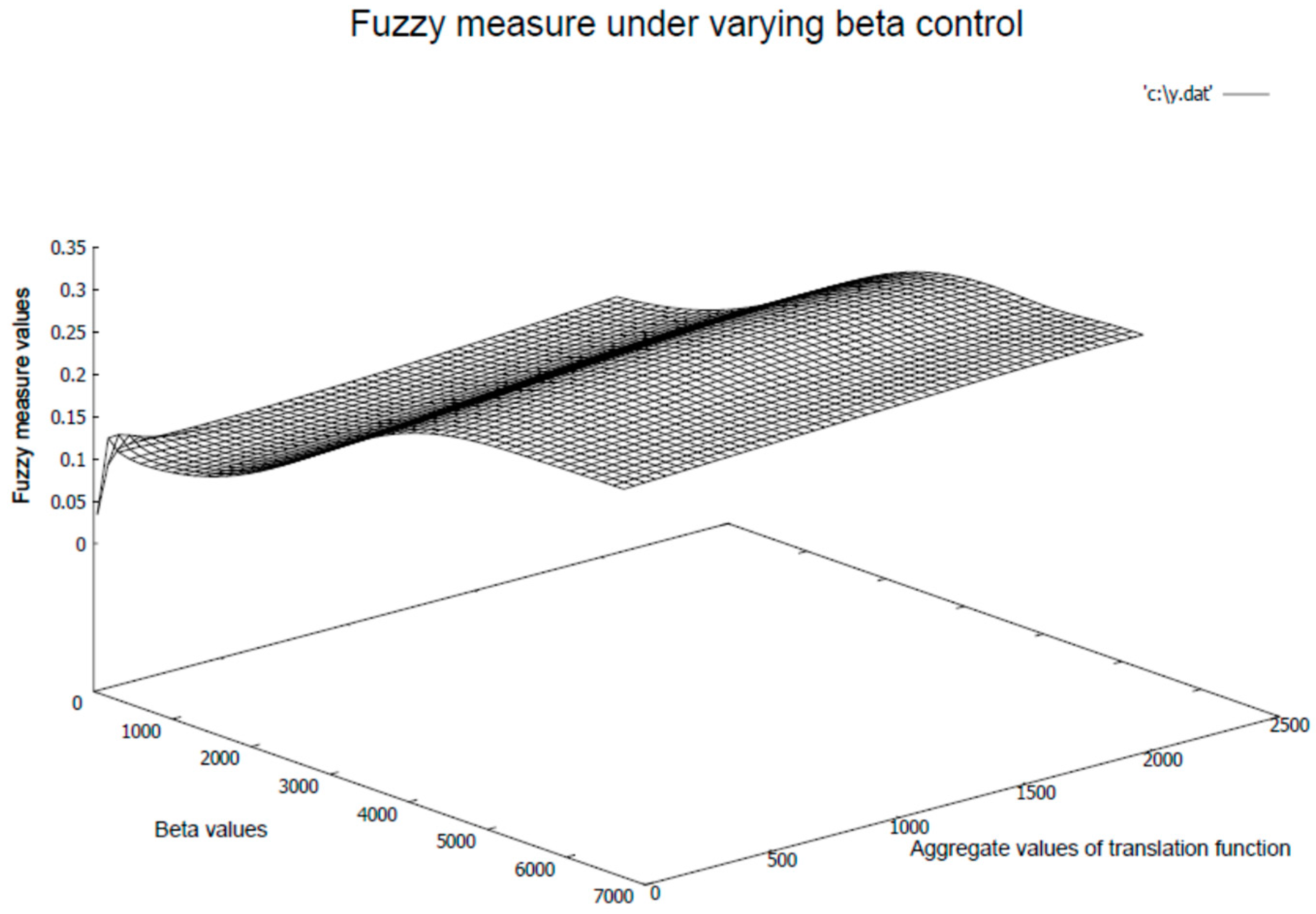
The fuzzy measures are computed considering two cases, such as (1) deterministic measures under sup(.) control, and (2) random measure under the control of randomized ${\beta }_i$ values maintaining conditions of fuzzy measures. The dynamics of the resulting fuzzy measures are presented in Figure 5 and Figure 6.

The sup(.) control considers a fixed beta value as a control parameter, based on a set of translation values, and it exerts a compressive effect on the distribution of measures. As a result, the domain of distribution of the fuzzy measure tends to cover [0, 1] entirely, as presented in Figure 5. Moreover, the covering measure distribution is nonlinear in nature. However, the randomized fuzzy measures are computed based on randomly generated beta control values, depending on the respective individual translation profiles. As a result, it generates a nonlinear measure surface with a saturation effect. 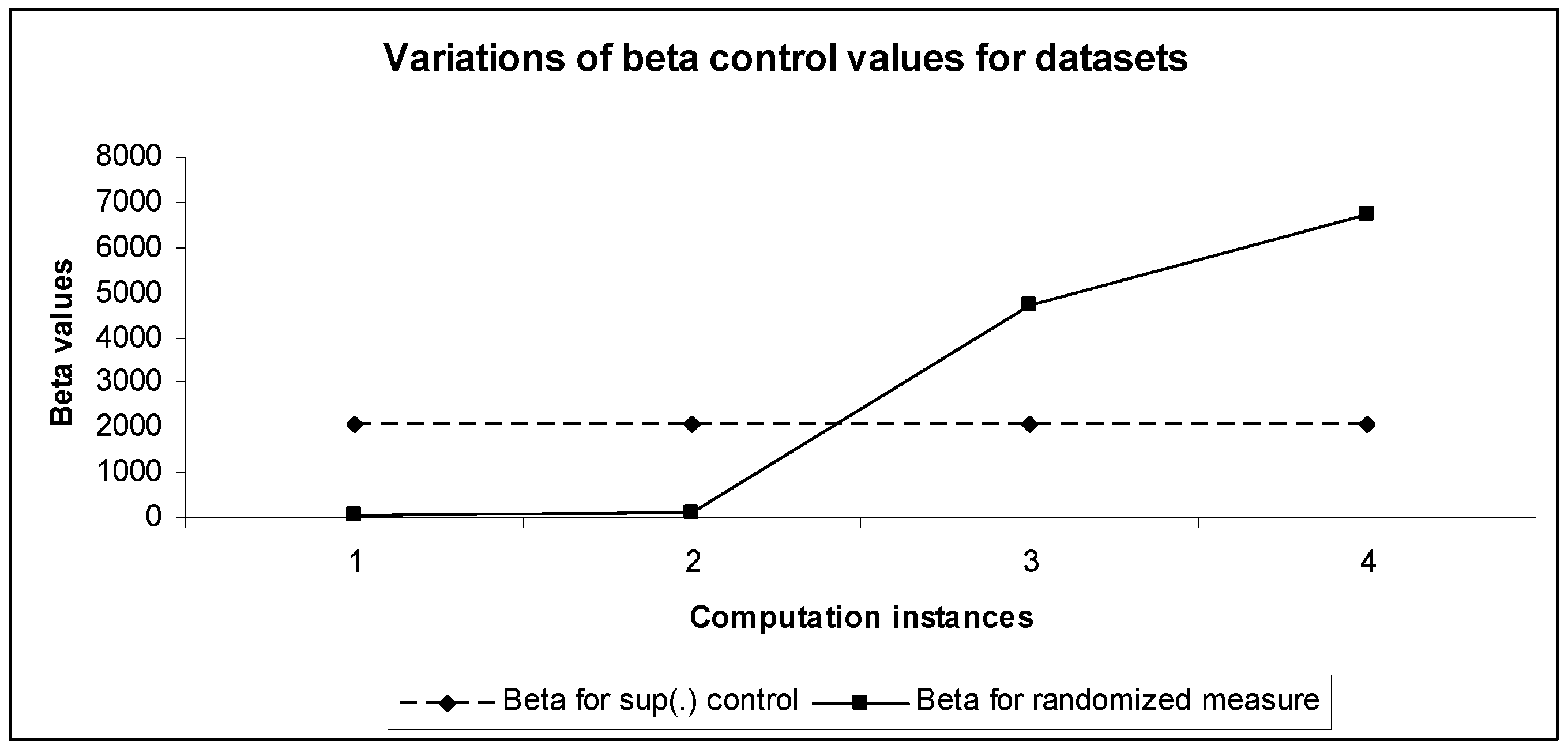The saturation effect depends upon two factors, namely (1) randomized distribution of the ${\beta }_i$ control parameter and (2) variations in the localized random measures based on distinctive individual ${\beta }_i$ values. The variations of the ${\beta }_i$ control parameters are presented in Figure 7. As the randomized control parameter is monotonically increased, the aggregated translation values incorporate saturation at a comparatively lower limit boundary (<1). However, both of the fuzzy measures are consistent in nature within the space.

6. Conclusions

The analytic understanding of topological fuzzy measures facilitates the construction of specific measure spaces along with its applications. The analysis and computation of topological fuzzy measures vary if the underlying spaces embed monoid algebraic structures. In this paper, the concept of topologically distributed monoid spaces is presented, and a set of novel theorems is constructed in order to gain analytical insights into fuzzy measures in such spaces. The fuzzy measure of the distributed monoid spaces can be computed with diverse distribution profiles covering the entire measure range, using a specific control parameter. The measures are finite in nature and the equivalent topological fuzzy measures in two locally homeomorphic monoid spaces can be formulated if the underlying space is Hausdorff. The proposed topological fuzzy measure is consistent under compression. In compact spaces, the covering topological fuzzy measure of the distributed monoids preserves the limiting unity measure. Furthermore, the minimal form of the fuzzy Haar measurability can be preserved in the topological distributed monoid spaces under certain conditions. The minimal Haar measurability of the proposed topological fuzzy measure considers the identity elements only. As a limiting case, the proposed measure does not consider the existence of a group structure in the underlying space. The topological fuzzy measures in the distributed monoid spaces can be computed under various translations, generating a variety of measure distributions and covers.