1. Introduction
Nowadays, in the open network environment, effectively managing and protecting digital multimedia content, as well as preventing increasingly serious computer crimes and information from being illegally leaked, deleted, and modified, have become a research hotspot in the field of information security. People first turn to traditional cryptography [
1], which ensures the message cannot be overheard or destroyed by using secret keys with different algorithms [
2,
3,
4]; consequently, the eavesdropper cannot see or understand the secret information. Nevertheless, at the same time, distinctive and meaningless secret key-based encryption results may unintentionally attract intruders’ attention. Furthermore, encryption algorithms are always very complicated, and the processes of encryption and decryption requires huge space and time complexity. To solve these problems, people have been looking for new solutions as an effective complement to the traditional cryptographic system. In such efforts, secret sharing and information hiding are significantly concerned.
Secret sharing serves to enhance security features and prevent authority fraud by avoiding the loss, modification, or destruction of important hidden information. The first secret sharing scheme is the threshold secret sharing scheme based on the Lagrange interpolating polynomial and finite geometry, which was proposed in 1979 by Shamir [
5] and Blakley [
6], independently. In their schemes, a dealer partitions a secret into
n shadows, which are distributed to
n participants. It takes at least
k (
k n) participants to work together to recover the secret, and less than
k will not release any valuable information. Thus, the advantages of a secret sharing scheme are as follows: (1) Preventing the excessive concentration of power to lead to abuse due to shared features; (2) ensuring the security and integrity of the secret key as enough shares must be provided to restore the original image and secret; and (3) increasing the reliability of the transmission process of secret information without increasing the risk. With the advent of secret sharing and in-depth research, secret sharing schemes based on different access structures have been increasingly proposed and applied in the last decade.
In 1994, at the European cryptography conference, a new branch of the secret sharing field, the visual secret sharing (VSS) scheme—or visual encryption (VC), as some people call it—was put forward by Naor and Shamir [
7]. VSS uses several random-like images called shadows that do not make any sense, instead of the original image, to transfer information over the Internet. By superposing the shadows, secret images can be easily recovered because VSS depends only on the human visual system (HVS) and has no need to apply the complex calculations of the traditional cryptographic system. In fact, it has no need for any cryptology knowledge or computer help in restoring a secret. Hence, VSS has a wide range of practical applications and has been extensively studied in the literature (e.g., References [
8,
9,
10,
11,
12,
13,
14]). However, this method faces the pixel expansion problem and suffers from the management problem. As we know, a VSS with less pixel expansion will have a smaller probability of making mistakes in reconstructing the secret image. Another problem that should not be ignored is that, during the transmission of shares, the noise-like shares increase transmission risk. Thus, it is important to find a method for eliminating pixel expansion and reducing the transmission risk in VSS schemes, especially for medical, military, or artistic images.
In order to solve the problems mentioned thus far and achieve higher security, secret sharing technology, in combination with information hiding (i.e., information hiding based VSS, or IH-VSS), is valued and has become a hot research topic in recent years. The purpose of information hiding is to cover up the secret using technical means. If human eyes cannot see the existence of the transmission of information from the surface, the information can be forwarded and the detection by third-party recipients can be avoided. Because information hiding is less likely to attract the attention of attackers or regulators, the hidden secret is less likely to be leaked. Information hiding technology consists mainly of two parts: An information-embedding algorithm and a hidden information detection/extraction algorithm (detector). Secure parameters may be required to detect/recover the hidden secret information from a cover carrier. Under the premise that secret parameters are unknown, it is difficult for a third party to get or delete from the carrier—or even find the secret information.
Through the combination of information hiding and visual secret sharing (IH-VSS), the defects of secret sharing and/or drawbacks of information hiding will be significantly weakened, thereby making covert communication more secure. Hence, many studies related to IH-VSS scheme using a meaningful cover image have been conducted, such as [
15,
16,
17,
18,
19,
20]. However, one common problem of these studies is that they could not restore the shadow image to the cover image. In 2010, a reversible image sharing scheme based on a Sudoku matrix to preserve the fidelity of valuable host images was proposed [
21] to successfully camouflage the shadows into the cover image with satisfactory quality, accompanied with distortion limited within a range of [0, 3]. Shortly after [
21] was published, an updated version of it was put forward that not only enhanced visual quality, but also had a larger capacity for embedded secret data [
22]. Subsequently, a low computational complexity Quadri-Directional Searching Algorithm (QDSA) for secret image sharing was proposed [
23], thereby enabling the modification of the original cover pixel values to be limited within a small range according to the value of ω. Moreover, the shadow images can achieve excellent visual quality, as demonstrated by [
24], followed by a (2, 2)-threshold reversible IH-VSS scheme that achieve high quality and have authentication ability by skillfully employing a turtle shell matrix [
25]. In addition to the above papers, some scholars have also designed different secret sharing schemes that feature the enhanced security of hidden secret messages. For example, in 2017, Cheng et al. [
26] used meaningful image shadows that are based on gray code to offer fairly high security. In [
27], He et al. proposed a high quality and high security image sharing. Recently, an adaptive method with a greatly enhanced embedding capacity under less execution time was proposed; it is obviously superior to many current algorithms in performance efficiency [
28].
The algorithms described thus far are all related to IH-VSS and have distinctive approaches that differ from one another, yet none of them are exempt from considering the trade-off between the embedding capacity and image quality of the generated shadows. In this paper, with no time-consuming mathematical operations involved, we proposed a 2-2 threshold IH-VSS scheme using a meaningful image as the cover image through which the avoidance of the pixel expansion problem caused by the noisy-like shadows of the traditional Shamir’s algorithm can be realized. In the algorithm, we first append part of the information from the cover image to the end of the secret and hide the secret using Kim et al.’s M matrix. Next, pixel pairs of the cover image with partial modification and stego-image are switched according to the sequence of {0, 1} generated by a random number generator. During the extraction and restoration phase, when the two participants collect the valid shadows, they can calculate the random number Num according to the pre-determined algorithm and then generate the corresponding {0, 1} string to recover the hidden secret information and further obtain the intact cover image. In this way, the embedding rate of 1.59 bpp (bits per pixel) along with PSNR of 54.34 dB are realized. Moreover, a good balance between the high embedding capacity and PSNR is achieved. Furthermore, if one participant provides a fake shadow or maliciously wants to obtain information about another participant, the Num, which is key information for pixel switching between the two shadows, cannot be derived correctly. In other words, the security of the hidden secret is guaranteed. Experimental results show that, by increasing the embedded payload of secret information, the PSNR value remains above 50 dB, which is quite high; furthermore, the small distortion between shadow1 and shadow2 and the cover image adds a lot of imperceptibility and security to our proposed IH-VSS scheme. It is also noted that our proposed IH-VSS scheme is completely reversible and friendly, with highly execution efficiency, which makes the application of our proposed scheme more extensive.
The rest of this paper is organized as follows.
Section 2 discusses Shamir’s secret sharing system and Kim et al.’s EMD-2 scheme. The IH-VSS scheme we propose is introduced in
Section 3, followed by the experimental results and performance analysis in
Section 4. Finally, the conclusions are presented in
Section 5.
2. Related Works
To give readers enough background knowledge for our proposed scheme,
Section 2 briefly reviews Shamir’s secret sharing [
2], and Kim et al.’s EMD-2 scheme [
29].
2.1. Shamir’s Secret Sharing
Shamir [
5] and Blakley [
6] independently proposed the first secret sharing scheme in 1979, focusing on the concept of the (
k,
n) threshold secret sharing scheme. Some important notions were defined in their schemes. For example, the image held by a participant is called a secret share or a sub-secret and shadow. Secret sharing schemes are usually established by trusted distributors who calculate all the shares and distribute them over secure channels to participants. The threshold
k has the important meaning that the possible values for secret
S seem as likely as with no knowledge when the number of shares does not reach the lower limit
k. In other words, the secret
S cannot be reconstructed with fewer than
k pieces. If
k =
n, then every shadow derived from the original secret
S is required to reconstruct the secret.
In Shamir’s (
k,
n) [
5] (where 1
) threshold secret sharing scheme, the secret data can be converted to (or can be made) a number, which we call
I. The domain of secrets and shares is the elements of a finite filed
, where
is a prime number (
>
I). To split
I into
n shares, the dealer determines and constructs a (
k − 1)-degree polynomial as
then uses it through the following steps:
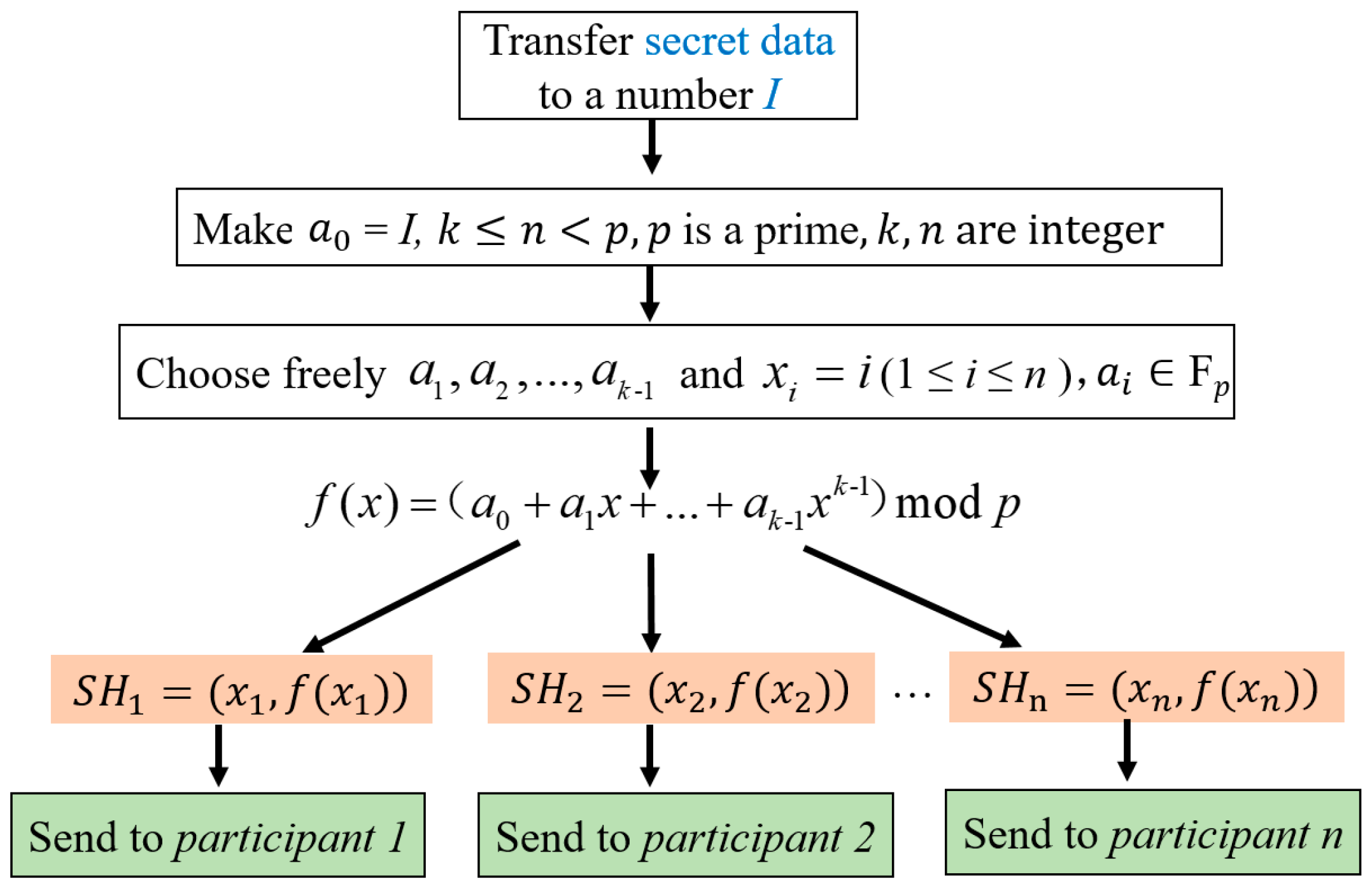
- Step 1.
Make = I.
- Step 2.
Choose (k − 1) integer values randomly within [0, − 1].
- Step 3.
Select freely for the ith (1 ≤ i ≤ n) share a value of x, denoted as , and all xi must be distinct from one another.
- Step 4.
Calculate a corresponding value of
for each chosen
xi, using Equation (1):
- Step 5.
Sent the corresponding (, )—the generated share SHi—to the ith participant.
- Step 6.
Perform Step 3 to Step 5 until each of the n participants gets the corresponding share SHj (1 ≤ j ≤ n).
The following figure is the flow chart of Shamir’s secret sharing scheme (
Figure 1).
Thus, the secret share formation and distribution phase is completed. When necessary, the following steps can be performed to extract secret information.
- Step 1.
Collect at least
k secret shares
SHj (1 ≤
j ≤
k) from the
n participants to form the following equations:
where
and
are 2
k known values from the
k secret shares.
- Step 2.
Use the Lagrange polynomial interpolation method to solve the
k unknowns values
and
in the
k equations in Equation (3) and regenerate the (
k − 1)-degree polynomial function
given by Equation (1) to be:
- Step 3.
Figure out the solution for the secret value
according to Equation (4)
Hence, the secret message I =
is revealed. According to Shamir’s (
k,
n) [
5], if fewer than
k shares are collected, the
k unknown coefficients cannot be figured out and the desired secret data
cannot be extracted.
Example: Assume that the threshold is k = 3, we will generate a function which = I, where I = 1234 is the secret number derived from secret data. Therefore, = I = 1234. Then at random we obtain = 166, = 94. Our polynomial which is used to produce secret shares is therefore: . In order to have 6 valuable information of the secret, we select freely for the ith (1 ≤ i ≤ n) share a value of x, denoted as , which is distinct from one another, and calculate 6 values on the function . Thus, we get 6 shares as = (1, 1494), = (2, 1942), = (3, 2578), = (4, 3402), = (5, 4414) and = (6, 5614), which will be delivered to n = 6 participants.
The correspondent reconstruction process of secret data is as follows: According to the threshold
k = 3, in order to reconstruct the secret any 3 of
will be enough. Let us consider
= (2, 1942),
= (4, 3402),
= (5, 4414). We will compute Lagrange basic polynomials on the basis of Equation (4):
Secret is the free coefficient, which means I = 1234.
Regarding the characteristics of our proposed IH-VSS, we use the (2, 2) threshold for example in this paper. It can be extended to an (n, n) threshold.
2.2. Kim et al.’s EMD-2 Scheme
In 2006, Zhang and Wang proposed the first exploiting modification direction (EMD) scheme [
30] providing good stego-image quality with the PSNR of more than 52dB and a considerable embedding rate of
by modifying at most one least-significant bit of
n pixel value. In 2010, Kim et al. developed the novel information hiding method called EMD-2 [
29], which improved EMD by allowing at most two pixels to be modified and using different directions of modification to represent different secret data.
In Kim et al.’s EMD-2 scheme, a pixel group is defined as
, where
. Follow Kim et al.’s definition, we think that in the case of
n = 1, the processing is carried out with a pixel as the unit, without forming a pixel group. Under such a condition, it can be reduced to the LSB (least significant bits) [
31] information hiding algorithm; and we will not discuss it in detail for we have benefited from a lot of treatises which have made detailed exposition to this problem.
is an
n-dimensional space that can be mapped to a value by function
. The basic elements
bi where
is used as an input to the function
f as a weighted sum with modulo (2
+ 1).
where
and
Here
d is the secret data to be hidden, and
f is the value calculated by Equation (6) associated with the pixel group
Pn. The subscript value
v is calculated using Equation (9).
The vector of the treated pixel value
can be acquired using Equation (10).
where
is the exponential vector when the number
v is associated with the basis vector
which has been defined in Equation (7).
Actually, when
n = 2, the best choice of the basis vector is
(see Equation (7)); meanwhile,
(see Equation (8)). We use these parameters in our proposed scheme because we use (2, 2) threshold as an example in this paper. This basis vector can produce numbers from 0 to 8.
Table 1 summarizes the details of the nine numbers and the corresponding coefficient vectors named
Ci, where
Combine the lowest three digits
C0 of 0 is [0, 0].
C1 = [1, 0].
C2 = [−1, 1], etc. Note that the number 0 can be generated by the basis vector as
. In addition,
C1 is [1, 0]; thus, the number 1 is generated by
. All nine numbers from 0 to 8 can be generated using Equation (6) by the linear combination of the basic elements with their associated coefficients.
In order to make it more intuitive and convenient to apply in our subsequent processes of the IH-VSS scheme, the calculation process we just mentioned can be projected as the generation of a matrix called
M. In the matrix, under the function of mod 9, the difference value between the two adjacent elements in the same row of the reference matrix
M is set to 1, and the difference value between the two adjacent elements in the same column is set to 3. An example of the reference matrix
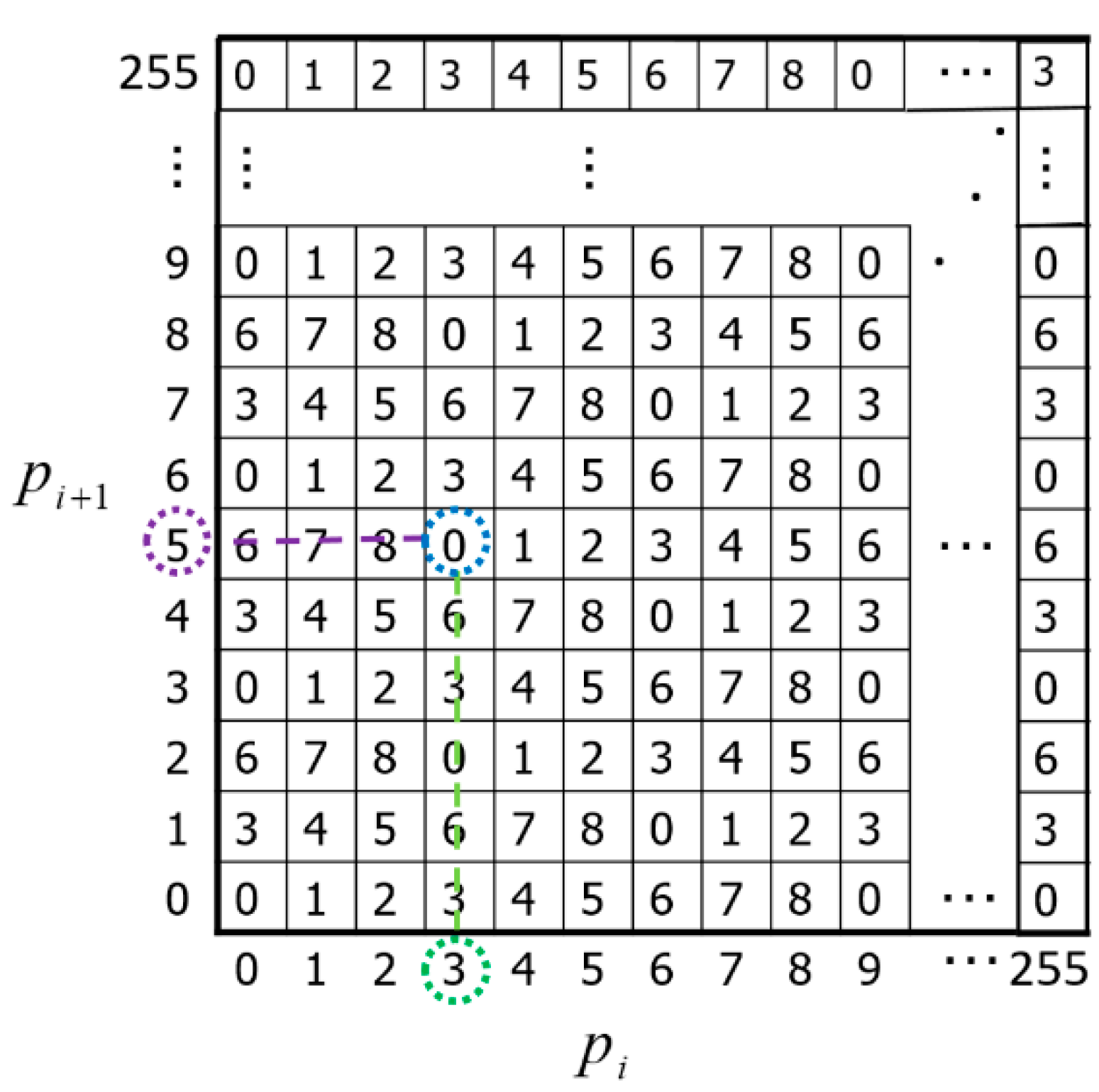
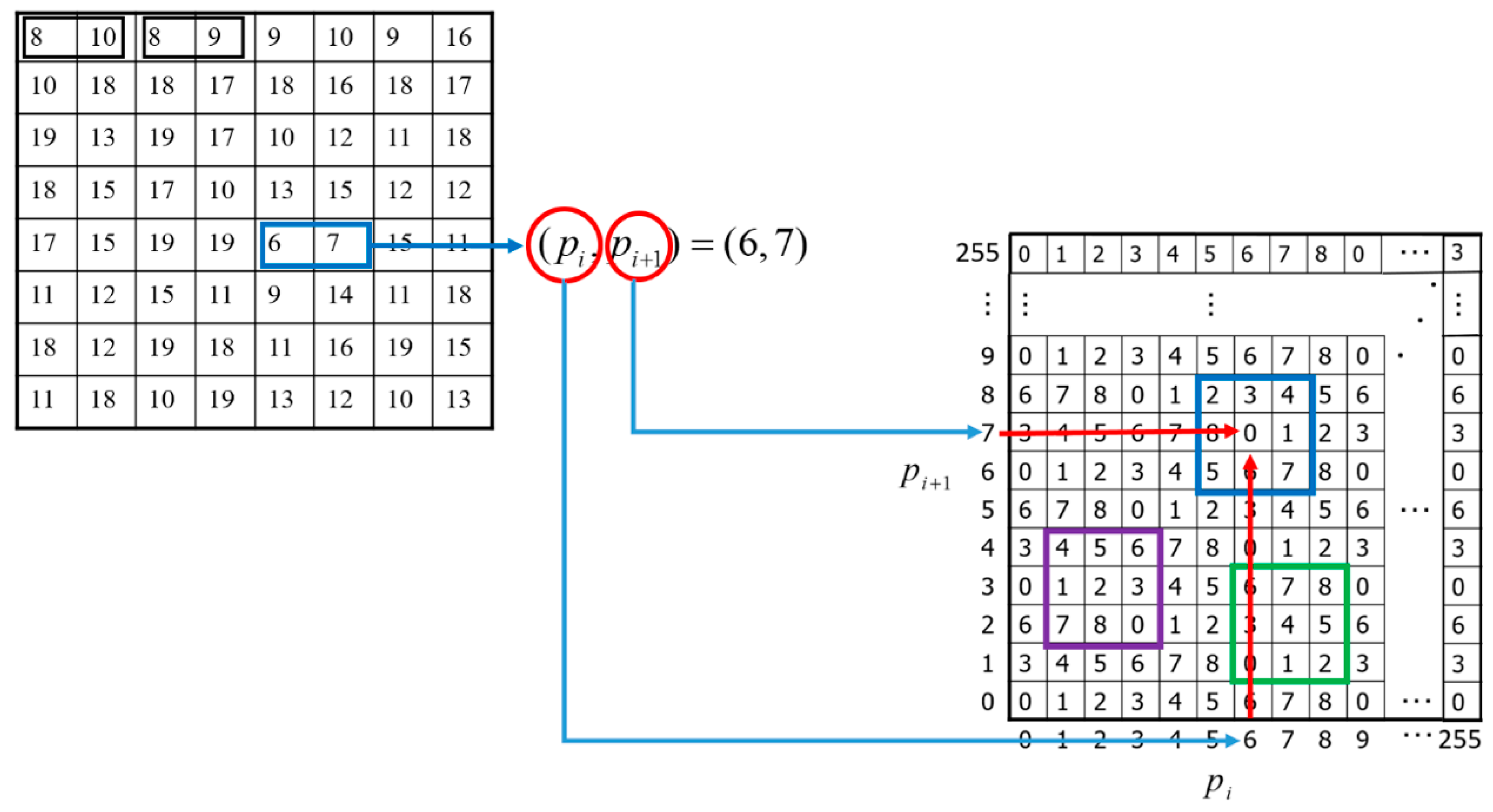
M with a size of 256 × 256 is shown in
Figure 2. The column value
pi and the row value
pi+1 in
M represent the grayscale values of the pixel pair (
pi,
pi+1) in the cover image.
According to Equations (6)–(8), each pixel pair (pi, pi+1) is located in the element function in M. By using Equation (11), we can calculate all the values of the matrix.
Here, two examples are given to demonstrate how
M matrix maps a pixel pair into a value. For pixel pair (3, 5), as illustrated in
Figure 2, its derived value is 0 based on Equation (11)
M (3, 5) = (3 × 1 + 5 × 3) mod 9 = 0. For pixel pair (123, 150), its derived value is 6 based on Equation (11)
M (123, 150) = (123 × 1 + 150 × 3) mod 9 = 6.
3. Proposed Scheme
This section presents a (2, 2)-threshold IH-VSS scheme based on Kim et al.’s
M matrix, which has the feature of high embedding capacity, without distortion and low computational complexity. In our scheme, three entities are involved:
dealer D and two participants (i.e.,
participant 1 and
participant 2). Given a secret message and a meaningful cover image, two meaningful shadows are created and distributed to participants by
dealer D. At the time of need, the two shadows are given by the designated legal participants, and their secret information can be extracted using our proposed extracting algorithm; at the same time, the cover image is restored. The concealment and sharing process will be introduced in
Section 3.2 and
Section 3.3, respectively. The hidden secret extraction procedure will proceed when the involved participants gather all shadows together. Meanwhile, the cover image can be reconstructed without loss. The corresponding process is discussed in
Section 3.4.
3.1. Preliminary Phase
Here, a secret data S, which is (or can be transferred into) a binary string, will be concealed. An H × W grayscale image, denoted as O = {oi|i = 1, 2, …, H × W} is used as the cover image, where , H is the height and W is the width of the image. Our proposed IH-VSS scheme applies a reversible data hiding scheme to embed secret data S along with the lowest three digits of the first four pixels in the original cover image into two meaningful grayscale images. Once the concealment phase is complete, each pixel pair in the stego-image carries one secret digit in the 9-base system; hence, the maximum hiding capacity using the proposed IH-VSS scheme is n = 415,498 (512 × 512 × log29/2) bits when the cover grayscale image has 512 × 512 pixels and the embedding rate is 1.59 = 0.5 × log29 bpp.
In the proposed (2, 2) IH-VSS scheme, the pre-process is listed as follows.
- Step 1:
Design a pixel value random diffusion function
. Here
3LSB means the three least significant bits of a pixel value, and
Rand means that the
3LSBs are given a value between ‘000’ and ‘111’ in a binary system with equal probability, as shown in
Figure 3. This function makes the three LSBs of a pixel value
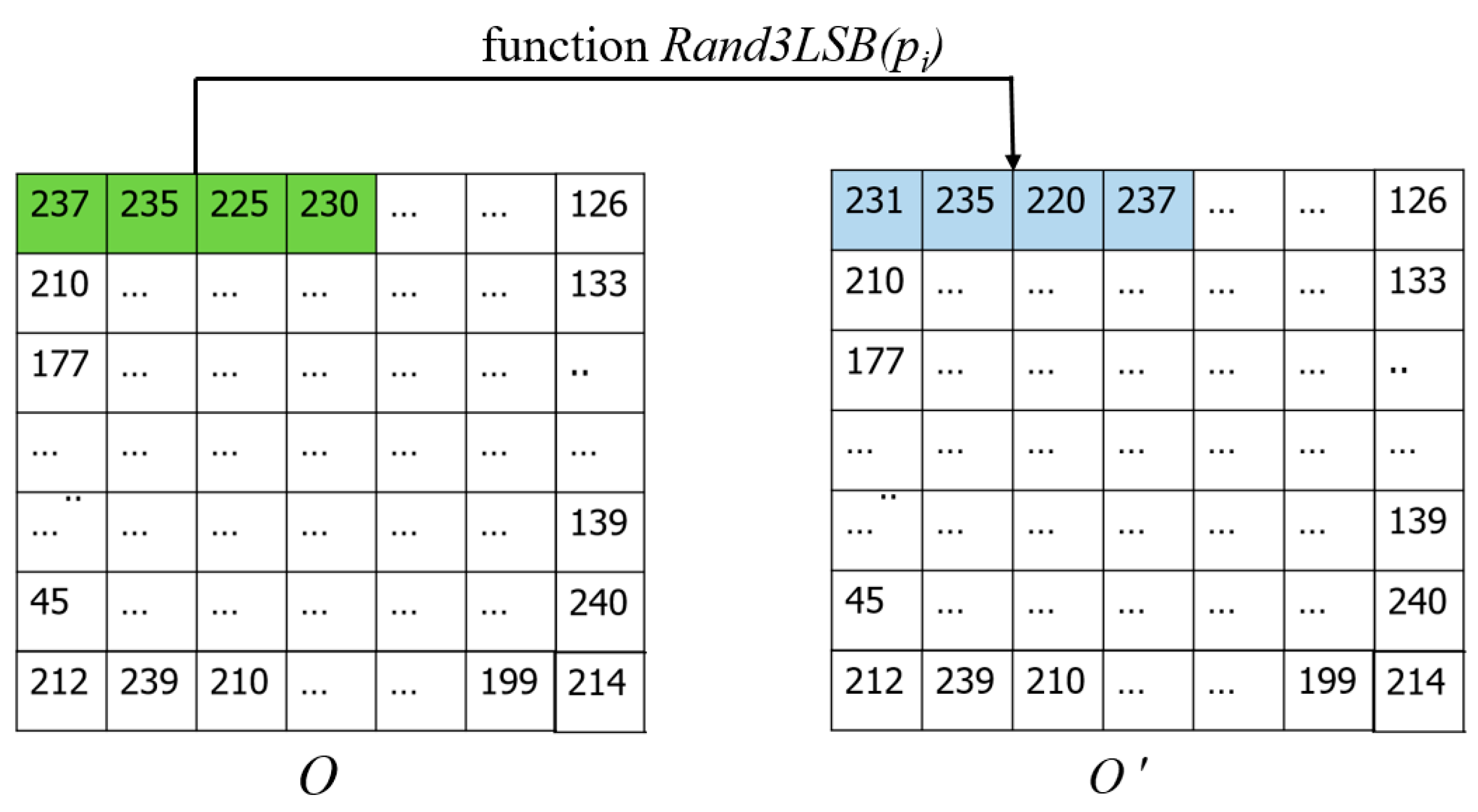
of a cover image slightly altered with randomness on a small scale. Such an arrangement can keep the pixel value still in the range of [0, 255], and the underflow and overflow problems do not exist in our IH-VSS scheme. Thus, the least significant three bits of the binary number are randomly changed to a new value that differs from the original value in the range [0, 7]. As a result, the severe pixel distortion problem can also be avoided.
- Step 2:
Process the first four pixels of the cover image
with the random diffusion function
. After being handled, collect the four processed pixels and the rest of the original pixels of the cover image
and denote them as image
. The first four pixels of image
are called
,
,
and
. The relevant preprocessing is illustrated in
Figure 4.
- Step 3:
Consider the pixel values of a grayscale image, which range between
, as a one-dimensional array.
is the first pixel value and
is the second pixel value. The subscript of
increases continuously until the maximum value is
. Define pixel pair
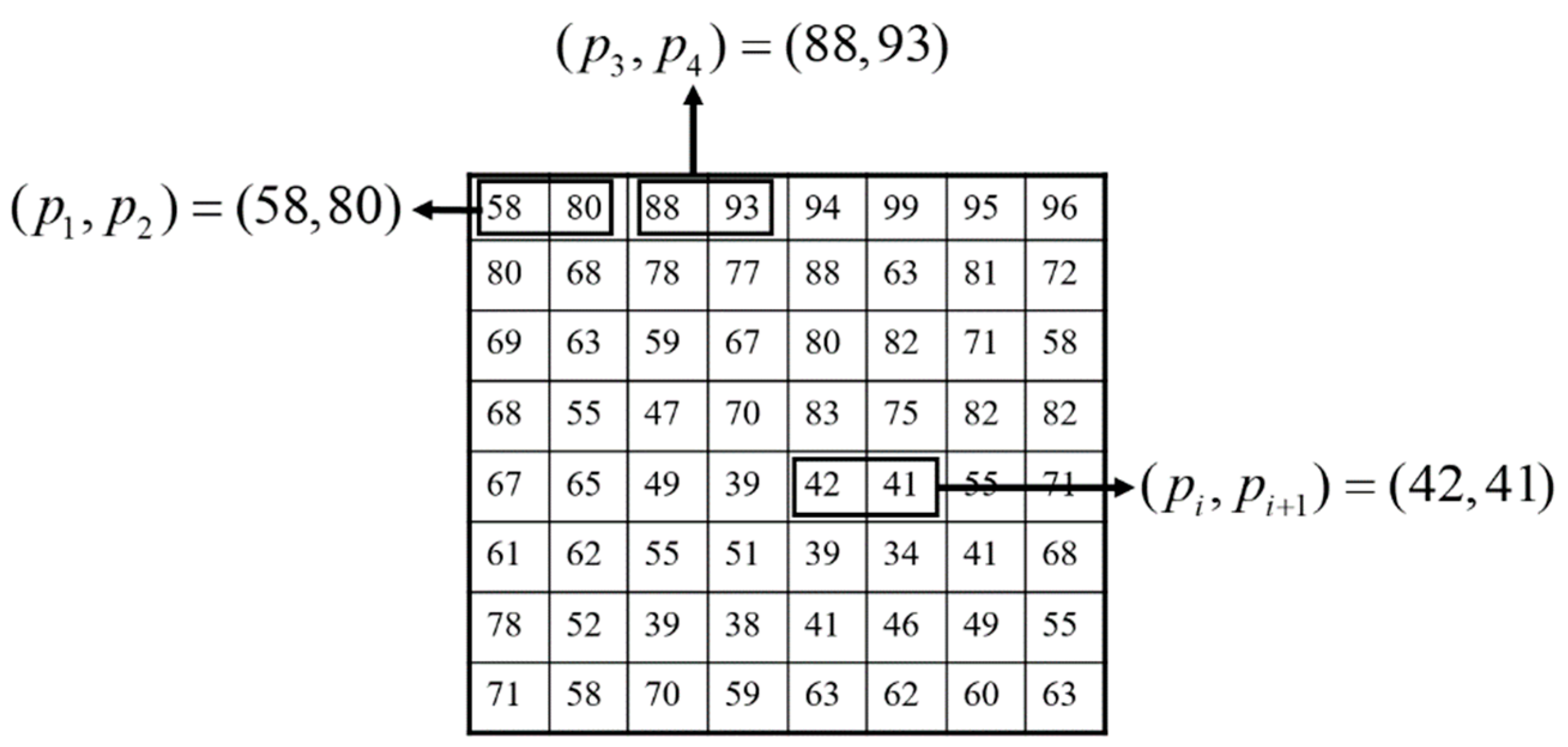
that is constituted by the grayscale values of two adjacent pixels
and
. For example, pixel
has a pixel grayscale value of 42 and pixel
has grayscale value of 41. The resulting pixel pair is
, as shown in
Figure 5.
- Step 4:
Define a matrix
M with the size of 256 × 256 according to Kim et al.’s EMD-2 algorithm. In the matrix
M, any 3 × 3 square, for example, the green, blue and purple square demonstrated in
Figure 6, has 9 numbers that can be used to conceal a secret value ranging from 0 to 8, as shown in
Table 2 according to
Figure 6.
is pixel pair of
after being hidden. Since each pixel pair we processed is targeted at the pixel pairs with the same position in the cover image and stego-image, their subscripts are one-to-one correspondence.
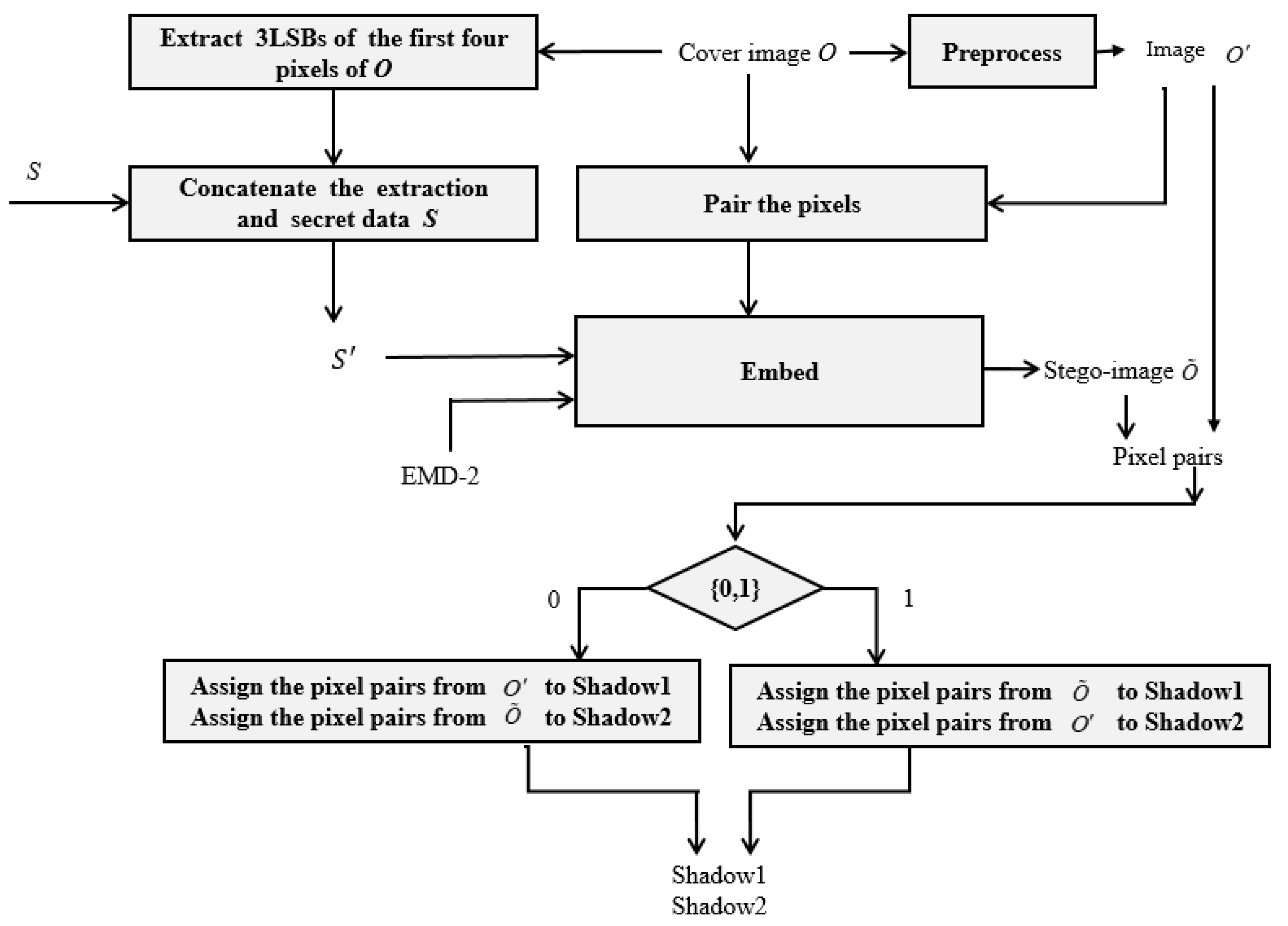
3.2. Concealment Phase
A secret data
S and an
H ×
W grayscale cover image are given, then the concealment phase can be executed as the flowchart of
Figure 7.
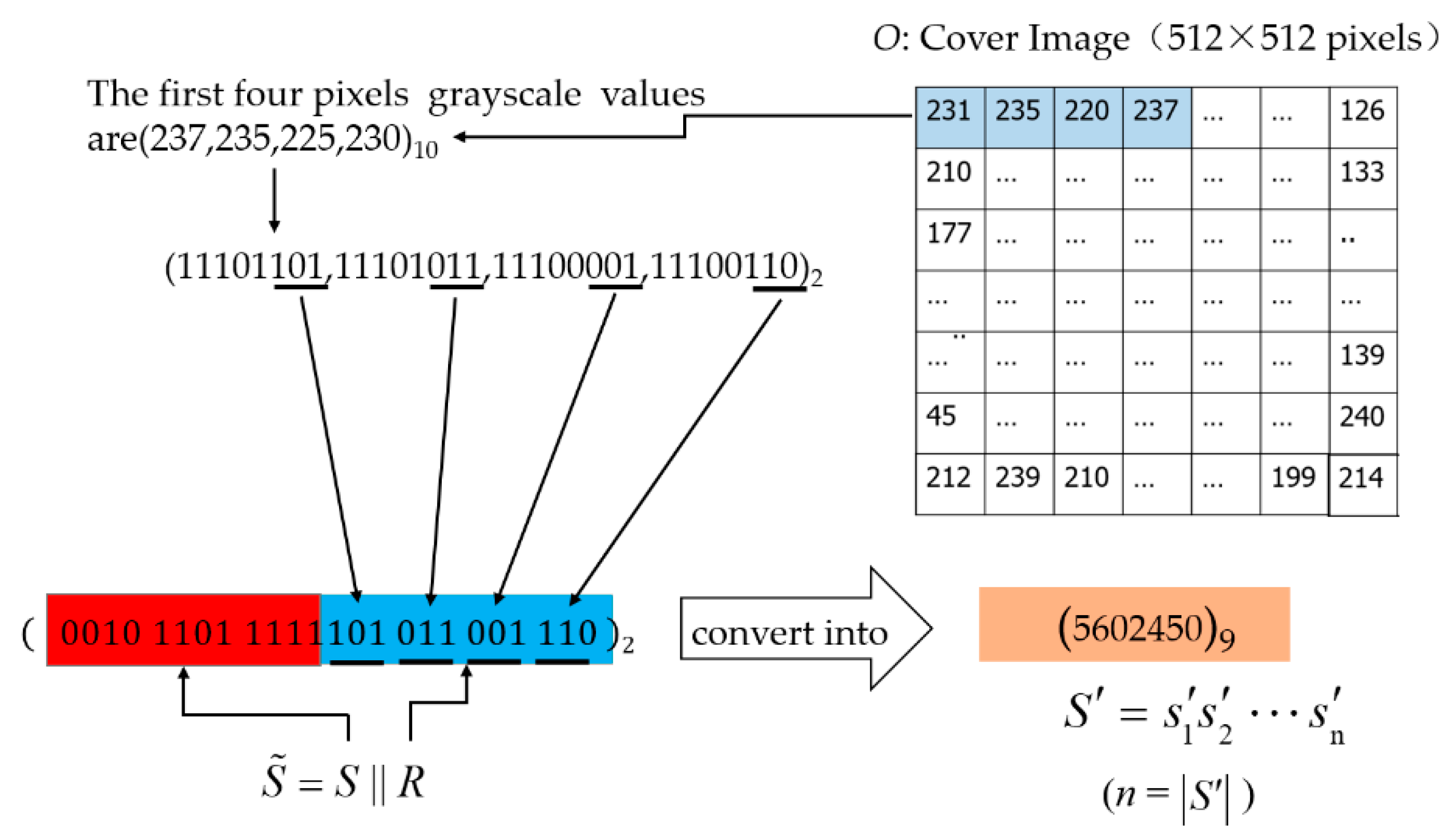
- Step 1:
Name the first four pixels of cover image as o1, o2, o3, and o4.
- Step 2:
Combine the lowest three digits of
o1,
o2,
o3, and
o4 to form
R = (101 011 001 110)
2. Define the sign of operation
as a concatenate function. Following the previous example, if
= 001011011111, then
, and the final number
represented by a number in 9-base system is (5602450)
9. We specify that
is in the binary number,
is the 9-base number corresponding to
, and actually, they have the same value. In addition, we express
in this form
, where
is the length of the number string
, and
is every digit in this number. This preprocessing procedure is illustrated in
Figure 8.
- Step 3:
Conduct the function to generate the seed of the function, where function controls random number generation so that the same string of {0, 1} will be generated by on the secret distributor and receiver, which allows encrypt and decrypt participants to use the same {0, 1} string.
- Step 4:
Pair each of the remaining pixels in image with their adjacent pixels to form non-overlapping pixel pairs, such as . Thus, there will be pixel pairs that can be used to embed secret information . As the cover image can be selected at will, the number of pixels of its height and width do not have to be even, so their product may be odd. Thus, we get the maximum number of the pixel pairs through floor function on .
- Step 5:
Embed secret information into each pixel pair with the concealment algorithm according to the following four sub-steps.
- Step 5.1:
Calculate the value
m =
M(
,
) to obtain the value
m by mapping
and
to matrix
M defined in
Figure 2 and Equation (11).
- Step 5.2:
Compare m and the . If they are equal, no change is required, (, ) in cover image will be copied to (, ) in stego-image. Otherwise, set m as the center (, ) and form a 3 × 3 search area. In the 3 × 3 square search area, find the corresponding and whose intersection is in the M matrix. Here, a new pixel pair (, ) = () of the stego-image is derived to carry the secret digit . The subscripts of (, ) and (, ) are one-to-one correspondence, as discussed in Step 4 of preliminary phase. Thus, a pixel pairs (, ) of conceals a base-9 digit by set values of pixel pairs (, ) of stego image .
- Step 5.3:
Repeat the preceding steps until all pixel pairs of except the first four pixels have been processed. Hence, the stego-image is obtained.
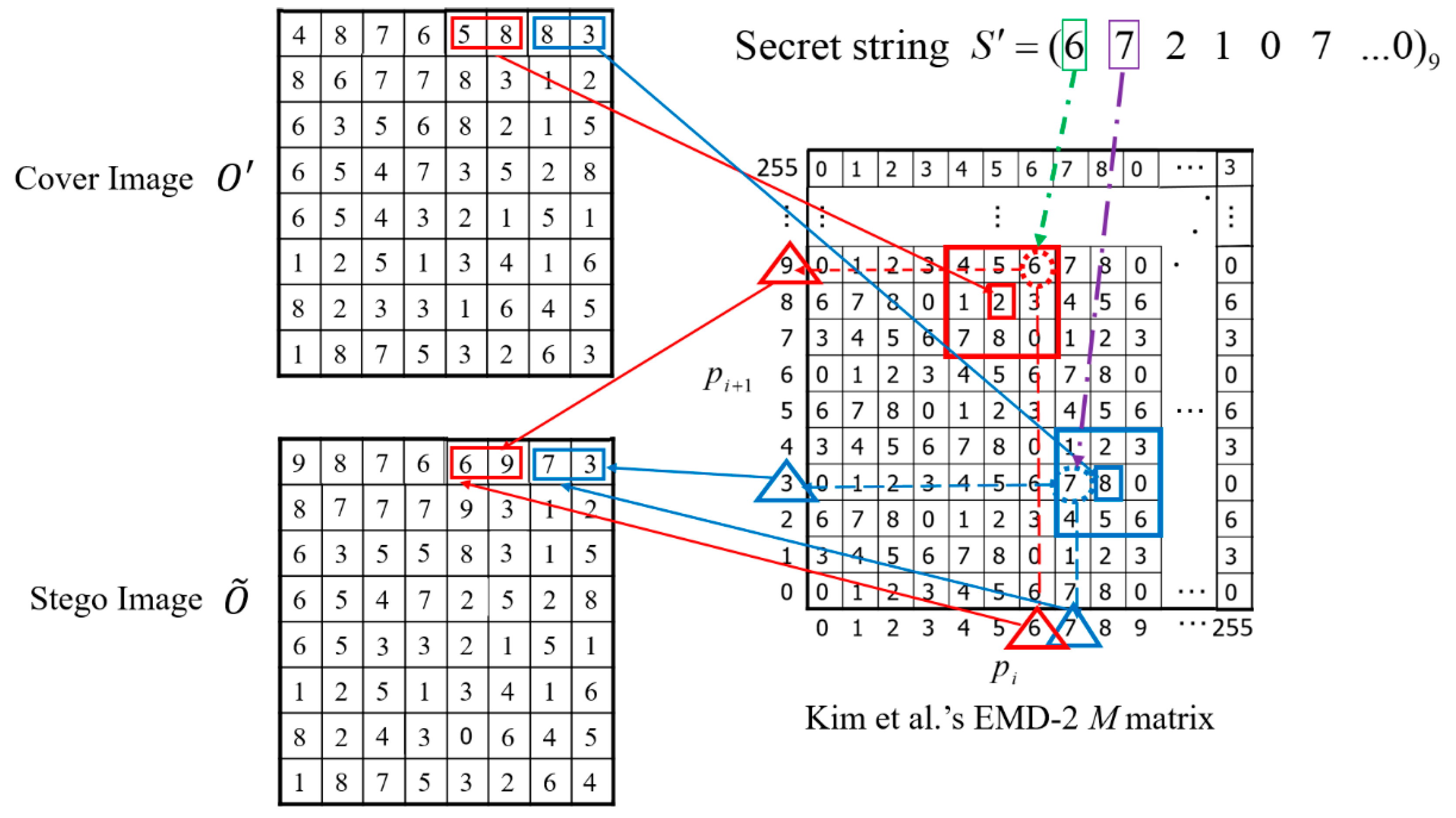
Example: To give a clear demonstration of our concealment phase, here, two pixel pair (
,
) of
, set as (5, 8) and (8, 3), the secret digit
= 6 and
= 7 are used. Since (
,
) = (5, 8), 5 is mapped to column
x and 8 is mapped to row
y of matrix
M. In other words, a base-9 digit ‘2’ can be found by using
M (5, 8) = 2, which is demonstrated as the center of the red rectangle in
Figure 9. But the base-9 digit ’2’ is not the same as
= 6 which is the number we need to hide at present, therefore, a 3 × 3 sized square is set as the search area around the center (5, 8), and a new pair (6, 9) =
(6) can be found because its intersection of column 6 and row 9 in matrix
M is 6. Thus, the pixel pair (
,
) = (5, 8) in
is changed to (
,
) = (6, 9) in
to carry secret digit
= 6. For the next pixel pair (8, 3), we can get the center of blue square
M (8, 3) = 8 in
Figure 9, which will be used to hide
= 7. Thus, we have to find 7 in the 3 × 3 search area around the center
M (8, 3) = 8. Then a new pair (
,
) = (7, 3) =
(7) can be found and set as the pixel pair to represent (
,
) = (8, 3) to carry secret digit
= 7. The detail is illustrated in
Figure 9.
3.3. Shadow Generation Phase
Once stego-image is constructed, it can cooperate with image to generate two meaningful shadows by conducting the following six steps.
- Step 1:
Combine the three LSBs of the first and second pixels of to form a 6-bits of binary string. Then transform the 6-bits binary string into the decimal number system and name it Num1. Next, combine the three LSBs of the third and fourth pixels of to form Num2. Finally, a decimal value named Num, which is the sum of Num1 and Num2, is derived.
- Step 2:
Set to get a binary string, such as (100010100110 1001 ……00101110)2, of which the length is not greater than .
- Step 3:
Generate the two shadows and . For shadow , the first two pixels are the same as those of image , but the following two pixels are derived from the Rand3LSB(pi) function with the third and the fourth pixels of image . On the contrary, the third and the fourth pixels of shadow are the same as those of image . But the first two pixels of shadow are derived from the Rand3LSB(pi) function with the first two pixels of image .
- Step 4:
Pair the adjacent pixels of image
and image
, except the first four pixels, to form non-overlapping pixel pairs. Use
as symbolic bits to decide to copy pixel pairs of
and
to shadow1
or shadow2
. When the current bit of
is ‘0’, the pixel pair of image
is copied to the corresponding position of shadow1
, and the pixel pair of image
is copied to the corresponding position of shadow2
. When the symbolic bit of
is ‘1’, the pixel pair of image
is copied to the corresponding position of shadow2
, and the pixel pair of image
is replicated to the corresponding position of shadow1
. The detailed shadow generation procedure is shown in
Figure 10.
Step 4 will be repeated until all pixel pairs of images
and
are processed.
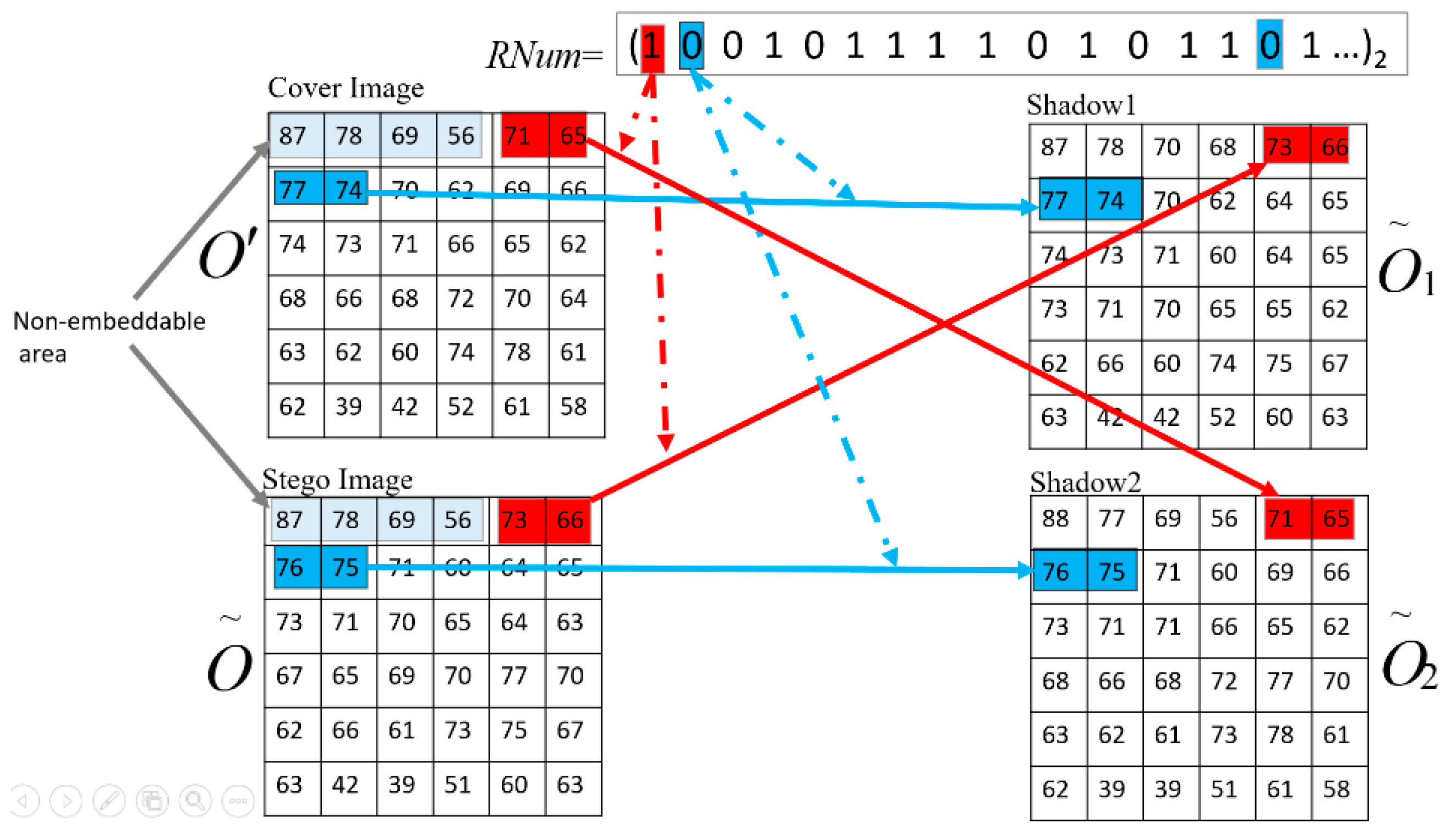
Example: We execute sequential processing of pixel pairs according to the ascending order of the subscript in the image and Rnum, thus = (71, 65) in , = (73, 66) in , ‘1’ in Rnum (all colored in red) are the first two pixel pairs and the first random bit we use to do with. As the symbolic bit is ‘1’, for , we make = = (73, 66); for , = = (71, 65) (see the red arrow). And then, the next bit is ‘0’ of Rnum (colored in blue), for , we make = = (77, 74); for , = = (76, 65) (see the blue arrow). And next, = = (70, 62) for , = = (71, 60) for , and so on.
- Step 5:
Set the LSB of the last pixel of shadow to 0 and name the final result shadow1. Set the LSB of the last pixel of shadow to 1 and name the final result shadow2. Send shadow1 to participant 1 and shadow2 to participant 2.
3.4. Extraction and Restoration Phase
- Step 1.
Collect shadows
and
from participants 1 and 2. Here, we assume two participants are credible and the received shadows are also reliable. According to the LSB of the past pixel of received shadows, shadows
and
can be determined, respectively. From the first pixel pair of
and the second pixel pair of
, the random number seed
Num can be derived. The
RNG(Num) function can then be performed, and images
and
can be restored according to the generated strings of 0 and 1. The restoration procedure is the inverse operation of
Figure 10.
- Step 2.
Search in Kim et al.’s M matrix according to images , , and the function ; the embedded information in each pixel pair can then be derived sequentially.
- Step 3.
Copy the last 12 bits of the secret information back to image derived in Step 1. Thus, the original image is restored exactly.
If the participant provides a forged image, the Num and the string of 0 and 1 based on the received forged image will be incorrect. Ultimately, the hidden secret message cannot be extracted.
4. Experimental Results and Analysis
Kim et al.’s data hiding strategy is employed in our proposed IH-VSS scheme to guarantee that two pixel pairs of shadows can carry a base-9 digit according to Equation (6). Hence, the embedding rate is 1.59 = 0.5 × log29 bpp. In other words, a 512 × 512-pixels grayscale image can embed secret bits.
In addition to the hiding capacity, the security and visual quality of shadows are crucial criteria used to evaluate the performance of VSS. The following subsections discuss the security analysis and visual quality. Comparisons among the four representative VSS schemes and our proposed scheme are demonstrated in
Section 4.3 to confirm the performance of our proposed IH-VSS on both hiding capacity and visual quality.
4.1. Security Analysis
This subsection examines the security capability of our proposed scheme. As previously discussed, the proposed IH-VSS scheme is a (2, 2)-threshold secret sharing scheme, in which the core idea is clearly defined that no single share can release any knowledge of the hidden secret message. However, it is possible that malicious users conduct a brute-force attack by randomly selecting pixel pairs from received shadows (i.e., , ) to try to reconstruct stego-image . To this end, the user must get the correct {0, 1} string. In a brute-force attack, the probability that a user will obtain the exact {0, 1} string is the reciprocal of , which is quite small and almost impossible to solve in real time. Thus, the security of the hidden secret message with our proposed IH-VSS scheme is guaranteed.
4.2. Visual Quality
In general, the
PSNR is used to measure the visual quality of the image after secret information is embedded into the cover image.
PSNR is defined as:
where
is the mean square error between the cover image and the shadow. For an
size grayscale cover image,
is defined as:
Here
denotes the pixel value of the original image, and
denotes the shadow’s pixel value at position
. Without a loss of generality, we believe that the difference between the cover image and shares is invisible to the naked eye when the
PSNR value exceeds 30 dB, and we conclude that the visual quality of shadows reaches an ideal level [
32].
The PSNR is often discussed with the embeddable secret capacity because they are the two major measurements of the performance of the VSS using the information hiding approach. The following figures show the contrasted PSNR value of images involved.
Figure 11a shows the original Lena. The two shadows shown in
Figure 11c,d have PSNR values of 55.98 dB and 55.91 dB, respectively, which are both meaningful images of size 512 × 512. As it is an accepted fact that when the value of PSNR is greater than 30, no difference can be detected directly through the human visual system. However, in the proposed scheme, PSNR value is often close to or more than 50 that makes the imperceptibility all the more salient. Furthermore, as is known to all, the pixel expansion is caused by shadows smaller than the cover image, which obviously does not exist in our scheme because shadows are the same size as the cover. Even when a large amount of the secret information is hidden, shares are visually no different from the original.
Another topic worth discussing is improvements to the produced shadow size. As we know, if the size of generated shadows is similar to or smaller than the size of the cover image, it is easier to manage and transmit the generated shadows. However, a tradeoff must be made between the size of the shadows and the size of the hidden secret. Smaller generated shadows may limit the size of hidden secret data even when relatively easier to manage and transmit. Thus, in the proposed IH-VSS scheme, the share size we define is the same as the cover image to keep the balance between the transmission efficiency and the size of the hidden secret message. Moreover, to enhance the security of the hidden secret message, the generated shadows are meaningful with the proposed IH-VSS scheme.
To enhance the security of the hidden secret message, the pixel pairs of the two generated intermediated shadows are switched with each other according to a binary random number string, except for the first four pixels, as shown in
Step 5 of shadow generation phase and
Figure 10. To further prove that such an arrangement does not affect the visual quality of the final generated shadows,
Table 3 shows the PSNRs of intermediate shadows and final shadows under different ECs, which increase from 13,000 to 415,485 bits. The column named image
(before exchange) shows the PSNR of image
before the exchange method, and it is as high as 84.99 dB when the EC is 415,485 bits because only four pixel values have changed, as we demonstrated in
Section 3.3. The column named image
(after exchange) indicates the PSNR of the stego-image, which carries the secret using Kim et al.’s EMD-2 algorithm. The PSNR is larger than 52 dB when the EC is over 400,000 bits, which is significantly higher than 30 dB because the difference between the two pixel values before and after the hidden information is controlled between [0, 7] using Kim et al.’s EMD-2 algorithm. We also found that the PSNR of image
increased with the happening of the exchange because the exchange of the original image pixel pairs making image
contains not only the stego-pixel pairs, but also some original pixel pairs. Therefore, the PSNR of image
remains at a very high level, as shown in
Table 3.
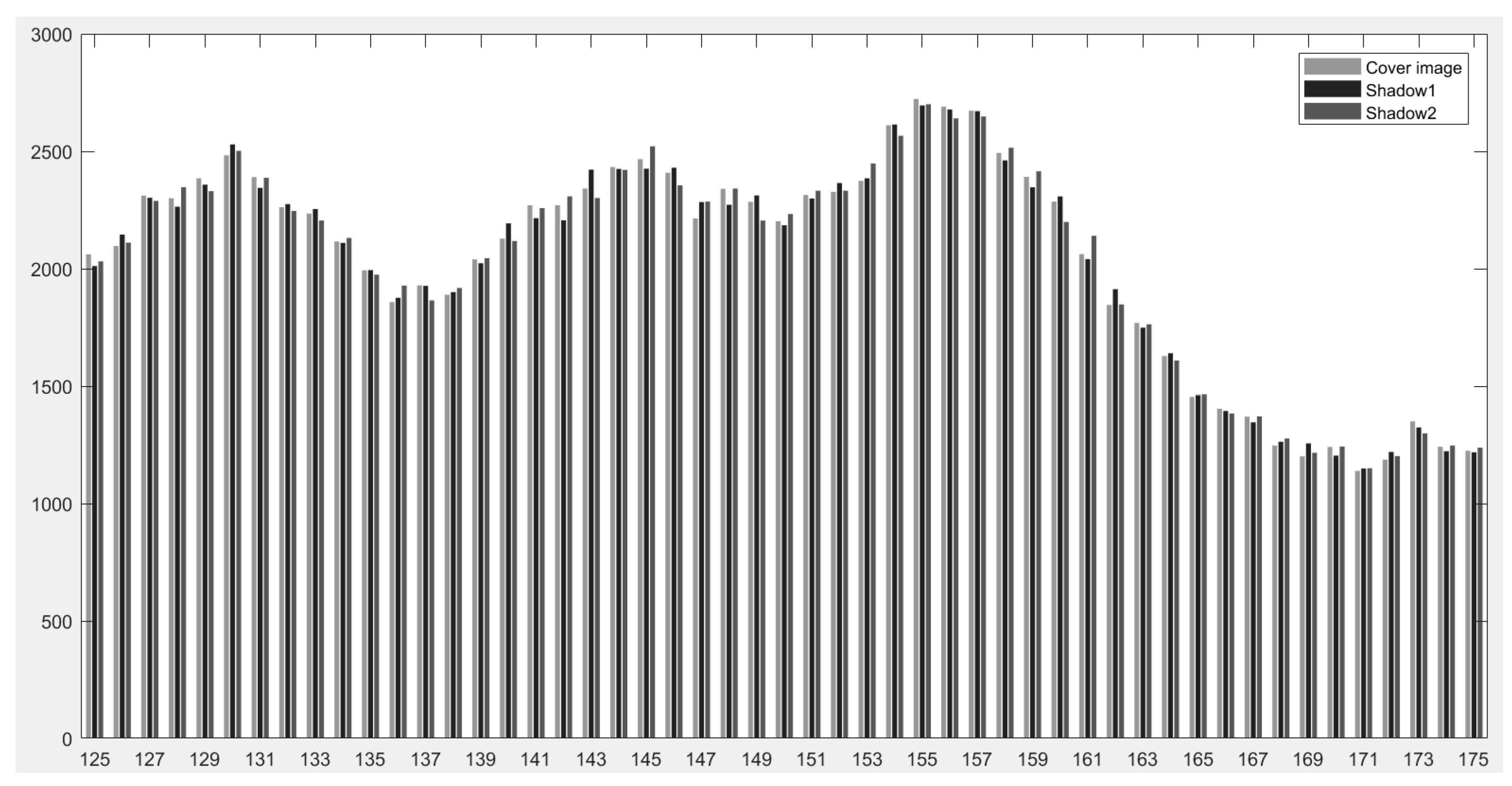
To demonstrate that the histograms of the original image “Lena” and its two shadows are similar, even when the size of our hidden secret message reaches the upper bound with our proposed IH-VSS, pixel values ranging from 125 to 175 is selected and demonstrated in
Figure 12. The reason we selected such pixel range because it is the middle range of the pixel value [0, 255] for a given grayscale image, and most of the pixels of the image are in this range, which makes the detailed phenomenon of the frequencies of the cover image and shadows can be shown. In general, the stego-pixel values could be different from the cover image after shadows carried the secret message. However,
Figure 12 shows that the difference of the frequencies is considerably small. This conclusion is further supported by
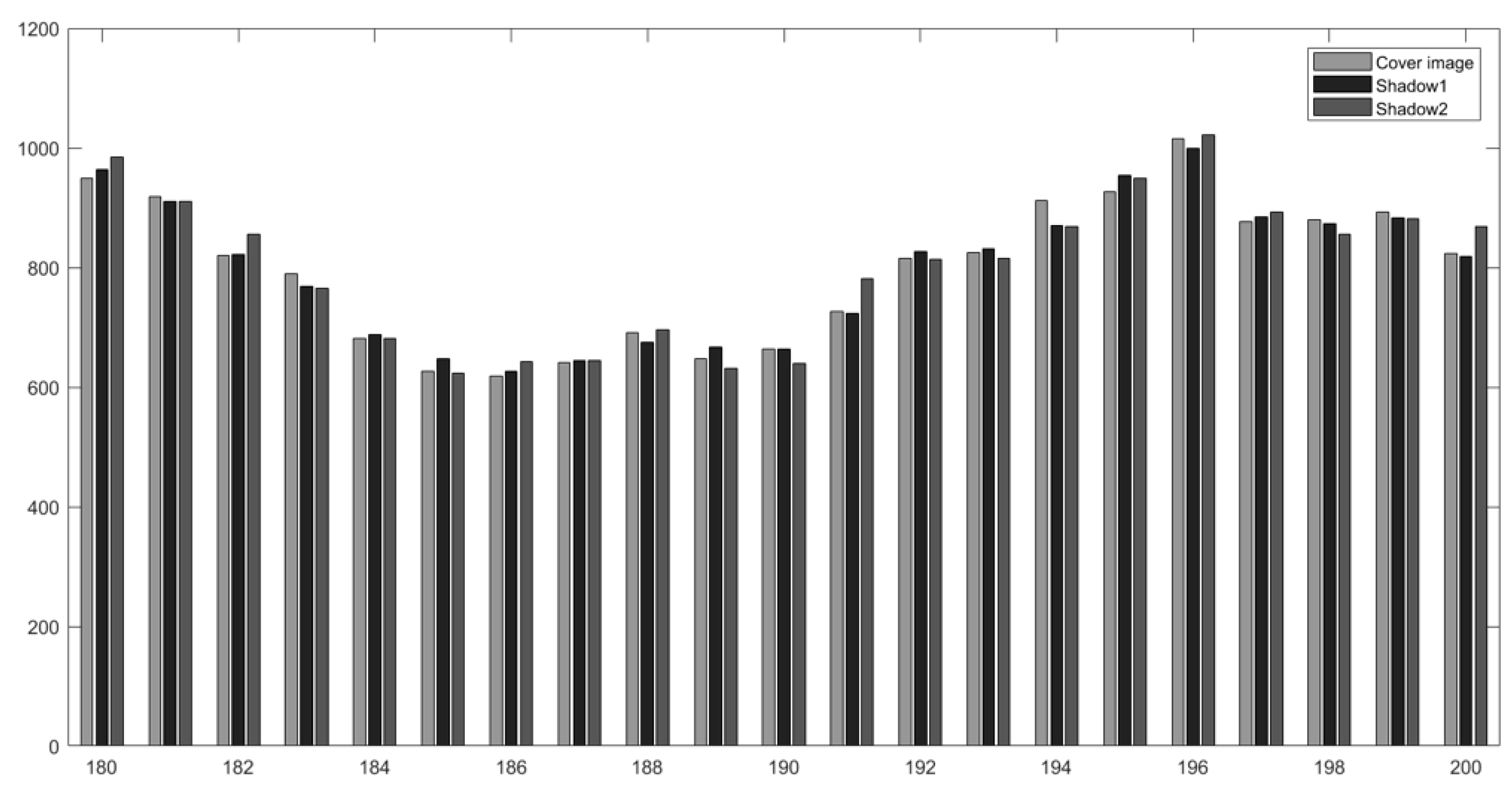
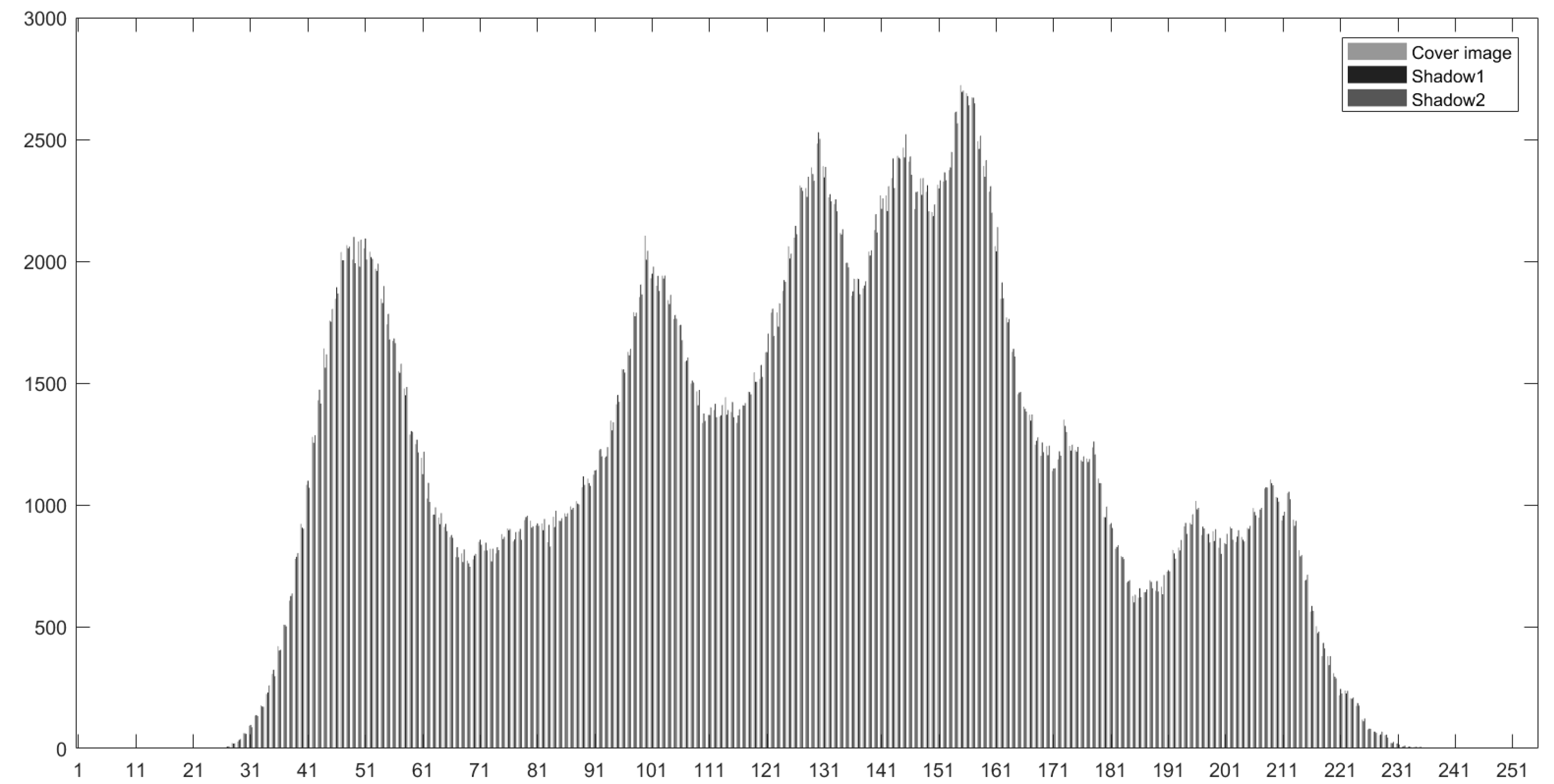
Figure 13 and
Figure 14 which show the pixel values ranging from 180 to 200 and 0 to 255 (all possible pixel values of an image), respectively.
Table 4 also demonstrates the pixel values with the top eight highest number of pixels of the cover image and the two shadows. The data of first line, colored in blue, tells that the pixel value 155 has the maximum number of 2723 in the cover image, correspondingly, the number in shadow1 and shadow2 is 2711 and 2714. These three numbers have similar values. On the other hand, the pixel value 130 has the 5th largest number of pixels (colored in light brown), 2493, 2572 and 2519 are the numbers in the cover image, shadow1 and shadow2, respectively. These three numbers are very close too. The same thing happens to the top eight, as shown in
Figure 14, in fact, to all the pixel values. Such results indicate that the proposed IH-VSS scheme is not only visually imperceptible, but also quantitatively negligible.
4.3. Comparisons with Four Existing Schemes
To evaluate the performance of the proposed VSS scheme, eight standard 512 × 512 grayscale images, as shown in
Figure 15, are used as test images. Here,
PSNR comparisons between the proposed scheme and four state-of-the-art (2, 2) IH-VSS schemes are listed in
Table 5.
Consider the bpp value of Cheng et al.’s [
26] is 0.5, and the maximum storage capacity of He et al.’s scheme [
27] can only reach a value of 69398 bits, which is far less from our algorithm, we do not regard them as comparison data here. Therefore, in
Table 5 only three existing schemes are used to compare with our proposed scheme. Among them, Chang et al.’s scheme [
24] applies a control parameter ω to determine the payload. Qin et al. [
33] use the matrix proposed by Zhang and Wang to embed a secret. Liu et al.’s scheme [
25] applies the turtle shell reference matrix during the shadow generation procedure. Chang et al.’s scheme (Th = 4) [
28] does not employ any reference matrix, but embeds the secret messages in the four LSB planes by combining LSB substitution and the exclusive or (XOR) operation to produce two shadow images. The comparisons show that the PSNR of the proposed scheme can be maintained at a high level-larger than 52 dB—when the embedding capacity reaches 415,485 bits.
Figure 15a–h uses the cover image to generate the corresponding shadow1 and shadow2 with different schemes. Again, it is proved that the proposed IH-VSS offers the highest PSNRs for two shadows no matter which cover image is adopted. Two reasons can explain this result. First, a finite change of pixel values is caused during the embedding procedure of Kim et al.’s EMD-2 algorithm. Second, the stego-pixel pairs of the two generated intermediate shadows are further switched by using the uniformly distributed pseudo-random string of {0, 1} generated by the function
at the end of the shadow generation phase. Thus, no matter which image is served as the cover image, PSNRs of the two shadows can be guaranteed to be greater than 50 and be very close.
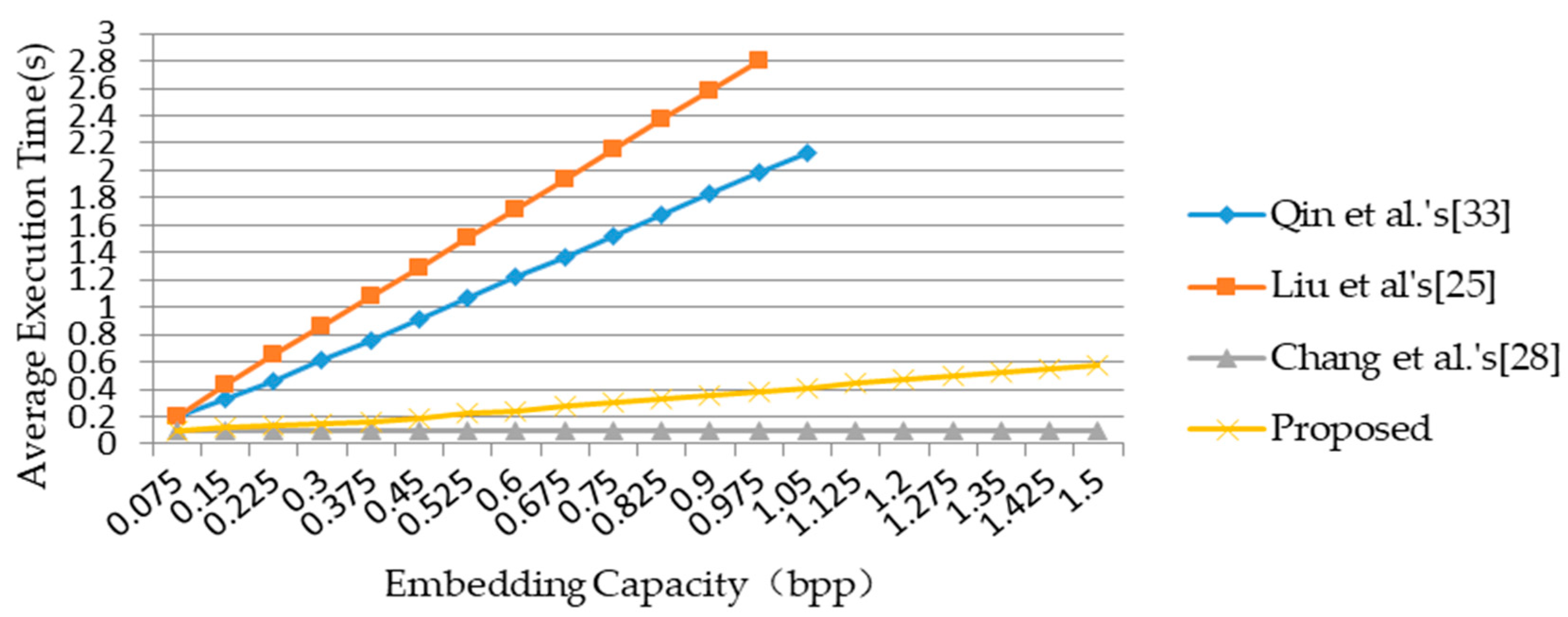
Figure 16 shows the average execution time of four schemes. Compared with schemes of Qin et al. [
33] and Liu et al. [
25], our proposed scheme requires less execution time, but takes more time than scheme of Chang et al. [
28]. Consider the average PNSR of generated shadows with our proposed scheme is 1.3 times more than that of Chang et al.’s scheme. We believe the execution time of our proposed scheme is acceptable.
Combined with
Table 5, it can be concluded that Chang et al.’s scheme sacrifices PSNR to achieve higher execution efficiency, while Qin et al.’s and Liu et al.’s work has the disadvantage of relatively smaller storage volume but higher PSNR. The proposed scheme, which makes a compromise between the amount of EC and PSNR, makes the PSNR close to or in most cases greater than 50 dB, while at the same time, the EC reaches more than 400,000 bits, and the execution efficiency is quite good.