Outage Probability Analysis in Relaying Cooperative Systems with NOMA Considering Power Splitting
Abstract
1. Introduction
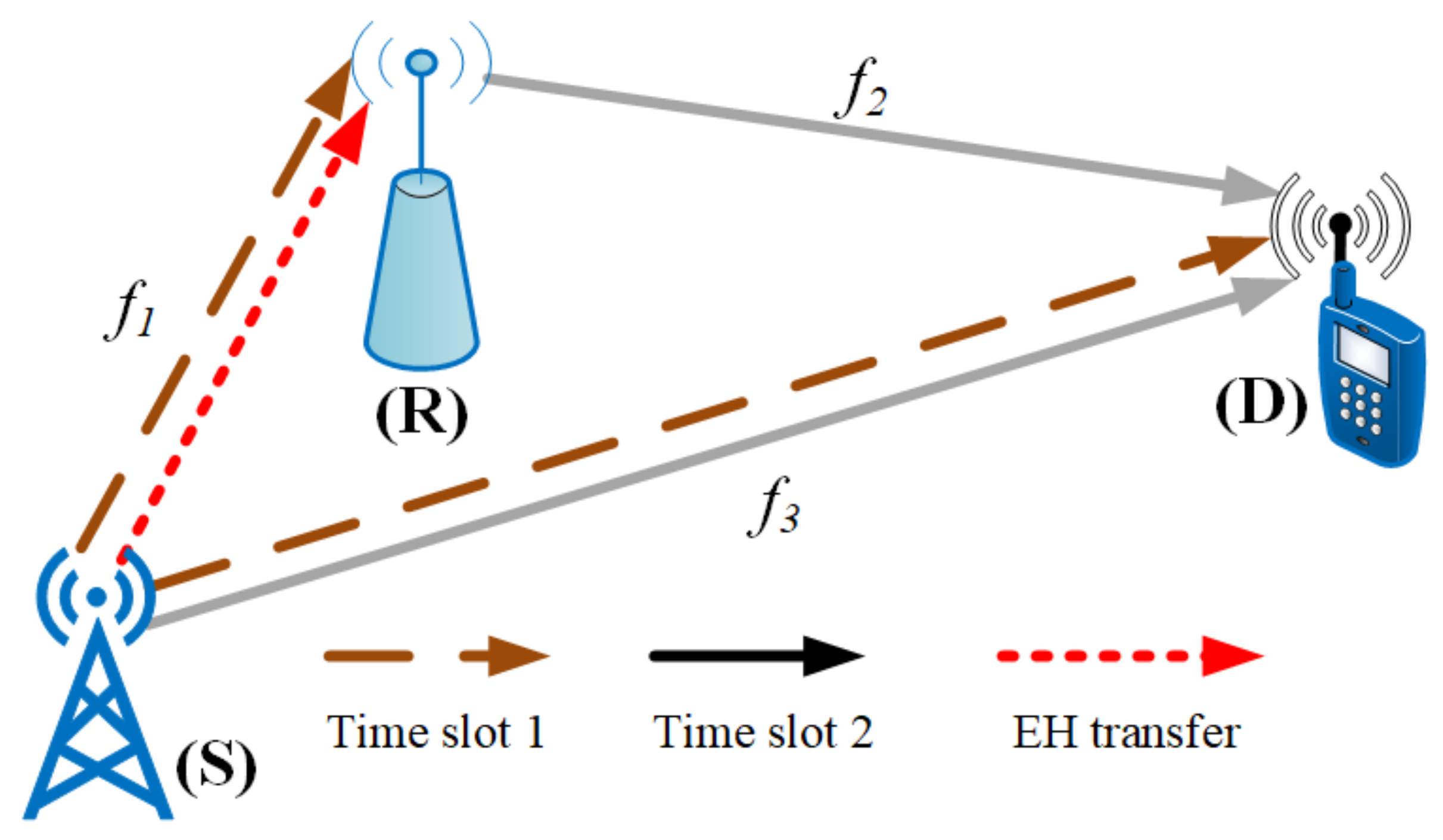
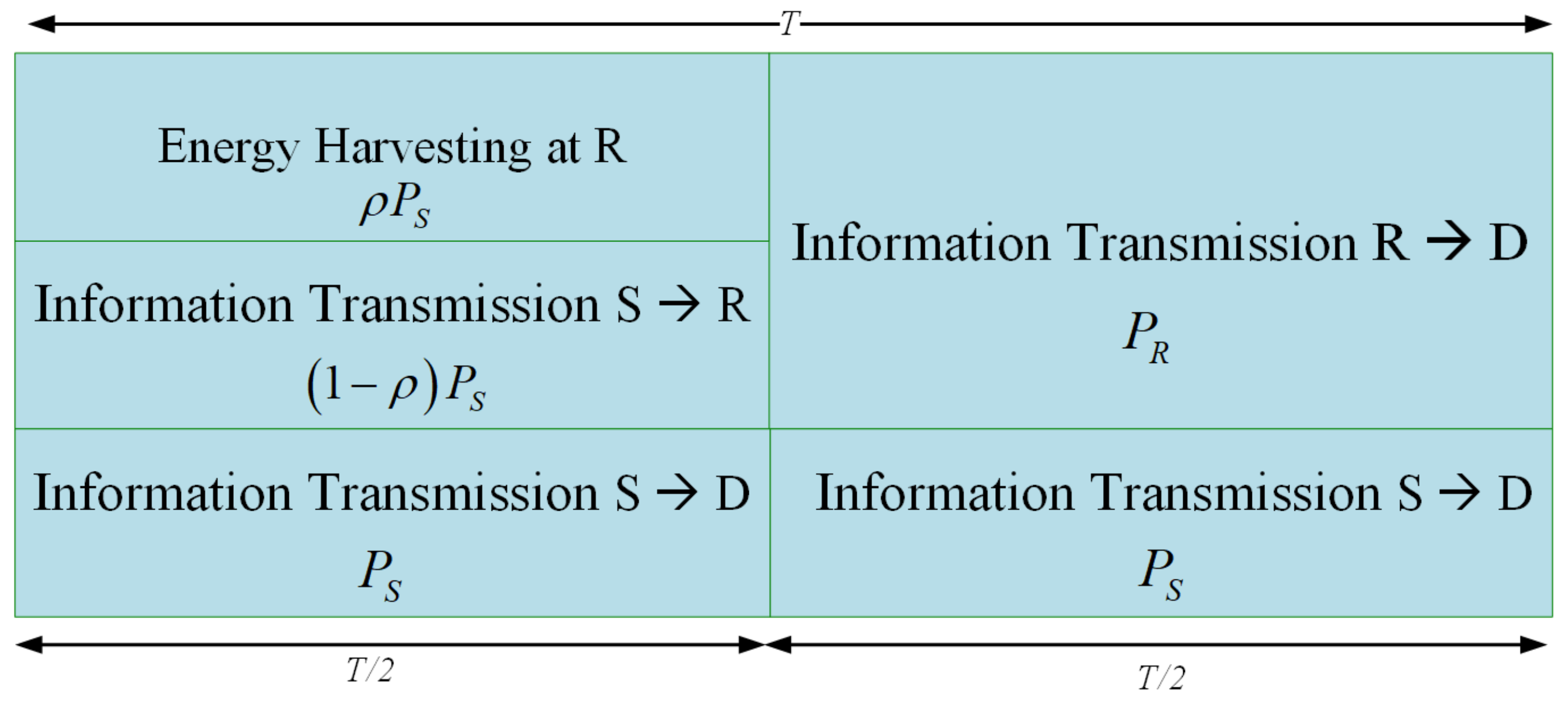
2. System Model
3. Performance Analysis
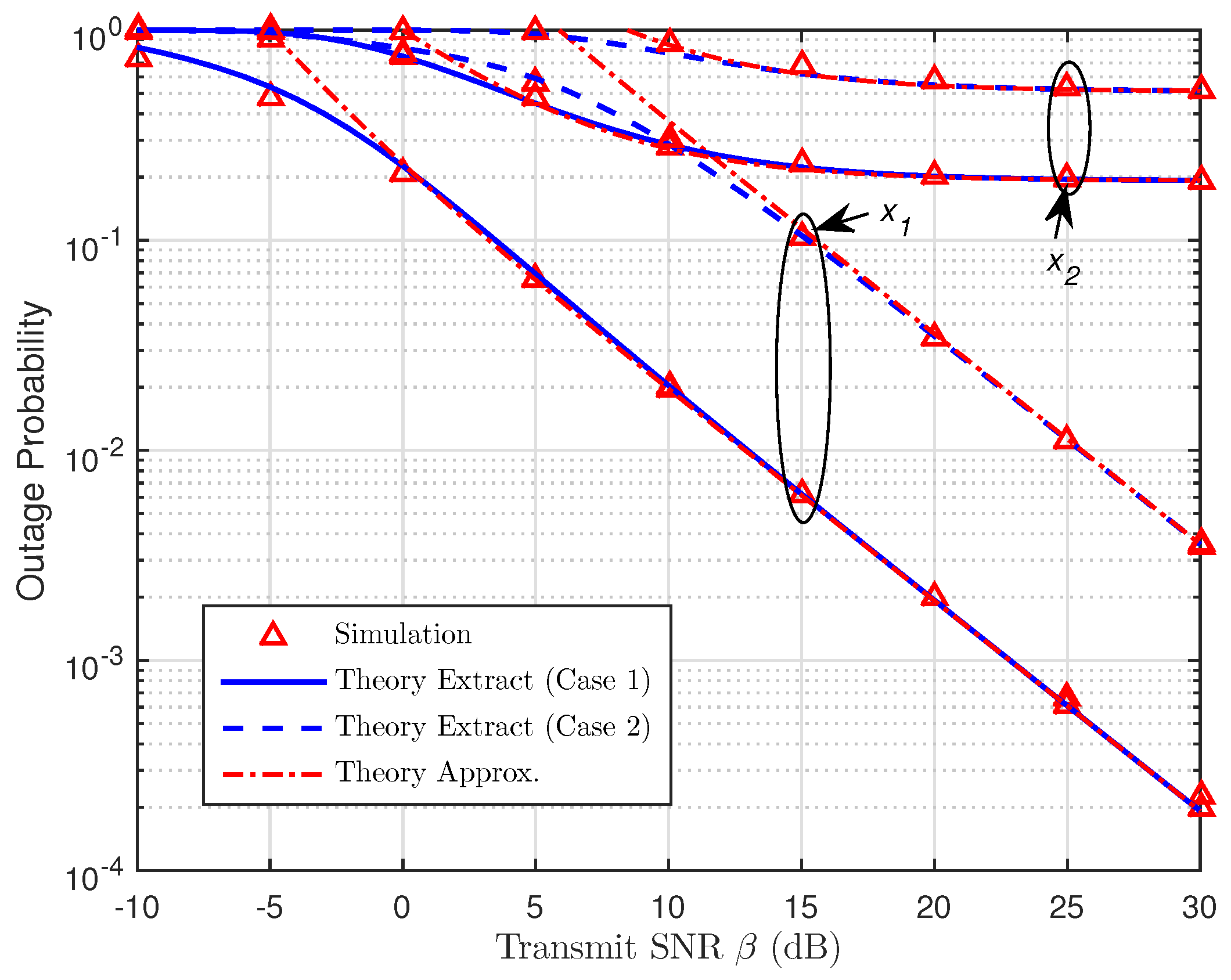
3.1. Exact Outage Performance
3.2. Approximate Outage Performance
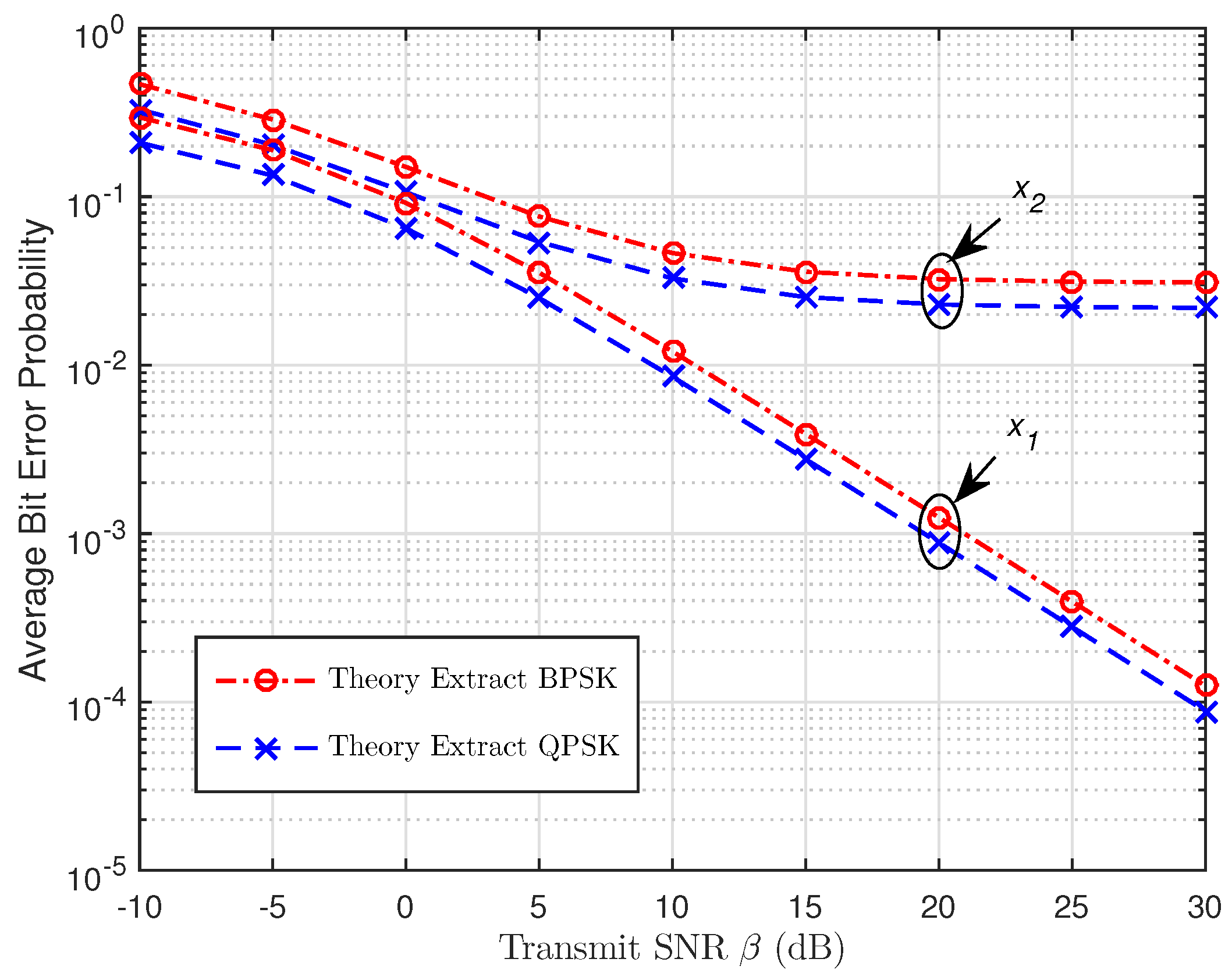
3.3. Average Bit Error Probability (ABEP)
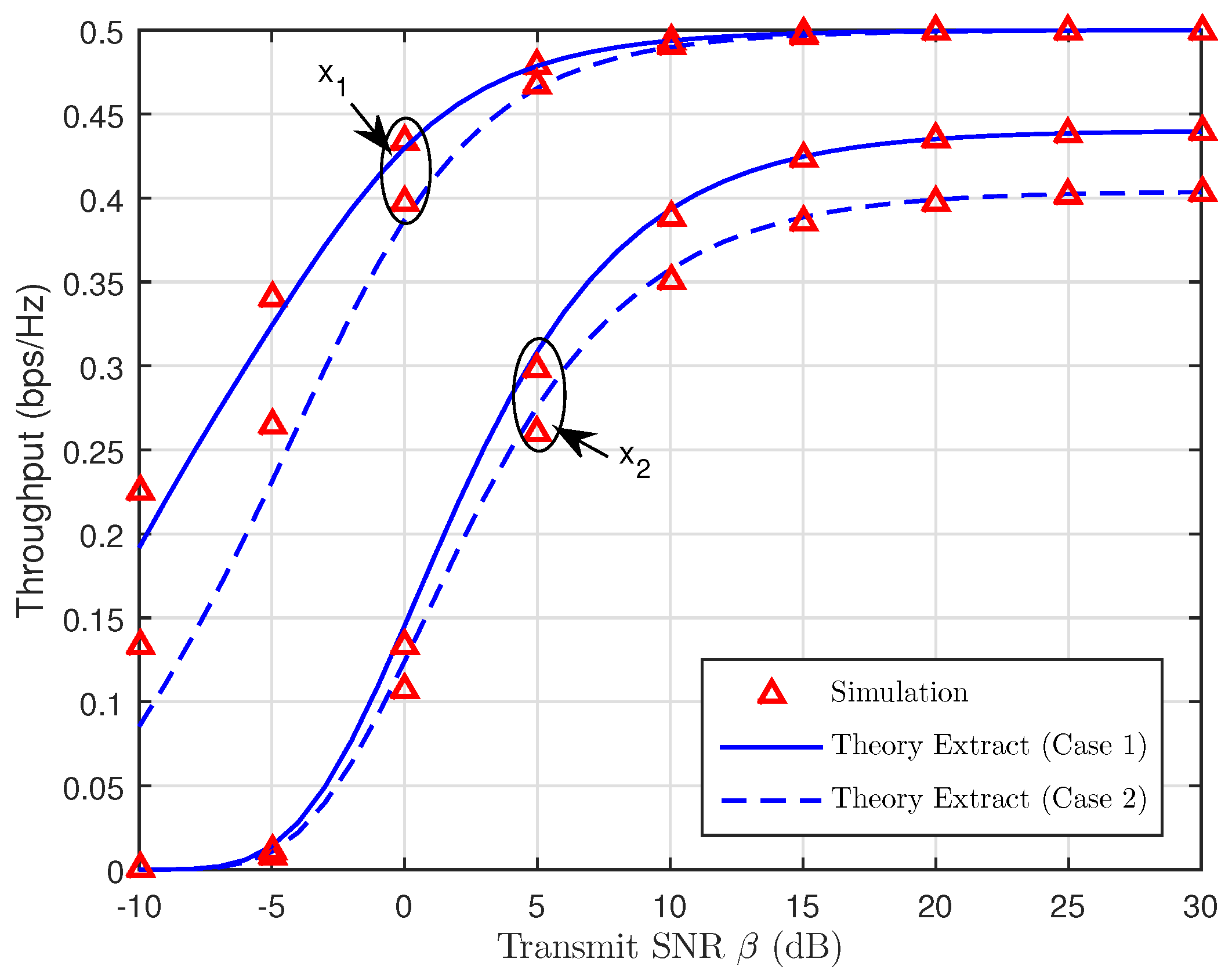
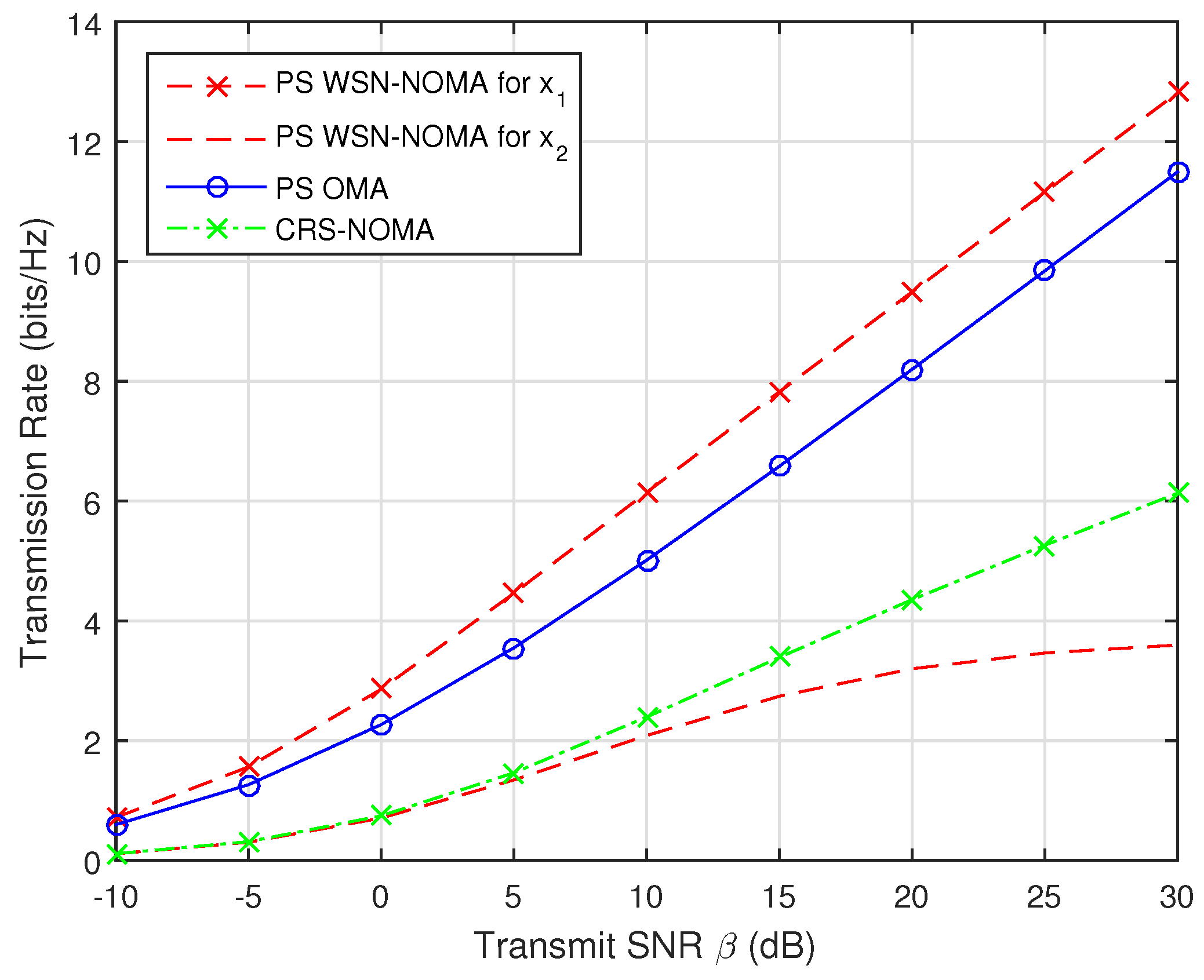
3.4. Throughput in Delay-Limited Transmission Mode
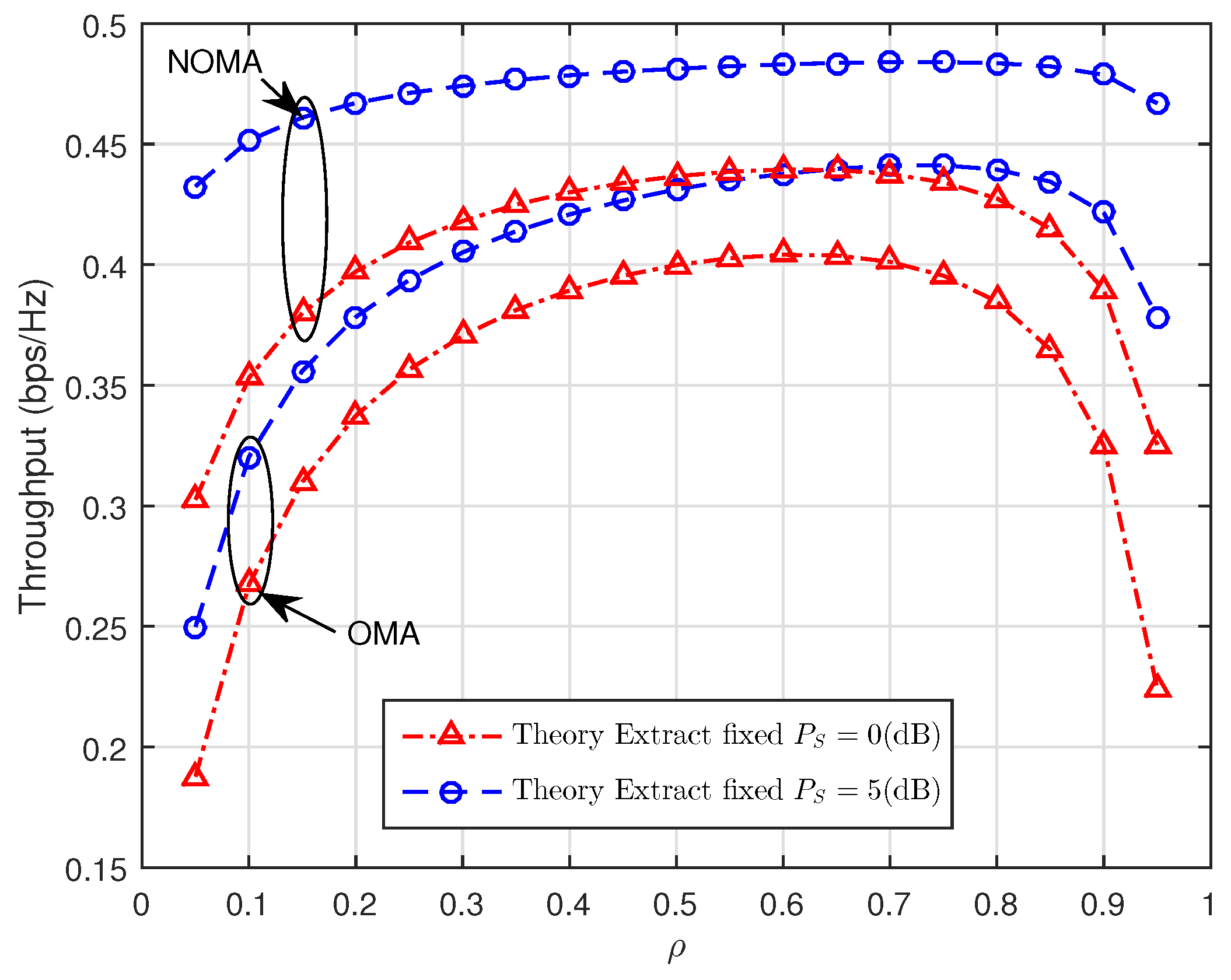
4. Numerical Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| NOMA | Non-orthogonal multiple access |
| SWIPT | Simultaneous wireless information and power transfer |
| WSN | wireless sensor network |
| EH | Energy harvesting |
| IT | Information transmission |
| SIC | Successive interference cancellation |
| PS | Power splitting |
| AF | Amplify-and-forward |
| DF | Decode-and-forward |
| OP | Outage probability |
| ABEP | Average bit error probability |
References
- Sudevalayam, S.; Kulkarn, P. Energy Harvesting Sensor Nodes: Survey and Implication. IEEE Commun. Surv. Tutor. 2011, 13, 443–461. [Google Scholar] [CrossRef]
- Tung, N.T. Heuristic Energy-Efficient Routing Solutions to Extend the Lifetime of Wireless Ad-Hoc Sensor Networks. In Intelligent Information and Database Systems. ACIIDS 2012; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7197, pp. 487–497. [Google Scholar]
- Tung, N.; Vinh, P. The Energy-Aware Operational Time of Wireless Ad-Hoc Sensor Networks. Mob. Netw. Appl. 2013, 18, 454–463. [Google Scholar] [CrossRef]
- Lu, X.; Wang, P.; Niyato, D.; Kim, D.I.; Hann, Z. Wireless Networks with RF Energy Harvesting: A Contemporary Survey. IEEE Commun. Surv. Tutor. 2015, 17, 757–7891. [Google Scholar] [CrossRef]
- Ku, M.L.; Li, W.; Chen, Y.; Liu, K.J.R. Advances in Energy Harvesting Communications: Past, Present, and Future Challenge. IEEE Commun. Surv. Tutor. 2016, 18, 1384–1412. [Google Scholar] [CrossRef]
- Liu, K.; Zhu, Q.; Wang, Y. Allocation Optimization for Multiple Energy-Harvesting Relay System Using SWIPT. Mob. Inf. Syst. 2018, 2018, 7102427. [Google Scholar] [CrossRef]
- Ni, Z.; Motani, M. Performance of Energy-Harvesting Receivers with Time-Switching Architecture. IEEE Trans. Wirel. Commun. 2017, 16, 7252–7263. [Google Scholar] [CrossRef]
- Zhou, Z.; Peng, M.; Zhao, Z.; Li, Y. Joint Power Splitting and Antenna Selection in Energy Harvesting Relay Channels. IEEE Signal Process. Lett. 2015, 16, 7252–7263. [Google Scholar] [CrossRef]
- Nguyen, H.S.; Nguyen, T.S.; Nguyen, M.T.; Voznak, M. Optimal Time Switching-Based Policies for Efficient Transmit Power in Wireless Energy Harvesting Small Cell Cognitive Relaying Networks. Wirel. Pers. Commun. 2015, 99, 1605–1624. [Google Scholar] [CrossRef]
- Zhong, S.; Huang, H.; Li, R. Outage probability of power splitting SWIPT two-way relay networks in Nakagami-m fading. EURASIP J. Wirel. Commun. Netw. 2018, 2018, 11. [Google Scholar] [CrossRef]
- Bai, X.; Shao, J.; Tian, J.; Shi, L. Power-Splitting Scheme for Nonlinear Energy Harvesting AF Relaying with Direct Link. Wirel. Commun. Mob. Comput. 2018, 2018, 7906957. [Google Scholar] [CrossRef]
- Wang, T.; Lu, G.; Ye, Y.; Reni, Y. Dynamic Power Splitting Strategy for SWIPT Based Two-Way Multiplicative AF Relay Networks with Nonlinear Energy Harvesting Model. Wirel. Commun. Mob. Comput. 2018, 2018, 1802063. [Google Scholar] [CrossRef]
- Kariminezhad, A.; Gherekhloo, S.; Sezgin, A. Optimal Power Splitting for Simultaneous Information Detection and Energy Harvesting. IEEE Signal Process. Lett. 2017, 24, 963–967. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, R.; Chua, K.C. Wireless Information and Power Transfer: A Dynamic Power Splitting Approach. IEEE Trans. Commun. 2013, 61, 3990–4001. [Google Scholar] [CrossRef]
- Alsharoa, A.; Ghazzai, H.; Kamal, A.E.; Kadri, A. Optimization of a Power Splitting Protocol for Two-Way Multiple Energy Harvesting Relay System. IEEE Trans. Green Commun. Netw. 2017, 1, 444–457. [Google Scholar] [CrossRef]
- Srivantana, T.; Maichalernnukul, K. Two-Way Multi-Antenna Relaying with Simultaneous Wireless Information and Power Transfer. Symmetry 2017, 9, 42. [Google Scholar] [CrossRef]
- Wu, F.; Xiao, L.; Yang, D.; Cuthbert, L.; Liu, X. Transceiver Design and Power Allocation for SWIPT in MIMO Cognitive Radio Systems. Symmetry 2018, 10, 647. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Ding, Z.; Wang, Z.; Chen, S.; Hanzo, L. A Survey of Non-Orthogonal Multiple Access for 5G. IEEE Commun. Surv. Tutor. 2018, 20, 2294–2323. [Google Scholar] [CrossRef]
- Luo, S.; The, K.C. Adaptive Transmission for Cooperative NOMA System with Buffer-Aided Relaying. IEEE Commun. Lett. 2017, 21, 937–940. [Google Scholar] [CrossRef]
- Alharbi, T.E.A.; So, D.K.C. Full-Duplex Decode-and-Forward Cooperative Non-Orthogonal Multiple Access. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; pp. 2577–2465. [Google Scholar]
- Zaidi, S.K.; Hasan, S.F.; Gui, X. Evaluating the Ergodic Rate in SWIPT-Aided Hybrid NOMA. IEEE Commun. Lett. 2018, 22, 1870–1873. [Google Scholar] [CrossRef]
- Ashraf, M.; Shahid, A.; Jang, J.W.; Lee, K.G. Energy Harvesting Non-Orthogonal Multiple Access System with Multi-Antenna Relay and Base Station. IEEE Access 2017, 5, 17660–17670. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, J. Performance analysis for non-orthogonal multiple access in energy harvesting relaying networks. IET Commun. 2016, 11, 1768–17740. [Google Scholar] [CrossRef]
- Lv, L.; Chen, J.; Ni, Q.; Ding, Z.; Jiang, H. Cognitive Non-Orthogonal Multiple Access with Cooperative Relaying: A New Wireless Frontier for 5G Spectrum Sharing. IEEE Commun. Mag. 2018, 56, 188–195. [Google Scholar] [CrossRef]
- Anwar, A.; Seet, B.C.; Din, Z. Non-Orthogonal Multiple Access for Ubiquitous Wireless Sensor Networks. Sensors 2018, 18, 516. [Google Scholar] [CrossRef] [PubMed]
- Song, M.; Zhen, M. Energy Efficiency Optimization For Wireless Powered Sensor Networks with Nonorthogonal Multiple Access. IEEE Sens. Lett. 2018, 2, 2475–1472. [Google Scholar] [CrossRef]
- Haci, H.; Zhu, H.; Wang, J. Performance of Non-orthogonal Multiple Access with a Novel Asynchronous Interference Cancellation Technique. IEEE Trans. Commun. 2017, 65, 1319–1335. [Google Scholar] [CrossRef]
- Zwillinger, D. Table of Integrals, Series, and Products, 8th ed.; Elsevier: New York, NY, USA, 2014. [Google Scholar]
- Cho, K.; Yoon, D. On the general BER expression of one and two dimensional amplitude modulations. IEEE Trans. Commun. 2002, 50, 1074–1080. [Google Scholar]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Throughput and ergodic capacity of wireless energy harvesting based DF relaying network. In Proceedings of the IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; pp. 4066–4071. [Google Scholar]
- Kim, J.B.; Lee, I.H. Capacity Analysis of Cooperative Relaying Systems Using Non-Orthogonal Multiple Access. IEEE Commun. Lett. 2015, 19, 1949–1952. [Google Scholar] [CrossRef]
| Symbols | Parameter Names | Values |
|---|---|---|
| Source rate | 1 (bps/Hz) | |
| PS ratio | 0.2 | |
| m | Path-loss | 2.7 |
| Energy harvesting efficiency | 0.8 | |
| Distance of S-D link | 1 | |
| Distance of S-R link | 0.3 | |
| Distance R-D link | ||
| Mean of the exponential RVs | 1 | |
| Mean of the exponential RVs | 1 | |
| Mean of the exponential RVs | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ly, T.T.H.; Nguyen, H.-S.; Nguyen, T.-S.; Huynh, V.V.; Nguyen, T.-L.; Voznak, M. Outage Probability Analysis in Relaying Cooperative Systems with NOMA Considering Power Splitting. Symmetry 2019, 11, 72. https://doi.org/10.3390/sym11010072
Ly TTH, Nguyen H-S, Nguyen T-S, Huynh VV, Nguyen T-L, Voznak M. Outage Probability Analysis in Relaying Cooperative Systems with NOMA Considering Power Splitting. Symmetry. 2019; 11(1):72. https://doi.org/10.3390/sym11010072
Chicago/Turabian StyleLy, Tran Thai Hoc, Hoang-Sy Nguyen, Thanh-Sang Nguyen, Van Van Huynh, Thanh-Long Nguyen, and Miroslav Voznak. 2019. "Outage Probability Analysis in Relaying Cooperative Systems with NOMA Considering Power Splitting" Symmetry 11, no. 1: 72. https://doi.org/10.3390/sym11010072
APA StyleLy, T. T. H., Nguyen, H.-S., Nguyen, T.-S., Huynh, V. V., Nguyen, T.-L., & Voznak, M. (2019). Outage Probability Analysis in Relaying Cooperative Systems with NOMA Considering Power Splitting. Symmetry, 11(1), 72. https://doi.org/10.3390/sym11010072







