Statistical Damage Model of Altered Granite under Dry-Wet Cycles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Research Background
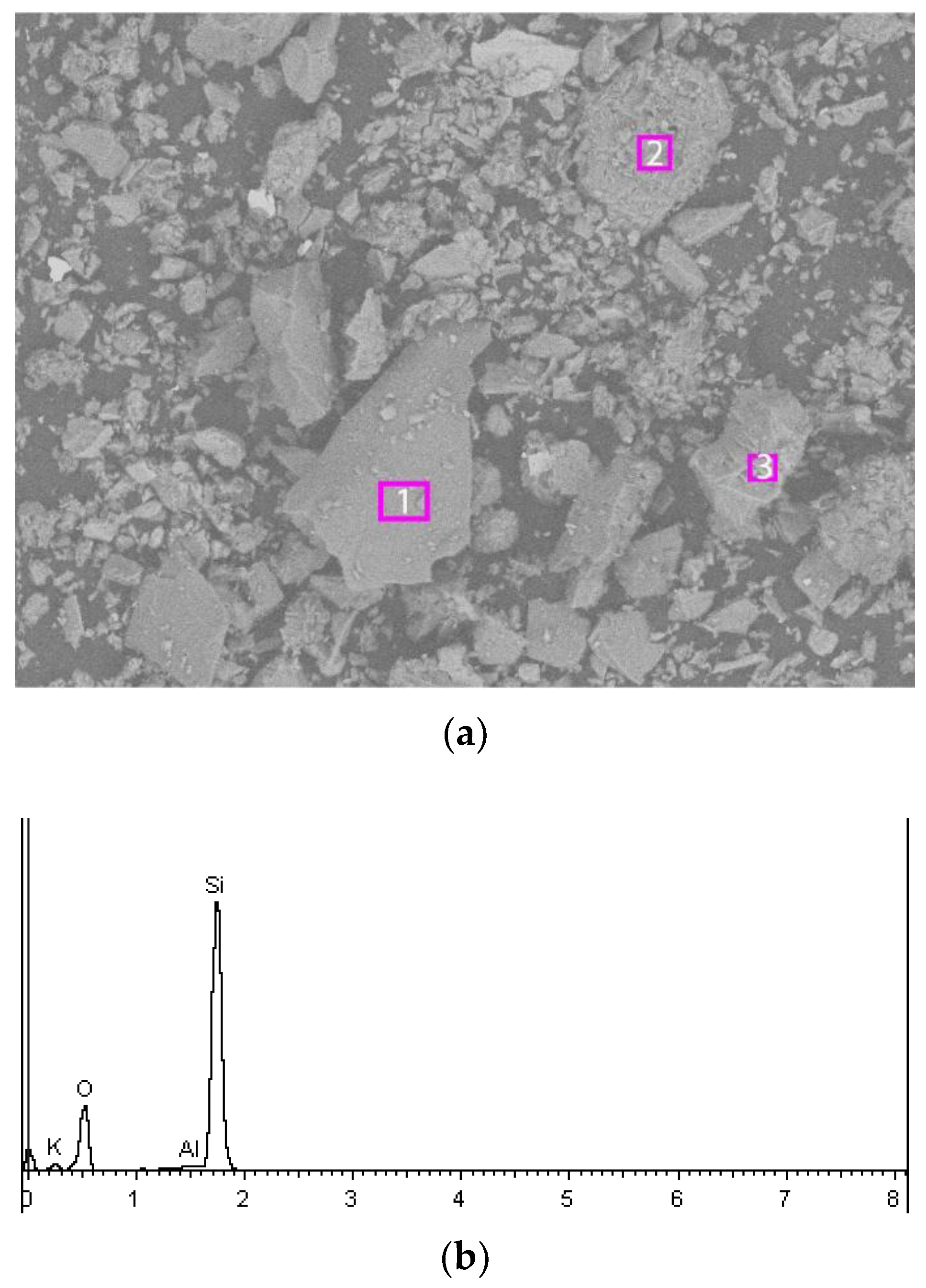
2.2. Sample Tested
2.3. Test of Dry-Wet Cycles
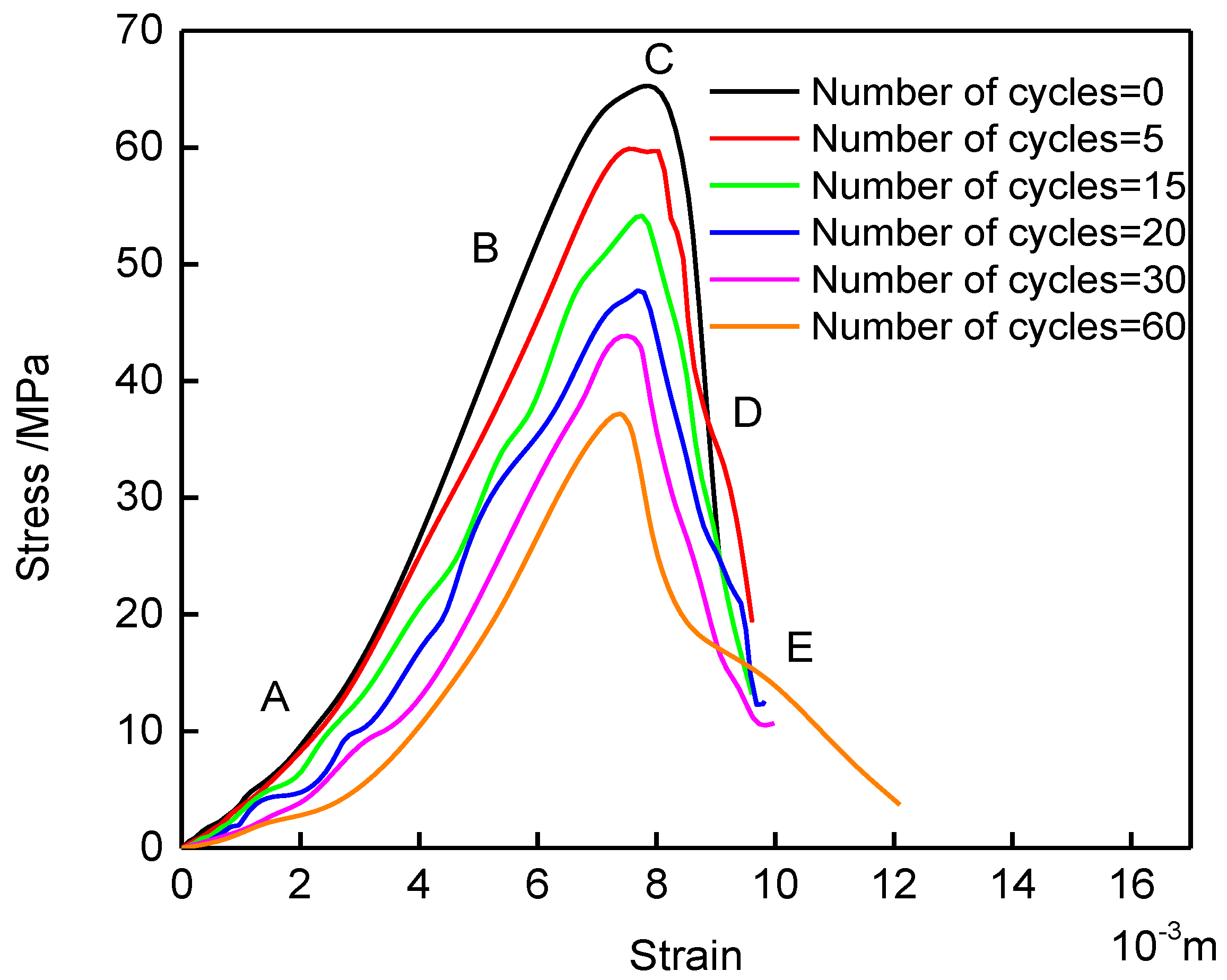
2.4. Results of Uniaxial Compression Test
3. Damage Variables under Dry-Wet Cycles
3.1. Hydraulic Damage Variable (Dw)
3.2. Loading Damage Variable (Dm)
3.3. Comprehensive Damage Variable (D)
4. Damage Constitutive Model under Dry-Wet Cycles
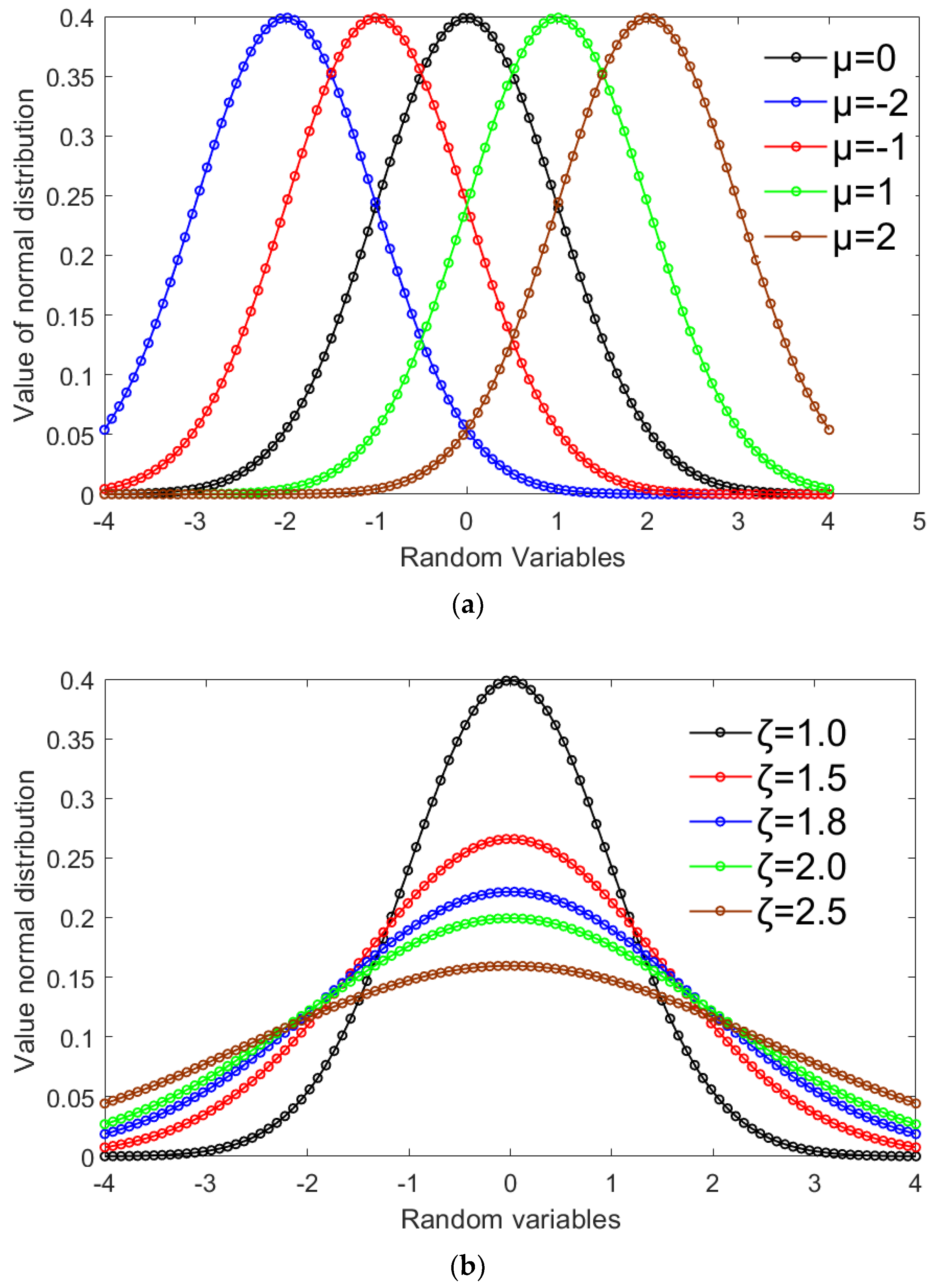
4.1. Damage Constitutive Model
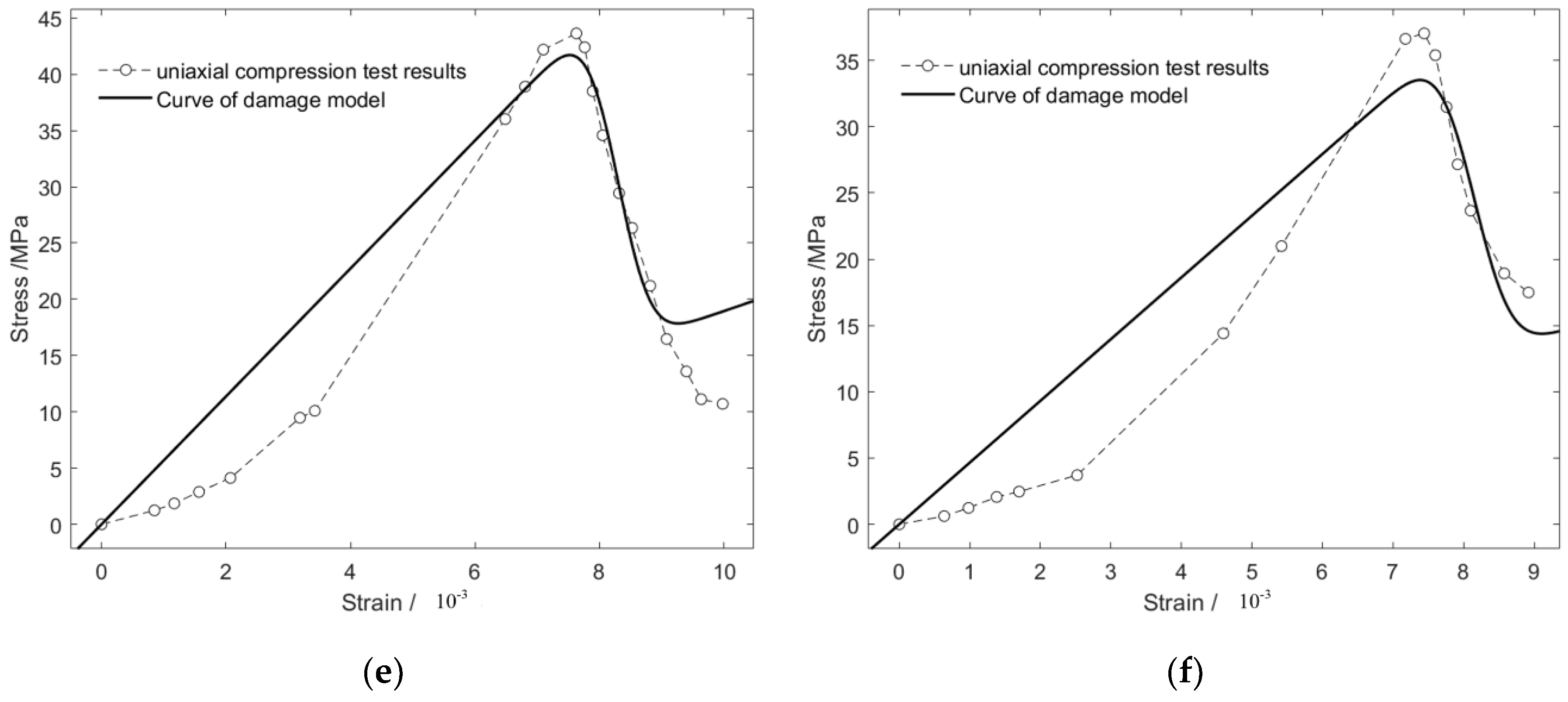
4.2. Comparison of Damage Model and Test Results
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Minardi, A.; Ferrari, A.; Ewy, R. Nonlinear Elastic Response of Partially Saturated Gas Shales in Uniaxial Compression. Rock Mech. Rock Eng. 2018, 3, 1–12. [Google Scholar] [CrossRef]
- Wang, Z.L.; Shi, H.; Wang, J.G. Mechanical Behavior and Damage Constitutive Model of Granite Under Coupling of Temperature and Dynamic Loading. Rock Mech. Rock Eng. 2018, 15, 1–16. [Google Scholar] [CrossRef]
- Liu, L.; Xu, W.Y.; Zhao, L.Y. An Experimental and Numerical Investigation of the Mechanical Behavior of Granite Gneiss Under Compression. Rock Mech. Rock Eng. 2016, 50, 1–8. [Google Scholar] [CrossRef]
- Berto, L.; Saetta, A.; Talledo, D. Constitutive model of concrete damaged by freeze–thaw action for evaluation of structural performance of RC elements. Constr. Build. Mater. 2015, 98, 559–569. [Google Scholar] [CrossRef]
- Raude, S.; Laigle, F.; Giot, R. A unified thermoplastic/viscoplastic constitutive model for geomaterials. Acta Geotech. 2016, 11, 849–869. [Google Scholar] [CrossRef]
- Parisio, F.; Vilarrasa, V.; Laloui, L. Hydro-mechanical Modeling of Tunnel Excavation in Anisotropic Shale with Coupled Damage-Plasticity and Micro-dilatant Regularization. Rock Mech. Rock Eng. 2018, 51, 3819–3833. [Google Scholar] [CrossRef]
- Kikumoto, M.; Nguyen, V.P.Q.; Yasuhara, H. Constitutive model for soft rocks considering structural healing and decay. Comput. Geotech. 2017, 91, 93–103. [Google Scholar] [CrossRef]
- Mortazavi, A.; Molladavoodi, H. A numerical investigation of brittle rock damage model in deep underground openings. Eng. Fract. Mech. 2012, 90, 101–120. [Google Scholar] [CrossRef]
- Cerfontaine, B.; Charlier, R.; Collin, F. Validation of a New Elastoplastic Constitutive Model Dedicated to the Cyclic Behavior of Brittle Rock Materials. Rock Mech. Rock Eng. 2017, 50, 2677–2694. [Google Scholar] [CrossRef]
- Li, X.; Cao, W.G.; Su, Y.H. A statistical damage constitutive model for softening behavior of rocks. Eng. Geotech. 2012, 113–114, 1–17. [Google Scholar] [CrossRef]
- Asadollahi, P.; Tonon, F. Constitutive model for rock fractures: Revisiting Barton’s empirical model. Eng. Geotech. 2010, 113, 11–32. [Google Scholar] [CrossRef]
- Unteregger, D.; Fuchs, B.; Hofstetter, G. A damage plasticity model for different types of intact rock. Int. J. Rock Mech. Min. Sci. 2015, 80, 402–411. [Google Scholar] [CrossRef]
- Amorosi, A.; Aversa, S.; Boldini, D. Application of a new constitutive model to the analysis of plate load tests in a pyroclastic rock. Int. J. Rock Mech. Min. Sci. 2015, 78, 271–282. [Google Scholar] [CrossRef]
- Özbek, A. Investigation of the effects of wetting–drying and freezing–thawing cycles on some physical and mechanical properties of selected ignimbrites. Bull. Eng. Geol. Environ. 2014, 73, 595–609. [Google Scholar] [CrossRef]
- Khanlari, G.; Abdilor, Y. Influence of dry-wet, freeze-thaw, and heat-cool cycles on the physical and mechanical properties of Upper Red sandstones in central Iran. Bull. Eng. Geol. Environ. 2015, 74, 1287–1300. [Google Scholar] [CrossRef]
- Qin, Z.; Chen, X.X.; Fu, H.L. Damage Features of Altered Rock Subjected to Drying-Wetting Cycles. Adv. Civ. Eng. 2018, 1, 1–10. [Google Scholar] [CrossRef]
- Chen, X.X.; Gong, Y.P. Features of Shear Strength Parameters Reflecting Damage to Rock Caused by Water Invasion-Loss Cycles. Geotech. Geol. Eng. 2018. [Google Scholar] [CrossRef]
- Krajcinovic, D. Damage mechanics. Mech. Mater 1989, 8, 117–197. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, W.H.; Yang, W.Q. Probability Theory and Mathematical Statistics; Higher Education Press: Beijing, China, 2016. [Google Scholar]
- Yan, C.F.; Xu, J. Probability Model of Rock Mass Strength Criterion and Its Application; Chongqing University Press: Chongqing, China, 1999. [Google Scholar]
- Cao, W.G.; Li, X.; Zhao, H. Damage constitutive model for strain-softening rock based on normal distribution and its parameter determination. J. Cent. South Univ. Technol. 2007, 14, 719–724. [Google Scholar] [CrossRef]
- Paisley, J.; Wang, C.; Blei, D.M. The Discrete Infinite Logistic Normal Distribution. Bayesian Anal. 2012, 15, 74–82. [Google Scholar] [CrossRef]
- Bian, K.; Liu, J.; Zhang, W. Mechanical Behavior and Damage Constitutive Model of Rock Subjected to Water-Weakening Effect and Uniaxial Loading. Rock Mech. Rock Eng. 2018. [Google Scholar] [CrossRef]
- Grgic, D. Constitutive modelling of the elastic–plastic, viscoplastic and damage behaviour of hard porous rocks within the unified theory of inelastic flow. Acta Geotech. 2016, 11, 95–126. [Google Scholar] [CrossRef]


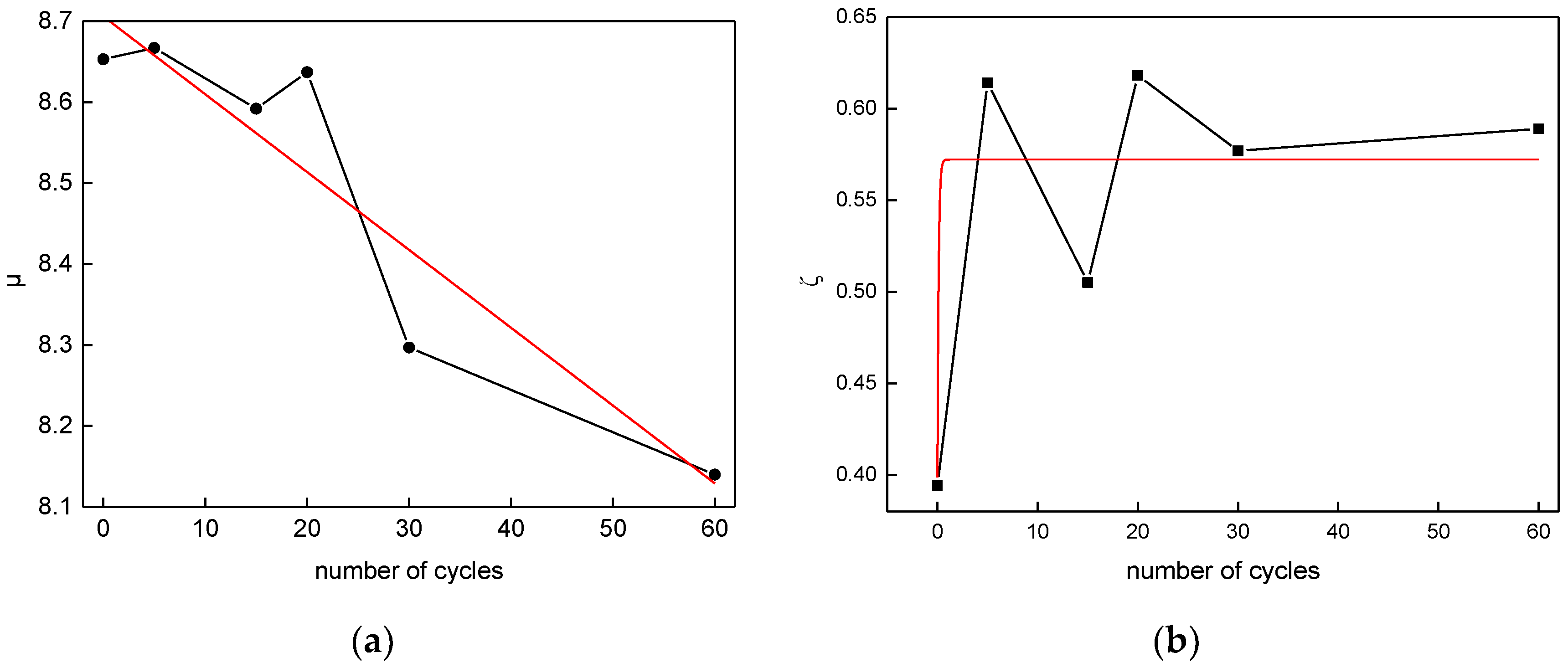

| Number of Cycles | μ | R2 | |
|---|---|---|---|
| 0 | 8.653 | 0.394 | 0.9758 |
| 5 | 8.667 | 0.614 | 0.9787 |
| 15 | 8.592 | 0.505 | 0.9622 |
| 20 | 8.637 | 0.618 | 0.9404 |
| 30 | 8.297 | 0.577 | 0.9132 |
| 60 | 8.140 | 0.589 | 0.9163 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; He, P.; Qin, Z.; Li, J.; Gong, Y. Statistical Damage Model of Altered Granite under Dry-Wet Cycles. Symmetry 2019, 11, 41. https://doi.org/10.3390/sym11010041
Chen X, He P, Qin Z, Li J, Gong Y. Statistical Damage Model of Altered Granite under Dry-Wet Cycles. Symmetry. 2019; 11(1):41. https://doi.org/10.3390/sym11010041
Chicago/Turabian StyleChen, Xuxin, Ping He, Zhe Qin, Jianye Li, and Yanping Gong. 2019. "Statistical Damage Model of Altered Granite under Dry-Wet Cycles" Symmetry 11, no. 1: 41. https://doi.org/10.3390/sym11010041
APA StyleChen, X., He, P., Qin, Z., Li, J., & Gong, Y. (2019). Statistical Damage Model of Altered Granite under Dry-Wet Cycles. Symmetry, 11(1), 41. https://doi.org/10.3390/sym11010041






