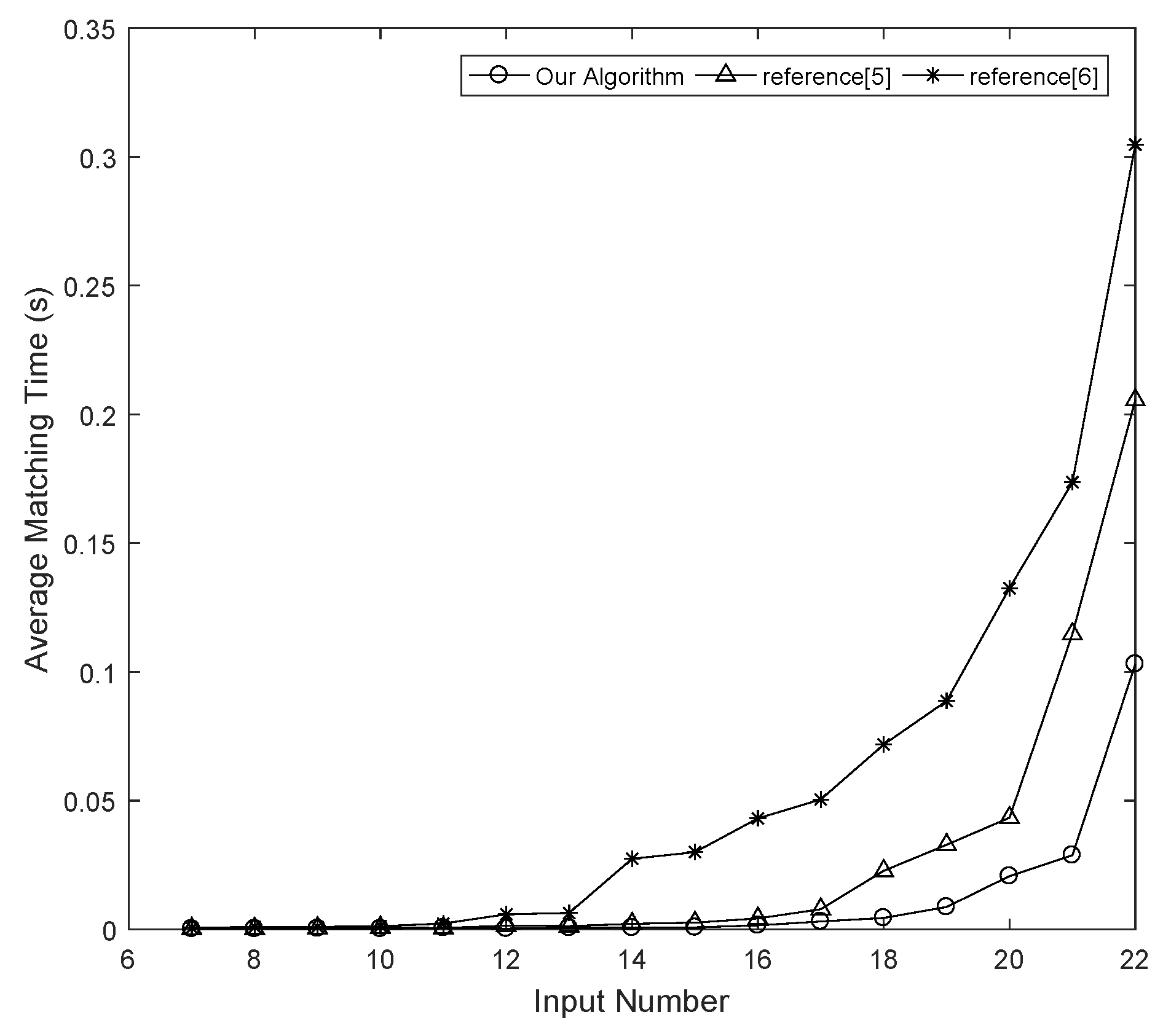
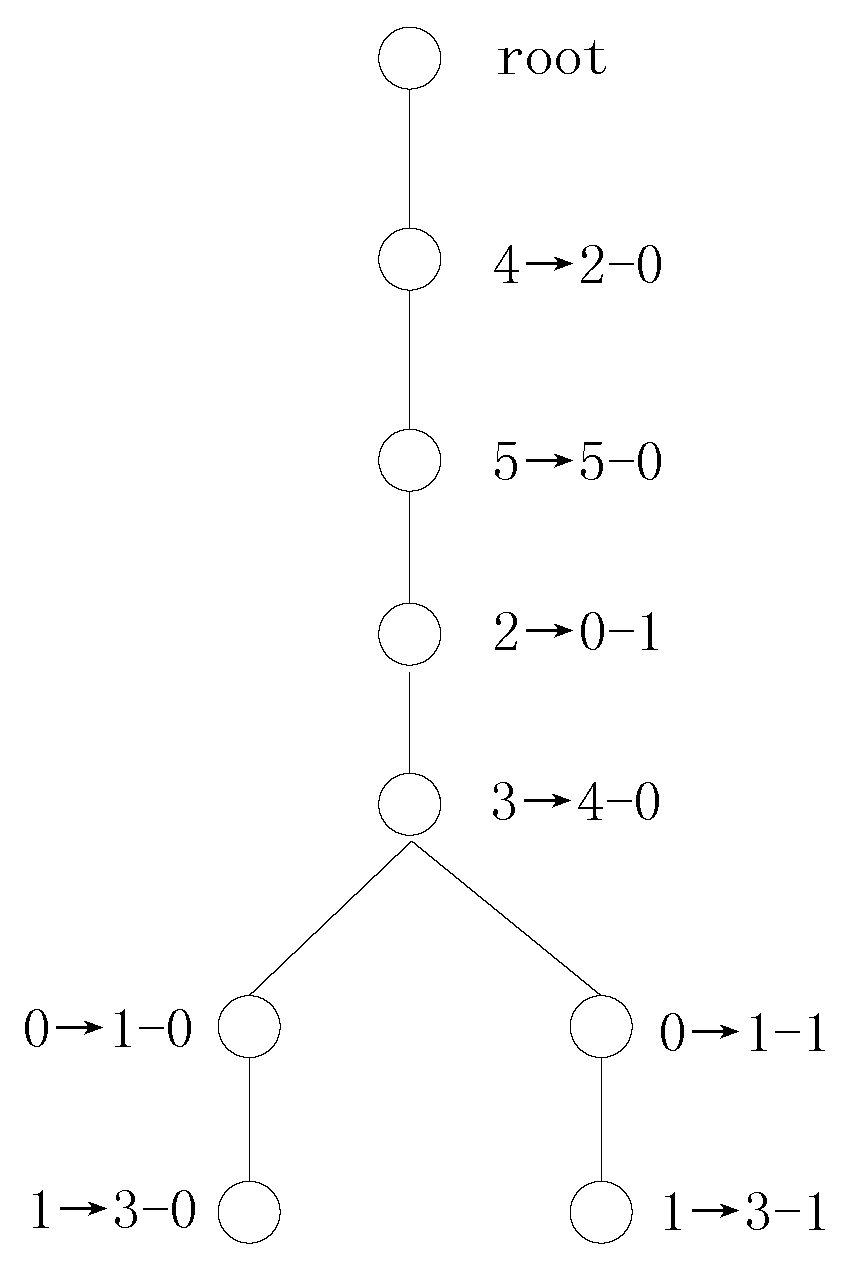The goal of the proposed algorithm is to reduce the size of the search space as much as possible, thereby improving the speed of NPN Boolean matching.
4.1. Boolean Difference
For n inputs, there are different Boolean functions. Many Boolean functions have one or more independent variables. Whether a variable of f is independent can be determined using cofactors.
The Boolean difference of a Boolean function
f with respect to
,
, is the Boolean function
, where
and
[
23].
Definition 2. (Boolean difference signature) The Boolean difference signature of a Boolean function f with respect to , , is the number of minterms of .
When a variable of f is NP transformed into , its Boolean difference signature does not change. Thus, Boolean difference signature, like cofactor signature, can be used to distinguish variables.
Example 1. Consider an 5-input Boolean function . Let us compute the 1st signature and the Boolean difference signature of each variable.
The 1st signatures of , , , and are , , , and , respectively. The variable is symmetric to . The Boolean difference signatures of the variables are 32, 12, 20, 28 and 12, respectively. From the 1st signatures and a symmetry check, we can distinguish variables , and . Variables and are both asymmetric variables and have the same 1st signature values. If we only utilize on their 1st signatures, the variables and cannot be distinguished. However, these two variables have different Boolean difference signatures. Thus, the variables and are actually different and can be distinguished.
Definition 3. (Independent variable) A variable of a Boolean function f is an independent variable if it satisfies .
NP transformations do not change the independence of a variable. Thus, an independent variable is still an independent variable after NP transformation.
Definition 4. (Independent-variable set) The independent-variable set of a Boolean function f, , is a set that consists of all independent variables of f.
Lemma 1. Two NPN-equivalent Boolean functions f and g have the same number of independent variables.
Proof. If the Boolean function f is NPN-equivalent to g, then f and g are in the same NPN equivalence class. There must exist an NP transformation T that can transform f into g or . After NP transformation, an independent variable is still an independent variable. Therefore, it can be deduced that f and g have the same number of independent variables. □
Property 1. The cofactor signature of a Boolean function f with respect to its variable is when the variable is an independent variable.
Proof. Since and and , it holds that . □
Because the positive cofactor signature is the same as the negative cofactor signature for an independent variable, the phases of independent variables cannot determined by using the phase assignment method presented in [
5,
6]. However, independent variables have no influence on a Boolean function. Thus, the proposed algorithm assigns a positive phase to all independent variables.
Example 2. Consider two 6-input Boolean functions and . Let us compute the SS vectors, Boolean difference signatures and independent-variable sets.
The SS vectors of f and g are as follows:
The Boolean difference signatures of the variables of f are 48, 48, 16, 16, 0 and 0. The Boolean difference signatures of the variables of g are 16, 48, 0, 48, 16 and 0. The independent-variable sets of f and g are and .
Definition 5. (Independent mapping set) The independent mapping set between Boolean functions f and g is .
Consider two NP-equivalent Boolean functions f and g with independent-variable sets of and , respectively. If we do not consider the symmetry and independence of variables, then there are groups of different variable mappings between and according to their 1st signatures. However, according to the properties of independent variables, we need to consider only the positive phase and create one independent-mapping set . Therefore, the search space is reduced significantly if there are independent variables in the Boolean functions.
In Example 2, the Boolean function
f has the three symmetry classes
,
and
, and the Boolean function
g has the three symmetry classes
,
and
if we do not consider the Boolean difference signatures. The symmetry class
of
f can be mapped to the symmetry classes
and
of
g using the method of reference [
5]. In other words, the symmetry classes
and
of Boolean function
f cannot be distinguished. However, the variables in
and
of Boolean function
f have different Boolean difference signatures. Thus, if we consider the Boolean difference signatures when searching the variable mappings, the symmetry class
of
f can be mapped only to the symmetry class
of
g, and the symmetry class
of
f can be mapped only to the symmetry class
of
g. There exists an independent-mapping set
.
Definition 6. (Structural difference signature vector) An n-input Boolean function f has a structural difference signature (SDS) vector , where .
The algorithm presented in [
5] groups variables by their 1st signature values. The algorithm proposed in this paper groups variables by their 1st signature values and Boolean difference signatures. We define the ’<’ relation between
and
as follows.
Definition 7. (<) The variables and have the relation if one of the following two cases is satisfied: (1) or (2) .
The group numbers of the variables are generated with the above ’<’ relation. The SDS vectors of f and g in example 2 are as follows: and . In the process of grouping variables of Boolean function f, we first compare their 1st signature and do not consider the order of positive and negative cofactor signature. Therefore, variables and are grouped into group 0. The varibales in symmetry class and have the same 1st signature, so we compare their Boolean difference signature. Because the Boolean difference signature of variables in is greater than that of variables in symmetry class , the group number of variables and are 1 and the group number of variables and are 2.
The SDS vector is a new signature vector that consists of the SS vector plus a Boolean difference mark. The variable mapping search and the transformation detection of our algorithm are based on two facts: (1) two NP-equivalent Boolean functions have the same SDS vectors; and (2) there exists a possible variable mapping between the variables and if they have the same SDS values.
4.2. SDS-Based Boolean Matching Algorithm
NPN Boolean matching is defined as follows:
Given two Boolean functions f and g, if there exists an NP transformation T that satisfies or , then f is NPN-equivalent to g.
Before searching the variable mappings, the proposed algorithm first determines whether there is an output negation for Boolean function
f. If there is, then our algorithm will match
f and
. The method of identifying the presence of an output negation is the same as that in reference [
5]. If
, then there is no output negation. There is an output negation if
. There is a tie if
. Our algorithm handles first the condition without output negation and then the condition with output negation if
f is not NP equivalent to
g.
The algorithm will terminate when it finds a transformation T that satisfies or when all candidate transformations have been checked and found not to satisfy . The algorithm will attempt all possible variable mappings, and thus, it will certainly find an NP transformation T between two NP-equivalent Boolean functions f and g .
The pseudo-code for NPN Boolean matching is given in Procedure 1.
In Procedure 1, is a tree that stores the NP transformations generated in the process of transformation detection. A candidate transformation is an unabridged branch in . and are the decomposition expressions for f and g, respectively. After the existence of an output negation has been determined, Procedure 1 calls Handle_SDS() to detect the NP transformations between f and g () and judge the NP equivalence of f and g .
Any one NP transformation between the Boolean functions f and g is composed of n variable mappings. Thus, the proposed algorithm searches variable mappings and generates NP transformations. In this paper, the necessary condition for two Boolean functions to be judged NP equivalent is that they must have the same SDS vector. For a variable mapping to be established between and , these two variables must satisfy the following conditions:
(1) and have the same 1st signature values, i.e., .
(2) and have the same Boolean difference signature, i.e., .
(3) and have the same symmetry class cardinality, i.e., .
(4) and have the same group number, i.e., .
| Procedure 1 NPN Boolean Matching. |
Input:f and g
Output: 0 or 1
function Matching()
Create BDD of f and g
Compute and
if then
if then
Return Handle_SDS()
else
if Handle_SDS()=1 then
Return 1
else
Return Handle_SDS(f,)
end if
end if
else
if then
Return Handle_SDS(f,)
else
Return 0
end if
end if
end function |
In the process of the variable mapping search, Handle_SDS() searches the variable mappings for each variable that has not been identified. A variable is identified when its phase and variable mappings are determined in a transformation. After searching all variable mapping sets, Handle_SDS() selects the minimal variable mapping set to handle. The minimal variable mapping set is the one with the lowest cardinality. There are eight possible cases for the variable mapping set of the variable of f, as follows.
(1) The variable is an asymmetric variable. The phase of is determined, and there is only one variable of g that has the same SDS values as those of . The variable mapping set of is a single-mapping set. , , and .
(2) The variable is an asymmetric variable. There exist multiple variables of g, where , that have the same SDS values as those of , and their phases are determined. The variable mapping set of is a multiple-mapping set. , where , and .
(3) The variable is an asymmetric variable. There exist one or more variables of g, where , that have the same SDS values as those of , and their phases are not determined. The variable mapping set of is a multiple-mapping set. , and .
(4) The variable is a symmetric variable, and its symmetry class is . There exists only one symmetry class of g whose variables have the same SDS values as those of the variables in , where , and the phase of is determined. The variable mapping set of , , is a single symmetry-mapping set, i.e., . There exists one group of variable mappings , where , between and .
(5) The variable is a symmetric variable, and its symmetry class is . There is only one symmetry class of g whose variables have the same SDS values as those of the variables in , where , and the phase of is not determined. The variable mapping set of , , is a multiple symmetry-mapping set: . There are two groups of variable mappings, , where , and , where , between and .
When the variable symmetry is checked, the phase relation between two symmetric variables is known. The variable mapping relations between and can be generated in the following way.
We first consider the case in which and have the same phase, i.e., there exists a variable mapping . A variable mapping exists in two cases: (1) is symmetric to and is symmetric to or (2) is symmetric to and is symmetric to . A variable mapping exists in two cases: (1) is symmetric to and is symmetric to or (2) is symmetric to and is symmetric to . Then, we consider the case in which and have the opposite phase, i.e., there exists a variable mapping . A variable mapping exists in two cases: (1) is symmetric to and is symmetric to or (2) is symmetric to and is symmetric to . A variable mapping exists in two cases: (1) is symmetric to and is symmetric to or (2) is symmetric to and is symmetric to . Thus, two groups of variable mappings between and will be generated via this method.
(6) The variable is a symmetric variable, and its symmetry class is . There exist multiple symmetry classes , where , whose variables have the same SDS values as the variables in , where , and the phase of is determined. The variable mapping set of , , is a multiple symmetry-mapping set: . There exists one group of variable mappings between and each , where .
(7) The variable is a symmetric variable, and its symmetry class is . There exist one or more symmetry classes , where , whose variables have the same SDS values as those of the variables of , where , and the phase of is not determined. The variable mapping set of , , is a multiple symmetry-mapping set: . There exist two groups of variable mappings between and each , where .
(8) The variable is an independent variable. The variable mapping set of is an independent mapping set.
All possible variable mapping sets are listed above. To generate an NP transformation, n variable mappings are needed for . Each node in the NP transformation tree, , represents a variable mapping, and all nodes in a given layer belong to the same variable mapping set. The methods for handling the variable mapping sets are as follows.
(1) If it is the first computation of SDS vectors, a check for independent variables is performed. If there are one or more independent variables, an independent-mapping set is created and added to , and the minimal variable mapping set is then sought among the remaining variables. If there are no independent variables, Handle_SDS() searches the variable mapping sets for all variables.
(2) If the current variable mapping set of is a single-mapping set, our algorithm adds the variable mapping in to . The variable is identified.
(3) If the current variable mapping set of is a single symmetry-mapping set and belongs to , where , then the group of variable mappings of is added to . To the NP transformation tree, m layers are added, where each layer contains a variable mapping node. The variables in the symmetry class are all identified.
(4) If the current variable mapping set of is a multiple-mapping set or a multiple symmetry-mapping set, then the cardinalities of the variable mapping sets are computed, and the minimal variable mapping set is recorded.
After searching all variable mapping sets, as in reference [
5], our algorithm updates the two decomposition expressions
and
in the case of a single-mapping set or a single symmetry-mapping set. Otherwise, our algorithm handles the minimal variable mapping set. If the cardinality
m of the minimal variable mapping set satisfies
, then
m branches will be generated in
. Each branch is handled in order.
The purpose of Procedure 2 is to search the variable mappings for all possible NP transformations. In the process of recursive_search, Procedure 2 uses the same methods applied in [
5] to find and prune error NP transformation branches. That is, the current branch will be pruned if the two SDS vectors are not the same or if the current variable mapping has a phase collision.
The pseudo-code for Procedure 2 is as follows.
| Procedure 2 recursive_search. |
Input:f, g, , , and
Output: 0 or 1
function handle_SDS()
if then
return VERIFY()
end if
UPDATE()
if then
return 0
end if
if then
Compute and
if then
Add independent mappings to
end if
end if
=32768
for all do
if then
Continue
end if
for all do
Search variable mappings
end for
Compute
if then
for all do
if then
return 0
else
Add to
end if
end for
else
if then
end if
end if
end for
if then
Update and
Return Handle_SDS()
else
for all do
if then
continue
else
Add to
Update and
Return Handle_SDS()
end if
end for
Return 0
end if
end function |
The meanings of conditions , , , , and and the operations that need to be performed when these conditions are satisfied are defined as follows:
: When is true, a candidate transformation is generated. Procedure 2 checks whether the current NP transformation T can transform f into g .
: When is true, the transformation tree is NULL, and this is the first time that the SDS vectors have been computed. Procedure 2 checks and handles the independent-mapping set between f and g .
: When is true, the current variable has already been identified, and Procedure 2 fetches the next to handle.
: When is true, the variable-mapping set of is a single-mapping set or a single symmetry-mapping set.
: When is true, there is a phase collision.
: When is true, the cardinality of the minimal variable mapping set is 1.
In the process of transformation detection, Procedure 2 attempts each variable mapping in each multiple-mapping set or each group of variable mappings in each multiple symmetry-mapping set. For two NP-equivalent Boolean functions f and g (), Procedure 2 must find a candidate transformation that satisfies . The purpose of VERIFY() is to check whether .
UPDATE() serves the following functions:
(1) Updates the SDS vector of f and the SDS vector of g by means of Shannon decomposition and the decomposition expressions and .
(2) Updates the phases of the variables in f and g.
(3) Checks the variable symmetry when the SDS vectors are computed for the first time.
(4) Groups the variables of f and g by their 1st signature values and Boolean difference signatures.
In Example 2, if we use the SS values to search the variable mappings, then there are one single symmetry-mapping set
and two multiple symmetry-mapping sets
and
, where
. Procedure 2 handles the single symmetry-mapping set
, and the variable mappings
and
are added to
.
and
are updated to
and
. After the SS vectors are updated, the 1st signatures of the remaining variables of
f and
g are all
. Therefore, the remaining four variables still cannot be distinguished, and there are two multiple symmetry-mapping sets,
and
. The first symmetry-mapping set
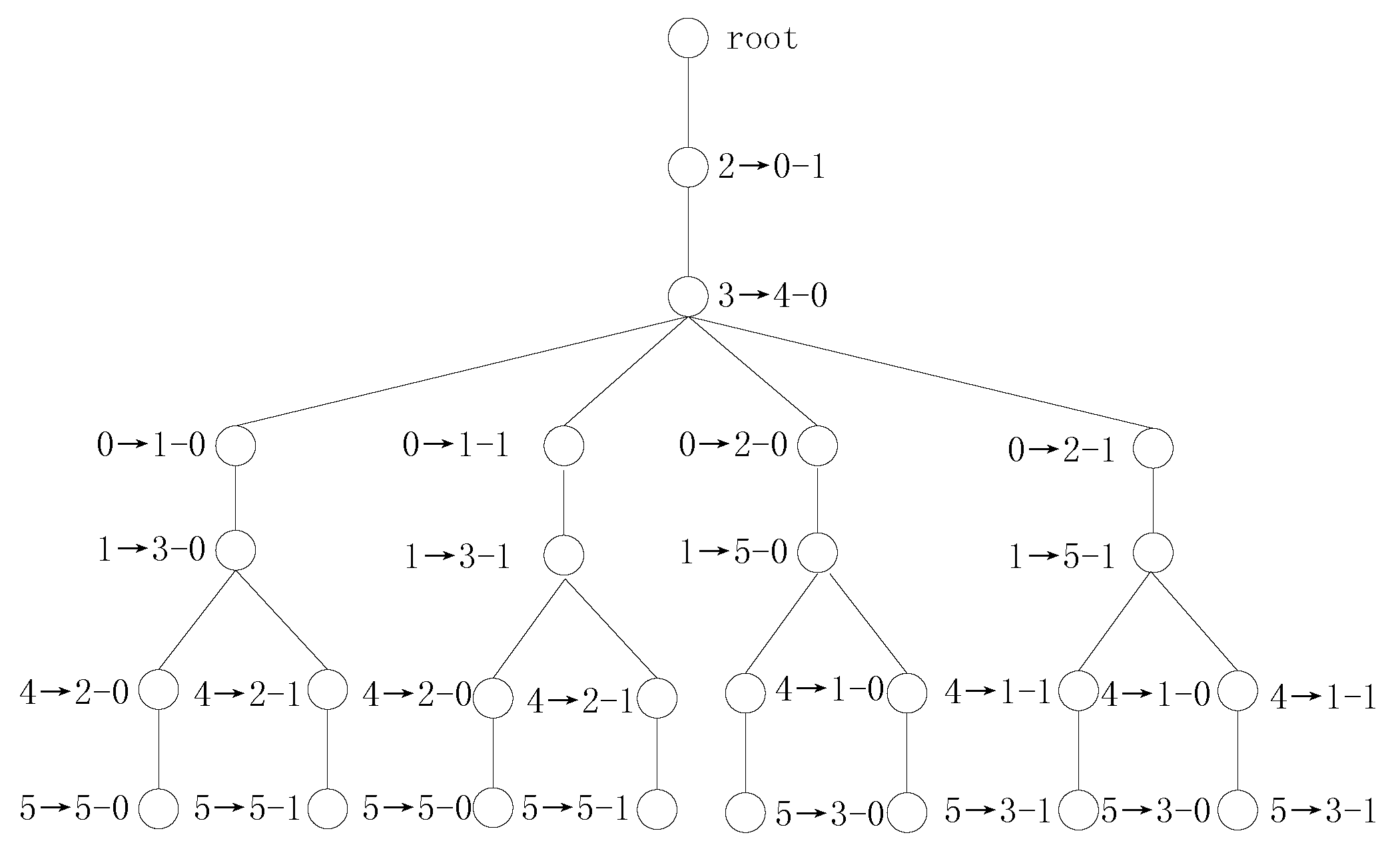
is selected to be handled. The transformation tree for Example 2 using SS vectors is shown in
Figure 1.
If we use the SDS values to search the variable mappings, then there are one independent-mapping set, one single symmetry-mapping set and one multiple symmetry-mapping set according to the first computed SDS vectors. Procedure 2 first adds the variable mappings and to the transformation tree. Then, the two variable mappings and of the symmetry mapping are added to the transformation tree. The catch is that the independent variable is not a splitting variable because the decomposition results obtained via Shannon expansion with the independent variable are unchanged. Thus, the decomposition expressions and are updated to and . UPDATE() is called to compute new SDS vectors, and the SDS vectors are updated in accordance with and .
In this way, Procedure 2 determines 4 variable mappings, namely,
,
,
and
, after the first variable mapping search for example 2. In the next variable mapping search, there is one multiple symmetry-mapping set,
. The transformation tree for Example 2 using SDS vectors is shown in
Figure 2.
From Example 2, we can see that the number of candidate transformations decreases from 8 to 2. The use of Boolean difference signatures helps to distinguish symmetry classes and , and we need to consider only the positive phase for independent variables. Thus, Boolean difference signatures are very beneficial for distinguishing variables.
In cell library binding, a benchmark Boolean circuit is found to realize another NPN equivalent Boolean function. Example 3 demonstrates the process of NPN equivalent matching by SS and SDS vectors respectively, and illustrates the validity of the SDS vectors proposed in this paper.
Example 3. Consider two 6-input Boolean functions and :
The transformation detection process using SS vectors is as follows:
(1) Compute the SS vectors of f and g. The results are:
From the above results, we can draw three conclusions: (1) these two SS vectors are the same; (2) the phases of the variable of f and the variable of g are determined; and (3) there is only one variable of g with the same SS values as those of the variable of f. Therefore, there is a single-mapping set . Concerning the splitting variables, the new splitting expressions are and .
(2) The algorithm enters the next iteration and computes the new SS vectors. The new SS vectors are:
The results show the following: (1) the two new SS vectors are the same; (2) the phases of all variables are determined; and (3) the next variable-mapping set to be handled is . Procedure 2 adds 5 nodes to the second layer of the transformation tree. Procedure 2 handles the first variable mapping in the order of the variable mappings in the set and updates and .
In the subsequent variable mapping search, the branch is pruned by a phase collision. The , and branches are pruned by having different SS vectors.
(3) Then, Procedure 2 handles the variable mapping and detects a candidate transformation . After verification, this transformation is found to satisfy . Therefore, f is NPN-equivalent to g.
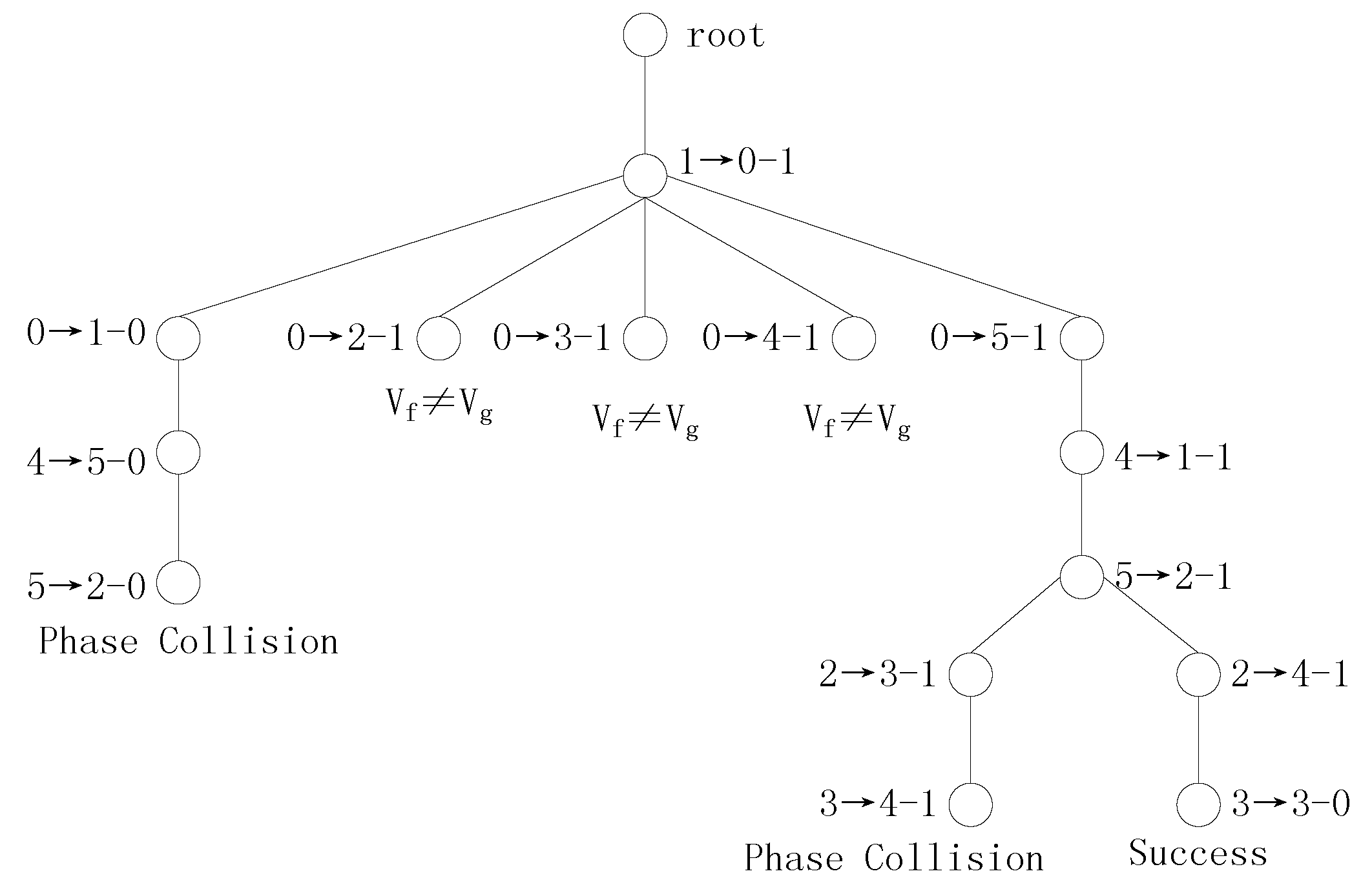
The transformation tree for Example 3 using SS vectors is shown in
Figure 3.
Figure 3 shows that this transformation tree for Example 3 has 6 branches and that the two Boolean functions are decomposed 4 times. Let us examine the detection process using SDS vectors.
(1) The SDS vectors of f and g are as follows:
From these results, we can draw the following conclusions: (1) these two SDS vectors are the same; (2) the phases of the variable of f and the variable of g are determined,; and (3) there is one single-mapping set to be used in the search. In Procedure 2, the splitting variables and are used to decompose f and g, respectively.
(2) The new SDS vectors are as follows:
From these two new SDS vectors, the following can be seen: (1) the phases of all variables are determined; and (2) all unidentified variables can be identified from their Boolean differences. A candidate transformation is generated, and this T is verified to be correct.
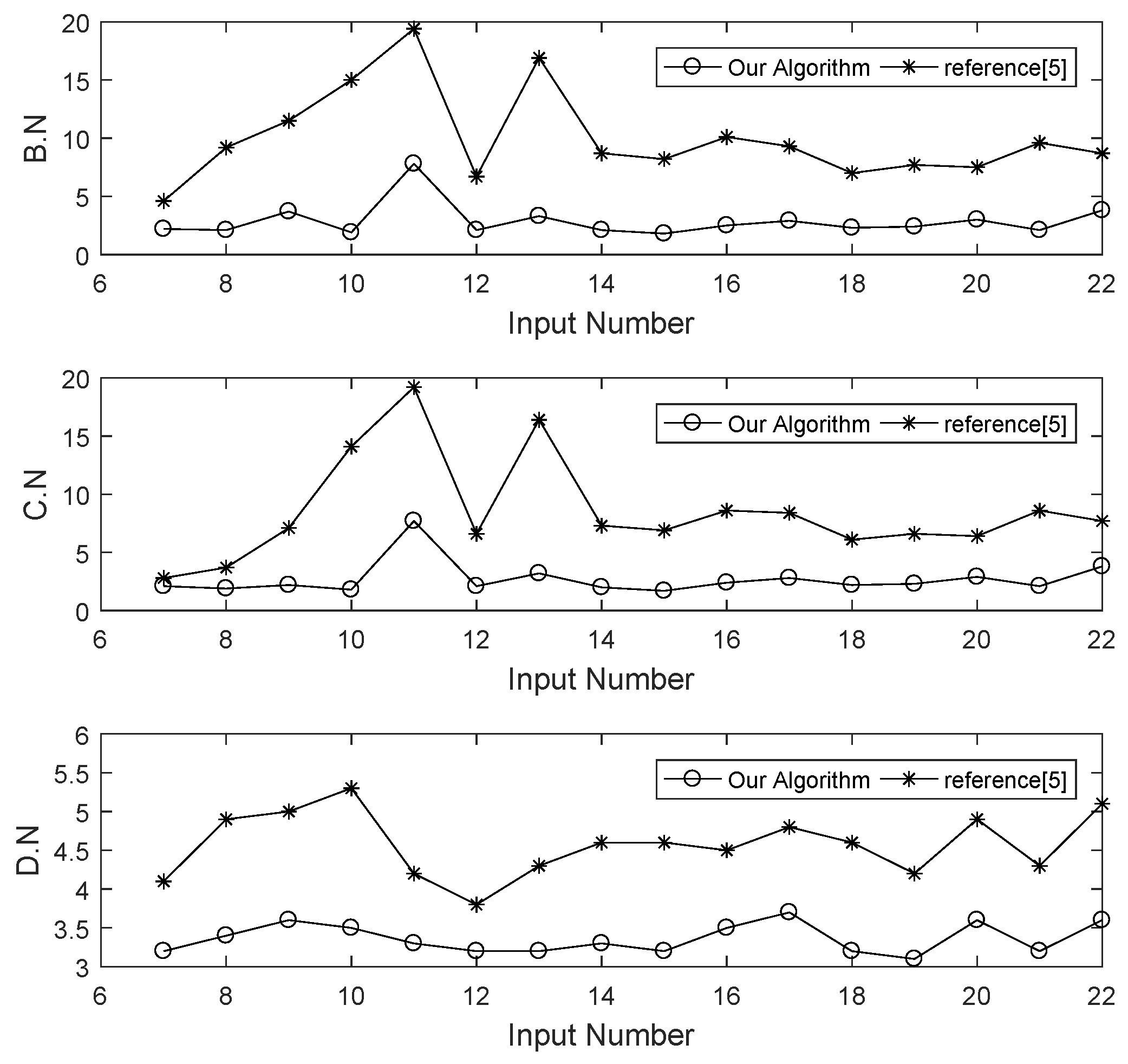
When SDS vectors are used to perform Boolean matching, the transformation tree for Example 3 contains only one candidate transformation. In the transformation detection process, the search space comprises all branches of the transformation tree, including unabridged and abridged branches. The unabridged branches are the candidate transformations, and the abridged branches are the pruned transformations. When the transformation tree possesses fewer branches, the algorithm considers a smaller search space. The purpose of decomposing the Boolean functions is to update the SDS vectors to search the new variable mappings. When the algorithm requires fewer decompositions, more variables are identified in each iteration. These three indicators can be used to measure how much of the search space our algorithm searches.
In the best case, the variable mapping set of every variable is a single-mapping set, and there is only one candidate transformation. In this case, the spatial complexity is , and the time complexity is . In the worst case, there are no symmetric variables, every variable has the same SDS value, and the phases of all variables cannot be determined in each SDS update. There are candidate transformations that need to be verified. The spatial complexity is , and the time complexity is .