Some Results on Multigranulation Neutrosophic Rough Sets on a Single Domain

Abstract

As a generalization of single value neutrosophic rough sets, the concept of multi-granulation neutrosophic rough sets was proposed by Bo et al., and some basic properties of the pessimistic (optimistic) multigranulation neutrosophic rough approximation operators were studied. However, they did not do a comprehensive study on the algebraic structure of the pessimistic (optimistic) multigranulation neutrosophic rough approximation operators. In the present paper, we will provide the lattice structure of the pessimistic multigranulation neutrosophic rough approximation operators. In particular, in the one-dimensional case, for special neutrosophic relations, the completely lattice isomorphic relationship between upper neutrosophic rough approximation operators and lower neutrosophic rough approximation operators is proved.

1. Introduction

In order to deal with imprecise information and inconsistent knowledge, Smarandache [1,2] first introduced the notion of neutrosophic set by fusing a tri-component set and the non-standard analysis. A neutrosophic set consists of three membership functions, where every function value is a real standard or non-standard subset of the nonstandard unit interval $]0^{-},1^{+}[$. Since then, many authors have studied various aspects of neutrosophic sets from different points of view, for example, in order to apply the neutrosophic idea to logics, Rivieccio [3] proposed neutrosophic logics which is a generalization of fuzzy logics and studied some basic properties. Guo and Cheng [4] and Guo and Sengur [5] obtained good applications in cluster analysis and image processing by using neutrosophic sets. Salama and Broumi [6] and Broumi and Smarandache [7] first introduced the concept of rough neutrosophic sets, handled incomplete and indeterminate information, and studied some operations and their properties.

In order to apply neutrosophic sets conveniently, Wang et al. [8] proposed single valued neutrosophic sets by simplifying neutrosophic sets. Single valued neutrosophic sets can also be viewed as a generalization of intuitionistic fuzzy sets (Atanassov [9]). Single valued neutrosophic sets have become a new majorly research issue. Ye [10,11,12] proposed decision making based on correlation coefficients and weighted correlation coefficient of single valued neutrosophic sets, and gave an application of proposed methods. Majumdar and Samant [13] studied similarity, distance and entropy of single valued neutrosophic sets from a theoretical aspect.

Şahin and Küçük [14] gave a subsethood measure of single valued neutrosophic sets based on distance and showed its effectiveness through an example. We know that there’s a certain connection among fuzzy rough approximation operators and fuzzy relations (resp., fuzzy topologies, information systems [15,16,17]). Hence, Yang et al. [18] firstly proposed neutrosophic relations and studied some kinds of kernels and closures of neutrosophic relations. Subsequently they proposed single valued neutrosophic rough sets [19] by fusing single valued neutrosophic sets and rough sets (Pawlak, [20]), and they studied some properties of single value neutrosophic upper and lower approximation operators. As a generalization of single value neutrosophic rough sets, Bao and Yang [21] introduced $p$-dimension single valued neutrosophic refined rough sets, and they also gave some properties of $p$-dimension single valued neutrosophic upper and lower approximation operators.

As another generalization of single value neutrosophic rough sets, Bo et al. [22] proposed the concept of multi-granulation neutrosophic rough sets and obtained some basic properties of the pessimistic (optimistic) multigranulation neutrosophic rough approximation operators. However, the lattice structures of those rough approximation operators in references [19,21,22], were not well studied. Following this idea, Zhao and Zhang [23] gave the supremum and infimum of the $p$-dimension neutrosophic upper and lower approximation operators, but they did not study the relationship between the $p$-dimension neutrosophic upper approximation operators and the $p$-dimension neutrosophic lower approximation operators, especially in the one-dimensional case. Inspired by paper [23], a natural problem is: Can the lattice structure of pessimistic (optimistic) multigranulation neutrosophic approximation operators be given?

In the present paper, we study the algebraic structure of optimistic (pessimistic) multigranulation single valued neutrosophic approximation operators.

The structure of the paper is organized as follows. The next section reviews some basic definitions of neutrosophic sets and one-dimensional multi-granulation rough sets. In Section 3, the lattice structure of the pessimistic multigranulation neutrosophic rough approximation operators are studied. In Section 4, for special neutrosophic relations, a one-to-one correspondence relationship between neutrosophic upper approximation operators and lower approximation operators is given. Finally, Section 5 concludes this article and points out the deficiencies of the current research.

2. Preliminaries

In this section, we briefly recall several definitions of neutrosophic set (here “neutrosophic set” refers exclusively to “single value neutrosophic set”) and one-dimensional multi-granulation rough set.

Definition 1

([8]). A neutrosophic set $B$ in $X$ is defined as follows: $\forall a\in X$,

$$B=(T_A(a),I_A(a),F_A(a)),$$

where $T_A(a)$, $I_A(a)$, $F_A(a)\in [0,1]$, $0\le \sup T_A(a)+\sup I_A(a)+\sup F_A(a)\le 3$. The set of all neutrosophic sets on $X$ will be denoted by $\mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$.

Definition 2

([11]). Let $C$ and $D$ be two neutrosophic sets in $X$, if

$$T_C(a)\le T_D(a),I_C(a)\ge I_D(a)and{F}_C(a)\ge F_D(a)$$

for each $a\in X$, then we called $C$ is contained in $D$, i.e., $C⋐D$. If $C⋐D$ and $D⋐C$, then we called $C$ is equal to $D$, denoted by $C=D$.

Definition 3

([18]). Let $A$ and $B$ be two neutrosophic sets in $X$,

(1) 

The union of$A$and$B$is a s neutrosophic set$C$, denoted by$A⋓B$, where$\forall x\in X$,

$$\begin{array}{c}{T}_C(a)=max\{T_A(a),T_B(a)\},I_C(a)=min\{I_A(a),I_B(a)\},and\\ F_C(a)=min\{F_A(a),F_B(a)\}.\end{array}$$

(2) 

The intersection of$A$and$B$is a neutrosophic set$D$, denoted by$A⋒B$, where$\forall x\in X$,

$$\begin{array}{c}{T}_D(a)=min\{T_A(a),T_B(a)\},I_D(a)=max\{I_A(a),I_B(a)\},and\\ F_D(a)=max\{F_A(a),F_B(a)\}.\end{array}$$

Definition 4

([18]). A neutrosophic relation $R$ in $X$ is defined as follows:

$$R=\{<(a,b),T_R(a,b),I_R(a,b),F_R(a,b)>\mid (a,b)\in X\times X\},$$

where $T_R:X\times X\to [0,1],I_R:X\times X\to [0,1],F_R:X\times X\to [0,1]$, and

$$0\le \sup T_R(a,b)+\sup I_R(a,b)+\sup F_R(a,b)\le 3.$$

The family of all neutrosophic relations in X will be denoted by$SVNR(X)$, and the pair$(X,R)$is called a neutrosophic approximation space.

Definition 5

([19]). Let $(X,R)$ be a neutrosophic approximation space, $\forall A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$, the lower and upper approximations of $A$ with respect to $(X,R)$, denoted by $\underset{\_}{R}(A)$ and $\overline{R}(A)$, are two neutrosophic sets whose membership functions are defined as: $\forall a\in X$,

$$T_{\underset{\_}{R}(A)}(a)=\underset{b\in X}{\wedge }\left[F_R(a,b)\vee T_A(b)\right],I_{\underset{\_}{R}(A)}(a)=\underset{b\in X}{\vee }\left[(1-I_R(a,b))\wedge I_A(b)\right],$$

$$F_{\underset{\_}{R}(A)}(a)=\underset{b\in X}{\vee }\left[T_R(a,b)\wedge F_A(b)\right],T_{\overline{R}(A)}(a)=\underset{b\in X}{\vee }\left[T_R(a,b)\wedge T_A(b)\right],$$

$$I_{\overline{R}(A)}(a)=\underset{b\in X}{\wedge }\left[I_R(a,b)\vee I_A(b)\right],F_{\overline{R}(A)}(a)=\underset{b\in X}{\wedge }\left[F_R(a,b)\vee F_A(b)\right].$$

The pair$(\underset{\_}{R}(A),\overline{R}(A))$is called the one-dimensional multi-granulation rough set (also called single value neutrosophic rough set or one-dimension single valued neutrosophic refined rough set) of A with respect to$(X,R)$.$\underset{\_}{R}$and$\overline{R}$are referred to as the neutrosophic lower and upper approximation operators,respectively.

Lemma 1

([19]). Let $R_1$ and $R_2$ be two neutrosophic relations in $X$, $\forall A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$, we have

(1) 

$\underset{\_}{R_1⋓R_2}(A)=\underset{\_}{R_1}(A)⋒\underset{\_}{R_2}(A)$;

(2) 

$\overline{R_1⋓R_2}(A)=\overline{R_1}(A)⋓\overline{R_2}(A)$;

(3) 

$\underset{\_}{R_1⋒R_2}(A)⋑\underset{\_}{R_1}(A)⋓\underset{\_}{R_2}(A)⋑\underset{\_}{R_1}(A)⋒\underset{\_}{R_2}(A)$;

(4) 

$\overline{R_1⋒R_2}(A)⋐\overline{R_1}(A)⋒\overline{R_2}(A).$

3. The Lattice Structure of the Pessimistic Multigranulation Neutrosophic Rough Approximation Operators

In this section, set $M=\{R_1,R_2,\cdots ,R_n\}={\left\{R_i\right\}}_{i=\overline{1,n}}$ is called a multigranulation neutrosophic relations set on $X$ if each $R_i$ is a neutrosophic relation on $X$. In this case, the pair $(X,M)$ will be called an $n$-dimensional multigranulation neutrosophic apptoximation space.

Definition 6

([22]). Let $(X,M)$ be an $n$-dimensional multigranulation neutrosophic apptoximation space. We define two pairs of approximation operators as follows, for all $\forall A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$ and $a\in X$,

$$M^O(A)=({\underset{\_}{M}}^O(A),{\overline{M}}^O(A)),M^P(A)=({\underset{\_}{M}}^P(A),{\overline{M}}^P(A)),$$

where

$$T_{{\underset{\_}{M}}^O(A)}(a)={\vee }_{i=1}^n{T}_{\underset{\_}{R_i}(A)}(a),I_{{\underset{\_}{M}}^O(A)}(a)={\wedge }_{i=1}^n{I}_{\underset{\_}{R_i}(A)}(a),F_{{\underset{\_}{M}}^O(A)}(a)={\wedge }_{i=1}^n{F}_{\underset{\_}{R_i}(A)}(a).$$

$$T_{{\overline{M}}^O(A)}(a)={\wedge }_{i=1}^n{T}_{\overline{R_i}(A)}(a),I_{{\overline{M}}^O(A)}(a)={\vee }_{i=1}^n{I}_{\overline{R_i}(A)}(a),F_{{\overline{M}}^O(A)}(a)={\vee }_{i=1}^n{F}_{\overline{R_i}(A)}(a).$$

$$T_{{\underset{\_}{M}}^P(A)}(a)={\wedge }_{i=1}^n{T}_{\underset{\_}{R_i}(A)}(a), I_{{\underset{\_}{M}}^P(A)}(a)={\vee }_{i=1}^n{I}_{\underset{\_}{R_i}(A)}(a), F_{{\underset{\_}{M}}^P(A)}(a)={\vee }_{i=1}^n{F}_{\underset{\_}{R_i}(A)}(a).$$

$$T_{{\overline{M}}^P(A)}(a)={\vee }_{i=1}^n{T}_{\overline{R_i}(A)}(a), I_{{\overline{M}}^P(A)}(a)={\wedge }_{i=1}^n{I}_{\overline{R_i}(A)}(a), F_{{\overline{M}}^P(A)}(a)={\wedge }_{i=1}^n{F}_{\overline{R_i}(A)}(a).$$

Then the pair$M^O(A)=({\underset{\_}{M}}^O(A),{\overline{M}}^O(A))$is called an optismistic multigranulation neutrosophic rough set, and the pair$M^P(A)=({\underset{\_}{M}}^P(A),{\overline{M}}^P(A))$is called an pessimistic multigranulation neutrosophic rough set${\overline{M}}^O$and${\overline{M}}^P$are referred to as the optimistic and pessimistic multigranulation neutrosophic upper approximation operators, respectively. Similarly,${\underset{\_}{M}}^O$and${\underset{\_}{M}}^P$are referred to as the optimistic and pessimistic multigranulation neutrosophic lower approximation operators, respectively.

Remark 1.

If$n=1$, then the multigranulation neutrosophic rough set will degenerated to a one-dimensional multi-granulation rough set (see Definition 5). In the following, the family of all multigranulation neutrosophic relations set on$X$will be denoted by$n-SVNR(X)$. Defined a relation$⊑$on$n-SVNR(X)$as follows:$M⊑N$if and only if$M_i⋐N_i$, then$(n-SVNR(X),⊑)$is a poset, where$M={\left\{M_i\right\}}_{i=\overline{1,n}}$and$N={\left\{N_i\right\}}_{i=\overline{1,n}}$.

$\forall {\left\{M^j\right\}}_{j\in \mathsf{\Lambda }}\subseteq n-SVNR(X)$, where$M^j={\left\{M_i^j\right\}}_{i=\overline{1,n}}$and$\mathsf{\Lambda }$be a index set, we can define union and intersection of$M^j$as follows:

$$\underset{j\in \mathsf{\Lambda }}{\vee }{M}^j={\left\{{⋓}_{j\in \mathsf{\Lambda }}{M}_i^j\right\}}_{i=\overline{1,n}},\underset{j\in \mathsf{\Lambda }}{\wedge }{M}^j={\left\{{⋒}_{j\in \mathsf{\Lambda }}{M}_i^j\right\}}_{i=\overline{1,n}},$$

where

$$\begin{array}{c}{T}_{{⋓}_{j\in \mathsf{\Lambda }}{M}_i^j}(a,b)=\underset{j\in \mathsf{\Lambda }}{\vee }{T}_{M_i^j}(a,b), I_{{⋓}_{j\in \mathsf{\Lambda }}{M}_i^j}(a,b)=\underset{j\in \mathsf{\Lambda }}{\wedge }{I}_{M_i^j}(a,b),\\ F_{{⋓}_{j\in \mathsf{\Lambda }}{M}_i^j}(a,b)=\underset{j\in \mathsf{\Lambda }}{\wedge }{F}_{M_i^j}(a,b),T_{{⋒}_{j\in \mathsf{\Lambda }}{M}_i^j}(a,b)=\underset{j\in \mathsf{\Lambda }}{\wedge }{T}_{M_i^j}(a,b),\\ I_{{⋒}_{j\in \mathsf{\Lambda }}{M}_i^j}(a,b)=\underset{j\in \mathsf{\Lambda }}{\vee }{I}_{M_i^j}(a,b),F_{{⋒}_{j\in \mathsf{\Lambda }}{M}_i^j}(a,b)=\underset{j\in \mathsf{\Lambda }}{\vee }{F}_{M_i^j}(a,b).\end{array}$$

Then$\underset{j\in \mathsf{\Lambda }}{\vee }{M}^j$and$\underset{j\in \mathsf{\Lambda }}{\wedge }{M}^j$are two multigranulation neutrosophic relations on$X$, and we easily show that$\underset{j\in \mathsf{\Lambda }}{\vee }{M}^j$and$\underset{j\in \mathsf{\Lambda }}{\wedge }{M}^j$are infimum and supremum of${\left\{M^j\right\}}_{j\in \mathsf{\Lambda }}$, respectively. Hence we can easily obtain the following theorem:

Theorem 1.

$(n-SVNR(X),⊑，\wedge ,\vee )$is a complete lattice,$\widetilde{X_n}=\{\underset{n}{\underbrace{X_n,X_n,\cdots ,X_n}}\}$and$\widetilde{{\varnothing }_N}=\{\underset{n}{\underbrace{{\varnothing }_N,{\varnothing }_N,\cdots ,{\varnothing }_N}}\}$are its top element and bottom element, respectively, where$X_n$and${\varnothing }_N$are two neutrosophic relations in$X$and defined as follows:$\forall (a,b)\in X\times X$,$T_{X_N}(a,b)=1$,$I_{X_N}(a,b)=0$,$F_{X_N}(a,b)=0$and$T_{{\varnothing }_N}(a,b)=0$,$I_{{\varnothing }_N}(a,b)=1$,$F_{{\varnothing }_N}(a,b)=1$. In particular,$(SVNR(X),⋐,⋓,⋒)$is a complete lattice.

Theorem 2.

Let$M={\left\{R_i\right\}}_{i=\overline{1,n}}$and$N={\left\{Q_i\right\}}_{i=\overline{1,n}}$be two multigranulation neutrosophic relations set on$X$,$\forall A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$, we have

(1) 

${\underset{\_}{M\vee N}}^O(A)⋐{\underset{\_}{M}}^O(A)⋒{\underset{\_}{N}}^O(A)$,${\underset{\_}{M\vee N}}^P(A)={\underset{\_}{M}}^P(A)⋒{\underset{\_}{N}}^P(A)$;

(2) 

${\overline{M\vee N}}^O(A)⋑{\overline{M}}^O(A)⋓{\overline{N}}^O(A)$,${\overline{M\vee N}}^P(A)={\overline{M}}^P(A)⋓{\overline{N}}^P(A)$;

(3) 

${\underset{\_}{M\wedge N}}^O(A)⋑{\underset{\_}{M}}^O(A)⋓{\underset{\_}{N}}^O(A)⋑{\underset{\_}{M}}^O(A)⋒{\underset{\_}{N}}^O(A)$,

${\underset{\_}{M\wedge N}}^P(A)⋑{\underset{\_}{M}}^P(A)⋓{\underset{\_}{N}}^P(A)⋑{\underset{\_}{M}}^P(A)⋒{\underset{\_}{N}}^P(A)$;

(4) 

${\overline{M\wedge N}}^O(A)⋐{\overline{M}}^O(A)⋒{\overline{N}}^O(A)$,${\overline{M\wedge N}}^P(A)⋐{\overline{M}}^P(A)⋒{\overline{N}}^P(A).$

Proof. 

We only show that the case of the optimistic multigranulation neutrosophic approximation operators.

(1)

$\forall a\in X$, by Lemma 1 and Definition 6, we have the following:

$$\begin{array}{l}{T}_{{\underset{\_}{M\vee N}}^O(A)}(a)\hfill \\ ={\vee }_{i=1}^n{T}_{\underset{\_}{R_i⋓Q_i}(A)}(a)={\vee }_{i=1}^n{T}_{\underset{\_}{R_i}(A)⋒\underset{\_}{Q_i}(A)}(a)\hfill \\ ={\vee }_{i=1}^n\left[T_{\underset{\_}{R_i}(A)}(a)\wedge T_{\underset{\_}{Q_i}(A)}(a)\right]\hfill \\ \le \left[{\vee }_{i=1}^n{T}_{\underset{\_}{R_i}(A)}(a)\right]\wedge \left[{\vee }_{i=1}^n{T}_{\underset{\_}{Q_i}(A)}(a)\right]\hfill \\ =T_{{\underset{\_}{M}}^O(A)}(a)\wedge T_{{\underset{\_}{N}}^O(A)}(a)\hfill \\ =T_{{\underset{\_}{M}}^O(A)⋒{\underset{\_}{N}}^O(A)}(a),\hfill \end{array}$$

$$\begin{array}{l}{I}_{{\underset{\_}{M\vee N}}^O(A)}(a)\hfill \\ ={\wedge }_{i=1}^n{I}_{\underset{\_}{R_i⋓Q_i}(A)}(a)={\wedge }_{i=1}^n{I}_{\underset{\_}{R_i}(A)⋒\underset{\_}{Q_i}(A)}(a)\hfill \\ ={\wedge }_{i=1}^n\left[I_{\underset{\_}{R_i}(A)}(a)\vee I_{\underset{\_}{Q_i}(A)}(a)\right]\hfill \\ \ge \left[{\wedge }_{i=1}^n{I}_{\underset{\_}{R_i}(A)}(a)\right]\vee \left[{\wedge }_{i=1}^n{I}_{\underset{\_}{Q_i}(A)}(a)\right]\hfill \\ =I_{{\underset{\_}{M}}^O(A)}(a)\vee I_{{\underset{\_}{N}}^O(A)}(a)\hfill \\ =I_{{\underset{\_}{M}}^O(A)⋒{\underset{\_}{N}}^O(A)}(a),\hfill \end{array}$$

$$\begin{array}{l}{F}_{{\underset{\_}{M\vee N}}^O(A)}(a)\hfill \\ ={\wedge }_{i=1}^n{F}_{\underset{\_}{R_i⋓Q_i}(A)}(a)={\wedge }_{i=1}^n{F}_{\underset{\_}{R_i}(A)⋒\underset{\_}{Q_i}(A)}(a)\hfill \\ ={\wedge }_{i=1}^n\left[F_{\underset{\_}{R_i}(A)}(a)\vee F_{\underset{\_}{Q_i}(A)}(a)\right]\hfill \\ \ge \left[{\wedge }_{i=1}^n{F}_{\underset{\_}{R_i}(A)}(a)\right]\vee \left[{\wedge }_{i=1}^n{F}_{\underset{\_}{Q_i}(A)}(a)\right]\hfill \\ =F_{{\underset{\_}{M}}^O(A)}(a)\vee F_{{\underset{\_}{N}}^O(A)}(a)\hfill \\ =F_{{\underset{\_}{M}}^O(A)⋒{\underset{\_}{N}}^O(A)}(a).\hfill \end{array}$$

Hence, ${\underset{\_}{M\vee N}}^O(A)⋐{\underset{\_}{M}}^O(A)⋒{\underset{\_}{N}}^O(A)$.

(2)

$\forall a\in X$, by Lemma 1 and Definition 6, we have the following:

$$\begin{array}{l}{T}_{{\overline{M\vee N}}^O(A)}(a)\hfill \\ ={\wedge }_{i=1}^n{T}_{\overline{R_i⋓Q_i}(A)}(a)={\wedge }_{i=1}^n{T}_{\overline{R_i}(A)⋓\overline{Q_i}(A)}(a)\hfill \\ ={\wedge }_{i=1}^n\left[T_{\overline{R_i}(A)}(a)\vee T_{\overline{Q_i}(A)}(a)\right]\hfill \\ \ge \left[{\wedge }_{i=1}^n{T}_{\overline{R_i}(A)}(a)\right]\vee \left[{\wedge }_{i=1}^n{T}_{\overline{Q_i}(A)}(a)\right]\hfill \\ =T_{{\overline{M}}^O(A)}(a)\vee T_{{\overline{N}}^O(A)}(a)=T_{{\overline{M}}^O(A)⋓{\overline{N}}^O(A)}(a),\hfill \end{array}$$

$$\begin{array}{l}{I}_{{\overline{M\vee N}}^O(A)}(a)\hfill \\ ={\vee }_{i=1}^n{I}_{\overline{R_i⋓Q_i}(A)}(a)={\vee }_{i=1}^n{I}_{\overline{R_i}(A)⋓\overline{Q_i}(A)}(a)\hfill \\ ={\vee }_{i=1}^n\left[I_{\overline{R_i}(A)}(a)\wedge I_{\overline{Q_i}(A)}(a)\right]\hfill \\ \le \left[{\vee }_{i=1}^n{I}_{\overline{R_i}(A)}(a)\right]\wedge \left[{\vee }_{i=1}^n{I}_{\overline{Q_i}(A)}(a)\right]\hfill \\ =I_{{\overline{M}}^O(A)}(a)\wedge I_{{\overline{N}}^O(A)}(a)=I_{{\overline{M}}^O(A)⋓{\overline{N}}^O(A)}(a),\hfill \end{array}$$

$$\begin{array}{l}{F}_{{\overline{M\vee N}}^O(A)}(a)\hfill \\ ={\vee }_{i=1}^n{F}_{\overline{R_i⋓Q_i}(A)}(a)={\vee }_{i=1}^n{F}_{\overline{R_i}(A)⋓\overline{Q_i}(A)}(a)\hfill \\ ={\vee }_{i=1}^n\left[F_{\overline{R_i}(A)}(a)\wedge F_{\overline{Q_i}(A)}(a)\right]\hfill \\ \le \left[{\vee }_{i=1}^n{F}_{\overline{R_i}(A)}(a)\right]\wedge \left[{\vee }_{i=1}^n{F}_{\overline{Q_i}(A)}(a)\right]\hfill \\ =F_{{\overline{M}}^O(A)}(a)\wedge F_{{\overline{N}}^O(A)}(a)=F_{{\overline{M}}^O(A)⋓{\overline{N}}^O(A)}(a).\hfill \end{array}$$

Hence, ${\overline{M\vee N}}^O(A)⋑{\overline{M}}^O(A)⋓{\overline{N}}^O(A)$.

(3)

$\forall a\in X$, by Lemma 1 and Definition 6, we have the following:

$$\begin{array}{l}{T}_{{\underset{\_}{M\wedge N}}^O(A)}(a)\hfill \\ ={\vee }_{i=1}^n{T}_{\underset{\_}{R_i⋒Q_i}(A)}(a)\ge {\vee }_{i=1}^n{T}_{\underset{\_}{R_i}(A)⋓\underset{\_}{Q_i}(A)}(a)\hfill \\ ={\vee }_{i=1}^n\left[T_{\underset{\_}{R_i}(A)}(a)\vee T_{\underset{\_}{Q_i}(A)}(a)\right]\hfill \\ =\left[{\vee }_{i=1}^n{T}_{\underset{\_}{R_i}(A)}(a)\right]\vee \left[{\vee }_{i=1}^n{T}_{\underset{\_}{Q_i}(A)}(a)\right]\hfill \\ =T_{{\underset{\_}{M}}^O(A)}(a)\vee T_{{\underset{\_}{N}}^O(A)}(a)\ge T_{{\underset{\_}{M}}^O(A)}(a)\wedge T_{{\underset{\_}{N}}^O(A)}(a),\hfill \end{array}$$

$$\begin{array}{l}{I}_{{\underset{\_}{M\wedge N}}^O(A)}(a)\hfill \\ ={\wedge }_{i=1}^n{I}_{\underset{\_}{R_i⋒Q_i}(A)}(a)\le {\wedge }_{i=1}^n{I}_{\underset{\_}{R_i}(A)⋓\underset{\_}{Q_i}(A)}(a)\hfill \\ ={\wedge }_{i=1}^n\left[I_{\underset{\_}{R_i}(A)}(a)\wedge I_{\underset{\_}{Q_i}(A)}(a)\right]\hfill \\ =\left[{\wedge }_{i=1}^n{I}_{\underset{\_}{R_i}(A)}(a)\right]\wedge \left[{\wedge }_{i=1}^n{I}_{\underset{\_}{Q_i}(A)}(a)\right]\hfill \\ =I_{{\underset{\_}{M}}^O(A)}(a)\wedge I_{{\underset{\_}{N}}^O(A)}(a)\le I_{{\underset{\_}{M}}^O(A)}(a)\vee I_{{\underset{\_}{N}}^O(A)}(a),\hfill \end{array}$$

$$\begin{array}{l}{F}_{{\underset{\_}{M\wedge N}}^O(A)}(a)\hfill \\ ={\wedge }_{i=1}^n{F}_{\underset{\_}{R_i⋒Q_i}(A)}(a)\le {\wedge }_{i=1}^n{F}_{\underset{\_}{R_i}(A)⋓\underset{\_}{Q_i}(A)}(a)\hfill \\ ={\wedge }_{i=1}^n\left[F_{\underset{\_}{R_i}(A)}(a)\wedge F_{\underset{\_}{Q_i}(A)}(a)\right]\hfill \\ =\left[{\wedge }_{i=1}^n{F}_{\underset{\_}{R_i}(A)}(a)\right]\wedge \left[{\wedge }_{i=1}^n{F}_{\underset{\_}{Q_i}(A)}(a)\right]\hfill \\ =F_{{\underset{\_}{M}}^O(A)}(a)\wedge F_{{\underset{\_}{N}}^O(A)}(a)\le F_{{\underset{\_}{M}}^O(A)}(a)\vee F_{{\underset{\_}{N}}^O(A)}(a).\hfill \end{array}$$

Hence, ${\underset{\_}{M\wedge N}}^o(A)⋑{\underset{\_}{M}}^o(A)⋓{\underset{\_}{N}}^o(A)⋑{\underset{\_}{M}}^o(A)⋒{\underset{\_}{N}}^o(A).$

(4)

$\forall a\in X$, by Lemma 1 and Definition 6, we have the following:

$$\begin{array}{l}{T}_{{\overline{M\wedge N}}^O(A)}(a)\hfill \\ ={\wedge }_{i=1}^n{T}_{\overline{R_i⋒Q_i}(A)}(a)\le {\wedge }_{i=1}^n{T}_{\overline{R_i}(A)⋒\overline{Q_i}(A)}(a)\hfill \\ ={\wedge }_{i=1}^n\left[T_{\overline{R_i}(A)}(a)\wedge T_{\overline{Q_i}(A)}(a)\right]\hfill \\ =\left[{\wedge }_{i=1}^n{T}_{\overline{R_i}(A)}(a)\right]\wedge \left[{\wedge }_{i=1}^n{T}_{\overline{Q_i}(A)}(a)\right]\hfill \\ =T_{{\overline{M}}^O(A)}(a)\wedge T_{{\overline{N}}^O(A)}(a)=T_{{\overline{M}}^O(A)⋒{\overline{N}}^O(A)}(a),\hfill \end{array}$$

$$\begin{array}{l}{I}_{{\overline{M\wedge N}}^O(A)}(a)\hfill \\ ={\vee }_{i=1}^n{I}_{\overline{R_i⋒Q_i}(A)}(a)\ge {\vee }_{i=1}^n{I}_{\overline{R_i}(A)⋒\overline{Q_i}(A)}(a)\hfill \\ ={\vee }_{i=1}^n\left[I_{\overline{R_i}(A)}(a)\vee I_{\overline{Q_i}(A)}(a)\right]\hfill \\ =\left[{\vee }_{i=1}^n{I}_{\overline{R_i}(A)}(a)\right]\vee \left[{\vee }_{i=1}^n{I}_{\overline{Q_i}(A)}(a)\right]\hfill \\ =I_{{\overline{M}}^O(A)}(a)\vee T_{{\overline{N}}^O(A)}(a)=I_{{\overline{M}}^O(A)⋒{\overline{N}}^O(A)}(a),\hfill \end{array}$$

$$\begin{array}{l}{F}_{{\overline{M\wedge N}}^O(A)}(a)\hfill \\ ={\vee }_{i=1}^n{F}_{\overline{R_i⋒Q_i}(A)}(a)\ge {\vee }_{i=1}^n{F}_{\overline{R_i}(A)⋒\overline{Q_i}(A)}(a)\hfill \\ ={\vee }_{i=1}^n\left[F_{\overline{R_i}(A)}(a)\vee F_{\overline{Q_i}(A)}(a)\right]\hfill \\ =\left[{\vee }_{i=1}^n{F}_{\overline{R_i}(A)}(a)\right]\vee \left[{\vee }_{i=1}^n{F}_{\overline{Q_i}(A)}(a)\right]\hfill \\ =F_{{\overline{M}}^O(A)}(a)\vee F_{{\overline{N}}^O(A)}(a)=F_{{\overline{M}}^O(A)⋒{\overline{N}}^O(A)}(a).\hfill \end{array}$$

Hence, ${\overline{M\wedge N}}^O(A)⋐{\overline{M}}^O(A)⋒{\overline{N}}^O(A).$ □

From Theorem 2, we can easily obtain the following corollary:

Corollary 1.

Let$M={\left\{R_i\right\}}_{i=\overline{1,n}}$and$N={\left\{Q_i\right\}}_{i=\overline{1,n}}$be two multigranulation neutrosophic relations set on$X$. If$M⊑N$, then$\forall A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$,

$${\underset{\_}{N}}^O(A)⋐{\underset{\_}{M}}^O(A),{\underset{\_}{N}}^P(A)⋐{\underset{\_}{M}}^P(A)),{\overline{M}}^O(A)⋐{\overline{N}}^O(A),{\overline{M}}^P(A)⋐{\overline{N}}^P(A).$$

Let $H_n^P=\{{\overline{M}}^P\mid M\in n-SVNR(X)\}$ and $L_n^P=\{{\underset{\_}{M}}^P\mid M\in n-SVNR(X)\}$ be the set of pessimistic multigranulation neutrosophic upper and lower approximation operators in $X$, respectively.

• Defined a relation $\widehat{\le }$ on $H_n^P$ as follows: ${\overline{M}}^P\widehat{\le }{\overline{N}}^P$ if and only if ${\overline{M}}^P(A)⋐{\overline{N}}^P(A)$ for each $A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$. Then $(H_n^P,\widehat{\le })$ is a poset.
• Defined a relation $\widehat{\le }$ on $L_n^P$ as follows: ${\underset{\_}{M}}^P\widehat{\le }{\underset{\_}{N}}^P$ if and only if ${\underset{\_}{N}}^P(A)⋐{\underset{\_}{M}}^P(A)$ for each $A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$. Then $(L_n^P,\widehat{\le })$ is a poset.

Let $H_n^O=\{{\overline{M}}^O\mid M\in n-SVNR(X)\}$ and $L_n^O=\{{\underset{\_}{M}}^O\mid M\in n-SVNR(X)\}$ be the set of optimistic multigranulation neutrosophic upper and lower approximation operators in $X$, respectively.

• Defined a relation $\widehat{\le }$ on $H_n^O$ as follows: ${\overline{M}}^O\widehat{\le }{\overline{N}}^O$ if and only if ${\overline{M}}^O(A)⋐{\overline{N}}^O(A)$ for each $A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$. Then $(H_n^O,\widehat{\le })$ is a poset.
• Defined a relation $\widehat{\le }$ on $L_n^O$ as follows: ${\underset{\_}{M}}^O\widehat{\le }{\underset{\_}{N}}^O$ if and only if ${\underset{\_}{N}}^O(A))⋐{\underset{\_}{M}}^O(A)$ for each $A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$. Then $(L_n^O,\widehat{\le })$ is a poset.

Theorem 3.

(1)$\forall {\left\{{\overline{M}}_i^P\right\}}_{i\in I}\subseteq$$(H_n^P,\widehat{\le })$and$I$be a index set, we can define union and intersection of${\overline{M}}_i^P$as follows:

$$\widehat{\underset{i\in I}{{\displaystyle \vee }}}{\overline{M}}_i^P={\overline{\underset{i\in I}{{\displaystyle \vee }}{M}_i}}^P,\widehat{\underset{i\in I}{{\displaystyle \wedge }}}{\overline{M}}_i^P={\overline{[\underset{i\in I}{{\displaystyle \wedge }}{M}_i]}}^P,$$

where$[\underset{i\in I}{{\displaystyle \wedge }}{M}_i]=\vee \{M\in n-SVNR(X)\mid \forall A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X),{\overline{M}}^P(A)⋐{⋒}_{i\in I}{\overline{M}}_i^P(A)\}.$Then$\widehat{\underset{i\in I}{{\displaystyle \vee }}}{\overline{M}}_i^P$and$\widehat{\underset{i\in I}{{\displaystyle \wedge }}}{\overline{M}}_i^P$are supremum and infimum of${\left\{{\overline{M}}_i^P\right\}}_{i\in I}$, respectively.

(2)$\forall {\left\{{\underset{\_}{M}}_i^P\right\}}_{i\in I}\subseteq$$(L_n^P,\widehat{\le })$and$I$be a index set, we can define union and intersection of${\underset{\_}{M}}_i^P$as follows:

$$\widehat{\underset{i\in I}{{\displaystyle \vee }}}{\underset{\_}{M}}_i^P={\underset{\_}{\underset{i\in I}{{\displaystyle \vee }}{M}_i}}^P,\widehat{\underset{i\in I}{{\displaystyle \wedge }}}{\underset{\_}{M}}_i^P={\underset{\_}{[\underset{i\in I}{{\displaystyle \vee }}{M}_i]}}^P,$$

where$[\underset{i\in I}{{\displaystyle \vee }}{M}_i]=\vee \{M\in n-SVNR(X)\mid \forall A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X),{⋓}_{i\in I}{\underset{\_}{M}}_i^P(A)⋐{\underset{\_}{M}}^P(A)\}.$Then$\widehat{\underset{i\in I}{{\displaystyle \vee }}}{\underset{\_}{M}}_i^P$and$\widehat{\underset{i\in I}{{\displaystyle \wedge }}}{\underset{\_}{M}}_i^P$are supremum and infimum of${\left\{{\underset{\_}{M}}_i^P\right\}}_{i\in I}$, respectively.

Proof. 

We only show (1).

Let $M=\underset{i\in I}{{\displaystyle \vee }}{M}_i$, then $M_i⊑M$ for each $i\in I.$ By Corollary 1, we have ${\overline{M_i}}^P(A)⋐{\overline{M}}^P(A)$ for any $A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$. Thus ${\overline{M_i}}^P\widehat{\le }{\overline{M}}^P$. If $M^{\star }$ is a multigranulation neutrosophic relations set such that ${\overline{M_i}}^P\widehat{\le }{\overline{M^{\star }}}^P$ for each $i\in I$, then $A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$, ${\overline{M_i}}^P(A)⋐{\overline{M^{\star }}}^P(A)$. Hence,

$${\overline{M}}^P(A)={\overline{\underset{i\in I}{{\displaystyle \vee }}{M}_i}}^P(A)={⋓}_{i\in I}{\overline{M_i}}^P(A)⋐{\overline{M^{\star }}}^P(A).$$

Thus ${\overline{M}}^P\widehat{\le }{\overline{M^{\star }}}^P.$ So $\widehat{\underset{i\in I}{{\displaystyle \vee }}}{\overline{M}}_i^P={\overline{\underset{i\in I}{{\displaystyle \vee }}{M}_i}}^P$ is the supremum of ${\left\{{\overline{M}}_i^P\right\}}_{i\in I}$.

Let $Q=[\underset{i\in I}{{\displaystyle \wedge }}{M}_i]$, then $\forall B\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$, we have

$${\overline{Q}}^P(B)={\overline{[\underset{i\in I}{{\displaystyle \wedge }}{M}_i]}}^P(B)⋐{⋒}_{i\in I}{\overline{M}}_i^P(B)⋐{\overline{M}}_i^P(B).$$

Thus ${\overline{Q}}^P\widehat{\le }{\overline{M}}_i^P$ for each $i\in I$. If $M^{\ast }$ is a multigranulation neutrosophic relations set such that ${\overline{M^{\ast }}}^P\widehat{\le }{\overline{M}}_i^P$ for each $i\in I$, then

$${\overline{M^{\ast }}}^P(A)⋐{⋒}_{i\in I}{\overline{M}}_i^P(A).$$

By the construction of $[\underset{i\in I}{{\displaystyle \wedge }}{M}_i]$, we can easily obtain $M^{\ast }⊑[\underset{i\in I}{{\displaystyle \wedge }}{M}_i]=Q$. Hence,

$${\overline{M^{\ast }}}^P\widehat{\le }{\overline{[\underset{i\in I}{{\displaystyle \wedge }}{M}_i]}}^P={\overline{Q}}^P,$$

So $\widehat{\underset{i\in I}{{\displaystyle \wedge }}}{\overline{M}}_i^P={\overline{[\underset{i\in I}{{\displaystyle \wedge }}{M}_i]}}^P$ is the infimum of ${\left\{{\overline{M}}_i^P\right\}}_{i\in I}$. □

Remark 2.

(1)$\forall A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$, ∀a ∈ X, we can calculate that the following formula holds.

$$T_{{\overline{\widetilde{{\varnothing }_N}}}^P(A)}(a)=0,I_{{\overline{\widetilde{{\varnothing }_N}}}^P(A)}(a)=1,F_{{\overline{\widetilde{{\varnothing }_N}}}^P(A)}(a)=1,$$

$$T_{{\underset{\_}{\widetilde{{\varnothing }_N}}}^P(A)}(a)=1,I_{{\underset{\_}{\widetilde{{\varnothing }_N}}}^P(A)}(a)=0,F_{{\underset{\_}{\widetilde{{\varnothing }_N}}}^P(A)}(a)=0.$$

Hence,$\forall M\in n-SVNR(X)$,${\overline{\widetilde{{\varnothing }_N}}}^P(A)⋐{\overline{M}}^P(A)$and${\underset{\_}{M}}^P(A)⋐{\underset{\_}{\widetilde{{\varnothing }_N}}}^P(A)$. It shows that${\overline{\widetilde{{\varnothing }_N}}}^P\widehat{\le }{\overline{M}}^P$and${\underset{\_}{\widetilde{{\varnothing }_N}}}^P\widehat{\le }{\underset{\_}{M}}^P$, i.e.,${\overline{\widetilde{{\varnothing }_N}}}^P$is the bottom element of$(H_n^P,\widehat{\le })$and${\underset{\_}{\widetilde{{\varnothing }_N}}}^P$is the bottom element of$(L_n^P,\widehat{\le })$. By Theorem 3, we have the following result: Both$(H_n^P,\widehat{\le },\widehat{\wedge },\widehat{\vee })$and$(L_n^P,\widehat{\le },\widehat{\wedge },\widehat{\vee })$are complete lattices.

(2) Similarly, we can prove that both$(H_n^O,\widehat{\le },\widehat{\wedge },\widehat{\vee })$and$(L_n^O,\widehat{\le },\widehat{\wedge },\widehat{\vee })$are complete lattices if we can use the generalization formula of

$${\overline{M\vee N}}^O(A)⋐{\overline{M}}^O(A)⋓{\overline{N}}^O(A)and{\underset{\_}{M\vee N}}^O(A)⋑{\underset{\_}{M}}^O(A)⋒{\underset{\_}{N}}^O(A),$$

However, by Theorem 2, we known that

$${\overline{M\vee N}}^O(A)⋑{\overline{M}}^O(A)⋓{\overline{N}}^O(A) and {\underset{\_}{M\vee N}}^O(A)⋐{\underset{\_}{M}}^O(A)⋒{\underset{\_}{N}}^O(A).$$

So, naturally, there is the following problem:

How to give the supremum and infimum of the optimistic multigranulation neutrosophic rough approximation operators?

In the one-dimensional case, for convenience, we will use $H=\{\overline{R}\mid R\in SVNR(X)\}$ and $L=\{\underset{\_}{R}\mid R\in SVNR(X)\}$ to denote the set of neutrosophic upper and lower approximation operators in X, respectively. According to Lemma 1, Remark 2 and Theorem 3, we have the following result: both $(H,\le ,\wedge ,\vee )$ and $(L,\le ,\wedge ,\vee )$ are complete lattices (it is also the one-dimensional case of Reference [23]).

4. The Relationship between Complete Lattices $\mathbf{(}\mathit{H}\mathbf{,}\mathbf{\le }\mathbf{,}\mathbf{\wedge }\mathbf{,}\mathbf{\vee }\mathbf{)}$ and $\mathbf{(}\mathit{L}\mathbf{,}\mathbf{\le }\mathbf{,}\mathbf{\wedge }\mathbf{,}\mathbf{\vee }\mathbf{)}$

In this section, we will study the relationship between complete lattices $(H,\le ,\wedge ,\vee )$ and $(L,\le ,\wedge ,\vee )$. Set

$$\mathcal{A}=\{SVNR(X)\mid \forall R_1,R_2\in SVNR(X),\overline{R_1}\le \overline{R_2}\iff R_1⋐R_2\iff \underset{\_}{R_1}\le \underset{\_}{R_2}\}.$$

Firstly, we will give an example to illustrate that$\mathcal{A}$ is not an empty family.

Example 1.

Let$X=\left\{a\right\}$be a single point set,$R_1$and$R_2$are two single valued neutrosophic relations in$X$.

(1) 

If$\overline{R_1}\le \overline{R_2}$, then$R_1⋐R_2$. In fact, if$\overline{R_1}\le \overline{R_2}$, then$\overline{R_1}(A)⋐\overline{R_2}(A)$for each$A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(\{a\}).$

Thus, $\forall a\in X$,

$$T_{\overline{R_1}(A)}(a)\le T_{\overline{R_2}(A)}(a),I_{\overline{R_1}(A)}(a)\ge I_{\overline{R_2}(A)}(a),and{F}_{\overline{R_1}(A)}(a)\ge F_{\overline{R_2}(A)}(a).$$

Moreover,$T_{R_1}(a,a)\wedge T_A(a)\le T_{R_2}(a,a)\wedge T_A(a)$,$I_{R_1}(a,a)\vee I_A(a)\ge I_{R_2}(a,a)\vee I_A(a)$, and$F_{R_1}(a,a)\vee F_A(a)\ge F_{R_2}(a,a)\vee F_A(a).$Considering the arbitrariness of$A$, in particular, take$A=\{<a,(1,0,0)>\}$, we have$T_{R_1}(a,a)\le T_{R_2}(a,a)$,$I_{R_1}(a,a)\ge I_{R_2}(a,a)$and$F_{R_1}(a,a)\ge F_{R_2}(a,a).$

Hence,$R_1⋐R_2$.

Similarly, we also can show that the following result:

(2) 

If$\underset{\_}{R_1}\le \underset{\_}{R_2}$, then$R_1⋐R_2$.

So, by (1), (2) and Corollary 1, we have$SVNR(\{a\})\in \mathcal{A}$, i.e.,$\mathcal{A}$is not an empty family.

Now, we will give the relationship between complete lattices $(H,\le ,\wedge ,\vee )$ and $(L,\le ,\wedge ,\vee )$.

Proposition 1.

If$SVNR(X)\in \mathcal{A}$, then$[{⋒}_{i\in I}{R}_i]={⋒}_{i\in I}{R}_i=[{⋓}_{i\in I}{R}_i]$, where$I$is a index set, and$R_i\in SVNR(X)$for each$i\in I$.

Proof. 

We first show that $[{⋒}_{i\in I}{R}_i]={⋒}_{i\in I}{R}_i$. Let $R$ be a neutrosophic relation in $X$ such that ${⋒}_{i\in I}{\overline{R}}_i(A)⋑\overline{R}(A)$ for each $A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$, then ${\overline{R}}_i\ge \overline{R}$, this is equivalent to $R_i⋑R$ since $SVNR(X)\in \mathcal{A}$. Thus ${⋒}_{i\in I}{R}_i⋑R.$ Moreover, by the construction of $[{⋒}_{i\in I}{R}_i]$, we have ${⋒}_{i\in I}{R}_i⋑[{⋒}_{i\in I}{R}_i].$ On the other hand, we can show that ${⋒}_{i\in I}{\overline{R}}_i(A)⋑\overline{{⋒}_{i\in I}{R}_i}(A)$ for each $A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$. So

$$[{⋒}_{i\in I}{R}_i]=⋓\{R\in SVNR(X)\mid \forall A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X),{⋒}_{i\in I}{\overline{R}}_i(A)⋑\overline{R}(A)\}⋑{⋒}_{i\in I}{R}_i.$$

Hence $[{⋒}_{i\in I}{R}_i]={⋒}_{i\in I}{R}_i.$

Now, we show that ${⋒}_{i\in I}{R}_i=[{⋓}_{i\in I}{R}_i].$ Let $R$ be a single valued neutrosophic relation in such that ${⋓}_{i\in I}{\underset{\_}{R}}_i(A)⋐\underset{\_}{R}(A)$ for each $A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$, then ${\underset{\_}{R}}_i\ge \underset{\_}{R}$, this is equivalent to $R_i⋑R$ since $SVNR(X)\in \mathcal{A}$. Thus ${⋒}_{i\in I}{R}_i⋑R.$ Moreover, by the construction of $[{⋓}_{i\in I}{R}_i]$. We have ${⋒}_{i\in I}{R}_i⋑[{⋓}_{i\in I}{R}_i].$

On the other hand, we can show that ${⋓}_{i\in I}{\underset{\_}{R}}_i(A)⋐\underset{\_}{{⋒}_{i\in I}{R}_i}(A)$ for each $A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X)$. So

$$[{⋓}_{i\in I}{R}_i]=⋓\{R\in SVNR(X)\mid \forall A\in \mathbb{S}\mathbb{V}\mathbb{N}\mathbb{S}(X),{⋓}_{i\in I}{\underset{\_}{R}}_i(A)⋐\underset{\_}{R}(A)\}⋑{⋒}_{i\in I}{R}_i.$$

Hence, $[{⋓}_{i\in I}{R}_i]={⋒}_{i\in I}{R}_i.$

From above proved, we know that $[{⋒}_{i\in I}{R}_i]={⋒}_{i\in I}{R}_i=[{⋓}_{j\in J}{R}_j].$ □

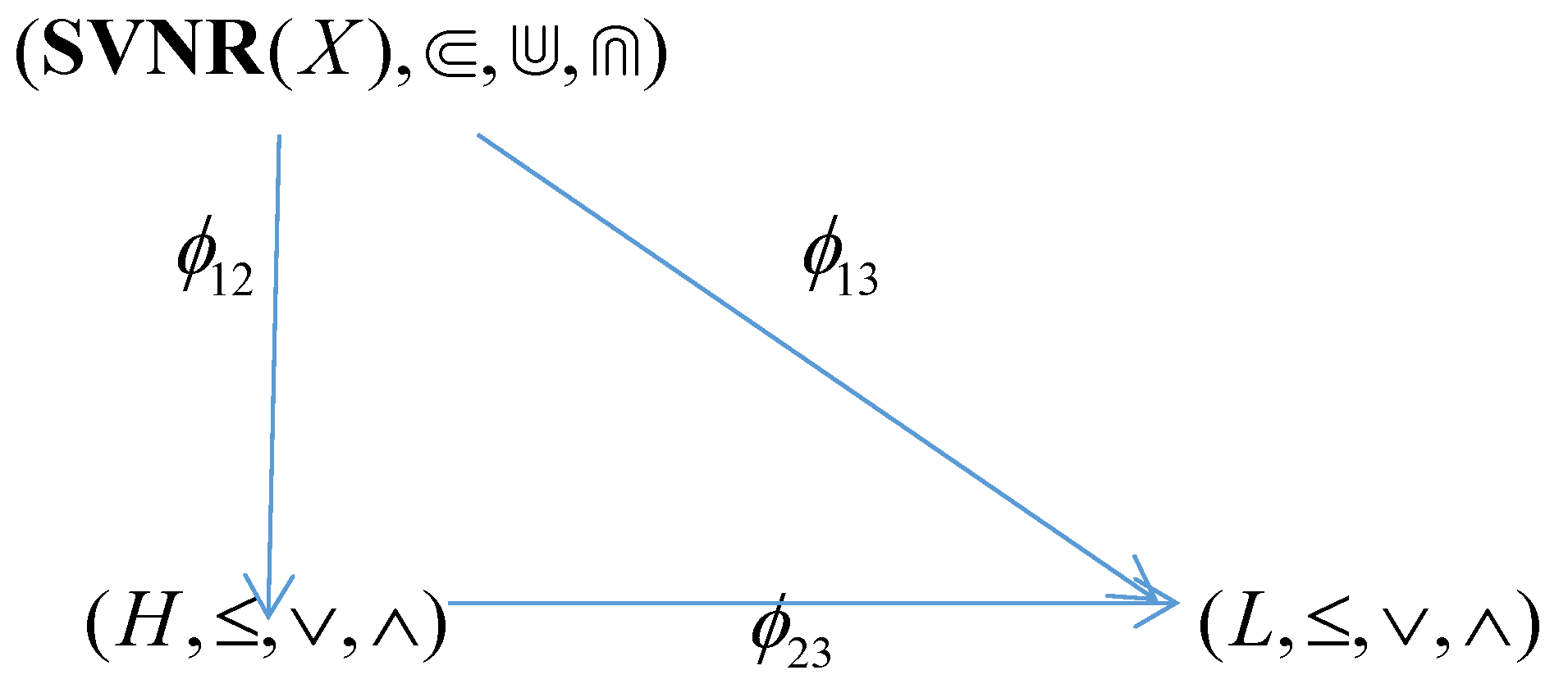
Theorem 4.

If$SVNR(X)\in \mathcal{A}$, then$(SVNR(X),⋐,⋓,⋒)$and$(H,\le ,\wedge ,\vee )$are complete lattice isomorphism.

Proof. 

Define a mapping ${\varphi }_{12}:SVNR(X)\to H$ as follows: $\forall R\in SVNR(X)$, ${\varphi }_{12}(R)=\overline{R}.$ Obviously, ${\varphi }_{12}$ is surjective. If $\overline{R_1}=\overline{R_2}$, notice that $SVNR(X)\in \mathcal{A}$, we know that $R_1=R_2.$ So ${\varphi }_{12}$ is one-one. $\forall {\left\{R_i\right\}}_{i\in I}\subseteq SVNR(X)$ and $I$ be a index set. By Theorem 3 and Proposition 1, we have

$${\varphi }_{12}({⋓}_{i\in I}{R}_i)=\overline{{⋓}_{i\in I}{R}_i}=\underset{i\in I}{{\displaystyle \vee }}\overline{R_i}=\underset{i\in I}{{\displaystyle \vee }}{\varphi }_{12}(R_i),$$

and

$${\varphi }_{12}({⋒}_{i\in I}{R}_i)=\overline{{⋒}_{i\in I}{R}_i}=\overline{[{⋒}_{i\in I}{R}_i]}=\underset{i\in I}{{\displaystyle \wedge }}\overline{R_i}=\underset{i\in I}{{\displaystyle \wedge }}{\varphi }_{12}(R_i).$$

Hence, ${\varphi }_{12}$ preserves arbitrary union and arbitrary intersection. □

From above proved, we know that $(SVNR(X),⋐,⋓,⋒)$ and $(H,\le ,\wedge ,\vee )$ are complete lattice isomorphism.

Theorem 5.

If$SVNR(X)\in \mathcal{A}$, then$(SVNR(X),⋐,⋓,⋒)$and$(L,\le ,\wedge ,\vee )$are complete lattice isomorphism.

Proof. 

Define a mapping ${\varphi }_{13}:SVNR(X)\to L$ as follows:$\forall R\in SVNR(X)$, ${\varphi }_{12}(R)=\underset{\_}{R}.$ Obviously, ${\varphi }_{13}$ is surjective. If $\underset{\_}{R_1}=\underset{\_}{R_2}$, notice that $SVNR(X)\in \mathcal{A}$, we know that $R_1=R_2.$ So ${\varphi }_{13}$ is one-one. $\forall {\left\{R_i\right\}}_{i\in I}\subseteq SVNR(X)$ and $I$ be an index set. By Theorem 3 and Proposition 1, we have

$${\varphi }_{13}({⋓}_{i\in I}{R}_i)=\underset{\_}{{⋓}_{i\in I}{R}_i}=\underset{i\in I}{{\displaystyle \vee }}\underset{\_}{R_i}=\underset{i\in I}{{\displaystyle \vee }}{\varphi }_{13}(R_i),$$

and

$${\varphi }_{13}({⋒}_{i\in I}{R}_i)=\underset{\_}{{⋒}_{i\in I}{R}_i}=\underset{\_}{[{⋓}_{i\in I}{R}_i]}=\underset{i\in I}{{\displaystyle \wedge }}\underset{\_}{R_i}=\underset{i\in I}{{\displaystyle \wedge }}{\varphi }_{13}(R_i).$$

Hence, ${\varphi }_{13}$ preserves arbitrary union and arbitrary intersection. □

From the above proof, we know that $(SVNR(X),⋐,⋓,⋒)$ and $(L,\le ,\wedge ,\vee )$ are complete lattice isomorphism.

Theorem 6.

If$SVNR(X)\in \mathcal{A}$, then$(H,\le ,\wedge ,\vee )$and$(L,\le ,\wedge ,\vee )$are complete lattice isomorphism.

Proof. 

Through Theorems 4 and 5, we immediately know that the conclusion holds. We can also prove it by the following way:

Define a mapping ${\varphi }_{23}:H\to L$ as follows: $\forall \overline{R}\in H$, ${\varphi }_{23}(\overline{R})=\underset{\_}{R}.$ Through Theorems 4 and 5, there must be one and only one $R\in SVNR(X)$ such that ${\varphi }_{23}(\overline{R})=\underset{\_}{R}$ for each $\underset{\_}{R}\in L.$ This shows ${\varphi }_{23}$ is surjective. If $\underset{\_}{R_1}=\underset{\_}{R_2}$, notice that $SVNR(X)\in \mathcal{A}$, we know that $\overline{R_1}=\overline{R_2}.$ So ${\varphi }_{23}$ is one-one. $\forall {\left\{\overline{R_i}\right\}}_{i\in I}\subseteq H$ and $I$ be a index set. Through Theorem 3 and Proposition 1, we have

$${\varphi }_{23}(\underset{i\in I}{{\displaystyle \vee }}\overline{R_i})={\varphi }_{23}(\overline{{⋓}_{i\in I}{R}_i})=\underset{\_}{{⋓}_{i\in I}{R}_i}=\underset{i\in I}{{\displaystyle \vee }}\underset{\_}{R_i}=\underset{i\in I}{{\displaystyle \vee }}{\varphi }_{13}(\overline{R_i}),$$

and

$${\varphi }_{13}(\underset{i\in I}{{\displaystyle \wedge }}\overline{R_i})={\varphi }_{13}(\overline{[{⋒}_{i\in I}{R}_i]})=\underset{\_}{[{⋒}_{i\in I}{R}_i]}=\underset{\_}{[{⋓}_{i\in I}{R}_i]}=\underset{i\in I}{{\displaystyle \wedge }}\underset{\_}{R_i}=\underset{i\in I}{{\displaystyle \wedge }}{\varphi }_{23}(\overline{R_i}).$$

Hence, ${\varphi }_{23}$ preserves arbitrary union and arbitrary intersection. So, $(H,\le ,\wedge ,\vee )$ and $(L,\le ,\wedge ,\vee )$ are complete lattice isomorphism. □

Remark 3.

Through Theorems 4–6, we can ascertain that${\varphi }_{12}$,${\varphi }_{13}$and${\varphi }_{23}$are isomorphic mappings among complete lattices. Moreover, the following diagram can commute, i.e.,${\varphi }_{23}\circ {\varphi }_{12}={\varphi }_{13}$(see Figure 1).

5. Conclusions

Following the idea of multigranulation neutrosophic rough sets on a single domain as introduced by Bo et al. (2018), we gave the lattice structure of the pessimistic multigranulation neutrosophic rough approximation operators. In the one-dimensional case, for each special $SVNR(X)$, we gave a one-to-one correspondence relationship between complete lattices $(H,\le )$ and $(L,\le )$. Unfortunately, at the moment, we haven’t solved the following problems:

(1)

Can the supremum and infimum of the optimistic multigranulation neutrosophic rough approximation operators be given?

(2)

For any set , are $(H,\le )$ and $(L,\le )$ isomorphic between complete lattices?