A Linguistic Neutrosophic Multi-Criteria Group Decision-Making Method to University Human Resource Management
Abstract
1. Introduction
2. New Operations and Distance Measure for LNNs
2.1. Linguistic Neutrosophic Set
2.2. New Operations for LNNs
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- ; and
- (5)
- .
- (1)
- ;
- (2)
- ;
- (3)
- ; and
- (4)
- .
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- ;
- (5)
- ; and
- (6)
- .
2.3. Distance between Two LNNs
- (1)
- ;
- (2)
- ;
- (3)
- ; and
- (4)
- .
3. Linguistic Neutrosophic Aggregation Operators
- (1)
- ;
- (2)
- ; and
- (3)
- , when, andis the distance betweenand.
3.1. Linguistic Neutrosophic Power Weighted Averaging Operator
3.2. Linguistic Neutrosophic Power Weighted Geometric Operator
4. MCGDM Method Based on the LNPWA and LNPWG Operators
5. A Case of Human Resource Management Problem
5.1. Problem Definition
5.2. Evaluation Steps of the Proposed Method
5.3. Sensitivity Analysis and Discussion
5.4. Comparison Analysis and Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Linguistic Scale Function
Appendix B. The Archimedean T-norm and T-conorm
Appendix C. The Proof of Theorem 2
Appendix D. The Proof of Theorem 3
References
- Abdullah, L.; Zulkifli, N. Integration of fuzzy AHP and interval type-2 fuzzy DEMATEL: An application to human resource management. Expert Syst. Appl. 2015, 42, 4397–4409. [Google Scholar] [CrossRef]
- Filho, C.F.F.C.; Rocha, D.A.R.; Costa, M.G.F. Using constraint satisfaction problem approach to solve human resource allocation problems in cooperative health services. Expert Syst. Appl. 2012, 39, 385–394. [Google Scholar] [CrossRef]
- Marcolajara, B.; ÚbedaGarcía, M. Human resource management approaches in Spanish hotels: An introductory analysis. Int. J. Hosp. Manag. 2013, 35, 339–347. [Google Scholar] [CrossRef]
- Bohlouli, M.; Mittas, N.; Kakarontzas, G.; Theodosiou, T.; Angelis, L.; Fathi, M. Competence assessment as an expert system for human resource management: A mathematical approach. Expert Syst. Appl. 2017, 70, 83–102. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Zhang, H.; Hu, J. A heterogeneous linguistic MAGDM framework to classroom teaching quality evaluation. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 4929–4956. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics: Neutrosophic Logic: Neutrosophy, Neutrosophic Set, Neutrosophic Probability; American Research Press: Rehoboth, DE, USA, 1999; pp. 1–141. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Wu, X.H.; Wang, J.Q.; Peng, J.J.; Qian, J. A novel group decision-making method with probability hesitant interval neutrosphic set and its application in middle level manager’ selection. Int. J. Uncertain. Quantif. 2018, 8, 291–319. [Google Scholar] [CrossRef]
- Ji, P.; Wang, J.Q.; Zhang, H.Y. Frank prioritized Bonferroni mean operator with single-valued neutrosophic sets and its application in selecting third-party logistics providers. Neural Comput. Appl. 2016, 30, 799–823. [Google Scholar] [CrossRef]
- Liang, R.; Wang, J.; Zhang, H. Evaluation of e-commerce websites: An integrated approach under a single-valued trapezoidal neutrosophic environment. Knowl.-Based Syst. 2017, 135, 44–59. [Google Scholar] [CrossRef]
- Liang, R.X.; Wang, J.Q.; Zhang, H.Y. A multi-criteria decision-making method based on single-valued trapezoidal neutrosophic preference relations with complete weight information. Neural Comput. Appl. 2017. [Google Scholar] [CrossRef]
- Liang, R.X.; Wang, J.Q.; Li, L. Multi-criteria group decision making method based on interdependent inputs of single valued trapezoidal neutrosophic information. Neural Comput. Appl. 2018, 30, 241–260. [Google Scholar] [CrossRef]
- Tian, Z.P.; Wang, J.; Wang, J.Q.; Zhang, H.Y. Simplified neutrosophic linguistic multi-criteria group decision-making approach to green product development. Group Decis. Negot. 2017, 26, 597–627. [Google Scholar] [CrossRef]
- Ji, P.; Zhang, H.Y.; Wang, J.Q. Selecting an outsourcing provider based on the combined MABAC–ELECTRE method using single-valued neutrosophic linguistic sets. Comput. Ind. Eng. 2018, 120, 429–441. [Google Scholar] [CrossRef]
- Karaaslan, F. Correlation coefficients of single-valued neutrosophic refined soft sets and their applications in clustering analysis. Neural Comput. Appl. 2017, 28, 2781–2793. [Google Scholar] [CrossRef]
- Ye, J. Single-valued neutrosophic clustering algorithms based on similarity measures. J. Classif. 2017, 34, 148–162. [Google Scholar] [CrossRef]
- Li, Y.Y.; Wang, J.Q.; Wang, T.L. A linguistic neutrosophic multi-criteria group decision-making approach with EDAS method. Arab. J. Sci. Eng. 2018. [Google Scholar] [CrossRef]
- Chen, Z.S.; Chin, K.S.; Li, Y.L.; Yang, Y. Proportional hesitant fuzzy linguistic term set for multiple criteria group decision making. Inf. Sci. 2016, 357, 61–87. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Wang, H. Extended hesitant fuzzy linguistic term sets and their aggregation in group decision making. Int. J. Comput. Intell. Syst. 2014, 8, 14–33. [Google Scholar] [CrossRef]
- Wang, X.K.; Peng, H.G.; Wang, J.Q. Hesitant linguistic intuitionistic fuzzy sets and their application in multi-criteria decision-making problems. Int. J. Uncertain. Quantif. 2018, 8, 321–341. [Google Scholar] [CrossRef]
- Tian, Z.P.; Wang, J.Q.; Zhang, H.Y.; Wang, T.L. Signed distance-based consensus in multi-criteria group decision-making with multi-granular hesitant unbalanced linguistic information. Comput. Ind. Eng. 2018, 124, 125–138. [Google Scholar] [CrossRef]
- Zhang, H.M. Linguistic intuitionistic fuzzy sets and application in MAGDM. J. Appl. Math. 2014, 2014. [Google Scholar] [CrossRef]
- Chen, Z.C.; Liu, P.H.; Pei, Z. An approach to multiple attribute group decision making based on linguistic intuitionistic fuzzy numbers. Int. J. Comput. Intell. Syst. 2015, 8, 747–760. [Google Scholar] [CrossRef]
- Peng, H.G.; Wang, J.Q. A multicriteria group decision-making method based on the normal cloud model with Zadeh’s Z-numbers. IEEE Trans. Fuzzy Syst. 2018. [Google Scholar] [CrossRef]
- Peng, H.G.; Zhang, H.Y.; Wang, J.Q. Cloud decision support model for selecting hotels on TripAdvisor.com with probabilistic linguistic information. Int. J. Hosp. Manag. 2018, 68, 124–138. [Google Scholar] [CrossRef]
- Luo, S.Z.; Zhang, H.Y.; Wang, J.Q.; Li, L. Group decision-making approach for evaluating the sustainability of constructed wetlands with probabilistic linguistic preference relations. J. Oper. Res. Soc. 2018. [Google Scholar] [CrossRef]
- Fang, Z.B.; Ye, J. Multiple attribute group decision-making method based on linguistic neutrosophic numbers. Symmetry 2017, 9, 111. [Google Scholar] [CrossRef]
- Li, Y.Y.; Zhang, H.Y.; Wang, J.Q. Linguistic neutrosophic sets and their application in multicriteria decision-making problems. Int. J. Uncertain. Quantif. 2017, 7, 135–154. [Google Scholar] [CrossRef]
- Fan, C.X.; Ye, J.; Hu, K.L.; Fan, E. Bonferroni mean operators of linguistic neutrosophic numbers and their multiple attribute group decision-making methods. Information 2017, 8, 107. [Google Scholar] [CrossRef]
- Shi, L.L.; Ye, J. Cosine measures of linguistic neutrosophic numbers and their application in multiple attribute group decision-making. Information 2017, 8, 117. [Google Scholar]
- Liang, W.Z.; Zhao, G.Y.; Wu, H. Evaluating investment risks of metallic mines using an extended TOPSIS method with linguistic neutrosophic numbers. Symmetry 2017, 9, 149. [Google Scholar] [CrossRef]
- Herrera, F.; Martínez, L. A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2000, 8, 746–752. [Google Scholar]
- Delgado, M.; Verdegay, J.L.; Vila, M.A. Linguistic decision-making models. Int. J. Intell. Syst. 1992, 7, 479–492. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, X.; Yang, Y.; Liu, Y.; Chen, X. New doctors ranking system based on VIKOR method. Int. Trans. Oper. Res. 2018. [Google Scholar] [CrossRef]
- Li, D.Y.; Meng, H.J.; Shi, X.M. Membership clouds and membership cloud generators. Comput. Res. Dev. 1995, 32, 16–21. [Google Scholar]
- Bordogna, G.; Fedrizzi, M.; Pasi, G. A linguistic modeling of consensus in group decision making based on OWA operators. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 1997, 27, 126–133. [Google Scholar] [CrossRef]
- Doukas, H.; Karakosta, C.; Psarras, J. Computing with words to assess the sustainability of renewable energy options. Expert Syst. Appl. 2010, 37, 5491–5497. [Google Scholar] [CrossRef]
- Wang, J.Q.; Wu, J.T.; Wang, J.; Zhang, H.Y.; Chen, X.H. Interval-valued hesitant fuzzy linguistic sets and their applications in multi-criteria decision-making problems. Inf. Sci. 2014, 288, 55–72. [Google Scholar] [CrossRef]
- Yager, R.R. The power average operator. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2001, 31, 724–731. [Google Scholar] [CrossRef]
- Jiang, W.; Wei, B.; Zhan, J.; Xie, C.; Zhou, D. A visibility graph power averaging aggregation operator: A methodology based on network analysis. Comput. Ind. Eng. 2016, 101, 260–268. [Google Scholar] [CrossRef]
- Gong, Z.; Xu, X.; Zhang, H.; Aytun Ozturk, U.; Herrera-Viedma, E.; Xu, C. The consensus models with interval preference opinions and their economic interpretation. Omega 2015, 55, 81–90. [Google Scholar] [CrossRef]
- Liu, P.D.; Qin, X.Y. Power average operators of linguistic intuitionistic fuzzy numbers and their application to multiple-attribute decision making. J. Intell. Fuzzy Syst. 2017, 32, 1029–1043. [Google Scholar] [CrossRef]
- Yager, R.R. Applications and extensions of OWA aggregations. Int. J. Man-Mach. Stud. 1992, 37, 103–132. [Google Scholar] [CrossRef]
- Yager, R.R. On ordered weighted averaging aggregation operators in multicriteria decision making. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Yager, R.R. Families of OWA operators. Fuzzy Sets Syst. 1993, 59, 125–148. [Google Scholar] [CrossRef]
- Huang, J.J.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2011. [Google Scholar]
- Baykasoğlu, A.; Gölcük, İ. Development of an interval type-2 fuzzy sets based hierarchical MADM model by combining DEMATEL and TOPSIS. Expert Syst. Appl. 2017, 70, 37–51. [Google Scholar] [CrossRef]
- Joshi, D.; Kumar, S. Interval-valued intuitionistic hesitant fuzzy Choquet integral based TOPSIS method for multi-criteria group decision making. Eur. J. Oper. Res. 2016, 248, 183–191. [Google Scholar] [CrossRef]
- Mehrdad, A.M.A.K.; Aghdas, B.; Alireza, A.; Mahdi, G.; Hamed, K. Introducing a procedure for developing a novel centrality measure (Sociability Centrality) for social networks using TOPSIS method and genetic algorithm. Comput. Hum. Behav. 2016, 56, 295–305. [Google Scholar]
- Afsordegan, A.; Sánchez, M.; Agell, N.; Zahedi, S.; Cremades, L.V. Decision making under uncertainty using a qualitative TOPSIS method for selecting sustainable energy alternatives. Int. J. Environ. Sci. Technol. 2016, 13, 1419–1432. [Google Scholar] [CrossRef]
- Xu, Z.S. A method based on linguistic aggregation operators for group decision making with linguistic preference relations. Inf. Sci. 2004, 166, 19–30. [Google Scholar] [CrossRef]
- Chou, Y.C.; Sun, C.C.; Yen, H.Y. Evaluating the criteria for human resource for science and technology (HRST) based on an integrated fuzzy AHP and fuzzy DEMATEL approach. Appl. Soft Comput. 2012, 12, 64–71. [Google Scholar] [CrossRef]
- Yu, D.; Wu, Y.; Lu, T. Interval-valued intuitionistic fuzzy prioritized operators and their application in group decision making. Knowl.-Based Syst. 2012, 30, 57–66. [Google Scholar] [CrossRef]
- Yu, S.M.; Wang, J.; Wang, J.Q.; Li, L. A multi-criteria decision-making model for hotel selection with linguistic distribution assessments. Appl. Soft Comput. 2018, 67, 741–755. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, T.; Yin, S.; Gao, H. Data-based optimal control for networked double-layer industrial processes. IEEE Trans. Ind. Electron. 2017, 64, 4179–4186. [Google Scholar] [CrossRef]
- Qiu, J.; Wei, Y.; Karimi, H.R.; Gao, H. Reliable control of discrete-time piecewise-affine time-delay systems via output feedback. IEEE Trans. Reliab. 2017, 67, 79–91. [Google Scholar] [CrossRef]
- Liu, A.Y.; Liu, F.J. Research on method of analyzing the posterior weight of experts based on new evaluation scale of linguistic information. Chin. J. Manag. Sci. 2011, 19, 149–155. [Google Scholar]
- Klement, E.P.; Mesiar, R. Logical, Algebraic, Analytic, and Probabilistic Aspects of Triangular Norms; Elsevier: New York, NY, USA, 2005. [Google Scholar]
- Beliakov, G.; Pradera, A.; Calvo, T. Aggregation Functions: A Guide for Practitioners; Springer: Berlin, Germany, 2007; Volume 12, pp. 139–141. [Google Scholar]
| Distance | |||||
|---|---|---|---|---|---|
| 2.1903 | 2.1162 | 1.6257 | 1.7055 | 0.7132 | |
| 2.3229 | 2.0653 | 1.5863 | 1.7175 | 0.698 | |
| 1.3743 | 2.8968 | 2.3562 | 0 | 0.7926 | |
| 2.3229 | 2.0653 | 1.5863 | 1.7175 | 0.698 | |
| 2.9288 | 0.561 | 0 | 2.3562 | 0.499 | |
| 2.3222 | 2.0656 | 1.5864 | 1.7174 | 0.6981 |
| Distance | |||||
|---|---|---|---|---|---|
| 2.2863 | 1.5118 | 1.1097 | 0.7259 | 0.5942 | |
| 2.711 | 1.3681 | 0.9082 | 0.9641 | 0.5445 | |
| 1.9575 | 2.1815 | 1.7206 | 0 | 0.6659 | |
| 2.9016 | 0.8254 | 0.3432 | 1.4138 | 0.4709 | |
| 3.0628 | 0.5194 | 0 | 1.7205 | 0.4224 | |
| 2.8615 | 0.9176 | 0.4412 | 1.3295 | 0.4844 |
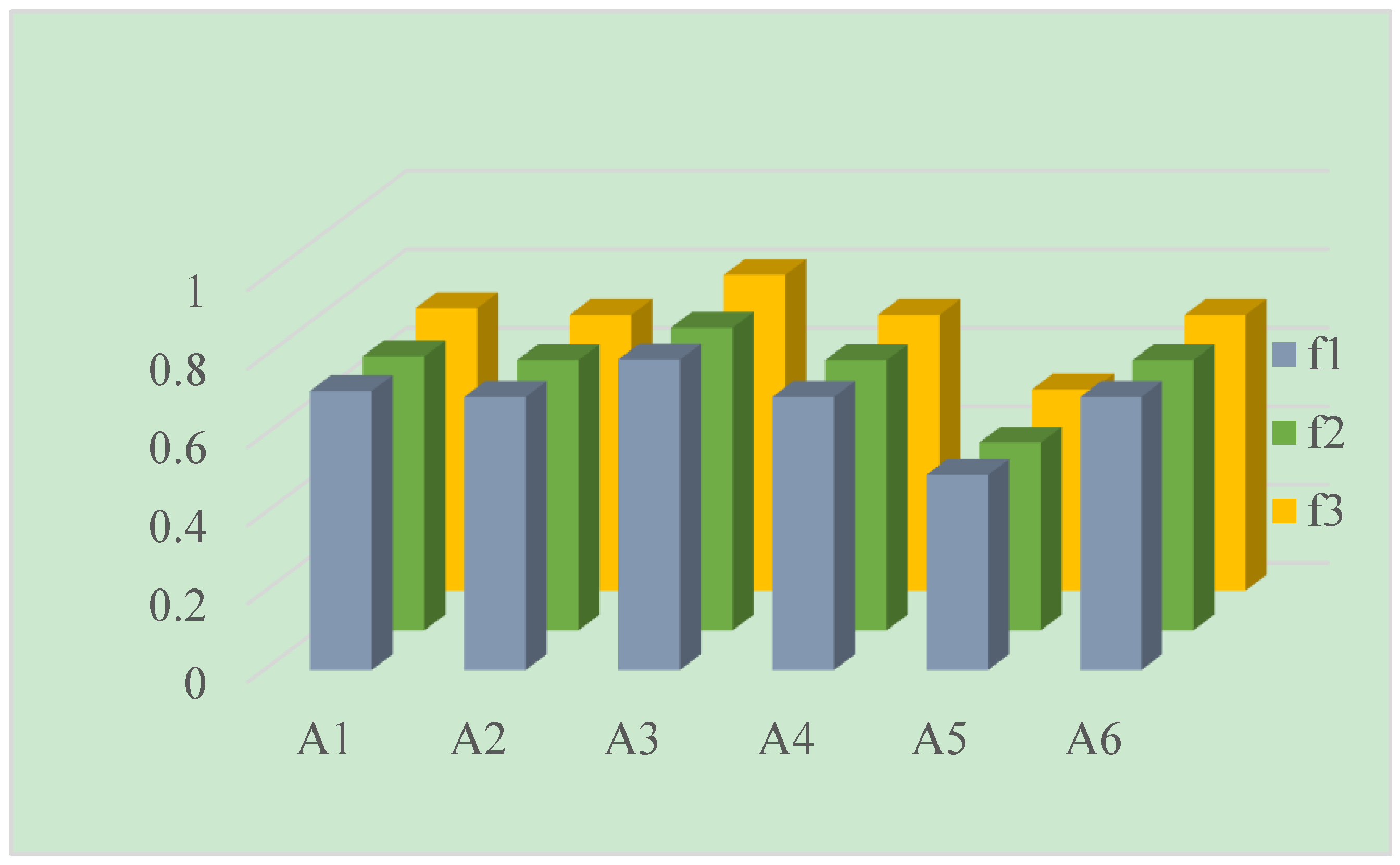
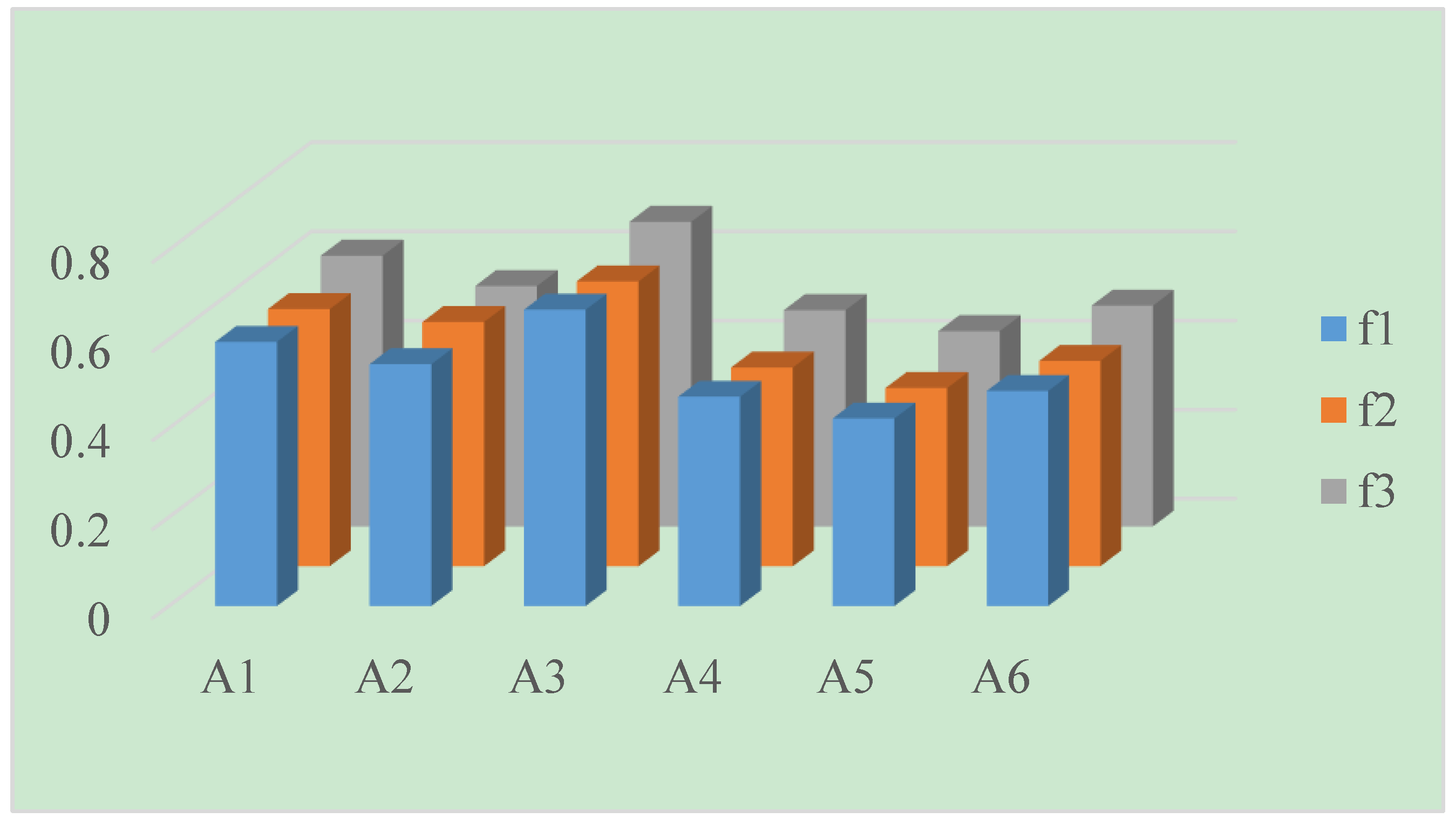
| Alternatives | Ranking Results | |||||||
|---|---|---|---|---|---|---|---|---|
| LNPWA | 0.713 | 0.698 | 0.793 | 0.698 | 0.499 | 0.698 | ||
| LNPWG | 0.594 | 0.544 | 0.666 | 0.471 | 0.422 | 0.484 | ||
| LNPWA | 0.7 | 0.69 | 0.773 | 0.69 | 0.48 | 0.69 | ||
| LNPWG | 0.578 | 0.549 | 0.64 | 0.447 | 0.401 | 0.462 | ||
| LNPWA | 0.721 | 0.704 | 0.806 | 0.704 | 0.514 | 0.704 | ||
| LNPWG | 0.608 | 0.54 | 0.684 | 0.486 | 0.439 | 0.496 | ||
| Ranking by LNPWA operator | Ranking by LNPWG operator | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, R.-x.; Jiang, Z.-b.; Wang, J.-q. A Linguistic Neutrosophic Multi-Criteria Group Decision-Making Method to University Human Resource Management. Symmetry 2018, 10, 364. https://doi.org/10.3390/sym10090364
Liang R-x, Jiang Z-b, Wang J-q. A Linguistic Neutrosophic Multi-Criteria Group Decision-Making Method to University Human Resource Management. Symmetry. 2018; 10(9):364. https://doi.org/10.3390/sym10090364
Chicago/Turabian StyleLiang, Ru-xia, Zi-bin Jiang, and Jian-qiang Wang. 2018. "A Linguistic Neutrosophic Multi-Criteria Group Decision-Making Method to University Human Resource Management" Symmetry 10, no. 9: 364. https://doi.org/10.3390/sym10090364
APA StyleLiang, R.-x., Jiang, Z.-b., & Wang, J.-q. (2018). A Linguistic Neutrosophic Multi-Criteria Group Decision-Making Method to University Human Resource Management. Symmetry, 10(9), 364. https://doi.org/10.3390/sym10090364




